2. 北京卫星导航中心, 北京市永丰路5128号, 100094;
3. 信息工程大学地理空间信息学院, 郑州市科学大道62号, 450001
全球卫星导航系统(GNSS)是以时间测量为基础的系统[1], 卫星钟差预报在系统时间同步[2]、系统自主运行与自主导航[3]、实时精密单点定位应用[4]等方面具有重要的作用和意义。因此,针对卫星钟差预报建立了多种模型,例如常用的一次多项式(LP)模型、二次多项式(QP)模型、灰色模型(GM模型)、时间序列ARIMA模型(ARIMA模型)、谱分析(SA)模型(也称为附有周期项的二次多项式模型)、Kalman滤波(KF)模型、神经网络模型以及这些模型的改进模型[5-9]。其中,文献[9]在建立卫星钟差预报的小波神经网络时发现,通过相邻历元卫星钟差数据之间的一次差分可以得到较高精度的预报结果。之后,有学者进行了更进一步的研究[10-11]。但对相关研究进行总结分析可知,其仍存在较多的局限性,例如现有的研究主要是通过一次差分处理来改进某种特定模型的预报效果。同时,对于常用钟差预报模型基于一次差分预报原理的效果对比的研究相对较少,而且不够充分、全面。基于此,本文系统地对比LP、QP、GM、SA、ARIMA、KF等6种常用钟差预报模型基于一次差分预报原理进行钟差预报时的效果及其相关特性,从不同角度对预报结果进行分析,一定程度上明确了哪些模型在何种预报条件下对于哪些类型的卫星及其星载钟能够取得相对较好的短期预报结果,进一步验证了钟差一次差分预报原理的有效性和适应条件,丰富和完善了钟差一次差分预报原理的理论体系。
1 钟差一次差分预报原理与常用钟差预报模型的相关说明 1.1 钟差一次差分预报原理的说明和分析钟差一次差分预报原理可以表述为[1, 9, 11]: 已知的历史钟差数据记为L={l(i), i=1, 2, …, n}, 相邻2个历元的钟差值l(i)、l(i-1) (i=2, …, n)作差得到其所对应的一次差分数据序列ΔL={Δl(i), i=1, 2, …, (n-1)}, 用ΔL确定特定的钟差预报模型之后,预报Δl(n-1)对应时刻之后连续的m(m > 1)个不同时刻的一次差分序列ΔL1={Δl(j), j=n, n+1, …, n+m-1}, 则所需预报历元时刻的钟差值为:
| $l(j)=l(n)+\sum\limits_{n}^{j} \Delta l(k), n<j \leqslant n+m-1 \\ m、n、k \in N^{*}$ | (1) |
从上面公式可知,钟差一次差分预报原理对已知钟差数据l(n)的依赖程度高,本文采取文献[12]的策略确保该数值的可靠性。同时可以看出,经过钟差数据相邻历元间的一次差分,会得到1组有效数字位数减少且便于准确拟合的数据序列。这是由于,为了记录高精度的时间信息,卫星钟差数据的有效位数通常比较多、数值比较大,而导航系统星载原子钟在1 h这种短时间内相邻时刻输出的变化相对稳定,相邻历元间的钟差数值变化不大;卫星钟差数据在进行相邻历元一次差分之后,可以在一定程度上消除原钟差序列趋势项和可能存在的系统误差的影响。这些特性使得钟差一次差分预报原理从理论上比常规卫星钟差建模预报策略更具优势。但根据误差传播定律可知,钟差数据作差得到的一次差分数据序列的误差会变大,这在一定程度上影响和制约钟差一次差分预报原理的性能。因此,需要根据实验验证其效果、确定其使用方法。
1.2 几种常用钟差预报模型的说明1) 在卫星钟差数据拟合和预报之前,使用中位数(MAD)方法[1, 12]进行数据预处理。
2) 在进行模型参数解算时,估值方法统一采用最小二乘法。
3) 对于SA模型周期项的确定和选取,借鉴已有研究对卫星钟差周期项分析的结果。考虑到下文中是以GPS卫星钟差数据为例进行拟合预报,而对于GPS卫星钟差的周期特性,Senior等[13]给出了详细的分析,因此本文取12 h和6 h作为SA模型的主周期项。
4) 在使用ARIMA模型进行钟差拟合预报时,先利用自相关函数和偏相关函数的截尾性初步确定模型和模型的阶数,然后基于赤池信息量准则(Akaike information criterion, AIC)来准确确定模型的阶数[1]。
5) 针对KF模型拟合预报过程中协方差矩阵的确定,使用孙启松等[14]提出的基于方差递推法来确定噪声矩阵的KF模型,进行钟差拟合预报。
6) 采用均方根误差(RMS)对预报结果的精度进行对比与分析,RMS的计算公式为:
| $\mathrm{RMS}=\sqrt{\frac{1}{n} \sum\limits_{i=1}^{n} \text { error }_{i}^{2}}, \mathrm{error} _{i}=l_{i}-\hat{l}_{i}$ | (2) |
式中,errori为预报误差,
在对一次差分预报原理进行说明和分析的基础上,结合对几种常用钟差预报模型的说明,给出本文各模型进行钟差预报时的主要工作流程,见图 1。
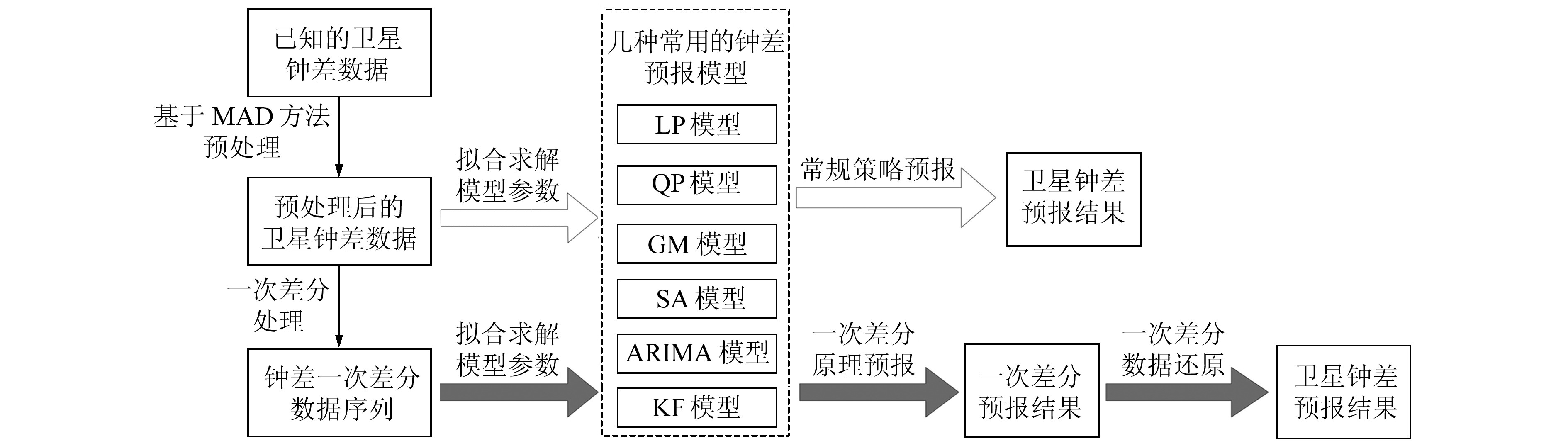
|
图 1 卫星钟差预报的主要工作流程 Fig. 1 The main working principle flow of SCB prediction |
采用IGS提供的GPS系统15 min采样间隔的精密钟差数据进行实验分析。数据采集时间为2015-04-07~21, 选取数据连续、完整的卫星进行钟差预报实验,表 1中加粗的卫星号为实验所用卫星。
使用前1 d的卫星钟差数据拟合后预报接下来1 d的钟差,连续预报14次。分别统计每次预报结果前3 h、前6 h、前12 h和前24 h的预报精度,通过对比6种常用模型(其中ARIMA模型记为AM模型)分别在常规建模条件与一次差分预报原理条件下的预报结果,分析基于钟差一次差分预报原理的特性。其中,基于钟差一次差分预报原理条件下的6种常用模型分别记作DLP模型、DQP模型、DGM模型、DSA模型、DAM模型和DKF模型。最后,按照卫星钟的类型给出几种常用钟差预报模型在不同预报时长下14次连续预报结果的RMS平均值的变化情况(图 2, 加D的图例表示一次差分预报结果); 给出实验分析所用全部卫星分别在常规建模条件下和一次差分预报原理条件下不同预报时长的卫星钟差预报结果精度的平均值。
|
|
表 1 数据采集时间段内GPS在轨卫星钟的类型 Tab. 1 Types of GPS satellite clocks in orbit during data acquisition period |
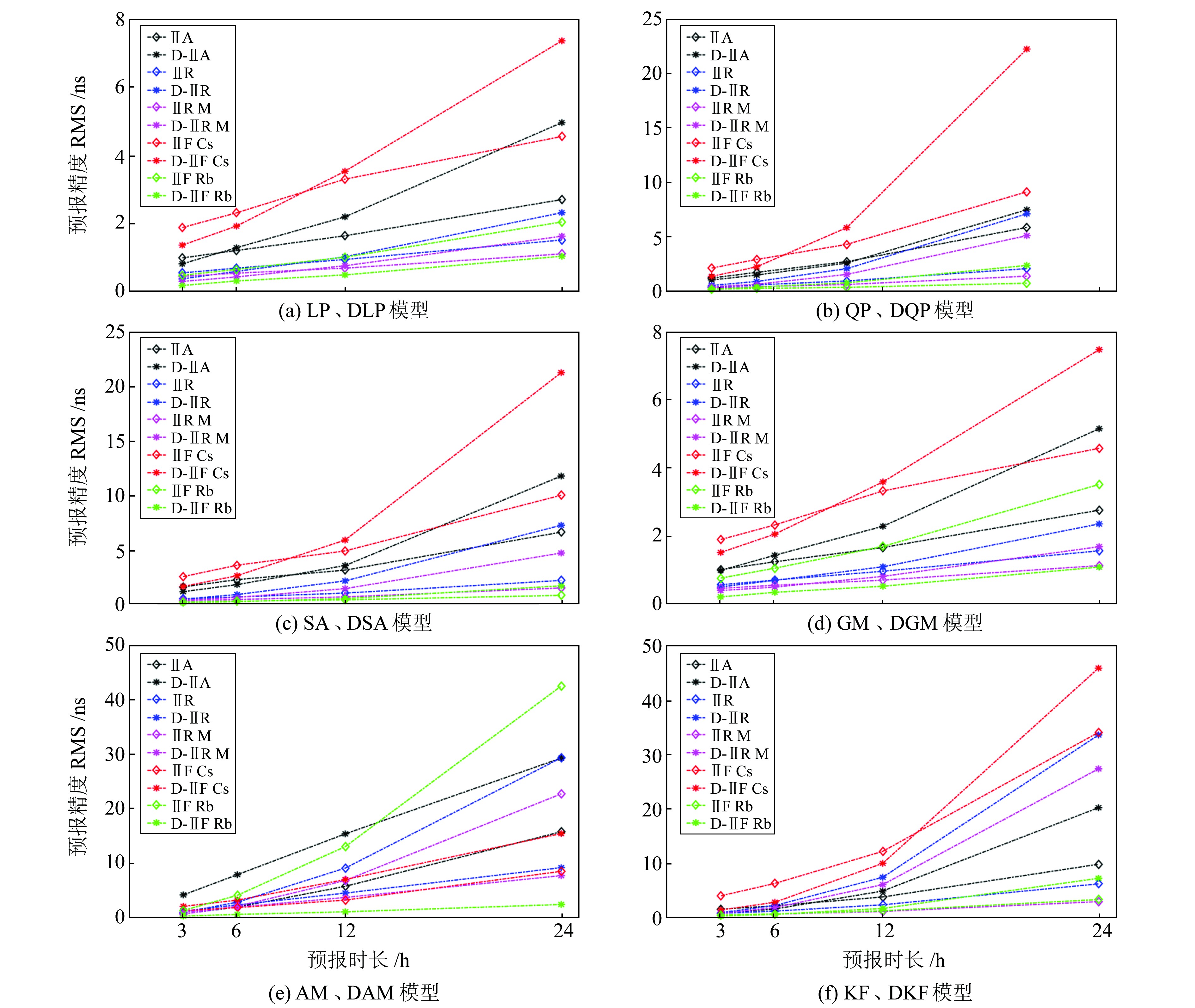
|
图 2 几种常用钟差预报模型不同预报时长下预报结果的RMS平均值 Fig. 2 RMS mean values of prediction results under different prediction durations of several common clock bias prediction models |
|
|
表 2 各模型不同预报时长下所有卫星预报精度的对比 Tab. 2 Comparison of prediction accuracy of all satellites under different prediction durations of each model |
分析图表结果可知:
1) 对比LP模型与DLP模型,在3 h和6 h的预报中,DLP模型的预报精度优于LP模型。特别是在3 h的预报中,对于5种不同类型的卫星钟,DLP模型的预报精度都最高,并且就该时段所有卫星预报精度的平均值而言,DLP模型的预报精度较LP模型提高了近50%。但随着预报时间的增加,DLP模型预报精度迅速变差,较LP模型的优势逐渐变弱。在12 h的预报中,其预报精度略好于LP模型;而在24 h的预报中,其预报精度比LP模型差。同时,对于ⅡF Rb钟,4个时间段的预报中,DLP模型都优于LP模型,并且3 h的预报中,前者明显优于后者,即使在24 h的预报中,前者也比后者的精度高出近50%。因此,基于钟差一次差分预报原理可以提高LP模型的短期预报精度,特别是对GPS ⅡF Rb钟钟差预报的改善效果最显著。
2) 对比QP模型与DQP模型,对于3 h和6 h的预报精度,DQP模型优于QP模型的次数相对较少,而对于12 h和24 h的预报精度,几乎每次都是QP模型优于DQP模型;同时,QP模型基于钟差一次差分预报原理的预报结果与卫星及其星载钟类型有较为密切的关系:对于ⅡA Rb钟的3 h、6 h和12 h预报,ⅡF Rb钟的3 h钟差预报,ⅡF Cs钟的3 h和6 h钟差预报,DQP模型的预报精度都优于QP模型。此外,随着预报时长的增加,DQP模型预报精度迅速变差且精度明显低于QP模型。因此,采用一次差分预报原理可以提高QP模型对GPS ⅡA Rb钟、ⅡF Rb钟和ⅡF Cs钟的短期预报精度。
3) 对比SA模型与DSA模型,对于3 h的预报精度,DSA模型总体上优于SA模型,而其他3个时段则相反;同样,SA模型基于钟差一次差分预报原理的预报结果与卫星及其星载钟类型有一定的关系,在3 h的预报中,除了ⅡR-M Rb钟,对于其他4类卫星的钟差预报精度,DSA模型优于SA模型;而在6 h的预报中,对于ⅡA Rb钟、ⅡF Rb钟和ⅡF Cs钟的预报,也是DSA模型优于SA模型。此外,与DQP模型类似,DSA模型的预报精度随预报时长的增加迅速变差且精度明显低于SA模型。综合分析可知,采用一次差分预报原理可以提高SA模型对GPS ⅡA Rb钟、ⅡF Rb钟和ⅡF Cs钟的短期预报精度。
4) 对比GM模型与DGM模型,对于3 h的预报精度,DGM模型均优于GM模型,并且对于5种不同类型的卫星钟,DGM模型的预报精度更高;对于6 h和12 h的预报精度,DGM模型整体优于GM模型。但随着预报时长的增加,DGM模型的预报精度迅速变差,其较GM模型的优势逐渐变弱,在24 h的预报中,其预报精度比GM模型差。同时,对于ⅡF Rb钟的预报精度,4个时段中,DGM模型较GM模型均高出70%左右。因此,钟差一次差分预报原理可以提高GM模型的短期预报精度,特别是对GPS ⅡF Rb钟预报效果的改善最为显著。
5) 对比AM模型与DAM模型,对于3 h的预报精度,总体上AM模型要优于DAM模型,而其他3个时段则是DAM模型的预报精度高,这种情况与其他几种常用模型基于一次差分预报原理的情况相反。同时从图 2中可以看出,AM模型基于钟差一次差预报原理的预报结果与卫星及其星载钟类型有一定的关系,对于ⅡF Rb钟的3 h预报精度,DAM模型优于AM模型;而在6 h、12 h和24 h的预报中,对于ⅡR Rb钟、ⅡR-M Rb钟和ⅡF Rb钟的预报精度,DAM模型优于AM模型。同时,DAM模型的预报精度随预报时长的增加相对缓慢地变差,但精度明显优于AM模型(AM模型存在模式识别比较困难和定阶不准的不足,所以其预报精度明显差于另外几种常用模型)。综合分析可知,采用一次差分预报原理可以在一定程度上改善AM模型对GPS ⅡR Rb钟、ⅡR-M Rb钟和ⅡF Rb钟进行钟差预报时存在的模式识别困难和定阶不准的不足,进而提高AM模型的预报精度,特别是对ⅡF Rb钟预报效果的改善最为显著。
6) 对比KF模型与DKF模型,对于3 h的预报精度,DKF模型总体上优于KF模型,而其他3个时段则是KF模型更优;同样,KF模型基于钟差一次差分预报原理的预报结果也与卫星及其星载钟的类型有一定的关系:在3 h和6 h的预报中,对于ⅡA Rb钟、ⅡF Rb钟和ⅡF Cs钟的预报精度,DKF模型优于KF模型。同时,DKF模型的预报精度随预报时长的增加迅速变差,且其精度明显低于KF模型。因此,采用一次差分预报原理可以提高KF模型对GPS ⅡA Rb钟、ⅡF Rb钟和ⅡF Cs钟的短期预报精度。
7) 对上述各模型基于钟差一次差分预报原理进行预报过程中出现的情况进行分析表明,在建模数据一定的条件下,随着预报时间的增长,各模型预报结果的精度均有所降低,而且除了AM模型之外,其余几种模型采用一次差分预报原理时精度的降低比常规建模条件下精度降低得更迅速。这主要是因为,钟差一次差分可以在一定程度上消除原钟差序列趋势项的影响,得到1组有效数字位数减少、便于更加准确拟合的数据序列,同时,经过一次差分处理,可以消除钟差序列中可能存在的系统误差。但根据误差传播定律可知,作差后所得数据的误差会变大,所以会出现短期预报时一次差分预报原理能够提高预报精度,但随着预报时间的增加,预报误差会迅速积累,从而导致采用一次差分预报原理的精度降低得更迅速,特别是QP模型和KF模型表现最为显著。
3 结语在卫星钟差数据和卫星钟差预报模型给定的条件下,通过对卫星钟差数据一次差分处理并基于一次差分数据进行卫星钟差建模预报可以在一定程度上提高卫星钟差的短期预报精度,同时一次差分后的钟差数据便于进行异常值的探测和数据预处理等,这使得在卫星钟差的短期预报应用中,无需改变已有的预报模型和方法,只需在数据层面进行一次差分便可提高现有卫星钟差预报体系的预报精度,其对于卫星钟差预报的实际工程应用具有重要的参考价值。
| [1] |
王宇谱. GNSS星载原子钟性能分析与卫星钟差建模预报研究[D]. 郑州: 信息工程大学, 2017 (Wang Yupu. Research on Modeling and Prediction of the Satellite Clock Bias and Performan Evaluation of GNSS Satellite Clocks[D]. Zhengzhou: Information Engineering University, 2017)
(  0) 0) |
| [2] |
Liu Q, Chen X H, Zhang Y S, et al. A Novel Short-Medium Term Satellite Clock Error Prediction Algorithm Based on Modified Exponential Smoothing Method[J]. Mathematical Problems in Engineering, 2018, 1-7
(  0) 0) |
| [3] |
席超, 蔡成林, 李思敏, 等. 基于ARMA模型的导航卫星钟差长期预报[J]. 天文学报, 2014, 55(1): 78-89 (Xi Chao, Cai Chenglin, Li Simin, et al. Long-Term Satellite Clock Bias Prediction Based on ARMA Model[J]. Acta Astronomica Sinica, 2014, 55(1): 78-89 DOI:10.3969/j.issn.0001-5245.2014.01.007)
(  0) 0) |
| [4] |
Huang G W, Zhang Q, Xu G C. Real-Time Clock Offset Prediction with an Improved Model[J]. GPS Solutions, 2014, 18(1): 95-104 DOI:10.1007/s10291-013-0313-0
(  0) 0) |
| [5] |
王宇谱, 吕志平, 王宁, 等. 顾及卫星钟随机特性的抗差最小二乘配置钟差预报算法[J]. 测绘学报, 2016, 45(6): 646-655 (Wang Yupu, Lü Zhiping, Wang Ning, et al. Prediction of Navigation Satellite Clock Bias Considering Clock's Stochastic Variation Behavior with Robust Least Square Collocation[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(6): 646-655)
(  0) 0) |
| [6] |
黄观文, 崔博斌, 张勤, 等. 附加周期和神经网络补偿的实时钟差预报模型[J]. 宇航学报, 2018, 39(1): 83-88 (Huang Guanwen, Cui Bobin, Zhang Qin, et al. Real-Time Clock Offset Prediction Model with Periodic and Neural Network Corrections[J]. Journal of Astronautics, 2018, 39(1): 83-88)
(  0) 0) |
| [7] |
Strandjord K L, Axelrad P. Improved Prediction of GPS Satellite Clock Sub-Daily Variations Based on Daily Repeat[J]. GPS Solutions, 2018, 22(3): 58 DOI:10.1007/s10291-018-0723-0
(  0) 0) |
| [8] |
于烨, 张慧君, 李孝辉. 含误差预报校正的GM(1, 1)卫星钟差预报新方法[J]. 测绘科学, 2019, 44(4): 8-14 (Yu Ye, Zhang Huijun, Li Xiaohui. A New Method of GM(1, 1)Satellite Clock Bias Prediction with Error Prediction Correction[J]. Science of Surveying and Mapping, 2019, 44(4): 8-14)
(  0) 0) |
| [9] |
王宇谱, 吕志平, 陈正生, 等. 卫星钟差预报的小波神经网络算法研究[J]. 测绘学报, 2013, 42(3): 323-330 (Wang Yupu, Lü Zhiping, Chen Zhengsheng, et al. Research on the Algorithm of Wavelet Neural Network to Predict Satellite Clock Bias[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(3): 323-330)
(  0) 0) |
| [10] |
梁月吉, 任超, 杨秀发, 等. 基于一次差的灰色模型在卫星钟差预报中的应用[J]. 天文学报, 2015, 56(3): 264-277 (Liang Yueji, Ren Chao, Yang Xiufa, et al. Grey Model Based on First Difference in the Application of the Satellite Clock Bias Prediction[J]. Acta Astronomica Sinica, 2015, 56(3): 264-277)
(  0) 0) |
| [11] |
王宇谱, 吕志平, 周海涛, 等. 基于修正钟差一次差分数据的卫星钟差预报[J]. 大地测量与地球动力学, 2016, 36(12): 1 073-1 077 (Wang Yupu, Lü Zhiping, Zhou Haitao, et al. Satellite Clock Bias Prediction Based on Modified Single Difference Data of Clock Bias[J]. Journal of Geodesy and Geodynamics, 2016, 36(12): 1 073-1 077)
(  0) 0) |
| [12] |
王宇谱, 张胜利, 徐金锋, 等. 改进中位数方法的BDS卫星钟差数据预处理策略[J]. 测绘科学, 2019, 44(2): 109-115 (Wang Yupu, Zhang Shengli, Xu Jinfeng, et al. Data Preprocessing Strategy for BDS Satellite Clock Bias Data Based on an Improved Median Absolute Deviation Method[J]. Science of Surveying and Mapping, 2019, 44(2): 109-115)
(  0) 0) |
| [13] |
Senior K L, Ray J R, Beard R L. Characterization of Periodic Variations in the GPS Satellite Clocks[J]. GPS Solutions, 2008, 12(3): 211-225 DOI:10.1007/s10291-008-0089-9
(  0) 0) |
| [14] |
孙启松, 王宇谱. 基于方差递推法的Kalman滤波在钟差预报中的应用[J]. 测绘与空间地理信息, 2016, 39(6): 93-95 (Sun Qisong, Wang Yupu. Clock Bias Prediction by Application of Kalman Filter Based on Recursive Variance Method[J]. Geomatics and Spatial Information Technology, 2016, 39(6): 93-95 DOI:10.3969/j.issn.1672-5867.2016.06.028)
(  0) 0) |
2. Beijing Satellite Navigation Center, 5128 Yongfeng Road, Beijing 100094, China;
3. School of Surveying and Mapping, Information Engineering University, 62 Kexue Road, Zhengzhou 450001, China
 2021, Vol. 41
2021, Vol. 41

