2. 河南城建学院测绘与城市空间信息学院, 河南省平顶山市龙翔大道, 467036;
3. 华东交通大学土木建筑学院, 南昌市双港东大街808号, 330013
学者们对TEC预测模型进行了大量研究[1-9]。常用的短期预测方法主要包括经典数学统计法[1-2]和人工智能法[4-6]。但由于电离层复杂的时空变化特性[7], 经典数学统计方法难以得到理想的预测效果[8]。而人工智能法受主观因素的影响,缺乏客观理论依据,稳定性较差[4]。
灰色预测模型在短期预测中运用较广,但无法精确地预测具有非线性特征的TEC数据[6]。人工神经网络在电离层非线性预测中具有较高的精度,但其预测参数的选取较为复杂,网络算法优化较为困难[4]。ARMA预测模型方法较为简单,但其在极值点附近的预测精度较差[3]。因单一模型难以满足TEC预测所需要的精度要求,本文基于ARMA模型,结合经验小波变换(empirical wavelet transform, EWT), 提出一种短期组合预测模型EWT-ARMA。
1 模型原理 1.1 EWT方法EWT是一种新型的自适应信号处理方法[10], 其核心思想是根据信号划分的结果选择合适的滤波器组,提取出具有傅里叶频谱特性的调幅-调频(amplitude modulated frequency modulated, AM-FM)组件。首先对信号频谱进行自适应分割[11], 然后对分割的信号频谱特征构造合适的正交小波滤波器组,提取出AM-FM组件,最后利用Hilbert变换对不同的AM-FM组件进行处理,获取相应的瞬时频率和瞬时幅值[12]。具体过程可参考文献[10]。
最终,重构的原始信号f(t)表达式为:
| $f(t) = W_f^\varepsilon (0, t)*{\phi _1}(t) + \sum\limits_{n = 1}^N {W_f^\varepsilon } (n, t)*{\psi _n}(t)$ | (1) |
式中,*为卷积运算符,
针对TEC含量的随机特性,在ARMA预测模型的基础上,结合EWT方法,组成电离层短期预测模型。首先对电离层数据进行EWT分解,得到具有不同特征的若干分量,然后对各分量进行ARMA模型预测,预测结果进行重构得到最终的电离层TEC预测值。具体步骤如下[7]。
1) 利用EWT方法将TEC数据时间序列x(t)进行分解,得到N+1个模态分量,其中包含1个经验尺度分量和N个经验小波分量。
2) 对N+1个模态分量进行ARMA(p, q)模型预测。设xt(t=1, 2, 3, …)为电离层TEC值组成的时间序列数据,对于任意的t, 满足:
| $\begin{array}{l} {x_t} - {\varphi _1}{x_{t - 1}} - {\varphi _2}{x_{t - 2}} - \cdots - {\varphi _p}{x_{t - p}} = \\ {\varepsilon _t} - {\theta _1}{\varepsilon _{t - 1}} - {\theta _2}{\varepsilon _{t - 2}} - \cdots - {\theta _q}{\varepsilon _{t - q}} \end{array}$ | (2) |
式中,xt由1个经验尺度分量f0(t)和N个经验小波分量fk(t)组成,即xt={fk(t), k=0, 1, 2, …, N}, ε={εt, t=0, ±1, …}是均值为0、方差为δ2的白噪声序列。xt表示滑动平均序列ARMA(p, q)过程,其中p为移动模型(AR)的阶数,q为滑动模型(MA)的阶数,当p=0时,它是MA(q)模型,当q=0时,它是AR(p)模型。
引进后移算子B, 式(2)可表达为:
| $B{x_t} = {x_{t - 1}}, {B^k}{x_t} = {x_{t - k}}$ | (3) |
记算子多项式为:
| $\begin{array}{l} \varphi B = 1 - {\varphi _1}B - {\varphi _2}{B^2} - \cdots - {\varphi _P}{B^P}\\ \theta B = 1 - {\theta _1}B - {\theta _2}{B^2} - \cdots - {\theta _q}{B^q} \end{array}$ | (4) |
则式(3)可表示为:
| $\varphi(B) x_{t}=\theta(B) \varepsilon_{t}$ | (5) |
ARMA属于线性模型,根据电离层TEC时间序列数据,采用AIC定阶准则选定p、q, 使其满足:
| $\min \mathrm{AIC}=n \ln \hat{\delta}_{\varepsilon}^{2}+2(p+q+1)$ | (6) |
式中,n为样本数目,
3) 根据步骤2), 对经验尺度分量和经验小波分量进行预测,重构预测结果,得到最终的TEC预测值。
2 实例计算与分析本文选用IGS提供的2 h时间分辨率的电离层格网点上的数据对组合模型进行实验分析。参考文献[7], 提取2018年年积日1~30、101~130、201~230、301~330等4个时间段内的低纬(5°N, 120°E)、中纬(45°N, 120°E)和(45°N, 60°W)及高纬(85°N, 120°E)4个不同地理位置共16组电离层数据进行分析。分别利用前25 d的TEC真实值预测后5 d的TEC值,后5 d的TEC真实值作为检测值与预测值进行对比,验证模型的预测效果。利用EWT方法对16组TEC真实数据进行模态分解,每组数据得到5~6个不同的经验小波分量和1个经验尺度分量,然后对各分量进行ARMA模型建模、预测,得到各分量的预测值,最后将各分量的预测值重构得到最终预测结果,并与真实值进行对比。为了验证本文组合模型预测结果的优劣性,采用均方根误差RMSE和平均相对精度P作为评定模型预测结果的指标,并与ARMA模型的预测结果进行对比:
| $\mathrm{RMSE}=\sqrt{\frac{1}{n} \sum\limits_{i=1}^{n}\left(\hat{x}_{i}-x_{i}\right)^{2}}$ | (7) |
| $P=1-\sum\limits_{i=1}^{n} \frac{\left|\hat{x}_{i}-x_{i}\right|}{x_{i}}$ | (8) |
式中,n为TEC预测数据的个数,
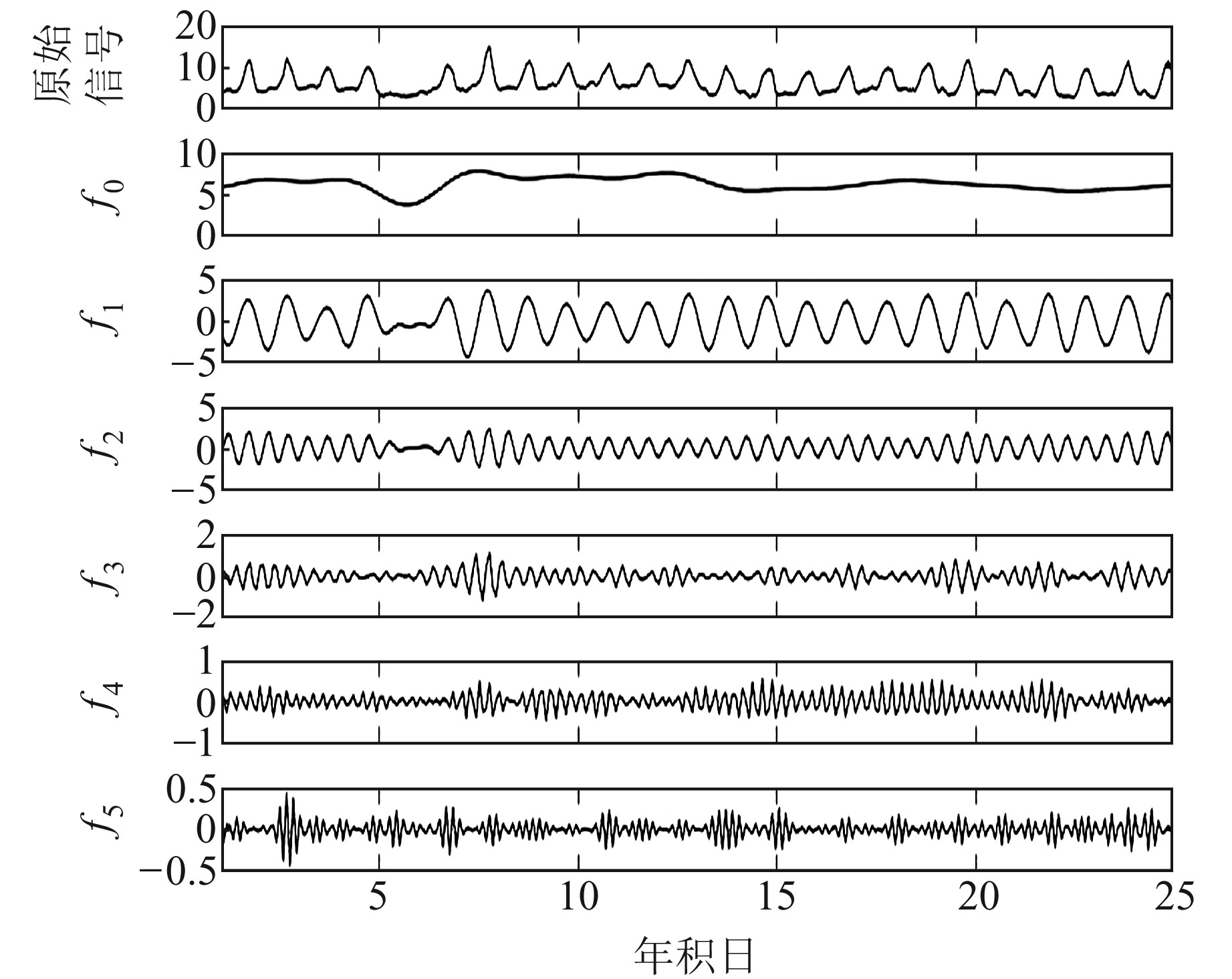
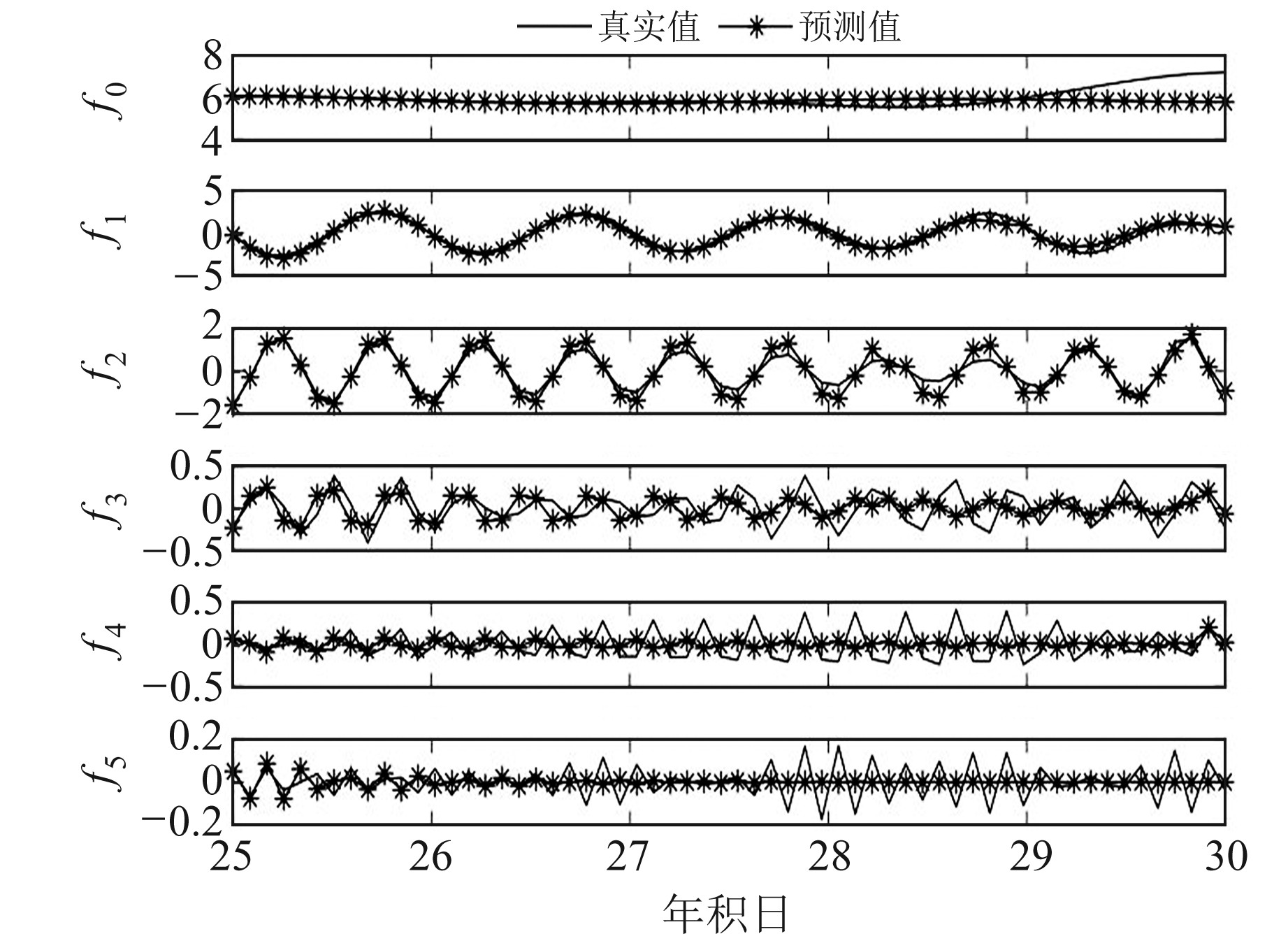
选择2018年年积日1~30(45°N, 60°W)的1组数据进行具体分析。首先提取该组电离层时间序列数据,利用EWT分解前25 d的TEC数据(图 1)。可以看出,TEC原始数据被分解成了1个经验尺度分量f0和5个经验小波分量f1~f5, 分解的分量呈现出从低频到高频变化的特点,且原有数据的能量分解后主要集中在经验尺度分量f0和经验小波分量f1、f2。对各分量25 d的数据进行ARMA建模,预测后5 d的数据,并与真实值对比(图 2)。可以看出,经验尺度分量f0和经验小波分量f1、f2预测效果较好,预测值与真实值偏差很小,分量f3~f5预测效果较差,但其所占能量比重小,不会对最终预测效果产生较大影响。将所有分量的预测值重构得到最终的TEC预测值。图 3为组合模型和ARMA模型的预测值与真实值的对比图。可以看出,采用ARMA模型进行预测时,在极值点附近偏差较大,达到2~3 TECu, 而本文组合模型预测值与真实值趋势符合较好,在极值点附近的偏差也减小到1 TECu左右。
|
图 1 年积日1~25(45°N, 60°W)原始信号和信号分解图 Fig. 1 Original signal and signal exploded view of doy 1~25(45°N, 60°W) |
|
图 2 年积日26~30(45°N, 60°W)各分量预测值与真实值的对比图 Fig. 2 Comparison between predicted TEC and true TEC of each component of doy 26~30(45°N, 60°W) |

|
图 3 2种模型在年积日26~30(45°N, 60°W)的TEC预测值对比图 Fig. 3 Comparison of TEC predicted values of two models of doy 26 ~ 30(45°N, 60°W) |
为了从整体上检验组合模型的预测效果,引进残差绝对值Δ进行说明,其表达式为:
| $\Delta=\left|\hat{x}_{i}-x_{i}\right|$ | (9) |
式中,
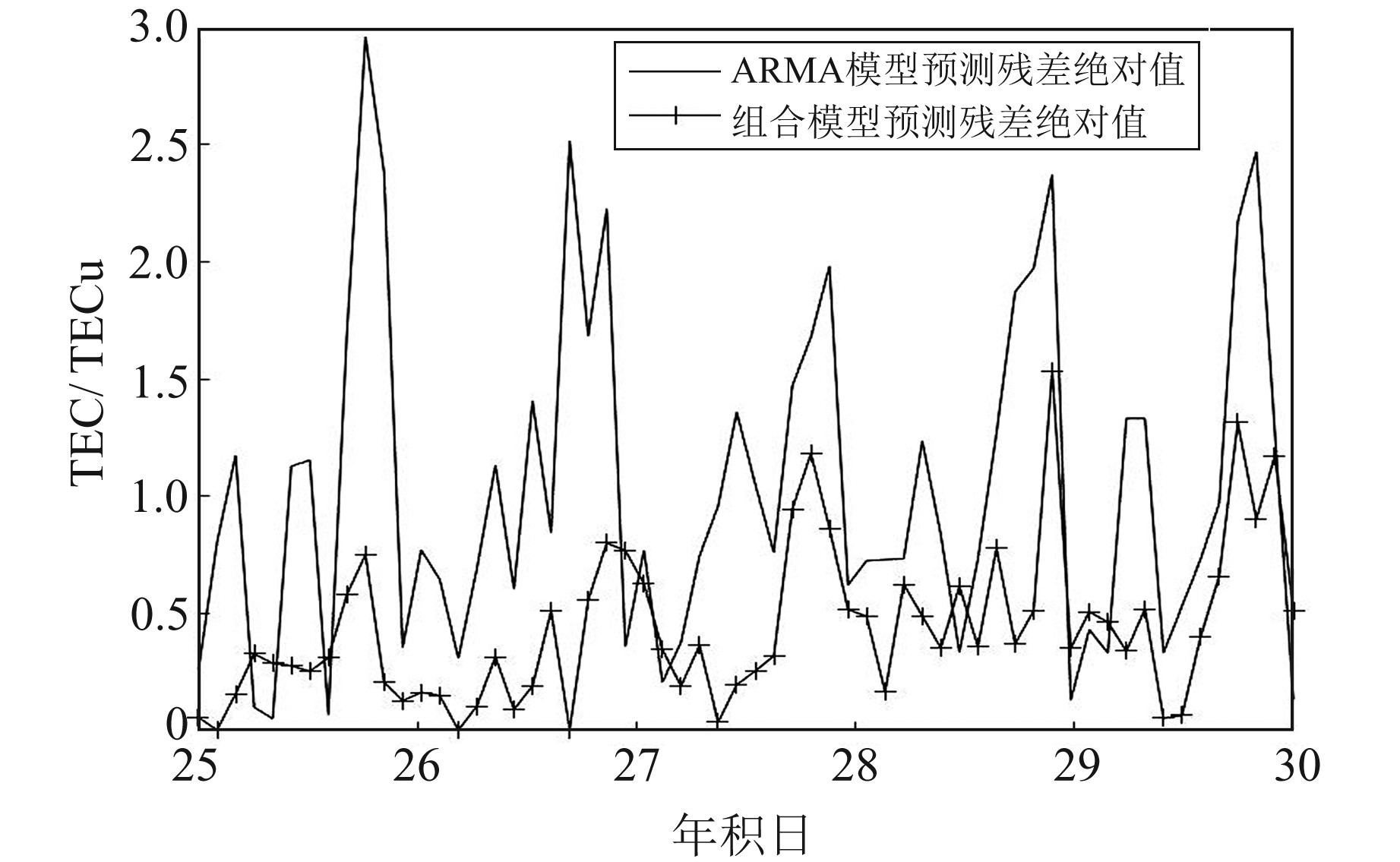
图 4为2种模型在2018年年积日26~30的TEC预报残差绝对值对比图。可以看出,ARMA模型预测的残差绝对值在1.5 TECu以内比重较大,部分超过2 TECu, 而组合模型预测的残差绝对值大部分在1 TECu以内,极少部分超过1 TECu。从整体来看,组合模型比ARMA模型预测效果更好。
|
图 4 2种模型在年积日26~30(45°N, 60°W)的TEC预报残差绝对值对比图 Fig. 4 Comparison of TEC residual absolute values of prediction of two models of doy 26 ~ 30(45°N, 60°W) |
表 1为2018年年积日26~30的4个不同地理位置的预报残差绝对值百分比统计表。表中显示,ETW-ARMA组合模型的残差绝对值均值小于1 TECu的占比为81.8%, 相比ARMA模型提高了20.1%。ETW-ARMA组合模型的残差绝对值均值大于3 TECu的占比为0.6%, 相比ARMA模型降低了5.2%。由此表明,本文组合模型的整体预测效果更优。同时,2种模型的残差绝对值均主要集中在2 TECu以内,符合IGS给出的3 TECu的精度范围[3]。
|
|
表 1 4个不同地理位置预报残差绝对值百分比统计 Tab. 1 Percentage statistics of forecast residual absolute value for four different geographical positions |
以2018年年积日201~230的TEC数据为例进行分析,表 2给出了同一时间段5 d内不同经纬度的均方根误差和平均相对精度的实验结果。从表中可以看出,同一时段相同位置处,组合模型的预测效果普遍比ARMA模型好;同一时段相同经度下,纬度越高,2种模型预测的平均相对精度越大,均方根误差越小;同一时段相同纬度下,不同经度间预测的平均相对精度和均方根误差没有明显变化。2018年为太阳活动低年,为验证EWT-ARMA组合模型在太阳活动高年的预测效果,用相同方法对2014年(太阳活动高年)的数据进行实验。表 3为2种模型在2014年年积日226~230的预测误差对比表。可以看出,2种模型在太阳活动高年的预测效果与太阳活动低年相同,组合模型的预测效果普遍优于ARMA模型的预测效果。
|
|
表 2 2018年年积日226~230不同模型的预测误差对比 Tab. 2 Comparison of prediction errors of different models of doy 226~230 in 2018 |
|
|
表 3 2014年年积日226~230不同模型的预测误差对比 Tab. 3 Comparison of prediction errors of different models of doy 226~230 in 2014 |
表 4给出了2种模型在太阳活动低年和太阳活动高年的4个时段5 d内的整体预测误差情况对比。结果显示,4个不同时段中,EWT-ARMA组合模型的预测效果均比单一ARMA模型更好。在太阳活动低年和太阳活动高年,ARMA模型预测的平均相对精度分别为83.0%和86.3%, 组合模型的则分别为87.8%和89.1%;ARMA模型预测的均方根误差分别为1.61和3.64, 组合模型预测的则分别为1.22和2.93, 证明组合模型比ARMA模型更优。对比太阳活动低年,2种模型在太阳活动高年预测时相对精度更高、均方根误差更大。
|
|
表 4 4个时段5 d内的预测误差对比 Tab. 4 Comparison of forecast errors within 5 d of four periods |
在表 4的基础上,给出4个时段前1 d内整体的预测误差对比(表 5)。结果表明,在前1 d内,太阳活动低年和太阳活动高年EWT-ARMA组合模型的平均相对精度比ARMA单一模型分别提高了7%和6.1%, 均方根误差则分别降低了0.82和1.71。对比组合模型5 d内的平均相对精度87.8%和89.1%, 前1 d内的平均相对精度为92.1%和94.5%, 表明组合模型在前1 d内的整体预测效果更好。
|
|
表 5 4个时段前1 d内的预测误差对比 Tab. 5 Comparison of prediction errors within one day earlier of four periods |
针对电离层预测模型中ARMA模型预测精度较低、极值点附近预测效果较差的问题,本文提出利用EWT-ARMA组合模型对电离层TEC数据进行预测分析,并与ARMA模型预测效果进行比较。对太阳活动低年和太阳活动高年的各16组数据进行实验,得出以下结论。
1) 利用ETW方法对电离层数据进行分解,对分解的各分量进行ARMA预测,预测结果重构得到最终的TEC值。与ARMA预测方法对比表明,组合模型整体预测精度更高。
2) 太阳活动低年和太阳活动高年的实验结果表明,相较于ARMA模型的平均相对精度,本文组合模型5 d内的平均相对精度分别提高了4.8%和2.8%, 前1 d内组合模型的平均相对精度分别提高了7%和6.1%, 表明本文预测方法效果更好,在前1 d内的预测精度更优。
本文将EWT方法应用到非线性、非平稳的电离层信号研究当中,给类似特性的信号提供了一种新的研究思路。但ARMA时间序列预测模型本身存在一定的局限性,结合经验小波变换的同时也增加了预测的工作量。此外,电离层复杂的时空变化特性也给预测带来一定的影响,建立一个更加完善的电离层预测模型还有待进一步的研究。
致谢: 感谢IGS中心提供电离层TEC格网数据。
| [1] |
Muhtarov P, Kutiev I. Autocorrelation Method for Temporal Interpolation and Short-Term Prediction of Ionospheric Data[J]. Radio Science, 1999, 34(2): 459-464 DOI:10.1029/1998RS900020
(  0) 0) |
| [2] |
Liu R Y, Liu S L, Xu Z H, et al. Application of Autocorrelation Method on Ionospheric Short-Term Forecasting in China[J]. Chinese Science Bulletin, 2006, 51(3): 352-357 DOI:10.1007/s11434-006-0352-9
(  0) 0) |
| [3] |
李磊, 张淑芳, 王轶卓, 等. 利用ARMA模型进行电离层TEC预报[J]. 应用基础与工程科学学报, 2013, 21(5): 814-822 (Li Lei, Zhang Shufang, Wang Yizhuo, et al. Ionospheric Total Electron Content Prediction Based on ARMA Model[J]. Journal of Basic Science and Engineering, 2013, 21(5): 814-822 DOI:10.3969/j.issn.1005-0930.2013.05.002)
(  0) 0) |
| [4] |
Acharya R, Roy B, Sivaraman M R, et al. Prediction of Ionospheric Total Electron Content Using Adaptive Neural Network with In-Situ Learning Algorithm[J]. Advances in Space Research, 2011, 47(1): 115-123 DOI:10.1016/j.asr.2010.08.016
(  0) 0) |
| [5] |
Huang Z, Yuan H. Ionospheric Single-Station TEC Short-Term Forecast Using RBF Neural Network[J]. Radio Science, 2014, 49(4): 283-292 DOI:10.1002/2013RS005247
(  0) 0) |
| [6] |
毛文军, 常文龙. 基于灰色组合模型的电离层电子含量预报[J]. 测绘科学, 2016, 41(1): 39-43 (Mao Wenjun, Chang Wenlong. Prediction of Ionospheric VTEC Using Grey Time Series Combination Model[J]. Science of Surveying and Mapping, 2016, 41(1): 39-43)
(  0) 0) |
| [7] |
汤俊, 姚宜斌, 陈鹏, 等. 利用EMD方法改进电离层TEC预报模型[J]. 武汉大学学报: 信息科学版, 2013, 38(4): 408-411 (Tang Jun, Yao Yibin, Chen Peng, et al. Prediction Models of Ionospheric TEC Improved by EMD Method[J]. Geomatics and Information Science of Wuhan University, 2013, 38(4): 408-411)
(  0) 0) |
| [8] |
张禄. 基于时间序列、神经网络、灰色和组合预测对电离层TEC的预测研究[D]. 南京: 南京信息工程大学, 2012 (Zhang Lu. Based on the Time Series, Neural Network, Grey and Combination Forecasting of Ionospheric TEC Forecast Research[D]. Nanjing: Nanjing University of Information Science and Technology, 2012)
(  0) 0) |
| [9] |
赵传华, 党亚民, 秘金钟. 组合方法在电离层TEC短期预报中的应用[J]. 大地测量与地球动力学, 2012, 32(3): 76-79 (Zhao Chuanhua, Dang Yamin, Bei Jinzhong. Application of Combination Method in Ionosphere TEC Short-Term Forecast[J]. Journal of Geodesy and Geodynamics, 2012, 32(3): 76-79)
(  0) 0) |
| [10] |
Gilles J. Empirical Wavelet Transform[J]. IEEE Transactions on Signal Processing, 2013, 61(16): 3 999-4 010 DOI:10.1109/TSP.2013.2265222
(  0) 0) |
| [11] |
王莹. 基于成分分解的自适应滤波降噪方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2017 (Wang Ying. Research on Adaptive Filter Denoising Method Based on Component Decomposition[D]. Harbin: Harbin Institute of Technology, 2017)
(  0) 0) |
| [12] |
孙国强, 梁智, 俞娜燕, 等. 基于EWT和分位数回归森林的短期风电功率概率密度预测[J]. 电力自动化设备, 2018, 38(8): 158-165 (Sun Guoqiang, Liang Zhi, Yu Nayan, et al. Short-Term Wind Power Probability Density Forecasting Based on EWT and Quantile Regression Forest[J]. Electric Power Automation Equipment, 2018, 38(8): 158-165)
(  0) 0) |
2. School of Surveying and Urban Spatial Information, Henan University of Urban Construction, Longxiang Road, Pingdingshan 467036, China;
3. School of Civil Engineering and Architecture, East China Jiaotong University, 808 East-Shuanggang Street, Nanchang 330013, China
 2021, Vol. 41
2021, Vol. 41


