JCZ-1超宽频带地震仪是“八五”期间研制的频带为DC~20 Hz的地震观测仪器[1],具有高灵敏度、低噪声等特点,观测范围可从高频地震波至固体潮[2]。截至2019年,国内已有17个台站安装JCZ系列超宽频带地震仪,可为地震信号监测提供大量数据。由于地球内部结构复杂,地震仪器采集到的地震信息往往伴随着各种噪声,为压制背景噪声,保留地震数据波形,需保持较高的信噪比,这对于后续地震数据分析处理具有重要意义。
JCZ系列地震仪可获取大量来自地球内部的地震信息,除去有效信号外,还包含各种噪声(主要分为相干噪声和随机噪声[3])。但目前有关该仪器的地震数据去噪处理等方面的研究方法较为单一,本文对地震信号降噪处理中的小波阈值法进行去噪研究,重点探讨小波基函数的选取、小波分解几何尺度参数的确定及软阈值、硬阈值函数的选取对去噪结果的影响等。同时探讨在小震和中强震两种情况下用相同方法处理的去噪效果,并选择合适的小波基与几何尺度用于震例数据去噪对比。结果发现,选取不同的阈值函数在不同震级的地震数据处理中会表现出不同的去噪效果。
1 小波变换与去噪理论在地震信号处理中,傅里叶变换是一种常用的方法,但该方法在处理非平稳信号时不能在时域和频域联合分析[1]。因此,小波变换应运而生,其具有局部化时频分析功能,时频窗口的大小可以随着频率的高低而变化。当地震信号的低频部分较为平缓时,所含的频率成分较多,小波分析可通过降低时间分辨率来提高频率分辨率;当地震信号的高频部分包含很多瞬态变化的特征时,小波分析可通过提高时间分辨率来关注信号的瞬态特征,从而降低频率分辨率[4]。
设地震信号函数为x(t),其连续小波变换的时域表达式为[1]:
| $ \begin{array}{l} {\rm{CWT}}\left( {a, b} \right) = {\left| a \right|^{ - \frac{1}{2}}}\int_{ - \infty }^{ + \infty } {x\left( t \right)} {\psi ^*}\left( {\frac{{t - b}}{a}} \right){\rm{d}}t, \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;a > 0, b \in R \end{array} $ | (1) |
式中,a为伸缩因子,b为平移因子。a、b均连续变化,ψ*(t)是ψ(t)的共轭,称为小波变换系数。在实际运用中,需要将参数a、b进行离散化:
| $ \begin{array}{l} a = a_0^i, {a_0} > 1, i \in z\\ b = ka_0^i{b_0}, {b_0} > 0, k \in z \end{array} $ | (2) |
则离散化的小波函数表达式为:
| $ \begin{array}{l} \;\;\;{\psi _{j, k}}\left( t \right) = a_0^{ - \frac{j}{2}}\psi (a_0^{ - j}(t - ka_0^j{b_0})), \\ j = 0, \pm 1, \pm 2, \ldots ;k = 0, \pm 1, \pm 2 \end{array} $ | (3) |
降噪的含义是在进行地震信号去噪时尽量将无用的信息从原始信号中去除[4],应满足两条准则:1)降噪处理后的信号大部分情况下应与原始信号具有同等的光滑性;2)降噪处理后的信号和原始信号的方差估计应在最坏情况下方差最小[4]。本文小波阈值去噪算法如图 1所示。

|
图 1 小波阈值去噪算法 Fig. 1 The algorithm of wavelet threshold denoising |
对于去噪后结果的评价,传统的评价标准有信噪比、平滑度、均方根误差、互相关系数等。由于JCZ超宽频带地震仪采集到的信号是地震信号与噪声信号的混合信号,很难得到地震信号的纯信号,无法使用信噪比进行真正意义上的计算评价。文献[5]将去噪后的信号当作纯信号,将原始信号当作带噪信号,提出相对信噪比概念,计算公式为:
| $ {\rm{SN}}{{\rm{R}}^*} = \frac{{P_1^2}}{{{{({P_2} - {P_1})}^2}}} $ | (4) |
式中,SNR*为相对信噪比,P1为小波去噪后的波形,P2为原始波形。相对SNR值越大,表示原始波形越接近去噪后的波形,说明去噪后的波形噪声依然很高,去噪效果不理想;相对SNR值越小,表示原始波形越远离去噪后的波形,说明去噪后的波形噪声较小,去噪效果明显。对于互相关系数[6]的计算,因为理论参考信号未知,即理论地震信号未知,计算准确度不高,因此本文未采取该衡量标准。平滑度指标的数学解释为当信号足够长时,去噪后信号的一阶差分与原始信号的一阶差分的方差根之比[7],其值越小,去噪效果越好,计算公式为:
| $ r = \frac{{\sqrt {\sum\limits_{i = 1}^{n - 1} {{{\left[ {f'\left( {i + 1} \right) - f'\left( i \right)} \right]}^2}} } }}{{\sqrt {\sum\limits_{i = 1}^{n - 1} {{{\left[ {f\left( {i + 1} \right) - f\left( i \right)} \right]}^2}} } }} $ | (5) |
均方根误差是指原始信号与去噪信号之间方差的平方根[8],将采集到的噪声与地震信息的混合信号作为原始信号,将小波去噪后的信号作为去噪信号。该指标可体现信号的整体偏差信息,数值越小说明去噪效果越好,计算公式为:
| $ {\rm{RMSE}} = \sqrt {\frac{{\sum\limits_{i = 1}^n {{{\left[ {f\left( i \right) - f'\left( i \right)} \right]}^2}} }}{n}} $ | (6) |
平均绝对误差可体现去噪后信号与原始信号之间的相似性,数值越小表示去噪效果越好,计算公式为:
| $ 平均绝对误差= \frac{{\sum\limits_{i = 1}^n {\left| {f\left( i \right) - f'\left( i \right)} \right|} }}{n} $ | (7) |
式(5)~(7)中,f(i)为地震计采集到的原始信号,f′(i)为小波去噪后的信号。
每种评价指标均从单一方面评价小波去噪的效果,当真值未知时,任何一种评价指标都无法满足质量评价的需求[8]。经过一系列实验发现,在选取小波基的实验过程中,并不是每种评价标准都能较好地反映不同小波基的去噪效果。在选取小波基的实验中,RMSE值与相对SNR值作为评判标准的效果比平均绝对误差和平滑度差,其值变化不明显,所以选择平滑度与平均绝对误差作为小波去噪效果的评价指标。对于分解与重建尺度的选取,去噪后信号的均方根误差的变化量较小,可以作为最佳分解尺度[9]。
2.2 小波基选取小波变换具有许多小波基可供选择,不同的小波基对地震信号去噪结果的影响也不同。对于小波基的选择,首先理论上要求其具有一定的紧支性、平滑性、对称性和消失矩阶数等,能较好处理地震信号的小波基函数主要有biorthogonal小波、daubechies小波、coifmant小波、symletsA小波[5]。在此基础上,使用实验方法对上述4种小波基进行地震信号的降噪处理。本文实验使用控制变量法,对于小波基的选取,只设置小波基变量,分解层数均设置为1,阈值均采用Birge-Massart阈值,信号上作用阈值的方法均使用硬阈值处理,其中Birge-Massart策略的经验系数设置为2。
本文实验数据均来自武汉水院地震台运行的JCZ-1超宽频带地震仪记录的数据,其中小波基与尺度实验数据为2016-03-22 00:00开始采集的连续24 h的垂直方向数据,数据格式为miniSEED,从第380 000点开始截取,直至第720 000点,信号长度为340 000。利用4种常用方法进行实验分析,首先在各自的小波簇内进行比较以确定较好的小波基,然后在选出的4种较好的小波基中进行比较,最终选出最有效的小波基。
由表 1可以看出,在db系列的小波基中,采用db6小波基的平滑度最小,平均绝对误差也最小,说明采用db6小波基是该小波基系列的最佳选择。
|
|
表 1 db小波基实验数据 Tab. 1 Experimental data of db wavelet basis |
由表 2可以看出,采用coif1小波基的平滑度在coif小波基中最小,表明去噪后的信号局部无过多的突变信息,说明去噪后信号的光滑性最好;但其平均绝对误差却很大,表明去噪后的信号与原始信号的相似程度较小;同时小波基coif1的消失矩阶数过小,反映小波去噪后的信号重构能量不集中,因此未选择小波基coif1。由表 2可知,从小波基coif1到小波基coif5,随着平滑度的不断增大,平均绝对误差不断减小,证明小波基无法很好地兼顾平滑性和紧支集性的特点。综上所述,选取coif3作为该系列的小波基。
|
|
表 2 coif小波基实验数据 Tab. 2 Experimental data of coif wavelet basis |
由表 3可以明显看出,采用小波基bior1.1~bior1.5去噪后信号的平滑度明显不够,并且平均绝对误差相对较大,这是因为这几个小波基的支撑长度较小。采用小波基bior2.6~bior3.3去噪后信号的光滑性可得到保证,但其平均绝对误差也相对较大,因为这些小波基随着滤波器长度的增加,紧支集区间也在变大,使得去噪后信号的平滑度较好,但同时也导致去噪后信号的局部性下降。采用小波基bior3.5~bior4.4去噪后信号的平滑度较好,平均绝对误差较小,并且这些小波基的消失矩阶数较高,信号重构后能量比较集中。综上可知,bior系列中可选择平滑度和紧支集性都较好的bior3.5小波基。
|
|
表 3 bior小波基实验数据 Tab. 3 Experimental data of bior wavelet basis |
由表 4可以看出,小波基sym4、sym6和sym8的平滑度与平均绝对误差都较好,比sym系列中其余小波基的效果更好。但对于小波基sym8,其消失矩阶数过高,会导致信号重构后能量过于集中;对于小波基sym4,虽然其平滑度最好,但相比于小波基sym6和sym8,其平均绝对误差过大,表明采用sym4小波基去噪后的信号无过多的局部突变,但会去除过多的有用信息。综上可知,sym系列可选择小波基sym6。
|
|
表 4 sym小波基实验数据 Tab. 4 Experimental data of sym wavelet basis |
在每个小波基系列中选出较优的小波基后,再对这4个小波基进行对比,选出最终的小波基(表 5)。
|
|
表 5 选出的4种小波基实验数据 Tab. 5 Experimental data of four selected wavelet bases |
由表 5可以看出,采用小波基bior3.5去噪后信号的光滑度和平均绝对误差最好,因此本文选择bior3.5作为小波基对JCZ超宽频带地震仪的地震数据进行去噪。
2.3 分解和重构尺度选取在小波进行地震信号去噪时,分解和重构的尺度对去噪结果具有很大影响,如果小波分解和重构尺度过小,会导致原始地震信号中还存在一定的噪声数据,消噪效果不理想;如果小波分解和重构尺度过大,会导致去噪后信息大量丢失,信噪比严重下降,同时使计算机处理数据的运算量变大[6]。结合前人的研究成果[10-12],本文设置8组对照实验,采用控制变量法选用bior3.5小波基,分解和重建尺度为1~8次,使用Birge-Massart阈值,信号上作用阈值的方法均使用硬阈值处理,其中Birge-Massart策略的经验系数设置为2(表 6)。
|
|
表 6 不同尺度下的实验数据 Tab. 6 Experimental data at different scales |
通过计算发现,平均绝对误差随分解尺度的增加而不断增大,相对SNR值则不断减小;平滑度在分解尺度1~5不断增加,随后不断减少;RMSE值随着分解尺度的增大而不断增大,这表明对于本文地震数据去噪分解尺度的选取无法直接使用以上4种评价指标[8],而去噪后信号的均方根误差变化量较小时的分解尺度可作为最佳分解尺度[9]。本文通过计算去噪后信号的均方根误差变化量(表 7)发现,当分解尺度为5时变化量最小,因此本文选择分解和重构尺度为5,其中均方根误差变化量计算公式为:
| $ {\rm{ver}}\left( m \right) = |{\rm{RMSE}}\left( {m + 1} \right) - {\rm{RMSE}}\left( m \right)| $ | (8) |
|
|
表 7 不同尺度下的均方根误差变化量 Tab. 7 Variation of root mean square error at different scales |
式中,ver(m)为尺度m+1与尺度m间的均方根误差变化量,RMSE(m)为第m分解尺度下的均方根误差。
2.4 小波阈值选取常用的小波阈值选取方法主要有2种:一是根据原始信号确定各级阈值,原理是基于原始信号的信噪比建立不同的数学模型求取阈值,如本文在选取小波基和分解及构建尺度设计的实验中使用的Birge-Massart阈值[4];二是根据样本数估计选取阈值,原理是在最坏情况下根据降噪信号与原始信号方差最小原则来确定统一阈值[4]。在实验分析中,除使用Birge-Massart阈值法外,还使用常用的rigrsure、sqtwolog、heursure和minimaxi阈值法进行实验对比分析。
2.5 小波阈值函数选取在已选取小波阈值的基础上,通常采用2种方法将阈值作用到待处理的地震信号上:一是将待处理的地震信号中绝对值小于阈值的点设为零,也称为硬阈值;另一种方法是在硬阈值基础上使数据处理边界出现不连续的点收缩到零[4]。
2.6 两种不同震级地震数据的去噪实验不同频带和振幅的地震数据在相同的去噪方法下会表现出不同的效果。为了探讨小震和中强震在相同方法下的小波阈值去噪效果,本文使用控制变量法,除地震数据不同外,其余处理方式完全一致,处理方案使用前文选取的小波基与尺度。小震使用JCZ-1超宽频带地震仪于2018-08-04在新疆库尔勒台记录到的新疆库尔勒2.4级地震的垂直向数据,数据从第1 617 400点开始,到第1 622 600点结束。中强震使用JCZ-1超宽频带地震仪于2012-12-30在新疆库尔勒台记录到的日本本州4.9级地震的垂直向数据,数据从第466 600点开始,到第495 400点结束。
由图 2~11可以看出,无论是在小震还是在中强震的实际去噪处理中,rigrsure阈值、sqtwolog阈值、heursure阈值和minimaxi阈值在实际地震中的去噪效果均不明显。由于实际的地震信号噪声源较多,频谱覆盖较广,基于样本数估计选取的阈值在实际信号中具有局限性[3]。在小震的小波阈值去噪中,Birge-Massart阈值去噪过度,会去除很多有用信息;在中强震的小波阈值去噪中,Birge-Massart阈值去噪效果较好,可去除地震数据中较多的“毛刺”背景噪声,保留有效信息。上述分析表明,在对实际的地震信号进行小波阈值去噪处理时,需要进行实际分析才能选出较好的阈值方法。
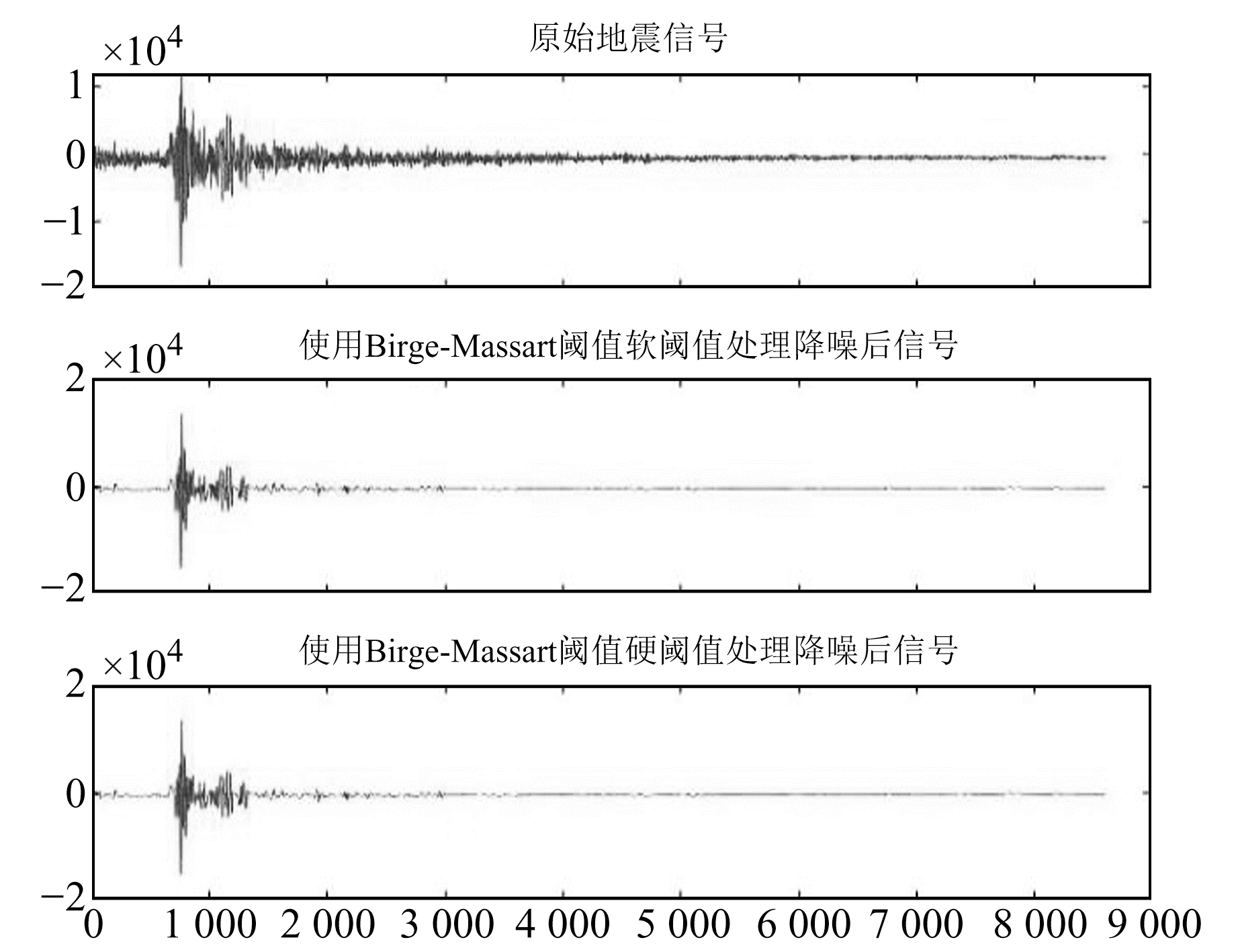
|
图 2 小震Birge-Massart阈值软、硬阈值处理后数据与原始数据对比 Fig. 2 Comparison of the small earthquake data processed by the Birge-Massart soft and hard thresholds and the original data |

|
图 3 小震rigrsure阈值软、硬阈值处理后数据与原始数据对比 Fig. 3 Comparison of the small earthquake data processed by the rigrsure soft and hard thresholds and the original data |
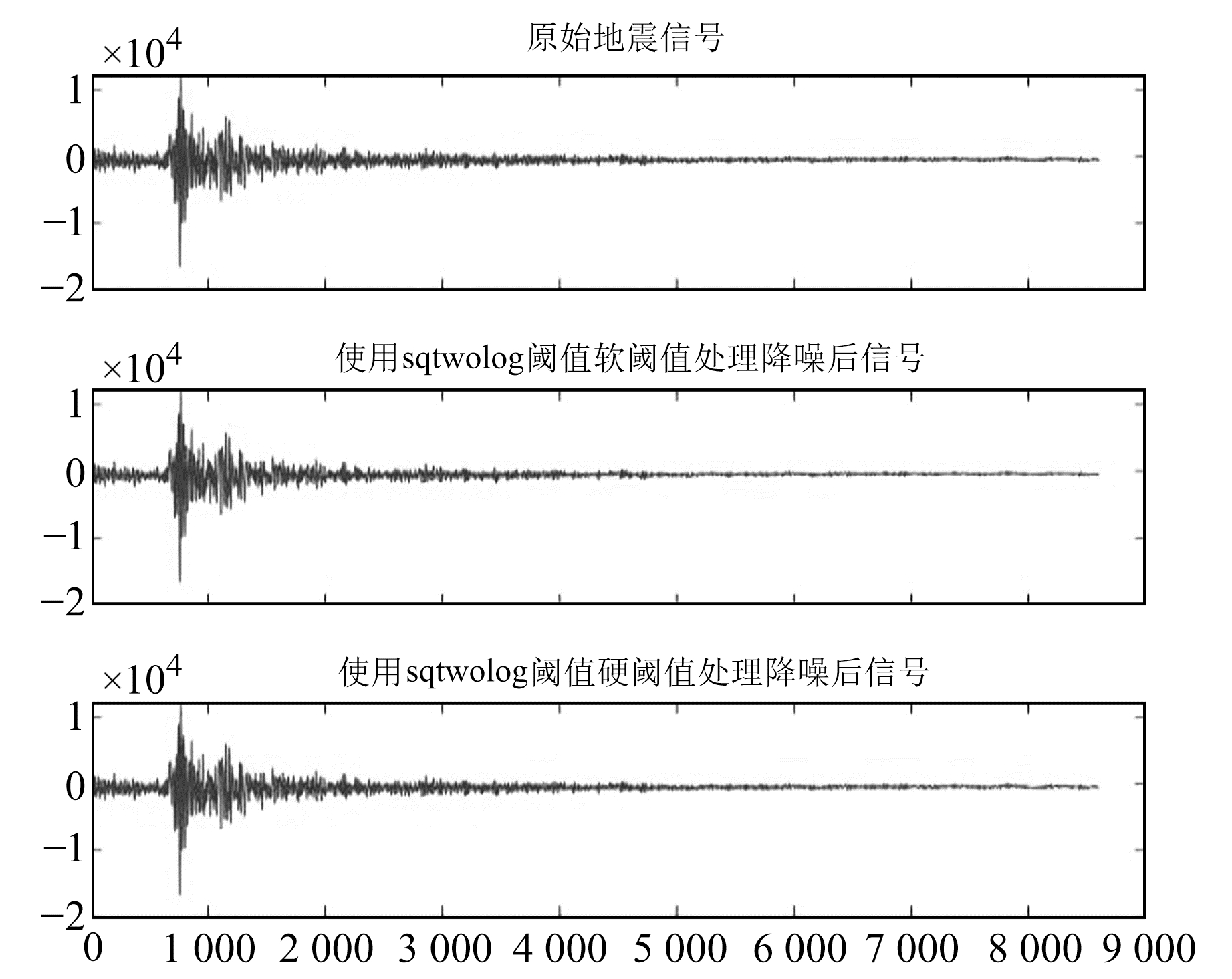
|
图 4 小震sqtwolog阈值软、硬阈值处理后数据与原始数据对比 Fig. 4 Comparison of the small earthquake data processed by the sqtwolog soft and hard thresholds and the original data |
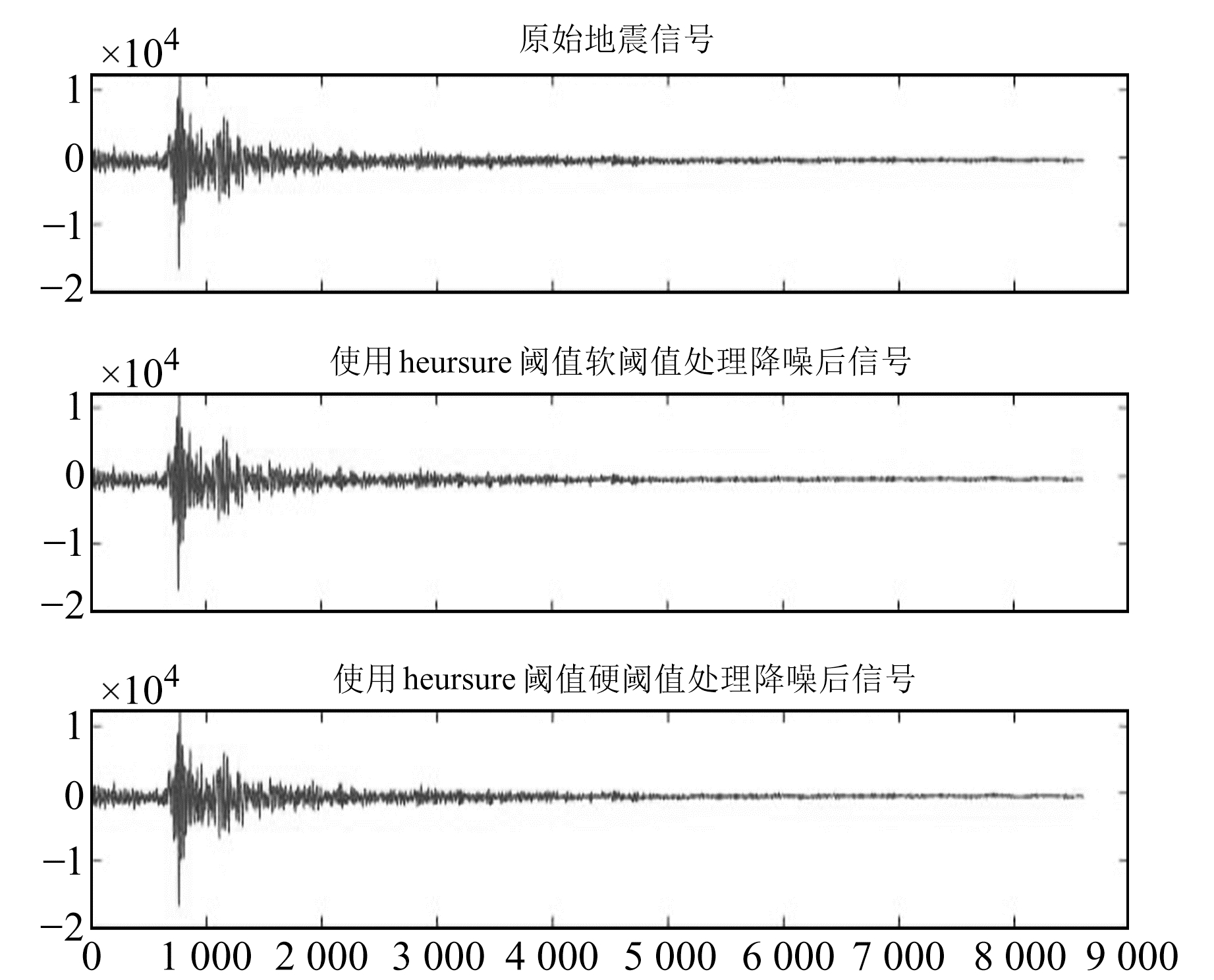
|
图 5 小震heursure阈值软、硬阈值处理后数据与原始数据对比 Fig. 5 Comparison of the small earthquake data processed by the heursure soft and hard thresholds and the original data |
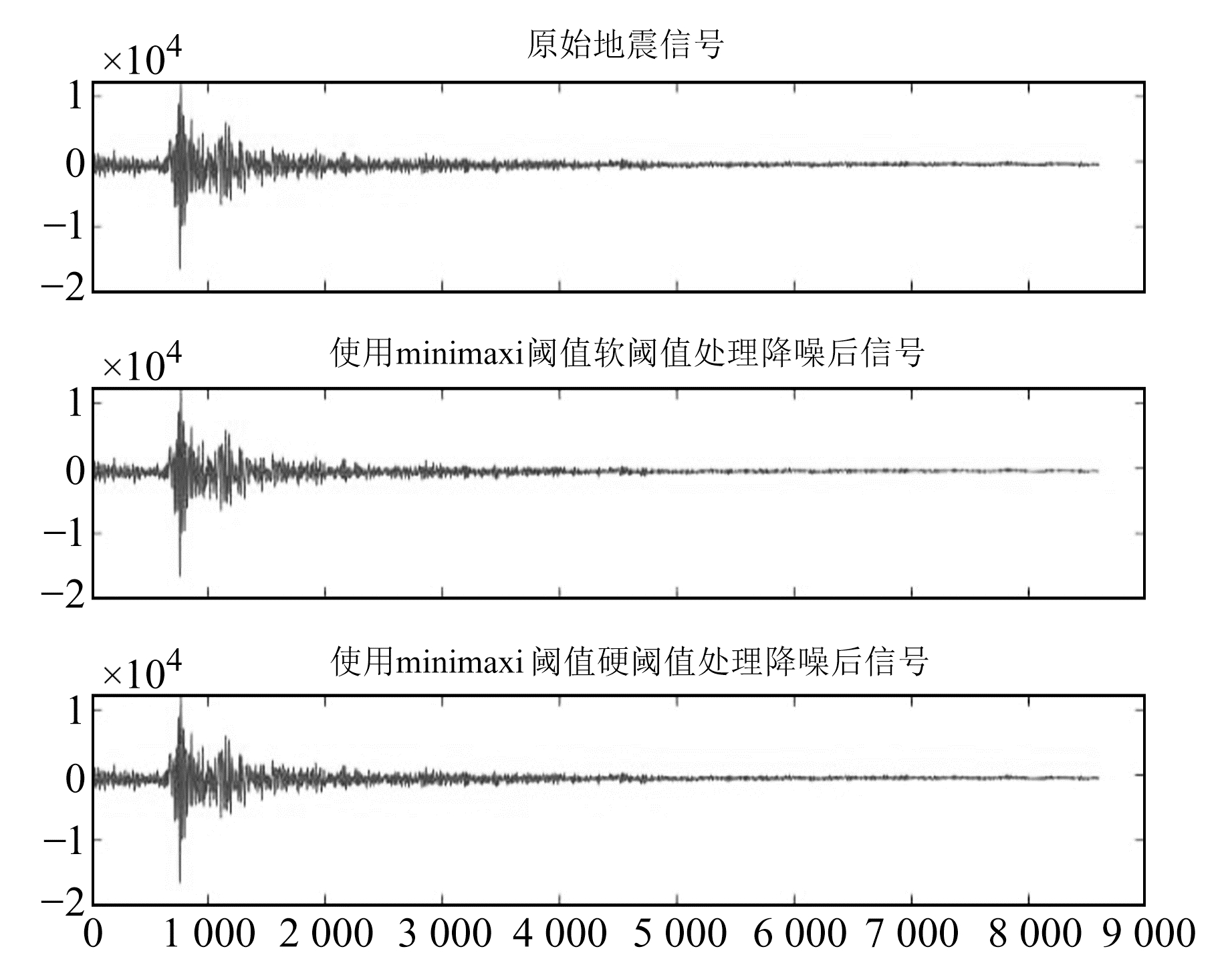
|
图 6 小震minimaxi阈值软、硬阈值处理后数据与原始数据对比 Fig. 6 Comparison of the small earthquake data processed by the minimaxi soft and hard thresholds and the original data |
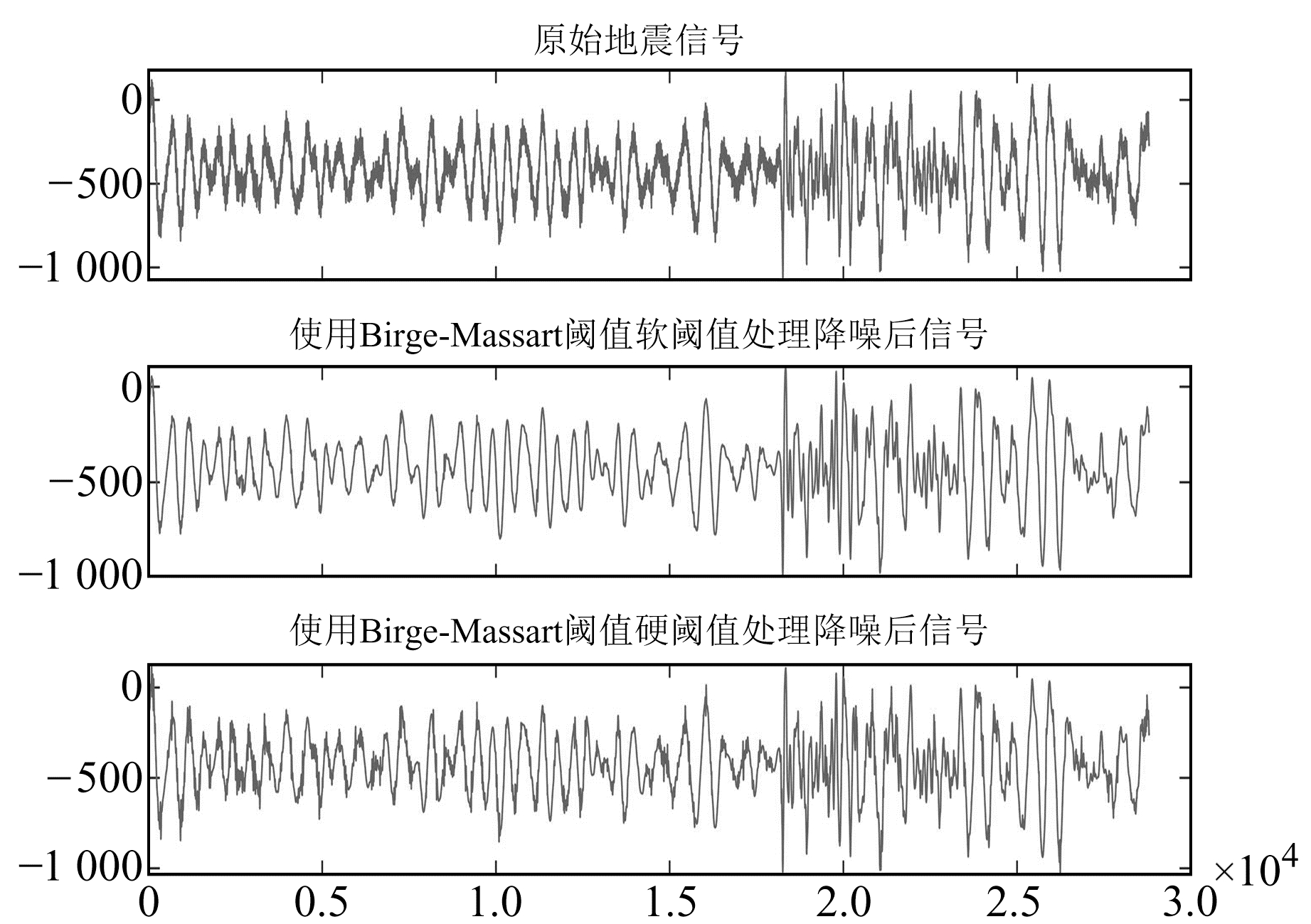
|
图 7 中强震Birge-Massart阈值软、硬阈值处理后数据与原始数据对比 Fig. 7 Comparison of the moderate-strong earthquake data processed by the Birge-Massart soft and hard thresholds and the original data |
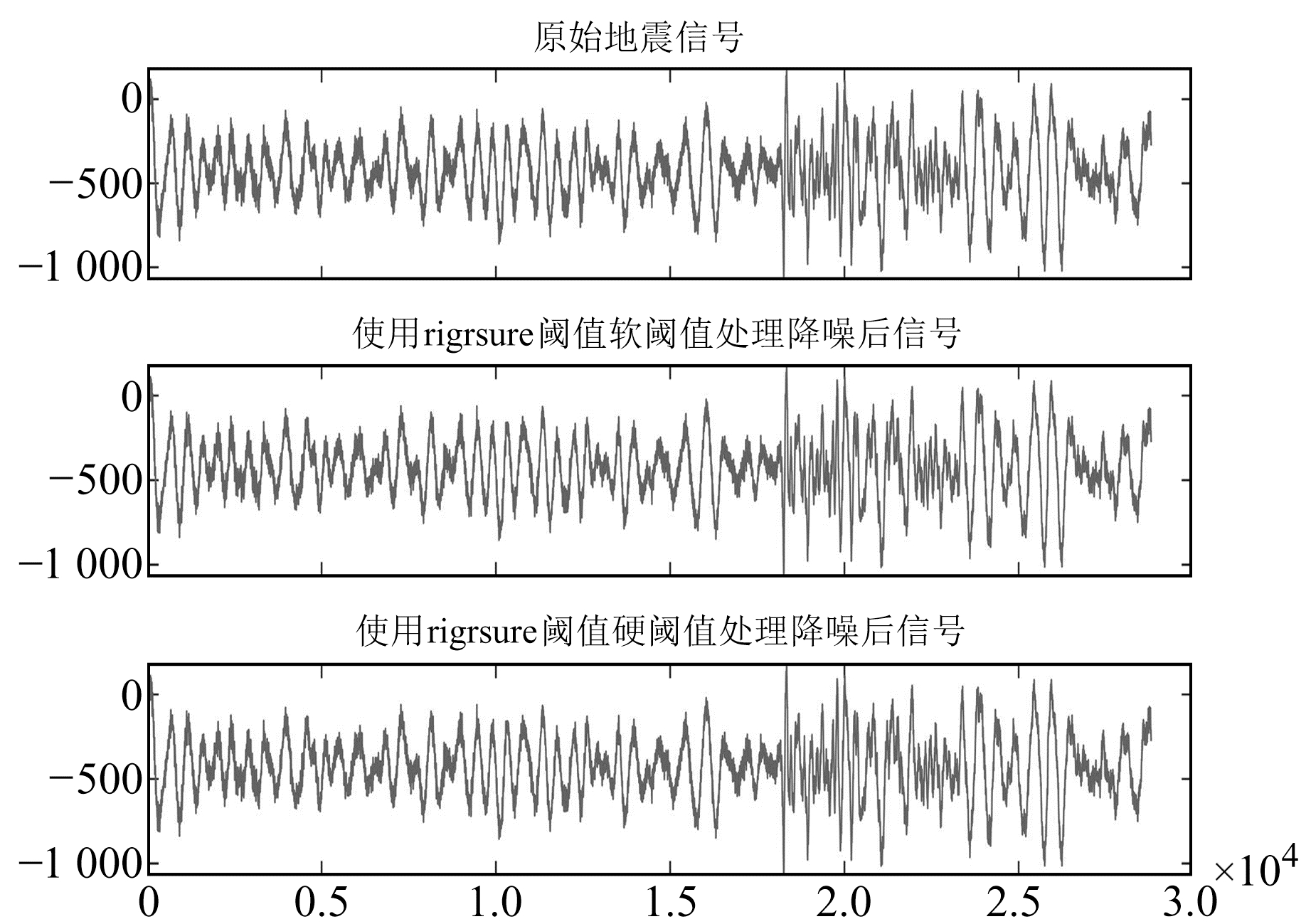
|
图 8 中强震rigrsure阈值软、硬阈值处理后数据与原始数据对比 Fig. 8 Comparison of the moderate-strong earthquake data processed by the rigrsure soft and hard thresholds and the original data |
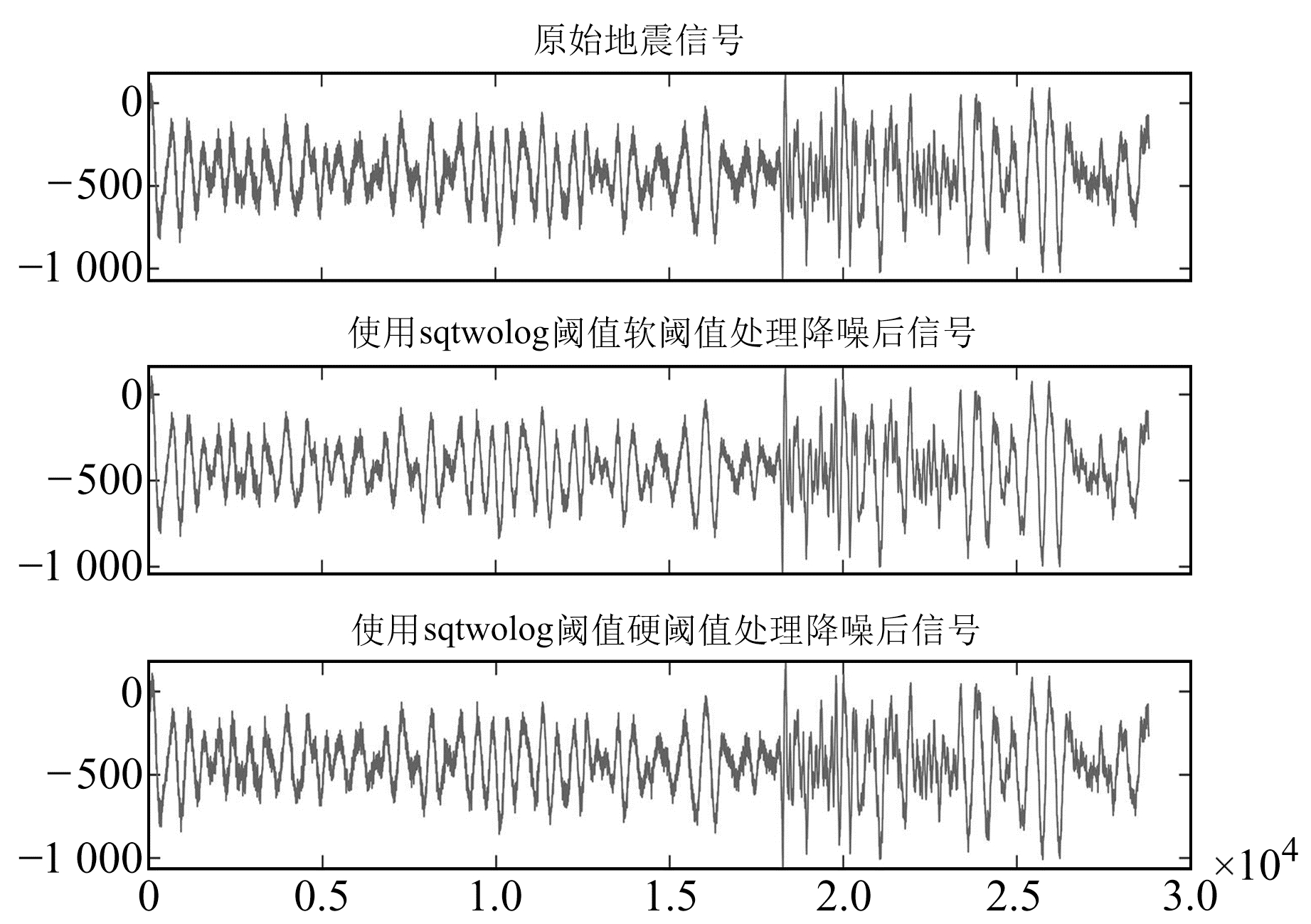
|
图 9 中强震sqtwolog阈值软、硬阈值处理后数据与原始数据对比 Fig. 9 Comparison of the moderate-strong earthquake data processed by the sqtwolog soft and hard thresholds and the original data |
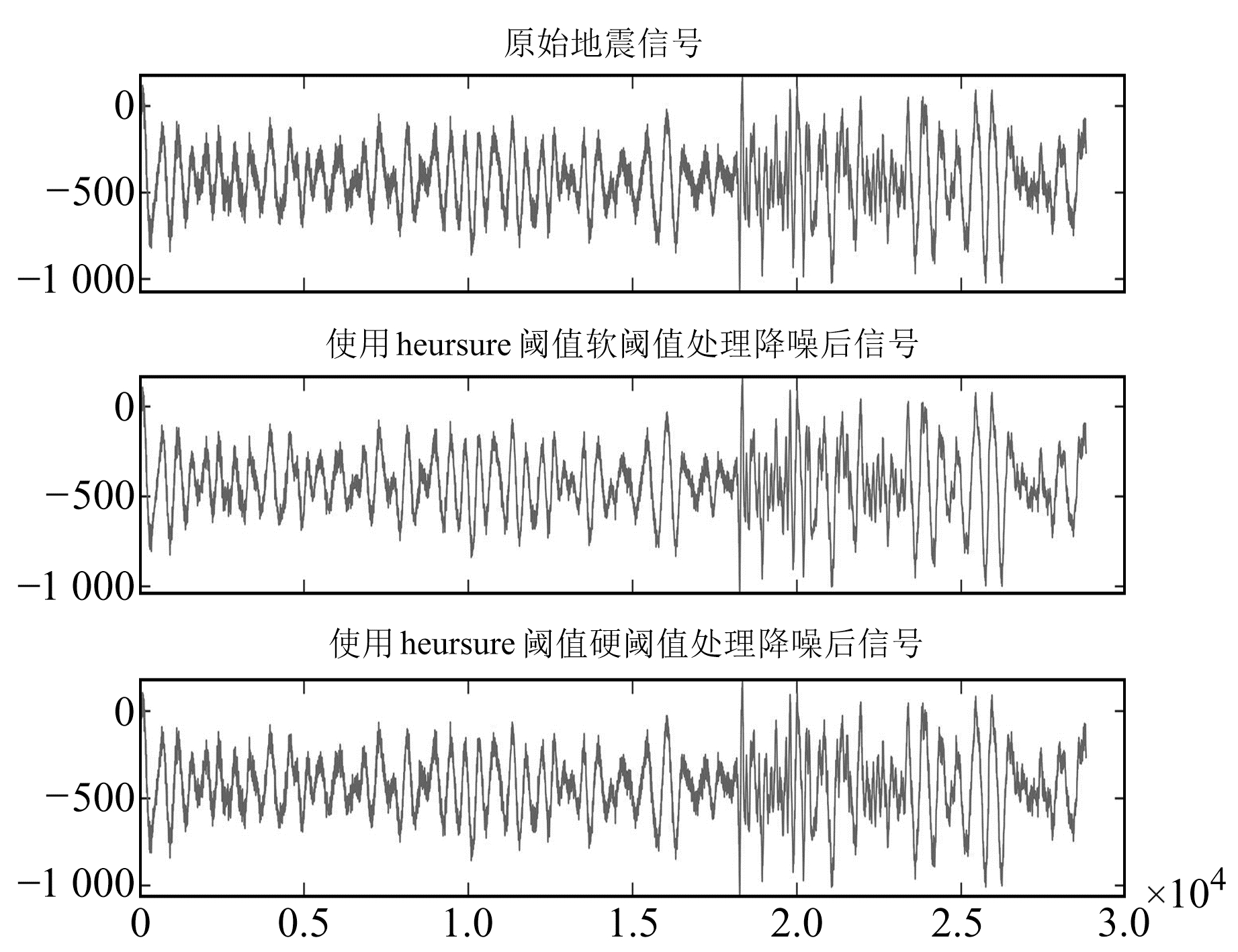
|
图 10 中强震heursure阈值软、硬阈值处理后数据与原始数据对比 Fig. 10 Comparison of the moderate-strong earthquake data processed by the heursure soft and hard thresholds and the original data |
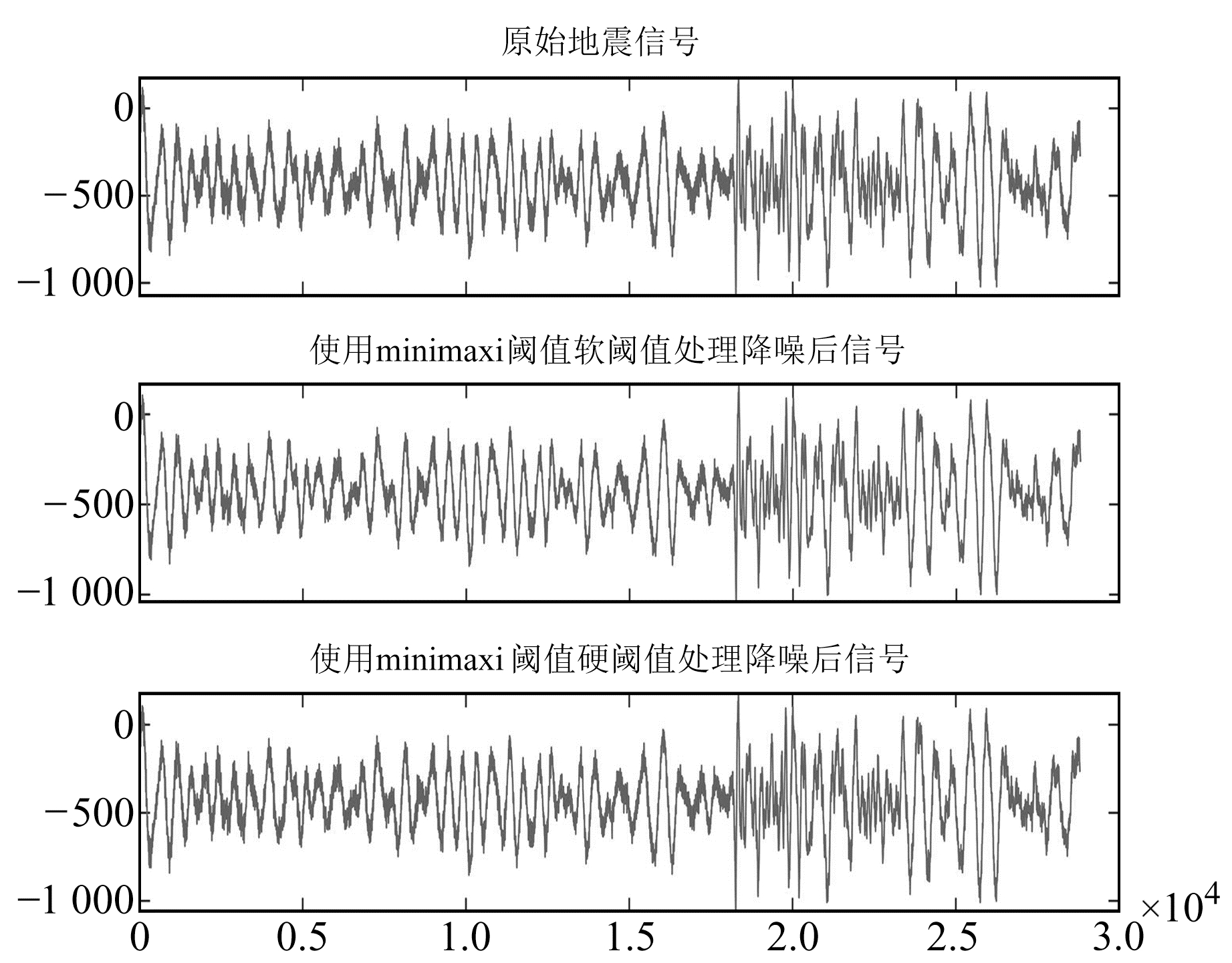
|
图 11 中强震minimaxi阈值软、硬阈值处理后数据与原始数据对比 Fig. 11 Comparison of the moderate-strong earthquake data processed by the minimaxi soft and hard thresholds and the original data |
图 12~13为小震与中强震采用Birge-Massart阈值去噪前后的频谱图对比。从图中可以看出,在采用相同的阈值进行去噪时,针对不同震级的地震会表现出不同的去噪效果。对于小震,Birge-Massart阈值不仅会将高频段信息去除,也同样会使低频段信息失真;对于中强震,Birge-Massart阈值可去除高频段中部分噪声,但会保留低频段的大部分有效信息。

|
图 12 小震信号所选数据及去噪后频谱 Fig. 12 Selected data of small earthquake signal and spectrum after denoising |
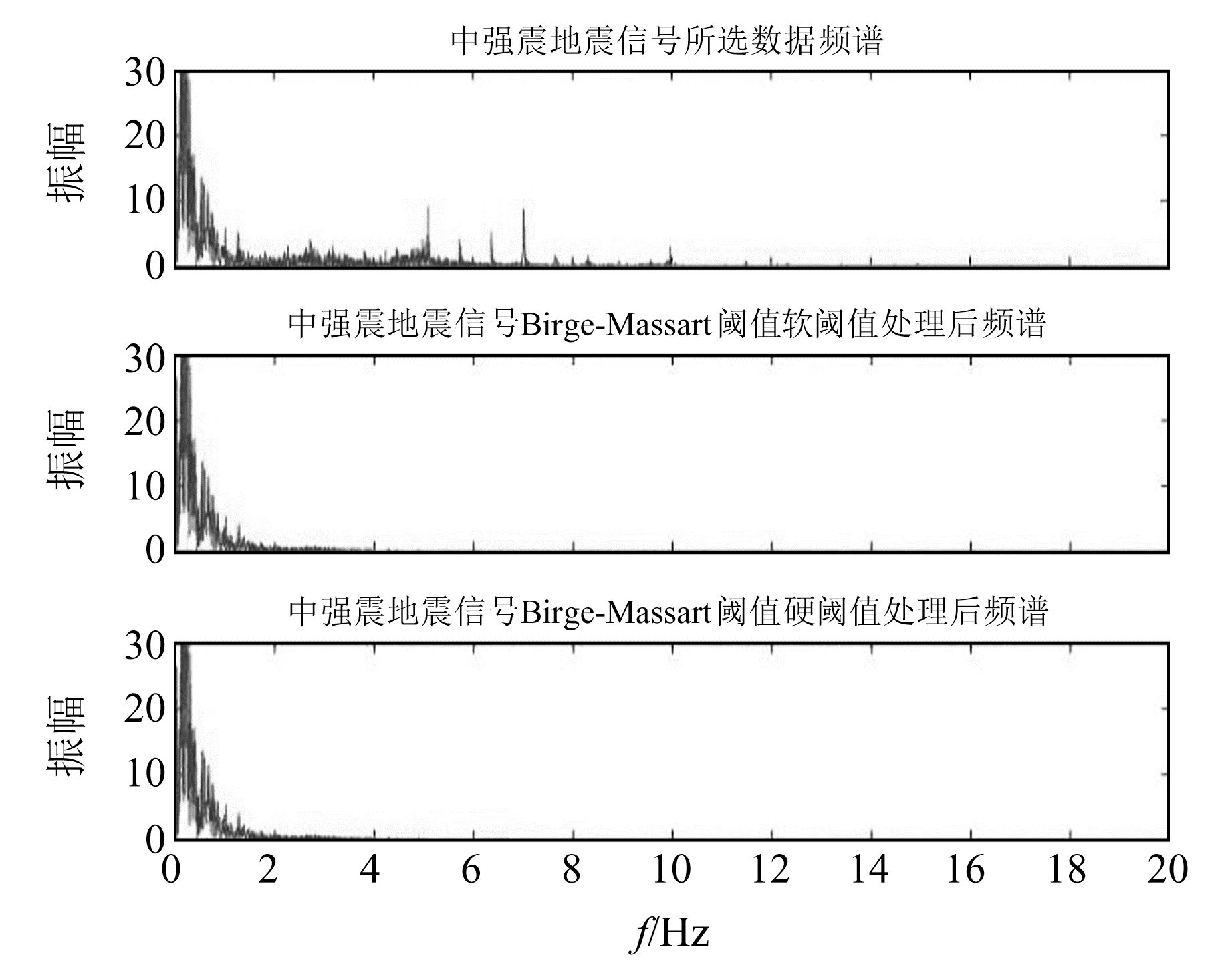
|
图 13 中强震所选数据及去噪后频谱 Fig. 13 Selected data of moderate-strong earthquake signal and spectrum after denoising |
计算中强震去噪后的评价指标,并对比软阈值与硬阈值处理的效果(表 8)。
|
|
表 8 中强震Birge-Massart小波阈值处理评价指标 Tab. 8 Evaluation index of medium-strong earthquake Birge-Massart wavelet threshold processing |
由表 8可以看出,在Birge-Massart小波软、硬阈值处理后相对SNR值、平均绝对误差及RMSE值都较为接近,但软阈值处理后的平滑度明显优于硬阈值,这也表明软阈值和硬阈值处理的特点:硬阈值函数在均方根误差上优于软阈值,软阈值函数处理后的重建信号比较光滑。综合各项指标来看,在Birge-Massart小波阈值去噪中,软阈值处理的效果比硬阈值好。
2.7 实际去噪后P波初动的判别探讨JCZ系列超宽频带地震仪在全国17个台站均有布设,地震仪的安置对背景噪声具有一定要求,因此这些地震仪采集到的地震数据中背景噪声均较小,从而使P波初动、S波与面波大部分都能被辨别出来。本文选取武汉水院地震台采集到的2017-01-16苏门答腊岛6.0级地震数据,原始数据中P波初动不明显,经过去噪后能够较好地判断出P波初动(图 14~15)。
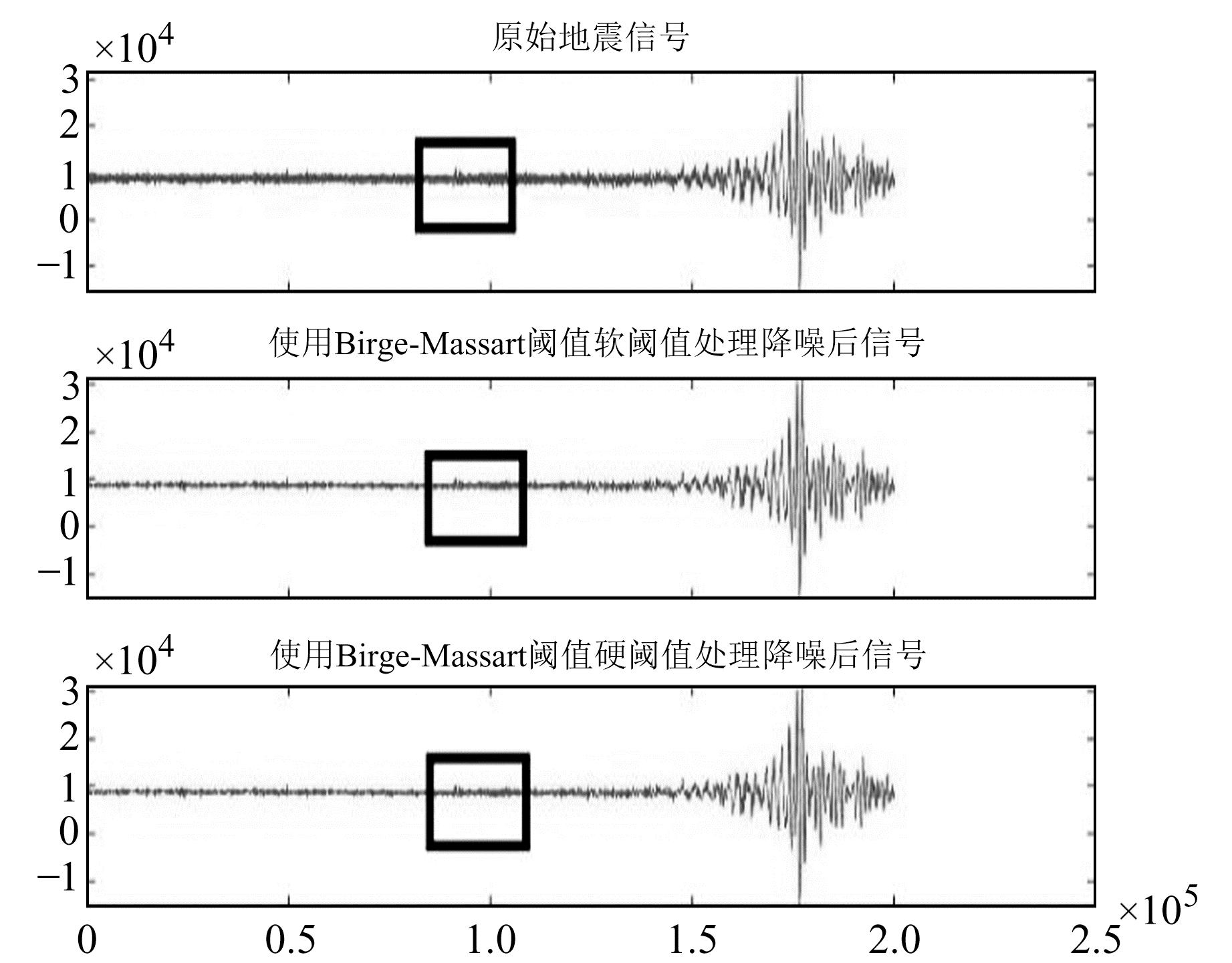
|
图 14 原始数据P波初动判别 Fig. 14 P wave first motion discrimination from original data |
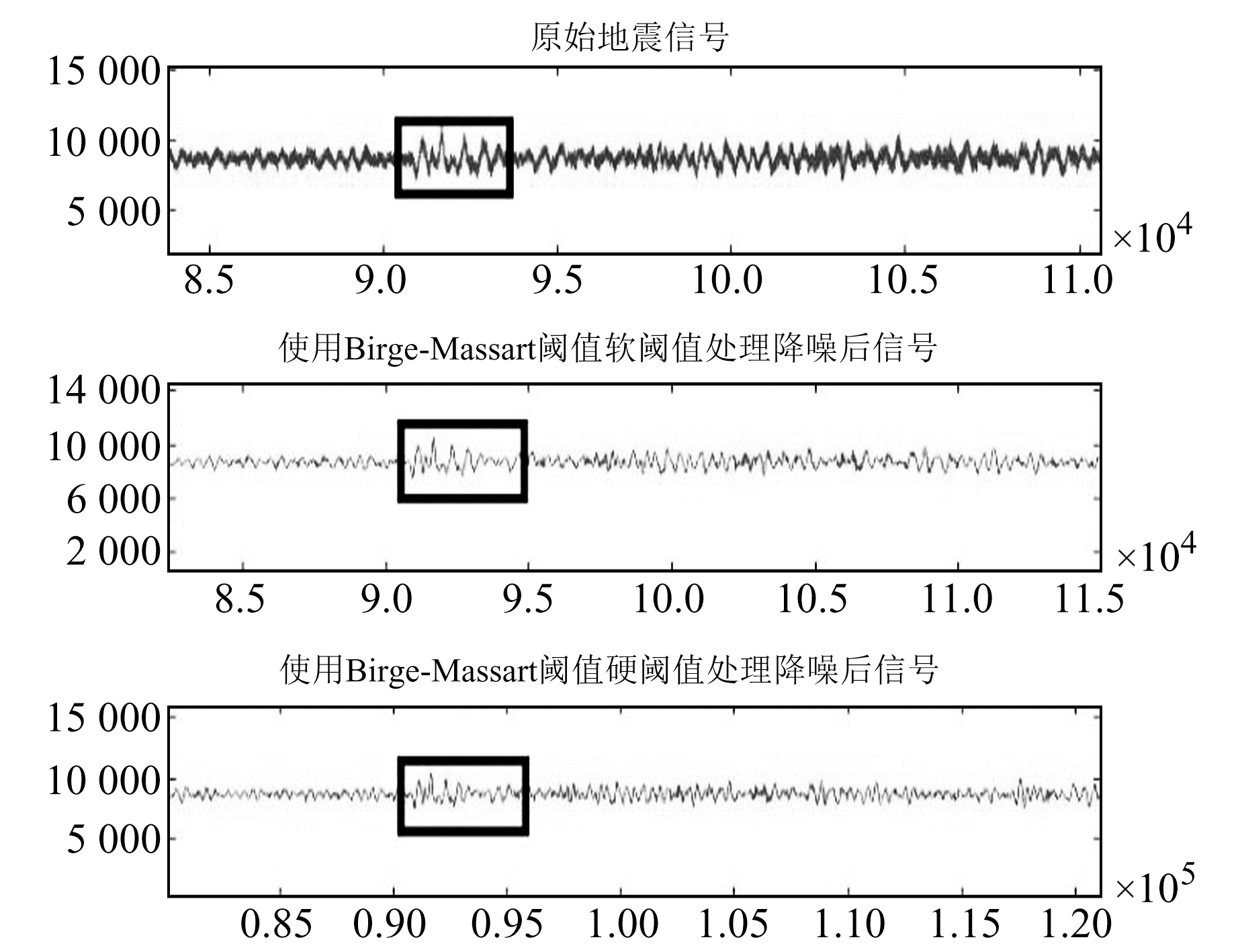
|
图 15 P波初动判别 Fig. 15 P wave first motion discrimination |
由图 14~15可知,在去噪之前,由于周围存在噪声,即使对信号作局部放大观察,也不能很好地判断P波初动的位置;但经过Birge-Massart阈值处理后,将P波初动周围的噪声进行压制,可以较好地观察出P波初动的位置,尤其是经过软阈值处理后效果更好。
3 结语本文使用控制变量法设置实验,对JCZ系列超宽频带地震仪采集到的地震数据采用小波阈值法进行去噪处理。去噪步骤可分为小波基选取、小波分解与重建尺度选取、阈值选取及阈值作用方式选取,并重点讨论小波去噪后信号评价指标的选取。对于原始信号中含有噪声的情况,单一的评价指标不能很好地判断去噪效果,需要多种指标联合评价。本文对于阈值处理方式仅分别讨论硬阈值与软阈值处理方法,其实也可将软、硬阈值结合起来进行数据比较分析,这也是后续研究的重点。通过对比相同方案下的去噪结果可知,在实际地震数据去噪中,基于样本估计选取的阈值具有一定局限性;在不同震级的地震中,相同阈值的去噪效果可能并不相同。在对P波初动不明显的地震数据进行去噪后发现,小波阈值去噪对于P波初动的判别具有一定意义。
| [1] |
皮誉洋, 周云耀, 吕永清. Morlet变换在超宽频带地震仪记录的汶川震前数据处理中的应用[J]. 大地测量与地球动力学, 2018, 38(9): 974-978 (Pi Yuyang, Zhou Yunyao, Lü Yongqing. Application of Morlet Transform in Pre-Earthquake Data Processing of Wenchuan Earthquake Recorded by Ultra Broadband Seismograph[J]. Journal of Geodesy and Geodynamics, 2018, 38(9): 974-978)
(  0) 0) |
| [2] |
蔡亚先, 吕永清, 周云耀, 等. JCZ-1超宽频带地震计[J]. 地壳形变与地震, 1995, 15(3): 1-8 (Cai Yaxian, Lü Yongqing, Zhou Yunyao, et al. JCZ-1 Ultra Broadband Seismometer[J]. Crustal Deformation and Earthquake, 1995, 15(3): 1-8)
(  0) 0) |
| [3] |
段瑞敏. 基于小波变换的地震信号降噪技术研究[D]. 武汉: 中国地震局地震研究所, 2016 (Duan Ruimin.Research on Seismic Signal Denoising Technology Based on Wavelet Transform[D]. Wuhan: Institute of Seismology, CEA, 2016)
(  0) 0) |
| [4] |
董长虹. Matlab小波分析工具箱原理与应用[M]. 北京: 国防工业出版社, 2004 (Dong Changhong. Matlab Wavelet Analysis Toolbox Principle and Application[M]. Beijing: National Defense Industry Press, 2004)
(  0) 0) |
| [5] |
何思源, 李贵元, 刘华姣, 等. 最优小波基选择法在测震数据干扰处理中的研究与应用[J]. 华南地震, 2019, 39(3): 49-56 (He Siyuan, Li Guiyuan, Liu Huajiao, et al. Application and Research of Optimal Wavelet Base Selection Method in Seismic Data Processing[J]. South China Journal of Seismology, 2019, 39(3): 49-56)
(  0) 0) |
| [6] |
陶珂, 朱建军. 多指标融合的小波去噪最佳分解尺度选择方法[J]. 测绘学报, 2012, 41(5): 749-755 (Tao Ke, Zhu Jianjun. A Hybrid Indicator for Determining the Best Decomposition Scale of Wavelet Denoising[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 749-755)
(  0) 0) |
| [7] |
张春蕾. 变形信号的去噪方法与去噪效果评价指标改进[J]. 浙江测绘, 2010(1): 13-14 (Zhang Chunlei. Denoising Method of Deformation Signal and Improvement of Denoising Effect Evaluation Index[J]. Zhejiang Surveying and Mapping, 2010(1): 13-14)
(  0) 0) |
| [8] |
朱建军, 章浙涛, 匡翠林, 等. 一种可靠的小波去噪质量评价指标[J]. 武汉大学学报: 信息科学版, 2015, 40(5): 688-694 (Zhu Jianjun, Zhang Zhetao, Kuang Cuilin, et al. A Reliable Evaluation Indicator of Wavelet De-Noising[J]. Geomatics and Information Science of Wuhan University, 2015, 40(5): 688-694)
(  0) 0) |
| [9] |
文鸿雁. 基于小波理论的变形分析模型研究[D]. 武汉: 武汉大学, 2004 (Wen Hongyan. Research on Deformation Analysis Model Based on Wavelet Transform Theory[D]. Wuhan: Wuhan University, 2004)
(  0) 0) |
| [10] |
柳建新, 韩世礼, 马捷. 小波分析在地震资料去噪中的应用[J]. 地球物理学进展, 2006, 21(2): 541-545 (Liu Jianxin, Han Shili, Ma Jie. Application of Wavelet Analysis in Seismic Data Denoising[J]. Progress in Geophysics, 2006, 21(2): 541-545)
(  0) 0) |
| [11] |
李艳飞, 秦飞龙, 周仲礼. 改进的小波变换算法在地震数据降噪处理中的应用[J]. 软件, 2013, 34(6): 40-43 (Li Yanfei, Qin Feilong, Zhou Zhongli. Application of Improved Wavelet Transformation Algorithm in Seismic Data Denoising[J]. Computer Engineering and Software, 2013, 34(6): 40-43)
(  0) 0) |
| [12] |
安蕴. 基于MATLAB的小波分析用于地震信号的去噪研究[D]. 太原: 中北大学, 2012 (An Yun.MATLAB-Based Wavelet Analysis for Seismic Signal Denoising Research[D]. Taiyuan: North University of China, 2012)
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41


