基坑沉降变形的影响因素包括地下水位、土体强度、围护结构特征和施工方法等[1],这些影响因素存在无法定量分析、时序性强和随机性高等特点[2]。由于多重影响因素同时作用于基坑工程,基坑沉降呈现非线性和非稳态性特征,因此精确预测基坑沉降较为困难。传统预测方法存在诸多局限性[3],时间序列方法要求监测数据平稳以及符合正态分布;神经网络模型对监测数据量的需求较大,并且容易收敛于局部最小值。
支持向量机(support vector machine, SVM)作为常用的变形预测模型,在处理高维数据、非线性问题上具有良好的鲁棒性和泛化能力[4]。针对SVM模型存在参数选择困难的问题,提出采用粒子群算法对SVM模型进行参数寻优处理。粒子群算法(particle swarm optimization, PSO)、鱼群算法和蚁群算法是主要的三大寻优算法[5],其中鱼群算法收敛速度较慢,蚁群算法容易陷入局部最优和难以解决连续域问题,而PSO算法具有搜索效率高、控制参数少和收敛性能好的优点[6]。
经过PSO优化的SVM模型广泛应用于基坑变形监测、特征自动提取和机器故障诊断等领域。赵艳楠等[7]通过PSO-SVM模型选取合适的滑坡变形影响因子来确定样本数据集,通过属性约简对样本数据的粗差和干扰属性进行剔除;文献[8]采用PSO算法优化SVM模型的补偿参数和核函数,并将其应用于油井井下工况特征的自动提取;文献[9]基于多流形学习组合PSO算法来优化SVM参数,组合算法具有良好的机器故障诊断能力。而当前的基坑沉降预测模型普遍存在以下不足[10]:1)基坑沉降变形的影响因素众多,而绝大多数因素不能进行定量和定性分析;2)大多数模型都是基于单点数据建模,未考虑其他影响因素;3)未对预测模型的最优样本数据进行分析。针对上述缺点,本文提出在最优样本下建立顾及邻近点的改进PSO-SVM模型,组合多尺度一维小波分解函数和柯西分布函数来改进PSO-SVM模型,并成功应用于基坑沉降预测。顾及邻近点的改进PSO-SVM模型能及时有效地作出预警,对基坑工程的安全运营具有重要作用。
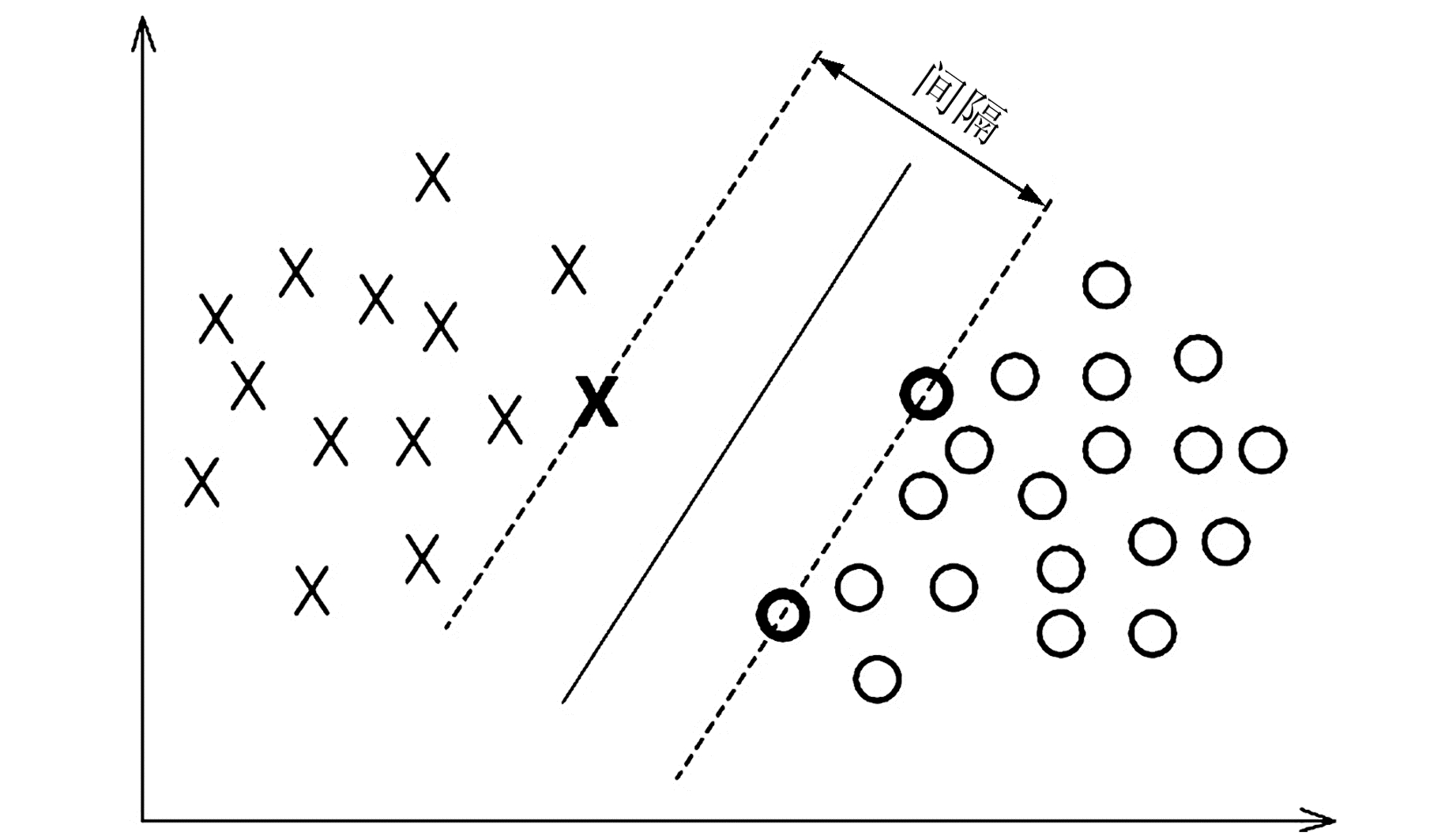
1 基本原理 1.1 SVM模型SVM作为基坑沉降变形预测的常用模型,其原理是对给定的样本数据进行分类,通过确定决策边界来实现数据的归类处理。为了使分类精准度最高,需要通过某种衡量方式确定一条最好的决策边界(图 1),称为最大边界[11]。
|
图 1 决策边界示意图 Fig. 1 Diagram of decision boundary |
寻找最大边界的衡量方式称为最大间隔分类器,其目标函数可定义为
| $ {y_i}\left( {{\mathit{\boldsymbol{\omega }}^{\rm{T}}}{x_i} + b} \right) = {\hat \gamma _i} > \hat \gamma ,i = 1, \cdots ,n $ | (1) |
可知,其导出的内容为约束条件。其中几何间隔可定义为:
| $ \tilde \gamma = y\gamma = \frac{{\hat \gamma }}{{\left\| \mathit{\boldsymbol{\omega }} \right\|}} $ | (2) |
令
| $ \max \frac{1}{\|\boldsymbol{\omega}\|}, y_{i}\left(\boldsymbol{\omega}^{\mathrm{T}} x_{i}+b\right) \geqslant 1, i=1, \cdots, n $ | (3) |
在约束条件yi(ωTxi+b)≥1, i=1, …, n中,将1/‖ω‖数值最大化,则1/‖ω‖为几何间隔
| $ \min \frac{1}{2}\|\boldsymbol{\omega}\|^{2}, y_{i}\left(\boldsymbol{\omega}^{\mathrm{T}} x_{i}+b\right) \geqslant 1, i=1, \cdots, n $ | (4) |
通过给每个约束条件附加一个拉格朗日乘子α来定义拉格朗日函数:
| $ L(\boldsymbol{\omega}, b, \alpha)=\frac{1}{2}\|\boldsymbol{\omega}\|^{2}-\sum\limits_{i=1}^{n} \alpha_{i}\left(y_{i}\left(\boldsymbol{\omega}^{\mathrm{T}} x_{i}+b\right)-1\right) $ | (5) |
将拉格朗日函数L(ω, b, α)分别对ω和b求偏导[10],并且将偏导得到的结果代入原式可得:
| $ {\min \frac{1}{2}\sum\limits_{n = 1}^N {\sum\limits_{m = 1}^N {{\alpha _n}} } {\alpha _m}{y_i}{y_j}\left( {{x_i} \cdot {x_j}} \right) - \sum\limits_{i = 1}^N {{\alpha _i}} } $ | (6) |
| $ {{\rm{ s}}{\rm{. t}},\sum\limits_{i = 1}^N {{\alpha _i}} {y_i} = 0,{\alpha _i} \ge 0,i = 1, \cdots ,N} $ | (7) |
粒子群优化算法来源于生物种群的行为特征[12],算法的粒子速度随着适应度值进行动态调整,可完成粒子的寻优求解。PSO优化算法可改进SVM模型中的正则化学习因子c与核参数g。
在D维空间中,包含n个粒子的种群X=(X1, X2, …, Xn),第i个粒子表示D维向量空间Xi=[xi1, xi2, …, xiD]T,根据目标函数可计算得到每个粒子位置Xi对应的适应度值。第i个粒子的速度Vi=[Vi1, Vi2, …, ViD]T,个体极值Pi=[Pi1, Pi2, …, PiD]T,其种群的全局极值Pg=[Pg1, Pg2, …, PgD]T。粒子群的更新公式为:
| $ {V_{id}^{k + 1} = \omega V_{id}^k + {c_1}{r_1}\left( {P_{id}^k - X_{id}^k} \right) + {c_2}{r_2}\left( {P_{gd}^k - X_{id}^k} \right)} $ | (8) |
| $ {X_{id}^{k + 1} = X_{id}^k + V_{id}^{k + 1}} $ | (9) |
式中,w是惯性权重,k为迭代次数,Vid为粒子速度,c1和c2为加速度因子,r1和r2为[0, 1]之间的随机数。w影响着粒子群的全局和局部搜索能力,而PSO-SVM模型存在w为固定值的缺点。
1.3 改进的PSO-SVM模型针对PSO-SVM模型w为固定值的缺点,提出改进的PSO-SVM(improved PSO-SVM, IPSO-SVM)模型,算法设计包括:1)引入标准柯西分布公式对惯性权重的取值进行改进;2)采用一维小波分解函数对样本数据进行粗差检验和去噪处理;3)确定适应度函数;4)初始化种群和速度;5)计算适应度函数;6)适应度标定;7)速度更新和个体更新;8)输出最优解。流程如图 2所示。

|
图 2 IPSO-SVM模型结构流程 Fig. 2 Flow chart of the IPSO-SVM model |
1) 引入标准柯西分布密度函数对惯性权重w进行改进,可克服w为固定值的缺点。柯西分布密度函数[13]能够在算法前期取较大的w值,以提高算法的全局搜索能力;在后期取较小的w值,以提高算法的局部搜索能力:
| $ w = \gamma p(x) = \frac{1}{{{\rm{ \mathsf{ π} }}\left( {1 + {x^2}} \right)}} $ | (10) |
2) 针对基坑沉降监测的样本数据具有随机性和非平稳性的特点[14],本文采用小波分解函数对样本数据进行粗差检验和去噪处理。小波分解函数的阈值取[C, L]=wavedec(y, 3, ‘sym4’),其中C为分解结构变量,L为样本数据长度变量,y为样本数据,分解层数为3次,小波类型为sym4。
3) 随机初始化粒子位置和粒子速度,并根据适应度函数计算粒子适应度值。设置PSO算法的运行参数,包括迭代次数和种群规模以及个体和速度的最大最小值。
4) 迭代寻优。首先进行粒子位置和速度更新,然后根据新粒子的适应度值进行个体极值和群体极值更新。
5) 最优解计算。yi(ωTxi+b)≥1, i=1, …, n为约束条件,目标函数为:
| $ \min \frac{1}{2}{\left\| \mathit{\boldsymbol{\omega }} \right\|^2},{y_i}\left( {{\mathit{\boldsymbol{\omega }}^{\rm{T}}}{x_i} + b} \right) \ge 1,i = 1, \cdots ,n $ | (11) |
利用拉格朗日乘子法对ω和b求偏导,进行最优解求取,求解公式为:
| $ \begin{array}{*{20}{l}} {\min \frac{1}{2}\sum\limits_{n = 1}^N {\sum\limits_{m = 1}^N {{\alpha _n}} } {\alpha _m}{y_i}{y_j}\left( {{x_i} \cdot {x_j}} \right) - \sum\limits_{i = 1}^N {{\alpha _i}} }\\ {{\rm{ s}}{\rm{.t}}{\rm{. }}\sum\limits_{i = 1}^N {{\alpha _i}} {y_i} = 0,{\alpha _i} \ge 0,i = 1, \cdots ,N} \end{array} $ | (12) |
深圳市地铁轨道交通13号线长约22.45 km,全程为地下线。13号线基坑工程重点监测对象包括基坑周围地表土体沉降、基坑周边地下水位、基坑支撑轴力、基坑南北端头井和标准段桩体位移以及周边建构筑物沉降。桩体水平位移监测是在围护桩钢筋上安装PVC测斜管,采用测斜仪进行监测。桩顶水平位移监测是根据现场通视情况采用坐标法进行。桩顶、建筑物、地表、管线、立柱的竖向位移监测是通过联测监测点之间的二等水准闭(附)合线路,由线路的工作点来测量各监测点的高程。
本节实验选取13号线留仙洞站基坑工程2号监测轴中一组邻近监测点DBC-02-1、DBC-02-2和DBC-02-3在2019-04-29~10-14期间的150期数据进行基坑沉降研究。实验包括模型最优训练样本数量研究、顾及邻近点的PSO-SVM模型和顾及邻近点的改进PSO-SVM模型研究。研究过程分为20期短期样本、50期中短期样本、100期中长期样本和150期长期样本,分别采用数据的前90%作为建模的训练数据集,通过对比模型的预测结果与后10%的数据来验证预测精度。样本数据分类见表 1。
|
|
表 1 训练和验证样本数量对比 Tab. 1 Comparison of training and validation sample size |
针对大多数传统预测模型未进行最优训练样本研究的缺点,本文提出在短期样本数量20期、中短期样本数量50期、中长期样本数量100期和长期样本数量150期情况下,选取PSO-SVM模型进行最优训练样本寻求实验。选取均方差、平均相对误差和最佳适应度值作为评定指标。适应度函数求解的均方误差值为最佳适应度值,数值越大精度越高[15]。预测精度对比见表 2。
|
|
表 2 不同样本数量下的预测精度对比 Tab. 2 Accuracy comparison under different sample size |
由表 2预测结果可知,在50期数据条件下,平均相对误差为5.5%,预测结果精度不佳;随着数据量增加到100期和150期,预测结果的均方差和平均相对误差趋于稳定,拟合效果一般;而在短期20期数据条件下,PSO-SVM模型的预测性能最优。
2.2 顾及邻近点的PSO-SVM模型针对传统PSO-SVM模型基于单点数据建模未考虑其他影响因素的缺点,本文通过相关性分析发现,时间、历史数据和邻近点沉降变形值与监测数据存在较强关联性,因此引入邻近点等相关因素建立PSO-SVM模型。其中相关性分析见表 3和表 4。
|
|
表 3 相邻监测点间的相关系数 Tab. 3 Correlation coefficient between the adjacent monitoring point |
|
|
表 4 历史数据之间的相关系数 Tab. 4 Correlation coefficient between historical data |
从表 3可以看出,3个监测点的相关系数均在0.87以上,表明3个监测点之间存在较强关联性,因此选取一组3个监测点进行沉降规律研究。
从表 4可以看出,DBC-02历史数据之间的相关系数在0.89以上,表明沉降数据和历史数据之间存在较强关联性,因此可通过研究历史数据来分析沉降规律。
综上分析可知,基坑沉降的变形时间、历史数据和邻近点都是影响沉降变形的相关因素。建立顾及邻近点的PSO-SVM模型,预测分析结果对比见表 5。
|
|
表 5 3种模型预测结果对比 Tab. 5 Comparison of prediction results of three models |
由表 5可知,顾及双因素的PSO-SVM模型的预测效果优于单因素的PSO-SVM模型,顾及邻近点的PSO-SVM模型的均方差、平均相对误差和最佳适应度值3项精度指标均最优。均方差从0.175 mm2优化至0.039 mm2,平均相对误差从5.455%减少至2.663%。因此本文顾及邻近点建立的PSO-SVM模型不仅考虑了实际的影响因子,而且可优化模型的拟合性能。
为研究不同样本数据量对顾及邻近点的PSO-SVM模型拟合精度的影响,本文设计20期、50期和100期数据下三因素的模型对比实验。预测结果见表 6。
|
|
表 6 3种样本数量下模型预测结果对比 Tab. 6 Comparison of prediction results under three sample sizes |
由表 6可知,顾及邻近点的PSO-SVM模型适用于短期样本下的模型拟合预测,在短期样本数据下模型的拟合效果最佳,而该模型在中长期样本数据下存在预测精度不佳和后期趋同性强的缺点。
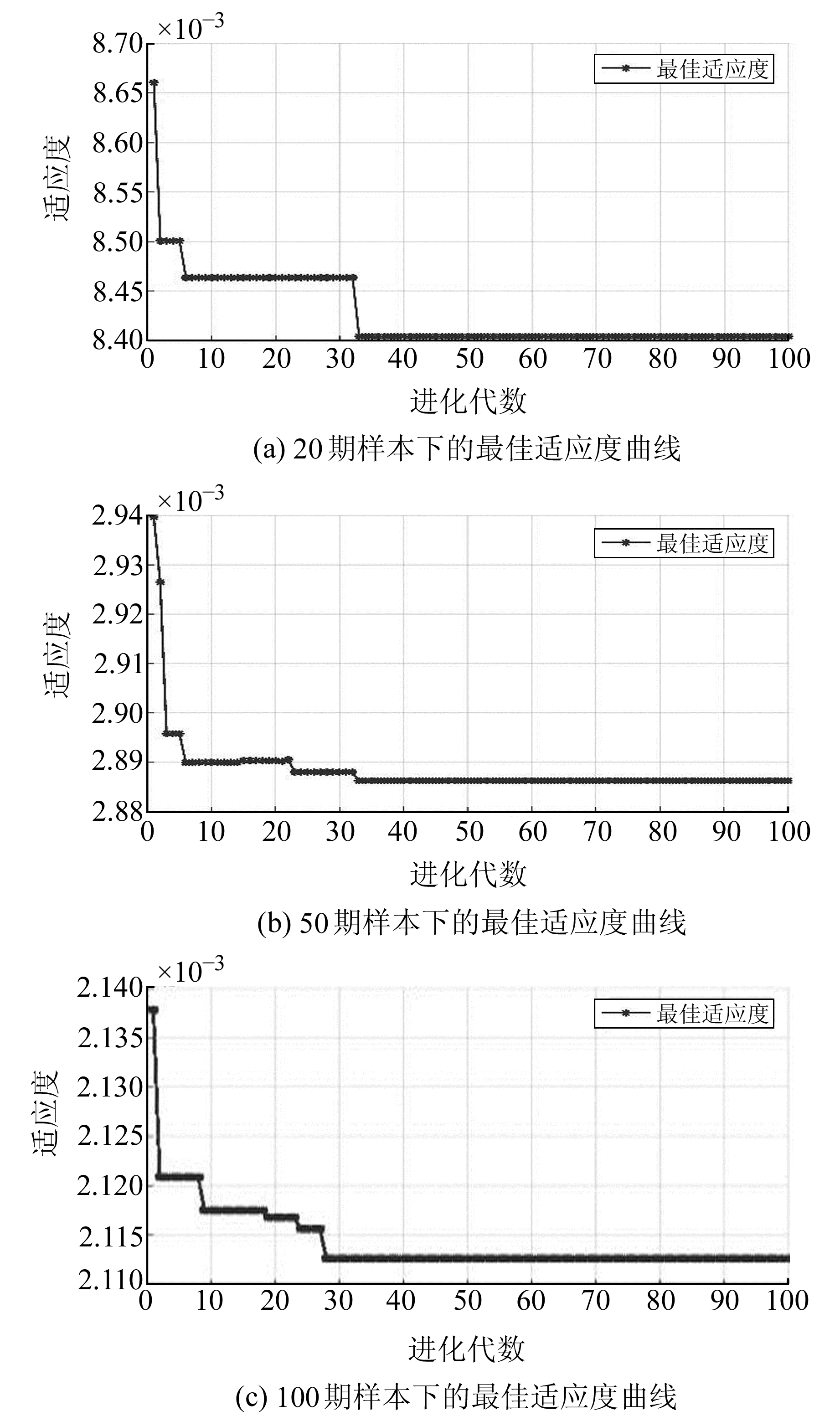
图 3为3种样本数量下的最佳适应度曲线,由图可知,3次拟合的训练程度合适,其中20期样本下拟合效果最好,最佳适应度值为0.008;而50期和100期的最佳适应度值分别为0.003和0.002。
|
图 3 3种样本数量下的最佳适应度曲线 Fig. 3 Best fitness curves under three kinds of sample size |
由此可知,顾及邻近点的PSO-SVM模型不适用于中长期样本数据下的拟合预测,需要针对该缺陷作进一步的算法改进。
2.3 顾及邻近点的改进PSO-SVM模型针对顾及邻近点的PSO-SVM模型在中长期样本数据下预测精度不佳的缺点,本文提出组合多尺度一维小波分解函数和柯西分布函数改进顾及邻近点的PSO-SVM模型。沉降变形量的时间序列曲线是一种连续的一维渐变模型,当样本数据中存在测量粗差时会导致时间序列严重失真,因此本文采用多尺度一维小波分解函数对样本数据进行粗差检验和平滑处理。粒子群算法在前期全局搜索能力较弱,在后期缺乏局部搜索能力,针对该缺点引入柯西分布密度函数对惯性权重w的取值进行改进。柯西分布密度函数能够在算法前期取较大的w值,提高算法的全局搜索能力;在后期取较小的w值,提高算法的局部搜索能力。
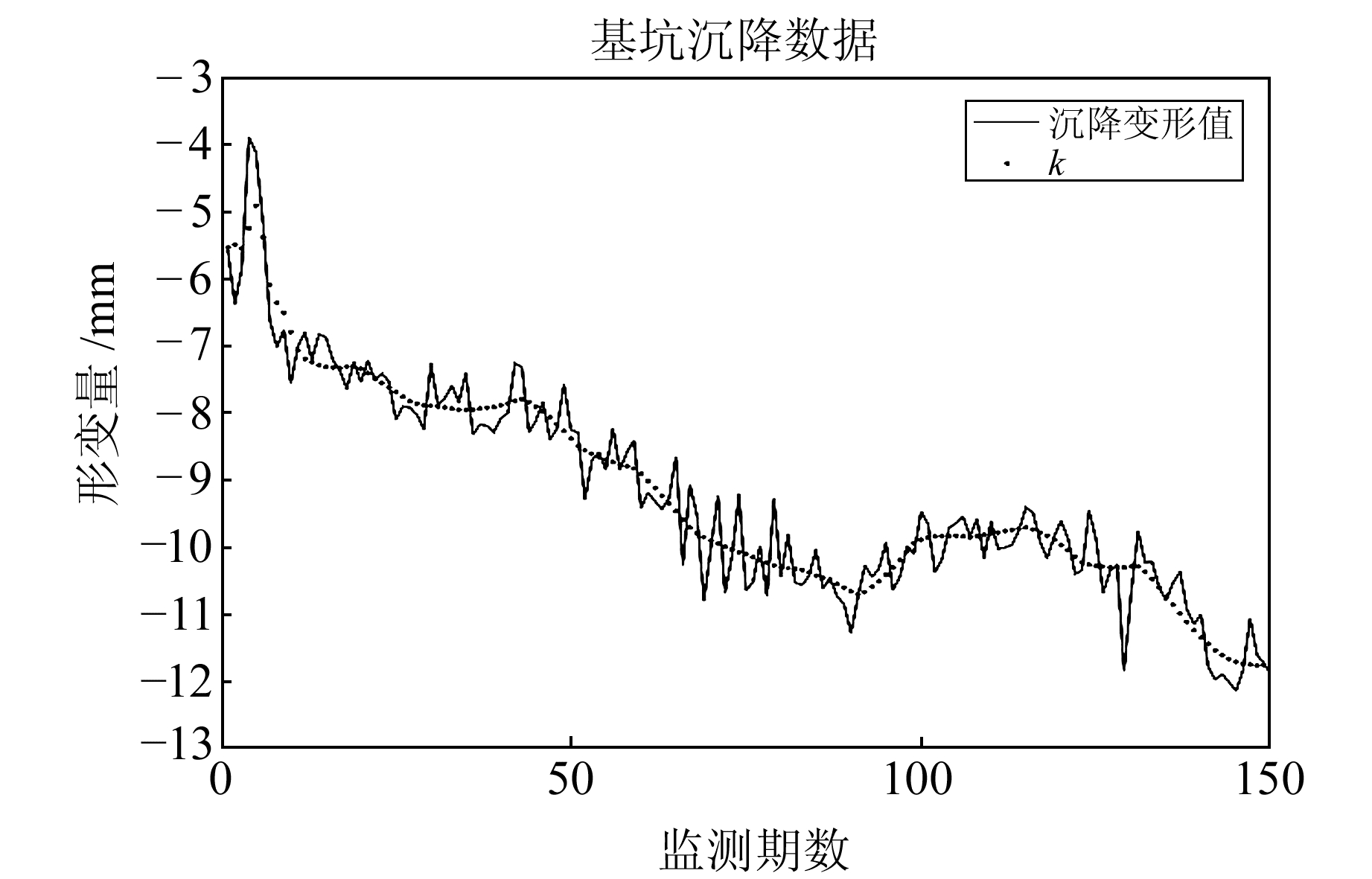
为验证顾及邻近点的IPSO-SVM模型在不同样本数量下的适应性和有效性,分别设计在20期、50期和100期样本条件下的拟合实验,前90%的样本为训练数据,后10%为验证样本。实验过程直到函数分解3次时其细节分量周期满足精度要求,其中多小波分解效果如图 4所示。预测精度对比见表 7和表 8。
|
图 4 小波分解效果 Fig. 4 Wavelet decomposition effect |
|
|
表 7 3种样本数量下模型的均方根误差对比 Tab. 7 Comparison of root mean square errors under three sample sizes |
|
|
表 8 3种样本数量下模型的平均相对误差对比 Tab. 8 Comparison of mean relative errors under three sample sizes |
由表 7和表 8可知,在样本数据从短期增加至长期的过程中,顾及邻近点的PSO-SVM模型的预测精度呈现逐渐降低的趋势;而改进的模型预测结果的均方根误差趋于稳定,约为0.08 mm2,平均相对误差逐渐变小。在不同样本期数下,改进的模型预测结果的均方根误差平均减小85.1%,平均相对误差减小84.7%。顾及邻近点的IPSO-SVM模型中多尺度一维小波分解函数能够平滑样本数据,柯西分布密度函数可提升PSO-SVM模型的全局搜索能力和局部搜索能力,改进的模型适用于不同样本条件下的变形预测,且预测精度更高。
3 结语基坑沉降模型是一个不等时的复杂非线性模型,为及时有效地对沉降变形作出预警,本文对顾及邻近点的PSO-SVM模型与顾及邻近点的IPSO-SVM模型为主体的基坑沉降变形预测建模进行研究。具体研究内容如下:
1) 针对传统模型未对最优训练样本数据量进行研究的缺点,选取PSO-SVM模型在4种不同样本数量情况下的结果进行分析。实验结果表明,在20期数据条件下,PSO-SVM模型的拟合性能最优。
2) 针对传统PSO-SVM模型基于单点数据建模的缺点,引入时间、历史数据和邻近点沉降变形值改进PSO-SVM模型。结果表明,在最佳训练样本数据下,顾及邻近点的PSO-SVM模型优于单因素的PSO-SVM模型,且在短期样本数据下拟合效果最佳,但不适用于中长期样本数据下的拟合预测。
3) 针对顾及邻近点的PSO-SVM模型在中长期样本数据下预测精度不佳的缺点,本文提出组合多尺度一维小波分解函数和柯西分布函数改进顾及邻近点的PSO-SVM模型。研究结果表明,在不同样本期数下,顾及邻近点的IPSO-SVM模型预测结果的均方根误差平均减小85.1%,平均相对误差减小84.7%,表明其适应性强、拟合精度高。
| [1] |
冯腾飞, 刘小生, 钟钰, 等. 基于IABC优化LSSVR的变形预测研究[J]. 大地测量与地球动力学, 2019, 39(1): 98-102 (Feng Tengfei, Liu Xiaosheng, Zhong Yu, et al. Research on Deformation Prediction Based on LSSVR Optimized by IABC[J]. Journal of Geodesy and Geodynamics, 2019, 39(1): 98-102)
(  0) 0) |
| [2] |
袁志明, 李沛鸿, 钟亮, 等. 基于LSTM-GM神经网络模型的深基坑沉降变形预测[J]. 江西理工大学学报, 2020, 41(1): 8-14 (Yuan Zhiming, Li Peihong, Zhong Liang, et al. Settlement Deformation Prediction of Deep Foundation Pit Based on LSTM-GM Neural Network Model[J]. Journal of Jiangxi University of Science and Technology, 2020, 41(1): 8-14)
(  0) 0) |
| [3] |
刘贺, 张弘强, 刘斌. 基于粒子群优化神经网络算法的深基坑变形预测方法[J]. 吉林大学学报: 地球科学版, 2014, 44(5): 1 609-1 614 (Liu He, Zhang Hongqiang, Liu Bin. A Prediction Method for the Deformation of Deep Foundation Pit Based on the Particle Swarm Optimization Neural Network[J]. Journal of Jilin University: Earth Science Edition, 2014, 44(5): 1 609-1 614)
(  0) 0) |
| [4] |
刘江华, 程君实, 陈佳品. 支持向量机训练算法综述[J]. 信息与控制, 2002, 31(1): 45-50 (Liu Jianghua, Cheng Junshi, Chen Jiapin. Support Vector Machine Training Algorithm: A Review[J]. Information and Control, 2002, 31(1): 45-50)
(  0) 0) |
| [5] |
李素, 袁志高, 王聪, 等. 群智能算法优化支持向量机参数综述[J]. 智能系统学报, 2018, 13(1): 70-84 (Li Su, Yuan Zhigao, Wang Cong, et al. Optimization of Support Vector Machine Parameters Based on Group Intelligence Algorithm[J]. CAAI Transactions on Intelligent Systems, 2018, 13(1): 70-84)
(  0) 0) |
| [6] |
Li G S, Chou W S. Path Planning for Mobile Robot Using Self-Adaptive Learning Particle Swarm Optimization[J]. Science China Information Sciences, 2018, 61(5)
(  0) 0) |
| [7] |
赵艳楠, 王霞. 基于Shearlet变换的单波段遥感图像拼接技术研究[J]. 科学技术与工程, 2014, 14(6): 218-221 (Zhao Yannan, Wang Xia. Research on Single Band Remote Sensing Image Based on the Algorithm of Shearlet[J]. Science Technology and Engineering, 2014, 14(6): 218-221)
(  0) 0) |
| [8] |
Liu B, Liu K Z, Wang Y Y, et al. A Hybrid Deep Sea Navigation System of LBL/DR Integration Based on UKF and PSO-SVM[J]. Robot, 2015, 37(5): 614-620
(  0) 0) |
| [9] |
Wang H J, Xu X L, Rosen B G. Fault Diagnosis Model Based on Multi-Manifold Learning and PSO-SVM for Machinery[J]. Chinese Journal of Scientific Instrument, 2014, 35(S2): 210-214
(  0) 0) |
| [10] |
尤军, 殷耀国, 李辉, 等. 基于MATLAB的深基坑沉降监测预报模型优选[J]. 中国科技论文, 2015, 10(15): 1 772-1 777 (You Jun, Yin Yaoguo, Li Hui, et al. The Preferred Model Base on MATLAB for Settlement Observation and Prediction of Deep Foundation Pits[J]. China Sciencepaper, 2015, 10(15): 1 772-1 777)
(  0) 0) |
| [11] |
Li M W, Kang H G, Zhou P F, et al. Hybrid Optimization Algorithm Based on Chaos, Cloud and Particle Swarm Optimization Algorithm[J]. Journal of Systems Engineering and Electronics, 2013, 24(2): 324-334 DOI:10.1109/JSEE.2013.00041
(  0) 0) |
| [12] |
李荣雨, 程磊. 基于SVM最优决策面的决策树构造[J]. 电子测量与仪器学报, 2016, 30(3): 342-351 (Li Rongyu, Cheng Lei. Building Decision Tree Based on SVM Optimal Decision Surface[J]. Journal of Electronic Measurement and Instrumentation, 2016, 30(3): 342-351)
(  0) 0) |
| [13] |
Ma J Q, Geng J H. Cauchy Prior Distribution-Based AVO Elastic Parameter Estimation via Weakly Nonlinear Waveform Inversion[J]. Applied Geophysics, 2013, 10(4): 442-452 DOI:10.1007/s11770-013-0393-1
(  0) 0) |
| [14] |
刘晓杰, 范虹, 党小虎. 结合二维EEMD和小波分解的遥感图像纹理方向检测[J]. 地理与地理信息科学, 2016, 32(1): 66-70 (Liu Xiaojie, Fan Hong, Dang Xiaohu. Detection Method for Remote Sensing Image Texture Direction Based on Bi-Dimensional EEMD and Wavelet Transform[J]. Geography and Geo-Information Science, 2016, 32(1): 66-70)
(  0) 0) |
| [15] |
陈家骐, 华建兵, 段园煜, 等. 基于粒子群优化的DGM(1, 1) 模型在基坑变形安全预测中的研究[J]. 中国安全生产科学技术, 2019, 15(3): 161-166 (Chen Jiaqi, Hua Jianbing, Duan Yuanyu, et al. Study on DGM(1, 1) Model Based on Particle Swarm Optimization in Predicting Deformation Safety of Foundation Pit[J]. Journal of Safety Science and Technology, 2019, 15(3): 161-166)
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41


