2. 国家遥感中心绵阳科技城分部,四川省绵阳市青龙大道中段59号,621010
矿山地表沉降机理复杂,通常单一预测模型预测数据的精度较低,不能反映矿区地表的真实情况。将单一预测模型进行组合,提取各模型的有效信息来提高预测精度是当前的发展趋势[1-4]。差分整合移动平均自回归(autoregressive integrated moving average, ARIMA)模型和Holt-Winters模型都是基于时间序列变化的预测模型,适用于矿山地表沉降时序变化预测。本文基于诱导有序加权平均(IOWA)算子,以SBAS-InSAR监测值作为实际值,将ARIMA模型和Holt-Winters模型进行加权组合,以期为矿山地表沉降监测预测提供新方法。
1 SBAS沉降监测及组合预测模型建立 1.1 SBAS-InSAR技术原理小基线集(small baseline subset, SBAS)技术可有效改善D-InSAR时空失相干、大气延迟等缺陷,其原理是将传统D-InSAR的监测形变结果作为单一观测值,并根据最小二乘法得到高精度的形变序列[5]。由于实验研究目标为地表垂向沉降变化,因此本文忽略地表水平位移的影响,将LOS向形变转至垂向形变。
1.2 基于IOWA算子的ARIMA和Holt-Winters模型的组合预测方法原理ARIMA模型是针对非平稳时间序列建模的常见模型。ARIMA(p, d, q)称为差分整合移动平均自回归模型,其中AR为自回归项,p为自回归阶数,MA为移动平均项,q为移动平均阶数,d为差分阶数。ARIMA(p, d, q)模型可表示为:
| $ \left( {1 - \sum\limits_{i = 1}^p {{\varphi _i}} {L^i}} \right){(1 - L)^d}{X_t} = \left( {1 + \sum\limits_{i = 1}^q {{\theta _i}} {L^i}} \right){\varepsilon _t} $ | (1) |
式中,L为滞后算子,d∈Z,d>0。当差分阶数d=0时,ARIMA模型等同于ARMA模型(即平稳时间序列模型)[6]。本文研究数据均为平稳时序数据,故d均为0。
指数平滑预测法是以具有某种指标的本期监测数据和预测数据为基础,引入平滑系数,以求取平均数的一种时间序列预测法,其预测公式为:
| $ {y^\prime }_{t + 1} = a{y_t} + (1 - a){y^\prime }_t $ | (2) |
式中,y′t+1为第t+1期预测值,yt为第t期监测值,y′t为第t期预测值。
Holt-Winters线性指数平滑法是在上述一次指数平滑的基础上进行二次指数平滑,其公式为:
| $ S_{t}^{(2)}=a S_{t}^{(1)}+(1-a) S_{t-1}^{(2)} $ | (3) |
式中,St(2)为第t期的二次指数平滑值,St(1)为第t期的一次指数平滑值,St-1(2)为第t-1期的二次指数平滑值,a为平滑系数[7]。
诱导有序加权平均(IOWA)算子是根据有序加权平均(OWA)算子发展而来的新型加权方法,基于IOWA算子的组合预测模型可以有效克服传统组合预测方法在某个时间点预测精度不同的缺点。IOWA算子原理如下:
假设存在一组监测值xi(i=1, 2, …, N), 采用m种可行的单预测模型进行预测,第t种方法在时刻i的预测值(或拟合值)为xti(t=1, 2, …, m)。设L=(l1, l2, …, lm)为m种单项预测在组合预测中的加权系数,且满足:
| $ \sum\limits_{t = 1}^m {{l_t}} = 1,{l_t} \ge 0,t = 1,2, \cdots ,m $ | (4) |
根据加权算术平均数计算公式,令
| $ {{\hat x}_i} = \sum\limits_{t = 1}^m {{l_t}} {x_{ti}},i = 1,2, \cdots ,N $ | (5) |
则称
第t种方法在时刻i的预测精度pti可表示为:
| $ {p_{ti}} = \left\{ {\begin{array}{*{20}{l}} {1 - \left( {{x_i} - {x_{ti}}} \right)/{x_i},\left( {{x_i} - {x_{ti}}} \right)/{x_i} < 1}\\ {0,\left( {{x_i} - {x_{ti}}} \right)/{x_i} \ge 1} \end{array}} \right. $ | (6) |
利用m种方法获得预测值及其预测精度,可构成一个二维数组(p1i, x1i), (p2i, x2i), …, (pmi, xmi),将pti按从大到小排序,设a-index(ti)是序号为t的预测精度的下标,令
| $ \begin{array}{*{20}{c}} {{F_L}\left( {\left( {{p_{1i}},{x_{1i}}} \right),\left( {{p_{2i}},{x_{2i}}} \right), \cdots ,\left( {{p_{mi}},{x_{mi}}} \right)} \right) = }\\ {\sum\limits_{t = 1}^m {{l_t}} {x_{a - {\mathop{\rm index}\nolimits} (ti)}}} \end{array} $ | (7) |
则式(7)称为由预测精度序列p1i, p2i, …, pmi所产生的IOWA组合预测值。
从式(7)可以看出,组合预测的赋权系数与单项预测方法无关,而与单项预测方法在各个时间点的预测精度大小密切相关[8]。
令ea-index(ti)=xi-xa-index(ti),则以误差平方和为准则的基于IOWA的组合预测最优化模型可表示为:
| $ \begin{array}{*{20}{c}} {\min S(L) = \sum\limits_{t = 1}^m {\sum\limits_{g = 1}^M {{l_t}} } {l_g}\left( {\sum\limits_{i = 1}^N {{e_{a - {\mathop{\rm index}\nolimits} (ti)}}} {e_{a - {\mathop{\rm index}\nolimits} (gi)}}} \right)}\\ {{\rm{ s}}{\rm{.t}}{\rm{. }}\left\{ {\begin{array}{*{20}{l}} {\sum\limits_{t = 1}^m {{l_t}} = 1}\\ {l \ge 0} \end{array}} \right.} \end{array} $ | (8) |
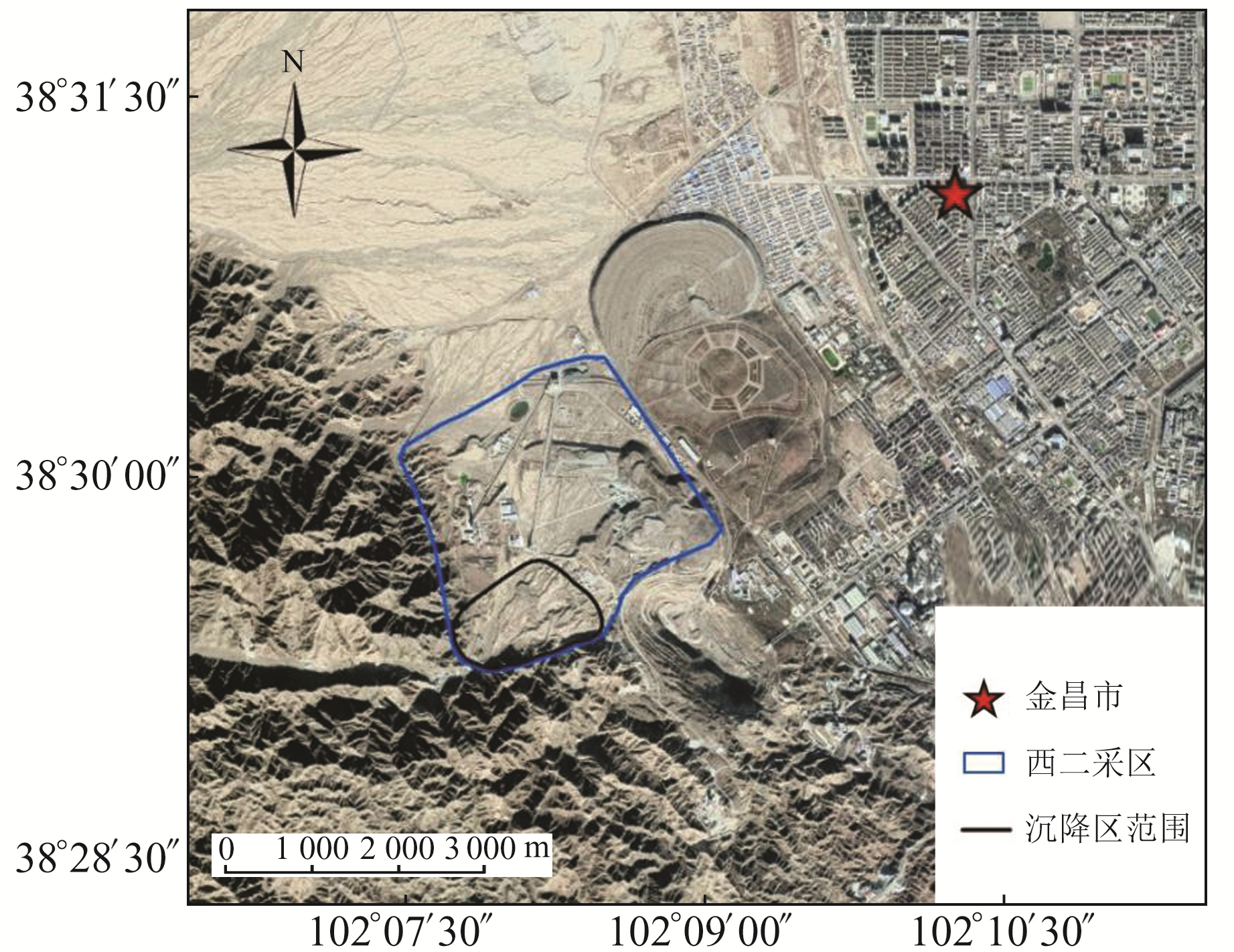
本文以金昌市龙首矿西二采区为研究区(以下简称西二采)。西二采位于我国甘肃省金昌市,其沉降区面积约1.1 km2,如图 1所示,矿区地势较平坦,平均海拔为1 500~1 800 m。矿区地表水系不发育,常年干枯,属温带大陆性气候。近年由于地下不断开采,导致地表塌陷,裂缝明显,从而对镍矿资源开采产生极大的安全隐患。
|
图 1 研究区概况 Fig. 1 Overview of the study area |
选取时间跨度为2019-04-03~2020-01-28的连续26景SAR数据C波段的升轨Sentinel-1A斜距单视复数(SLC)影像,周期为12 d,分辨率为5 m×20 m,实验参数详见表 1。影像预处理过程中引入AUX_POEORB精密定轨星历数据,数据处理时选用分辨率为30 m的SRTM DEM数据去除地形相位。
|
|
表 1 实验数据参数 Tab. 1 Parameters of experimental data |
实验选取覆盖研究区的26景Sentinel-1A升轨SAR影像,基于SARscape5.2.1版本进行SBAS数据处理。为获取可靠的形变监测结果,设置临界基线阈值为2 %,时间基线为150,并引入30 m分辨率的SRTM DEM数据去除地形相位。剔除效果较差的干涉对后,最终选取172个干涉对进行差分干涉处理;设置解缠相干系数阈值为0.2,并选取47个稳定控制点进行轨道精化和重去平;进行形变速率反演和地理编码,去除大气相位等误差影响,得到视线(LOS)向年平均沉降速率和时序累积沉降结果并转至垂向形变,其中累积垂向沉降值见图 2。

|
图 2 累积沉降值 Fig. 2 Cumulative settlement |
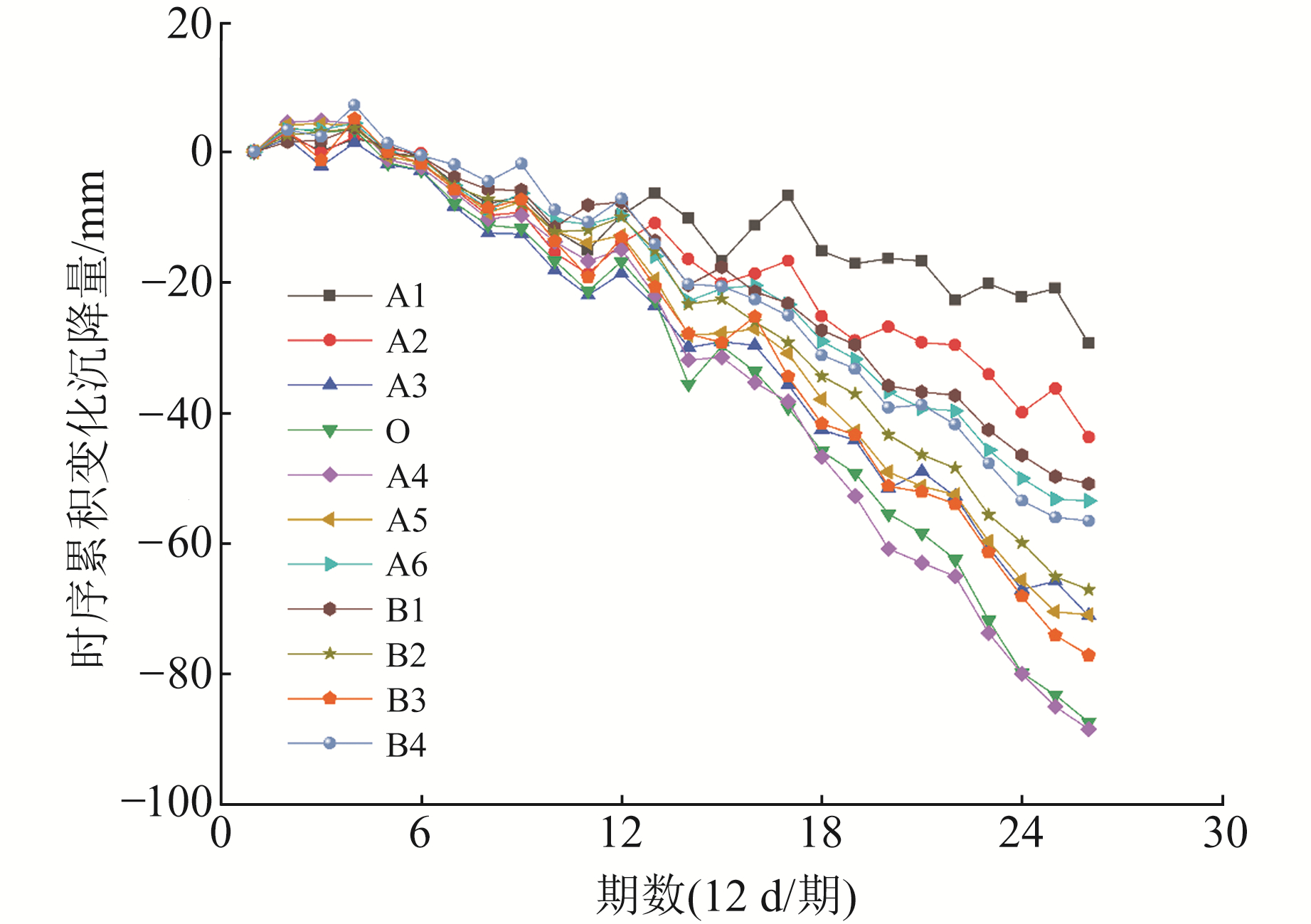
由图 2可以看出,矿区在监测时段内由地下开采引起的最大累积垂向沉降值达到-94.5 mm。为便于后文分析矿区地表沉降预测,将26景影像视为26期时序沉降变化,其中每12 d视为1期,并选取11个监测点进行时序沉降监测分析,包含沿走向分布的6个监测点(A1~A6)、沿倾向分布的4个监测点(B1~B4)及交点O。各点沉降变化曲线如图 3所示,从图中可以看出,1~4期各监测点呈轻微抬升趋势;5~12期各监测点呈沉降趋势,且各点累积沉降值相差较小;12~26期整体沉降速率加快,其中接近沉降中心的A4点累积沉降变化最大,A1点距离沉降中心最远,累积沉降变化最小。
|
图 3 各点沉降变化曲线 Fig. 3 Settlement curve of each point |
由于缺少地面观测点数据,故将SBAS-InSAR监测数据作为实际值,选取前23期(每期时间间隔为12 d)监测数据对后3期(2020-01-04~28)数据进行预测,并将后3期SBAS监测值与预测值进行对比分析。为证明本文提出的组合预测模型在矿区沉降预测中的可行性,建立3种方案进行分析:方案1采用ARIMA模型进行预测,方案2采用Holt-Winters指数平滑模型进行预测,方案3采用基于IOWA算子的ARIMA和Holt-Winters指数平滑组合模型进行预测。
方案1和方案2采用IBM SPSS Statistics 24.0软件进行时间序列预测分析,得到各预测模型前23期数据拟合度(表 2)、ARIMA模型预测值(表 3)和Holt-Winters模型预测值(表 4)。
|
|
表 2 各模型拟合度 Tab. 2 Fitness of each model |
|
|
表 3 ARIMA模型预测值 Tab. 3 Predictive value of ARIMA model |
|
|
表 4 Holt-Winters模型预测值 Tab. 4 Predictive value of Holt-Winters model |
从表 2可以看出,ARIMA模型的均方根误差RMSE平均值为3.44,略高于Holt-Winters模型,因此Holt-Winters模型的拟合度整体上优于ARIMA模型。但从表 3、4可以看出,2种预测模型的预测值与实际值在不同期数不同点的精度存在差异,例如A1点在ARIMA模型下3期预测值的相对误差分别为19.23 %、0.14 %和18.64 %,在Holt-Winters模型下3期预测值的相对误差分别为4.14 %、6.39 %和20.55 %,因此引入IOWA算子可克服单一预测方法在不同时间点预测精度不同的缺点。
方案3基于IOWA算子,由式(11)计算IOWA组合预测值,以A1点为例:
| $ \begin{array}{c} {f_L}\left[ {\left( {{p_{1,24}},{x_{1,24}}} \right),\left( {{p_{2,24}},{x_{2,24}}} \right)} \right] = \\ {l_1}{x_{a - {\mathop{\rm index}\nolimits} (1,24)}} + {l_2}{x_{a - {\mathop{\rm index}\nolimits} (2,24)}} \end{array} $ |
| $ \begin{array}{c} {f_L}\left[ {\left( {{p_{1,25}},{x_{1,25}}} \right),\left( {{p_{2,25}},{x_{2,25}}} \right)} \right] = \\ {l_1}{x_{a - {\mathop{\rm index}\nolimits} (1,25)}} + {l_2}{x_{a - {\mathop{\rm index}\nolimits} (2,25)}} \end{array} $ |
| $ \begin{array}{c} {f_L}\left[ {\left( {{p_{1,26}},{x_{1,26}}} \right),\left( {{p_{2,26}},{x_{2,26}}} \right)} \right] = \\ {l_1}{x_{a - {\mathop{\rm index}\nolimits} (1,26)}} + {l_2}{x_{a - {\mathop{\rm index}\nolimits} (2,26)}} \end{array} $ |
得出:
| $ \begin{array}{c} {f_L}[(0.808, - 17.93),(0.959, - 21.28)] = \\ - 21.28{l_1} - 17.93{l_2} \end{array} $ |
| $ \begin{array}{c} {f_L}[(0.999, - 20.99),(0.936, - 22.30)] = \\ - 20.99{l_1} - 22.30{l_2} \end{array} $ |
| $ \begin{array}{c} {f_L}[(0.814, - 23.87),(0.794, - 23.31)] = \\ - 23.87{l_1} - 23.31{l_2} \end{array} $ |
将其代入式(12),整理得到最优化模型:
| $ \begin{array}{*{20}{c}} {\min S\left( {{l_1},{l_2}} \right) = 1{\kern 1pt} {\kern 1pt} {\kern 1pt} 463.2l_1^2 + 1{\kern 1pt} {\kern 1pt} {\kern 1pt} 361.66l_2^2 + }\\ {2{\kern 1pt} {\kern 1pt} {\kern 1pt} 811.6{l_1}{l_2} - 3{\kern 1pt} {\kern 1pt} {\kern 1pt} 225.42{l_1} - 3{\kern 1pt} {\kern 1pt} {\kern 1pt} 098.15{l_2} + 1{\kern 1pt} {\kern 1pt} {\kern 1pt} 793.00} \end{array} $ |
| $ {{\rm{ s}}{\rm{.t}}{\rm{. }}\left\{ {\begin{array}{*{20}{l}} {{l_1} + {l_2} = 1}\\ {{l_1} \ge 0,{l_2} \ge 0} \end{array}} \right.} $ |
同理可得到其他点的最优化模型。利用编程或MATLAB最优化工具箱可计算出A1点基于IOWA算子的组合预测模型的最优权系数为:
| $ {l_1} = 1,{l_2} = 0 $ |
则A1点的预测值分别为-21.28 mm、-20.99 mm和-23.87 mm。
从A1点组合预测模型的IOWA最优权系数可以看出,该方法在A1点的组合预测是将2个单一模型中预测精度更高的值作为其组合预测值。表 5为基于IOWA算子的组合预测模型的预测值。
|
|
表 5 组合预测模型预测值 Tab. 5 Predictive value of combined model |
为验证上述组合预测模型的有效性,选取均方误差MSE和平均绝对误差MAE作为主要评价指标(表 6)。
|
|
表 6 预测精度比较 Tab. 6 Comparison of prediction accuracy |
从表 6可以看出,基于IOWA算子的组合模型在各点的均方误差MSE和平均绝对误差MAE均比单一模型小,表明该组合模型的预测精度更高,具有一定的有效性。
3 结语以金昌市龙首矿西二采为研究区,采用26景SAR影像进行SBAS地表沉降监测,得到该地区26期时序沉降变化与累积沉降值。以SBAS监测值为实际值,基于前23期监测值分别采用ARIMA模型和Holt-Winters模型进行拟合并预测后3期沉降值。结果表明,单一模型在不同点不同时期的预测精度存在差异,其中ARIMA模型在A1、A2、A3点第25期的预测精度更高,Holt-Winters模型则在B1~B4点的预测精度更高。根据各单一模型的预测值特点,本文基于IOWA算子将ARIMA模型和Holt-Winters模型进行组合,在最优权系数赋值时按照单一模型的预测精度大小进行赋值,组合模型可有效克服传统单一赋权的缺陷,其精度优于各单一模型。
| [1] |
陈银翠, 徐良骥, 余礼仁. 融合D-InSAR与GIS技术的矿区开采沉陷形变监测及预测方法[J]. 测绘通报, 2019(7): 54-58 (Chen Yincui, Xu Liangji, Yu Liren. The Method of Mining Subsidence Deformation Monitoring and Prediction Based on D-InSAR with GIS Technology[J]. Bulletin of Surveying and Mapping, 2019(7): 54-58)
(  0) 0) |
| [2] |
鲁小红. 最优权组合预测法在采煤沉陷变形预测中的应用[J]. 测绘通报, 2020(4): 111-115 (Lu Xiaohong. Application of Optimal Weight Combination Method in Predicting Coal Mining Subsidence Deformation[J]. Bulletin of Surveying and Mapping, 2020(4): 111-115)
(  0) 0) |
| [3] |
严剑锋, 邓喀中. 基于BP网络与WPGM(1, 1)组合模型的地面沉降预测[J]. 合肥工业大学学报: 自然科学版, 2013, 36(3): 361-364 (Yan Jianfeng, Deng Kazhong. Combination Model of BP Network and WPGM(1, 1) for Land Subsidence Prediction[J]. Journal of Hefei University of Technology: Natural Science, 2013, 36(3): 361-364)
(  0) 0) |
| [4] |
徐青, 郭伟, 何松. 基于Logistic-ARMA组合模型对基坑开挖过程地表沉降的预测研究[J]. 安全与环境工程, 2017, 24(3): 160-163 (Xu Qing, Guo Wei, He Song. Forecast of Surface Subsidence Induced by Foundation Pit Excavation Based on Logistic-ARMA Model[J]. Safety and Environmental Engineering, 2017, 24(3): 160-163)
(  0) 0) |
| [5] |
李金超, 高飞, 鲁加国, 等. 基于SBAS-InSAR和GM-SVR的居民区形变监测与预测[J]. 大地测量与地球动力学, 2019, 39(8): 837-842 (Li Jinchao, Gao Fei, Lu Jiaguo, et al. Deformation Monitoring and Prediction of Residential Areas Based on SBAS-InSAR and GM-SVR[J]. Journal of Geodesy and Geodynamics, 2019, 39(8): 837-842)
(  0) 0) |
| [6] |
周杰, 任光辉, 贺宏斌, 等. 指数平滑模型与ARIMA模型在湖南省血吸虫病流行趋势预测中的应用[J]. 中国血吸虫病防治杂志, 2020, 32(3): 236-241 (Zhou Jie, Ren Guanghui, He Hongbin, et al. Application of the Exponential Smoothing Model and ARIMA Model in Prediction of the Endemic Situation of Schistosomiasis in Hunan Province[J]. Chinese Journal of Schistosomiasis Control, 2020, 32(3): 236-241)
(  0) 0) |
| [7] |
张璇. 基于数据挖掘的铁路货运量预测应用研究[D]. 成都: 西南交通大学, 2016 (Zhang Xuan. Research of Railway Freight Volume Forecasting Based on Data Mining[D]. Chengdu: Southwest Jiaotong University, 2016)
(  0) 0) |
| [8] |
陈华友, 刘春林. 基于IOWA算子的组合预测方法[J]. 预测, 2003, 22(6): 61-65 (Chen Huayou, Liu Chunlin. A Kind of Combination Forecasting Method Based on Induced Ordered Weighted Averaging(IOWA) Operators[J]. Forecasting, 2003, 22(6): 61-65)
(  0) 0) |
2. Mianyang Science and Technology City Division, National Remote Sensing Center of China, 59 Mid-Qinglong Avenue, Mianyang 621010, China
 2021, Vol. 41
2021, Vol. 41


