2. 山东科技大学测绘与空间信息学院,青岛市前湾港路579号,266590
卫星钟差(satellite clock bias,SCB)预报是卫星导航定位系统中一项极其重要的工作[1],可靠程度高的钟差预报结果有利于提高精密单点定位(PPP)的精度[2]。地面基于卫星精密星历所预报的钟差也可作为卫星导航所需要的先验信息[3]。卫星钟差的高精度预报已成为精密导航定位中一项关键技术[4],尽管IGS已发布了轨道精度达到cm级的实时精密轨道产品,但由于其钟差的外推精度不足,该产品无法应用于实时精密导航定位; 另外IGS还发布了实时精密钟差,其精度可达0.1 ns,但传输稳定性较差[5]。研究表明,白噪声调相、白噪声调频、闪变噪声调相、闪变噪声调频及随机游走调频等5种噪声会严重影响卫星原子钟的稳定性,导致频标的频率发生随机变化,使得卫星钟差预报难以达到较高精度[6-7]。为得到高精度的卫星预报钟差,国内外学者进行了大量研究,针对卫星钟差的特点提出一系列钟差预报模型,其中常用的钟差预报模型包括二次多项式(QP)模型、附有周期项的二次多项式模型(SA)、灰色系统(GM(1, 1))模型和人工神经网络(artificial neural network,ANN)模型等[8-14]。
卫星钟差数据变化复杂,难以采用严密的数学表达式进行表示,而Elman神经网络是一种拥有局部记忆单元和局部反馈连接的递归神经网络,具备强大的计算能力,可以动态映射任意非线性时间序列[15],同时拥有动态反馈能力,能有效降低钟差预报过程中出现的误差累积效应。本文以IGS提供的30 s采样率的精密钟差序列作为原始数据,对其进行一次差处理并建模,分别采用Elman模型、二次多项式模型、附有周期项的二次多项式模型和灰色模型进行卫星钟差预报,并对比分析各模型对各类原子钟预报不同时长的精度及稳定性,以验证Elman模型的可行性。
1 常用预报模型 1.1 二次多项式模型(QP模型)用于卫星钟差预报的二次多项式模型的观测方程[11]为:
| $ x_{i}=a_{0}+a_{1}\left(t_{i}-t_{0}\right)+a_{2}\left(t_{i}-t_{0}\right)^{2}+\varepsilon $ | (1) |
式中,xi为ti时刻的卫星钟差,ti(i=1, 2, …, n)为历元时刻,t0为卫星钟参考时刻,a0、a1和a2分别为参考时刻t0的相位、钟速及钟漂,ε为频率随机误差。
当拥有2个以上钟差数据时,利用最小二乘原理即可求得参数最或然值
SA模型是在二次多项式模型的基础上附加考虑周期项的钟差预报模型[2],其表达式为:
| $ \begin{aligned} x_{i} &=a_{0}+a_{1}\left(t_{i}-t_{0}\right)+a_{2}\left(t_{i}-t_{0}\right)^{2}+\\ & \sum\limits_{k=1}^{p} A_{k} \sin \left[2 \pi f_{k}\left(t_{i}-t_{0}\right)+\varphi_{k}\right]+\varepsilon \end{aligned} $ | (2) |
式中,a0、a1、a2和ε所代表的含义与式(1)相同,p为主要周期函数的个数,Ak、fk、φk分别为对应周期项的振幅、频率和相位。
与二次多项式模型相同,利用最小二乘原理求得参数最或然值,再代入式(2)即可求得预报历元的钟差。附加周期项的二次多项式模型虽然考虑了钟差周期性变化的影响,提高了短期钟差预报的精度,但该模型同样受多项式模型主体的影响,随着预报时间的增加,预报精度逐渐降低。
1.3 灰色系统模型(GM(1, 1)模型)灰色系统模型[12]表达式为:
| $ x^{(0)}(k+1)=\left(1-\mathrm{e}^{a}\right)\left[x^{(0)}(1)-\frac{u}{a}\right] \mathrm{e}^{-a(k-1)} $ | (3) |
式中,k=1, 2, …, n; a和u为常量参数,分别为发展系数和灰色作用量。
模型参数
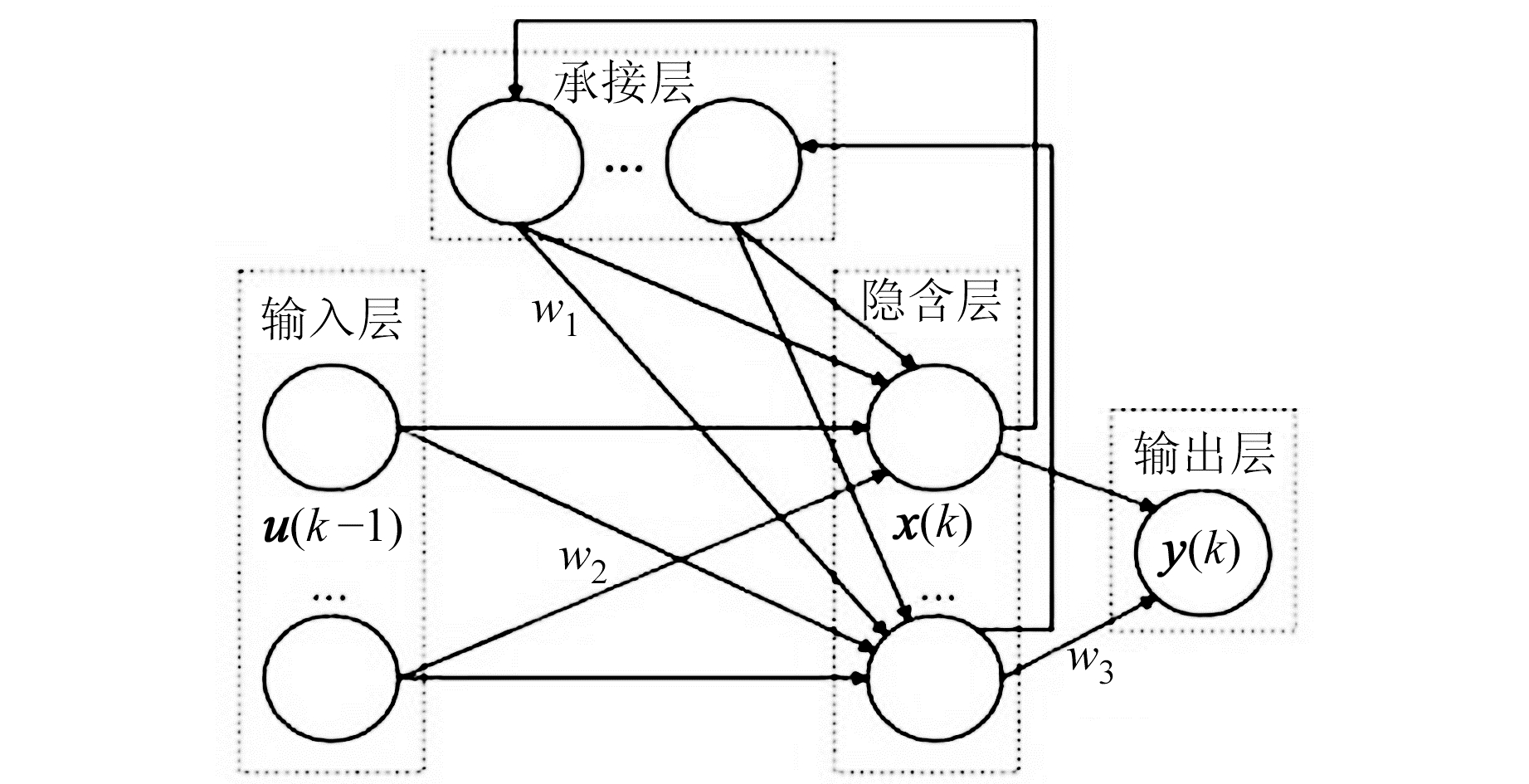
Elman神经网络通过在传统的BP神经网络结构中增加一个承接层,以接收反馈信号和连接记忆上一时刻隐含层的输出状态,并与该时刻的网络输入共同作为隐含层的输入,从而使网络训练具备局部反馈和动态记忆的特性[16]。这种方式使Elman神经网络表现出较强的记忆性和时序性,在关于时间序列的问题上具有较好的适配度[17]。Elman神经网络由输入层、隐含层、承接层和输出层构成,具体如图 1所示。
|
图 1 Elman神经网络结构 Fig. 1 Elman neural network structure |
Elman神经网络通过输入层神经元传输信号,同时隐含层神经元采用Sigmoid函数作为激励函数,通过输出层神经元起到线性加权的作用,其表达式为:
| $ \begin{array}{c} \boldsymbol{x}(k)=f\left(w_{1} * \boldsymbol{x}_{c}(k)+w_{2} * \boldsymbol{u}(k-1)\right) \end{array} $ | (4) |
| $ \boldsymbol{x}_{c}(k)=\boldsymbol{x}(k-1) $ | (5) |
| $ \boldsymbol{y}_{k}=g\left(w_{3} * \boldsymbol{x}(k)\right) $ | (6) |
式中,yk为m维输出层节点向量,x(k)为n维隐含层节点向量,u为r维输入层节点向量,xc为n维反馈状态向量,w1为承接层到隐含层的连接权值,w2为输入层到隐含层的连接权值,w3为隐含层到输出层的连接权值,g(*)为输出神经元的传递函数,f(*)为隐含层神经元的传递函数。
Elman神经网络的连接权值可采用附加动量的梯度下降反向传播算法进行修正,同时将误差平方和函数作为学习指标,其表达式为:
| $ E(w)=\sum\limits_{k=1}^{\infty}\left(\boldsymbol{y}_{k}(w)-\tilde{\boldsymbol{y}}_{k}(w)\right)^{2} $ | (7) |
式中,
采用Elman神经网络模型预报钟差,其关键在于针对卫星钟差的特点选择最佳的网络结构。目前,神经网络结构中每层神经元数量的确定并无明确规范,因此需要根据实际情况来确定[18]。研究表明,输出层神经元的个数通常与需要输出的数据类型的个数相同[19],此处输出的数据类型只有1种,因此输出层神经元个数为1。
Elman神经网络隐含层神经元个数的确定对模型预报的精度极为关键,如果隐含层的神经元个数较多,则网络的结构会更加稳定,映射非线性函数的能力也将加强,但会降低网络训练的收敛速度; 如果隐含层神经元个数较少,网络结构则会过于简单,计算时间减少,但会导致模型预报能力不足,预报精度也会大大降低。因此需要在保证模型预报能力的前提下,选择合适的隐含层神经元数量。
为得到最佳的网络结构,本文选择GPS week 20 100(2018-07-15)数据进行建模,选择不同个数的隐含层神经元预报其后1 d的钟差。图 2为隐含层神经元个数为3~11时钟差预报结果的RMS变化情况。

|
图 2 隐含层神经元变化时钟差预报结果的RMS变化情况 Fig. 2 RMS of clock bias prediction result when hidden layer neuron changes |
从图 2可以看出,隐含层神经元个数为5时,钟差预报结果的RMS最小。随着神经元个数的增加,RMS存在一定波动,但达不到最小值。当神经元个数为3时,其RMS也较小,而此时的预报结果也能达到要求。由此说明,神经元个数的选择受人为经验影响,本文选择神经元个数为5,即为最优的网络结构。
研究表明,卫星钟差数据不可避免会含有误差,而使用一次差分数据进行钟差预报可减小误差的影响,从而提高预报精度[20]。但常用的预报模型采用一次差分处理后的数据进行预报会使精度不稳定,而GM(1, 1)模型在预报钟差时已经对数据进行自减和自增,再进行一次差处理会导致模型的预报性能无法定性[21]。因此,本文利用Elman预报模型一次差分处理后的新样本数据进行卫星钟差预报,而常用模型不进行一次差分处理。在预报过程中得到一部分预测值后,需要通过移动窗口法得到连续的预测值,最后将所有的一阶差分预测值恢复成钟差预测值。
3 预报实验及分析为验证本文提出的预报模型的可行性,使用IGS提供的30 s采样率的精密钟差序列,从不同建模数据量和预报时长的角度,采用4种模型对GPS卫星进行1 d、7 d、30 d的钟差预报实验。本文实验以GPS week 20 100~20 142(2018-07-15~08-14)共31 d的数据为例,考虑到不同类型的星载原子钟(包括Block IIR铷钟、Block IIR-M铷钟、Block IIF铯钟和Block IIF铷钟)可能会对预报效果产生影响,故随机选取各类原子钟的其中1颗卫星进行实验,本文实验所选卫星为PRN08、PRN12、PRN22和PRN26。在预报实验中,采用均方根误差(RMS)和极差(最大误差与最小误差之差,记为Range)作为统计指标,并以对应的IGS精密钟差数据作为真值进行预报效果分析[22]。RMS计算公式为:
| $ \mathrm{RMS}=\sqrt{\frac{\sum\limits_{i=1}^{n}\left(\text { error }_{i}\right)^{2}}{n}} $ | (8) |
式中,
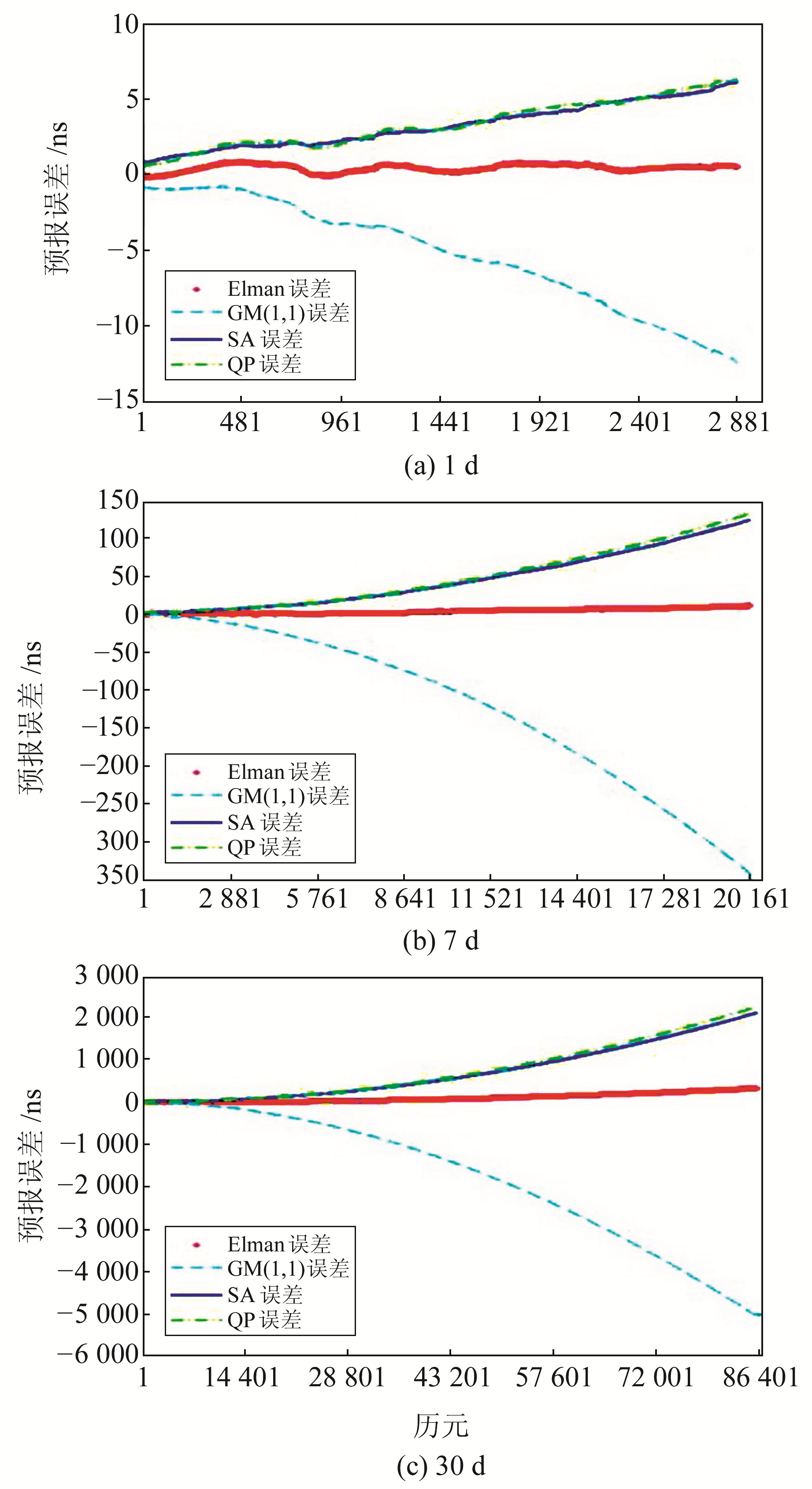
为分析Elman模型的预报效果,分别采用QP模型、SA模型、GM(1, 1)模型和Elman模型(网络结构为1-5-1-1)对GPS week 20 100数据进行建模,预报其后1 d、7 d、30 d的钟差,分别对应短期、中期、长期钟差预报。以PRN26为例,图 3为不同模型不同预报时长的钟差预报误差,表 1~3为各卫星钟差预报的结果统计。
|
图 3 钟差预报误差 Fig. 3 Clock bias prediction error |
|
|
表 1 1 d钟差预报结果统计 Tab. 1 1-day clock bias prediction result |
|
|
表 2 7 d钟差预报结果统计 Tab. 2 7-days clock bias prediction result |
|
|
表 3 30 d钟差预报结果统计 Tab. 3 30-days clock bias prediction result |
从图 3可以看出,在进行短期、中期和长期钟差预报时,Elman模型的预报误差曲线均保持在0值附近,而其他常用模型的误差曲线呈现随时间不断递增的趋势,说明Elman模型在一定程度上可抑制因预报时间增长导致误差不断累积的问题,表明该模型的预报效果优于其他常用模型。
从表 1(单位ns)可以看出,在卫星钟差短期预报实验中,PRN12和PRN08的预报精度为ns级,PRN22和PRN26的预报精度为亚ns级。其中,PRN12工作时间较长,卫星钟性能下降导致预报精度稍低,而PRN08的卫星钟为铯钟,精度相对较低。对比各模型对同一卫星的预报精度发现,无论是星载铷钟还是星载铯钟,Elman模型的预报精度和稳定性均明显优于3种常用模型。以PRN26的预报效果为例,其预报精度分别提高89.1%、88.8%和89.8%,稳定性分别提高67.0%、68.0%和69.6%。因此,在短期钟差预报中,Elman模型的钟差预报效果优于3种常用模型。
从表 2和3(单位ns)可以看出,随着预报时长的增加,各模型进行中长期钟差预报的精度和稳定性均迅速降低。在进行中期钟差预报时,以PRN26的预报效果为例,Elman模型的预报精度比3种常用模型分别提升96.8%、91.3%和91.8%,其稳定性也有一定提升。
在进行长期钟差预报时发现,PRN08存在多天数据缺失的现象,因此只选用PRN12、PRN22和PRN26这3颗卫星参与30 d的钟差预报实验。其中,Elman模型的预报精度在600 ns以内,其余3种模型的预报精度基本都超过600 ns,部分甚至超过1 000 ns,无法满足精密定位的需求。以PRN26的预报效果为例,Elman模型的预报精度比3种常用模型分别提升93.8%、84.9%和85.9%,其预报稳定性也高出其余模型1个数量级。总体来说,Elman模型的预报精度和稳定性明显优于3种常用模型。
4 结语为提高卫星钟差预报的精度和稳定性,本文提出基于Elman神经网络的钟差预报模型,并通过短期、中期和长期预报实验,得到4种模型不同预报时长的预报结果。在对钟差预报结果进行对比分析后,得出以下结论:
1) 在卫星钟差短期预报中,无论是星载铯钟还是星载铷钟,4种模型的钟差预报精度均能达到ns级,而使用Elman模型预报钟差时,部分卫星的预报精度甚至可达到亚ns级,其钟差预报稳定性也有较大提升。
2) 随着预报时长的增加,各类模型进行卫星钟差中长期预报的误差不断累积,导致各模型预报钟差的精度和稳定性迅速降低。但与3种常用模型相比,Elman模型的预报精度和稳定性仍有明显提升。
本文提出的Elman模型较3种常用钟差预报模型具有更高的预报精度,表明Elman神经网络在卫星钟差预报中具有可行性。
| [1] |
王利, 张勤, 黄观文, 等. 基于指数平滑法的GPS卫星钟差预报[J]. 武汉大学学报: 信息科学版, 2017, 42(7): 995-1 001 (Wang Li, Zhang Qin, Huang Guanwen, et al. GPS Satellite Clock Bias Prediction Based on Exponential Smoothing Method[J]. Geomatics and Information Science of Wuhan University, 2017, 42(7): 995-1 001)
(  0) 0) |
| [2] |
郑作亚, 党亚民, 卢秀山, 等. 附有周期项的预报模型及其在GPS卫星钟差预报中的应用研究[J]. 天文学报, 2010, 51(1): 95-102 (Zheng Zuoya, Dang Yamin, Lu Xiushan, et al. Prediction Model with Periodic Item and Its Application to the Prediction of GPS Satellite Clock Bias[J]. Acta Astronomica Sinica, 2010, 51(1): 95-102)
(  0) 0) |
| [3] |
杨宇飞, 杨元喜, 王威, 等. MGEX钟差产品精度分析[J]. 测绘科学技术学报, 2018, 35(5): 441-445 (Yang Yufei, Yang Yuanxi, Wang Wei, et al. Accuracy Assessment for IGS MGEX Clock Products[J]. Journal of Geomatics Science and Technology, 2018, 35(5): 441-445)
(  0) 0) |
| [4] |
Bhattarai S. Satellite Clock Time Offset Prediction in Global Navigation Satellite System[D]. London: University of London, 2015
(  0) 0) |
| [5] |
Strandjord K L, Axelrad P. Improved Prediction of GPS Satellite Clock Sub-Daily Variations Based on Daily Repeat[J]. GPS Solutions, 2018, 22(3): 58 DOI:10.1007/s10291-018-0723-0
(  0) 0) |
| [6] |
王宁. BDS星载原子钟钟差数据预处理与钟性能分析研究[D]. 郑州: 信息工程大学, 2017 (Wang Ning. Study on the Methods of Clock Bias Data Preprocessing and Performance Analysis for On-Board Atomic Clocks of BDS[D]. Zhengzhou: Information Engineering University, 2017)
(  0) 0) |
| [7] |
Allan D W. Time and Frequency(Time-Domain) Characterization, Estimation, and Prediction of Precision Clocks and Oscillators[J]. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 1987, 34(6): 647-654 DOI:10.1109/T-UFFC.1987.26997
(  0) 0) |
| [8] |
廖汐琳, 李浩军, 赵润根. GPS卫星钟差高精度模型化及在精密单点定位中的应用[J]. 大地测量与地球动力学, 2018, 38(8): 836-839 (Liao Xilin, Li Haojun, Zhao Rungen. Modeling of GPS Satellite Clock Error and Its Application in Precise Point Positioning[J]. Journal of Geodesy and Geodynamics, 2018, 38(8): 836-839)
(  0) 0) |
| [9] |
李成龙, 陈西宏, 刘继业, 等. 利用自适应TS-IPSO优化的灰色系统预报卫星钟差[J]. 武汉大学学报: 信息科学版, 2018, 43(6): 854-859 (Li Chenglong, Chen Xihong, Liu Jiye, et al. Predicting Satellite Clock Errors Using Grey Model Optimized by Adaptive TS-IPSO[J]. Geomatics and Information Science of Wuhan University, 2018, 43(6): 854-859)
(  0) 0) |
| [10] |
王国成, 柳林涛, 徐爱功, 等. 径向基函数神经网络在GPS卫星钟差预报中的应用[J]. 测绘学报, 2014, 43(8): 803-807 (Wang Guocheng, Liu Lintao, Xu Aigong, et al. The Application of Radial Basis Function Neural Network in the GPS Satellite Clock Bias Prediction[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(8): 803-807)
(  0) 0) |
| [11] |
Han T. Fractal Behavior of BDS-2 Satellite Clock Offsets and Its Application to Real-Time Clock Offsets Prediction[J]. GPS Solutions, 2020, 24(2): 35 DOI:10.1007/s10291-019-0950-z
(  0) 0) |
| [12] |
马卓希, 杨力, 贾小林. BDS星载原子钟周期项特性及预报研究[J]. 大地测量与地球动力学, 2017, 37(3): 292-296 (Ma Zhuoxi, Yang Li, Jia Xiaolin. Research on Prediction and Characterization of Periodic Variations in BDS Satellite Clocks[J]. Journal of Geodesy and Geodynamics, 2017, 37(3): 292-296)
(  0) 0) |
| [13] |
路晓峰, 杨志强, 贾小林, 等. 灰色系统理论的优化方法及其在卫星钟差预报中的应用[J]. 武汉大学学报: 信息科学版, 2008, 33(5): 492-495 (Lu Xiaofeng, Yang Zhiqiang, Jia Xiaolin, et al. Parameter Optimization Method of Gray System Theory for the Satellite Clock Error Predicting[J]. Geomatics and Information Science of Wuhan University, 2008, 33(5): 492-495)
(  0) 0) |
| [14] |
雷雨, 赵丹宁, 蔡宏兵. 利用结构自适应极端学习机预报导航卫星钟差[J]. 武汉大学学报: 信息科学版, 2018, 43(5): 664-668 (Lei Yu, Zhao Danning, Cai Hongbing. Prediction of Navigation Satellite Clock Offset by Adaptive Extreme Learning Machine[J]. Geomatics and Information Science of Wuhan University, 2018, 43(5): 664-668)
(  0) 0) |
| [15] |
邹丽萍, 宫响, 庄述鹏. 基于Elman神经网络的日总辐射曝辐量预估[J]. 青岛科技大学学报: 自然科学版, 2019, 40(5): 112-118 (Zou Liping, Gong Xiang, Zhuang Shupeng. Estimate of Daily Irradiation Exposure of Global Radiation Using Elman Neural Network[J]. Journal of Qingdao University of Science and Technology: Natural Science, 2019, 40(5): 112-118)
(  0) 0) |
| [16] |
王述红, 任艺鹏, 邢观华. 一种改进AFSA-Elman边坡位移预测网络[J]. 东北大学学报: 自然科学版, 2019, 40(1): 115-120 (Wang Shuhong, Ren Yipeng, Xing Guanhua. An Improved AFSA-Elman Slope Displacement Prediction Network[J]. Journal of Northeastern University: Natural Science, 2019, 40(1): 115-120)
(  0) 0) |
| [17] |
戴文战, 娄海川, 杨爱萍. 非线性系统神经网络预测控制研究进展[J]. 控制理论与应用, 2009, 26(5): 521-530 (Dai Wenzhan, Lou Haichuan, Yang Aiping. An Overview of Neural Network Predictive Control for Nonlinear Systems[J]. Control Theory and Applications, 2009, 26(5): 521-530)
(  0) 0) |
| [18] |
王宇谱, 吕志平, 崔阳, 等. 利用遗传小波神经网络预报导航卫星钟差[J]. 武汉大学学报: 信息科学版, 2014, 39(7): 809-814 (Wang Yupu, Lü Zhiping, Cui Yang, et al. Predicting Navigation Satellite Clock Bias Using a Genetic Wavelet Neural Network[J]. Geomatics and Information Science of Wuhan University, 2014, 39(7): 809-814)
(  0) 0) |
| [19] |
张雨浓, 肖秀春, 陈扬文, 等. Hermite前向神经网络隐节点数目自动确定[J]. 浙江大学学报: 工学版, 2010, 44(2): 271-275 (Zhang Yunong, Xiao Xiuchun, Chen Yangwen, et al. Number Determination of Hidden-Layer Nodes for Hermite Feed-Forward Neural Network[J]. Journal of Zhejiang University: Engineering Science, 2010, 44(2): 271-275)
(  0) 0) |
| [20] |
王宇谱, 吕志平, 陈正生, 等. 一种新的钟差预处理方法及在WNN钟差中长期预报中的应用[J]. 武汉大学学报: 信息科学版, 2016, 41(3): 373-379 (Wang Yupu, Lü Zhiping, Chen Zhengsheng, et al. A New Data Preprocessing Method for Satellite Clock Bias and Its Application in WNN to Predict Medium-Term and Long-Term Clock Bias[J]. Geomatics and Information Science of Wuhan University, 2016, 41(3): 373-379)
(  0) 0) |
| [21] |
王宇谱, 吕志平, 陈正生, 等. 卫星钟差预报的小波神经网络算法研究[J]. 测绘学报, 2013, 42(3): 323-330 (Wang Yupu, Lü Zhiping, Chen Zhengsheng, et al. Research on the Algorithm of Wavelet Neural Network to Predict Satellite Clock Bias[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(3): 323-330)
(  0) 0) |
| [22] |
王宇谱. 导航卫星原子钟钟差预报理论与方法研究[D]. 郑州: 信息工程大学, 2014 (Wang Yupu. Research on the Prediction Theories and Methods of Atomic Clock Bias for Navigation Satellites[D]. Zhengzhou: Information Engineering University, 2014)
(  0) 0) |
2. College of Geodesy and Geomatics, Shandong University of Science and Technology, 579 Qianwangang Road, Qingdao 266590, China
 2021, Vol. 41
2021, Vol. 41


