扩展卡尔曼滤波是高斯白噪声假设条件下常见的非线性滤波算法，已在导航定位、目标跟踪和制导控制等领域得到广泛运用^[1]。当高斯白噪声假设条件不符时会发生滤波精度下降的现象，为此许多学者提出基于模型补偿算法的自适应滤波理论，主要有Sage-Husa滤波、渐消滤波、抗差自适应滤波等^[2-3]，这些滤波方法在处理非高斯噪声污染问题时，真实噪声模型往往通过具有更大方差的高斯分布来涵盖。近年来，一种源于高斯混合模型(Gaussian mixture model, GMM)的多模近似方法为解决非高斯噪声问题提供了另一可行途径，比采用膨大方差的高斯分布近似法具有更高精度^[4-7]，在一定程度上可解决非线性非高斯模型的状态估计问题。但GMM建模参数不能随非高斯噪声统计特性的变化而变化，这种局限性使得高斯和滤波不能有效应对非高斯噪声的时变性。

本文在分析GMM分解特性的基础上研究高斯分量间位移参数对高斯和扩展卡尔曼滤波(Gaussian sum extend Kalman filter，GSEKF)拟合精度的影响，通过参数自适应技术获取最优位移参数，并对GMM进行实时修正，从而提升时变非高斯噪声环境下GSEKF的估计精度和稳定性。实验结果表明，本文探讨的参数自适应GSEKF算法在处理时变非高斯噪声问题上具有可行性。

1 问题描述

GNSS/SINS紧组合定姿定位系统具有较好的导航精度和抗干扰能力，在处于大失准角和高机动状况时，传统线性化模型会降低解算精度，需建立非线性数学模型^[8]。设k时刻状态向量X_k为包含姿态、速度、位置、陀螺漂移、加速度计漂移、GNSS时钟偏置和时钟漂移的18维列向量，其中姿态可用四元数表示，状态方程可概括为:

$ \boldsymbol{X}_{k}=f\left(\boldsymbol{X}_{k-1}\right)+\boldsymbol{G}_{k} \boldsymbol{W}_{k} $

(1)

式中，f(·)为非线性函数，G_k为噪声系数阵，W_k为过程噪声，具体设置见文献[1]。

GNSS观测数据经卫星钟差、电离层延迟和对流层延迟改正后，整理得到量测方程为:

$ \boldsymbol{L}_{k}=h\left(\boldsymbol{X}_{k}\right)+\boldsymbol{v}_{k} $

(2)

式中，h(·)为非线性函数，${{\boldsymbol{v}}_k} = \left[ {v_{{\rho _k}}^1, \cdots ,v_{{\rho _k}}^m,v_{{{\dot \rho }_k}}^1,} \right.{\left. { \cdots v_{{{\dot \rho }_k}}^m} \right]^{\rm{T}}} $ 为接收机噪声、多路径效应和轨道预测残差等引起的量测噪声向量，$ \boldsymbol{L}_{k}=\left[\rho_{k}^{1}, \cdots, \rho_{k}^{m}, \dot{\rho}_{k}^{1},\right.\left.\cdots \cdot \dot{\rho}_{k}^{m}\right]^{\mathrm{T}}$为伪距ρ和$ \dot{\rho}$伪距率组成的观测量，上标m为卫星数。

文献[9-10]对GNSS噪声残余项进行Allan方差分析，发现其与零均值高斯白噪声的特性不符，为非高斯与高斯的混合分布，且由于受到外界因素影响，具有一定时变性。因此，为改进组合导航定姿定位性能，需在滤波计算中顾及非高斯时变噪声的影响。

1.1 GMM建模

在非高斯环境下，利用GMM将式(2)中量测噪声分布模型近似为2个高斯分量的形式^[7]:

$ p(\boldsymbol{v}) \approx \varepsilon N\left(\boldsymbol{v}_{A} ; \boldsymbol{\mu}_{A}, \boldsymbol{\varSigma}_{A}\right)+(1-\varepsilon) N\left(\boldsymbol{v}_{B} ; \boldsymbol{\mu}_{B}, \boldsymbol{\varSigma}_{B}\right) $

(3)

式中，N(v; μ, Σ)为由均值μ和协方差Σ构成的高斯分量，下标A和B分别代表 2个不同的高斯分量; $ \boldsymbol{\mu}_{\mathrm{A}}=\boldsymbol{\mu}+d \sqrt{\lambda} \boldsymbol{u}, \boldsymbol{\mu}_{\mathrm{B}}=\boldsymbol{\mu}-d \sqrt{\lambda} \boldsymbol{u}, \boldsymbol{\varSigma}_{\mathrm{A}}=\boldsymbol{\varSigma}_{\mathrm{B}}=\boldsymbol{\varSigma}-d^{2} \lambda \boldsymbol{u} \boldsymbol{u}^{\mathrm{T}}, \lambda$，λ和u分别为协方差Σ的最大特征值和最大特征向量，d为影响2个高斯分量均值距离的位移参数，常根据协方差矩阵的最大特征值近似为2个等距离的高斯分量，即d=0.5;ε为具有不可测性和时变性的干扰噪声频率因子。

1.2 GMM局限性分析

非高斯噪声通过GMM分解可得到其分布模型的近似形式，然而现实导航测量环境具有动态性和复杂性等特点，故干扰噪声频率因子ε也会发生改变。这种不确定性使经典GMM对非高斯噪声建模存在一定局限性，若直接将其应用于动态导航GSEKF算法中则不能有效应对复杂的时变非高斯噪声环境，从而会引起滤波随机模型失配，严重时会降低估计精度。

2 位移参数自适应GSEKF算法 2.1 位移参数特性分析

GMM分解过程中位移参数d可限定2个不同高斯分量均值之间的距离。由式(3)可知，当d < 0.5时，分量(1－ε)N(v_B; μ_B, Σ_B)比分量εN(v_A; μ_A, Σ_A)弱; 当d>0.5时则相反。以往在非高斯噪声发生变化时，d=0.5的经验性取值并不具有最优性，若d能随时跟踪调整，则算法将具有一定的自适应能力。

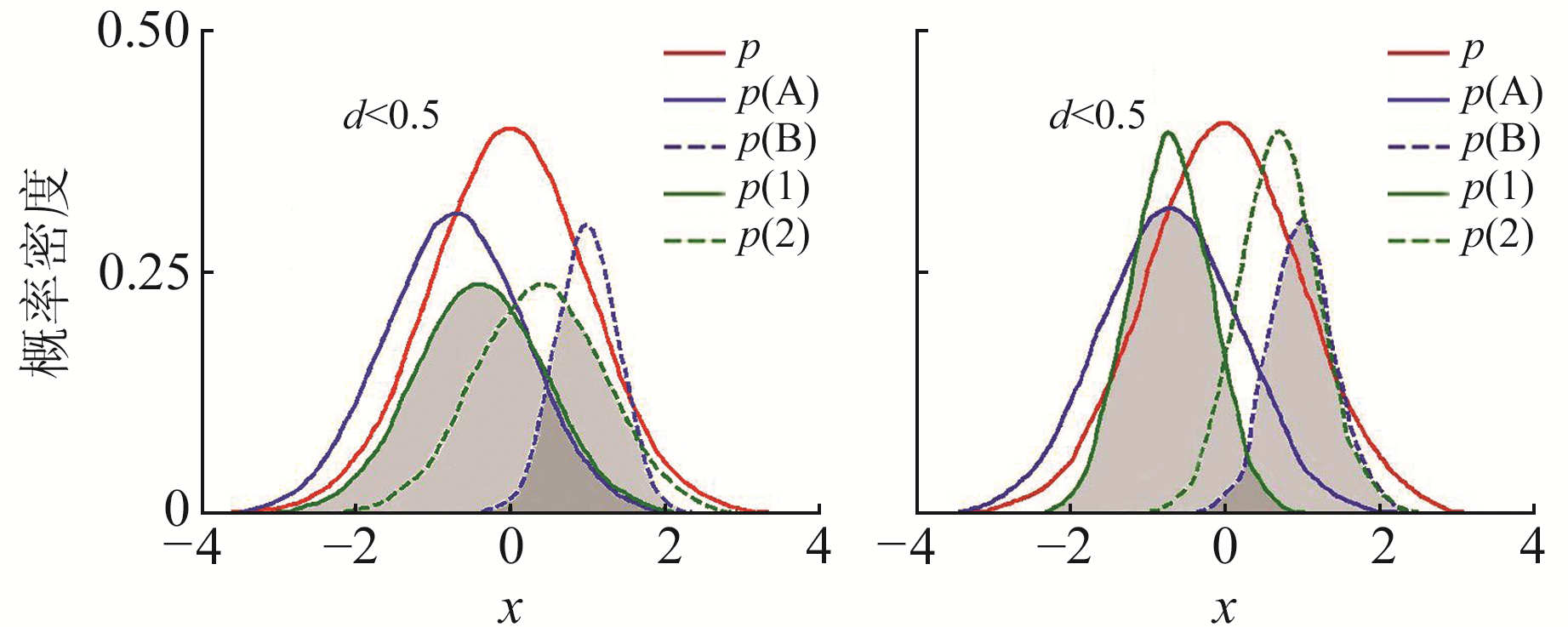
图 1为位移参数d与GMM分解过程的关系，红线p代表真实非高斯噪声模型，蓝线p(A)和p(B)分别代表 2个不同的高斯分量。当d <0.5时，GMM实际计算区域为绿线p(1)、p(2)和x轴所包围的区域，记为M; 同理d>0.5时对应区域为N。阴影范围代表实际GMM对真实非高斯噪声的近似程度，重合度越高则拟合效果越好。由于非高斯噪声的时变性会引起干扰噪声频率因子ε随之改变，故当分量(1－ε)N(v_B; μ_B, Σ_B)发生强化时，区域M中2个高斯分量的均值会背离零均值方向，此时若使d>0.5，则区域N的滤波效果比区域M更优。

由此可见，位移参数d的自适应变化能较好地跟踪时变非高斯噪声，使GMM分解过程更合理，对实际非高斯噪声的拟合也更接近，可获得更精准的随机模型，从而改善GSEKF的估计效果。

2.2 算法原理

本文从高斯分解合理性的角度出发，通过代价函数、位移参数和步长来弥补GMM的缺陷，优化算法的自适应能力，设计一种位移参数自适应GSEKF算法，该算法过程可描述为:

1) 确定自适应步长l，设位移参数d的变化范围为[d_a, d_b]，令d=d_a; 设代价函数为p_g(L_k|L_k－1, d)，最大似然函数为H=0。

2) 计算滤波时间，更新预测值$ \overline{\boldsymbol{X}}_{k}$及预测协方差阵$ \boldsymbol{\varSigma}_{\bar{X}_{k}}$，即

$ \overline{\boldsymbol{X}}_{k}=\boldsymbol{\varPhi}_{k, k-1} \hat{\boldsymbol{X}}_{k-1} $

(4)

$ \boldsymbol{\varSigma}_{\bar{X}_{k}}=\boldsymbol{\varPhi}_{k, k-1} \boldsymbol{\varSigma}_{\hat{X}_{k-1}} \boldsymbol{\varPhi}_{k, k-1}^{\mathrm{T}}+\boldsymbol{\varSigma}_{W_{k}} $

(5)

式中，Φ_{k, k－1}为状态转移阵，Σ_Wk为过程噪声协方差阵。

3) 依据式(3)对非高斯量测噪声进行建模，并将其与EKF算法结合，使原先单个EKF分解为2个平行的EKF子滤波器:

$ \hat{\boldsymbol{X}}_{k}^{i}=\overline{\boldsymbol{X}}_{k}-\boldsymbol{K}_{k}^{i}\left(\boldsymbol{A}_{k} \overline{\boldsymbol{X}}_{k}-\boldsymbol{L}_{k}\right) $

(6)

$ \boldsymbol{\varSigma}_{\hat{X}_{k}^{i}}=\left(\boldsymbol{I}-\boldsymbol{K}_{k}^{i} \boldsymbol{A}_{k}\right) \boldsymbol{\varSigma}_{\bar{X}_{k}}\left(\boldsymbol{I}-\boldsymbol{A}_{k}^{\mathrm{T}} \boldsymbol{K}_{k}^{i \mathrm{~T}}\right)+\boldsymbol{K}_{k}^{i} \boldsymbol{\varSigma}_{k}^{i} \boldsymbol{K}_{k}^{i \mathrm{~T}} $

(7)

$ \boldsymbol{K}_{k}^{i}=\boldsymbol{\varPhi}_{k, k-1} \boldsymbol{A}_{k}\left[\boldsymbol{A}_{k} \boldsymbol{\varSigma}_{\bar{X}_{k}} \boldsymbol{A}_{k}^{\mathrm{T}}+\boldsymbol{\varSigma}_{k}^{i}\right]^{-1} $

(8)

式中，A_k为观测设计阵，K_kⁱ为增益矩阵，Σ_kⁱ为观测噪声协方差阵，i为子滤波器个数。

4) 计算似然函数，若p_g(L_k|L_k－1, d)≥H，则令$ H=p_{g}\left(\boldsymbol{L}_{k} \mid \boldsymbol{L}_{k-1}, d\right), \hat{d}=d \boldsymbol{, } d=d+l$。重复2)直至满足d>d_b时迭代终止，即得到最优位移参数。

5) 对各子滤波加权求和，得到量测更新后的均值$ \hat{\boldsymbol{X}}_{k}$及协方差阵$\boldsymbol{\varSigma}_{\hat{X}_{k}} $ :

$ \hat{\boldsymbol{X}}_{k}=\sum\limits_{i=1}^{2} \omega_{k}^{i} \hat{\boldsymbol{X}}_{k}^{i} $

(9)

$ \boldsymbol{\varSigma}_{\hat{X}_{k}}=\sum\limits_{i=1}^{2} \omega_{k}^{i}\left[\boldsymbol{\varSigma}_{\hat{X}_{k}^{i}}+\left(\hat{\boldsymbol{X}}_{k}^{i}-\hat{\boldsymbol{X}}_{k}\right)\left(\hat{\boldsymbol{X}}_{k}^{i}-\hat{\boldsymbol{X}}_{k}\right)^{\mathrm{T}}\right] $

(10)

$ \omega_{k}^{i}=\omega_{k-1}^{i} \boldsymbol{\beta}_{k}^{i} / \sum\limits_{i=1}^{2} \omega_{k-1}^{i} \boldsymbol{\beta}_{k}^{i} $

(11)

$ \boldsymbol{\beta}_{k}^{i} \approx N\left(\boldsymbol{L}_{k}-\boldsymbol{A}_{k} \overline{\boldsymbol{X}}_{k}, \boldsymbol{A}_{k} \boldsymbol{\varSigma}_{\bar{X}_{k}} \boldsymbol{A}_{k}^{\mathrm{T}}+\boldsymbol{\varSigma}_{k}^{i}\right) $

(12)

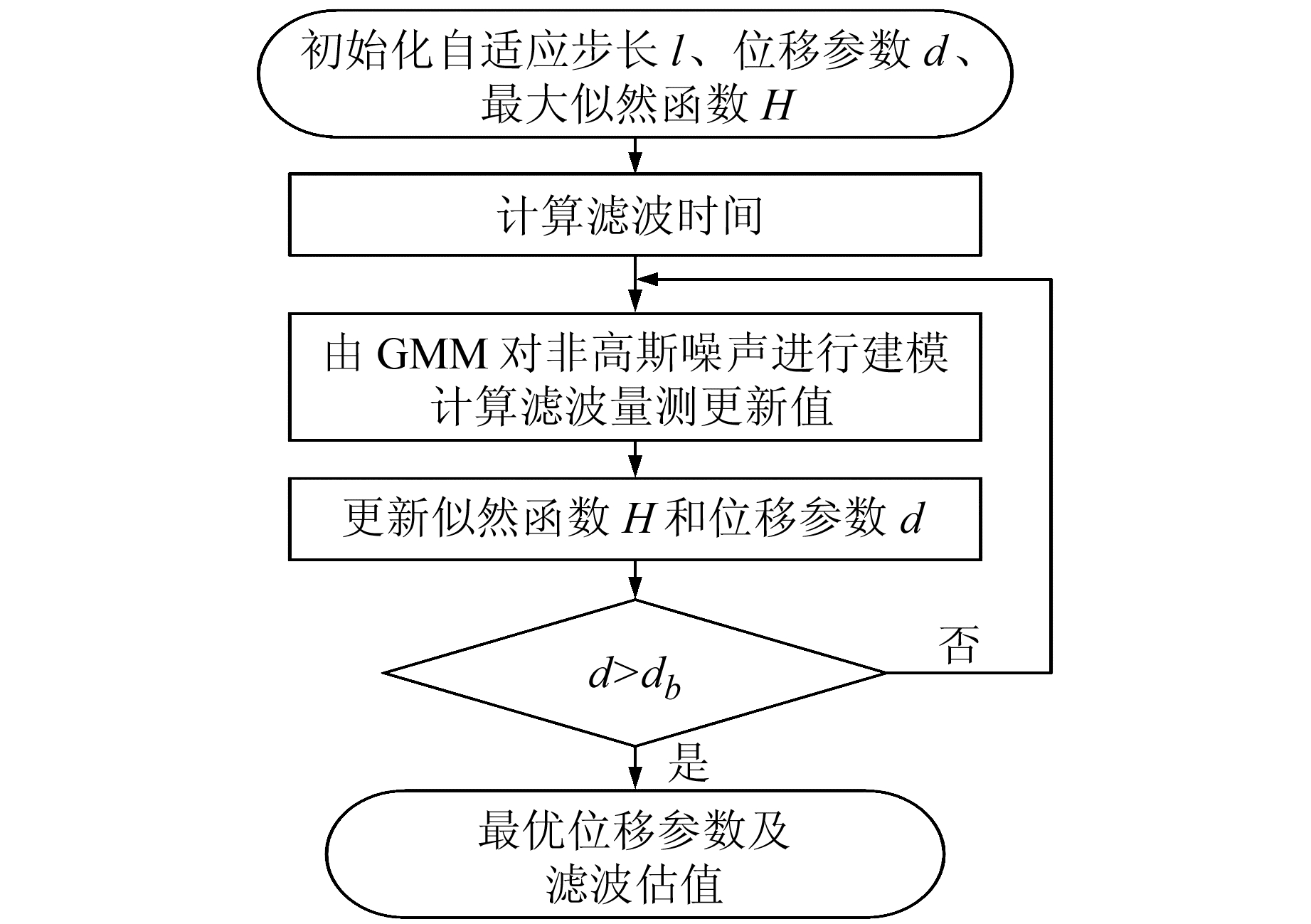
本文位移参数自适应GSEKF算法流程如图 2所示，通过位移参数d的自适应调节可弥补GMM的缺陷，在理论上具有更理想的估计精度。

3 算例与分析 3.1 仿真检校

本文通过GNSS/SINS紧耦合仿真测试平台验证算法的有效性。设置陀螺仪零偏为0.1°/h，陀螺仪随机游走为0.1°/$ \sqrt {{\rm{h}}} $，加速度计零偏为0.1 mg，随机游走为30 μg/$ \sqrt {{\rm{Hz}}} $ ，载体初始位置为126.67°E、45.79°N，初始姿态、速度及位置的标准差分别设为20″、10 cm/s和3 m。基于2019-10-16卫星星座分布和当前历元姿态仿真GNSS观测数据，仿真总时长为1 500 s，滤波周期为1 s。为考察算法对时变非高斯噪声的跟踪性能，模拟产生非高斯量测噪声分布满足p(v_k)≈εN(0, Σ_A)+(1-ε)N(0.5, Σ_B)，其中Σ_A=3Σ_B=diag(0.3²…0.3²)。

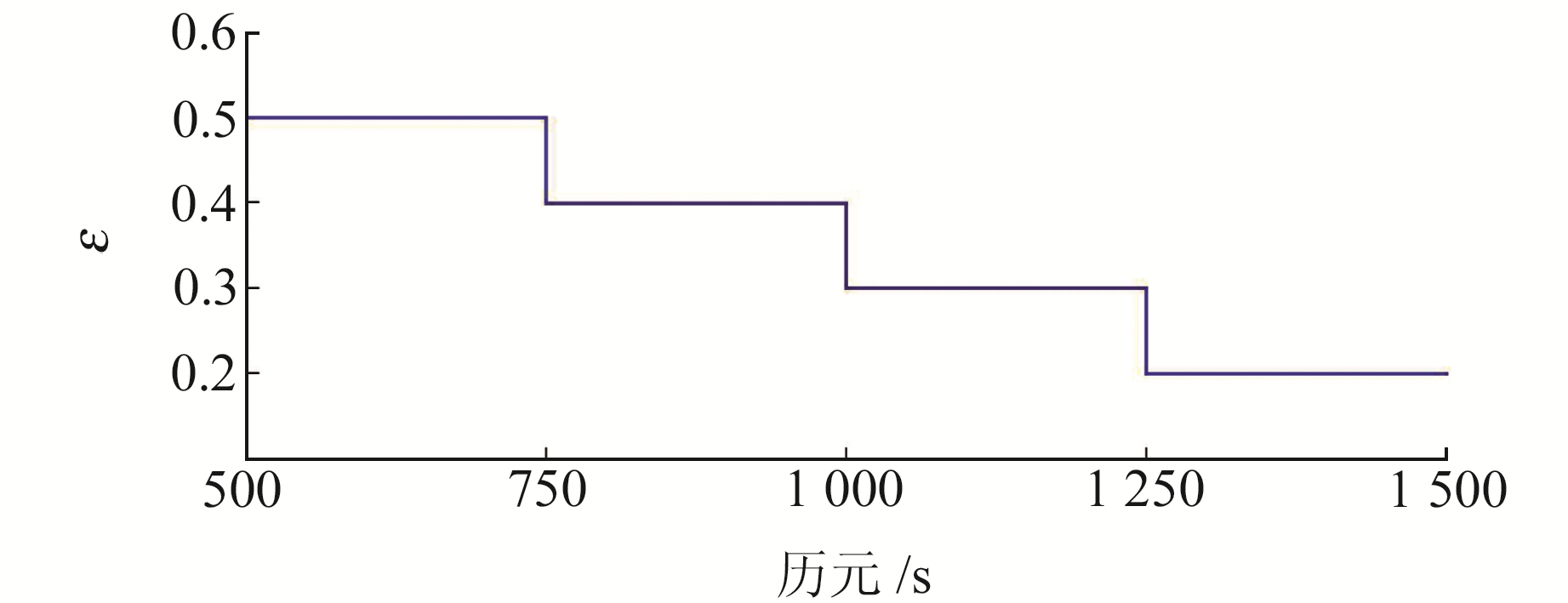
设置ε初值为0.5，并从500 s开始每隔250 s跳变1次，如图 3所示。用2种不同的滤波方案进行数据处理: 方案1，GSEKF算法; 方案2，位移参数自适应GSEKF算法。计算平台为Inter Core i7-8550u 1.8GHz，RAM 8GB，计算软件选用MATLAB R2014a。

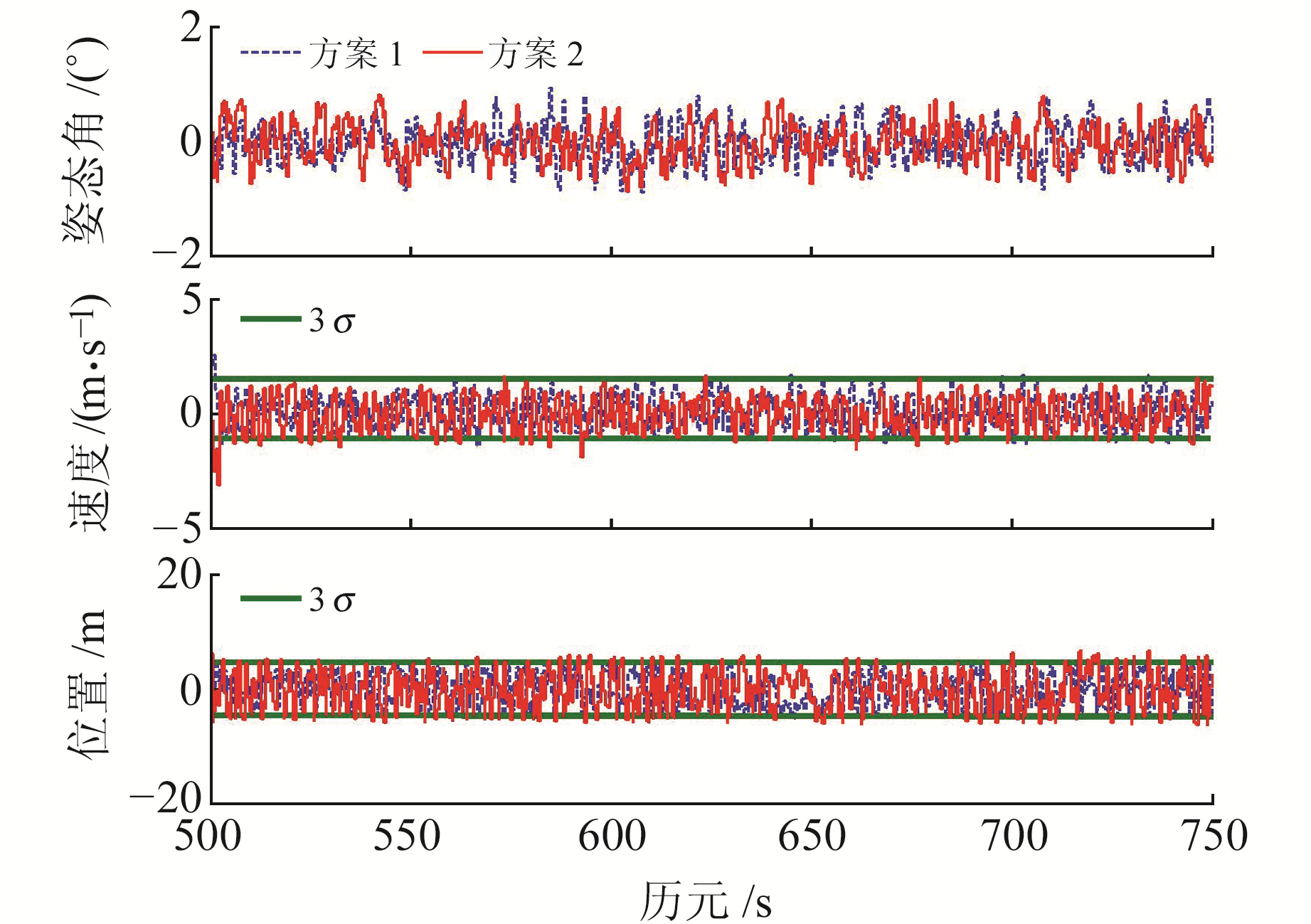
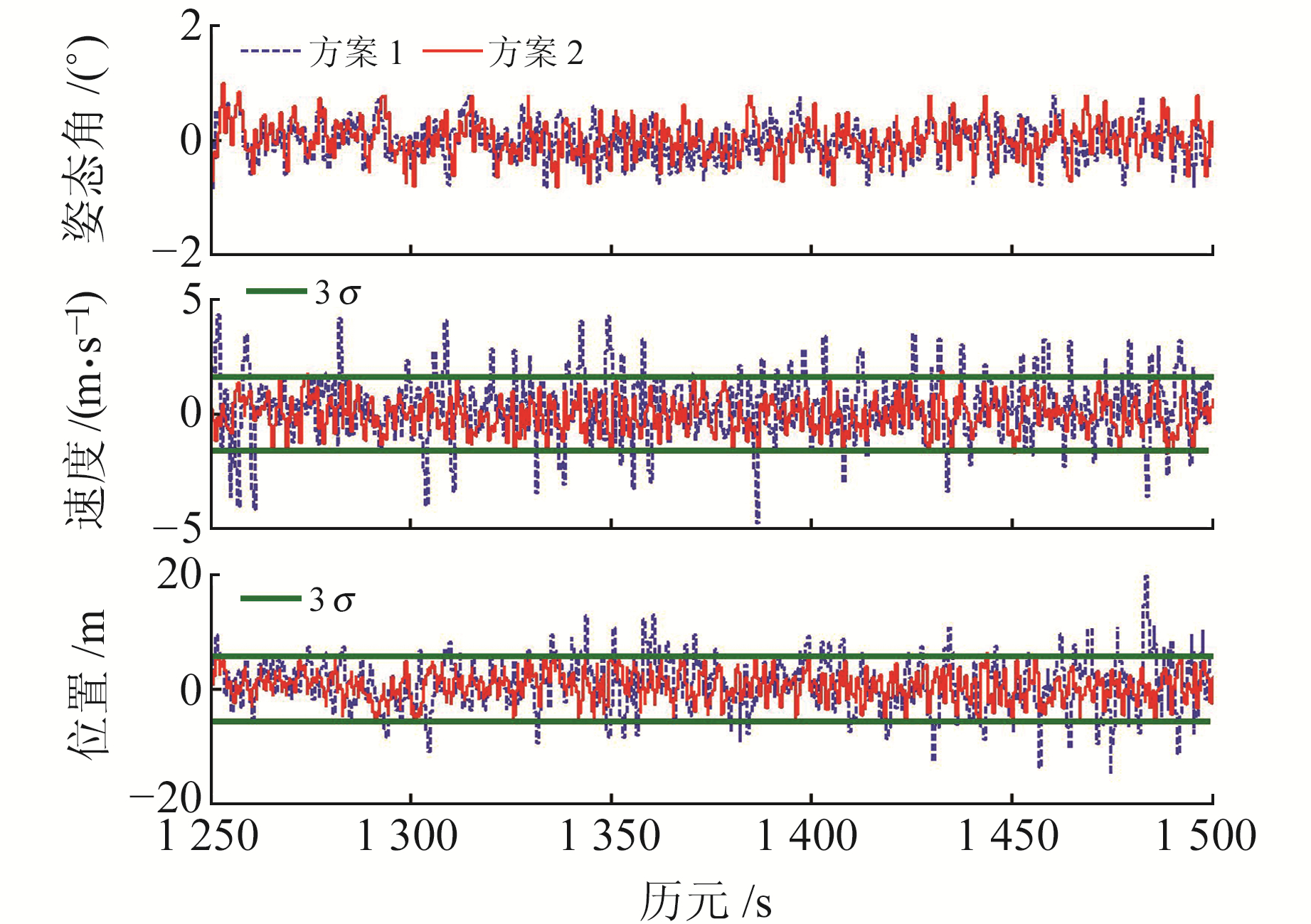
图 4为500~750 s滤波结果，在ε发生跳变前，方案1和方案2的估计结果相近，2个方案非高斯噪声建模较为准确，因此均能较好收敛。图 5为1 250~1 500 s滤波结果，由于方案1中GNSS量测噪声GMM建模不准确，导致姿态角估计结果较差，其相应的速度和位置估值也受到影响(多个历元点处的估值超过3σ误差界限); 而方案2利用自适应修正的位移参数可较好地跟踪时变非高斯噪声，取得比方案1更为稳定的滤波效果。

为体现算法比较的公正性，在相同参数条件下进行50次蒙特卡洛仿真实验，采用均方根误差(RMSE)和单位历元计算耗时进行量化比较。如表 1所示，方案1的估计误差略大，方案2由于对位移参数进行实时修正，使得GSEKF的随机模型具有自适应性，从而获得更高的滤波精度。但方案2需要对参数d进行迭代更新，因此耗时比方案1略长。

为进一步验证算法的性能，仿真不同历元数量的数据进行测试，结果如表 2所示。由表可知，历元数增加会使估计精度降低，但方案2始终优于方案1。以姿态估计为例，2 000个历元时方案2精度较方案1高约13%，4 000个历元时其精度优势更为明显，高约22%。由于姿态角精度会影响定位结果，因此方案2的位置估计精度也高于方案1。由此可见，方案2在复杂的时变非高斯噪声环境下可表现出较高的滤波精度，且在长航时导航解算中具有更好的滤波稳定性。

3.2 实验测试

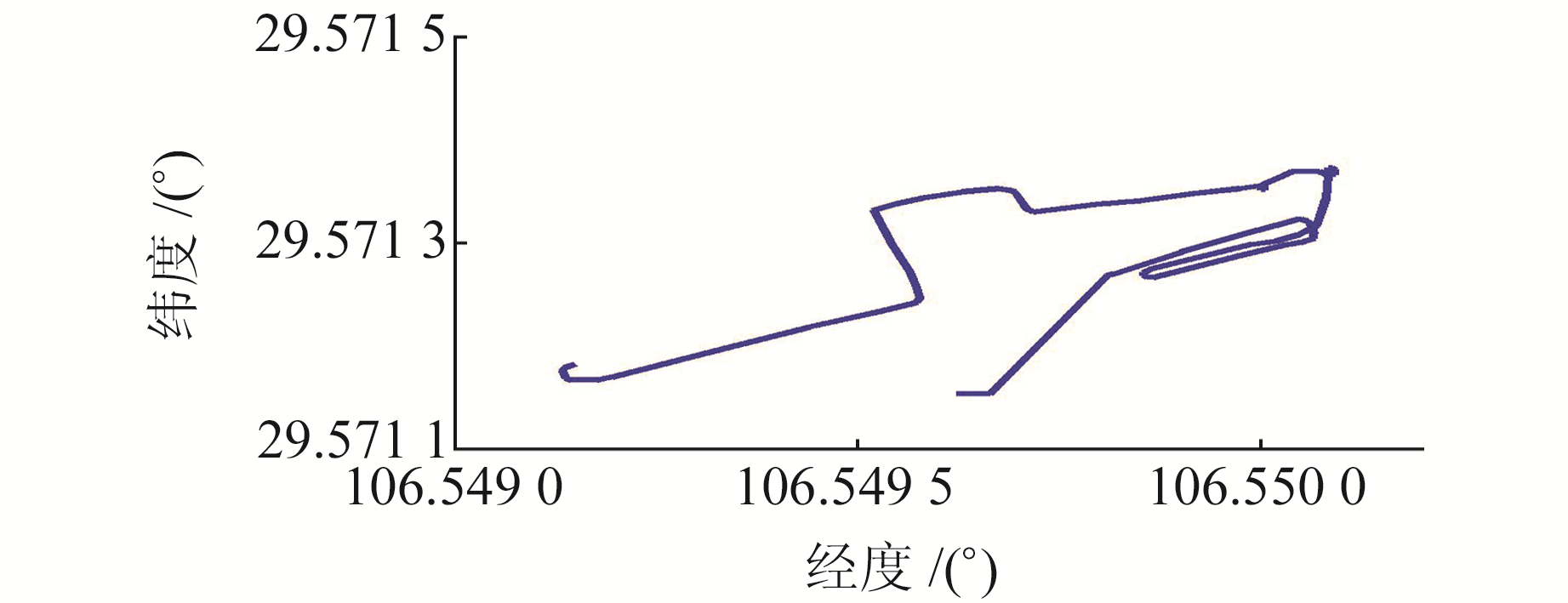
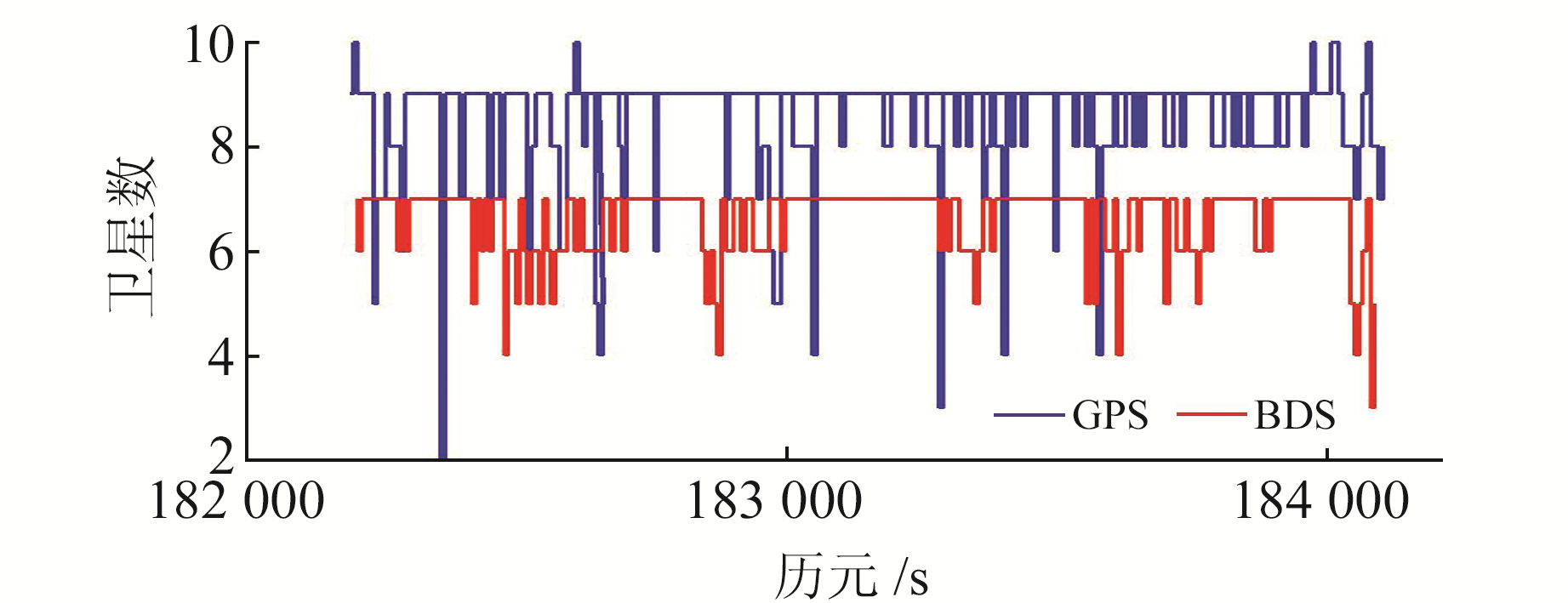
实验数据采集于GNSS/SINS组合导航装置，其中GNSS接收机可接收GPS和BDS双系统信号，采样率为1 Hz，三轴陀螺零偏稳定性小于0.5°/h，采样率为1 000 Hz。将基于光纤陀螺的GNSS/SINS高精度导航数据作为参考真值，并用于机动载体初始化。机动载体经过建筑物、树林和水面附近，其运动轨迹如图 6所示，GPS和BDS可见卫星状况如图 7所示，复杂变化的数据采集环境使得导航噪声具有时变性和非高斯特性。分别采用§3.1中方案1和方案2进行解算，滤波周期为1 s。

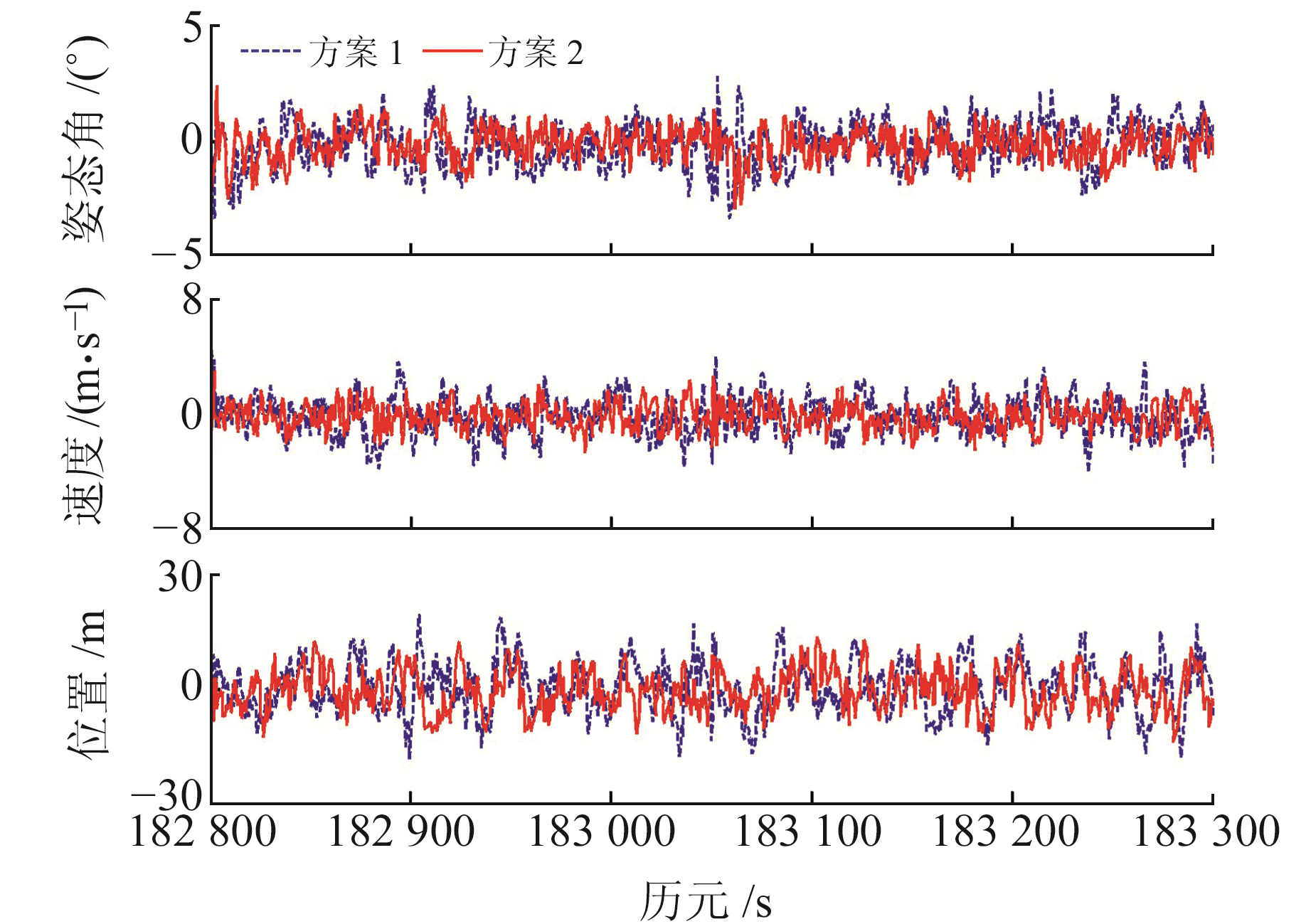
图 8为其中500个历元的滤波结果，从图中可以看出，方案2的滤波精度明显高于方案1，方案2估计误差(姿态、速度、位置)的最大值小于方案1。表 3为不同方案的量化比较结果，从表中可以看出，方案2优势明显，其滤波估计精度比方案1高(姿态提高4%、速度提高5%、位置提高7%)。在单位历元计算耗时方面，方案2略微增加，但未造成计算效率明显降低，这是因为位移参数自适应GSEKF算法虽然需要迭代计算位移参数，但可降低GMM的初值敏感性，加快GMM参数估计的收敛速度。由此说明，当机动载体导航环境发生改变时，本文讨论的顾及时变非高斯噪声的高斯和滤波算法能精化随机模型，进一步提高滤波性能。

4 结语

针对时变非高斯噪声下高斯和滤波精度和稳定性下降的问题，设计一种基于位移参数自适应调整的GSEKF算法，该算法可克服传统GMM的局限性，使GMM分解过程更加合理，可为复杂导航环境下的高精度定姿定位滤波解算提供可能。实验结果表明，在时变非高斯噪声导航环境下，本文算法可进一步改善滤波精度和自适应能力，且在长航时导航解算中能表现出更好的稳定性，对非线性非高斯滤波理论及组合导航定姿定位算法研究具有参考意义。