电离层通常指高度在60 ~ 2 000 km的大气层,是组成近地空间环境的关键要素之一。电离层总电子含量(TEC)是表征电离层形态结构、延迟特性的关键参数,电离层TEC的精确测定对于导航定位、地震前兆识别具有重要意义。当前国内外求取TEC的预测模型主要包含两类: 第1类是基于统计经验的模型[1],该类模型因使用方便且计算简单被广泛应用,但受电离层日夜变化、地域跨度等因素影响,预测效果并不理想[2]; 第2类是基于TEC观测数据,通过人工智能或数据挖掘等方法建立的模型,常用的有神经网络模型、时序分析模型等[3-5]。
机器学习与时序分析虽已广泛应用于TEC预测领域并取得良好效果,但对两者在不同外部环境下预测效果的对比分析较少。本文利用IGS中心提供的高精度TEC数据,分别采用BP神经网络及ARMA时序模型对武汉地区不同季节、电离层平静期和活跃期的TEC进行预测,并对不同样本长度对模型预测精度的影响进行分析,对健全和完善TEC预测体系具有积极意义。
1 基本理论 1.1 BP神经网络模型BP神经网络是模拟人脑神经系统结构特征而建立的函数模型,由大量神经元广泛互连形成,不同层神经元间通过权重连接。该模型具有非线性建模、函数逼近等功能,能以任意精度逼近任意N维到M维的映射,被广泛应用于电离层TEC预测领域[6]。作为一种单向传播的前向神经网络,BP神经网络模型一般包括输入层、隐含层(一个或多个)和输出层,并以误差平方和作为目标函数,采用梯度下降算法交替处理,随着“模式前向传播”和“误差反向传播”,直至目标函数取得最小值[7]。
任意连续函数均可仅用1层隐含层的BP神经网络进行逼近[8],因此本文进行TEC预测时选取只含1个隐含层的3层BP神经网络模型,以前7 d的电离层TEC值(共84个历元)作为输入,以后续3 d的电离层TEC值作为期望输出。在研究过程中,输入数据按照5:1:1随机分为3组,分别用于训练并调试网络、检验网络泛化能力及独立测试网络性能。综合考虑具有不同隐含层神经元个数的模型在验证集上的均方根误差,将隐含层神经元个数选定为25个,采用sigmoid函数作为激活函数(式(1)),输出层采用线性函数,设定初始学习速率为0.000 2,正则化系数为0.1:
| $ \operatorname{sigmoid}(z)=\frac{1}{1+\mathrm{e}^{-z}} $ | (1) |
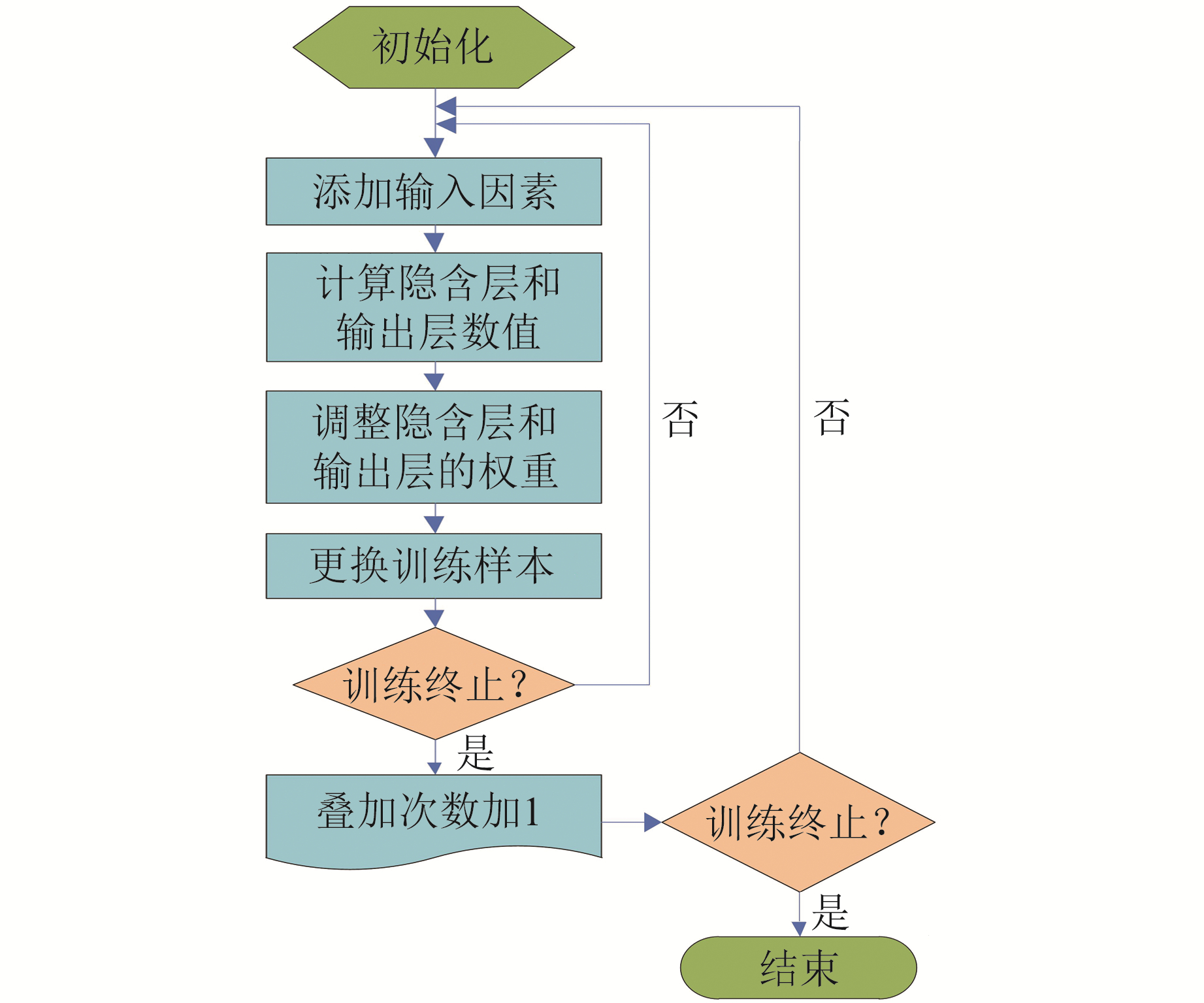
式中,z为输入因数x与权重因数w的向量积。确立模型结构后,利用BP网络对训练样本xm进行训练,以获取输入/输出参数间的权重系数w,并通过不断调试使模型训练达到要求,进而根据权重系数和预测时刻的输入参数确定预测结果(图 1)。
|
图 1 BP神经网络预测流程 Fig. 1 Prediction flow chart of BP neural network |
自回归移动平均方法(ARMA)是一种应用广泛且精确度较高的时序预测方法,对于时间序列{xt},若其零均值平稳且满足式(2)结构,则可称其为自回归移动平均模型,记作ARMA(p,q):
| $ \left\{\begin{array}{l} x_{t}=\phi_{1} x_{t-1}+\cdots+\phi_{p} x_{t-p}+\varepsilon_{t}- \\ \theta_{1} \varepsilon_{t-1}-\cdots-\theta_{q} \varepsilon_{t-q}, \phi_{p} \theta_{q} \neq 0 \\ E\left(\varepsilon_{t}\right)=0, \operatorname{var}\left(\varepsilon_{t}\right)=\sigma_{\varepsilon}^{2} \\ E\left(\varepsilon_{t} \varepsilon_{s}\right)=0, s \neq t \\ E\left(x_{s} \varepsilon_{t}\right)=0, \forall s<t \end{array}\right. $ | (2) |
式中,θq为模型系数,{εt}为白噪声序列。θq≠0可确保模型最高阶数为q,其余限制条件可确保{εt}为零均值白噪声。
在实际应用中,TEC受纬度、季节、地方时及太阳和地球活动等因素影响,呈现明显的年、季、日周期变化和随机波动,因此需要对TEC时序数据进行平稳化检验及差分处理。鉴于部分时间序列经多次差分均无法转为平稳序列或平稳性不明显,本文将TEC固定的周期性变化视为“周期效应”,采用式(3)分析并最大限度地减弱TEC序列中的周期性变化:
| $ x_{i j}=\bar{x} \times S_{i j} $ | (3) |
式中,xij为第i个周期第j个时刻的周期效应值;
对于包含n个周期,且每个周期含有m个时刻的目标序列(长度为m×n),各周期内各时刻的均值即为该时刻的长期平均值,可表示为:
| $ \bar{x}_{k}=\frac{\sum\limits_{i=1}^{n} x_{i k}}{n}, k=1, 2 \cdots, m $ | (4) |
该目标序列总平均数
| $ {{\bar x}_t} = \frac{{\sum\limits_{i = 1}^n {\sum\limits_{k = 1}^m {{x_{ik}}} } }}{{mn}} $ | (5) |
各时刻周期指数Sk可表示为:
| $ S_{k}=\frac{\bar{x}_{k}}{\bar{x}_{t}} $ | (6) |
当TEC序列满足零均值和平稳条件后,即可利用ARMA模型对其进行分析和建模,主要流程见图 2。

|
图 2 ARMA模型预测流程 Fig. 2 Prediction flow chart of ARMA model |
本文利用IGS发布的武汉地区经纬度为115.0°E、30.5°N的TEC时间序列数据,选取不同时段TEC序列,分别采用BP神经网络和ARMA模型进行不同季节时段、不同电离层活跃程度、不同样本长度对比预测,并将预测结果与IGS TEC发布值进行比对分析,通过定义相对精度P、日均相对精度Pave和均方差RMSE来评价预测效果[9-10]:
| $ \begin{array}{c} P=1-\frac{\left|I_{\mathrm{pre}}-I_{\mathrm{IGS}}\right|}{I_{\mathrm{IGS}}} \times 100 \% \end{array} $ | (7) |
| $ P_{\mathrm{ave}}=\frac{1}{N} \sum\limits_{r=1}^{n} P $ | (8) |
| $ \mathrm{RMSE}=\sqrt{\frac{1}{N} \sum\limits_{r=1}^{N}\left(I_{\mathrm{pre}}-I_{\mathrm{IGS}}\right)^{2}} $ | (9) |
式中,Ipre为预测值,IIGS为IGS发布的TEC观测值,N为当天观测的历元数。
2.1 不同季节时段对比预测分别选取2017-03-20~30、06-20~30、10-20~30、12-20~30四个不同季节时段的数据作为TEC预测建模数据,每个时段均以前7 d的IGS TEC数据作为样本序列预测后3 d的TEC值。两种模型不同季节时段的TEC预测结果如图 3所示,图 4为模型预测值与IGS TEC值的残差。

|
图 3 两种模型4个时段的预测结果 Fig. 3 Predicted results in four periods of two models |
由图 3可以看出,BP神经网络和ARMA模型在不同季节时段均表现优异,预测结果与IGS TEC发布值具有良好的一致性,初步印证两种模型在TEC预测建模中的合理性。结合图 4发现,两种模型在春、夏时段残差较小,预测效果优于秋、冬时段。从单时段表现来看,两种模型在春、夏时段的预测精度相当,但ARMA模型的预测残差在秋季时段波动较大,可能与9月初爆发的太阳耀斑对电离层的强扰动作用有关,而BP神经网络模型在冬季的预测效果最差。
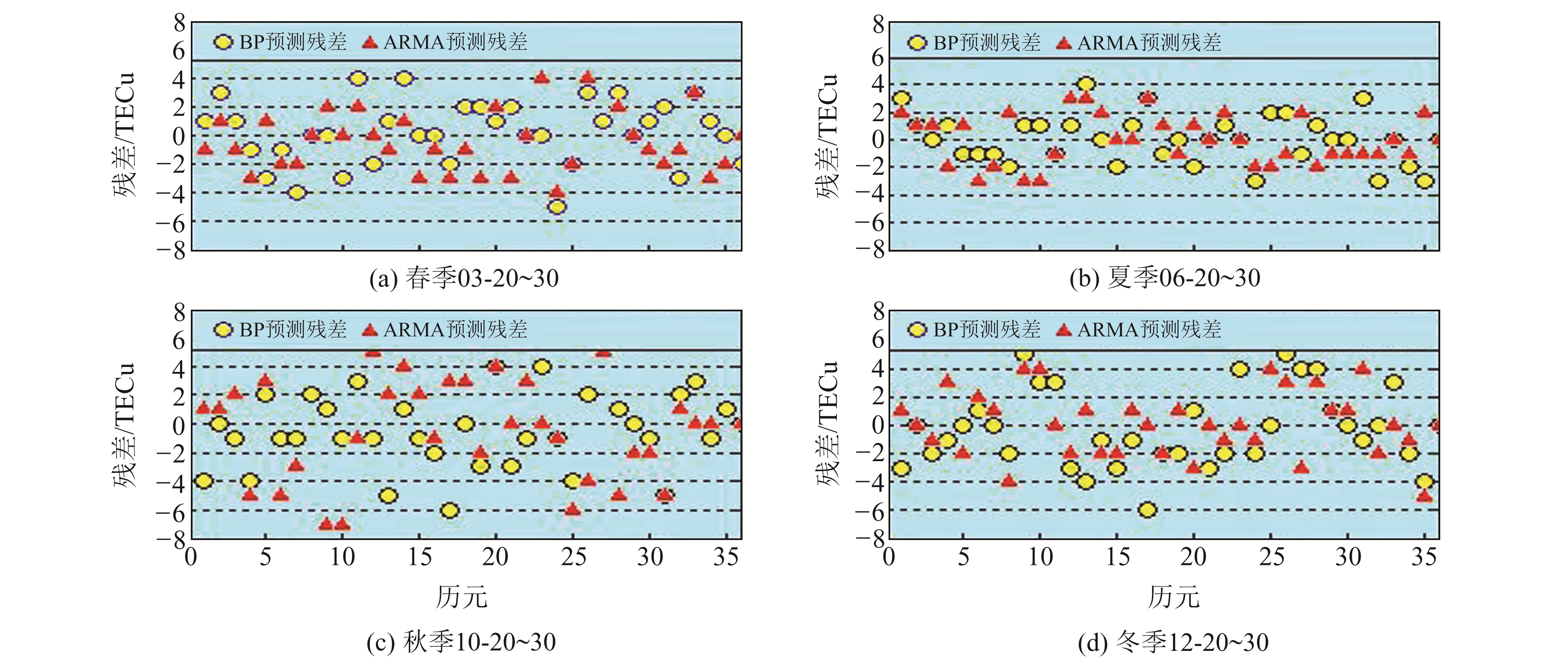
|
图 4 两种模型4个时段的预测残差 Fig. 4 Residual of predicted values in four periods of two models |
为更加详细地比较BP神经网络和ARMA模型的预测精度,分别统计两种模型在不同季节时段的预测值残差分布情况(表 1,单位%)。
|
|
表 1 不同时段TEC预测残差 Tab. 1 Residual of predicted values in different periods |
由表 1可知,两种模型在4个时段的预测残差约85%在3 TECu以内,约1/3小于1 TECu,残差大于3 TECu的部分约占10%。结合模型预测值的相对精度和均方根误差(表 2)可知,ARMA模型的总体预测精度略优于BP神经网络。分时段来看,ARMA模型在春、冬时段的预测效果明显优于BP神经网络,而BP神经网络在秋季时段的预测效果略优于ARMA模型,两者在夏季时段的预测效果相差较小。
|
|
表 2 不同时段TEC预测值均方根误差和相对精度统计 Tab. 2 Statistics of RMSE and relative accuracy of predicted values in different periods |
选取2017-07-06~15、09-06~15两个时段的数据分别作为电离层平静期与活跃期的TEC预测建模数据,每个时段均以前7 d的TEC数据作为样本序列预测后3 d的TEC值,两种模型的建模方案与数据处理方法不变,预测结果如图 5所示,图 6为模型预测值与原始值的残差。

|
图 5 平静期与活跃期两种模型TEC预测结果 Fig. 5 Comparison of predicted results in ionospheric quiet and active period |
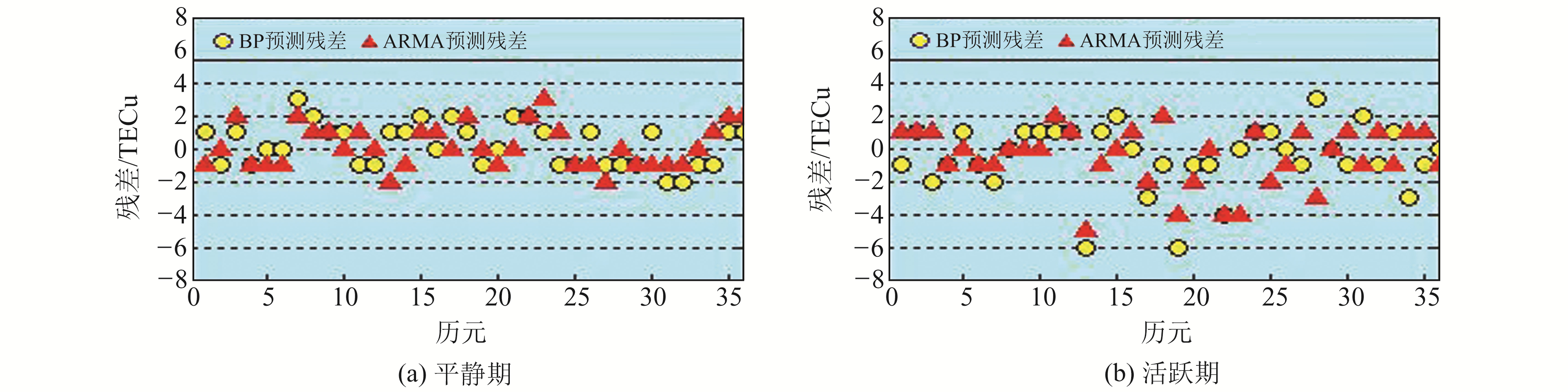
|
图 6 平静期与活跃期两种模型预测结果残差 Fig. 6 Residual of predicted values in ionospheric quiet and active period |
综合图 5和图 6发现,两种模型在电离层平静期和活跃期均能较好地反映TEC的变化特征。从整体效果来看,两种模型在平静期的预测效果优于活跃期; 从模型自身表现来看,两种模型在活跃期的精度相当,预测残差大部分在3 TECu以内,而BP神经网络模型在活跃期的拟合精度明显优于ARMA模型,说明ARMA模型对电离层活跃期的TEC不规则变化更加敏感,从而影响预测精度。统计BP神经网络和ARMA模型在平静期和活跃期预测残差,结果见表 3(单位%)和表 4(单位%)。
|
|
表 3 平静期TEC预测残差 Tab. 3 Residual of predicted values in ionosphericquiet period |
|
|
表 4 活跃期TEC预测残差 Tab. 4 Residual of predicted values in ionospheric active period |
由表 3和表 4分析发现,在平静期BP神经网络的预测残差约31.1%在1 TECu以内,约12.1%大于3 TECu; ARMA模型的预测残差约31.8%小于1 TECu,残差超过3 TECu的部分约占12.5%。由此可知,在平静期ARMA模型的预测效果略优于BP神经网络。在活跃期BP神经网络的预测残差约26.9%小于1 TECu,残差超过3 TECu的部分约占21.5%;ARMA模型中这两项数据分别为25.0%和24.5%,表明在活跃期BP神经网络的预测效果明显优于ARMA模型。两种模型的预测残差低于3 TECu的部分均占70%以上,因此无论在平静期或是活跃期,BP神经网络和ARMA模型都是较为理想的TEC预测方法。
分析两种模型在不同时期的均方根误差RMSE和相对精度Pave(表 5)发现,ARMA模型在平静期整体Pave高于BP神经网络,而Pave值在活跃期差异不明显。从单日表现来看,BP神经网络在首日预测精度最佳,而ARMA模型预测精度则在预测第2天达到峰值,推测该现象可能与预测样本长度有关,即7 d样本长度难以支撑预测精度的持续提升。
|
|
表 5 平静期和活跃期两种模型的预测值均方根误差和相对精度统计 Tab. 5 Statistics of RMSE and relative accuracy of predicted values in ionospheric quiet and active period |
选取2017-04-06~05-05电离层平静期武汉地区经纬度为115.0°E、30.5°N处的TEC时间序列数据,分别基于BP神经网络和ARMA模型采用7 d样本、14 d样本、21 d样本、28 d样本4种模式预测后3 d的TEC值,探究两种模型在不同样本长度下的预测效果,结果见图 7和图 8,表 6为不同预测模式的均方根误差与相对精度统计。
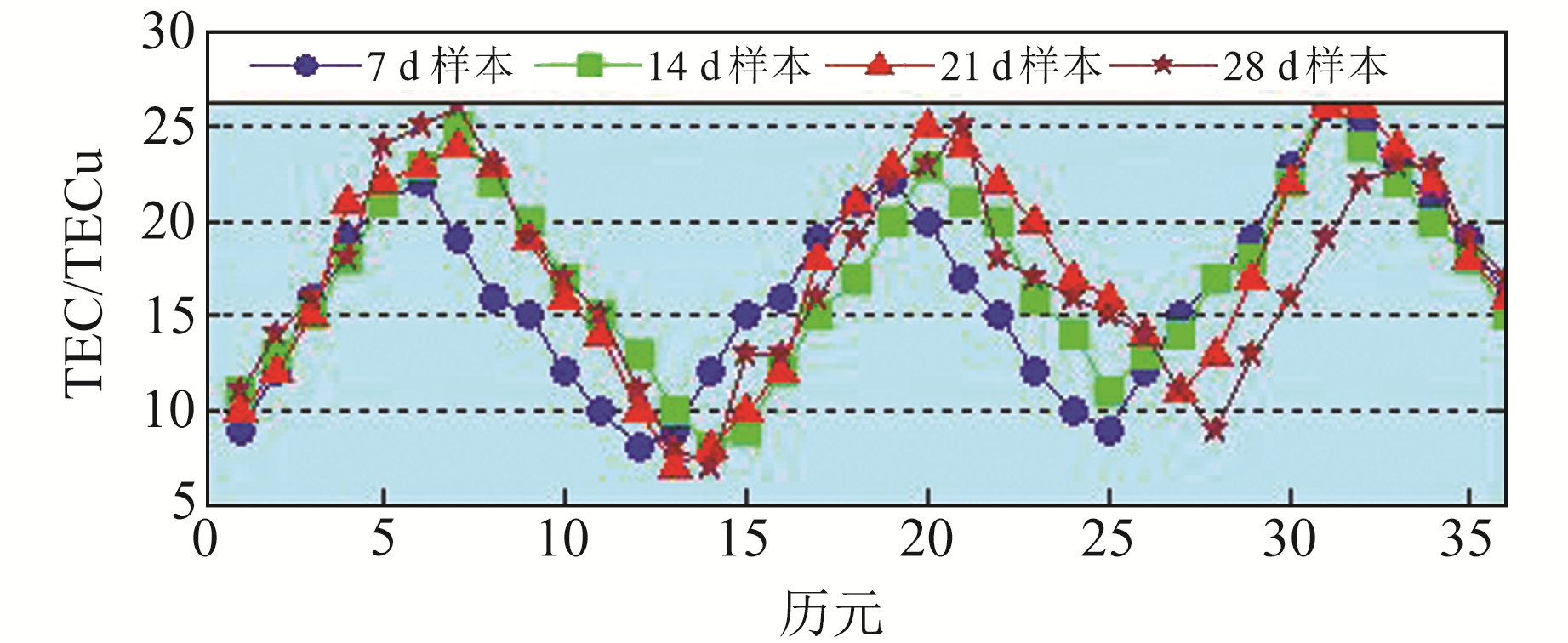
|
图 7 不同模式下BP神经网络预测结果 Fig. 7 Prediction results of BP neural network with different sample length |

|
图 8 不同模式下ARMA模型预测结果 Fig. 8 Prediction results of ARMA model with different sample length |
|
|
表 6 不同模式下两种模型均方根误差与相对精度统计 Tab. 6 Statistics of RMSE and relative accuracy of predicted values with different sample length |
综合图 7和表 6可以看出,样本长度对预测精度存在明显影响。ARMA模型在7 d样本处精度达到峰值,随着样本长度的增加,预测精度反而开始降低; BP神经网络模型在14 d样本处精度最高,但其RMSE较21 d样本明显偏大。21 d样本处3 d预测精度分别为92.2%、92.7%、92.6%,精度平稳可靠且RMSE最小。由此推断,BP神经网络模型在21 d样本处预测效果最佳。
因此可以推测,对于天数既定的TEC预测,当样本长度超过阈值后,两种模型的预测精度都难以进一步提升。同时也反映出对于3 d的TEC预测,ARMA模型在短样本模式下效果较好,而BP神经网络在较长样本模式预测中才能发挥明显优势。
3 结语本文基于BP神经网络模型和ARMA模型,利用IGS中心发布的武汉地区电离层TEC样本数据分别进行不同季节时段、不同太阳活动情况、不同样本长度下的TEC 3 d预测实验,并将预测结果与IGS中心提供的实测数据进行对比分析,得到如下结论:
1) 7 d样本模式下,两种模型在4个季节时段中的预测精度都能较好地反映武汉地区TEC的变化特征。从各时段预测残差可知,两种模型在春、夏时段的预测效果优于秋、冬时段; 而从单时段表现来看,两种模型在夏季时段的预测精度大致相同,ARMA模型在春、冬时段的预测效果优于BP神经网络。
2) 7 d样本模式下,两种模型在电离层平静期的预测精度相当; 而在电离层活跃期,由于BP神经网络具有良好的非线性预测与抗波动干扰能力,其预测精度优于ARMA模型。
3) ARMA模型在7 d样本模式下的平均精度最高,而BP神经网络在21 d样本模式下的预测效果最佳,即ARMA模型和BP神经网络的最佳样本长度分别为7 d和21 d。ARMA模型的短样本模式预报精度更高,BP神经网络在较长样本模式预测中才能发挥较好的效果。
| [1] |
方涵先, 翁利斌, 杨升高, 等. IRI、NeQuick和Klobuchar模式比较研究[J]. 地球物理学进展, 2012, 27(1): 1-7 (Fang Hanxian, Weng Libin, Yang Shenggao, et al. The Research of IRI、NeQuick and Klobuchar Models[J]. Progress in Geophysics, 2012, 27(1): 1-7)
(  0) 0) |
| [2] |
Luo W H, Liu Z Z, Li M. A Preliminary Evaluation of the Performance of Multiple Ionospheric Models in Low- and Mid-Latitude Regions of China in 2010-2011[J]. GPS Solutions, 2014, 18(2): 297-308 DOI:10.1007/s10291-013-0330-z
(  0) 0) |
| [3] |
袁天娇. 基于机器学习的电离层总电子含量经验预报模型[D]. 北京: 中国科学院大学, 2017 (Yuan Tianjiao. Empirical Model of Ionospheric Total Electron Content Using Machine Learning Technique[D]. Beijing: University of Chinese Academy of Sciences, 2017)
(  0) 0) |
| [4] |
张小红, 任晓东, 吴风波, 等. 自回归移动平均模型的电离层总电子含量短期预报[J]. 测绘学报, 2014, 43(2): 118-124 (Zhang Xiaohong, Ren Xiaodong, Wu Fengbo, et al. Short-Term TEC Prediction of Ionosphere Based on ARIMA Model[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(2): 118-124)
(  0) 0) |
| [5] |
田祥雨, 刘立龙, 陈军, 等. 基于ARIMA与Holt-Winters组合模型的电离层TEC预报[J]. 测绘科学技术学报, 2018, 35(1): 44-48 (Tian Xiangyu, Liu Lilong, Chen Jun, et al. Ionospheric TEC Prediction Based on Combination Model of ARIMA and Holt-Winters[J]. Journal of Geomatics Science and Technology, 2018, 35(1): 44-48)
(  0) 0) |
| [6] |
陈必焰, 戴吾蛟, 蔡昌盛, 等. 时间序列与神经网络组合方法在电离层TEC预报中的应用[J]. 工程勘察, 2011, 39(4): 64-68 (Chen Biyan, Dai Wujiao, Cai Changsheng, et al. An Application of Time Series and Neural Network Method in Ionospheric TEC Prediction[J]. Journal of Geotechnical Investigation and Surveying, 2011, 39(4): 64-68)
(  0) 0) |
| [7] |
付来迎. 经验模态分解在电离层TEC多尺度分析预测中的应用研究[D]. 南昌: 东华理工大学, 2016 (Fu Laiying. Application of Empirical Mode Decomposition in the Multi Scale Analysis and Prediction of Ionospheric TEC[D]. Nanchang: East China University of Technology, 2016)
(  0) 0) |
| [8] |
Hecht-Nielsen R. Neurocomputing: Picking the Human Brain[J]. IEEE Spectrum, 1988, 25(3): 36-41 DOI:10.1109/6.4520
(  0) 0) |
| [9] |
吉长东, 王强, 沈祎凡, 等. 自回归神经网络的电离层总电子含量预报[J]. 导航定位学报, 2018, 6(4): 96-101 (Ji Changdong, Wang Qiang, Shen Yifan, et al. TEC Prediction of Ionosphere Based on Nonlinear Auto Regressive Model[J]. Journal of Navigation and Positioning, 2018, 6(4): 96-101)
(  0) 0) |
| [10] |
陆建华, 王斌, 胡伍生. 利用BP神经网络改进电离层短期预报模型[J]. 测绘科学技术学报, 2017, 34(1): 1-4 (Lu Jianhua, Wang Bin, Hu Wusheng. Improved Prediction Model of Ionospheric TEC by BP Neural Network[J]. Journal of Geomatics Science and Technology, 2017, 34(1): 1-4)
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41

