2. 中国地震局地震预测研究所地震预测重点实验室,北京市复兴路63号,100036
获取高空间分辨率的重力异常场对研究地球形状、地球内部结构和物质迁移活动等重要地球物理问题至关重要,但受限于仪器精度和时间经济成本,现阶段难以直接通过地表重力观测手段获取高空间分辨率的重力异常场,而通常是通过对观测结果进行推估获取[1-2]。随着重力观测数据的不断积累,不同区域的重力观测数据覆盖率逐渐提升[3-4],同时大数据分析技术的兴起,使深度神经网络在各个方面取得广泛应用[5]。深度神经网络中的循环神经网络主要应用于序列数据分析,在数据趋势推估方面具有良好的效果[6]。
基于循环神经网络在数据推估方面的优势,本文首先对观测的自由空气重力异常数据进行随机采样,作为训练循环神经网络模型的数据集;然后基于长短期记忆循环神经网络,结合训练数据集对神经网络进行训练;最后通过比较分析神经网络和传统克里金方法计算结果的差异,对2种方法进行评价。
1 自由空气重力异常数据为方便对比循环神经网络和传统克里金插值方法的结果,采用2014和2017年鄂尔多斯西南缘地区的自由空气重力异常数据[7],该数据包含385个重力观测点。图 1为观测点空间分布图,圆点不同颜色表示自由空气重力异常值。重力异常观测仪器为Burris相对重力仪,采用A-B-C-…-C-B-A观测方式来提高观测精度,平差处理软件为LGADJ[8]。在经过正常场改正和高程改正后,可得到自由空气重力异常。

|
图 1 鄂尔多斯西南缘自由空气重力异常场 Fig. 1 Free-air gravity anomaly field in the southwestern margin of Ordos |
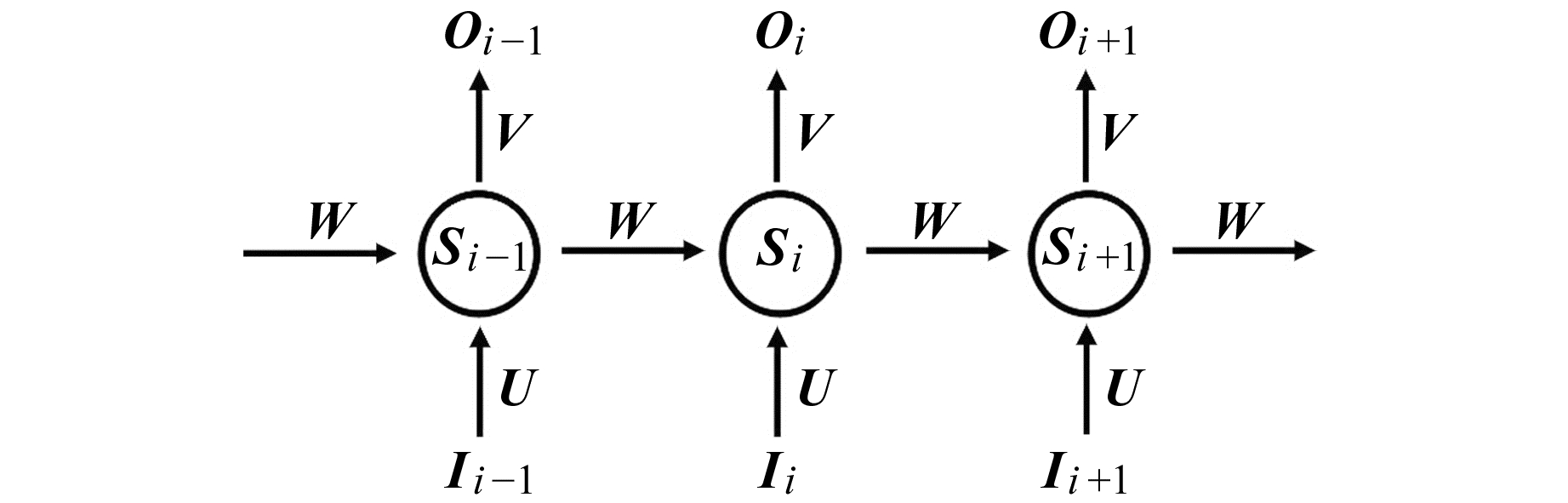
图 2为循环神经网络结构图,由输入层Ii、隐藏层Si和输出层Oi组成,其中I、S和O为向量。U为输入层到隐藏层的权重矩阵,V为隐藏层到输出层的权重矩阵,W为上一神经元的输出权重矩阵。上述各变量的关系可表示为:
|
图 2 循环神经网络结构 Fig. 2 Structure of recurrent neural network |
| $ \boldsymbol{O}_{i}=g\left(\boldsymbol{V} \boldsymbol{S}_{i}\right) $ | (1) |
| $\boldsymbol{S}_{i}=f\left(\boldsymbol{U} \boldsymbol{I}_{i}+\boldsymbol{W} \boldsymbol{S}_{i-1}\right) $ | (2) |
式中,f和g为激活函数,本文采用反正切函数作为激活函数[8]。
由式(1)和(2)可得:
| $\begin{array}{c} \boldsymbol{O}_{i}=g\left(\boldsymbol{V} f\left(\boldsymbol{U} \boldsymbol{I}_{i}+\boldsymbol{W} f\left(\boldsymbol{U} \boldsymbol{I}_{i-1}+\boldsymbol{W} f\left(\boldsymbol{U} \boldsymbol{I}_{i-2}+\right.\right.\right.\right. \\ \left.\left.\left.\boldsymbol{W} f\left(\boldsymbol{U}\boldsymbol{I}_{i-3}+\boldsymbol{\cdots}\right)\right)\right)\right) \end{array} $ | (3) |
由式(3)可知,循环神经网络可传递已知序列之间的信息,可利用已有数据之间的联系来推估未知数据,该特性可实现利用零散的观测数据推估整个研究区内观测数据的空间分布。将Si替换为Sij,j为隐藏层数,当j大于1时,表明神经网络包含多层结构。
2.2 长短期记忆神经元式(3)也同时表明该神经网络存在不足:在训练模型时需要采用梯度下降法,通过反向迭代来求解隐藏层Si,当数据序列很长时,在模型训练计算时会出现梯度爆炸和梯度弥散问题[9],即Si过大或趋于0。出现梯度爆炸和梯度弥散都将影响序列数据之间信息的传递,进而造成循环神经网络计算结果较差,无法满足应用研究的需求。为解决梯度爆炸和梯度弥散问题,长短期记忆神经元被引入到循环神经网络中,并已取得良好效果[6, 10]。
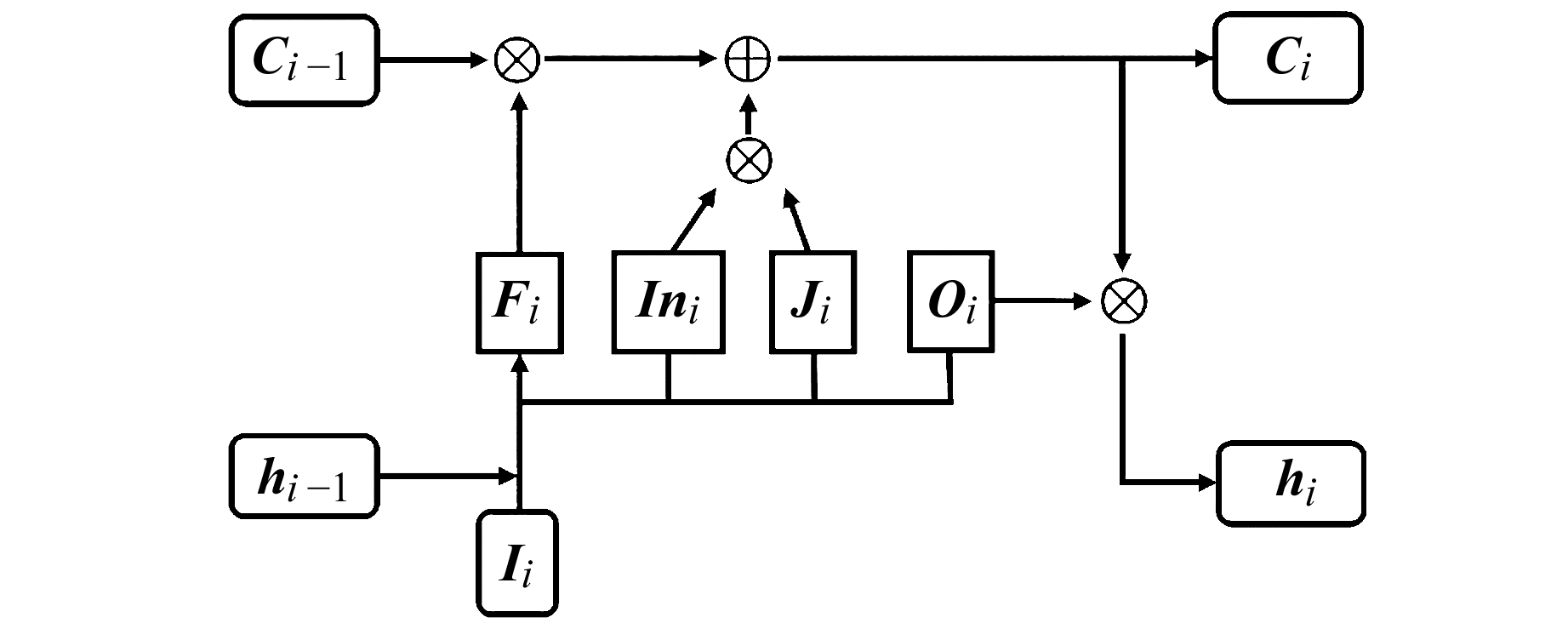
LSTM将RNN中Si替换为2个输出值进行处理,即神经元的当前状态值Ci和输出值hi。Ci可保存序列数据的长期状态,通过遗忘门(Fi)、输入门(Ii)和输出门(Oi)进行控制。图 3为LSTM神经元结构图,其中各变量之间的数学关系见式(4):
|
图 3 长短期记忆神经网络结构 Fig. 3 Structure of long short-term memory |
| $\begin{array}{l} \boldsymbol{I} \boldsymbol{n}_{i}=\tanh \left(\boldsymbol{W}_{x I n} \boldsymbol{I}_{i}+\boldsymbol{W}_{h I n} \boldsymbol{h}_{i-1}+b_{i}\right) \\ \boldsymbol{J}_{i}=\operatorname{sigm}\left(\boldsymbol{W}_{x j} \boldsymbol{I}_{i}+\boldsymbol{W}_{h j} \boldsymbol{h}_{i-1}+b_{j}\right) \\ \boldsymbol{F}_{i}=\operatorname{sigm}\left(\boldsymbol{W}_{x f} \boldsymbol{I}_{i}+\boldsymbol{W}_{h f} \boldsymbol{h}_{i-1}+b_{f}\right) \\ \boldsymbol{O}_{i}=\tanh \left(\boldsymbol{W}_{x o} \boldsymbol{I}_{i}+\boldsymbol{W}_{h o} \boldsymbol{h}_{i-1}+b_{o}\right) \\ \boldsymbol{C}_{i}=\boldsymbol{C}_{i-1} \odot \boldsymbol{F}_{i}+\boldsymbol{I}_{i} \odot \boldsymbol{J}_{i} \\ \boldsymbol{h}_{i}=\tanh \left(\boldsymbol{C}_{i}\right) \odot \boldsymbol{O}_{i} \end{array} $ | (4) |
式中,tanh和sigm分别为反正切函数和sigmoid函数,sigmoid函数取值范围为0~1,可对信息进行筛选,控制上一层信息进入该层的程度。⊙为元素积符号,W*和b*分别为权重矩阵和偏置项。结合图 3和式(4)可知,通过LSTM神经元可控制需要记忆和遗忘的数据信息,使隐藏层输出合适数值,并将数据信息状态通过Ci进行传递,从而解决梯度爆炸和梯度弥散问题。
神经网络训练的核心工作是对训练数据集进行多参数拟合。循环神经网络训练主要分3步进行:一是输出前向计算神经元;二是反向计算神经元的误差项δi,该项为误差函数对神经元i的加权输入矩阵的偏导数;三是计算每个权重的梯度,并利用随机梯度下降算法更新权重。同时,通过随机抛弃部分神经元参数的方式,防止出现过拟合情况,以获取最优的训练模型。在本文研究中,将输入层对应为训练数据集中重力观测点的位置信息,输出层则为训练数据集的自由空气重力异常。基于LSTM方法对自由空气重力异常数据进行训练,以获取合适的深度神经网络模型,并将其用于推估其他位置的重力异常值。
3 不同推估方法对比分析为研究循环神经网络对自由空气重力异常的推估能力,将传统克里金方法[11]获取的推估结果与LSTM循环神经网络的结果进行对比分析。LSTM循环神经网络采用4个隐藏层和每层72个神经元的网络结构进行训练,迭代次数为3 000次。基于图 1的观测数据,随机抽取50、100和150个点作为训练数据集,将剩余点作为测试数据集。对每个采样点数进行100次随机采样,各自生成100组训练数据集。使用LSTM和克里金方法分别进行推估计算,将推估结果与测试数据集进行求差并计算差异的标准差,结果如图 4所示。

|
图 4 基于观测数据的不同推估方法对比 Fig. 4 Comparison of different estimated methods based on observation data |
通过比较LSTM和克里金方法的结果可知,LSTM方法获取的100组随机数据的推估结果和测试数据集差异的标准差分布符合正态分布,结果较为稳定,且测试标准差小于克里金方法,相对而言克里金方法获取的结果较为分散。基于以上训练结果,本文认为利用LSTM循环神经网络方法推估的自由空气重力异常结果比传统克里金方法更为可靠。但训练神经网络所需的时间远大于克里金方法的计算时间,即使在使用GPU (Nvidia Tesla P4)训练的情况下,使用包含100个数据点的训练集,训练4层72个神经元所需的时间超过120 s,而克里金方法耗时则小于1 s,从效能角度考虑克里金方法仍占优势。随着计算机硬件能力和神经网络基础研究的发展,相信未来基于神经网络的推估方法会逐渐替代传统方法。
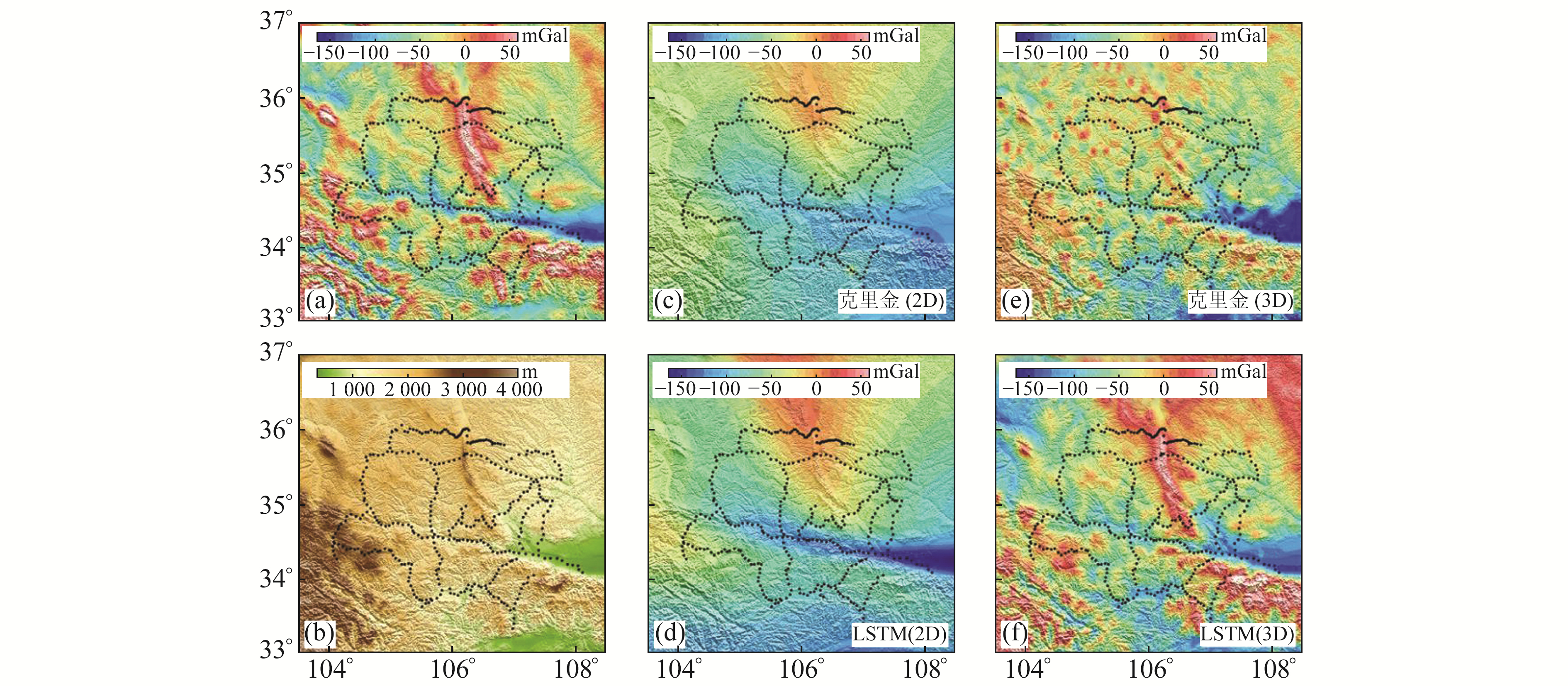
为进一步测试LSTM方法和传统克里金方法对实测数据的推估能力,基于图 1中数据分别使用2种方法推估计算鄂尔多斯西南缘的自由空气重力异常场(图 5)。为方便对比分析,分别绘制鄂尔多斯西南缘EIGEN-6C4模型[12]自由空气重力异常场(图 5(a))和高程空间分布结果(图 5(b)),高程数据提取自ETOPO1模型[13]。图 5(c)和5(d)分别为克里金方法和LSTM方法的推估结果,这2组结果是基于经度和纬度的二维推估计算结果,推估计算点为0.1°×0.1°网格数据。由图 5(a)、5(c)和5(d)可知,受限于观测点的分布(图 5中黑点),虽然2种方法推估的自由空气重力异常结果均不理想,但相对于克里金方法,LSTM方法推估的重力异常分布特征与模型数据更为接近,特别是在研究区中部和北部,LSTM方法可正确推估重力异常低值和高值区域。图 5(e)和5(f)为2种方法基于图 1中385个观测点数据的经度、纬度和高程数据进行的三维推估结果,推估计算点与二维方法一致。除经纬度信息外,还加入对应点的高程信息(图 5(b))。LSTM方法获取的结果与模型数据基本一致,且明显优于克里金方法,该结果表明加入高程数据作为约束条件对神经网络的训练更为有利,这与前人的研究结果一致[14]。
|
图 5 基于不同推估方法的鄂尔多斯西南缘自由空气重力异常场 Fig. 5 Free-air gravity anomaly field in the southwestern margin of Ordos based on different estimation methods |
基于观测的自由空气重力异常数据,对LSTM循环神经网络的推估能力进行分析,并与传统克里金方法的推估结果进行比较,得到以下结论:1)LSTM循环神经网络可利用有限的数据获取较好的推估结果。2)LSTM循环神经网络的推估能力优于传统克里金方法,但在运算效率上克里金方法表现更优。3)利用鄂尔多斯西南缘的观测数据对整个区域进行推估,结果表明,LSTM方法明显优于克里金方法,加入高程数据作为约束条件可有效提高LSTM方法推估自由空气重力异常场的精度。
| [1] |
Fu G Y, Gao S H, Freymueller J T, et al. Bouguer Gravity Anomaly and Isostasy at Western Sichuan Basin Revealed by New Gravity Surveys[J]. Journal of Geophysical Research: Solid Earth, 2014, 119(4): 3925-3938 DOI:10.1002/2014JB011033
(  0) 0) |
| [2] |
She Y W, Fu G Y, Wang Z H, et al. Gravity Anomalies and Lithospheric Flexure around the Longmenshan Deduced from Combinations of in Situ Observations and EGM2008 Data[J]. Earth, Planets and Space, 2016, 68(1): 163 DOI:10.1186/s40623-016-0537-7
(  0) 0) |
| [3] |
Fu G Y, She Y W. Gravity Anomalies and Isostasy Deduced from New Dense Gravimetry around the Tsangpo Gorge, Tibet[J]. Geophysical Research Letters, 2017, 44(20): 10233-10239 DOI:10.1002/2017GL075290
(  0) 0) |
| [4] |
申重阳, 杨光亮, 谈洪波, 等. 维西-贵阳剖面重力异常与地壳密度结构特征[J]. 地球物理学报, 2015, 58(11): 3952-3964 (Shen Chongyang, Yang Guangliang, Tan Hongbo, et al. Gravity Anomalies and Crustal Density Structure Characteristics of Profile Weixi-Guiyang[J]. Chinese Journal of Geophysics, 2015, 58(11): 3952-3964 DOI:10.3969/j.issn.0253-4975.2015.09.077)
(  0) 0) |
| [5] |
周志华. 机器学习[M]. 北京: 清华大学出版社, 2016 (Zhou Zhihua. Machine Learning[M]. Beijing: Tsinghua University Press, 2016)
(  0) 0) |
| [6] |
Jozefowicz R, Zaremba W, Sutskever I. An Empirical Exploration of Recurrent Network Architectures[C]. International Conference on Machine Learning, Lille, 2015
(  0) 0) |
| [7] |
Wang Z Y, Fu G Y, She Y W. Crustal Density Structure, Lithosphere Flexure Mechanism, and Isostatic State throughout the Qinling Orogen Revealed by in Situ Dense Gravity Observations[J]. Journal of Geophysical Research: Solid Earth, 2018, 123(11): 10026-10039 DOI:10.1029/2018JB016117
(  0) 0) |
| [8] |
刘冬至, 李辉, 刘绍府. 重力测量资料的处理系统——LGADJ[A]//国家地震局科技监测司. 地震预报方法实用化研究文集: 形变、重力、应变专辑[M]. 北京: 地震出版社, 1991 (Liu Dongzhi, Li Hui, Liu Shaofu. A Data Processing System of Gravity Surveying—LGADJ[A]//Science and Technology Monitoring Department of CEA.Practical Research Collection of Earthquake Prediction Methods(Special Issue on Deformation, Gravity and Strain Measurement)[M]. Beijing: Seismological Press, 1991)
(  0) 0) |
| [9] |
Bengio Y, Simard P, Frasconi P. Learning Long-Term Dependencies with Gradient Descent Is Difficult[J]. IEEE Transactions on Neural Networks, 1994, 5(2): 157-166 DOI:10.1109/72.279181
(  0) 0) |
| [10] |
Hochreiter S, Schmidhuber J. Long Short-Term Memory[J]. Neural Computation, 1997, 9(8): 1735-1780 DOI:10.1162/neco.1997.9.8.1735
(  0) 0) |
| [11] |
Kitanidis P K. Introduction to Geostatistics: Applications in Hydrogeology[M]. Cambridge: Cambridge University Press, 1997
(  0) 0) |
| [12] |
Förste C, Bruinsma S L, Abrikosov O, et al. EIGEN-6C4-The Latest Combined Global Gravity Field Model Including GOCE Data up to Degree and Order 1949 of GFZ Potsdam and GRGS Toulouse[C]. EGU General Assembly Conference, Vienna, 2014
(  0) 0) |
| [13] |
Amante C, Eakins B W. ETOPO11 Arc-Minute Global Relief Model: Procedures, Data Sources and Analysis[Z]. NOAA Technical Memorandum NESDIS NGDC-24, 2009
(  0) 0) |
| [14] |
任强强, 王跃钢, 腾红磊, 等. 基于小波神经网络的盲区重力数据预测[J]. 大地测量与地球动力学, 2016, 36(4): 359-363 (Ren Qiangqiang, Wang Yuegang, Teng Honglei, et al. The Gravity Data Forecast of Unmeasurable Zone Based on Wavelet Neural Network[J]. Journal of Geodesy and Geodynamics, 2016, 36(4): 359-363 DOI:10.14075/j.jgg.2016.04.018)
(  0) 0) |
2. Key Laboratory of Earthquake Forecasting, Institute of Earthquake Forecasting, CEA, 63 Fuxing Road, Beijing 100036, China
 2021, Vol. 41
2021, Vol. 41


