2. 火箭军士官学校,山东省青州市,262500;
3. 火箭军工程大学,西安市,710025
地磁场是一种随时间和空间变化的矢量场,在多个领域均有广泛应用,如空间天气监测和预报[1]、地震预报[2]、地磁导航与地磁寻的制导技术[3]等。地磁场的时空变化对于地磁场应用的精度和范围具有重要影响,因此对地磁变化场进行建模和预测在科学研究中具有重大意义[4]。现有资料表明[5-8],地磁场的成因机理极其复杂,很难通过机理建模的方法对其时空变化规律进行准确描述;部分针对地磁变化场的高精度预测方法,由于受地磁数据量限制,缺乏时间和空间上的广泛适用性。
目前,全球多个国家已建立地磁观测台站,以研究地磁场的时空变化,台站总数已达百余个。这些地磁台站分布在全球各地,24 h不间断测量,采样频率达1 kHz,观测数据量极大,其中必然蕴含着地球磁场变化在时间和空间上的分布规律。本文以现有地磁台站的观测数据为基础,分析地磁变化场数据在时空上的关联性,研究数据中蕴含的规律信息,并利用BP神经网络建立地磁变化场预测模型,以实现地磁变化场的时空预测。
1 地磁变化场时空关联性分析为说明地磁变化场在空间和时间上的关联性,以长春、乌鲁木齐、成都和兰州4个台站的数据为例,分析相同纬度不同经度、相同经度不同纬度、不同月同日及同月不同日的地磁数据,并通过定性(作图观察)和定量(计算相关系数)方法探讨其在时空上的关联性。
采用相关分析法对关联性进行定量计算。相关分析法是研究2个或2个以上变量之间的相关程度并用一定函数来表达相互关系的方法,相关变量之间不存在确定性关系,通常用相关系数R表述2个变量的密切程度,R绝对值越接近1表明相关性越好,其计算公式为:
| $R=\frac{\sum(x-\bar{x})(y-\bar{y})}{\sqrt{\sum(x-\bar{x})^{2} \sum(y-\bar{y})^{2}}} $ |
式中,
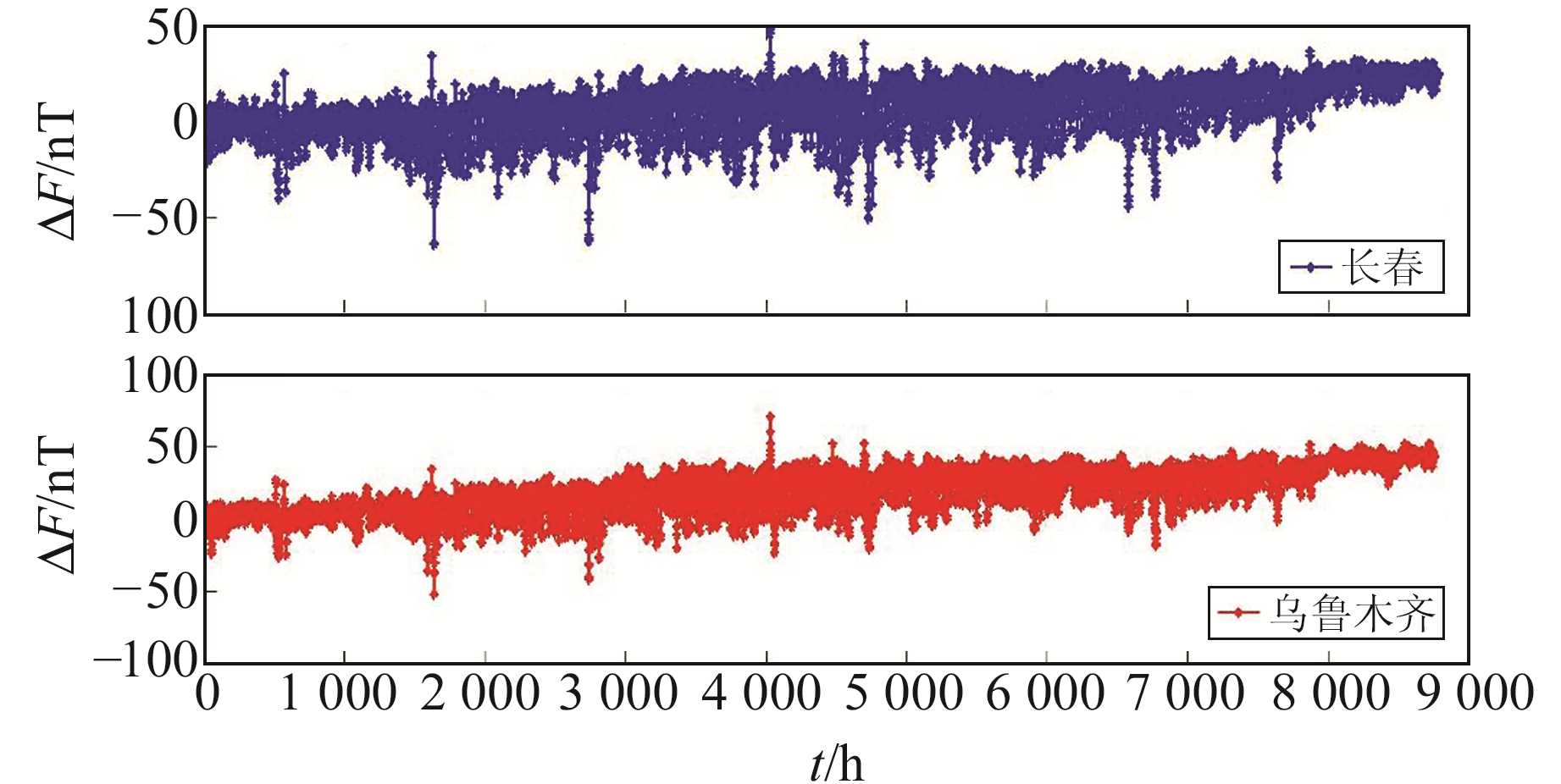
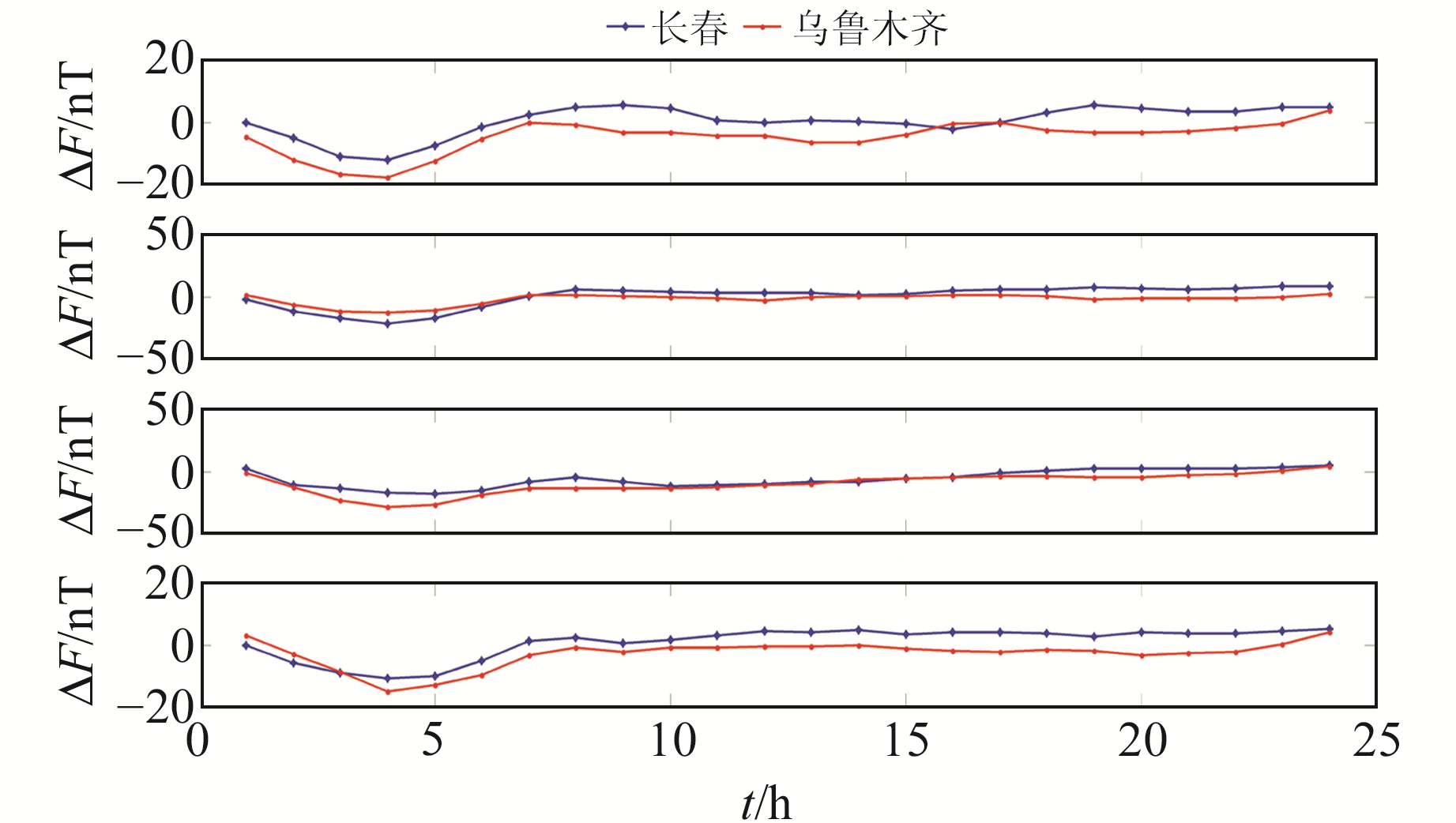
为研究地磁变化场在相同纬度不同经度的相关性,选取长春台(44.0°N、125.2°E)及乌鲁木齐台(43.8°N、87.8°E)数据,对其进行由宏观特性到个例的分析。图 1为2012年长春台和乌鲁木齐台全年的地磁变化场时均值,由图可知:1)从宏观上看,2个台站的地磁变化场时均值曲线的形态非常相似;2)2个台站尖峰值的出现均是由于磁暴,且出现尖峰值的时间几乎一致;3)2个台站数据的相关系数R=0.710 8。综上可知,相同纬度不同经度的地磁变化场具有较强的相关性。为更加精细地体现其相关性,任意抽取4 d的数据进行分析。图 2为2012-01-01~01-04长春台与乌鲁木齐台地磁变化场时均值变化曲线,经计算可知,2个台站每日的地磁变化场相关系数分别为0.871 5、0.903 3、0.924 8和0.963 3,相关系数较大,说明相同纬度不同经度的地磁变化场具有较强的相关性。
|
图 1 2012年长春台和乌鲁木齐台全年的地磁变化场时均值对比 Fig. 1 Hourly mean variable geomagnetic field during 2012 in Changchun station and Urumqi station |
|
图 2 2012-01-01~01-04长春台和乌鲁木齐台地磁变化场时均值曲线 Fig. 2 Hourly mean variable geomagnetic field from January 1, 2012 to January 4, 2012 in Changchun station and Urumqi station |
为研究地磁变化场在相同经度不同纬度的相关性,选取成都台(103.7°E、31.0°N)及兰州台(103.8°E、36.1°N)数据进行分析。通过计算可知,2个台站2012年全年数据的相关系数R=0.999 8,2012-01-01~01-04每日的地磁变化场相关系数分别为0.945 5、0.926 6、0.975 7和0.928 6,相关系数极大,说明相同经度不同纬度的地磁变化场也具有较强的相关性。
1.2 地磁变化场时均值在时间上的相关性分析选用长春台2012-01-01、04-01、07-01和10-01的地磁变化场时均值数据进行分析,结果见图 3。从图 3可以看出,不同月同日的地磁变化场时均值的变化趋势一致,仅幅值大小存在差别,这些差别在很大程度上由不同月份所造成。假设1月份为1,4月份为2,7月份为3,10月份为4,Rij为i与j的相关系数,经计算可得,R12=0.885 9,R13=0.699 0,R14=0.901 6,R23=0.771 5,R24=0.882 0,R34=0.828 8,说明不同月同日的地磁变化场具有较强的相关性。

|
图 3 长春台2012-01-01、04-01、07-01、10-01地磁变化场时均值 Fig. 3 Hourly mean variable geomagnetic field on January 1, April 1, July 1, October 1, 2012 in Changchun station |
选取长春台2012-01-01~01-04的地磁变化场时均值数据进行分析,结果见图 4。假设第1日为1,第2日为2,第3日为3,第4日为4,经计算可得,R12=0.921 9,R13=0.825 6,R14=0.885 8,R23=0.960 8,R24=0.923 0,R34=0.844 9,说明同一个区域同月不同日的地磁变化场也具有较强的相关性。

|
图 4 长春台2012-01-01~01-04地磁变化场时均值 Fig. 4 Hourly mean variable geomagnetic field from January 1, 2012 to January 4, 2012 in Changchun station |
综合分析可知,地磁变化场的观测数据包含地磁变化场在空间和时间上的变化规律,且地磁变化场与其相对应的地理经度、纬度及时间等要素之间具有复杂的非线性函数关系,属于高维问题。因此可将空间因素和时间因素作为神经网络的输入,通过数据驱动固化网络参数,进而表达地磁变化场在时间和空间上的复杂非线性映射关系。
2 基于神经网络的地磁变化场预测BP神经网络也称反向传播前馈性神经网络,具有强大的计算能力,可表达各种复杂映射,适用于反映地磁场的复杂非线性变化规律[9],且在地磁空间环境的预测预报方面具有较好的应用[10]。本文选用BP神经网络对地磁变化场进行时空预测,确定神经网络的输入量和参考输出,实现未知区域(无地磁台站)地磁变化场的预测。
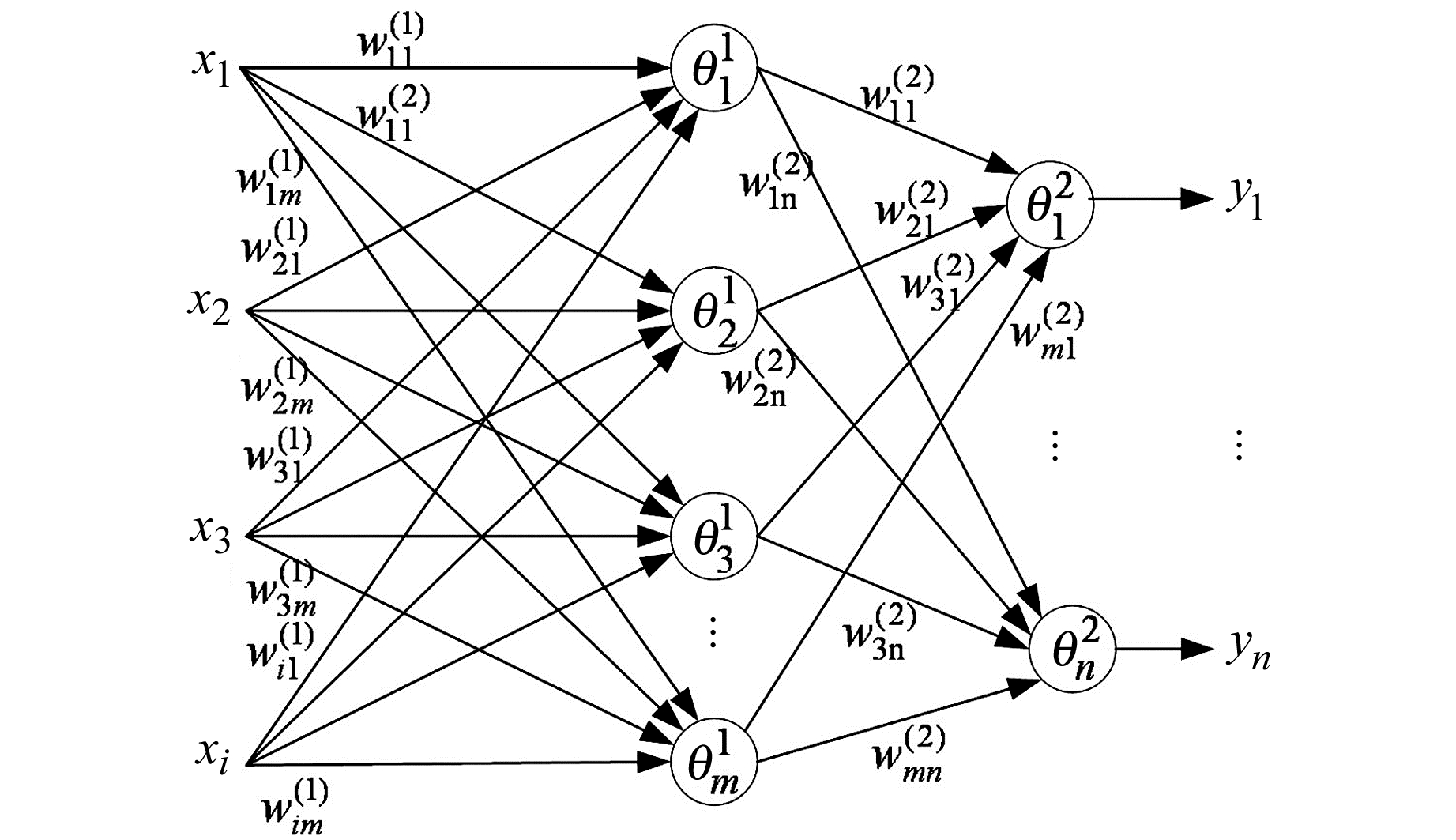
2.1 神经网络结构神经网络中隐含层神经元的传递函数设定为正切S型传递函数tansig,输出层神经元的传递函数为线性传递函数purelin,训练函数设定为Levenberg-Marquardt算法训练函数trainlm。神经网络参数设定后,可得到区域地磁变化场时空预测的BP神经网络结构示意图(图 5),其中所建网络的输入量个数为i,中间隐含层的节点数为m,输出量个数为n。
|
图 5 BP神经网络示意图 Fig. 5 Schematic diagram of BP neural network |
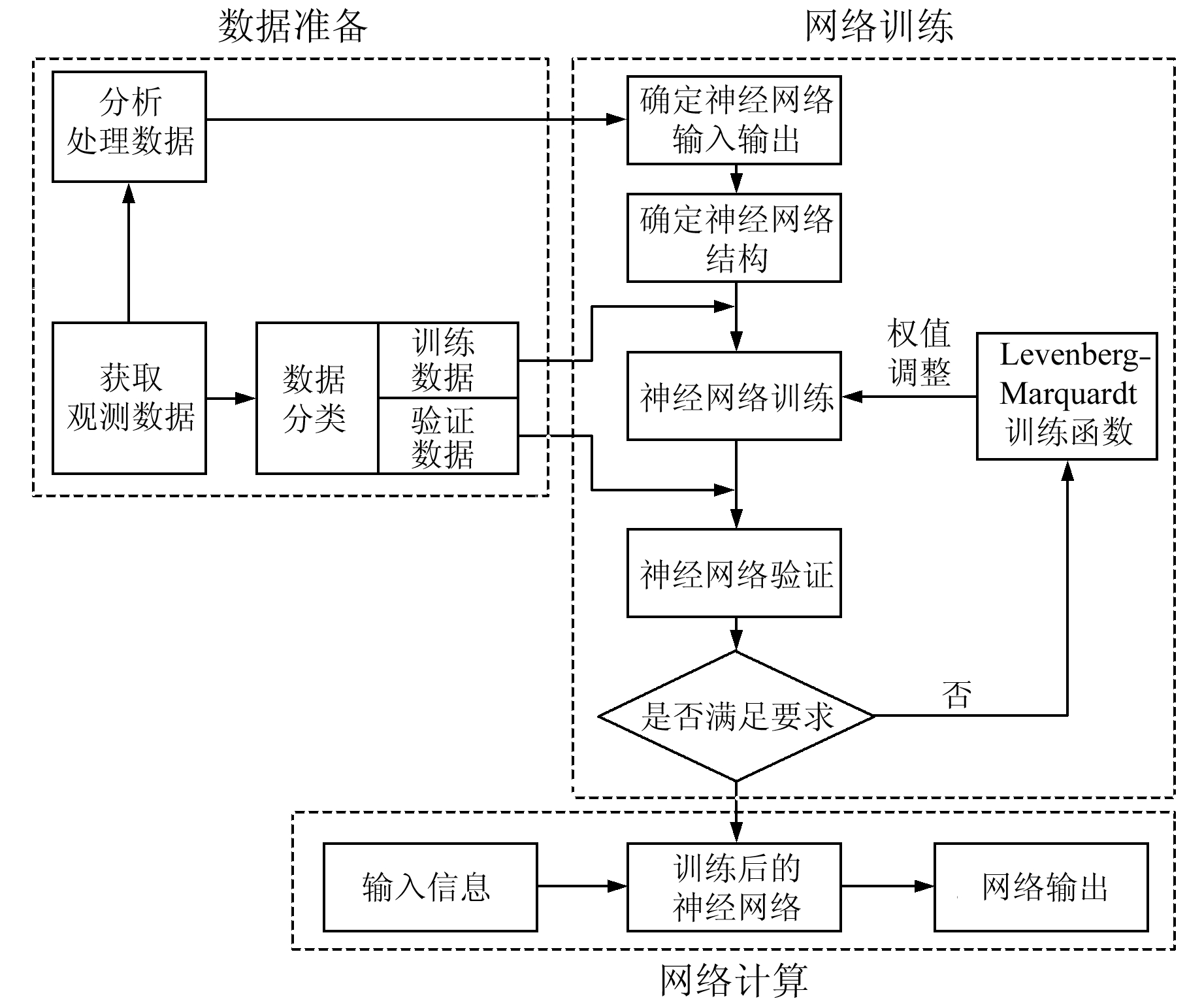
由于获取的数据信息量过大,因此首先需要分析并确定神经网络的输入和输出,然后将输入输出作为训练数据输入到神经网络,通过训练函数trainlm对神经网络各层之间的权系数进行调整。训练过程中权系数w可反映输入输出之间的映射关系,训练结束后可得到符合精度要求的神经网络结构,从而实现对地磁变化场进行时空预测。具体流程如图 6所示。
|
图 6 基于神经网络的地磁变化场预测示意图 Fig. 6 Schematic diagram of variable geomagnetic field forecasting based on neural network |
通过分析可知,地磁变化场在时间和空间上具有较好的相关性,因此可将时间因素和空间因素作为神经网络的输入。为了便于表达和计算,将1 a中每日及1 d中每小时进行编号,小时编号用t1表示,每日编号用t2表示,1 d中00:00~23:00的编号t1分别为1、2、3、…、24,1 a中01-01~12-31的编号t2分别为1、2、3、…、365(闰年为366)。尽管t1和t2具有不同取值,但不能将这些不同值直接作为神经网络的输入,因为当日23:00与次日00:00非常接近,当年12-31与次年01-01也非常接近,而神经网络并不能对其进行区分。因此,将24个世界时向圆周投影,并按照式(1)将地方时t1投影为x1和x2,将日期t2投影为x3和x4,从而完成时间的圆周投影:
| $\left\{\begin{array}{l} x_{1}=\cos \left(2 \pi t_{1} / 24\right) \\ x_{2}=\sin \left(2 \pi t_{1} / 24\right) \\ x_{3}=\cos \left(2 \pi t_{2} / 365\right) \\ x_{4}=\sin \left(2 \pi t_{2} / 365\right) \end{array}\right. $ | (1) |
神经网络输入的空间信息主要用经度λ和纬度φ来表示,但λ和φ实际对应一个圆心角,对其进行圆周投影就相当于将球面位置坐标放到平面上,其方法与世界时的圆周化相同,具体投影公式为:
| $ \left\{\begin{array}{l} x_{5}=\cos \lambda \\ x_{6}=\sin \lambda \\ x_{7}=\cos \varphi \\ x_{8}=\sin \varphi \end{array}\right. $ | (2) |
为更好地反映地磁场的变化规律,选取磁静日(Kp指数均小于等于2)00:00~02:00和22:00~24:00地磁场观测的平均值作为稳定磁场值,记为F。地磁变化场值ΔF为地磁场观测值F相对于稳定基准值F的变化量,即ΔF=F-F。因此,神经网络的输出为网络时空输入所对应的地磁变化场值ΔF,记为y。
2.3 神经网络训练、验证与预测确定神经网络的输入量为8,输出量为1。为更直观地说明输入输出数据的形式,统一数据的转化顺序为经度、纬度、日、时,假设位置为120°E、30°N,时间为03-01 06:00,变化磁场为20 nT,经过式(1)和式(2)转换,得到输入量和输出量分别为X=[-0.5,0.866,0.866,0.5,0.512 4,0.858 8,0,1]T,y=20。
将现有观测台站的可用数据按照上述输入量和输出量的形式进行表示,并将其分为训练数据和验证数据2类,训练数据(占总数量90%以上)用于对神经网络进行训练,验证数据用于验证训练后神经网络的正确性。最后将未知区域的输入量加入到已经训练好的神经网络中,实现对任意未知区域地磁变化场的预测。
3 地磁台站数据验证由于获取的数据量有限,无法对全球所有台站的地磁场数据进行收集整理,仅以我国地磁台站的数据信息为例,本文共收集10个地磁台站2008~2013年共6 a的地磁总场分钟值数据及磁暴数据(表 1)。
|
|
表 1 地磁台站信息 Tab. 1 Information of geomagnetic stations |
将观测数据中的异常值及磁暴数据进行剔除和修正后,取时均值用于计算。选取用于验证神经网络在时空域内求解地磁变化场有效性的数据,本文选取6个台站2010-06-01~06-02的数据进行分析,验证结果见图 7。选取用于验证神经网络仿真计算精度的数据,本文随机选取100个训练数据进行分析,结果见图 8。将剩余的数据作为训练数据,设定训练函数为Levenberg-Marquardt算法训练函数trainlm,训练100次后对结果进行验证。

|
图 7 地磁变化场时空计算结果 Fig. 7 The temporal and spatial calculation results of the variable geomagnetic field |

|
图 8 地磁变化场时空计算精度 Fig. 8 The temporal and spatial calculation accuracy of the variable geomagnetic field |
由图 7可知:1)神经网络求解的地磁变化场在06-01~06-02的变化情况与实际地磁变化场基本一致,说明其能够较好地反映地磁变化场在时间上的变化规律;2)各个台站06-01~06-02的地磁变化场无论是幅值还是相位都存在差异,神经网络计算对各台站之间的位置差异敏感,求解结果与实际变化情况基本一致,说明其能够较好地反映地磁变化场在空间上的分布规律。
由图 8可知,神经网络仿真计算的均方根误差RMS=4.8 nT,考虑到地磁变化场1 d内的波动幅度能达到几十nT,在一般扰动变化时能达到几百nT,且地磁变化场随时间和空间的变化规律非常复杂,因此本文建立的BP神经网络模型的计算精度能够满足一般科学研究对地磁变化场的精度需求。
4 结语本文综合分析了影响地磁变化场的时间和空间因素,基于国内多个地磁台站的观测数据构建用于地磁变化场预测的BP神经网络模型,并验证了模型的有效性,该研究思路和建模方法能够为地磁场建模和计算等相关研究提供借鉴。本文在地磁变化场数据处理时,仅对磁暴数据进行修正,但地磁变化场还受太阳风、空间粒子及其他外部环境影响,且本文仅基于陆上地磁台站的数据,对海上地磁变化场预测的适用性有待研究。后期将综合考虑各类影响因素,并通过增加各区域地磁台站数据等方式对所建立的神经网络模型进行训练,以提高地磁变化场的预测精度和适用范围。
| [1] |
Dugassa T, Habarulema J B, Nigussie M. Longitudinal Variability of Occurrence of Ionospheric Irregularities over the American, African and Indian Regions during Geomagnetic Storms[J]. Advances in Space Research, 2019, 63(8): 2609-2622 DOI:10.1016/j.asr.2019.01.001
(  0) 0) |
| [2] |
史坤朋, 郭金运, 刘智敏, 等. 2016-12-25智利MW7.6地震震前电离层TEC异常探测[J]. 大地测量与地球动力学, 2016, 38(9): 979-985 (Shi Kunpeng, Guo Jinyun, Liu Zhimin, et al. Detection of Ionospheric TEC Anomaly before Chile MW7.6 Earthquake on December 25, 2016[J]. Journal of Geodesy and Geodynamics, 2016, 38(9): 979-985)
(  0) 0) |
| [3] |
李婷, 张金生, 王仕成, 等. 基于改进地磁熵的地磁适配区选择准则[J]. 大地测量与地球动力学, 2014, 34(5): 151-155 (Li Ting, Zhang Jinsheng, Wang Shicheng, et al. Study on Selection of Geomagnetic Suitable Matching Area Based on Improved Geomagnetic Entropy[J]. Journal of Geodesy and Geodynamics, 2014, 34(5): 151-155)
(  0) 0) |
| [4] |
牛超, 刘代志, 李夕海, 等. 基于复杂度理论的地磁变化场时间序列特征分析[J]. 地球物理学报, 2014, 57(8): 2713-2723 (Niu Chao, Liu Daizhi, Li Xihai, et al. Feature Analysis of Geomagnetic Variation Time Series Based on Complexity Theory[J]. Chinese Journal of Geophysics, 2014, 57(8): 2713-2723)
(  0) 0) |
| [5] |
聂琳娟, 邱耀东, 申文斌, 等. IGRF12和WMM2015模型在中国区域的精度评估及其适用性分析[J]. 武汉大学学报: 信息科学版, 2017, 42(9): 1229-1235 (Nie Linjuan, Qiu Yaodong, Shen Wenbin, et al. Accuracy Evaluation and Applicability of IGRF12 and WMM2015 Model in Chinese Mainland[J]. Geomatics and Information Science of Wuhan University, 2017, 42(9): 1229-1235)
(  0) 0) |
| [6] |
康丽文, 边少锋, 陈洁. EMM-740模型与中国地磁台站年均值的差异分析[J]. 海洋测绘, 2019, 39(1): 27-30 (Kang Liwen, Bian Shaofeng, Chen Jie. Analysis on the Differences of EMM-740 Model and the Annual Mean of China's Geomagnetic Observatories[J]. Hydrographic Surveying and Charting, 2019, 39(1): 27-30)
(  0) 0) |
| [7] |
易世华, 刘代志, 何元磊, 等. 变化地磁场预测的支持向量机建模[J]. 地球物理学报, 2013, 56(1): 127-135 (Yi Shihua, Liu Daizhi, He Yuanlei, et al. Modeling and Forecasting of the Variable Geomagnetic Field by Support Vector Machine[J]. Chinese Journal of Geophysics, 2013, 56(1): 127-135)
(  0) 0) |
| [8] |
牛超, 李夕海, 易世华, 等. 地磁变化场的MEEMD-样本熵-LSSVM预测模型[J]. 武汉大学学报: 信息科学版, 2014, 39(5): 626-630 (Niu Chao, Li Xihai, Yi Shihua, et al. Forecasting Model of Geomagnetic Variation Field Based on Modified Ensemble Empirical Mode Decomposition-Sample Entropy-Least Square Support Vector Machine[J]. Geomatics and Information Science of Wuhan University, 2014, 39(5): 626-630 DOI:10.13203/j.whugis20130261)
(  0) 0) |
| [9] |
姚休义, 滕云田, 杨冬梅, 等. 基于神经网络的地磁观测数据重构研究[J]. 地球物理学报, 2018, 61(6): 2358-2368 (Yao Xiuyi, Teng Yuntian, Yang Dongmei, et al. Reconstruction of Geomagnetic Data Based on Artificial Neural Network[J]. Chinese Journal of Geophysics, 2018, 61(6): 2358-2368)
(  0) 0) |
| [10] |
Gururajan N, Prabhakaran V K. Prediction of Geomagnetic Variations Using ANN[J]. International Journal of Scientific Engineering and Technology, 2013, 2(5): 322-330
(  0) 0) |
2. Rocket Force Sergeant School, Qingzhou 262500, China;
3. Rocket Force University of Engineering, Xi'an 710025, China
 2021, Vol. 41
2021, Vol. 41

