在位场数据处理与转换过程中,数据区域边界往往易产生畸变等边界效应,给资料解释工作带来不利影响。为尽量减少甚至消除边界效应,保证处理后边界数据的真实性和完整性,以便利用实测位场数据进行地质解释,通常在处理前需要对位场数据进行必要的扩边处理。
扩边对位场数据处理造成的影响往往不可忽视[1-5],且扩边后的数据质量直接影响到处理后数据的精度。为此,很多学者围绕如何减少边界效应、提升处理结果可靠性等开展大量工作,并提出许多位场数据扩边方法,如余弦扩边方法[1]、区域场扩边方法[1]、最小曲率扩边方法[6]、三向扩边方法[7]、泛克里格扩边方法[8]、凸集投影(projection onto convex sets,POCS)扩边方法[9]等。但这些研究主要集中于扩边方法本身的效果与精度,而基于特定方法开展扩边的尺度对位场数据处理影响的研究却鲜有涉及。
为此,本文从扩边尺度对位场数据处理影响的角度展开研究,以线性三角插值法作为位场数据的扩边方法[10],对传统的四点切割算子和动态改进型插值切割算子进行改进[11],并基于改进后的完全圆周对称的动态改进型插值切割算子对理想模型在地表重力异常在不同深度层源进行切割分离。基于分离后的结果,从不同深度层源重力异常理论值和重力场源分离计算值之间的差异、扩边尺度与重力场源分离误差等角度研究扩边尺度对重力异常分层分离结果的影响,为后续位场数据处理过程中扩边尺度的合理选取提供参考依据。
1 插值切割分层分离原理及其技术流程 1.1 插值切割分层分离原理及改进插值切割法是在多次切割法的基础上发展而来的空间域划分区域和局部场的方法[12-14],通过引入半二阶差分量,可显著提升对异常特征的分辨能力[13],被认为是一种较好的位场分离技术。随着大深度位场向下延拓技术的发展,插值切割法在位场数据分离处理中得到广泛应用[15-18]。徐世浙等[17-18]发现不同深度地层的位场效应与切割半径之间关系密切,认为深度r以上地层的位场效应可以近似用切割半径r切割到的局部场表示,通过r1、r2两个不同半径切割即可获得r2-r1地层在地表的位场效应,插值切割分层分离技术即是基于该原理。
在大半径切割时,现有的切割算子存在不足,如四点圆周平均切割算子会产生严重的窗型震荡现象[19],动态改进型切割算子所采用的数据点无法完全均匀分布于切割半径所对应的圆周上[11],因此本文综合这2种切割算子的各自特点,对动态改进型切割算子进行改进,提出随切割半径增加而完全圆周对称的动态改进型插值切割算子,并基于新的切割算子对理想模型在地表的重力异常进行切割分离。基于相同的理想模型,将本文提出的新切割算子的切割分离结果与文献[11]的分离结果进行比较,两者结果基本一致,表明改进后的算法具有可行性。
完全圆周对称的动态改进型插值切割算子可确保用于计算的切割算子计算点均匀分布于切割半径所对应圆周上,且计算点数目随切割半径的增加而均匀增加。根据线性三角插值法,对网格数据进行插值,重新计算切割半径所对应圆周上的切割算子计算点处的位场值。基于插值后的切割半径所对应圆周上的计算点处的位场值,根据式(1)~(3)对位场进行切割分离[11]:
| $\begin{array}{l} A(x, y)=\frac{1}{N} \sum\limits_{i=1}^{N} G_{i}(r) \\ R(x, y)=(1-g) G(x, y)+g A(x, y) \\ S(x, y)=g[G(x, y)-A(x, y)] \end{array} $ | (1) |
式中,A(x, y)表示圆心为(x, y)、切割半径为r的圆周上N点位场的算术平均值,N随着切割半径的增加而增大,为切割半径4倍,即N=4r,且均匀分布于切割半径所对应的圆周上;G(x, y)、Gi(r)分别为圆心位于(x, y)处的位场值和切割半径为r的圆周上点i处的位场值,圆周上i处的位场值则是通过对位场网格数据进行插值计算获得;R(x, y)、S(x, y)分别为切割半径r所对应的区域场和局部场;权系数g由圆心处和圆周上的位场值共同确定,反映两者的线性程度,由式(2)和式(3)计算所得:
| $f_{i}(r)=\frac{\left[G_{i}(r)-G_{i}^{o}(r)\right]^{2}}{\left[G_{i}(r)-G_{i}^{o}(r)\right]^{2}+\left\{G(x, y)-\frac{1}{2}\left[G_{i}(r)+G_{i}^{o}(r)\right]\right\}^{2}} $ | (2) |
| $g=1-\frac{1}{\frac{N}{2}} \sum\limits_{i=1}^{\frac{N}{2}} f_{i}(r) $ | (3) |
式(2)中,Gio(r)为Gi(r)在切割半径为r的圆周上的对称点。
1.2 位场插值切割分层分离技术流程根据文献[10]中线性三角插值法对位场网格数据进行插值,计算1倍网格点距半径圆周上所对应的切割算子计算点处的位场值,由计算点处的位场值根据式(1)~(3)计算1倍网格点距切割算子,基于1倍网格点距切割算子对位场数据进行切割分离,获得的局部场可视为浅部1倍网格点距深度以上的重力效应。计算2倍网格点距半径圆周上所对应的切割算子计算点处的位场值,由计算点处的位场值根据式(1)~(3)计算2倍网格点距切割算子,基于2倍网格点距切割算子对位场数据进行切割分离,获得的局部场可视为浅部2倍网格点距深度以上的位场效应,该效应为第1、第2层地层的综合重力效应,则第2层地层的重力效应为第1、第2层的综合效应与第1层地层重力效应之差。依次类推,逐渐增加切割半径,完成不同深度地层重力效应的分离[15, 17]。
2 理想模型实验 2.1 模型设计参数本文以文献[11]中给出的三维组合模型作为此次计算的理想模型,如图 1所示,模型在25 km×25 km×5 km空间范围内布设球体、椭球体和棱柱体3种不同类型的密度异常体,模型设计参数见表 1。图 2为研究区理想模型重力异常在地表的空间分布,理想模型重力异常在地表 25 km×25 km范围内以网格点距为100 m、250×250的网格状点阵分布,模型重力异常值由Encom ModelVision软件计算获得。
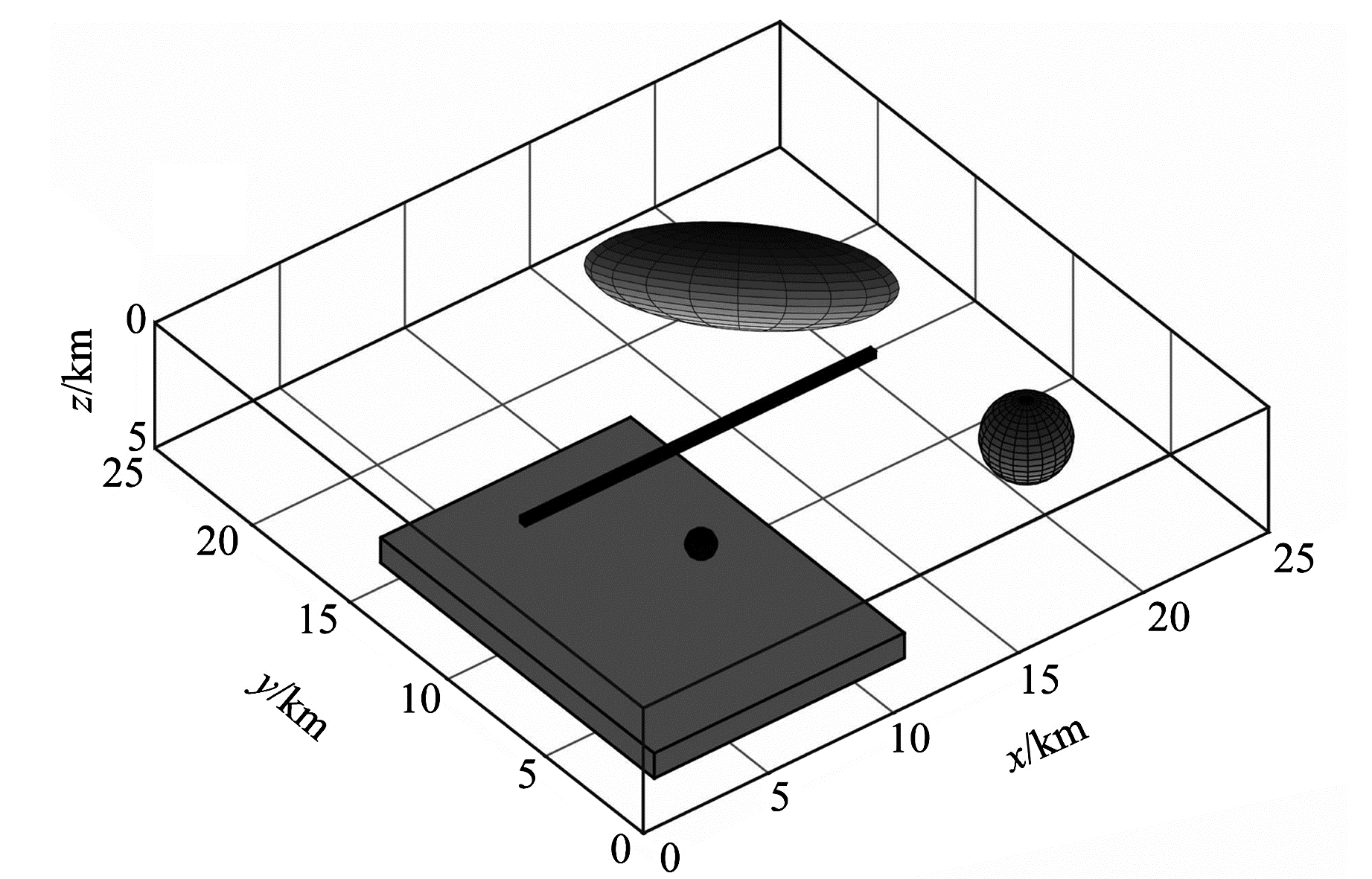
|
图 1 理想模型空间分布 Fig. 1 Space distribution of ideal model |
|
|
表 1 三维理想模型设计参数 Tab. 1 Parameters of ideal three dimensional model |

|
图 2 理想模型重力异常分布 Fig. 2 Gravity anomalies distribution of ideal model |
为了更直观地认识扩边尺度对重力异常分层分离处理的影响,本文基于改进后的完全圆周对称的动态改进型插值切割算子,对理想模型进行实验,以期为重力异常分层分离时扩边尺度的合理设置提供参考依据。
2.2.1 理想模型不同深度层源的理论重力异常值计算为确保理想模型切割分离出的不同深度层源在地表的重力异常值不产生边界效应,在地表重力异常切割分离前,以重力异常数据格网点距的整数倍为长度对研究区重力异常数据进行扩边。理想模型中各个异常体的埋设深度为0~5 km,模型重力异常数据的格网点距为100 m,若设定模型最大分离切割深度取50倍格网点距,则模型的最大切割深度为5 km,同时将各深度层源的切割迭代次数固定为20次,则需将研究区重力异常数据向四周扩充50×20个格网点距。如果理想模型在地表的重力异常数据扩边尺度足够,切割分离出的不同深度层源的重力异常则不会产生边界效应。基于理想模型分离的最大切割深度及其在地表重力异常数据的格网点距,本文对模型重力异常数据进行扩边,扩边后的数据为2 250×2 250点阵,扩边前后的数据区域范围如图 3所示(红色为研究区,蓝色为扩边区)。扩边后区域范围的地表重力异常通过Encom ModelVision软件计算获得,空间分布如图 4所示。分别以1~50倍格网点距为切割半径,根据§1.2的位场插值切割分层分离技术流程对扩边后的重力异常数据进行切割分离,并将获得的地表重力异常称为理想模型在不同深度层源的理论重力异常值。

|
图 3 研究区及其扩边后的区域分布 Fig. 3 Distribution of the study area and its expanded area |
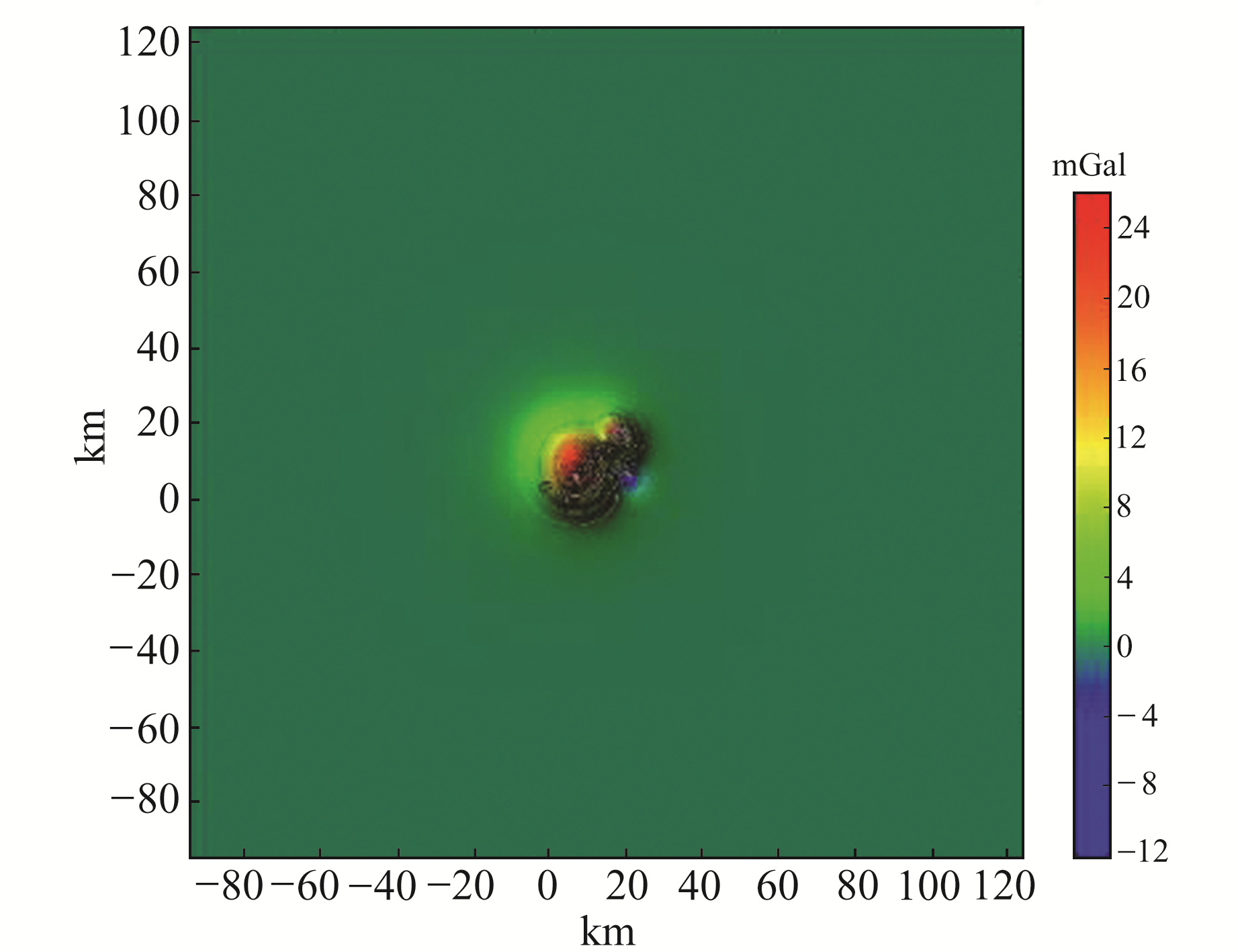
|
图 4 扩边后的重力异常分布 Fig. 4 Gravity anomalies distribution after edge expansion |
由前文可知,若扩边尺度足够,则切割分离出的不同深度层源在地表的重力异常值不会产生边界效应,否则,切割分离出的不同深度层源在地表的重力异常结果会包含边界效应。本文将含有边界效应的不同深度层源分离结果称为理想模型重力场源分离计算值,以相同的格网点距对研究区分别进行50、100和150倍格网点距扩边,同时基于线性三角插值法分别计算扩边尺度为50、100和150倍格网点距的区域范围地表重力异常。
根据分离技术流程,分别以1~50倍格网点距为切割半径对扩边尺度为50倍格网点距的理想模型重力异常进行切割分离,获得1~50倍格网点距的不同深度层源在地表的重力异常。若以理想模型的重力异常值作为参考,则可获得研究区不同深度层源在地表的重力异常理论值与重力场源分离计算值的差异,图 5为理想模型扩边尺度为50倍格网点距的重力异常理论值与重力场源分离计算值差异的空间分布。

|
图 5 扩边尺度为50倍格网点距的不同深度层源重力异常差异分布 Fig. 5 The distribution of gravity anomalies at different depths of layers with an expanded edge size of 50 times grid spacing |
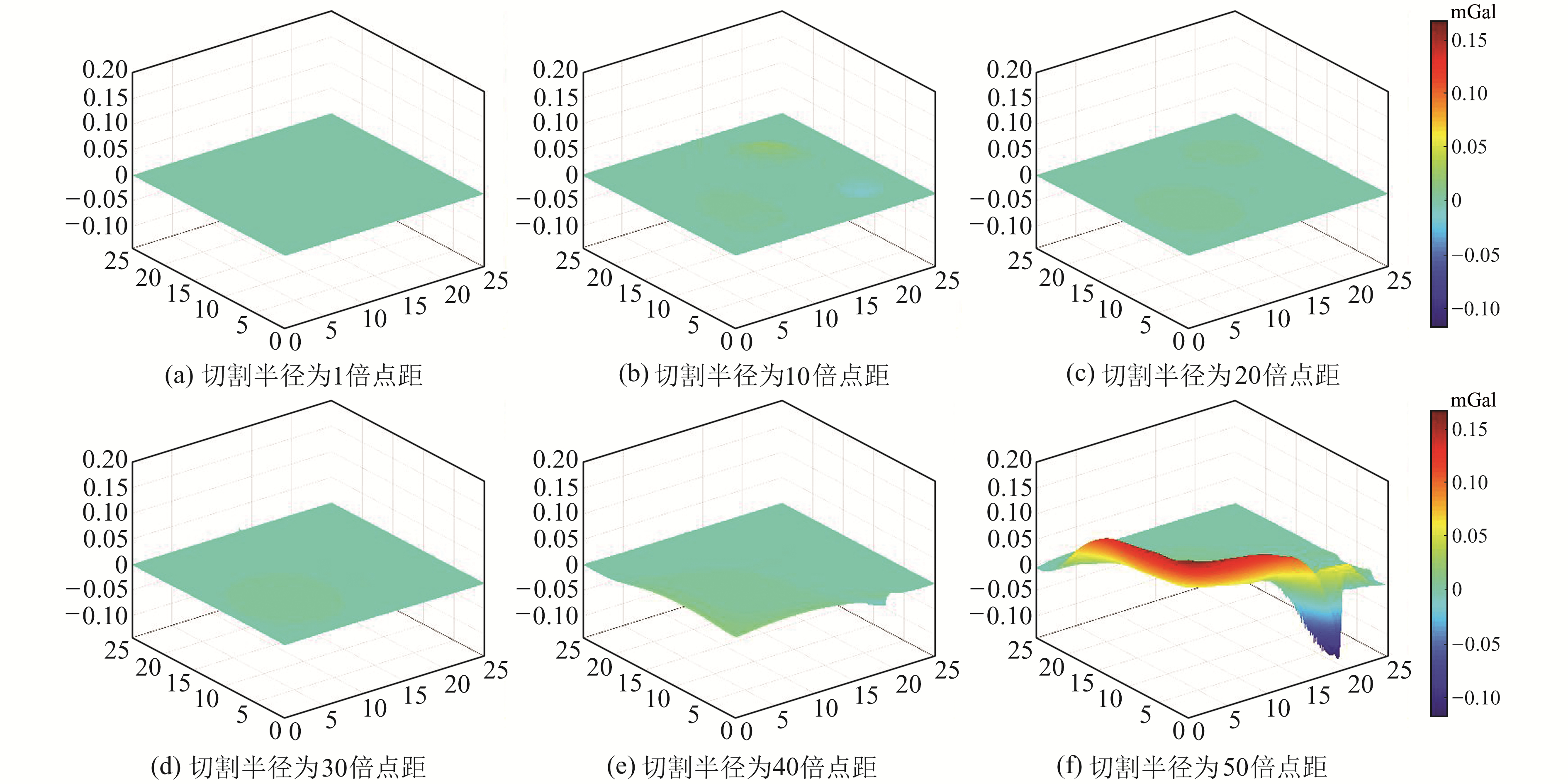
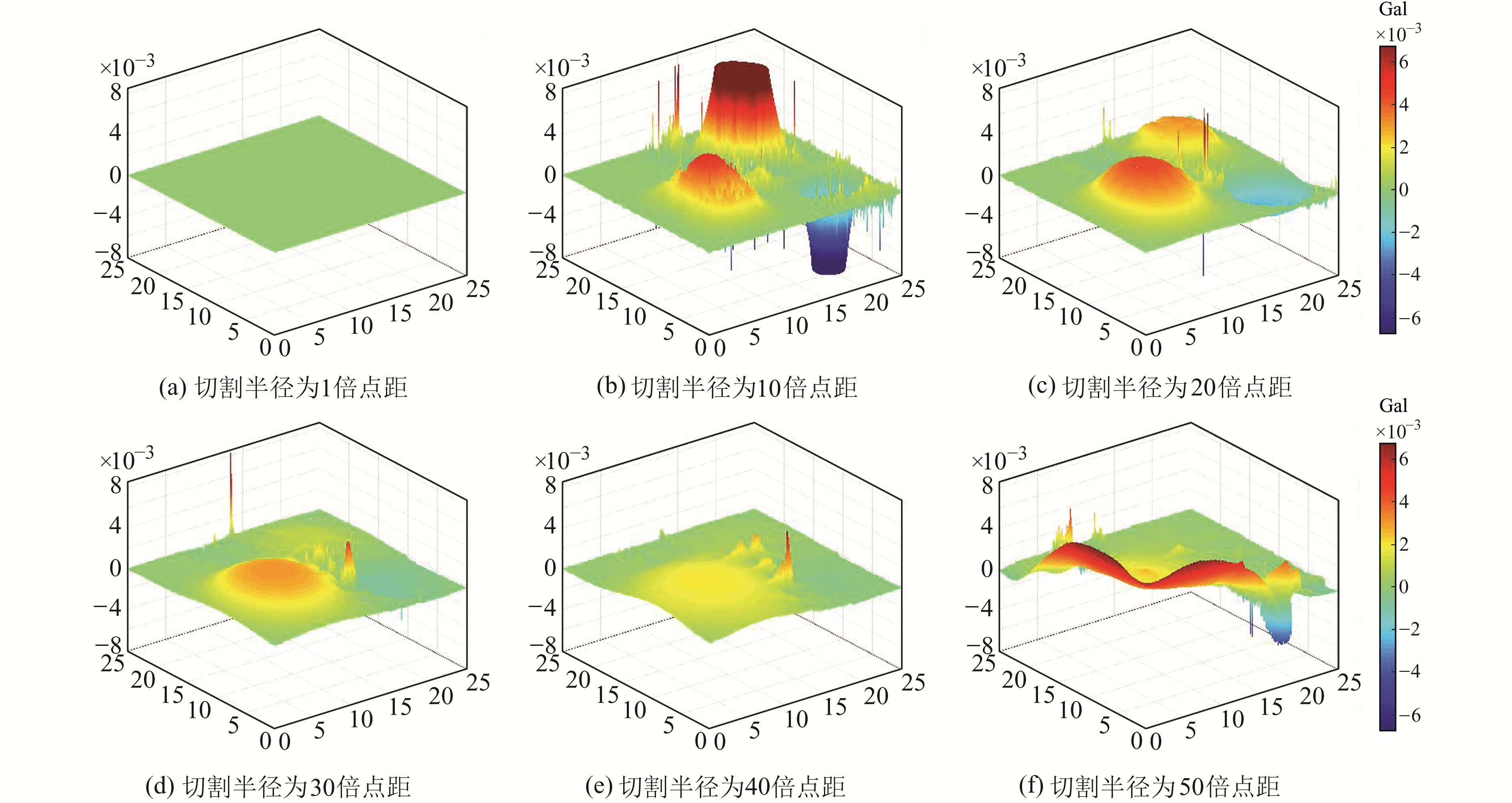
同理,计算获得扩边尺度为100倍和150倍格网点距的不同切割半径对应的深度层源在地表的重力异常差异,结果如图 6和7所示。
|
图 6 扩边尺度为100倍格网点距的不同深度层源重力异常差异分布 Fig. 6 The distribution of gravity anomalies at different depths of layers with an expanded edge size of 100 times grid spacing |
|
图 7 扩边尺度为150倍格网点距的不同深度层源重力异常差异分布 Fig. 7 The distribution of gravity anomalies at different depths of layers with an expanded edge size of 150 times grid spacing |
由图 5~7可以发现:1)理想模型重力异常分层分离结果中的边界效应与模型研究区数据的扩边尺度具有密切关系,若模型分层分离的深度相同,随着模型数据扩边尺度的增加,分层分离结果受到边界效应的影响则越弱;2)理想模型重力异常分离结果中的边界效应与其切割分离的深度具有密切关系,若模型研究区扩边尺度相同,切割分离的深度越深,分离后的结果中包含的边界效应则越明显;3)边界效应与异常体的规模也有一定关系,若模型研究区数据的扩边尺度、分层分离深度相同,异常体的规模越大,分层分离结果中的边界效应则越明显,扩边尺度需进一步增加,以减弱分层分离结果中的边界效应;4)若模型数据扩边尺度固定,分层分离结果中边界效应的空间展布不是由数据区域边界向中心区域均匀分布,而与异常体的规模和空间位置有关,异常的规模和幅度越大,边界效应则越明显。
2.2.3 扩边尺度与重力场源分离误差分析根据均方误差公式对扩边尺度与重力场源分离误差进行分析,分别统计理想模型在50、100和150倍格网点距扩边尺度条件下1~50倍格网点距对应的不同深度层源在地表的重力异常理论值与重力场源分离计算值差异的均方误差:
| $\delta=\sqrt{\frac{1}{M P} \sum\limits_{m=1}^{M} \sum\limits_{p=1}^{P}\left[v_{c}(m, n)-v_{t}(m, n)\right]^{2}} $ | (4) |
式中,M、P分别为理想模型重力异常格网的线数及其点数,vt、vc分别为理想模型不同深度层源在地表的重力异常理论值和重力场源分离计算值。δ计算结果如图 8所示。
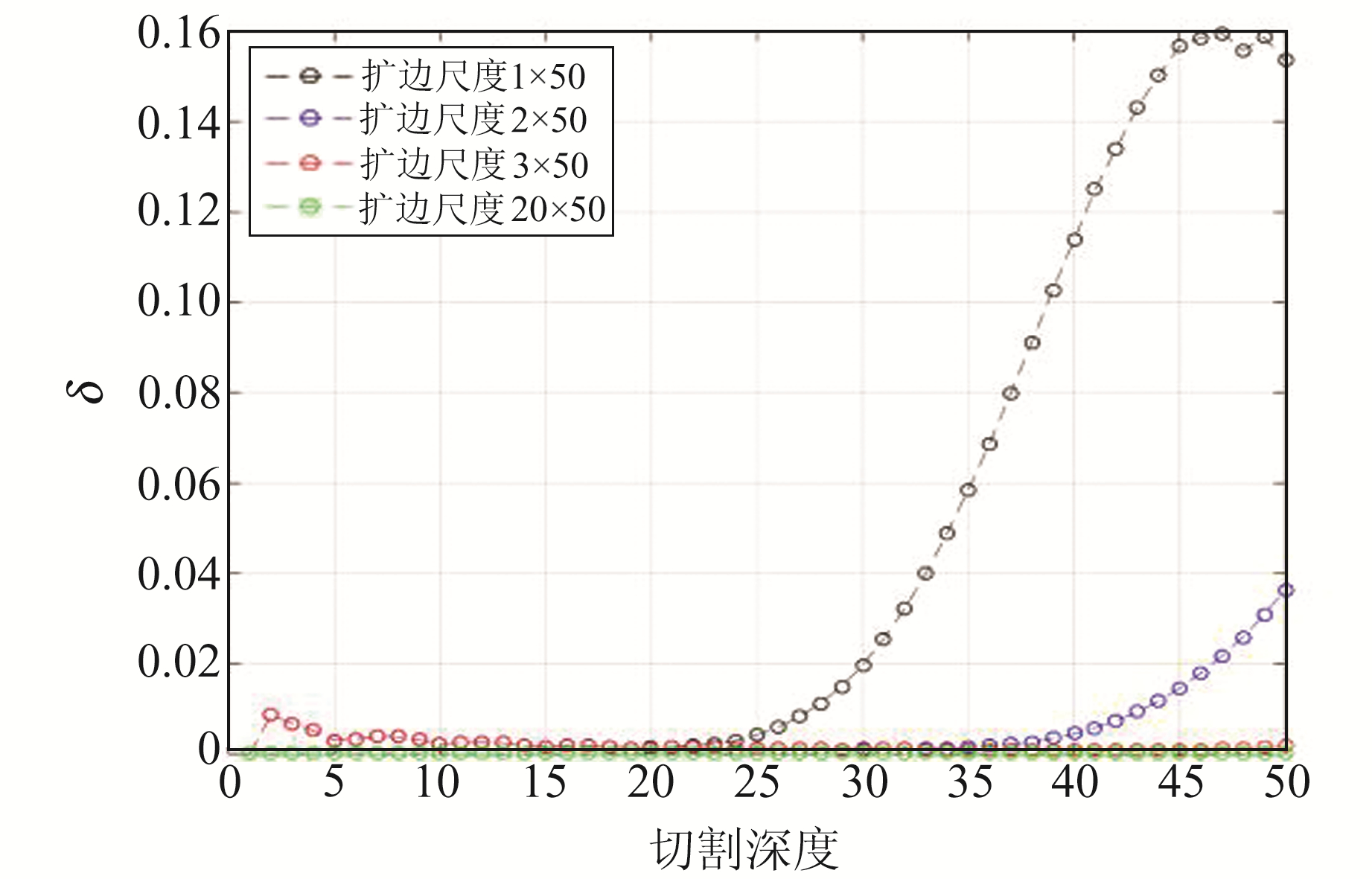
|
图 8 不同扩边尺度、不同深度层源重力异常差异均方误差 Fig. 8 The mean square error of gravity anomalies difference at different expanded edge sizes and depths |
图 8中横坐标为理想模型切割所选取的切割半径,最大切割半径为50倍格网点距;纵坐标为不同切割半径所对应的重力异常差异的均方误差。从图 8可以看出:1)当理想模型数据的扩边尺度一定时,随着切割半径的增加,即切割深度增加,不同深度层源的地表重力异常差异的均方误差不断增大,即分层分离结果中的边界效应越显著;2)当切割深度一定时,随着数据扩边尺度的增加,不同深度层源的重力异常差异的均方误差迅速衰减,表明扩边尺度越大,分层分离结果中的边界效应显著减弱;3)随着理想模型数据扩边尺度的增加,模型重力异常差异的均方误差衰减变缓,表明扩边尺度增加到一定程度再继续增加时,对边界效应的改善有限;4)理想模型数据的扩边尺度与切割的最大深度存在近似2∶1的关系,若要使不同深度层源的重力异常分离结果的边界效应不明显,则理想模型数据的扩边尺度不应小于最大切割深度的2倍;5)随着模型数据扩边尺度的增加,若用小尺度切割半径进行切割时,累积误差效应显著增加,表明模型数据的扩边尺度并非越大越好。
同理,分别计算理想模型数据的扩边尺度基数为40倍格网点距(40、80、120和800)、30倍格网点距(30、60、90和600)及20倍格网点距(20、40、60和400)条件下理想模型的地表重力异常理论值与重力场源分离计算值差异的均方误差,结果如图 9所示。
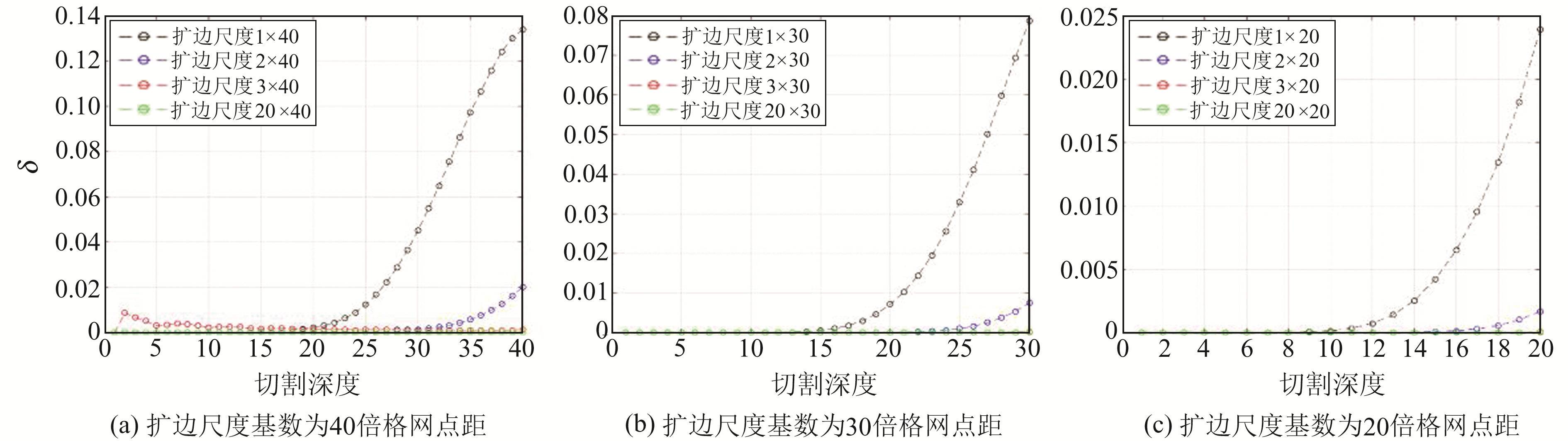
|
图 9 不同扩边尺度、不同深度层源重力异常差异的均方误差 Fig. 9 The mean square error of gravity anomalies difference at different expanded edge sizes and depths |
通过对比图 8和9可以发现,随着模型数据扩边尺度的增加,在减弱分离结果边界效应的同时也会使分离结果中引入计算误差。当模型数据的扩边尺度过大,且切割半径较小时,分离结果中计算误差显著,且随着扩边尺度增加,误差累积效应越明显,即数据的扩边尺度并非越大越好,适当即可,如模型数据的扩边尺度基于50倍和40倍格网点距(图 8和9(a))。当模型数据的扩边尺度较小、切割分离半径较大时,分离结果中包含的误差累积效应显著减弱,如模型数据扩边尺度基于30倍和20倍格网点距(图 9(b)和9(c))。
3 实际资料计算图 10为五河周边区域1∶20万比例尺的布格重力异常数据,插值后的数据格网间距为1 000 m×1 000 m,本文基于改进后的插值切割算子对研究区实测布格重力异常数据进行不同深度层源的切割分离,切割分离最大深度为10倍格网间距,即10 km,计算获得1 000 m、2 000 m、3 000 m和6 000 m不同深度层源在地表的重力异常,分离后的各深度层源在地表的重力异常如图 11所示。基于改进后的插值切割算子的分离结果与文献[11]基本一致,且随着切割深度的增加,两者一致性更好,但浅部分离结果(图 11(a))与文献[11]在异常幅度方面存在较为明显的差异,这种差异可能是由于本文与文献[11]使用不同分辨率的重力异常数据进行切割分离所致。
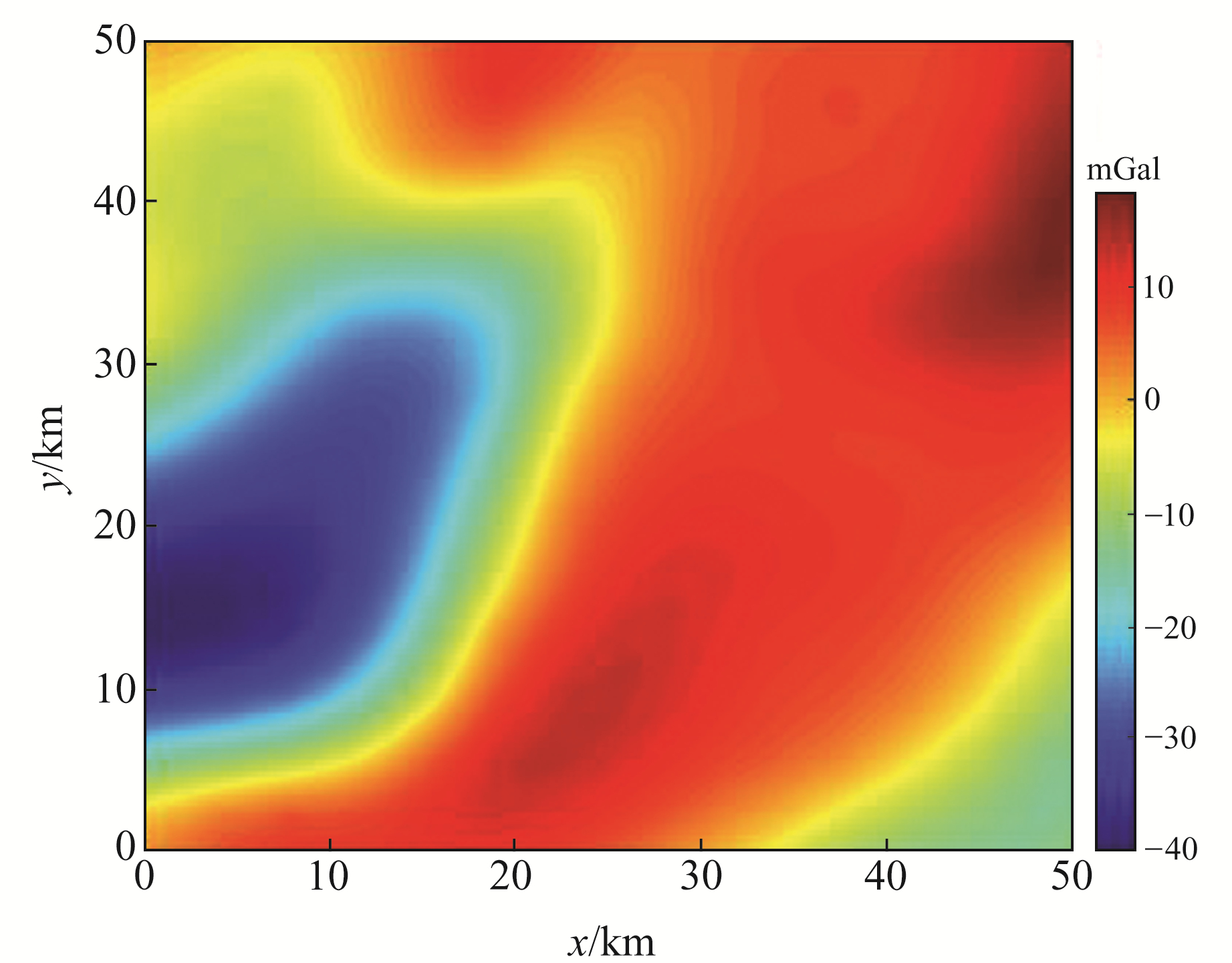
|
图 10 布格重力异常 Fig. 10 Bouguer gravity anomalies |

|
图 11 扩边尺度为40倍格网点距的不同深度层源重力异常在地表的空间分布 Fig. 11 The distribution of gravity anomalies at different depths of layers with an expanded edge size of 40 times grid spacing |
根据均方误差公式对实测布格重力异常数据的扩边尺度与重力场源分离误差进行分析,以40倍格网点距扩边尺度为参考,计算10、20和30倍格网点距扩边尺度条件下1~20倍格网点距对应的不同深度层源在地表的重力异常差异的均方误差,结果如图 12所示。图 12与图 8总体上表现出相似的特征,同时图 12的分层分离结果更好地说明在边缘区域存在较大异常时,需要在扩边尺度与最大切割深度近似2∶1的基础上进一步增加扩边尺度,以减弱分层分离结果中的边界效应,如扩边尺度与最大切割深度关系近似为3∶1。
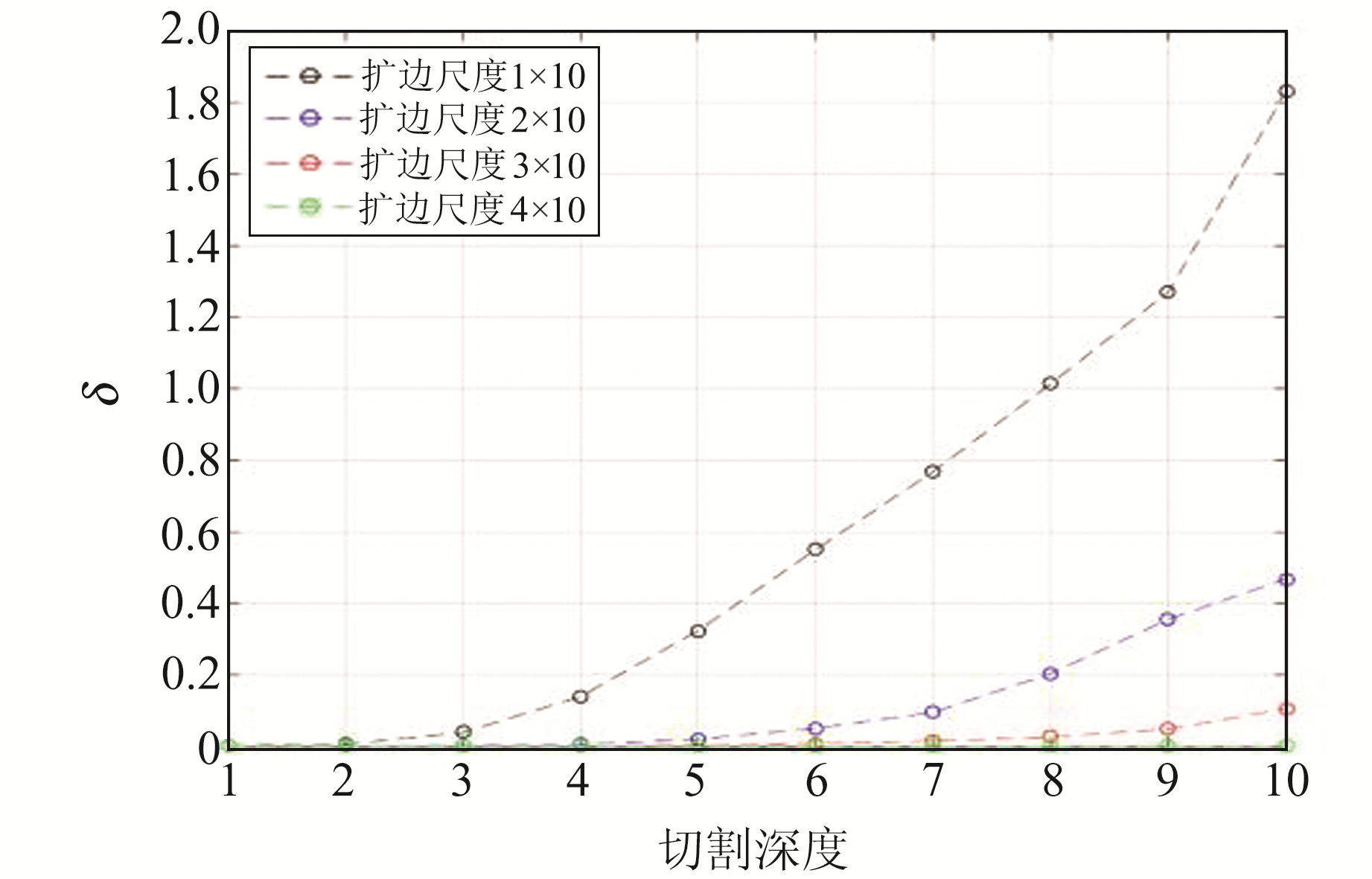
|
图 12 不同扩边尺度、不同深度层源重力异常差异的均方误差 Fig. 12 mean square error of gravity anomalies difference at different expanded edge sizes and depths |
本文基于改进后的插值切割算子,对三维组合理想模型在地表的重力异常进行不同深度层源的切割分离,从不同深度层源的重力异常差异、扩边尺度与重力场源误差分析方面,研究扩边尺度对重力异常分层分离处理的影响,为位场数据处理过程中扩边尺度的合理选取提供参考依据。
1) 实验结果表明,数据区域的边界效应与扩边尺度、分离切割深度、异常的规模和幅度及空间位置等因素相关。当切割分离深度、异常体的规模和异常幅度、空间位置一定时,数据扩边尺度越大,分层分离结果中的边界效应越弱;扩边尺度越小,边界效应越强。
2) 扩边尺度的选择应综合考虑分析资料所需满足的精度和数据计算效率,扩边尺度不宜过大,若扩边尺度过大,且切割半径较小,分离结果中计算误差显著,扩边尺度与重力异常分层分离的最大切割深度至少应满足2∶1的要求,才能明显改善边界效应和计算误差。对含有较大重力异常的边界进行切割分离时,应在2倍扩边尺度的基础上再进一步扩边,基于此关系,根据所要分离的最大切割深度确定数据区域的扩边尺度,或根据数据区域的扩边尺度确定最大切割深度。
3) 数据区域边界效应的空间展布不是由数据区域边界向中心区域均匀分布,而与异常体的规模和空间位置有关。
致谢: 本文得到中国地震局地震研究所胡敏章博士、合肥工业大学葛粲博士、中国地震局第一监测中心刘金钊博士的支持和帮助,在此表示诚挚感谢。
| [1] |
段本春, 徐世浙. 磁(重力)异常局部场与区域场分离处理中的扩边方法研究[J]. 物探化探计算技术, 1997, 19(4): 298-304 (Duan Benchun, Xu Shizhe. A Study of the Scheme of Extending Edge in the Processing of Separating Local Field from Regional Field for Magnetic/Gravity Anomaly[J]. Computing Techniques for Geophysical and Geochemical Exploration, 1997, 19(4): 298-304)
(  0) 0) |
| [2] |
姚长利, 管志宁, 高德章, 等. 低纬度磁异常化极方法——压制因子法[J]. 地球物理学报, 2003, 46(5): 690-696 (Yao Changli, Guan Zhining, Gao Dezhang, et al. Reduction-to-the-Pole of Magnetic Anomalies at Low Latitude with Suppression Filter[J]. Chinese Journal of Geophysics, 2003, 46(5): 690-696)
(  0) 0) |
| [3] |
张辉, 陈龙伟, 任治新, 等. 位场向下延拓迭代法收敛性分析及稳健向下延拓方法研究[J]. 地球物理学报, 2009, 52(4): 1107-1113 (Zhang Hui, Chen Longwei, Ren Zhixin, et al. Analysis on Convergence of Iteration Method for Potential Fields Downward Continuation and Research on Robust Downward Continuation Method[J]. Chinese Journal of Geophysics, 2009, 52(4): 1107-1113)
(  0) 0) |
| [4] |
张志厚, 徐世浙, 余海龙, 等. 位场向下延拓的迭代法的扩边方法[J]. 浙江大学学报: 工学版, 2013, 47(5): 918-924 (Zhang Zhihou, Xu Shizhe, Yu Hailong, et al. Study of Extending Methods of Iteration of Downward Continuation in Potential Field[J]. Journal of Zhejiang University: Engineering Science, 2013, 47(5): 918-924)
(  0) 0) |
| [5] |
骆遥, 吴美平. 位场向下延拓的最小曲率方法[J]. 地球物理学报, 2016, 59(1): 240-251 (Luo Yao, Wu Meiping. Minimum Curvature Method for Downward Continuation of Potential Field Data[J]. Chinese Journal of Geophysics, 2016, 59(1): 240-251)
(  0) 0) |
| [6] |
王万银, 邱之云, 刘金兰, 等. 位场数据处理中的最小曲率扩边和补空方法研究[J]. 地球物理学进展, 2009, 24(4): 1327-1338 (Wang Wanyin, Qiu Zhiyun, Liu Jinlan, et al. The Research to the Extending Edge and Interpolation Based on the Minimum Curvature Method in Potential Field Data Processing[J]. Progress in Geophysics, 2009, 24(4): 1327-1338)
(  0) 0) |
| [7] |
马国庆, 孟令顺, 杜晓娟, 等. 磁法数据处理中的扩边和优化中值滤波方法的研究[J]. 物探化探计算技术, 2010, 32(2): 194-199 (Ma Guoqing, Meng Lingshun, Du Xiaojuan, et al. The Study of Edge Expansion and Optimization Median Filtering Method in Magnetic Data Processing[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2010, 32(2): 194-199)
(  0) 0) |
| [8] |
李盼, 戴前伟, 吕宏安. 基于泛克里格方法的位场扩边处理[J]. 物探化探计算技术, 2018, 40(6): 741-747 (Li Pan, Dai Qianwei, Lü Hongan. The Edge Extending of Potential Field Data Based on Universal Kriging Interpolation Method[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2018, 40(6): 741-747)
(  0) 0) |
| [9] |
曾小牛, 李夕海, 刘继昊, 等. 基于凸集投影的重力数据扩充下延一体化方法[J]. 石油地球物理勘探, 2019, 54(5): 1166-1173 (Zeng Xiaoniu, Li Xihai, Liu Jihao, et al. An Integration of Interpolation Edge Padding and Downward Continuation for Gravity Data Based on the Projection onto Convex Sets[J]. Oil Geophysical Prospecting, 2019, 54(5): 1166-1173)
(  0) 0) |
| [10] |
Amidror I. Scattered Data Interpolation Methods for Electronic Imaging Systems: A Survey[J]. Journal of Electronic Imaging, 2002, 11(2): 157-176 DOI:10.1117/1.1455013
(  0) 0) |
| [11] |
葛粲, 任升莲, 李永东, 等. 重力异常分层分离方法改进及应用: 以安徽五河地区为例[J]. 地球物理学报, 2017, 60(12): 4826-4839 (Ge Can, Ren Shenglian, Li Yongdong, et al. Improvement and Application of the Layered Separation Method for Gravity Anomalies: An Example of the Wuhe Area, Anhui Province[J]. Chinese Journal of Geophysics, 2017, 60(12): 4826-4839)
(  0) 0) |
| [12] |
程方道, 刘东甲, 姚汝信. 划分重力区域场与局部场的研究[J]. 物化探计算技术, 1987, 9(1): 1-9 (Cheng Fangdao, Liu Dongjia, Yao Ruxin. A Study on the Identification of Regional and Local Gravity Fields[J]. Computing Techniques for Geophysical and Geochemical Exploration, 1987, 9(1): 1-9)
(  0) 0) |
| [13] |
文百红, 程方道. 用于划分磁异常的新方法——插值切割法[J]. 中南矿冶学院学报, 1990, 21(3): 229-235 (Wen Baihong, Cheng Fangdao. A New Interpolating Cut Method for Identifying Regional and Local Fields of Magnetic Anomaly[J]. Journal of Central-South Institute of Mining and Metallurgy, 1990, 21(3): 229-235)
(  0) 0) |
| [14] |
秦葆瑚. 用分层切割法研究复杂磁异常[J]. 物探化探计算技术, 1994, 16(2): 96-101 (Qin Baohu. Divisions of Complex Magnetic Anomaly by Layered Dividing Method[J]. Computing Techniques for Geophysical and Geochemical Exploration, 1994, 16(2): 96-101)
(  0) 0) |
| [15] |
徐世浙, 曹洛华, 姚敬金. 重力异常三维反演: 视密度成像方法技术的应用[J]. 物探与化探, 2007, 31(1): 25-28 (Xu Shizhe, Cao Luohua, Yao Jingjin. 3D Inversion of Gravity Anomaly: An Application of the Apparent Density Imagery Technology[J]. Geophysical and Geochemical Exploration, 2007, 31(1): 25-28)
(  0) 0) |
| [16] |
杨金玉, 徐世浙, 余海龙, 等. 视密度反演在东海及邻区重力异常解释中的应用[J]. 地球物理学报, 2008, 51(6): 1909-1916 (Yang Jinyu, Xu Shizhe, Yu Hailong, et al. Application of Apparent Density Inversion Method in the East China Sea and Its Adjacent Area[J]. Chinese Journal of Geophysics, 2008, 51(6): 1909-1916)
(  0) 0) |
| [17] |
徐世浙, 余海龙, 李海侠, 等. 基于位场分离与延拓的视密度反演[J]. 地球物理学报, 2009, 52(6): 1592-1598 (Xu Shizhe, Yu Hailong, Li Haixia, et al. The Inversion of Apparent Density Based on the Separation and Continuation of Potential Field[J]. Chinese Journal of Geophysics, 2009, 52(6): 1592-1598)
(  0) 0) |
| [18] |
徐世浙, 王华军, 余海龙, 等. 普光气田重力异常的视密度反演[J]. 地球物理学报, 2009, 52(9): 2357-2363 (Xu Shizhe, Wang Huajun, Yu Hailong, et al. Apparent Density Inversion of Gravity Anomalies of Puguang Gas Field[J]. Chinese Journal of Geophysics, 2009, 52(9): 2357-2363)
(  0) 0) |
| [19] |
邢怡, 滕菲, 张国利. 利用插值切割法研究重力区域场与局部场的分离[J]. 地质调查与研究, 2014, 37(3): 193-196 (Xing Yi, Teng Fei, Zhang Guoli. An Interpolating Cut Method for Separation of Regional and Local Gravity Field[J]. Geological Survey and Research, 2014, 37(3): 193-196)
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41

