干旱指数作为一种计算简单且容易理解的参数,成为目前量化和评估干旱的常用手段[1],如基于降雨的标准化降雨指数(SPI)[2]和基于降雨及其他气象要素(温度)的帕默尔指数(PDSI)[3]等,同时也有大量学者研究利用GRACE卫星反演的陆地水储量(TWS)变化进行干旱监测[4-8]。
目前利用最新的GRACE RL06时变重力场数据分析干旱时空特征的研究较少,本文以长江流域为例,基于最新GRACE卫星时变重力场数据反演的水储量变化,构造水储量亏损指数,探测并评估长江流域2003-01~2014-12的干旱事件,主要目的有:1)利用广义三角帽方法分析不同GRACE时变重力场数据产品反演长江流域水储量变化的不确定性;2)分析长江流域水储量变化的时变特征;3)利用水储量亏损指数分析长江流域干旱的时空特征,并与改进的帕默尔指数(scPDSI)[9]进行比较,验证水储量亏损指数在监测长江流域干旱方面的有效性。
1 研究区域长江流域横跨中国东部、中部和西部三大经济区,是中国第一大河,世界第三大流域,总面积约180万km2,约占中国国土面积的18.8%,其地处亚热带季风区,气候温暖湿润。长江中上游分界点为宜昌,中下游分界点为湖口,年平均气温约为14 ℃,年降雨量约为1 100 mm,年水面蒸发量约为990 mm[10]。受气候变化和人类活动的影响,长江流域在过去几年经历了数次极端干旱天气[11-13],监测干旱事件对长江流域水资源的合理利用与分配具有重要作用。
2 数据与方法 2.1 数据 2.1.1 GRACE数据本文利用CSR和JPL分别发布的3种GRACE时变重力场数据产品反演长江流域的水储量变化:1)最新的GRACE level-2 RL06版球谐系数(SH)时变重力场数据;2)level-3网格数据产品;3)月RL06 Mascon解数据产品。为方便表示,以上数据分别记为CSR_SH、JPL_SH和CSR_L3、JPL_L3及CSR_M、JPL_M,所有数据的时间分辨率都为1个月,时间跨度为2003-01~2014-12,缺少的月份利用相邻月份数据进行简单插值得到。
2.1.2 降雨数据降雨对长江流域干旱特征的研究具有重要意义。降雨数据取自GPM数据产品[14],其时间分辨率为1个月,空间分辨率为0.1°×0.1°,时间跨度与GRACE数据一致。
2.1.3 水文模型数据使用2种水文模型验证GRACE反演长江流域水储量变化的正确性:第1种为全球水文模型(WGHM),该模型不仅模拟了雪水当量、土壤水和植物冠层含水量,还输出地表水和地下水,其时空分辨率分别为0.5°×0.5°和1个月[15];第2种为GLDAS,该系统利用地表观测与卫星遥感观测数据,驱动CLM、MOSAIC、NOAH、VIC和CLSM陆面模型,并通过模型模拟与数据同化生成全球范围的地表状态变量(土壤水分和地表温度)及通量(蒸发和感热通量)数据[16]。本文使用GLDAS NOAH模型模拟输出,时空分辨率为1°×1°和1个月,该模型未模拟地表水和地下水分量。水文模型数据的时间跨度与GRACE数据一致。
2.1.4 scPDSI数据尽管帕默尔指数(PDSI)被较早提出,但其参数对不同区域的敏感性较高,且计算方案中土壤湿度的取值在观测资料缺乏的地区存在较大的不确定性。本文选用改进的帕默尔指数(scPDSI)[9],其优势是考虑了全球变暖和地球过去状态的变化,具有监测长期干旱事件的能力,还计算了潜在蒸散量,用实际植被代替参考作物,同时考虑了积雪的季节性动态变化,具有空间可比性。scPDSI数据的时空分辨率分别为2.5°×2.5°和1个月。
2.2 研究方法水储量亏损(WSD)是每月水储量变化与对应月份的平均气候之差,月平均气候定义为时间序列中所有该月水储量变化数据的平均值。水储量亏损(WSD)和水储量亏损指数(WSDI)的计算公式可表示为:
| $ {{\rm{WS}}{{\rm{D}}_{i, j}} = {\rm{TWS}}{{\rm{A}}_{i, j}} - \overline {{\rm{TWS}}{{\rm{A}}_j}} } $ | (1) |
| $ {{\rm{WSDI}} = \frac{{{\rm{WSD}} - \mu }}{\sigma }} $ | (2) |
式中,i为第i年,j为第j月,
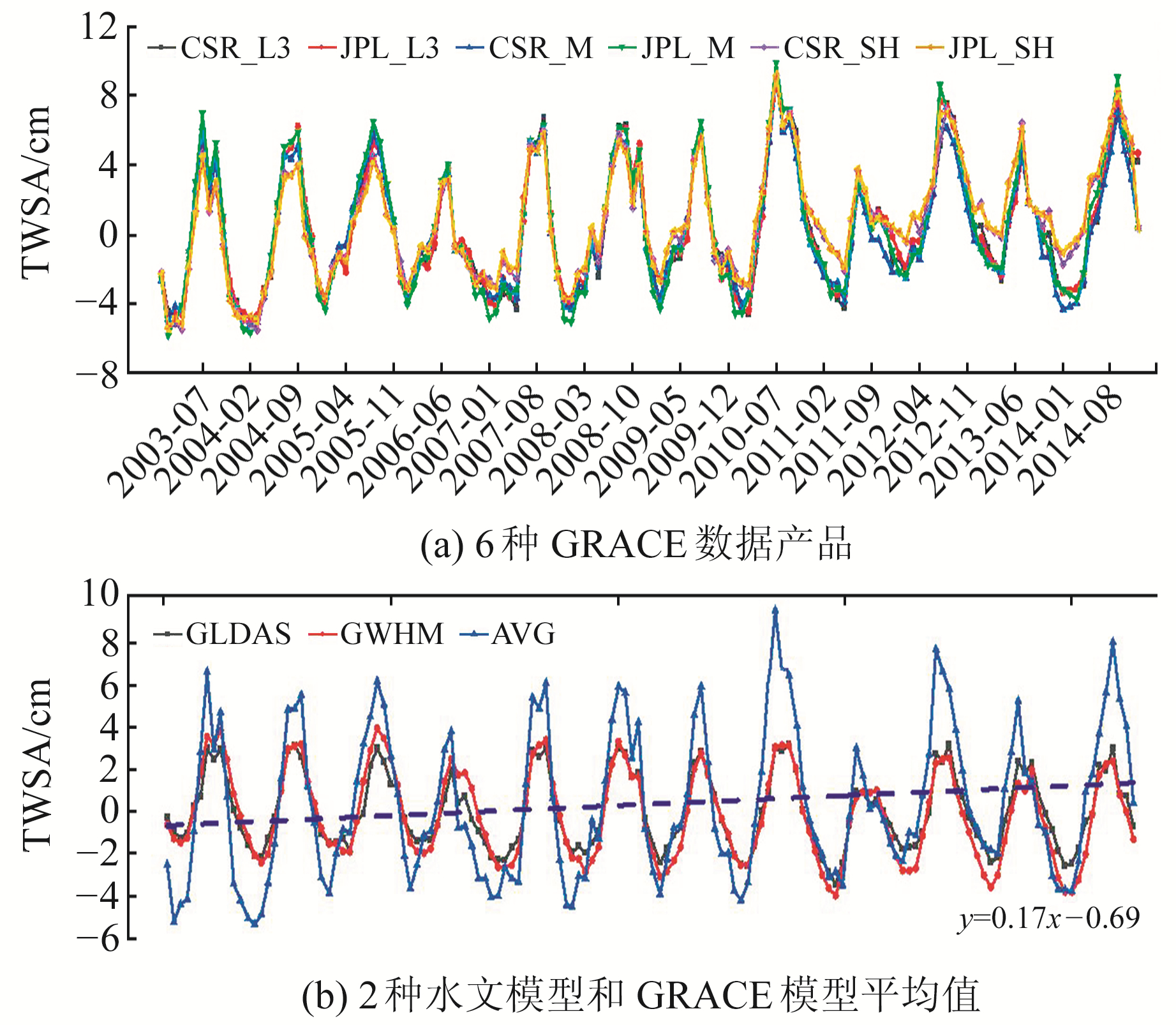
利用6种GRACE数据分别计算长江流域的水储量变化,结果见图 1。由图 1(a)可知,6种GRACE数据的结果具有很高的一致性;从振幅来看,Mascon解略大于level-3,SH解振幅最小。如表 1所示,CSR_M与JPL_SH之间的相关系数最低,而CSR_SH与JPL_SH之间的相关系数最高。结果表明,Mascon解目前在反演区域水储量变化方面确实具有更少的泄露误差,同时RL06版球谐系数产品的精度也在不断提高。无特殊说明,本文采用6种GRACE数据计算结果的平均值作为长江流域水储量变化的最终估值。图 1(b)将GRACE反演结果与GLDAS及WGHM等水文模型进行对比,从时间上看,GRCAE的反演结果与GLDAS及WGHM具有较高的一致性,相关系数分别为0.90和0.84;从振幅上看,GRACE反演的振幅大于2种水文模型,这是因为GRACE反演的水储量变化包括地球表面和次表面所有的水文信息,而水文模型通常遗漏某些水文分量。另外WGHM的振幅略大于GLDAS,这是因为WGHM还模拟了地表水和地下水,而GLDAS只输出雪水当量、土壤水和植物冠层含水量。图 2(b)中蓝色虚线为平均值的线性拟合结果,可以看出,长江流域水储量变化在此期间呈小幅上升趋势,约为0.17 cm/a(通过了M-K趋势检测)。利用广义三角帽方法[17]计算6种GRACE数据产品的不确定性,其中JPL_M的不确定性最小,为3.51 mm,而JPL_SH的不确定性最大,为10.71 mm。
|
图 1 长江流域水储量变化 Fig. 1 The TWSA of Yangtze |
|
|
表 1 不同数据源计算的长江流域水储量变化的相关系数和不确定性 Tab. 1 Correlation matrix and uncertainty of Yangtze TWSA from different data |
|
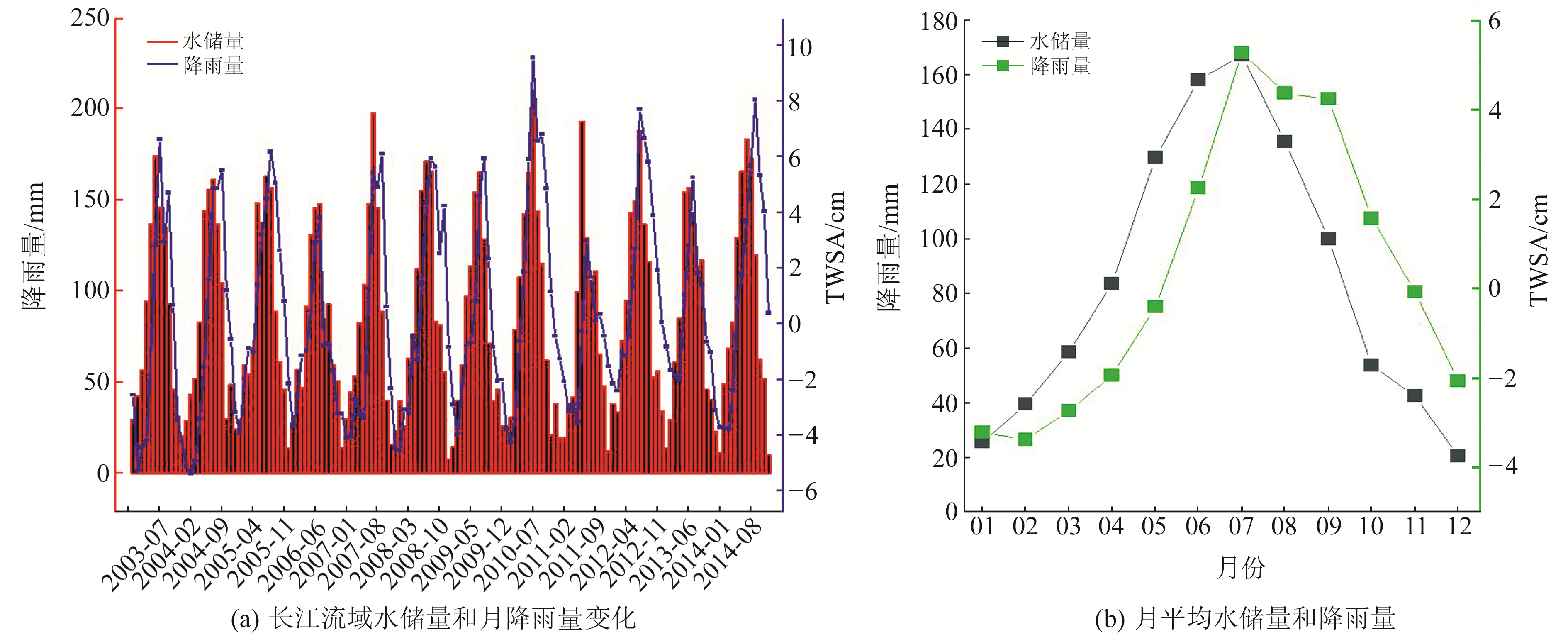
图 2 水储量及降雨量 Fig. 2 Water storage and precipitation |
图 2(a)为长江流域的水储量变化和月累积降雨变化,可以看出,二者具有较高的一致性,相关系数达0.67,表明降雨是影响长江流域水储量变化的重要因素。图 2(b)为长江流域长期月平均水储量与降雨量,可以看出,长江流域的水储量和降雨量都具有明显的季节性变化,冬季(12月~次年1月)降水量为全年最少,春季(3~5月)降水量逐月增加,夏季(6~7月)长江中下游月降水量超过170 mm,而水储量则在每年7月达到峰值,约为5.27 cm,冬季达到低谷,约为-3.3 cm。
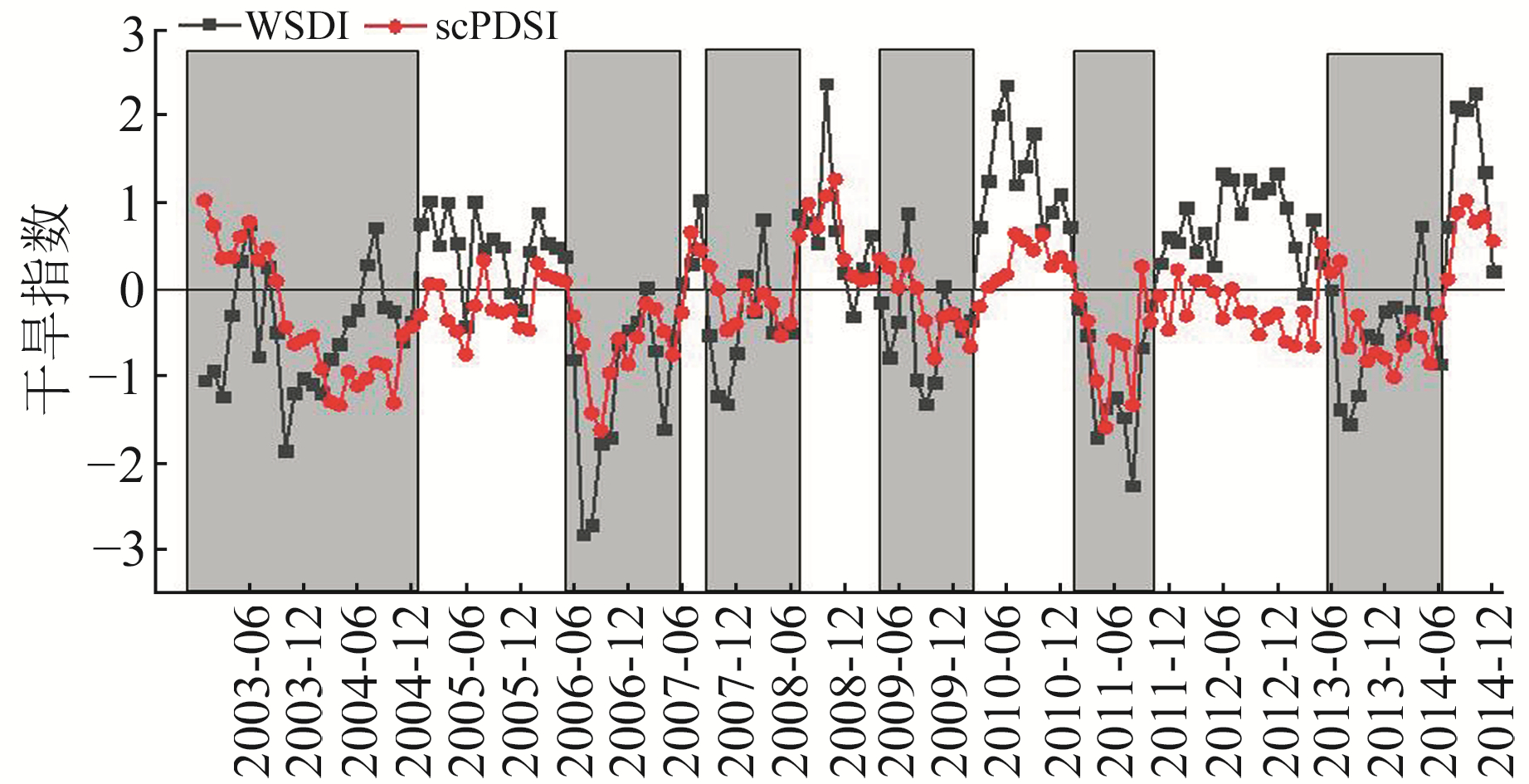
3.2 干旱监测根据定义,WSDI连续3个月或以上为负值时判定为1次干旱事件,而WSDI在干旱事件期间取值为不超过2个月的正值则定义为干旱异常事件,也属于干旱月。为对比分析WSDI与scPDSI,将所有scPDSI的取值向上调整1个数值(因为scPDSI取值小于-1时定义为干旱),并采取与WSDI同样的准则监测长江流域的干旱。图 3为长江流域WSDI和scPDSI时间序列,图中阴影部分表示利用WSDI探测到的长江流域干旱事件,同时计算各干旱事件的量级和强度[1],结果见表 2。可以看出,2003-01~2014-12长江流域共经历了6次干旱事件,其中持续时间最长的是2003-02开始的干旱,持续时间为2 a;2006年夏天和2011年春天同样检测到干旱事件,这与前人的研究结论[11-12]一致,而这2次干旱也是研究期间最严重的干旱事件,强度分别达到2.15和1.97。
|
图 3 长江流域WSDI和scPDSI时间序列 Fig. 3 Time series of WSDI and scPDSI in Yangtze |
|
|
表 2 利用WSDI监测长江流域干旱事件总结 Tab. 2 Summary table of WSDI-identified drought events |
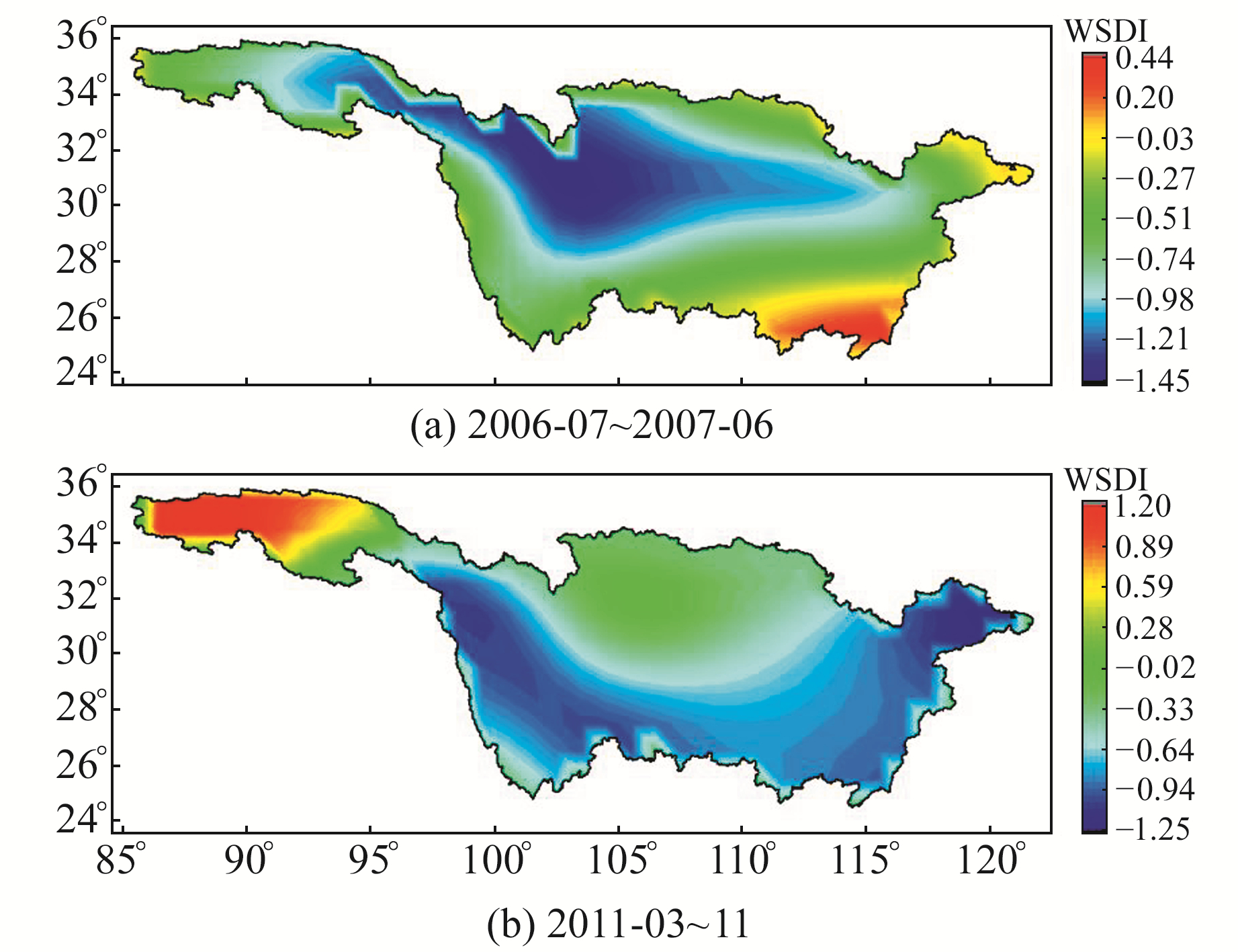
以2006-07和2011-03这2次最严重的干旱事件为例,分别计算平均WSDI的空间分布。图 4(a)为2006-07~2007-06长江流域平均WSDI的空间分布,可以看出,在此期间几乎整个长江流域的WSDI均为负值,即处于干旱状态,仅东南角的平均WSDI略大于零,这可能与长江流域降雨的空间分布有关;另外,长江流域中部地区的干旱程度明显大于其他区域。图 4(b)为2011-03~11长江流域平均WSDI的空间分布,不同于2006年的干旱事件,此次干旱主要集中于长江流域的下游、中游及上游东南地区,而上游西北地区水储量明显处于丰盈状态,可能与唐古拉山等山脉雪水融化有关。
|
图 4 长江流域平均WSDI空间分布 Fig. 4 Spatial distribution of mean WSDI in Yangtze |
scPDSI也监测到了6次干旱事件(2003-10~2006-01、2006-06~2007-06、2008-02~06、2009-09~2010-03、2011-02~2013-04、2013-08~2014-06),与WSDI监测到的干旱事件的发生和结束时间略有不同,这可能是因为WSDI主要与水储量变化有关,而scPDSI主要与降雨、温度等其他气象要素有关,也可能与两者的模型误差有关,两者的相关系数为0.53。由此可知,WSDI确实可以有效监测长江流域的干旱事件。
4 结语随着GRACE时变重力场数据产品质量的提高及GRACE Follow-on卫星的成功发射,利用GRACE卫星监测大尺度范围的干旱越来越受到关注。本文利用6种不同的GRACE模型数据计算长江流域的水储量变化,并利用GPM产品计算其降雨变化,同时构造水储量亏损指数(WSDI)来监测长江流域的干旱事件,并和改进的帕默尔指数(scPDSI)进行对比,得出以下结论:
1) 长江流域的水储量与降雨呈明显的季节性变化。陆地水储量在每年7月达到峰值,约为5.27 cm;而降雨量在每年夏季达到峰值,约为170 mm。降雨量与水储量变化的相关系数为0.67,表明降雨是影响长江流域陆地水储量变化的重要因素。
2) 利用广义三角帽方法分析了6种不同模型数据的不确定性,结果表明,目前Mascon解的时空分辨率优于SH解,JPL_M、CSR_M、CSR_L3、JPL_L3、CSR_SH和JPL_SH的不确定性分别为3.51 mm、3.78 mm、5.45 mm、9.87 mm、9.12 mm及10.71 mm。
3) 利用WSDI监测到长江流域2003-01~2014-12共经历6次干旱,其中持续时间最长的干旱事件始于2003-02,持续时间达2 a;而最严重的干旱事件发生于2006年春季和2011年夏季,强度分别为2.15和1.97。WSDI的空间分布表明,2006-07~2007-06几乎整个长江流域都处于干旱状态,而2011-03~11干旱主要集中于长江流域下游、中游及上游东南地区。另外,WSDI与scPDSI的相关系数为0.53,表明WSDI可有效监测长江流域的干旱。
| [1] |
Zargar A, Sadiq R, Naser B, et al. A Review of Drought INDICES[J]. Environmental Reviews, 2011, 19(1): 333-349
(  0) 0) |
| [2] |
Nie N, Zhang W C, Chen H, et al. A Global Hydrological Drought Index Dataset Based on Gravity Recovery and Climate Experiment (GRACE) Data[J]. Water Resources Management, 2018, 32(4): 1 275-1 290 DOI:10.1007/s11269-017-1869-1
(  0) 0) |
| [3] |
Dai A G, Trenberth K E, Qian T T. A Global Dataset of Palmer Drought Severity Index for 1870-2002: Relationship with Soil Moisture and Effects of Surface Warming[J]. Journal of Hydrometeorology, 2004, 5(6): 1 117-1 130 DOI:10.1175/JHM-386.1
(  0) 0) |
| [4] |
Yirdaw S Z, Snelgrove K R, Agboma C O. GRACE Satellite Observations of Terrestrial Moisture Changes for Drought Characterization in the Canadian Prairie[J]. Journal of Hydrology, 2008, 356(1-2): 84-92 DOI:10.1016/j.jhydrol.2008.04.004
(  0) 0) |
| [5] |
Chen J L, Wilson C R, Tapley B D, et al. 2005 Drought Event in the Amazon River Basin as Measured by GRACE and Estimated by Climate Models[J]. Journal of Geophysical Research Atmospheres, 2009, 114(B5)
(  0) 0) |
| [6] |
Lenk O. Satellite Based Estimates of Terrestrial Water Storage Variations in Turkey[J]. Journal of Geodynamics, 2013, 67: 106-110 DOI:10.1016/j.jog.2012.04.010
(  0) 0) |
| [7] |
Thomas A C, Reager J T, Famiglietti J S, et al. A GRACE-Based Water Storage Deficit Approach for Hydrological Drought Characterization[J]. Geophysical Research Letters, 2014, 41(5): 1 537-1 545 DOI:10.1002/2014GL059323
(  0) 0) |
| [8] |
李琼, 罗志才, 钟波, 等. 利用GRACE时变重力场探测2010年中国西南干旱陆地水储量变化[J]. 地球物理学报, 2013, 56(6): 1 843-1 849 (Li Qiong, Luo Zhicai, Zhong Bo, et al. Terrestrial Water Storage Changes of the 2010 Southwest China Drought Detected by GRACE Temporal Gravity Field[J]. Chinese Journal of Geophysics, 2013, 56(6): 1 843-1 849)
(  0) 0) |
| [9] |
Schrier G, Barichivich J, Briffa K R, et al. A scPDSI-Based Global Data Set of Dry and Wet Spells for 1901-2009[J]. Journal of Geophysical Research: Atmospheres, 2013, 118(10): 4 025-4 048 DOI:10.1002/jgrd.50355
(  0) 0) |
| [10] |
Sun Z L, Zhu X F, Pan Y Z, et al. Drought Evaluation Using the GRACE Terrestrial Water Storage Deficit over the Yangtze River Basin, China[J]. Science of the Total Environment, 2018, 634: 727-738 DOI:10.1016/j.scitotenv.2018.03.292
(  0) 0) |
| [11] |
Long D, Yang Y T, Wada Y, et al. Deriving Scaling Factors Using a Global Hydrological Model to Restore GRACE Total Water Storage Changes for China's Yangtze River Basin[J]. Remote Sensing of Environment, 2015, 168: 177-193 DOI:10.1016/j.rse.2015.07.003
(  0) 0) |
| [12] |
Zhang Z Z, Chao B F, Chen J L, et al. Terrestrial Water Storage Anomalies of Yangtze River Basin Droughts Observed by GRACE and Connections with ENSO[J]. Global and Planetary Change, 2015, 126: 35-45 DOI:10.1016/j.gloplacha.2015.01.002
(  0) 0) |
| [13] |
Zhang D, Zhang Q, Werner A D, et al. GRACE-Based Hydrological Drought Evaluation of the Yangtze River Basin, China[J]. Journal of Hydrometeorology, 2016, 17(3): 811-828 DOI:10.1175/JHM-D-15-0084.1
(  0) 0) |
| [14] |
Prakash S, Mitra A K, Pai D S, et al. From TRMM to GPM: How Well can Heavy Rainfall be Detected from Space?[J]. Advances in Water Resources, 2016, 88: 1-7 DOI:10.1016/j.advwatres.2015.11.008
(  0) 0) |
| [15] |
Döll P, Kaspar F, Lehner B, et al. A Global Hydrological Model for Deriving Water Availability Indicators: Model Tuning and Validation[J]. Journal of Hydrology, 2003, 270(1-2): 105-134 DOI:10.1016/S0022-1694(02)00283-4
(  0) 0) |
| [16] |
刘任莉, 佘敦先, 李敏, 等. 利用卫星观测数据评估GLDAS与WGHM水文模型的适用性[J]. 武汉大学学报:信息科学版, 2019, 44(11): 1 596-1 604 (Liu Renli, She Dunxian, Li Min, et al. Using Satellite Observations to Assess Applicability of GLDAS and WGHM Hydrological Model[J]. Geomatics and Information Science of Wuhan University, 2019, 44(11): 1 596-1 604)
(  0) 0) |
| [17] |
姚朝龙, 李琼, 罗志才, 等. 利用广义三角帽方法评估GRACE反演中国大陆地区水储量变化的不确定性[J]. 地球物理学报, 2019, 62(3): 883-897 (Yao Chaolong, Li Qiong, Luo Zhicai, et al. Uncertainties in GRACE-Derived Terrestrial Water Storage Changes over Mainland China Based on a Generalized Three-Cornered Hat Method[J]. Chinese Journal of Geophysics, 2019, 62(3): 883-897)
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41


