2. 南京信息工程大学遥感与测绘工程学院,南京市宁六路219号,210044
在水准测量中,两个测量点之间的高差是指一点的水准面相对于另一点水准面的垂直距离。高差是由重力位差来确定的[1], 但在实际测量中,测量路径不同,所得到的高差是不相同的,这对测量工作中的精度评定是不利的。而力高结合几何上的高差测量和重力测量,使得高差与路径无关,同时可以保证在同一个等位面上有相同的高程[2-3]。在计算力高的公式中,涉及到正常重力平均值的选取时大多以大地纬度45°处的正常重力值作为平均值,但这样做并不科学,且容易引起系统性误差。
要想从地球向各大行星发射探测器,惯性导航技术至关重要,加速度计是惯性导航中的关键器件,而正常重力平均值的取值是否合理将直接影响到加速度计的精度[4]。为了在未来能够更顺利地探索太阳系甚至更远的星系,就需要进一步研究各天体的正常重力平均值所在的地心纬度随椭球第一偏心率变化的规律。本文将正常重力公式进行级数展开,利用牛顿迭代法等方法推导出正常重力平均值处地心纬度关于椭球第一偏心率的函数式。
1 正常重力平均值及其取值的地心纬度有研究表明,当正常重力平均值取大地纬度为35.358 7°处的正常重力值时,随着第一偏心率的增大,正常重力平均值处的纬度逐渐增大[5]。考虑到重力为引力和离心力之和,而引力为两质点之间的作用力,对地球而言,质点取在地心更为合理。
以地理纬度60°为例,其地心纬度为59.836°,两者相差0.164°,相当于9.84′,这在天体上的差距是较大的。因此,考虑利用地心纬度来推算正常重力平均值处纬度与第一偏心率的关系式。
正常重力公式为[6]:
| $ \gamma = \frac{{{\gamma _e}\left( {1 + k{{\sin }^2}(B)} \right)}}{{\sqrt {1 - {e^2}{{\sin }^2}(B)} }} $ | (1) |
式中,
在计算机代数系统中,将大地纬度B表示成地心纬度φ的闭合表达式:
| $ \left\{ \begin{array}{l} {\sin ^2}B = \frac{{{{\sin }^2}\varphi }}{{1 - 2{e^2} + {e^4} + 2{e^2}{{\sin }^2}\varphi - {e^4}{{\sin }^2}\varphi }}\\ {\cos ^2}B = \frac{{1 - 2{e^2} + {e^4}}}{{\frac{1}{{{{\cos }^2}\varphi }} - 2{e^2} + {e^4}}} \end{array} \right. $ | (2) |
将式(2)代入式(1),得到正常重力值与地心纬度φ的函数关系式:
| $ {\gamma _\varphi } = \frac{{{\gamma _e}\left( {1 + k\frac{{{{\sin }^2}\varphi }}{{1 - 2{e^2} + {e^4} + 2{e^2}{{\sin }^2}\varphi - {e^4}{{\sin }^2}\varphi }}} \right)}}{{\sqrt {1 - {e^2}\frac{{{{\sin }^2}\varphi }}{{1 - 2{e^2} + {e^4} + 2{e^2}{{\sin }^2}\varphi - {e^4}{{\sin }^2}\varphi }}} }} $ | (3) |
根据正常重力公式[7]及椭球大地测量学知识,可以得到:
| $ {\bar \gamma _E} = \frac{{\int_0^{2{\rm{ \mathsf{ π} }}} {\int_{ - \frac{{\rm{ \mathsf{ π} }}}{2}}^{\frac{{\rm{ \mathsf{ π} }}}{2}} \gamma } (\varphi )Mr{\rm{d}}\varphi {\rm{d}}\lambda }}{{\int_0^{2{\rm{ \mathsf{ π} }}} {\int_{ - \frac{{\rm{ \mathsf{ π} }}}{2}}^{\frac{{\rm{ \mathsf{ π} }}}{2}} M } r{\rm{d}}\varphi {\rm{d}}\lambda }} $ | (4) |
式中,
要想探究正常重力平均值与地心纬度的关系,需要将子午圈曲率半径M和平行圈曲率半径r转化成地心纬度φ的函数关系式:
| $ \left\{ {\begin{array}{*{20}{l}} {\quad {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} M = }\\ {\frac{{a\left( {1 - {e^2}} \right)}}{{{{\left( {1 - {e^2}\frac{{{{\sin }^2}\varphi }}{{1 - 2{e^2} + {e^4} + 2{e^2}{{\sin }^2}\varphi - {e^4}{{\sin }^2}\varphi }}} \right)}^{3/2}}}}}\\ {r = \frac{{a\sqrt {\frac{{1 - 2{e^2} + {e^4}}}{{1/{{\cos }^2}\varphi - 2{e^2} + {e^4}}}} }}{{\sqrt {1 - {e^2}\frac{{{{\sin }^2}\varphi }}{{1 - 2{e^2} + {e^4} + 2{e^2}{{\sin }^2}\varphi - {e^4}{{\sin }^2}\varphi }}} }}} \end{array}} \right. $ | (5) |
根据式(4),首先计算分子部分,积分后可得:
| $ \begin{array}{*{20}{c}} {\int_{ - {\rm{ \mathsf{ π} }}/2}^{{\rm{ \mathsf{ π} }}/2} \gamma (\varphi )Mr{\rm{d}}\varphi = }\\ {{a^2}{\gamma _e}\left( {{a_0} + {a_2}{e^2} + {a_4}{e^4} + {a_6}{e^6} + {a_8}{e^8}} \right)} \end{array} $ | (6) |
式中,
| $ \begin{array}{*{20}{c}} {\int_{ - {\rm{ \mathsf{ π} }}/2}^{{\rm{ \mathsf{ π} }}/2} M r{\rm{d}}\varphi = }\\ {\frac{2}{{105}}{a^2}\left( {105 - 70{e^2} + 21{e^4} + 12{e^6} + 9{e^8}} \right)} \end{array} $ | (7) |
利用计算机代数系统[8-9]将得到的正常重力平均值对第一偏心率e进行级数展开:
| $ {\bar \gamma _{Es}} = {b_0} + {b_2}{e^2} + {b_4}{e^4} + {b_6}{e^6} + {b_8}{e^8} + o{[e]^9} $ | (8) |
式中,b0=9.786 77, b2=1.598 37, b4=-9.135 31×1010, b6=2.435 19×1013, b8=5.541 12×1025。
若代入CGCS2000坐标系中的各参数值,可以求得在正常椭球上的正常重力平均值为γCGCS2000=979.77。
为求得正常重力平均值处的地心纬度,令正常椭球上的正常重力平均值公式与正常重力公式相等,建立方程式,得到:
| $ \begin{array}{l} \frac{{{\gamma _e}\left( {\begin{array}{*{20}{l}} {147{\kern 1pt} {\kern 1pt} {\kern 1pt} 840(3 + k) + 14{\kern 1pt} {\kern 1pt} {\kern 1pt} 784( - 15 + 7k){e^2} + }\\ {21{\kern 1pt} {\kern 1pt} {\kern 1pt} 648(7 + 5k){e^4} + 88(1{\kern 1pt} {\kern 1pt} {\kern 1pt} 389 + 1{\kern 1pt} {\kern 1pt} {\kern 1pt} 267k){e^6} + }\\ {(115{\kern 1pt} {\kern 1pt} {\kern 1pt} 907 + 112{\kern 1pt} {\kern 1pt} {\kern 1pt} 881k){e^8}} \end{array}} \right)}}{{4{\kern 1pt} {\kern 1pt} 224\left( {105 - 70{e^2} + 21{e^4} + 12{e^6} + 9{e^8}} \right)}}\\ = \frac{{{\gamma _e}\left( {1 + k\frac{{{{\sin }^2}\varphi }}{{1 - 2{e^2} + {e^4} + 2{e^2}{{\sin }^2}\varphi - {e^4}{{\sin }^2}\varphi }}} \right)}}{{\sqrt {1 - {e^2}\frac{{{{\sin }^2}\varphi }}{{1 - 2{e^2} + {e^4} + 2{e^2}{{\sin }^2}\varphi - {e^4}{{\sin }^2}\varphi }}} }} \end{array} $ | (9) |
在计算机代数系统中,两边同时约去γe,方程式的左边部分是e的函数式Y,设t=sin2φ,再将上式两端平方,经过整理得到:
| $ \begin{array}{*{20}{c}} {{{\sin }^2}\varphi = }\\ {\frac{{\left( {\begin{array}{*{20}{l}} { - 4{e^2} + 10{e^4} - 8{e^6} + 2{e^8} - 2k + 4{e^2}k - 2{e^4}k + }\\ {3{e^2}{Y^2} - 8{e^4}{Y^2} + 7{e^6}{Y^2} - 2{e^8}{Y^2} \mp {{\left( { - 1 + {e^2}} \right)}^2}}\\ {Y\sqrt {4{e^2}k + 4{k^2} + {e^4}{Y^2}} } \end{array}} \right)}}{{2\left( {\begin{array}{*{20}{l}} {4{e^4} - 4{e^6} + {e^8} + 4{e^2}k - 2{e^4}k + {k^2} - }\\ {2{e^4}{Y^2} + 3{e^6}{Y^2} - {e^8}{Y^2}} \end{array}} \right)}}} \end{array} $ | (10) |
将各参数代入式(10)求出φ0作为初始值,利用符号迭代法[10]求得正常椭球上正常重力平均值处的地心纬度与第一偏心率的函数关系式为:
| $ \varphi = {c_0} + {c_2}{e^2} + {c_4}{e^4} + {c_6}{e^6} + {c_8}{e^8} $ | (11) |
式中,c0=0.615 48,c2=-0.047 14,c4=1.358 36,c6=80.102 1,c8=4 789.14。
代入椭球第一偏心率的数值,得到正常椭球上正常重力平均值所在的地心纬度为35.252°。因此,在正常椭球上正常重力的平均值应当取地心纬度为35.252°处的正常重力值。
2 正常重力平均值所处地心纬度随椭球第一偏心率的变化规律为探讨太阳系中部分天体的正常重力平均值处地心纬度的变化规律,假设第一偏心率发生变化,推导正常椭球上正常重力平均值处地心纬度关于第一偏心率的函数关系式,并画出函数图像。
2.1 正常重力平均值处地心纬度随第一偏心率的变化规律当第一偏心率e变化时,需要考虑到
| $ \begin{array}{l} k = \frac{{b{\gamma _p} - a{\gamma _e}}}{{a{\gamma _e}}} = \frac{1}{{{e^2} - 1}} + \frac{5}{2}m + 1 = \\ {\kern 1pt} {\kern 1pt} \frac{1}{{{e^2} - 1}} + 1 + 0.008{\kern 1pt} {\kern 1pt} {\kern 1pt} 653{\kern 1pt} {\kern 1pt} {\kern 1pt} 52\sqrt {1 - {e^2}} \end{array} $ | (12) |
式中,
| $ \varphi=c_{0}+c_{2} e^{2}+c_{4} e^{4}+c_{6} e^{6}+c_{8} e^{8} $ | (13) |
式中,c0=0.615 48,c2=-0.047 141,c4=1.353 81,c6=80.252 4,c8=4 821.66。
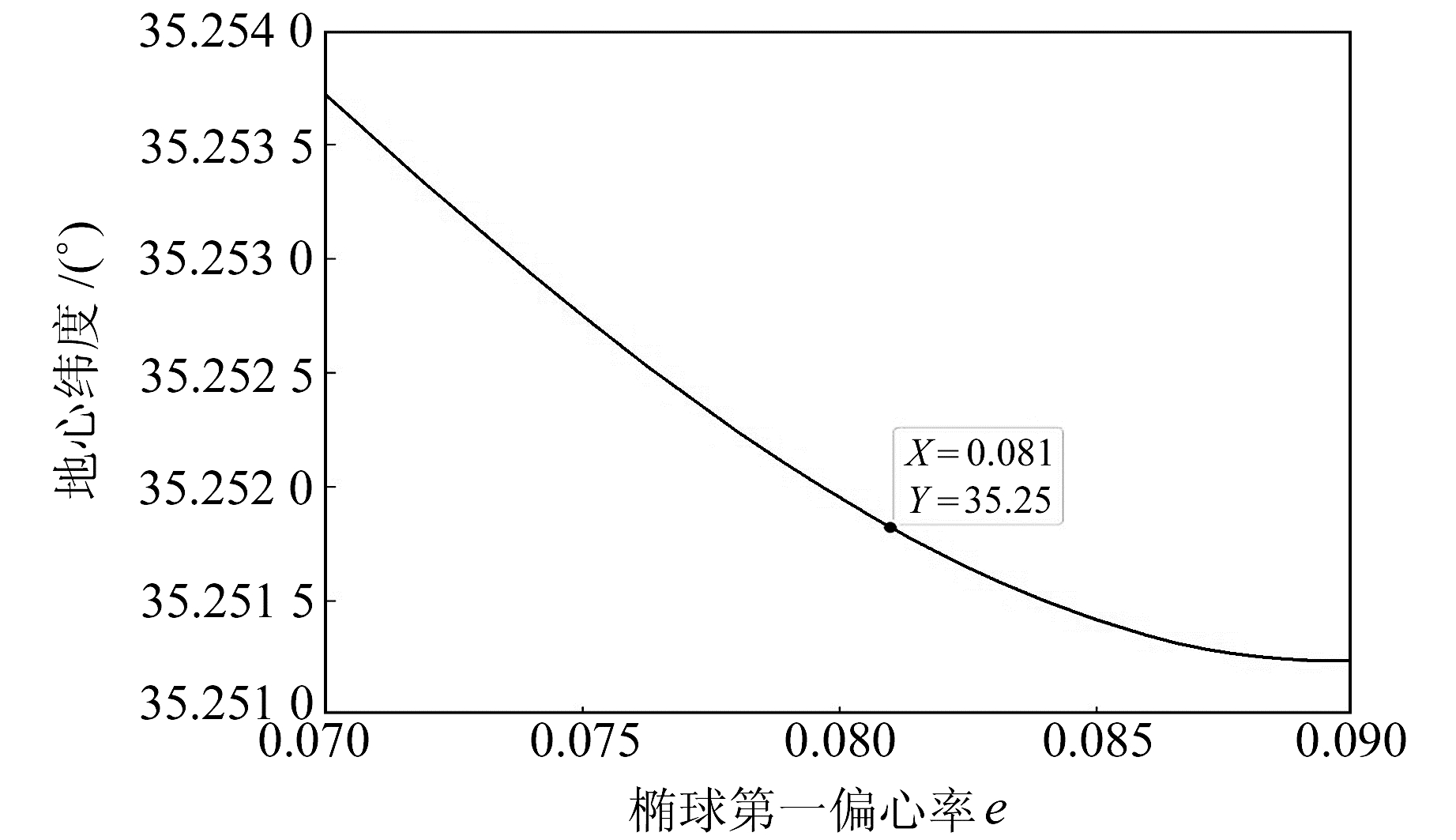
为了得到正常重力平均值处地心纬度与第一偏心率的变化规律,在地球椭球第一偏心率(e=0.081 082 029)附近选定变化区间(0.07, 0.09),并画出图形(图 1)。
|
图 1 正常重力平均值处地心纬度随第一偏心率变化而变化的曲线 Fig. 1 The geocentric latitude at the average normal gravity varying with the first eccentricity |
从图 1可以看出,正常重力平均值所处的地心纬度会随第一偏心率的增大而逐渐减小,图中标出的坐标为地球偏心率和正常重力平均值所处的地心纬度。
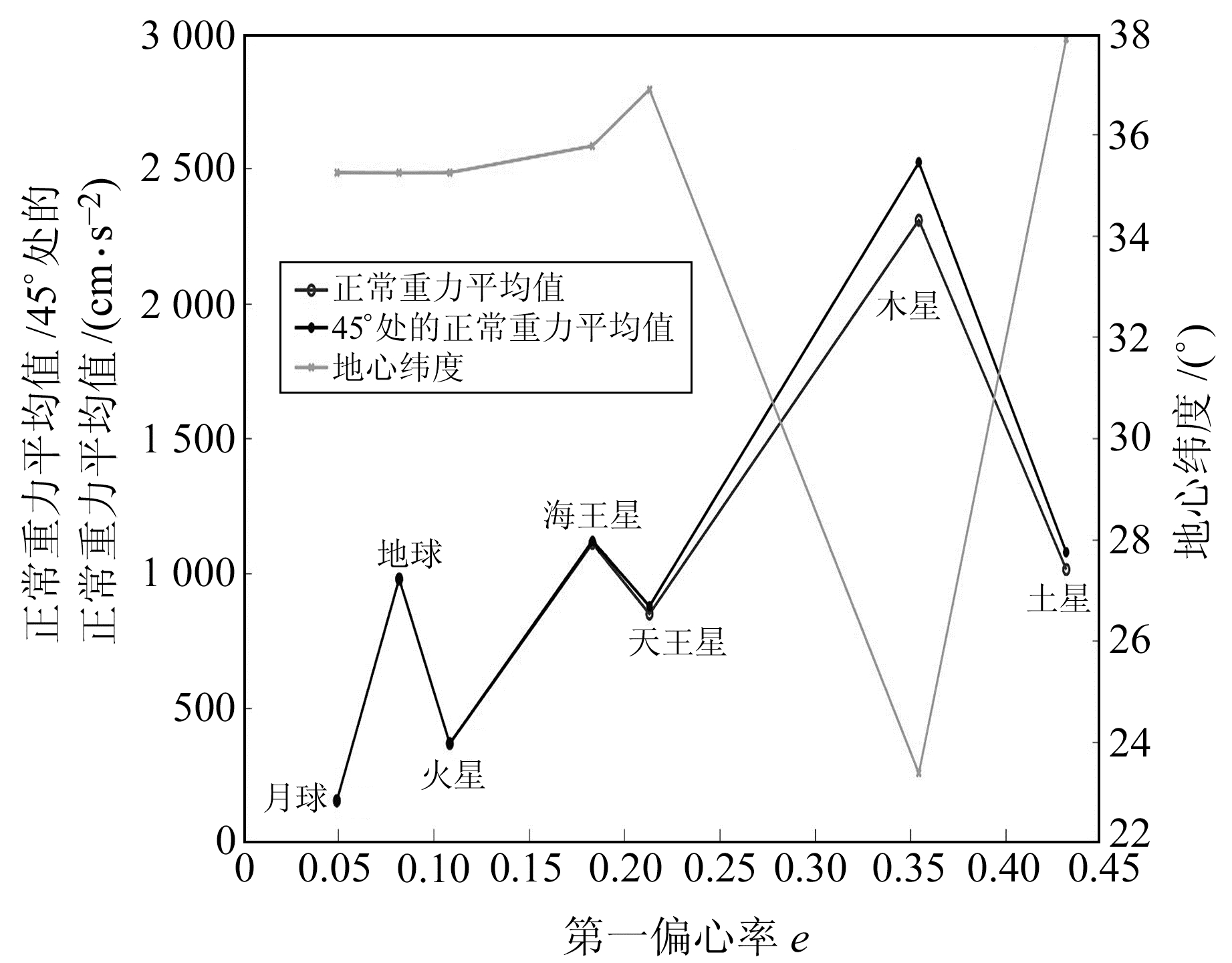
2.2 正常重力平均值处地心纬度随部分天体第一偏心率的变化规律太阳系中部分天体正常重力平均值处地心纬度及其平均值数据如表 1所示,利用MATLAB对表格中的数据进行成图,得到图 2。
|
|
表 1 部分天体正常重力平均值所处地心纬度及平均值数据的汇总 Tab. 1 Summary of the latitude and average data of the gravity average of some normal ellipsoid of celestial bodies |
|
图 2 太阳系中部分天体的正常重力平均值及其所在的地心纬度随第一偏心率变化而变化的曲线 Fig. 2 The average normal gravity values of some objects in the solar system and their geocentric latitudes varying with the first eccentricity |
如表 1所示,当第一偏心率增大时,距离地球由近及远的天体中正常椭球上正常重力平均值处的地心纬度基本稳定在35°~38°之间,只有木星相距较大;另外,木星也是所有天体中正常重力平均值与45°处正常重力平均值相差最大的。从图 2可以看出,当第一偏心率较小时,正常重力平均值和45°处的正常重力平均值的差值较小;当第一偏心率较大时,二者差值较大。
3 结语本文主要研究正常重力平均值的取值问题,并探讨假设第一偏心率为变量时,对于太阳系中各天体是否仍存在相符的变化规律。
1) 正常重力平均值的选取影响到加速度计的精度,而加速度计的精度是影响惯性导航精度最直接和最重要的因素。因此,取地心纬度35.252°处的正常重力值作为正常重力平均值更严谨。
2) 推导得出正常重力平均值处地心纬度关于椭球第一偏心率的函数关系式,并得到部分天体数据的验证,发现地心纬度会随第一偏心率增大而增大的变化规律。
3) 太阳系中天体的正常重力平均值处地心纬度大多稳定在35°~38°之间,当椭球第一偏心率在0~0.2之间时,本文求得的正常重力平均值与45°处的正常重力平均值相差较小;但当椭球第一偏心率大于0.25时,两者的差值较大。另外,木星的正常重力平均值处地心纬度与其他天体相差较大,值得进一步研究。
| [1] |
Feremeev B, Yourkina M N. Height Theory of Earth Gravity[M]. Moscow: Mincral Press, 1972
(  0) 0) |
| [2] |
张赤军. 力高在全球垂直基准中的作用及其精确推求[J]. 海洋测绘, 2001, 21(2): 2-7 (Zhang Chijun. The Role of Force Height in Global Vertical Datum and Its Exact Derivation[J]. Hydrographic Surveying and Charting, 2001, 21(2): 2-7)
(  0) 0) |
| [3] |
张赤军, 许厚泽. 略论位(重力)基数测量在水利建设中的应用[J]. 物探与化探, 2002, 26(1): 68-70 (Zhang Chijun, Xu Houze. A Tentative Discussion on the Application of Gravity Potential Base Survey to the Construction of Water Conservancy Projects[J]. Geophysical and Geochemical Exploration, 2002, 26(1): 68-70)
(  0) 0) |
| [4] |
李爽, 彭玉明, 陆宇平. 火星EDL导航、制导与控制技术综述与展望[J]. 宇航学报, 2010, 31(3): 621-627 (Li Shuang, Peng Yuming, Lu Yuping. Review and Prospect of Mars EDL Navigation Guidance and Control Technologies[J]. Journal of Astronautics, 2010, 31(3): 621-627 DOI:10.3873/j.issn.1000-1328.2010.03.001)
(  0) 0) |
| [5] |
边少锋, 席梦寒, 纪兵, 等. 正常椭球重力平均值处纬度与偏心率的表达式[J]. 海洋测绘, 2019, 39(5): 9-13 (Bian Shaofeng, Xi Menghan, Ji Bing, et al. Expression of Latitude at the Average of the Normal Ellipsoidal Gravity and Eccentricity[J]. Hydrographic Surveying and Charting, 2019, 39(5): 9-13)
(  0) 0) |
| [6] |
孔祥元, 郭际明, 刘宗泉. 大地测量学基础[M]. 武汉: 武汉大学出版社, 2010 (Kong Xiangyuan, Guo Jiming, Liu Zongquan. Fundamentals of Geodesy[M]. Wuhan: Wuhan University Press, 2010)
(  0) 0) |
| [7] |
魏子卿. 正常重力公式[J]. 测绘学报, 2003, 32(2): 95-101 (Wei Ziqing. Normal Gravity Formulae[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(2): 95-101 DOI:10.3321/j.issn:1001-1595.2003.02.001)
(  0) 0) |
| [8] |
李厚朴, 边少锋, 钟斌. 地理坐标系计算机代数精密分析理论[M]. 北京: 国防工业出版社, 2015 (Li Houpu, Bian Shaofeng, Zhong Bin. Computer Algebra Precision Analysis Theory of Geographic Coordinate System[M]. Beijing: National Defense Industry Press, 2015)
(  0) 0) |
| [9] |
边少锋, 李厚朴. 大地测量计算机代数分析[M]. 北京: 科学出版社, 2018 (Bian Shaofeng, Li Houpu. Computer Algebraic Analysis of Geodesy[M]. Beijing: Science Press, 2018)
(  0) 0) |
| [10] |
陈成, 边少锋, 李厚朴. 一种解算椭球大地测量学反问题的方法及应用[J]. 海洋测绘, 2015, 35(6): 8-13 (Chen Cheng, Bian Shaofeng, Li Houpu. A Method for Solving Inverse Problems of Ellipsoidal Geodesy and Its Application[J]. Hydrographic Surveying and Charting, 2015, 35(6): 8-13)
(  0) 0) |
2. School of Remote Sensing and Geomatics Engineering, Nanjing University of Information Science and Technology, 219 Ningliu Road, Nanjing 210044, China
 2021, Vol. 41
2021, Vol. 41

