2. 中国地震局地壳应力研究所,北京市安宁庄路1号,100085;
3. 南京工业大学测绘科学与技术学院,南京市浦珠南路30号,211800
一直以来,郯庐断裂带中段及北段的研究成果较为丰富[1-6],而南部苏皖段的研究工作起步相对较晚[1-2],对于郯庐断裂带苏皖段地质结构和块体作用形式的认识存在分歧[3-4, 6]。本文从可准确观测记录的震级和频次入手,借以数理统计方法研究区域内近50 a的G-R关系变化和b值时空演化特征,并对研究区的地震活动水平和构造应力状态进行分析。
1 G-R关系及b值古登堡-里克特关系(Gutenberg-Richter)是地球物理学中描述震级与频度的重要统计公式[7],其一般表达式为:
| $ \lg N=a-b M $ | (1) |
式中,M为震级,N为区域内震级大于等于M的地震次数。a值描述区域的总体地震活动水平,反映总体震级大小; b值反映区域内不同震级对应的地震分布关系,b值大则大震发生次数比小震少,反之则比小震多。研究发现,在震级过小或过大时G-R关系有一定的偏离,虽有学者对其作过改进,但a、b值仍包含丰富的地震活动信息,尤其是b值历来都是地震预测和特征判别的重要参考指标[8-10]。
2 资料选取与地震目录完整性 2.1 研究对象及时空范围为研究郯庐断裂带苏皖段的G-R关系和b值时空特征,选取中国地震台网中心发布的1970~2019年地震目录资料,研究范围为115°~121°E、30°~35°N,该范围被认为是郯庐断裂带苏皖段活动的直接影响区域,其地震震级和频次能直接体现苏皖段断层的活动性。总体来说,研究区内部地震频率有一定的差异,具有东强西弱、南密北疏的特点,郯庐断裂带影响区域东侧的地震密集且震级较高,西侧则较少且较弱; 而33°N以北区域地震较少,以南区域地震频率相对较高且震级较大。从城市地震活跃程度来看,地震较为活跃的地区为江苏盐城、淮安、镇江、常州和安徽六安、淮南、蚌埠以及邻近的湖北黄冈一带。
2.2 地震资料选取为准确计算G-R关系及b值,应具备准确充足的观测数据和合理的数学模型。由于小震的频散不充分且信噪比低,在大范围(一级板块尺度或跨越完整断裂带以上)和长周期(100 a以上)内一般采用面波震级MS作为计算震级,且在6~8级地震时关系式的符合程度较高[10]。由于郯庐断裂带苏皖段6级以上的地震发生频次很低,样本量过少,计算的不确定性较大; 且大震复发周期长,记录周期小于实际的大震复发周期,而小震复发周期短,依一定时间的近震资料分析其规律及区域应力结果较为可靠。因此,在本文研究的时空范围内不宜采用面波震级MS作为计算震级。
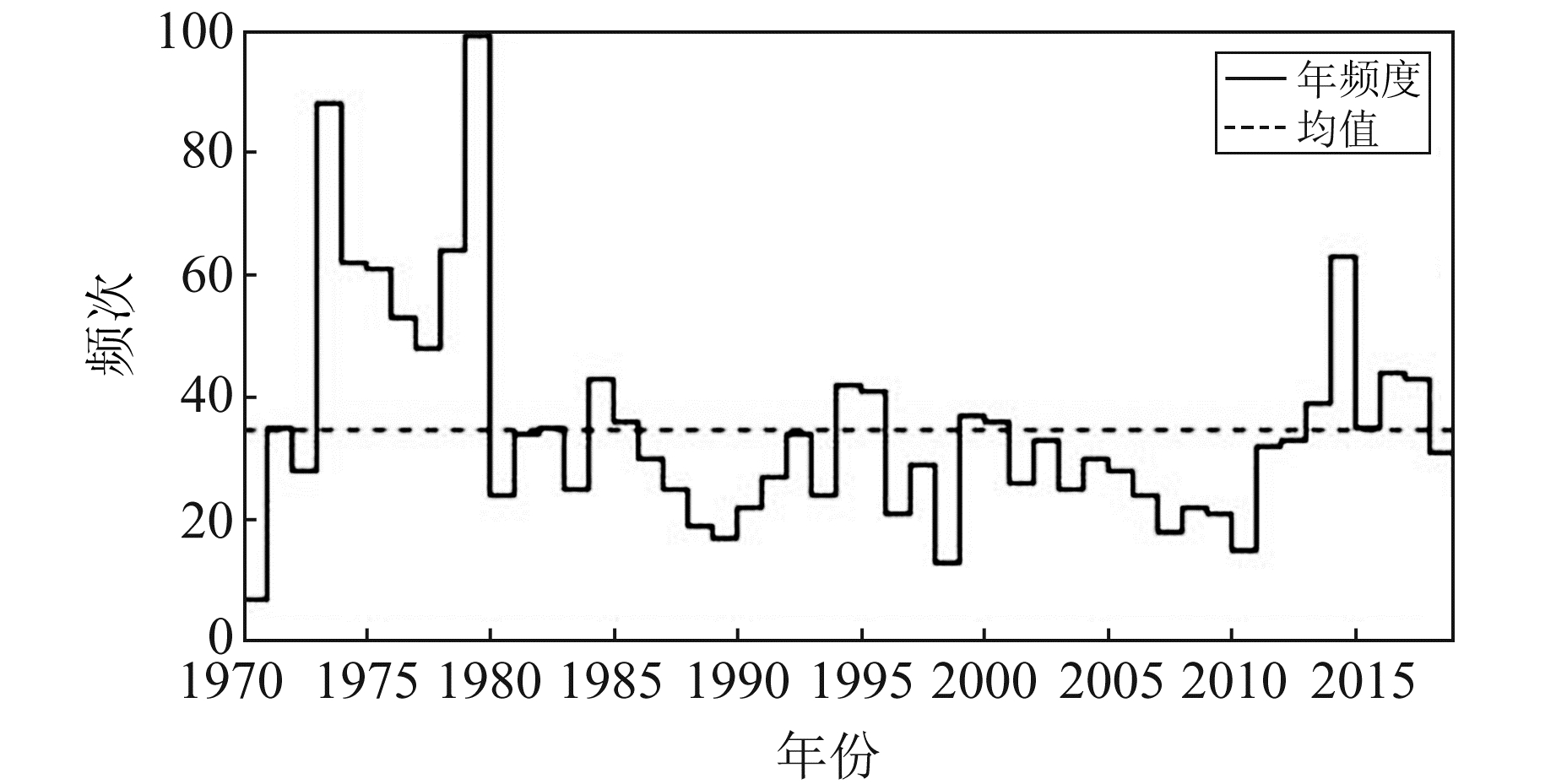
有研究认为,地方震级ML在5级以上时因近台超限易产生较大误差,ML为2.5~4.5时误差较小[10]。研究区2.5级及以上地震中约0.6%的地震为5级以上地震,占比极小,且MS与ML表示的震级在7级以下时基本相同[11],因此本文震例资料采用地方震级ML为计算震级,研究区内ML≥2.5地震的年频度见图 1。
|
图 1 研究区地震数量年频度 Fig. 1 Yearly frequency of the number of earthquakes in the research area |
地震目录的完整性对b值计算尤为重要,因台网监测能力较弱造成的小震资料缺失会使b值偏低[12],通常用最小完备震级MC(一定时空范围内可被台网准确监测到的最小震级)来评价台站的测震能力。本文依据研究区5级以上地震的发生时刻和区域地震监测台网改造,将研究时段划分为1970~1986年、1987~1996年、1997~2007年、2008~2019年4个时段进行MC分析。
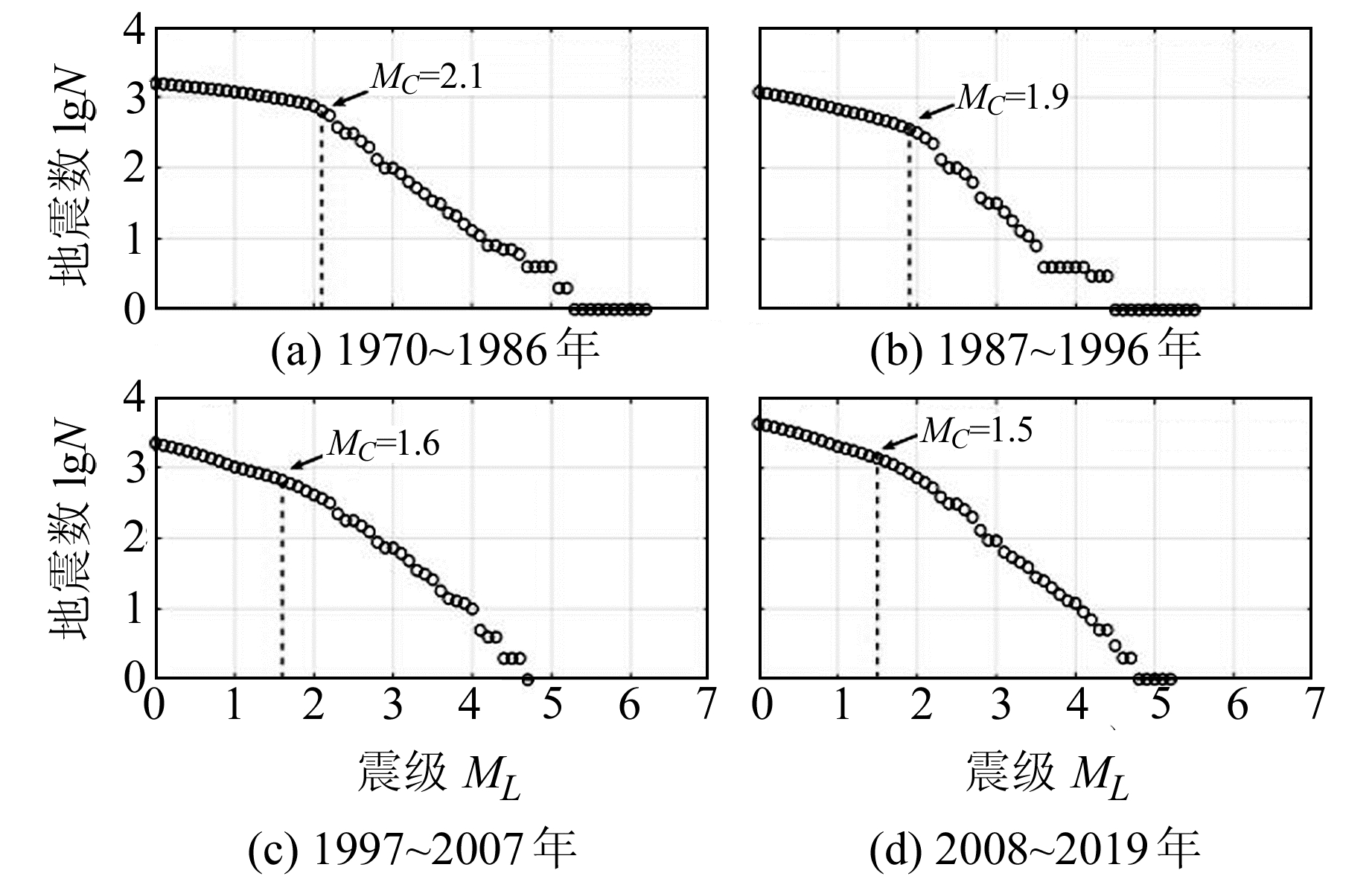
通过对华北板块地震资料完整性进行研究认为,华北地区最小完备震级为0.5~3.0[12],总体测震能力有明显提高的趋势。本文采用最大曲率法[13]对研究区4个时段的MC进行计算,以震级频度曲线函数一阶导数极大值对应的震级为最小完备震级[14],计算结果见图 2。
|
图 2 区域地震完整性分析 Fig. 2 The earthquake integrity analysis of the research area |
由图 2可以看出,4个时段的MC依次为2.1、1.9、1.6和1.5,区域内台站监测能力在逐步提升。鉴于最大MC约为2.1且计算误差在±0.2以内,由此认为,本文取ML≥2.5的地震数据为b值计算的源数据是可信的。
3 b值计算方法b值常用的计算方法有最小二乘法(LSM)、极大似然法(MLE)及相关改进方法。从本质上,最小二乘法是估计函数模型参数,而极大似然法是估计概率模型参数[15]。本文采用极大似然法来计算b值。
设某区域某时段发生震级分别为Mi(i=1,2,3, …, N)的地震,震级为随机变量且服从指数分布,这N个地震可认为是来自呈指数分布的总体样本的一组子样本。依条件概率乘法定理,考虑最小完备震级MC在此处的实际意义,则若干独立地震同时发生的概率似然函数为:
| $ L = \prod\limits_{i = 1}^N {\left( {\lambda {{\rm{e}}^{ - \lambda \left( {{M_i} - {M_C}} \right)}}} \right)} = {\lambda ^N}\prod\limits_{i = 1}^N {{{\rm{e}}^{ - \lambda \left( {{M_i} - {M_C}} \right)}}} $ | (2) |
概率最大处即为似然函数的极大值点,即参数λ为某值时,若干地震Mi发生的概率最大。对式(2)两边同时取对数,则:
| $ \ln L = N\ln \lambda - \lambda \sum\limits_{i = 1}^N {\left( {{M_i} - {M_C}} \right)} $ | (3) |
极大似然估计量是微分方程的解,在似然函数满足连续、可微的正则条件下,对式(3)两边同时作λ的微分,则:
| $ \frac{{{\rm{d}}\ln L(\lambda )}}{{{\rm{d}}\lambda }} = \frac{N}{\lambda } - \lambda \sum\limits_{i = 1}^N {\left( {{M_i} - {M_C}} \right)} = 0 $ | (4) |
得到参数λ的估值:
| $ \hat \lambda = \frac{N}{{\sum\limits_{i = 1}^N {\left( {{M_i} - {M_C}} \right)} }} = \frac{1}{{{{\bar M}_i} - {M_C}}} $ | (5) |
式中,
将基本关系式(1)作换底公式,则有:
| $ \frac{{\ln N}}{{\ln 10}} = a - bN{\rm{ 或 }}\ln N = a\ln 10 - bM\ln 10 $ | (6) |
设aln10为α,bln10为β,则式(6)可写为:
| $ \ln N = \alpha - \beta M{\rm{ 或 }}N = {{\rm{e}}^{a - \beta M}} $ | (7) |
因只选取MC以上震例为研究样本,则:
| $ {N_{{\rm{total }}}} = N\left( {{M_C}} \right) - N\left( {{M_{\max }}} \right) = {{\rm{e}}^{\alpha - \beta M}} - {{\rm{e}}^{\alpha - \beta {M_{\max }}}} $ | (8) |
根据定义,震级M处的概率分布函数为:
| $ F(M) = \frac{{N\left( {{M_C}} \right) - N(M)}}{{{N_{{\rm{total }}}}}} = \frac{{N\left( {{M_C}} \right) - {{\rm{e}}^{\alpha - \beta M}}}}{{{N_{{\rm{total }}}}}} $ | (9) |
求导后,其概率密度函数为:
| $ \begin{array}{l} \frac{{{\rm{d}}F(M)}}{{{\rm{d}}M}} = f(M) = \frac{{\beta {{\rm{e}}^{ - \beta M}}}}{{{{\rm{e}}^{ - \beta {M_C}}} - {{\rm{e}}^{ - \beta {M_{\max }}}}}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} M \in \left[ {{M_C},{M_{\max }}} \right] \end{array} $ | (10) |
将β=bln10代入式(10),则概率密度函数为:
| $ \begin{array}{l} f(M) = b\ln 10\frac{{{{10}^{ - bM}}}}{{{{10}^{ - b{M_C}}} - {{10}^{ - b{M_{\max }}}}}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} M \in \left[ {{M_C},{M_{\max }}} \right] \end{array} $ | (11) |
当
| $ \begin{array}{l} f(M) = \beta {{\rm{e}}^{ - \beta \left( {M - {M_C}} \right)}} = b\ln 10 \times {{\rm{e}}^{ - b\ln 10\left( {M - {M_C}} \right)}} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} b\ln 10 \times {10^{ - b\left( {M - {M_C}} \right)}} \end{array} $ | (12) |
而之前推导的
| $ \hat \lambda = \frac{1}{{{{\bar M}_i} - {M_C}}} = \beta = b\ln 10 $ | (13) |
依
| $ \hat b = \frac{{\lg e}}{{{{\bar M}_i} - {M_C}}} $ | (14) |
对郯庐断裂带苏皖段G-R关系进行分阶段分析,并从时间和空间上对b值进行扫描,依据b值所指示的中强震关联性和构造意义进行讨论。
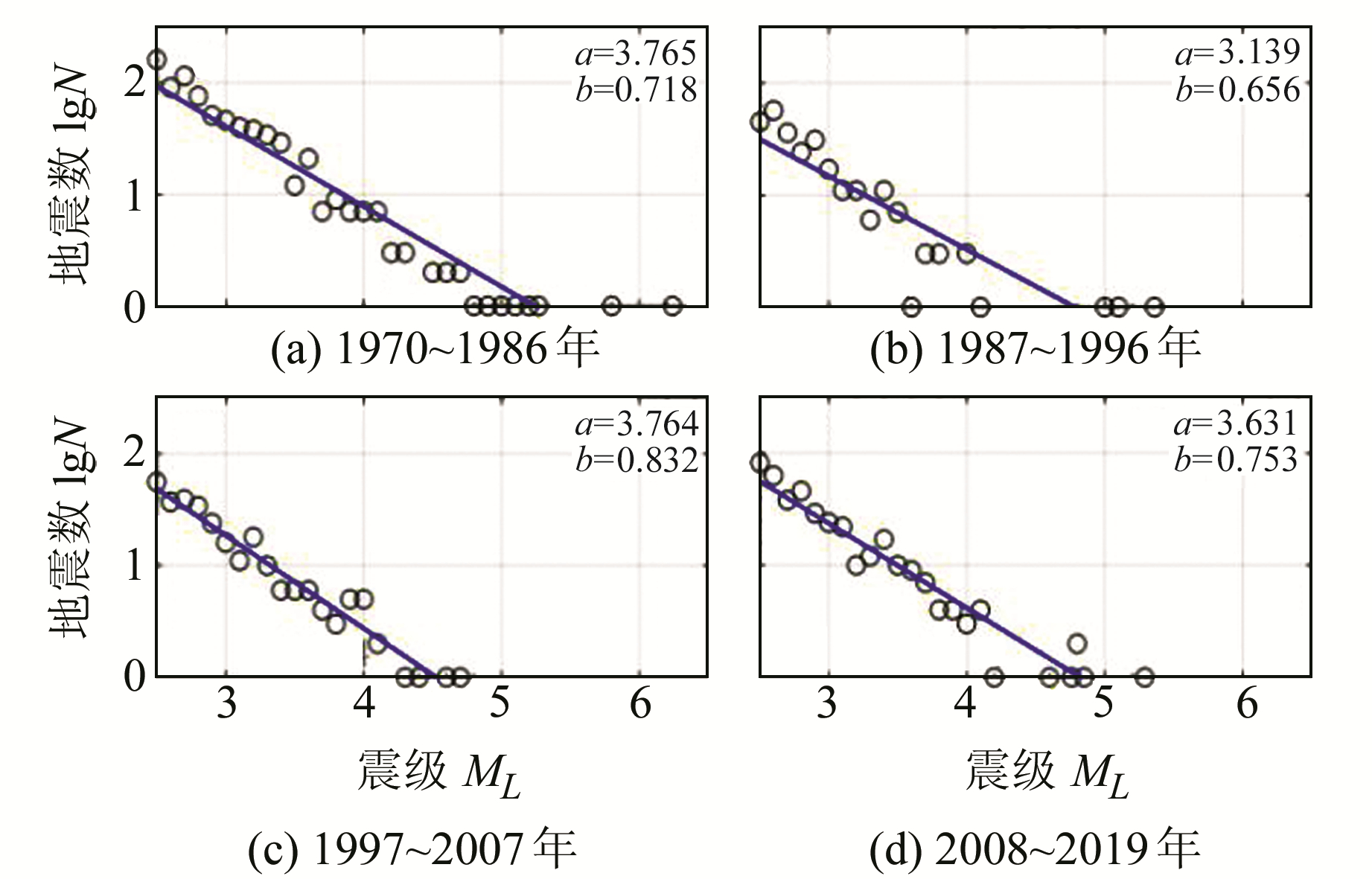
4.1 b值的时间扫描对研究区4个时段内ML≥2.5的震例进行polyfit数值拟合,G-R关系标准差RMSE为±0.25,确定系数R-square在0.8以上,具体结果见图 3。
|
图 3 研究区G-R关系 Fig. 3 The G-R relationship of the research area |
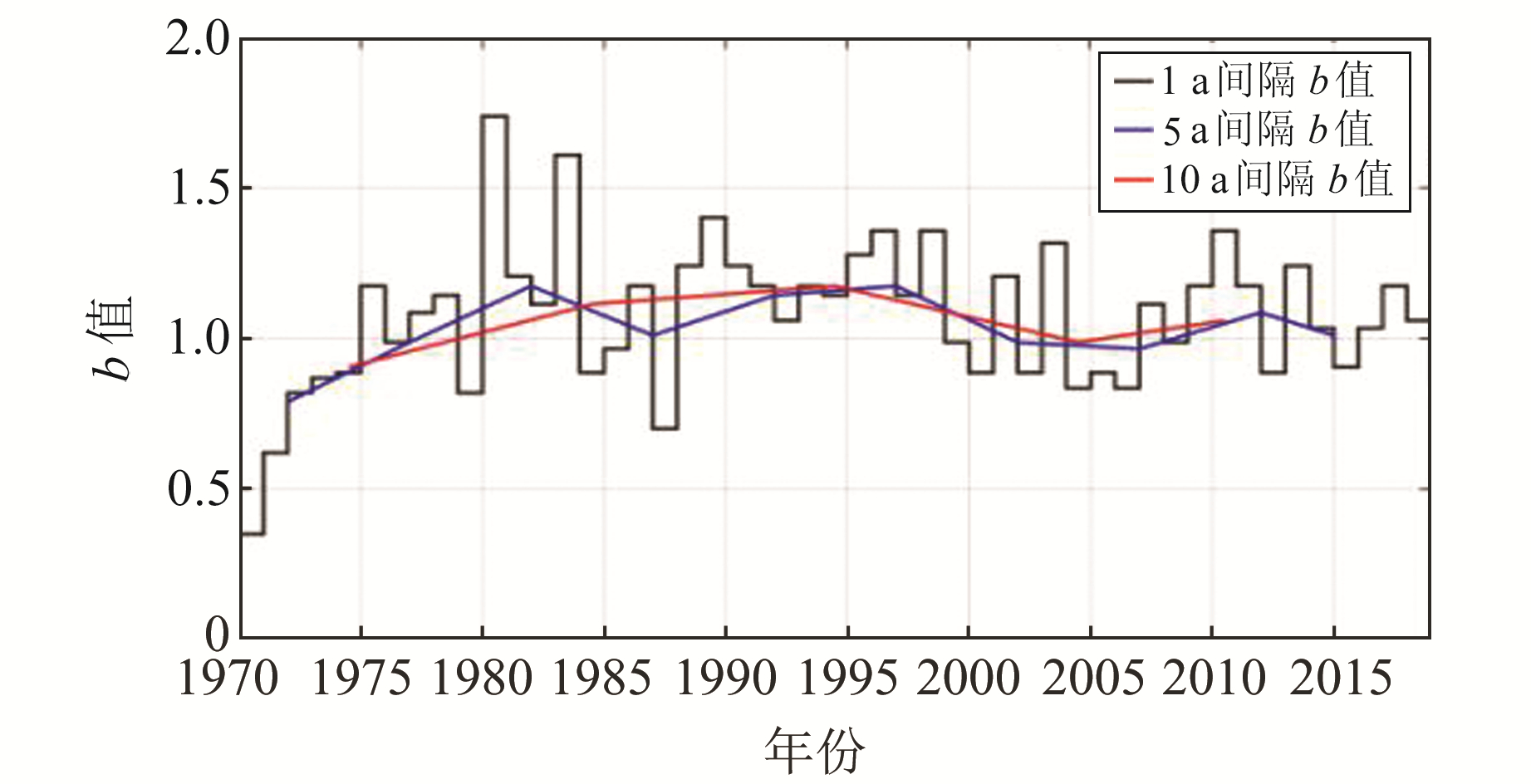
由图 3中的a值可知,研究区50 a来总体发震水平较平均,1987~1996年地震活动相对平静; 由b值可以看出,1970~1996年b值偏低,1997~2018年b值较高,整体呈由低到高再到低的过程。分别以1 a、5 a和10 a为间隔研究b值的变化特征,研究区内b值与时间的关系见图 4。
|
图 4 b值-时间关系 Fig. 4 The temporal variation of b value |
从图 4可以看出,研究区内b值5 a及1 a的中短期变化无一致的趋势特征,长期变化呈缓慢的升-降过程,可认为b值的变化与选取周期的长短关系不大,且在无大震发生的情况下,短周期的b值变化无特殊意义,长期来看研究区近50 a的b值均值约为1.05。
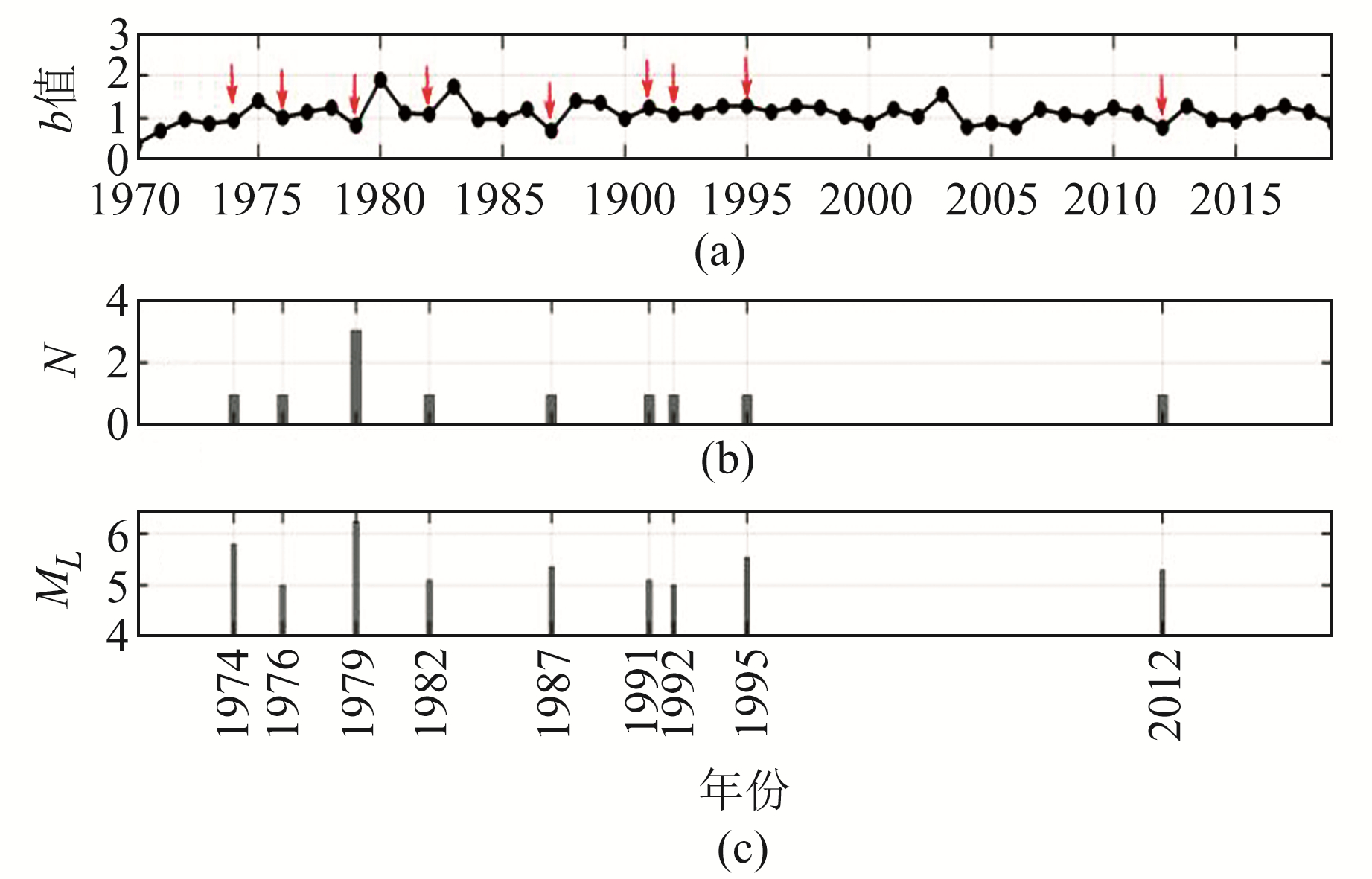
4.2 b值时间特征与5级以上地震的关联性选取研究区11次5级以上地震事件(表 1)进行响应关系分析,以推断和理解b值与中强震的关联性[16]。经整理分析得到研究区b值、发震时间和5级以上地震的关系,具体见图 5。
|
|
表 1 研究区5级以上地震事件统计 Tab. 1 Statistics of earthquake events with ML≥5 in the research area |
|
图 5 苏皖段b值、发震时间和5级以上地震的关系 Fig. 5 Relationship between b value, time of occurrence and earthquakes with M≥5.0 in Jiangsu-Anhui section |
由图 5可以看出,在研究区11次5级以上中强地震事件中,有9次在发生之前出现b值下降的现象,但降幅不大。
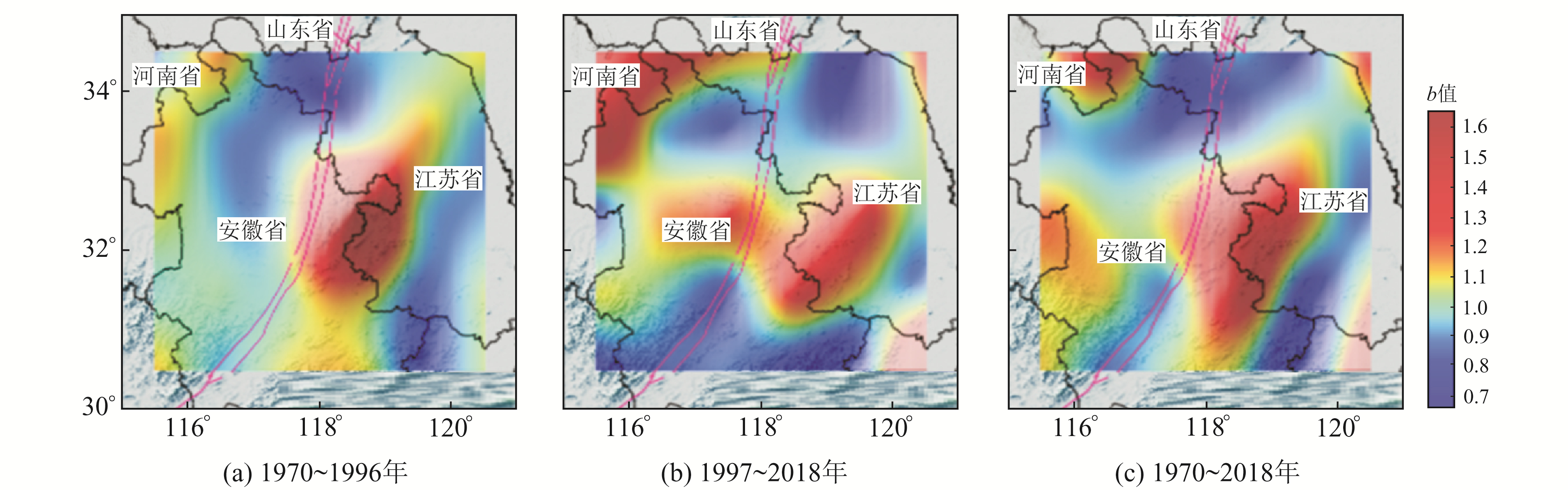
4.3 b值的空间扫描采用网格法对b值进行空间扫描,顾及普遍划分标准和研究区选取的实际范围及样本数量,本文确定基本格网大小为1°×1°,并将研究区划分为30个格网,搜索步长为0.5°,并要求格网内的地震数目大于20,震级差大于1.5级。这种选取方式以样本实际为出发点,从样本量和震级跨度2个方面保证b值的相对合理性与精度。图 6为郯庐断裂带苏皖段影响区在1970~1996年及1997~2018年2个阶段和近50 a的b值总体空间分布状态。
|
图 6 苏皖段b值空间分布 Fig. 6 Spatial distribution of b value of Jiangsu-Anhui section |
由图 6可知,郯庐断裂带苏皖段影响区内b值大小的空间分布不一,最大差异可达1倍。从空间分布看,b值较低区域为苏北盆地及以南区域; 从时间演化看,苏北盆地一直是低b值区域,而合肥盆地及大别造山带等地区经历了b值由高到低的演化过程。
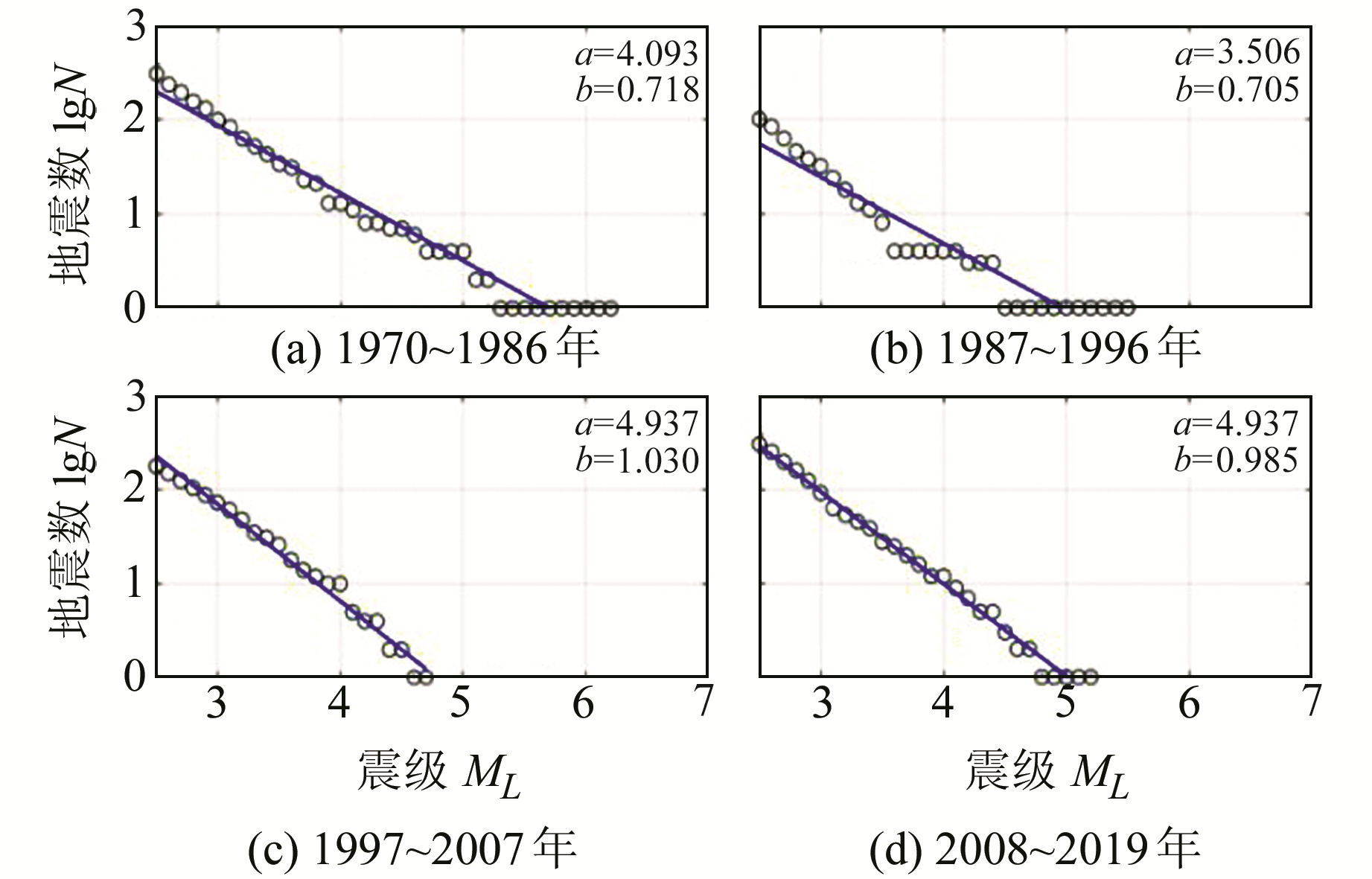
4.4 与苏鲁段b值时空特征对比山东、江苏、安徽等地是郯庐断裂带中南段的主要影响区域,其中苏鲁交汇地区的b值、构造及地震活动性等对本文的苏皖段研究有重要意义。对郯庐断裂带苏鲁段影响区(115°~120°E,33°~36°N)的b值时空特征进行分析,G-R关系拟合结果见图 7。对比图 3和7可以看出,郯庐断裂带苏皖段的a值普遍比苏鲁段的低,反映苏皖段的地震活动性比苏鲁段弱; 还可看出,苏皖段的b值相较苏鲁段大小相近或略小,指示苏皖段也有地壳应力偏高的特征。
|
图 7 苏鲁交汇段研究区G-R关系 Fig. 7 The G-R relationship of the Jiangsu-Shandong intersection research area |
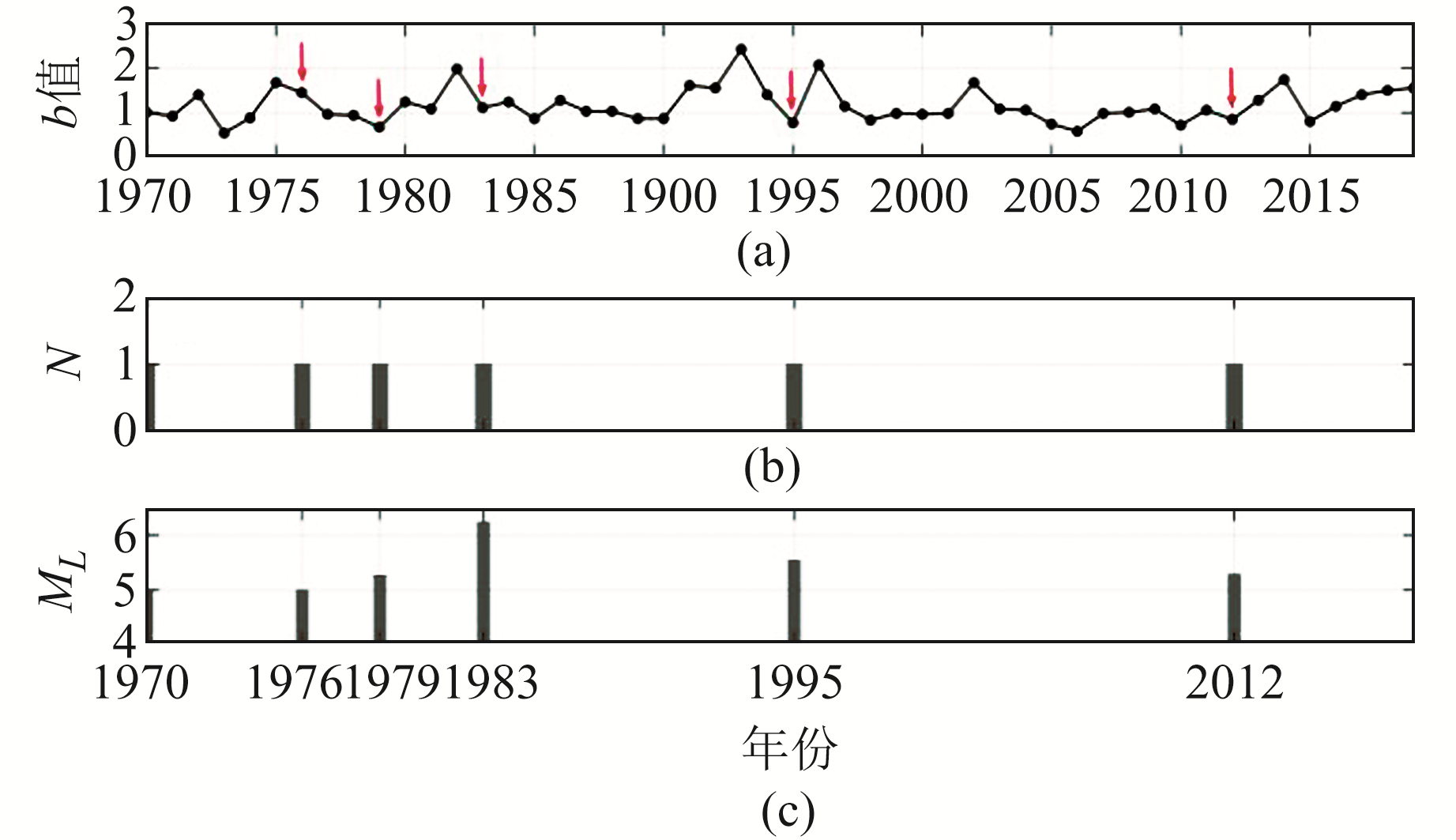
由苏鲁段b值与发震时间及5级以上地震映震关系的研究(图 8)可知,苏皖段11次5级以上地震中有9次在发震前出现b值下降的情况,但降幅较小; 而苏鲁段有6次5级以上地震在发生前b值有一定程度的下降,推测苏皖段b值的短期映震关联度比苏鲁段低。另外,郯庐断裂带苏皖段和苏鲁段影响区的b值在震后均出现上升,可能与震后区域应力得到释放有关。
|
图 8 苏鲁交汇段b值、发震时间和5级以上地震的关系 Fig. 8 Relationship between b value, time of occurrence and M≥5.0 earthquakes in Jiangsu-Shandong section |
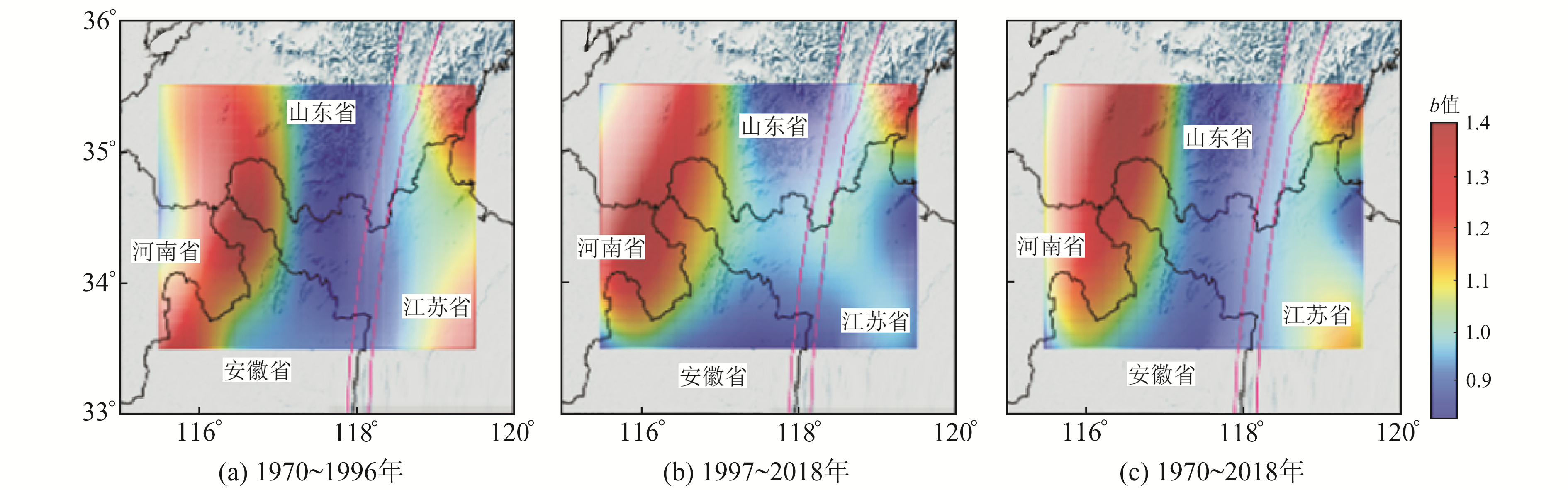
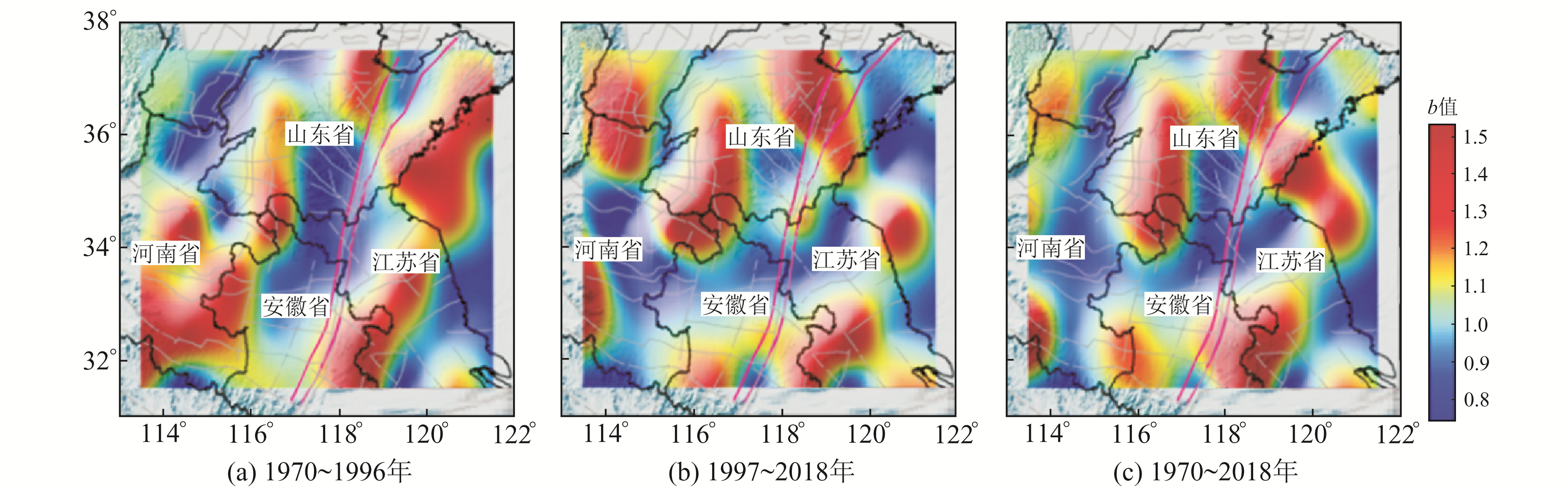
为揭示郯庐断裂带苏皖段b值的空间分布特征,以同样的方法对郯庐断裂带苏鲁段影响区同时段数据进行b值空间扫描,结果见图 9。再将苏皖段以北及更大区域纳入空间扫描范围,得到的结果见图 10。以不同区域范围b值的空间分布扫描结果为基础,对b值指示的区域构造应力作进一步研究。
|
图 9 苏鲁段区域b值空间分布 Fig. 9 Spatial distribution of b value of Jiangsu-Shandong section |
|
图 10 苏皖段邻区b值空间分布 Fig. 10 Spatial distribution of b value in Jiangsu-Anhui section |
b值不只是表征地震前兆和余震活动的统计参数[17],也有直接的物理指示意义,可为区域构造应力承受水平和应力场状态分析提供依据。跟据岩石力学相关概念,有:
| $ b = c(1 - F) $ | (15) |
式中,c为数值大小为1左右的常数,F为区域内地壳介质构造破裂概率(0≤F≤1)。一般来说,F升高时b值下降,F下降时b值升高,b值的区域时空分布演化特征可为推断研究区在时段内所受的平均应力和应力变化提供参考。由b值的应力指示意义可以看出:
1) 郯庐断裂带苏皖段影响区内的高构造应力区主要对应苏北盆地及以南区域和苏鲁造山带南缘,合肥盆地及大别造山带区域的构造应力也相对偏高,涉及的地区主要有淮北-宿迁-盐城沿线、常州-宣城沿线和合肥-潜山沿线等。从时间尺度看,1997年之前研究区内构造应力主要集中在淮北-徐州沿线和盐城-常州-宣城沿线,1997~2018年构造应力集中区分别向连云港-盐城沿线和安庆-铜陵-宣城沿线迁移。常州-宣城沿线应力集聚趋势较明显,应引起注意。
2) 郯庐断裂苏鲁段影响区内西侧的构造应力较高,高构造应力区与鲁西隆起带南部、苏北盆地及以南地区和苏鲁造山带南缘较为吻合,涉及的城市主要有枣庄、徐州、宿迁、连云港等。从时间尺度看,1997年以前研究区内构造应力主要集中在枣庄-徐州一带,1997~2018年构造应力集中区分别向枣庄以北和徐州以南迁移,连云港和宿迁以东有应力集聚趋势,值得关注。
3) 基于b值指示的构造应力意义,结合郯庐断裂带苏皖段和苏鲁段的地质特征,可为地壳构造应力解释找到相关依据。地质调查资料显示,郯庐断裂带苏皖段南部有大量未固结的构造岩(断层泥或角砾),说明其形成后未经压实埋藏,某些区域活断层切入到第四系松散沉积层内或前第四系固结岩层逆冲在第四系地层之上,指示第四纪以来的地壳应力活动,也是构造应力偏高的标志。
另外可看出,郯庐断裂带宿迁地区b值偏低,指示了高构造应力,自宿迁-泗洪向南进入安徽省界后至嘉山、合肥一带b值逐渐增大,说明该区域地震活动性不强。结合断层闭锁特征的研究[18]认为,郯庐断裂带宿迁泗洪以南至合肥一带的闭锁程度相对较高,也未曾发生较大破裂,目前b值指示的构造应力虽不高,但结合该段断层的闭锁特征认为,其应力易于积累,存在发生中强地震的危险。
5 结语通过对1970年以来郯庐断裂带苏皖段影响区及邻区的地震资料进行分析,得出以下结论:
1) 采用最大曲率法计算的区域最小完备震级依次减小,可看出郯庐断裂带苏皖段、苏鲁段及邻区的台网测震能力逐步增强,选取ML≥2.5地震数据来分析G-R关系和b值合理可行,可为相关研究提供依据。本文从指数函数的概率分布严密推导了b值的极大似然计算方法,比最小二乘法更科学合理。
2) 根据研究区b值的时间分布特征,1 a左右短期的b值变化与5级以上中强地震的映震关系明显,即中强地震在短期临震阶段b值会有一定下降,对应率达80%以上,中长期的b值变化与5级以上地震没有明显的关联。另外,苏皖段b值的短期映震关联度比苏鲁段低,相关结论可用于区域震情研判。
3) 根据研究区b值的空间分布特征,苏北盆地整体及以南地区和合肥盆地南缘的构造应力相对较高,与区内超高压变质带的分布有较好的一致性,该区域可能处于孕震阶段,应重点关注。此外,郯庐断裂带苏皖段南部的闭锁特征较北部更强,邻区的b值分布特征显示,鲁苏皖交界处和苏鲁以东的黄海海域处于应力偏高状态。
4) 本文仅选取距今约50 a的地震资料,从长周期大尺度角度看,对于地壳应力演化难以形成轮回和覆盖,但本文研究可为区域现代地质构造和板块动力学等研究提供一定的借鉴。
致谢: 感谢中国地震局地壳应力研究所和宿迁市地震服务中心提供相关资料。
| [1] |
沈小七, 姚大全, 郑海刚, 等. 郯庐断裂带重岗山-王迁段晚更新世以来的活动习性[J]. 地震地质, 2015, 37(1): 139-148 (Shen Xiaoqi, Yao Daquan, Zheng Haigang, et al. The Research on Activity Behavior of Chonggangshan-Wangqian Segment of Tan-Lu Fault Zone since Late Pleistocene[J]. Seismology and Geology, 2015, 37(1): 139-148 DOI:10.3969/j.issn.0253-4967.2015.01.011)
(  0) 0) |
| [2] |
张鹏, 李丽梅, 冉勇康, 等. 郯庐断裂带安丘-莒县断裂江苏段晚第四纪活动特征研究[J]. 地震地质, 2015, 37(4): 1 162-1 176 (Zhang Peng, Li Limei, Ran Yongkang, et al. Research on Characteristics of Late Quaternary Activity of the Jiangsu Segment of Anqiu-Juxian Fault in the Tanlu Fault Zone[J]. Seismology and Geology, 2015, 37(4): 1 162-1 176)
(  0) 0) |
| [3] |
黄耘, 李清河, 张元生, 等. 郯庐断裂带鲁苏皖段及邻区地壳速度结构[J]. 地球物理学报, 2011, 54(10): 2 549-2 559 (Huang Yun, Li Qinghe, Zhang Yuansheng, et al. Crustal Velocity Structure Beneath the Shandong-Jiangsu-Anhui Segment of the Tancheng-Lujiang Fault Zone and Adjacent Areas[J]. Chinese Journal of Geophysics, 2011, 54(10): 2 549-2 559)
(  0) 0) |
| [4] |
王鑫, 张景发, 姜文亮, 等. 基于布格重力数据研究郯庐断裂带江苏段深部构造[J]. 地球物理学进展, 2015, 30(4): 1 516-1 525 (Wang Xin, Zhang Jingfa, Jiang Wenliang, et al. Deep Structures of Jiangsu Segment of Tan-Lu Fault Zone Derived from Bouguer Gravity Data[J]. Progress in Geophysics, 2015, 30(4): 1 516-1 525)
(  0) 0) |
| [5] |
徐锡伟, 吴熙彦, 于贵华, 等. 中国大陆高震级地震危险区判定的地震地质学标志及其应用[J]. 地震地质, 2017, 39(2): 219-275 (Xu Xiwei, Wu Xiyan, Yu Guihua, et al. Seismo-Geological Signatures for Identifying M≥7.0 Earthquake Risk Areas and Their Premilimary Application in Mainland China[J]. Seismology and Geology, 2017, 39(2): 219-275 DOI:10.3969/j.issn.0253-4967.2017.02.001)
(  0) 0) |
| [6] |
李云平, 吴时国, 韩文功, 等. 合肥盆地和郯庐断裂带南段深部地球物理特征研究[J]. 地球物理学报, 2006, 49(1): 115-122 (Li Yunping, Wu Shiguo, Han Wengong, et al. A Study on Geophysical Features of Deep Structures of the Hefei Basin and the Southern Tan-Lu Fault Zone[J]. Chinese Journal of Geophysics, 2006, 49(1): 115-122 DOI:10.3321/j.issn:0001-5733.2006.01.016)
(  0) 0) |
| [7] |
Gutenberg B, Richter C F. Seismicity of the Earth and Associated Phenomena[M]. Princeton: Princeton University Press, 1954
(  0) 0) |
| [8] |
郑确, 刘财, 田有, 等. 地震活动性中震级-频度关系研究进展与再认识[J]. 地球物理学进展, 2018, 33(5): 1 879-1 889 (Zheng Que, Liu Cai, Tian You, et al. Review and Further Understanding of Frequency-Magnitude Distribution in Seismicity[J]. Progress in Geophysics, 2018, 33(5): 1 879-1 889)
(  0) 0) |
| [9] |
史海霞, 孟令媛, 张雪梅, 等. 汶川地震前的b值变化[J]. 地球物理学报, 2017, 61(5): 1 874-1 882 (Shi Haixia, Meng Lingyuan, Zhang Xuemei, et al. Decrease in b-Value Prior to the Wenchuan Earthquake(MS8.0)[J]. Chinese Journal of Geophysics, 2017, 61(5): 1 874-1 882)
(  0) 0) |
| [10] |
陈培善, 白彤霞, 李保昆. b值和地震复发周期[J]. 地球物理学报, 2003, 46(4): 510-519 (Chen Peishan, Bai Tongxia, Li Baokun. b-Value and Earthquake Occurrence Period[J]. Chinese Journal of Geophysics, 2003, 46(4): 510-519 DOI:10.3321/j.issn:0001-5733.2003.04.013)
(  0) 0) |
| [11] |
汪素云, 俞言祥. 震级转换关系及其对地震活动性参数的影响研究[J]. 震灾防御技术, 2009, 4(2): 141-149 (Wang Suyun, Yu Yanxiang. Research on Empirical Relationship of Earthquake Magnitude Scales and Its Influence on Seismicity Parameters[J]. Technology for Earthquake Disaster Prevention, 2009, 4(2): 141-149 DOI:10.3969/j.issn.1673-5722.2009.02.002)
(  0) 0) |
| [12] |
任雪梅.地震区划中b值统计的若干问题研究[D].北京: 中国地震局地球物理研究所, 2011 (Ren Xuemei. Study on the Estimation of b Value on Seismic Zontion[D]. Beijing: Institute of Geophysics, CEA, 2011)
(  0) 0) |
| [13] |
龙锋, 闻学泽, 倪四道. 区域最小完整性震级时空分布的确定:以龙门山断裂带为例[J]. 地震, 2009, 29(3): 27-36 (Long Feng, Wen Xueze, Ni Sidao. Determination of Temporal-Spatial Distribution of the Regional Minimum Magnitudes of Completeness: Application to the Longmenshan Fault Zone[J]. Earthquake, 2009, 29(3): 27-36)
(  0) 0) |
| [14] |
黄亦磊, 周仕勇, 庄建仓. 基于地震目录估计完备震级方法的数值实验[J]. 地球物理学报, 2016, 59(4): 1 350-1 358 (Huang Yilei, Zhou Shiyong, Zhuang Jiancang. Numerical Tests on Catalog-Based Methods to Estimate Magnitude of Completeness[J]. Chinese Journal of Geophysics, 2016, 59(4): 1 350-1 358)
(  0) 0) |
| [15] |
吴果, 周庆, 冉洪流. 震级-频度关系中b值的极大似然法估计及其影响因素分析[J]. 地震地质, 2019, 41(1): 21-43 (Wu Guo, Zhou Qing, Ran Hongliu. The Maximum Likelihood Estimation of b-Value in Magnitude-Frequency Relation and Analysis of Its Influencing Factors[J]. Seismology and Geology, 2019, 41(1): 21-43)
(  0) 0) |
| [16] |
高斯阳, 屠泓为, 张朋涛, 等. 2016年门源6.4级地震序列b值变化特征及周期谱分析[J]. 地球物理学进展, 2019, 34(6): 2 152-2 157 (Gao Siyang, Tu Hongwei, Zhang Pengtao, et al. Comprehensive Analysis on 2016 Menyuan M6.4 Earthquake Sequence of b Value and Periodic Spectrum[J]. Progress in Geophysics, 2019, 34(6): 2 152-2 157)
(  0) 0) |
| [17] |
Felzer K. Simulated Aftershock Sequences for an M7.8 Earthquake on the Southern San Andreas Fault[J]. Seismological Research Letters, 2009, 80(1): 21-25 DOI:10.1785/gssrl.80.1.21
(  0) 0) |
| [18] |
李腊月, 李玉江, 张风霜, 等. 郯庐断裂带中南段闭锁特征与地震危险性分析[J]. 地质学报, 2020, 94(2): 467-479 (Li Layue, Li Yujiang, Zhang Fengshuang, et al. Fault Blocking Characteristics and Seismic Hazard Analysis in the Middle and Southern Segments of the Tan-Lu Fault Zone[J]. Acta Geologica Sinica, 2020, 94(2): 467-479 DOI:10.3969/j.issn.0001-5717.2020.02.008)
(  0) 0) |
2. Institute of Crustal Dynamics, CEA, 1 Anningzhuang Road, Beijing 100085, China;
3. School of Geomatics Science and Technology, Nanjing Technology University, 30 South-Puzhu Road, Nanjing 211800, China
 2021, Vol. 41
2021, Vol. 41

