2020-01-23 22:26四川省石渠县(32.97°N,98.87°E)发生MS4.3地震,震源深度13 km,是继2017-05-16石渠MS4.4地震后近年发生的第2次中强地震。震区地处青藏高原,与青海、西藏接壤,属于三省交界地区,平均海拔超过4 200 m,地质构造上位于松潘-甘孜地块,为巴颜喀拉前陆盆地褶皱带,新生代以来以间歇性强烈抬升为主,地震活动性较强[1]。
本文利用国家测震台网数据备份中心提供的四川、青海、西藏、甘肃等区域地震台网宽频带固定台站近震数字波形资料,采用gCAP全波形反演方法[2-3]对石渠MS4.3地震的震源机制和震源深度进行反演,并从速度结构模型、定位误差、数据质量等方面对反演结果的可靠性进行评价,结合区域地质构造和余震序列的空间展布特征,探讨石渠地震可能的发震构造,为震区周边的地震危险性分析提供数据基础。
1 地质构造背景研究区位于三叠系松潘-甘孜地块,属于地中海-喜马拉雅构造带[4],地块呈倒三角形夹持于羌塘地体、东昆仑-西秦岭造山带和龙门山逆冲推覆带之间[5]。松潘-甘孜地块北面以东昆仑深断裂、玛沁-略阳深断裂为界,与秦岭大别皱褶系及柴达木盆地相分割; 西南方向以金沙江-红河深断裂北段为界,与羌塘地块相接; 东南以龙门山深断裂为界,与四川盆地相邻。块体内部主要分为3个部分,鲜水河深断裂以北为巴颜喀拉地槽褶皱带,甘孜-理塘深断裂以西为义敦地槽褶皱带,2条深大断裂的中间部分为雅江地槽褶皱带。达日断裂、玉科-泥曲断裂、巴颜喀拉山主峰断裂、炉霍-道孚断裂、长沙贡玛断裂、杂孕楚玛尔河断裂、曲麻莱断裂、甘孜-理塘断裂、玉树-甘孜断裂等众多NW向的断裂带近似平行分布于块体内。
鲜水河深大断裂带为一条NW向的弧形左旋走滑深大断裂带,自泸定向北,经康定、炉霍至长沙贡玛进入青海省境内,贯穿整个川西高原[6]。该断裂具有长期活动性,最早始于二叠纪,地震频发,自有记录以来共发生7级以上地震20余次[7]。长沙贡玛断裂与炉霍-道孚断裂北西延伸段交汇于石渠县境内,黄仕华等[8]认为长沙贡玛断裂为炉霍-道孚断裂带的次级断裂,其左行剪切活动强烈,长沙贡玛断裂石渠段自有记录以来共发生4级以上地震8次。此外,广义的鲜水河断裂带包括玉树-甘孜断裂带,而狭义的鲜水河断裂带、安宁河-则木河断裂带及小江断裂带为研究区内地壳运动变形最强烈的断裂带[4]。
2 研究方法gCAP(generalized cut and paste)方法[2]采用全波形反演震源机制,将体波和面波部分分别进行拟合,可克服只利用体波或面波进行求解的局限性。对于双力偶震源,设u(t)为观测位移,则相应的理论位移s(t)可表示为:
| $ s(t)=M_{0} \sum\limits_{i=1}^{3} A_{i}(\phi-\theta, \delta, \lambda) G_{i}(t) $ | (1) |
式中,i=1, 2, 3分别对应垂直走滑型、垂直倾滑型及倾角45°倾滑型断层,M0为标量地震矩,Ai为辐射系数,ϕ为台站方位角,Gi为格林函数,θ、δ、λ分别为走向、倾角和滑动角。
| $ u(t)=s(t) $ | (2) |
设θ、δ、λ的取值范围分别为0≤θ≤2π、0≤δ≤π/2、0≤λ≤2π,通过格点搜索方法对非线性式(2)进行求解,从而对实际观测位移进行评估。
误差函数可表示为:
| $ e=\left\|\left(\frac{r}{r_{0}}\right)^{p}\right\| \cdot\|u-s\| $ | (3) |
式中,r为台站震中距,r0为选定的参考震中距,p为比例因子[2]。在实际反演过程中,体波和面波需要根据实际情况给予不同的比例因子,从而避免面波部分的拟合误差占据主要权重[9]。根据前人研究成果[10],设置体波p为1,面波p为0.5,并由此计算实际观测波形与理论波形之间的误差函数,寻找最优震源机制参数,最终获得地震的震源机制解、震源深度及矩震级。
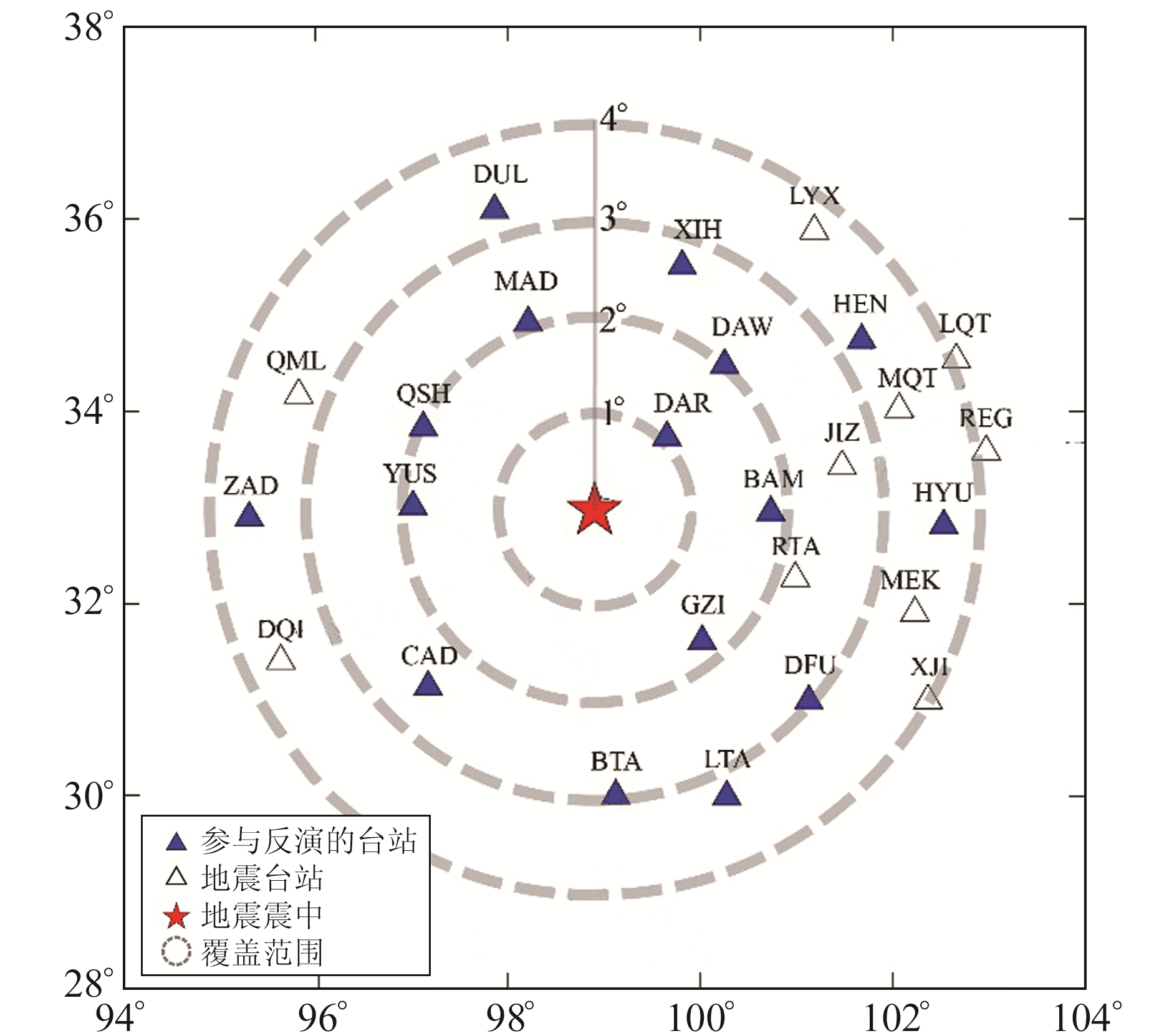
3 数据与模型 3.1 台站分布与数据来源利用国家测震台网数据备份中心提供的四川、青海、西藏、甘肃区域地震台网宽频带固定台站近震资料,选取震中距为0°~4°共26个台站的波形数据,并筛选出16个P波初动清晰且分布均匀的台站(图 1)波形作为最终参与反演的数据对象,包含青海台网10个台站、四川台网5个台站、西藏台网1个台站,研究所用的地震事件目录从中国地震台网中心获取。
|
图 1 地震震中和台站分布 Fig. 1 Distribution of earthquake epicenters and stations |
石渠MS4.3地震涉及区域位于松潘-甘孜地块,选取参与反演的台站震中距较小,均在4°以内。利用地震震中的地理坐标,采用crust2.0(http://igppweb.ucsd.edu/~gabi/crust2.html)速度模型[11]给出震中的速度结构,并设置品质因子Q值,其中QS(S波品质因子)为500,QP(P波品质因子)为QS值的2倍,表 1为研究区平均地壳速度结构模型。
|
|
表 1 研究区地壳速度模型 Tab. 1 The crustal velocity model of study area |
采用频率-波数(F-K)方法[12]计算不同深度、不同震中距的理论格林函数。设置深度为0~30 km,步长为1 km,采样率为0.2 s,计算选取的16个台站的震中距,结果介于111~360 km,其中震中距最大为DUL台,相距357.9 km; 最小为DAR台,相距111.2 km。
3.4 数据处理对震中距为0°~4°、三分量齐全的近震数据进行格式转换,将seed格式波形数据转为SAC格式。截取P波理论到时前10 s至后800 s波形,对原始波形数据进行去趋势、去均值、去倾斜、去仪器响应等处理,再采用0.2 s重采样,利用0.05~2.00 Hz Butterworth带通滤波器进行滤波,以降低高频噪声的影响。将坐标转换至大圆路径,将三分量E(水平东西向)、N(水平南北向)、Z(垂直向)旋转为R(径向)、T(切向)、Z(垂直向)后手动拾取P波初动到时。采用gCAP方法进行全波形反演时,设定体波时窗长度为30 s,面波时窗长度为60 s,由于石渠MS4.3地震震级偏小,为保证结果的可靠性并提高信噪比,将波形数据截断为体波(Pnl)部分和面波(S)部分,分别采用4阶Butterworth带通滤波器进行滤波,以减少噪声和地壳精细结构对数据的影响。体波部分滤波频段为0.05~0.15 Hz,面波部分滤波频段为0.06~0.1 Hz,震源机制解和震级的搜索步长分别设置为5和0.1。
利用频率-波数方法计算理论地震波形分别对频率和波数进行的积分[13],使用传播矩阵计算地震的全波场位移,最终获得不同频率的体波和面波理论地震波形[14]。利用格点搜索和互相关方法将实际地震波形与理论地震波形进行拟合[13],同时进行全局搜索,寻找误差函数最小的震源机制解[2]。
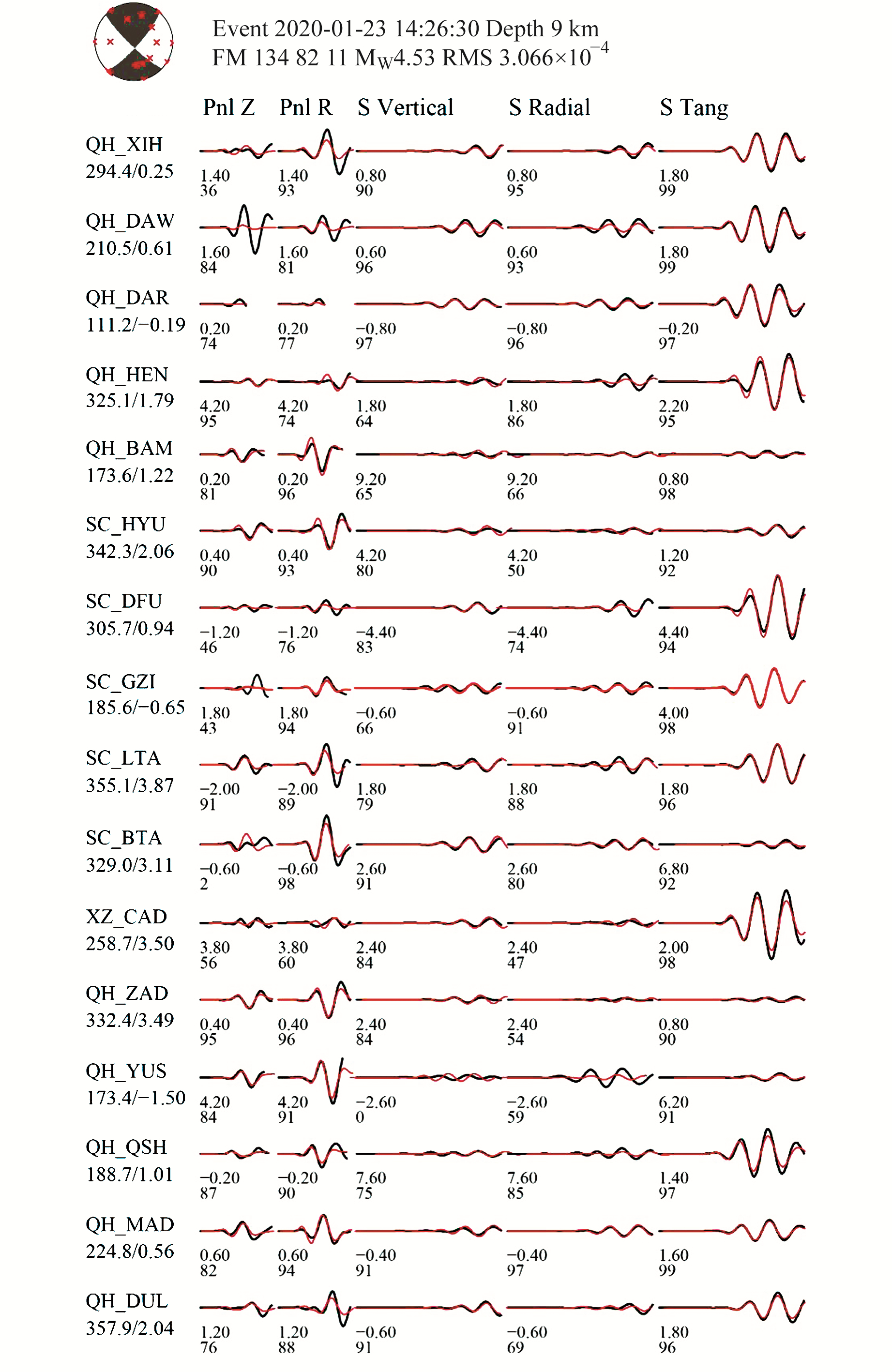
4 结果 4.1 震源机制解利用gCAP方法反演得到四川石渠MS4.3地震的最佳震源机制解,节面Ⅰ走向134°,倾角82°,滑动角11°; 节面Ⅱ走向42°,倾角79°,滑动角171°。P、T轴的方位角分别为-92°、-1.5°,倾角分别为2.0°、13.4°。由图 2可知,在参与反演的16个台站记录的80个震相数据中,56个震相数据的相关系数大于0.8,占总数的70%;40个震相数据的相关系数大于0.9,占总数的50%,属强相关,均方根误差(RMS)为3.066×10-4,波形拟合较好,各震源机制参数结果的可信度高。
|
波形的滤波范围: Pnl部分为0.05~0.15 Hz,S部分为0.06~0.1 Hz, 波形下方数字表示理论波形相对实际波形的时移(单位s)和相关系数, 时移为正值表示理论波形比实际观测快, 相关系数用百分比表示; 左侧大写字母表示台网名和台站名, 其下方数字为震中距(单位km)和相对偏移时间(单位s); 台站波形按方位角排列 图 2 震源机制解及理论地震波形(红色)和观测地震波形(黑色)对比 Fig. 2 The result of focal mechanism solution and comparison between synthetic(red) and observed(black) waveforms |
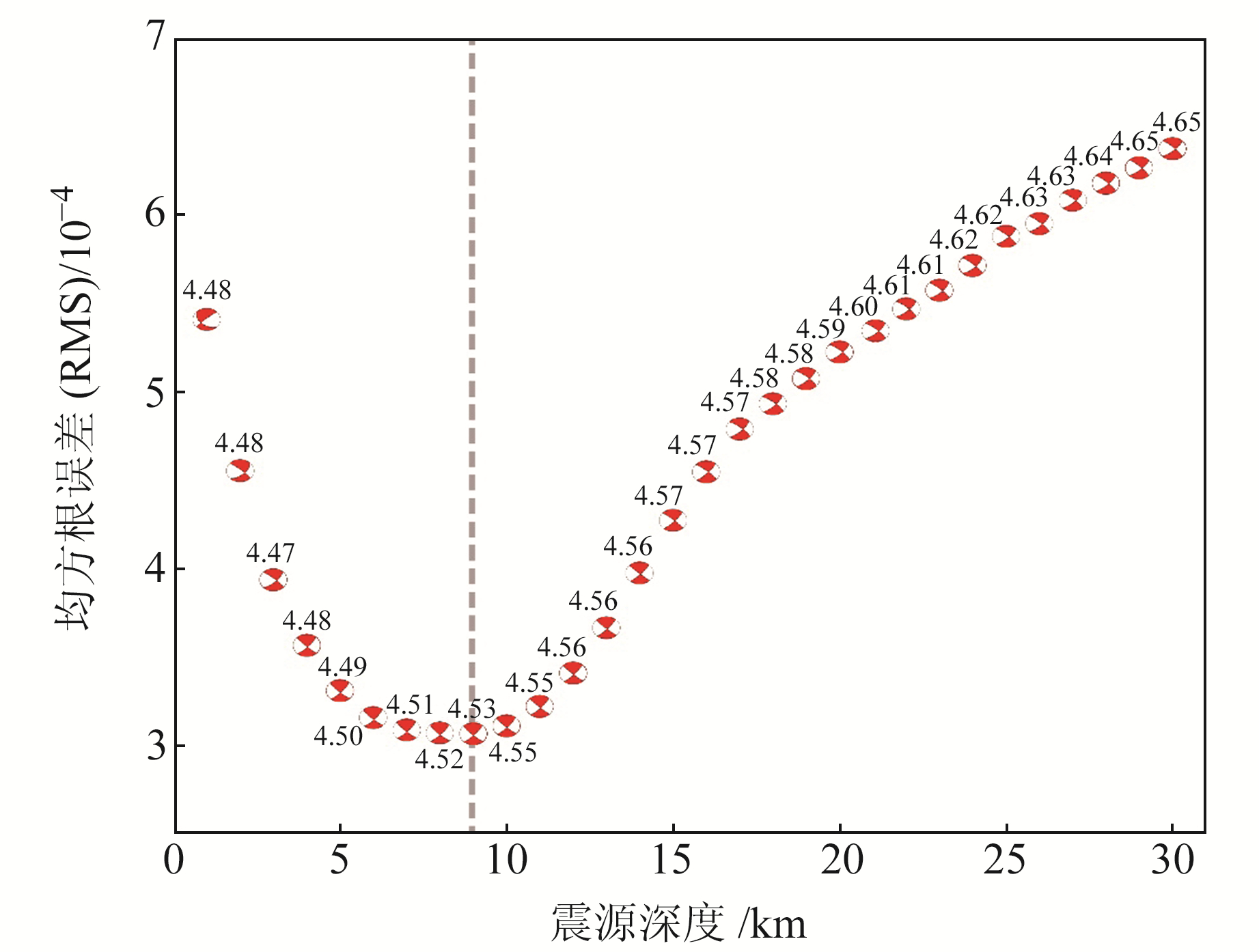
将震源机制解的反演误差作为震源深度函数[15],分析误差随震源深度的变化关系。利用不同深度的最佳震源机制解结果,以波形最小拟合均方根误差作为四川石渠MS4.3地震的最佳质心深度,由图 3可知,除1 km和2 km深度外,反演得到的震源机制解在不同深度上的变化较小,表明该地震以走滑型为主,反演的震源机制解稳定性和可靠性较高。该地震的最佳质心深度为9 km,震级为MW 4.53,属于浅源地震。
|
图 3 震源机制解随不同震源深度变化及拟合均方根误差 Fig. 3 Variation of focal mechanism solution with different focal depths and RMS |
在求解震源机制解的过程中,主要有3个方面的因素会对结果的可靠性造成影响:1)地壳速度结构误差,包括S波、P波速度及品质因子大小; 2)震中定位的准确性; 3)数据质量的影响。为测试震源机制解结果的稳定性和可靠性,本文将从这3个方面对结果进行分析。
5.1 速度结构模型误差影响根据品质因子Q值的变化[16],对速度结构模型中的QS和QP进行调整(表 2),重新计算格林函数并进行gCAP反演。从表 3可以看出,震源机制解和最佳质心深度无变化,均方根误差(RMS)减小了0.001×10-4,震级变化了0.01,表明品质因子Q值几乎不影响震源机制解和质心深度,对震级影响较小。
|
|
表 2 Q值调整后的研究区地壳速度模型 Tab. 2 The crustal velocity model of study area after Q value adjustment |
为测试S波和P波速度的影响,将波速分别增加和减小5%,得到新的速度结构模型,再次计算格林函数并进行gCAP反演。利用高速异常速度模型反演的结果为:节面Ⅰ走向133°,倾角82°,滑动角10°; 震级MW4.57,质心深度9 km。利用低速异常速度模型反演的结果为:节面Ⅰ走向134°,倾角80°,滑动角12°; 震级MW4.47,质心深度7 km。与crust2.0速度模型相比,走向差为0°~1°,倾角差为0°~2°,滑动角最大差为1°,震级差最大为0.06,深度差为2 km。结果表明,增加S波和P波速度的扰动对震源机制解的影响较小,对震级和质心深度存在一定影响。分析可知,改变品质因子Q值和S波、P波速度对震源机制解结果的影响较小,同时也说明gCAP方法对地壳速度结构模型的依赖程度较小。
5.2 定位误差影响通常情况下,地震的定位误差不超过3 km[13],本文将震中位置分别向东、南、西、北各移动5 km,测试定位精确度对震源机制解的影响。从表 3可以看出,改变震中位置对震源机制解中滑动角的影响较大,对走向和倾向的影响很小,结果均为走滑型地震。矩震级和地震质心深度分别相差0.04~0.06和2~4 km,影响相对较大。
|
|
表 3 不同影响因素下震源机制解结果 Tab. 3 The focal mechanism solution under different conditions |
在初始反演时,选取数据质量较好、方位角分布均匀的16个台站进行震源机制反演,结果发现波形拟合较好。为测试数据质量对结果的影响,将已剔除的7个台站波形数据加入反演计算,结果见表 3。从表中可以看出,震源机制解中3个角度值的变化量最大为3°,矩震级相差0.05,质心深度相差2 km。进一步将信噪比最差的3个台站波形数据加入计算,即26个台站全部参与反演,计算结果与23个台站参与计算的结果一致。因此认为,反演获得的震源机制解的变化量在5°以内,反演结果较为稳定。
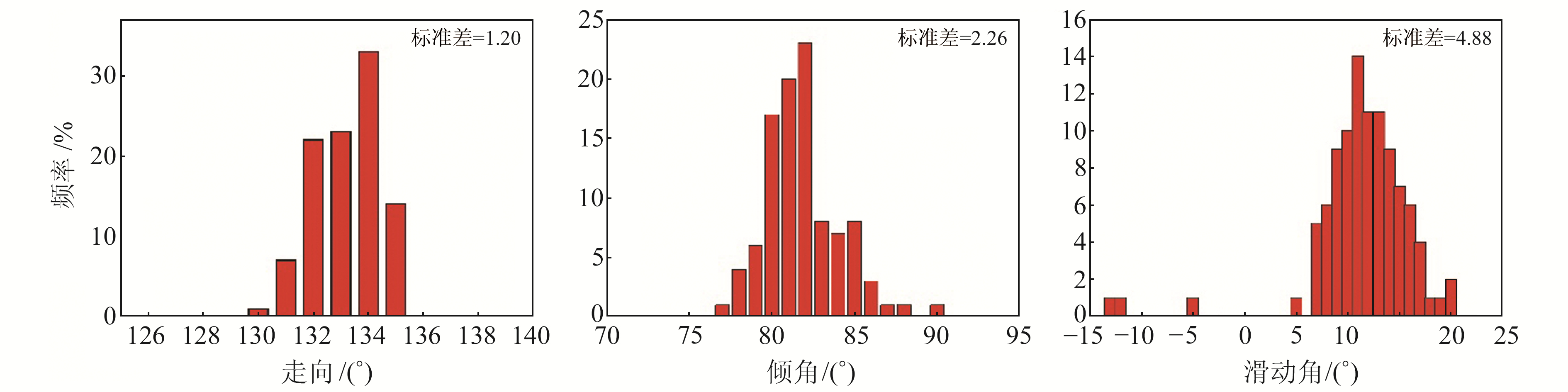
5.4 误差估计利用gCAP方法进行震源机制求解的过程属于非线性反演,本文采用Sheng等[17]的误差估计方式,利用bootstrap方法[18]分析震源机制解的误差,以便进一步评估结果的准确性和稳定性。将最终反演的16个台站作为抽样对象,每个样本抽取按照放回抽样的方式从波形数据集中随机选择,允许某些台站的波形记录被重复选取,同时也存在部分台站未被采样。重复进行1 000次抽样,获得震源机制的反演结果。bootstrap方法的计算结果表明,走向、倾角、滑动角的标准差分别为1.20°、2.26°和4.88°。根据误差评估方法以2倍标准差作为结果的误差,最终获得石渠MS4.3地震震源机制解的走向、倾角、滑动角误差分别为2.40°、4.52°和9.76°。图 4为1 000个震源机制解的频数分布,从图中可以看出,走向、倾角、滑动角的分布高度集中,表明震源机制解的结果较为可靠。
|
图 4 bootstrap抽样计算的震源机制解结果 Fig. 4 The focal mechanism solution obtained by bootstrap sampling |
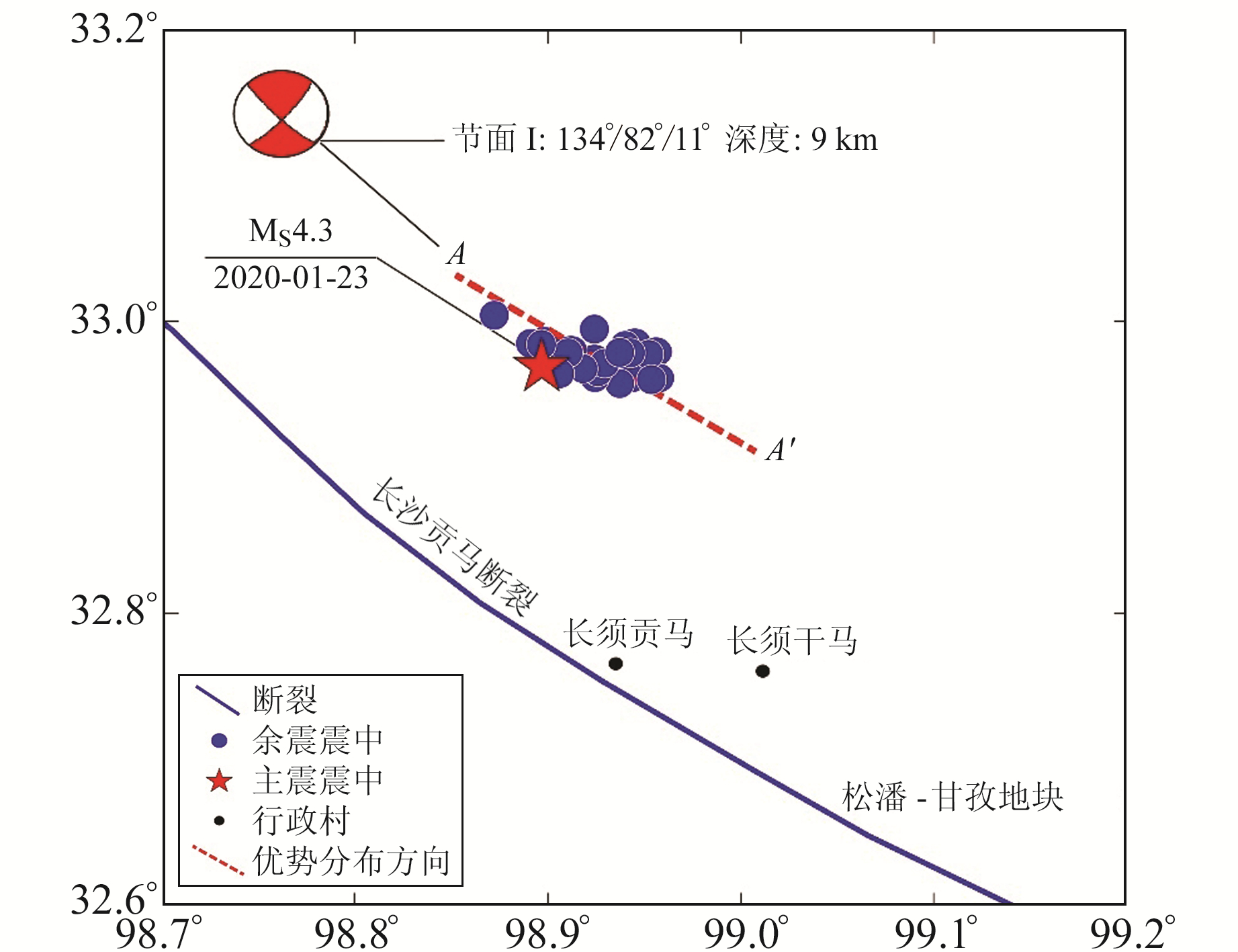
石渠MS4.3地震的震源机制解为节面Ⅰ走向134°,倾角82°,滑动角11°; 节面Ⅱ走向42°,倾角79°,滑动角171°,而实际的发震构造需要根据震中区域的地质构造特征及余震的震中分布进行推测分析[15]。石渠MS4.3地震发生后,截至2020-03-25共记录到可定位余震36次,利用HypoDD相对定位法[19]对地震序列进行重定位后发现,余震分布集中。从图 5可以看出,余震序列展布方向为NW向,主要分布在主震偏NE侧附近,具有向NE向倾斜的趋势。震源区附近发育有长沙贡玛断裂,走向NW,倾向NE,倾角为60°~75°,为左旋走滑型逆断层。震源区内的剪切作用是最重要的发震力学因素,由于NW向断裂在构造上受到的剪切应力较NE向大,受到的正压应力比NE向小[6],容易产生剪切滑动,而长沙贡玛断裂左行剪切活动强烈也可印证这一特点[8]。
|
图 5 石渠MS4.3地震余震序列重定位结果与震源机制 Fig. 5 The relocation results of aftershock sequences and focal mechanisms of Shiqu MS4.3 earthquake |
根据震源区的地质构造特征,综合余震分布特点及震源机制解认为,节面Ⅰ与长沙贡玛断裂属性一致,且余震序列优势分布方向也与节面Ⅰ吻合。因此,将节面Ⅰ作为四川石渠MS4.3地震的发震构造更为合理,即长沙贡玛断裂为地震的发震断层,其走向、倾角和滑动角分别为134°、82°和11°,为左旋走滑型地震。
6 结语1) 利用gCAP方法反演获得四川石渠MS4.3地震的震源机制解,结果表明,该地震为走滑型地震,不同震源深度的震源机制解反演得到的最佳质心深度为9 km,矩震级为MW4.53。
2) 为测试震源机制解的稳定性和可靠性,从地壳速度结构误差、震中定位的准确性和数据质量影响等3个方面进行综合分析认为,当反演获得的震源机制解的变化量在5°以内时,反演结果较为稳定,可靠性较高,震源机制解可被接受。
3) 使用bootstrap方法对震源机制解的误差进行分析,计算1 000次bootstrap抽样结果的震源机制解,获得石渠地震震源机制解的走向、倾角、滑动角的误差分别为2.40°、4.52°和9.76°,表明震源机制解结果较为可靠。
4) 四川石渠MS4.3地震余震序列展布方向为NW向,主要分布在主震偏NE侧附近,具有向NE向倾斜的趋势。震源机制解节面Ⅰ与长沙贡玛断裂的特征相吻合,余震序列的优势分布方向与节面Ⅰ走向一致。综合震源区地质构造特征、主震震源机制及余震序列的空间分布特征认为,此次地震的发震断层为节面Ⅰ,即长沙贡玛断裂,走向、倾角和滑动角分别为134°、82°和11°,为左旋走滑型地震。
致谢: 感谢中国地震台网中心、四川省地震台网和中国地震局地球物理研究所“国家数字测震台网数据备份中心”为本文研究提供相关数据; 感谢朱露培教授提供gCAP程序包,本文部分图件使用GMT进行绘制。重庆市地震局黄世源高级工程师、中国科学院精密测量科学与技术创新研究院盛敏汉博士及四川省地震局李大虎高级工程师在本文分析过程中提供了大力支持,在此一并表示衷心感谢!
| [1] |
王新民. 石渠地震震害损失的评估及其背景条件[J]. 四川地质学报, 1993, 13(4): 304-309 (Wang Xinmin. Assessment and Background Conditions of Losses Caused by Earthquake Disaster of Shiqu Earthquake[J]. Acta Geologica Sichuan, 1993, 13(4): 304-309)
(  0) 0) |
| [2] |
Zhu L P, Helmberger D V. Advancement in Source Estimation Techniques Using Broadband Regional Seismograms[J]. Bulletin of the Seismological Society of America, 1996, 86(5): 1 634-1 641
(  0) 0) |
| [3] |
Zhu L P, Ben-Zion Y. Parametrization of General Seismic Potency and Moment Tensors for Source Inversion of Seismic Waveform Data[J]. Geophysical Journal International, 2013, 194(2): 839-843 DOI:10.1093/gji/ggt137
(  0) 0) |
| [4] |
李坪. 鲜水河-小江断裂带[M]. 北京: 地震出版社, 1993 (Li Ping. The Xianshuihe-Xiaojiang Fault Zone[M]. Beijing: Seismological Press, 1993)
(  0) 0) |
| [5] |
王海燕, 高锐, 张季生, 等. 松潘-甘孜地块地壳性质再研究[J]. 地质科学, 2016, 51(1): 41-52 (Wang Haiyan, Gao Rui, Zhang Jisheng, et al. Research of the Crustal Property of the Songpan-Garze Block[J]. Chinese Journal of Geology, 2016, 51(1): 41-52 DOI:10.3969/j.issn.0563-5020.2016.01.005)
(  0) 0) |
| [6] |
四川省地质矿产局. 四川省区域地质志[M]. 北京: 地质出版社, 1991 (Bureau of Geology and Mineral Resources of Sichuan Province. Regional Geology of Sichuan Province[M]. Beijing: Geological Publishing House, 1991)
(  0) 0) |
| [7] |
张世民, 谢富仁. 鲜水河-小江断裂带7级以上强震构造区的划分及其构造地貌特征[J]. 地震学报, 2001, 23(1): 36-44 (Zhang Shimin, Xie Furen. Seismo-Tectonic Divisions of Strong Earthquakes(MS≥7.0) and Their Tectonic Geomorphology along Xianshuihe-Xiaojiang Fault Zone[J]. Acta Seismologica Sinica, 2001, 23(1): 36-44 DOI:10.3321/j.issn:0253-3782.2001.01.005)
(  0) 0) |
| [8] |
黄仕华, 刘汉强. 青海达日县桑日麻地区发现道孚-炉霍断裂带北西延伸踪迹[J]. 四川地质学报, 2006, 26(3): 129-132 (Huang Shihua, Liu Hanqiang. NW-Trending Extending of the Dawu-Luhuo Fracture Zone to Sangruma, Darlag, Qinghai[J]. Acta Geologica Sichuan, 2006, 26(3): 129-132 DOI:10.3969/j.issn.1006-0995.2006.03.001)
(  0) 0) |
| [9] |
孟庆君. CAP方法和深度震相确定地震震源参数研究[D].合肥: 中国科学技术大学, 2013 (Meng Qingjun. Research about Focal Parameters Using CAP and Depth Phases[D]. Hefei: University of Science and Technology of China, 2013)
(  0) 0) |
| [10] |
郑建常, 林眉, 王鹏, 等. CAP方法反演震源机制的误差分析:以胶东半岛两次显著中等地震为例[J]. 地球物理学报, 2015, 58(2): 453-462 (Zheng Jianchang, Lin Mei, Wang Peng, et al. Error Analysis for Focal Mechanisms from CAP Method Inversion: An Example of 2 Moderate Earthquakes in Jiaodong Peninsula[J]. Chinese Journal of Geophysics, 2015, 58(2): 453-462)
(  0) 0) |
| [11] |
Laske G, Masters G, Reif C. CRUST2.0: A New Global Crustal Model at 2×2 Degrees[EB/OL]. https://igppweb.ucsd.edu/gabi/crust2.html, 2001
(  0) 0) |
| [12] |
Zhu L P, Rivera L A. A Note on the Dynamic and Static Displacements from a Point Source in Multilayered Media[J]. Geophysical Journal International, 2002, 148(3): 619-627 DOI:10.1046/j.1365-246X.2002.01610.x
(  0) 0) |
| [13] |
谢祖军, 郑勇, 倪四道, 等. 2011年1月19日安庆ML4.8地震的震源机制解和深度研究[J]. 地球物理学报, 2012, 55(5): 1 624-1 634 (Xie Zujun, Zheng Yong, Ni Sidao, et al. Focal Mechanism and Focal Depth of the 19 January 2011 Anqing Earthquake[J]. Chinese Journal of Geophysics, 2012, 55(5): 1 624-1 634)
(  0) 0) |
| [14] |
李锋, 缪阿丽, 李迎春, 等. 2018-04-06无为ML4.1地震震源机制和深度及发震构造研究[J]. 大地测量与地球动力学, 2019, 39(8): 790-793 (Li Feng, Miao Ali, Li Yingchun, et al. Focal Mechanism and Depth and Seismogenic Structure of the Wuwei ML4.4 Earthquake, April 6, 2018[J]. Journal of Geodesy and Geodynamics, 2019, 39(8): 790-793)
(  0) 0) |
| [15] |
徐志国, 梁姗姗, 刘杰, 等. 2017年新疆精河MS6.6主震震源机制解反演及余震序列重定位[J]. 地球物理学进展, 2019, 34(4): 1357-1365 (Xu Zhiguo, Liang Shanshan, Liu Jie, et al. Focal Mechanism Solution and Relocation of the Aftershock Sequences of the 2017 Jinghe MS6.6 Earthquake in Xinjiang[J]. Progress in Geophysics, 2019, 34(4): 1357-1365)
(  0) 0) |
| [16] |
汪素云, 裴顺平, Thomas M H, 等. 利用ML振幅研究地壳横波Q值Ⅱ:Q横向变化特征[J]. 地球物理学报, 2008, 51(1): 133-139 (Wang Suyun, Pei Shunping, Thomas M H, et al. Crustal S-Wave Q Estimated from ML Amplitude Ⅱ: Q Lateral Variation in China[J]. Chinese Journal of Geophysics, 2008, 51(1): 133-139 DOI:10.3321/j.issn:0001-5733.2008.01.017)
(  0) 0) |
| [17] |
Sheng M H, Chu R S, Wang Y, et al. Inversion of Source Mechanisms for Single-Force Events Using Broadband Waveforms[J]. Seismogical Research Letters, 2020, 91(3): 1 820-1 830 DOI:10.1785/0220190349
(  0) 0) |
| [18] |
Efron B, Tibshirani R. Bootstrap Methods for Standard Errors, Confidence Intervals, and Other Measures of Statistical Accuracy[J]. Statistical Science, 1986, 1(1): 54-77 DOI:10.1214/ss/1177013815
(  0) 0) |
| [19] |
Waldhauser F, Ellsworth W L. A Double-Difference Earthquake Location Algorithm: Method and Application to the Northern Hayward Fault, California[J]. Bulletin of the Seismological Society of America, 2000, 90(6): 1 353-1 368 DOI:10.1785/0120000006
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41


