随着我国大坝等水利工程建造数量的大幅度增加,大坝的安全性受到社会各界的广泛关注。目前,对观测得到的大坝变形多源监测数据进行准确预报与反演是保障大坝安全的重要手段[1]。大坝变形的影响因素主要可以分为水压、温度和时效3类,水压因素直接作用在大坝上,与水库水位变化有密切关系; 温度因素间接作用于大坝,温差和边界约束是产生应力的主要原因[2]; 而时效因素是许多非线性因素的综合,对于混凝土大坝,主要反映了坝体混凝土材料特性(如混凝土徐变、老化等)、坝基岩体的材料特性(如岩石蠕变、节理裂隙等)、坝体结构缺陷(如施工质量等)、坝基结构缺陷(如软弱结构面等)等因素对变形效应量的影响[3],另外水位、温度和时效之间也存在着一定的相关性。由于各种影响因素的内在联系错综复杂,主次关系变化不定,所以高效地预测大坝变形依旧存在着很多挑战。
随着人工神经网络的不断发展和模糊数学理论的完善,不少学者将二者结合应用于大坝变形预测,这些改进方法虽然对传统神经网络进行了优化,预测精度有所提高,但模型方法参数较多,建模过程繁琐,导致建模比较困难。而基于深度学习算法的全连接神经网络包括多层隐藏层,可实现无监督学习,从而以更少的模型参数、更快的收敛速度和更高的拟合精度来逼近现实[4],在水质预测[5]、大气污染预测[6]、降雨预测[7]等领域应用较多,而在大坝变形预测领域应用较少。
本文利用丰满大坝实测的多源监测数据,建立基于最优学习算法的深度全连接神经网络预测模型,对丰满大坝位移变形量进行预测,并将预测结果与传统BP神经网络的预测结果进行对比,以验证本文深度全连接神经网络预测模型预测大坝位移变形的可行性和优越性。
1 构建深度全连接神经网络 1.1 全连接神经网络全连接神经网络与传统神经网络相比更强调网络的深度。隐藏层和输出层层数之和为网络的深度,记为d,隐藏层可由多层构成,记为hi,隐藏层对应的激活函数记为Ai。
隐藏层第1层的输出值h1为:
| $ h_{1}=A_{1}\left(W_{1} x+b_{1}\right) $ | (1) |
隐藏层其他层的输出值hi为:
| $ h_{i}=A_{i}\left(W_{i} h_{i-1}+b_{i}\right), 1<i<d $ | (2) |
式中,Wi为权重值,bi为偏置。
常见的激活函数包括对数S型函数sigmoid、双曲正切函数tanh和线性整流函数ReLu。
1.2 优化学习算法梯度下降法是目前使用最为广泛的优化算法,也是传统神经网络和机器学习最常用的优化方法,主要包括批量梯度下降法(BGD)和随机梯度下降法(SGD)。其中,BGD的每步迭代使用全部的训练数据,所以参数更新方向比较稳定,但收敛速度较慢,比较耗时; 而SGD的每步迭代随机选取训练样本,收敛速度较快,但由于训练样本的随机性,参数更新不稳定,因此二者都存在比较大的缺陷。随着深度学习的兴起,很多深度优化算法被提出并用于对网络的优化训练。
1.2.1 小批量梯度下降法(MBGD)MBGD[8]是BGD和SGD两种梯度下降法的综合体现,在每步迭代过程中从n个训练样本随机抽取m(m < n)个样本。该方法结合了BGD和SGD各自的优点,相对于BGD,每次学习的速率得到提升; 相对于SGD,降低了收敛波动性,参数更新方向更加稳定。
1.2.2 动量法(momentum)动量法[9]是为解决SGD更新方向完全依赖当前batch从而使更新十分不稳定而提出的。在更新时通过动量因子保留之前的更新方向,并加入该轮的梯度,从而提高学习效率,增加稳定性,能有效避免模型陷入局部最优。具体迭代更新公式为:
| $ {g \leftarrow \frac{1}{m}{\nabla _\theta }\sum\limits_{i = 1}^m L \left( {f\left( {{x^{(i)}};\theta } \right),{y^{(i)}}} \right)} $ | (3) |
| $ {v \leftarrow \gamma v + \eta g} $ | (4) |
式中,γ为动量因子,一般设置为0.9,η为学习率,θ 为初始参数,v为下降动量。
1.2.3 自适应学习率的优化算法(AdaGrad)AdaGrad算法[10]是借鉴模型引入正则化项以缓减过拟合现象的思路提出的,该算法可以解决梯度消失的问题。参数更新的迭代过程为:
| $ {g \leftarrow \frac{1}{m}{\nabla _\theta }\sum\limits_{i = 1}^m L \left( {f\left( {{x^{(i)}};\theta } \right),{y^{(i)}}} \right)} $ | (5) |
| $ {r \leftarrow r + g \odot g} $ | (6) |
| $ {\Delta \theta \leftarrow - \frac{\eta }{{\sqrt r + \delta }} \odot g} $ | (7) |
| $ {\theta \leftarrow \theta + \Delta \theta } $ | (8) |
式中,η为全局学习率,δ为数值稳定量,θ为初始参数,r为梯度累计量。
RMSProp算法[11]是AdaGrad算法的扩展算法,将AdaGrad算法迭代过程式(6)修改为式(9),能有效克服AdaGrad算法梯度急剧减小的问题。具体参数更新为:
| $ r = \rho r + (1 - \rho )g \odot g $ | (9) |
式中,ρ为指数衰减率。
1.2.4 自适应矩估计优化算法(Adam)Adam算法[12]是利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率,将momentum法和RMSprop算法的优势相结合。参数更新的迭代过程为:
| $ g \leftarrow \frac{1}{m}{\nabla _\theta }\sum\limits_{i = 1}^m L \left( {f\left( {{x^{(i)}};\theta } \right),{y^{(i)}}} \right) $ | (10) |
| $ m \leftarrow {p_1}m + \left( {1 - {p_1}} \right) $ | (11) |
| $ gv \leftarrow {p_2}v + \left( {1 - {p_2}} \right)g \odot g $ | (12) |
由于m和v的初始值取0,所以需要对 m和v进行纠正:
| $ \hat m \leftarrow \frac{m}{{1 - p_1^t}} $ | (13) |
| $ \hat v \leftarrow \frac{v}{{1 - p_2^t}} $ | (14) |
| $ \Delta \theta \leftarrow - \eta \frac{{\hat m}}{{\sqrt {\hat v} + \delta }} $ | (15) |
| $ \theta \leftarrow + \Delta \theta $ | (16) |
式中,m和v分别为对梯度的一阶矩估计和二阶矩估计,和为对
1) 数据预处理。训练样本和测试样本的划分及数据标准化处理。
2) 网络构建。确定网络结构,激活函数和损失函数的选取。
3) 优化算法的选取。将经过标准化处理的训练样本数据输入步骤2)的网络模型,经过多轮调试,设置MBGD、momentum法、RMSprop算法和Adam算法的相关参数,利用设置好的4种深度优化学习算法对网络模型进行优化训练,通过观察训练损失函数值的变化曲线,选取最合适的优化学习算法,得到基于最优学习算法的大坝变形预测模型。
4) 模型预测。将测试样本数据中各影响因子输入步骤3)的网络模型,对大坝位移值进行预测。
5) 模型评价。通过MAE、MAPE和RMSE三种评价指标对预测模型进行评价。
2 实例分析 2.1 数据预处理本文选取丰满大坝某坝段监测点1985-01-04~1988-04-09共187期的多源监测数据进行分析,选取前160期监测数据作为训练样本,后27期监测数据作为测试样本。
为消除不同量纲对模型带来的影响并提高神经网络的运行效率和预测精度,需要对原始数据进行预处理。本文使用min-max标准化将原始数据映射到[0~1]之间,具体计算公式为:
| $ y = \frac{{x - \min (x)}}{{\max (x) - \min (x)}} $ | (17) |
相应的反归一化处理计算公式为:
| $ x=y(\max (x)-\min (x))+\min (x) $ | (18) |
式中,y为预处理后的样本数据,x为原始样本数据,min(x)和max(x)为样本中各输入对应的最小值和最大值。
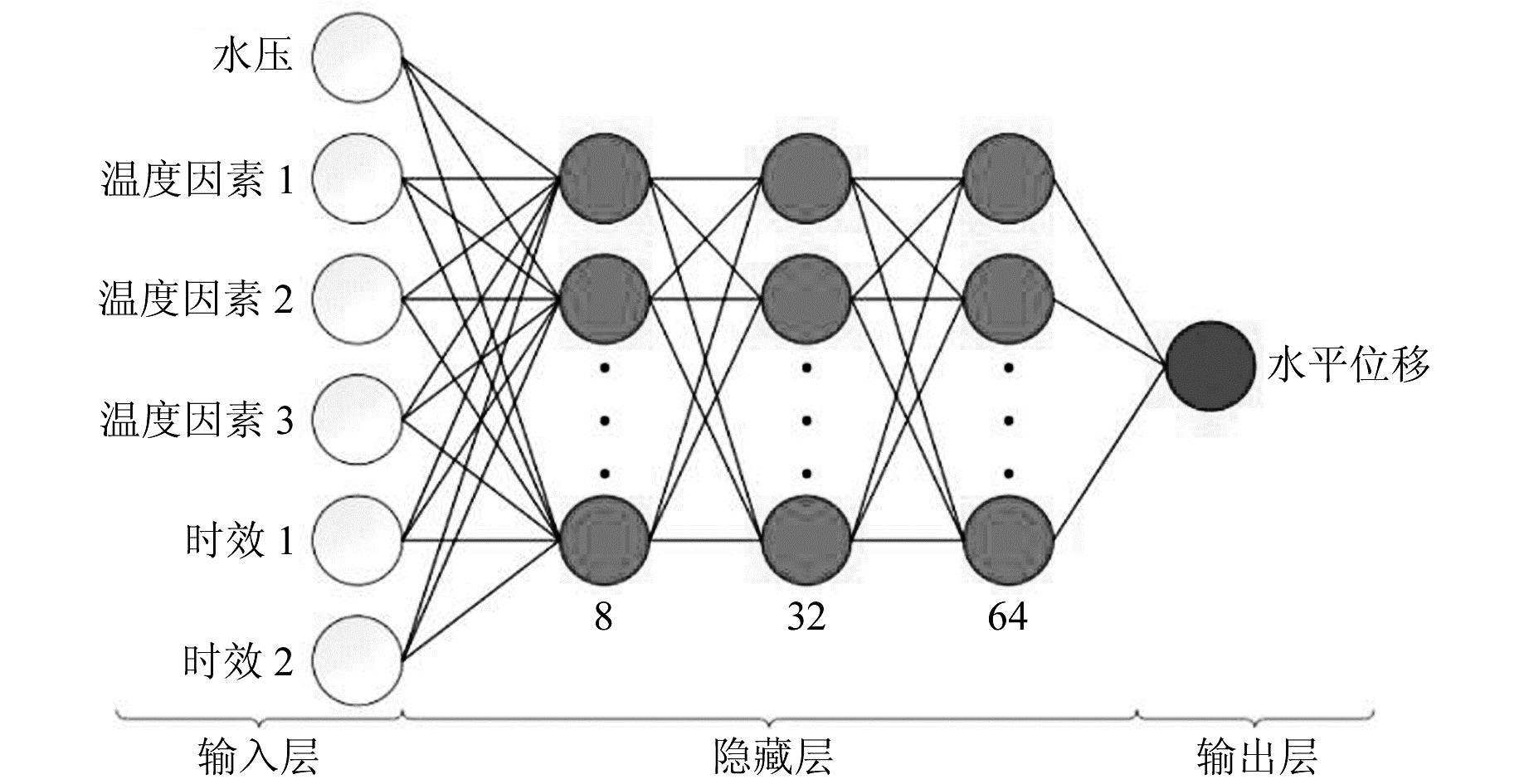
2.2 全连接神经网络的构建 2.2.1 网络结构的设置混凝土大坝位移量的影响因素有很多,其中主要的影响因素有3类,即温度、水压和时效。温度因子取T0,正余弦谐波因子取sin(2πt/365)、sin(4πt/365)、cos(2πt/365)、cos(4πt/365),水压因子取H1、H12、H13,时效因子取θ、lnθ,其中θ=0.01t(t为本次观测距起始观测的累计天数)。胡纪元等[13]应用平均影响值(MIV)结合BP神经网络计算以上10个影响因子对大坝变形量的贡献值,并按照贡献值的大小排序,最终确定选取H1、T0、sin(2πt/365)、sin(4πt/365)、θ、lnθ等6个影响因子同样可以取得很好的预测效果,因此选取这6个影响因子作为本文全连接神经网络的输入。由于本文全连接神经网络是对大坝的位移值进行预测,最终输出为大坝的水平位移值,所以确定输出层的神经元个数取1。隐藏层层数和神经元数量过少不能深挖特征与目标之间的深层关系,过多又会导致模型参数多、训练耗时,还容易导致模型过拟合。本文采用试错法并结合Hecht-Nielsen理论确定隐藏层的层数和隐藏层神经元的数量[5],经过反复实验,最终确定隐藏层的层数为3,每层神经元的个数分别为8、32、64。因此,深度全连接神经网络的网络结构最终确定为6-8-32-64-1,具体如图 1所示。
|
图 1 深度全连接神经网络大坝变形预测模型结构 Fig. 1 Structure of dam deformation prediction model with deep fully connected neural network |
本文程序的实现基于python3.7环境和PaddlePaddle深度学习框架,隐藏层使用的激活函数是sigmoid函数,输出层采用的是tanh函数; 大坝位移预测属于回归问题,所以选用的损失函数为均方误差。
2.3 优化算法的选取 2.3.1 优化算法超参数的设置本文选用MBGD、momentum法、RMSprop算法和Adam算法等4种不同的优化学习算法对模型进行训练。经过多轮调试,最终确定最优学习率都取0.01,momentum法动量因子γ取0.9,RMSprop算法ρ值取0.95,δ采用默认值1×10-6; Adam算法δ采用默认值1×10-8,p1和p2分别取0.9和0.99;中间变量都默认取0,随机选取各初始参数。
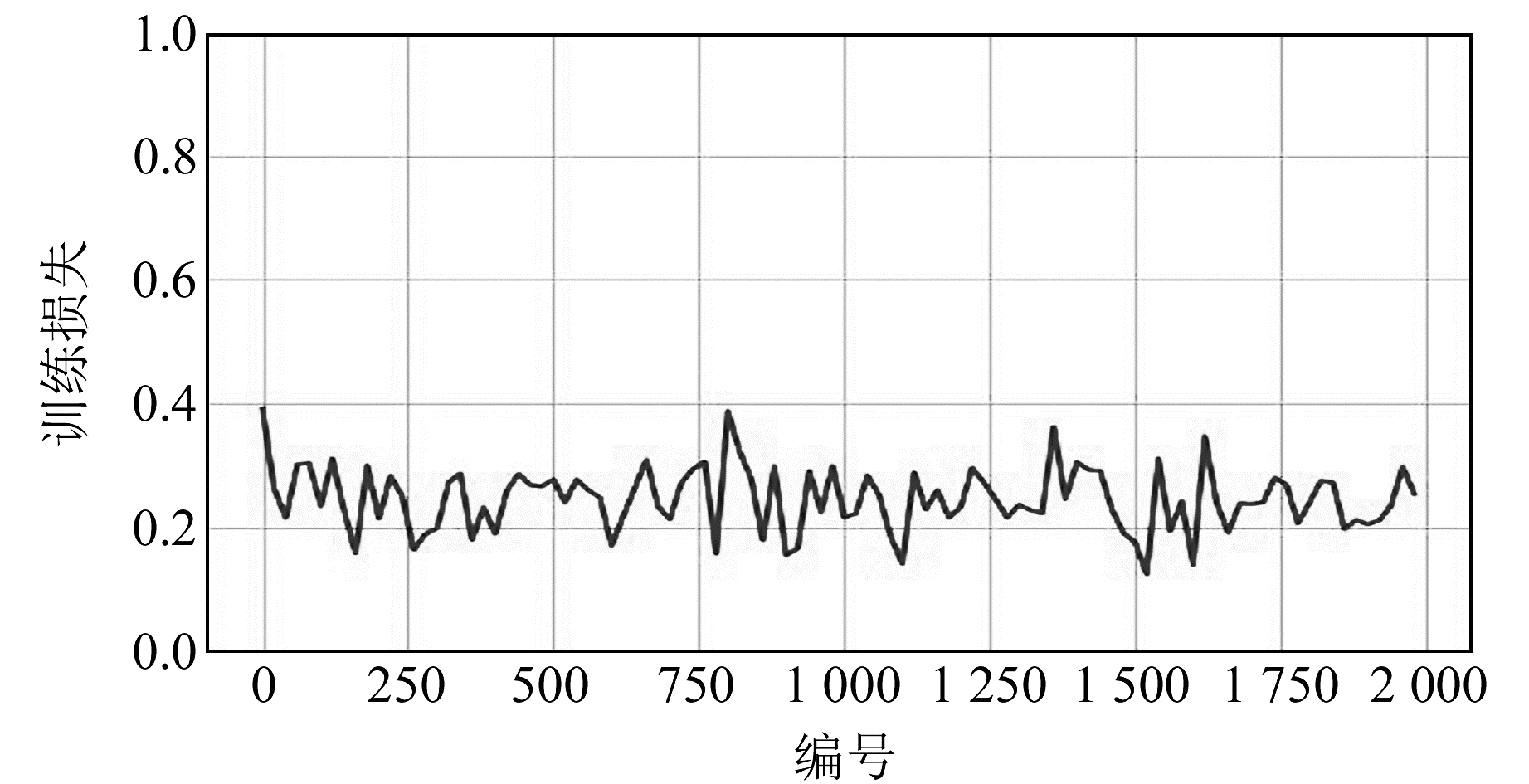
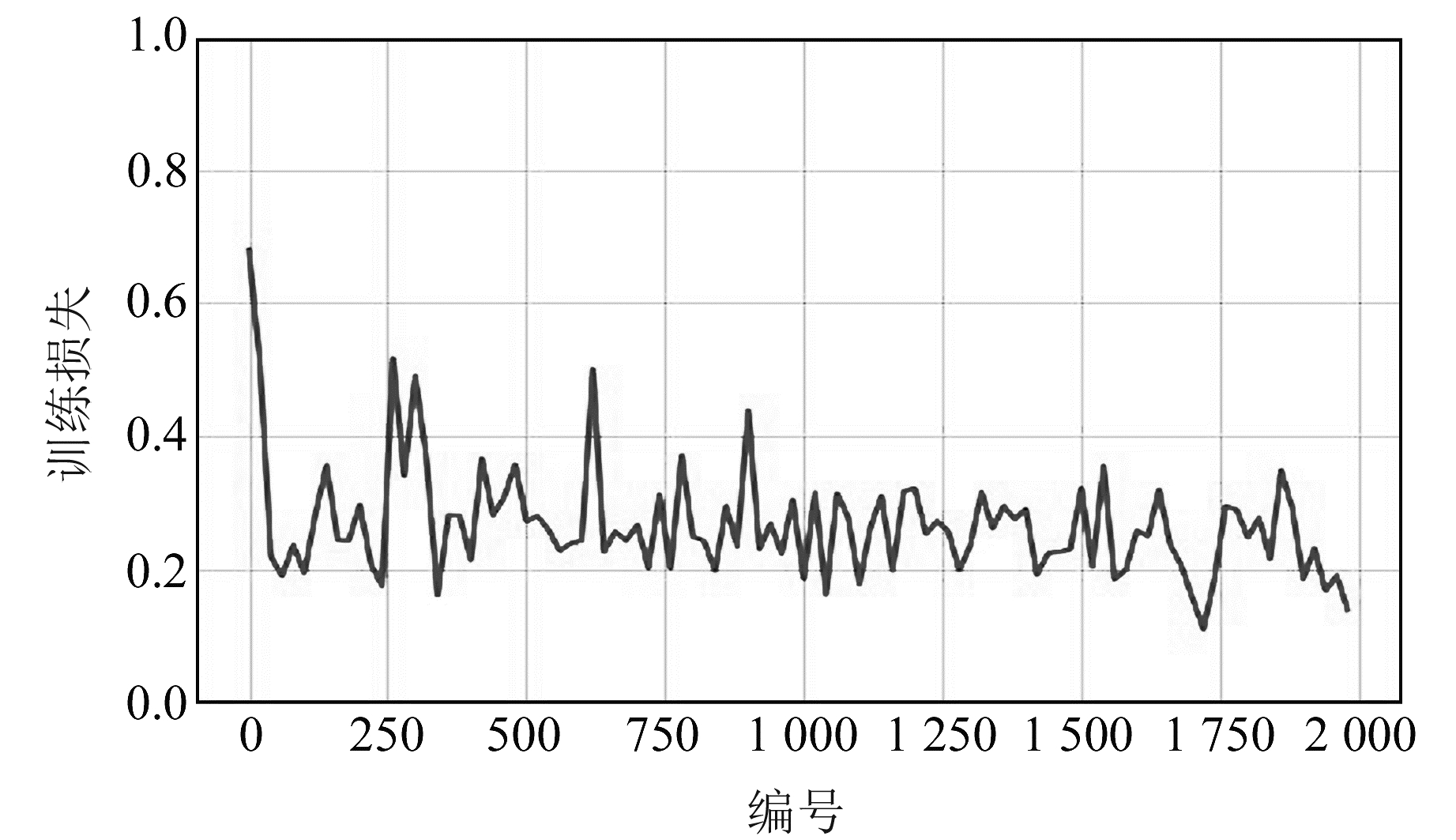
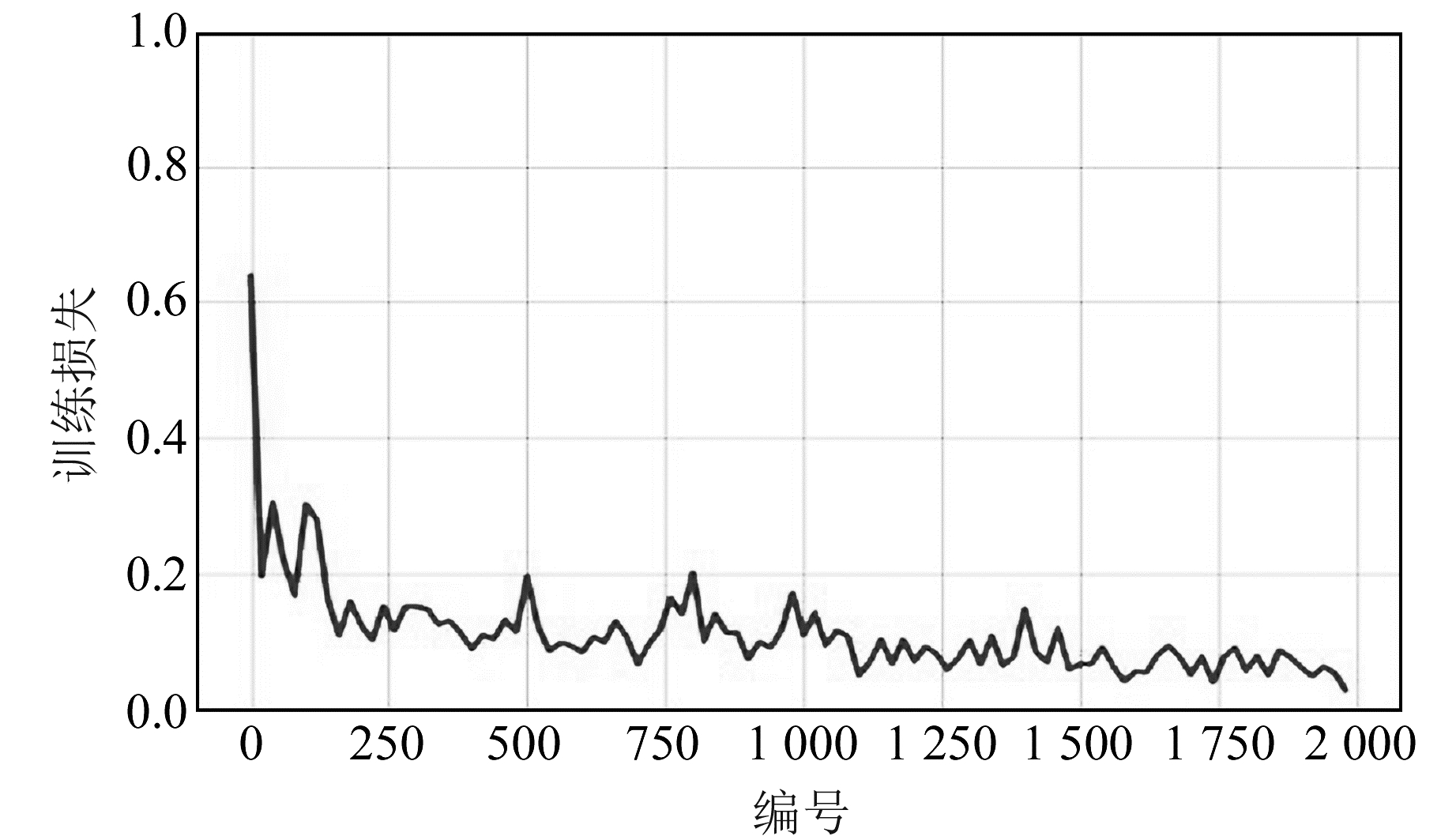
2.3.2 网络训练将经过标准化处理的训练样本数据各影响因素和对应的大坝实测位移量作为输入,采用设置好的4种优化算法对网络进行优化训练。本文训练采用双层循环,内层循环设置batch-size为10,即每次迭代随机抽取10组样本数据更新参数; 网络外层循环epoch-num取100,即进行100轮训练,在每轮迭代开始前要将训练数据进行随机打乱。通过观察各优化算法损失函数值的变化情况选择最合适的优化算法,将训练批次编号作为X轴,该批次的训练损失作为Y轴,4种优化算法损失函数值的变化曲线如图 2~5所示。通过观察可知,Adam算法的收敛速度最快、效率最高,并且最终损失值降到最低值0.027。
|
图 2 MBGD损失函数值变化曲线 Fig. 2 MBGD loss function value change curve |
|
图 3 Momentum法损失函数值变化曲线 Fig. 3 Momentum loss function value change curve |

|
图 4 RMSProp算法损失函数值变化曲线 Fig. 4 RMSProp loss function value change curve |
|
图 5 Adam算法损失函数值变化曲线 Fig. 5 Adam loss function value change curve |
通过对比发现,Adam算法为最优深度学习算法,所以本文运用基于Adam算法的深度全连接神经网络对大坝位移变形量进行预测。将标准化处理后的27期测试样本数据中各影响因子输入网络模型,预测所对应的位移变形量,然后通过反标准化处理得到最终的位移预测值,具体结果见表 1(单位mm)。为进一步评估本文神经网络的预测精度,利用传统BP神经网络对同样的大坝监测数据进行训练并预测,BP神经网络的隐藏层为1层,隐藏层神经元个数根据经验公式和反复实验取13,最终确定BP神经网络结构为6-13-1,训练方式为默认的梯度下降法,其他参数的设置和激活函数的选取与本文神经网络一致,预测结果见表 1(单位mm)。
|
|
表 1 两种神经网络预测结果对比 Tab. 1 Comparison of two neural network prediction results |
由表 1可知,本文深度全连接神经网络和传统BP神经网络都可以对大坝位移变形进行有效的预测,而本文神经网络的预测值与大坝位移的真实值更接近。为更加客观地评价本文深度全连接神经网络的预测精度,通过MAE、MAPE和RMSE三种评价指标进行评价,具体计算结果见表 2(单位mm)。由表可知,本文神经网络的预测精度更高,能更好地描述大坝位移的变形趋势。
|
|
表 2 两种模型3种指标的计算结果 Tab. 2 Calculation results of the three indicators of the two models |
本文通过PaddlePaddle深度学习框架,将深度全连接神经网络引入大坝变形监测领域,并选择最优的深度学习算法对深度全连接神经网络进行优化训练,建立了基于Adam算法的深度全连接神经网络大坝变形预测模型。通过实测的大坝多源监测数据验证表明,该预测模型既能增加传统神经网络的非线性学习能力,又能提高拟合预测的精度,很好地避免了模型的过拟合,可更加准确地描述大坝的真实状态,为大坝的安全施工和运行提供参考依据。
| [1] |
贾金生. 中国大坝建设60年[M]. 北京: 中国水利水电出版社, 2013 (Jia Jinsheng. Dam Construction in China Sixty-Year Review[M]. Beijing: China Water and Power Press, 2013)
(  0) 0) |
| [2] |
张婷婷, 陈宇清, 付慧. 大坝效应量及其分量分离的影响因素分析[J]. 水利科技与经济, 2011, 17(1): 56-57 (Zhang Tingting, Chen Yuqing, Fu Hui. Analysis on the Influencing Factors of Dam Effect Quantity and Its Component Separation[J]. Water Conservancy Science and Technology and Economy, 2011, 17(1): 56-57 DOI:10.3969/j.issn.1006-7175.2011.01.022)
(  0) 0) |
| [3] |
危文爽, 李民. 混凝土大坝的不可逆时效变形[J]. 武汉水利电力大学(宜昌)学报, 1997(4): 72-75 (Wei Wenshuang, Li Min. Unreverse Time-Dependent Displacement of Concrete Dam[J]. Journal of Wuhan University of Water Resources and Electric Power/Yichang, 1997(4): 72-75)
(  0) 0) |
| [4] |
陈先昌.基于卷积神经网络的深度学习算法与应用研究[D].杭州: 浙江工商大学, 2013 (Chen Xianchang. Research on Algorithm and Application of Deep Learning Based on Convolutional Neural Network[D]. Hangzhou: Zhejiang Gongshang University, 2013)
(  0) 0) |
| [5] |
刘世存, 杨薇, 田凯, 等. 基于多层全连接神经网络的白洋淀水质预测[J]. 农业环境科学学报, 2020, 39(6): 1 283-1 292 (Liu Shicun, Yang Wei, Tian Kai, et al. Water Quality Forecasting Based on Multilayer Fully Connected Neural Network for Baiyangdian Lake[J]. Journal of Agro-Environment Science, 2020, 39(6): 1 283-1 292)
(  0) 0) |
| [6] |
Pak U, Ma J, Ryu U, et al. Deep Learning-Based PM2.5 Prediction Considering the Spatiotemporal Correlations: A Case Study of Beijing, China[J]. Science of the Total Environment, 2020, 699
(  0) 0) |
| [7] |
Yu P S, Yang T C, Chen S Y, et al. Comparison of Random Forests and Support Vector Machine for Real-Time Radar-Derived Rainfall Forecasting[J]. Journal of Hydrology, 2017, 552: 92-104 DOI:10.1016/j.jhydrol.2017.06.020
(  0) 0) |
| [8] |
仝卫国, 李敏霞, 张一可. 深度学习优化算法研究[J]. 计算机科学, 2018, 45((增2): 155-159 (Tong Weiguo, Li Minxia, Zhang Yike. Research on Optimization Algorithm of Deep Learning[J]. Computer Science, 2018, 45(S2): 155-159)
(  0) 0) |
| [9] |
Sutskever I, Martens J, Dahl G, et al. On the Importance of Initialization and Momentum in Deep Learning[C]. Proceeding of the 30th International Conference on Machine Learning, Atlanta, 2013
(  0) 0) |
| [10] |
Duchi J C, Hazan E, Singer Y, et al. Adaptive Subgradient Methods for Online Learning and Stochastic Optimization[J]. Journal of Machine Learning Research, 2011(12): 257-269
(  0) 0) |
| [11] |
Dauphin Y N, Vries H, Chung J, et al. RMSProp and Equilibrated Adaptive Learning Rates for Non-Convex Optimization[Z]. arXiv: Learning, 2015(2)
(  0) 0) |
| [12] |
Kingma D P, Ba J. Adam: A Method for Stochastic Optimization[Z]. arXiv: Learning, 2014(12)
(  0) 0) |
| [13] |
胡纪元, 文鸿雁, 周吕, 等. 基于IPSO-BP模型的大坝多源监测数据预报与反演[J]. 大地测量与地球动力学, 2014, 34(4): 67-70 (Hu Jiyuan, Wen Hongyan, Zhou Lü, et al. Study on Dam Prediction and Inversion with Multi-Source Monitoring Data Based on IPSO-BP Model[J]. Journal of Geodesy and Geodynamics, 2014, 34(4): 67-70)
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41


