2021, Vol. 41
应用分块矩阵求逆解算约束秩亏间接平差模型
1. 合肥职业技术学院建筑工程学院，合肥市姥山南路1号，238000;
2. 桂林理工大学博文管理学院，桂林市雁山街317号，541006
2. 桂林理工大学博文管理学院，桂林市雁山街317号，541006
摘要：在通常的四分块矩阵求广义逆矩阵和凯利逆矩阵公式基础上，分析左上角子矩阵为秩亏、右下角子矩阵为零的特殊四分块矩阵的凯利逆矩阵存在条件，应用广义逆矩阵法和矩阵变换法推导该类特殊四分块矩阵的凯利逆矩阵显性表达公式，并用于解算约束秩亏间接平差模型的参数估计。实验数据表明，当满足存在性条件时，应用分块矩阵求逆公式解算约束秩亏间接平差模型的结果与间接平差模型的解算结果一致，表明推导的显性表达公式具有可行性。
关键词：测量平差；分块矩阵；广义逆矩阵；约束秩亏间接平差模型
在经典测量平差模型中，将附有限制条件的间接平差模型作为概括平差函数模型[1]具有列立误差方程式规律性强、参数平差值即为结果、便于编程计算等优点[2]，但该模型中满秩的误差方程包含已知数据，约束方程也由已知数据建立，会混淆已知数据和观测数据2类不同性质的数据。若将平差系统中所有点作为未知参数，利用观测数据建立误差方程，用已知数据建立约束方程或基准方程，两者联合组成约束秩亏间接平差模型，不仅可有效区分观测数据和已知数据，并且在理解参考系效应和内部噪声、评定观测值的内部符合精度、分析已知数据对平差结果的影响[3-4]等方面具有明显优势。因此，约束秩亏间接平差模型被广泛应用于变形监测、近景摄影测量、GPS测量、地球参考框架建立[5-8]等大地测量数据处理中。
国内学者对解算约束秩亏间接平差模型的方法进行过大量研究[9-12]，本文在这些研究基础上进一步分析约束秩亏间接平差模型的法方程系数四分块矩阵结构，研究其凯利逆矩阵的存在条件和显性表达式，并验证公式的正确性，为解算约束秩亏间接平差模型提供简单准确的方法。
1 特殊分块矩阵求逆 1.1 引理[13]引理1 设N为u×u非负定矩阵，C为s×u矩阵，N'bb=N+CTC，N'cc=CN'bb-CT，则：
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{N}}&{{\mathit{\boldsymbol{C}}^{\rm{T}}}}\\ \mathit{\boldsymbol{C}}&0 \end{array}} \right]^ - } = \\ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{N'}}_{bb}^ - - \mathit{\boldsymbol{N'}}_{bb}^ - {\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{N'}}_{cc}^ - \mathit{\boldsymbol{CN'}}_{bb}^ - }&{\mathit{\boldsymbol{N'}}_{bb}^ - {\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{N'}}_{cc}^ - }\\ {\mathit{\boldsymbol{N'}}_{cc}^ - \mathit{\boldsymbol{CN'}}_{bb}^ - }&{\mathit{\boldsymbol{N'}}_{cc}^ - {{\mathit{\boldsymbol{N'}}}_{cc}} - \mathit{\boldsymbol{N'}}_{cc}^ - } \end{array}} \right] \end{array} $ | (1) |
引理2 设实矩阵
| $ {\mathit{\boldsymbol{A}}^{ - 1}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{A}}_{11}^{ - 1} + \mathit{\boldsymbol{A}}_{11}^{ - 1}{\mathit{\boldsymbol{A}}_{12}}{\mathit{\boldsymbol{B}}^{ - 1}}{\mathit{\boldsymbol{A}}_{21}}\mathit{\boldsymbol{A}}_{11}^{ - 1}}&{ - \mathit{\boldsymbol{A}}_{11}^{ - 1}{\mathit{\boldsymbol{A}}_{12}}{\mathit{\boldsymbol{B}}^{ - 1}}}\\ { - {\mathit{\boldsymbol{B}}^{ - 1}}{\mathit{\boldsymbol{A}}_{21}}\mathit{\boldsymbol{A}}_{11}^{ - 1}}&{{\mathit{\boldsymbol{B}}^{ - 1}}} \end{array}} \right] $ | (2) |
设存在四分块矩阵
1) R(C)=s，表示C为行满秩矩阵。如果C行秩亏，R(C⋮0)必行秩亏，
2)
| $ R\left( {\begin{array}{*{20}{l}} \mathit{\boldsymbol{N}}\\ \mathit{\boldsymbol{C}} \end{array}} \right) \le R(\mathit{\boldsymbol{N}}) + R(\mathit{\boldsymbol{C}}) $ | (3) |
即
| $ u \le r + s{\rm{ 或 }}u - r \le s $ | (4) |
式(4)表明，C的行数大于等于N的秩亏数。
1.3 定理及证明设存在四分块矩阵
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{N}}&{{\mathit{\boldsymbol{C}}^{\rm{T}}}}\\ \mathit{\boldsymbol{C}}&0 \end{array}} \right]^{ - 1}} = \\ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{N'}}_{bb}^{ - 1} - \mathit{\boldsymbol{N'}}_{bb}^{ - 1}{\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{N'}}_{cc}^{ - 1}\mathit{\boldsymbol{CN'}}_{bb}^{ - 1}}&{\mathit{\boldsymbol{N'}}_{bb}^{ - 1}{\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{N'}}_{cc}^{ - 1}}\\ {\mathit{\boldsymbol{N'}}_{cc}^{ - 1}\mathit{\boldsymbol{CN'}}_{bb}^{ - 1}}&{{\mathit{\boldsymbol{I}}_s} - \mathit{\boldsymbol{N'}}_{cc}^{ - 1}} \end{array}} \right] \end{array} $ | (5) |
本文将通过广义逆矩阵法和矩阵变换法2种方法验证该表达式。
1.3.1 广义逆矩阵法设N为u×u非负定矩阵，C为s×u矩阵，N'bb=N+CTC，可得：
| $ {\mathit{\boldsymbol{N'}}_{bb}} = \mathit{\boldsymbol{N}} + {\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{I}}&{{\mathit{\boldsymbol{C}}^{\rm{T}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{N}}\\ \mathit{\boldsymbol{C}} \end{array}} \right] $ | (6) |
式中，[I CT]为u×(u+s)行满秩矩阵，
根据矩阵分解性质[15]，存在u×u满秩矩阵A，使得行满秩矩阵：
| $ \left[ \begin{array}{*{35}{l}} \mathit{\boldsymbol{I}} & {{\mathit{\boldsymbol{C}}}^{\text{T}}} \\ \end{array} \right]=\underset{u\times u}{\mathop{\mathit{\boldsymbol{A}}}}\,\left[ \begin{array}{*{35}{l}} \underset{u\times u}{\mathop{\mathit{\boldsymbol{I}}}}\, & \underset{u\times s}{\mathop{0}}\, \\ \end{array} \right] $ | (7) |
式中，
同理，存在u×u满秩矩阵B，使得列满秩矩阵：
| $ \left[ \begin{matrix} \mathit{\boldsymbol{N}} \\ \mathit{\boldsymbol{C}} \\ \end{matrix} \right]=\left[ \begin{matrix} \underset{u\times u}{\mathop{\mathit{\boldsymbol{I}}}}\, \\ \underset{s\times u}{\mathop{0}}\, \\ \end{matrix} \right]\underset{u\times u}{\mathop{\mathit{\boldsymbol{B}}}}\, $ | (8) |
所以，
| $ \begin{align} & {{{\mathit{\boldsymbol{{N}'}}}}_{bb}}=\mathit{\boldsymbol{N}}+{{\mathit{\boldsymbol{C}}}^{\text{T}}}\mathit{\boldsymbol{C}}=\left[ \begin{array}{*{35}{l}} \mathit{\boldsymbol{I}} & {{\mathit{\boldsymbol{C}}}^{\text{T}}} \\ \end{array} \right]\left[ \begin{array}{*{35}{l}} \mathit{\boldsymbol{N}} \\ \mathit{\boldsymbol{C}} \\ \end{array} \right]= \\ & \underset{u\times u}{\mathop{\mathit{\boldsymbol{A}}}}\,\left[ \begin{array}{*{35}{l}} \underset{u\times u}{\mathop{\mathit{\boldsymbol{I}}}}\, & \underset{u\times s}{\mathop{0}}\, \\ \end{array} \right]\left[ \begin{array}{*{35}{l}} \underset{u\times u}{\mathop{\mathit{\boldsymbol{I}}}}\, \\ \underset{s\times u}{\mathop{0}}\, \\ \end{array} \right]\underset{u\times u}{\mathop{\mathit{\boldsymbol{B}}}}\,=\underset{u\times u}{\mathop{\mathit{\boldsymbol{A}}}}\,\underset{u\times u}{\mathop{\mathit{\boldsymbol{B}}}}\, \\ \end{align} $ | (9) |
由于A、B均为u×u满秩矩阵，N'bb必满秩可逆，且
| $ R\left( {{{\mathit{\boldsymbol{N'}}}_w}} \right) = R\left( {\mathit{\boldsymbol{N'}}_{bb}^{ - 1}} \right) = u $ | (10) |
上述推算过程和结果表明，s×u行满秩矩阵和u×s列满秩矩阵相乘后可得s×s满秩矩阵。
根据矩阵秩基本性质[16]可知，任意矩阵左乘列满秩矩阵和右乘行满秩矩阵，该矩阵的秩不变。因此，s×u矩阵C右乘u×u行满秩矩阵N'bb-1得到的s×u矩阵CN'bb-1和矩阵C的秩均为s，所以CN'bb-1为s×u行满秩矩阵。
s×u行满秩矩阵CN'bb-1和u×s列满秩矩阵CT相乘得到s×s满秩矩阵CN'bb-1CT，因此，N'cc=CN'bb-1CT必满秩可逆。
根据广义逆的定义，凯利逆为广义逆的特殊逆，因此凯利逆N'bb-1、N'cc-1必满足引理1，将之代入式(1)可得：
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{N}}&{{\mathit{\boldsymbol{C}}^{\rm{T}}}}\\ \mathit{\boldsymbol{C}}&0 \end{array}} \right]^{ - 1}} = \\ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{N'}}_{bb}^ - - \mathit{\boldsymbol{N'}}_{bb}^ - {\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{N'}}_{cc}^ - \mathit{\boldsymbol{CN'}}_{bb}^ - }&{\mathit{\boldsymbol{N'}}_{bb}^ - {\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{N'}}_{cc}^ - }\\ {\mathit{\boldsymbol{N'}}_{cc}^ - \mathit{\boldsymbol{CN'}}_{bb}^ - }&{\mathit{\boldsymbol{N'}}_{cc}^ - {{\mathit{\boldsymbol{N'}}}_{cc}} - \mathit{\boldsymbol{N'}}_{cc}^ - } \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{N'}}_{bb}^{ - 1} - \mathit{\boldsymbol{N'}}_{bb}^{ - 1}{\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{N'}}_{cc}^{ - 1}\mathit{\boldsymbol{CN'}}_{bb}^{ - 1}}&{\mathit{\boldsymbol{N'}}_{bb}^{ - 1}{\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{N'}}_{cc}^{ - 1}}\\ {\mathit{\boldsymbol{N'}}_{cc}^{ - 1}\mathit{\boldsymbol{CN'}}_{bb}^{ - 1}}&{{\mathit{\boldsymbol{I}}_s} - \mathit{\boldsymbol{N'}}_{cc}^{ - 1}} \end{array}} \right] \end{array} $ | (11) |
得证。
1.3.2 矩阵变换法设
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{N}}&{{\mathit{\boldsymbol{C}}^{\rm{T}}}}\\ \mathit{\boldsymbol{C}}&0 \end{array}} \right]^{ - 1}} = \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{Q}}_{11}}}&{{\mathit{\boldsymbol{Q}}_{12}}}\\ {{\mathit{\boldsymbol{Q}}_{21}}}&{{\mathit{\boldsymbol{Q}}_{22}}} \end{array}} \right]\\ {\rm{或}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{N}}&{{\mathit{\boldsymbol{C}}^{\rm{T}}}}\\ \mathit{\boldsymbol{C}}&0 \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{{\bf{Q}}_{11}}}&{{\mathit{\boldsymbol{Q}}_{12}}}\\ {{\mathit{\boldsymbol{Q}}_{21}}}&{{\mathit{\boldsymbol{Q}}_{22}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}_u}}&{\mathop 0\limits_{u \times s} }\\ {\mathop 0\limits_{s \times u} }&{{\mathit{\boldsymbol{I}}_s}} \end{array}} \right] \end{array} $ | (12) |
则：
| $ \mathit{\boldsymbol{N}}{{\mathit{\boldsymbol{Q}}}_{11}}+{{\mathit{\boldsymbol{C}}}^{\text{T}}}{{\mathit{\boldsymbol{Q}}}_{21}}={{\mathit{\boldsymbol{I}}}_{u}} $ | (13) |
| $ \mathit{\boldsymbol{N}}{{\mathit{\boldsymbol{Q}}}_{12}}+{{\mathit{\boldsymbol{C}}}^{\text{T}}}{{\mathit{\boldsymbol{Q}}}_{22}}=\underset{u\times s}{\mathop{0}}\, $ | (14) |
| $ \mathit{\boldsymbol{C}}{{\mathit{\boldsymbol{Q}}}_{11}}=\underset{s\times u}{\mathop{0}}\, $ | (15) |
| $ \mathit{\boldsymbol{C}}{{\mathit{\boldsymbol{Q}}}_{12}}={{\mathit{\boldsymbol{I}}}_{s}} $ | (16) |
在式(15)左乘CT与式(13)相加可得：
| $ \left( \mathit{\boldsymbol{N}}+{{\mathit{\boldsymbol{C}}}^{\text{T}}}\mathit{\boldsymbol{C}} \right){{\mathit{\boldsymbol{Q}}}_{11}}+{{\mathit{\boldsymbol{C}}}^{\text{T}}}{{\mathit{\boldsymbol{Q}}}_{21}}={{\mathit{\boldsymbol{I}}}_{u}} $ | (17) |
同理，将式(16)左乘CT再与式(14)相加可得：
| $ \left( \mathit{\boldsymbol{N}}+{{\mathit{\boldsymbol{C}}}^{\text{T}}}\mathit{\boldsymbol{C}} \right){{\mathit{\boldsymbol{Q}}}_{12}}+{{\mathit{\boldsymbol{C}}}^{\text{T}}}\left( {{\mathit{\boldsymbol{Q}}}_{22}}-{{\mathit{\boldsymbol{I}}}_{s}} \right)=\underset{u\times s}{\mathop{0}}\, $ | (18) |
联立式(15)~式(18)，用矩阵形式可表示为：
| $ \left[ \begin{matrix} \mathit{\boldsymbol{N}}+{{\mathit{\boldsymbol{C}}}^{\text{T}}}\mathit{\boldsymbol{C}} & {{\mathit{\boldsymbol{C}}}^{\text{T}}} \\ \mathit{\boldsymbol{C}} & 0 \\ \end{matrix} \right]\left[ \begin{array}{*{35}{c}} {{\mathit{\boldsymbol{Q}}}_{11}} & {{\mathit{\boldsymbol{Q}}}_{12}} \\ {{\mathit{\boldsymbol{Q}}}_{21}} & {{\mathit{\boldsymbol{Q}}}_{22}}-{{\mathit{\boldsymbol{I}}}_{s}} \\ \end{array} \right]=\left[ \begin{matrix} {{\mathit{\boldsymbol{I}}}_{u}} & \underset{u\times s}{\mathop{0}}\, \\ \underset{s\times u}{\mathop{0}}\, & {{\mathit{\boldsymbol{I}}}_{s}} \\ \end{matrix} \right] $ | (19) |
式(19)四分块矩阵
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Q}}_{11}}}&{{\mathit{\boldsymbol{Q}}_{12}}}\\ {{\mathit{\boldsymbol{Q}}_{21}}}&{{\mathit{\boldsymbol{Q}}_{22}} - {\mathit{\boldsymbol{I}}_s}} \end{array}} \right] = {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{N}} + {\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{C}}}&{{\mathit{\boldsymbol{C}}^{\rm{T}}}}\\ \mathit{\boldsymbol{C}}&0 \end{array}} \right]^{ - 1}} = \\ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{N'}}_{bb}^{ - 1} - \mathit{\boldsymbol{N'}}_{bb}^{ - 1}{\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{N'}}_{cc}^{ - 1}\mathit{\boldsymbol{CN'}}_{bb}^{ - 1}}&{\mathit{\boldsymbol{N'}}_{bb}^{ - 1}{\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{N'}}_{cc}^{ - 1}}\\ {\mathit{\boldsymbol{N'}}_{cc}^{ - 1}\mathit{\boldsymbol{CN'}}_{bb}^{ - 1}}&{{\mathit{\boldsymbol{I}}_s} - \mathit{\boldsymbol{N'}}_{cc}^{ - 1}} \end{array}} \right] \end{array} $ | (20) |
可得：
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{N}}&{{\mathit{\boldsymbol{C}}^{\rm{T}}}}\\ \mathit{\boldsymbol{C}}&0 \end{array}} \right]^{ - 1}} = \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{Q}}_{11}}}&{{\mathit{\boldsymbol{Q}}_{12}}}\\ {{\mathit{\boldsymbol{Q}}_{21}}}&{{\mathit{\boldsymbol{Q}}_{22}}} \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{N'}}_{bb}^{ - 1} - \mathit{\boldsymbol{N'}}_{bb}^{ - 1}{\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{N'}}_{cc}^{ - 1}\mathit{\boldsymbol{CN'}}_{bb}^{ - 1}}&{\mathit{\boldsymbol{N'}}_{bb}^{ - 1}{\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{N'}}_{cc}^{ - 1}}\\ {\mathit{\boldsymbol{N'}}_{cc}^{ - 1}\mathit{\boldsymbol{CN'}}_{bb}^{ - 1}}&{{\mathit{\boldsymbol{I}}_s} - \mathit{\boldsymbol{N'}}_{cc}^{ - 1}} \end{array}} \right] \end{array} $ | (21) |
得证。
2 约束秩亏间接平差模型参数的应用 2.1 约束秩亏间接平差模型的参数估计约束秩亏间接平差模型可表示为：
| $ \underset{n\times 1}{\mathop{\mathit{\boldsymbol{V}}}}\,=\underset{n\times u}{\mathop{\mathit{\boldsymbol{B}}}}\,\underset{u\times 1}{\mathop{{\mathit{\boldsymbol{\hat{X}}}}}}\,-\underset{n\times 1}{\mathop{\mathit{\boldsymbol{L}}}}\, $ | (22) |
| $ \underset{s\times u}{\mathop{\mathit{\boldsymbol{C}}}}\,\underset{u\times 1}{\mathop{{\mathit{\boldsymbol{\hat{X}}}}}}\,=\underset{s\times 1}{\mathop{{{\mathit{\boldsymbol{W}}}_{X}}}}\, $ | (23) |
式(22)为秩亏间接平差模型的误差方程，V为n维观测误差向量，E(V)=0，D(V)=σ2P-1，B为误差方程的n×u系数矩阵，R(B)=r < u，u为未知参数个数，
上述参数估计为约束条件下的极值求解问题，按照拉格朗日乘数法构造函数：
| $ {\varphi = {\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{PV}} + 2{\mathit{\boldsymbol{K}}^{\rm{T}}}\left( {\mathit{\boldsymbol{C\hat X}} - {\mathit{\boldsymbol{W}}_X}} \right)} $ | (24) |
式中，K为对应于约束方程的s×1常数向量。解算该函数的极小值，只需令
| $ {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PB\hat X}} - {\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PL}} + {\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{K}} = 0} $ | (25) |
| $ {\mathit{\boldsymbol{C\hat X}} - {\mathit{\boldsymbol{W}}_X} = 0} $ | (26) |
令
| $ {\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{N}}&{{\mathit{\boldsymbol{C}}^{\rm{T}}}}\\ \mathit{\boldsymbol{C}}&0 \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\hat X}}}\\ \mathit{\boldsymbol{K}} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{W}}\\ {{\mathit{\boldsymbol{W}}_X}} \end{array}} \right] = 0} $ | (27) |
则：
| $ {\left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\hat X}}}\\ \mathit{\boldsymbol{K}} \end{array}} \right] = {{\left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{N}}&{{\mathit{\boldsymbol{C}}^{\rm{T}}}}\\ \mathit{\boldsymbol{C}}&0 \end{array}} \right]}^{ - 1}}\left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{W}}\\ {{\mathit{\boldsymbol{W}}_X}} \end{array}} \right]} $ | (28) |
式中，N为u×u阶秩亏矩阵，R(N)=R(B)=t < u，四分块矩阵无法应用通常的用分块矩阵求凯利逆的方法求解逆矩阵，但在满足存在条件1)和2)的情况下，采用本文推导的该类特殊四分块矩阵求解逆矩阵可得：
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\hat X}}}\\ \mathit{\boldsymbol{K}} \end{array}} \right] = {\left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{N}}&{{\mathit{\boldsymbol{C}}^{\rm{T}}}}\\ \mathit{\boldsymbol{C}}&0 \end{array}} \right]^{ - 1}}\left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{W}}\\ {{\mathit{\boldsymbol{W}}_X}} \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{N'}}_{bb}^{ - 1} - \mathit{\boldsymbol{N'}}_{bb}^{ - 1}{\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{N'}}_{cc}^{ - 1}\mathit{\boldsymbol{CN'}}_{bb}^{ - 1}}&{\mathit{\boldsymbol{N'}}_{bb}^{ - 1}{\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{N'}}_{cc}^{ - 1}}\\ {\mathit{\boldsymbol{N'}}_{cc}^{ - 1}\mathit{\boldsymbol{CN'}}_{bb}^{ - 1}}&{{\mathit{\boldsymbol{I}}_s} - \mathit{\boldsymbol{N'}}_{cc}^{ - 1}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{W}}\\ {{\mathit{\boldsymbol{W}}_X}} \end{array}} \right] \end{array} $ | (29) |
展开得：
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{X}} = \left( {{\mathit{\boldsymbol{N}}^{\prime - 1}} - \mathit{\boldsymbol{N}}_{bb}^{\prime - 1}{\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{N}}_{cc}^{\prime - 1}\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{N}}^{\prime - 1}}} \right)\mathit{\boldsymbol{W}} + }\\ {\mathit{\boldsymbol{N}}_{bb}^{\prime - 1}{\mathit{\boldsymbol{C}}^{\rm{T}}}{\mathit{\boldsymbol{N}}^{\prime - 1}}{\mathit{\boldsymbol{W}}_X} = \{ {{(\mathit{\boldsymbol{N}} + {\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{C}})}^{ - 1}} - }\\ {{{\left( {\mathit{\boldsymbol{N}} + {\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{C}}} \right)}^{ - 1}}{\mathit{\boldsymbol{C}}^{\rm{T}}}{{\left[ {\mathit{\boldsymbol{C}}\left( {\mathit{\boldsymbol{N}} + {\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{C}}} \right){\mathit{\boldsymbol{C}}^{\rm{T}}}} \right]}^{ - 1}}}\\ {\left. {\mathit{\boldsymbol{C}}{{\left( {\mathit{\boldsymbol{N}} + {\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{C}}} \right)}^{ - 1}}} \right\}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PL}} + {{\left( {\mathit{\boldsymbol{N}} + {\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{C}}} \right)}^{ - 1}}{\mathit{\boldsymbol{C}}^{\rm{T}}}}\\ {{{\left[ {\mathit{\boldsymbol{C}}\left( {\mathit{\boldsymbol{N}} + {\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{C}}} \right){\mathit{\boldsymbol{C}}^{\rm{T}}}} \right]}^{ - 1}}{\mathit{\boldsymbol{W}}_X}} \end{array} $ | (30) |
式(30)即为约束秩亏间接平差模型参数估计的一般显性表达式。
2.2 数值算例在图 1所示的水准网中，已知水准点A和B的高程分别为HA=237.483 m、HB=233.868 m，为求P1、P2点的高程，进行水准测量，表 1为测量高差和水准路线。分别采用约束秩亏间接平差模型和间接平差模型解算待求点P1、P2的高程，并对结果进行比较。
|
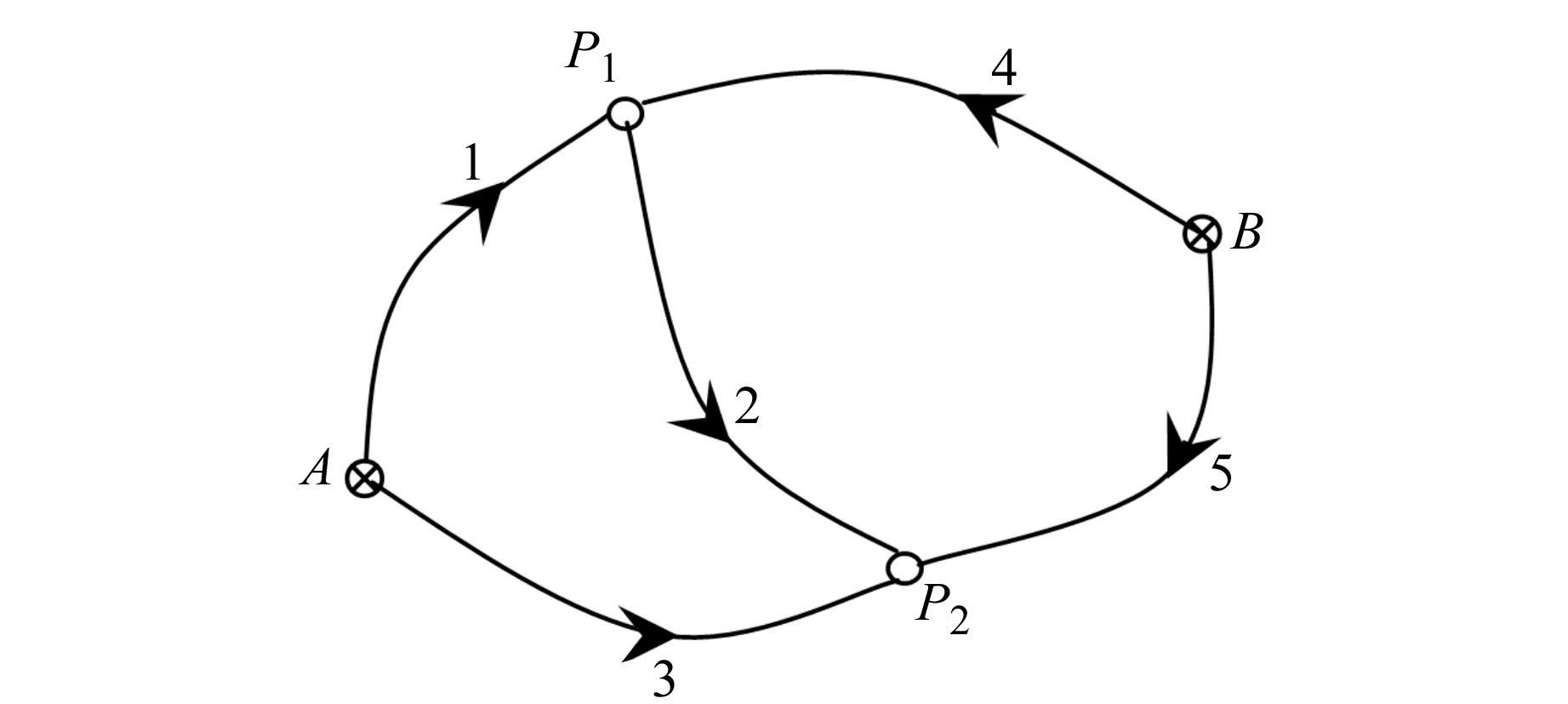
图 1 水准网 Fig. 1 Leveling network |
|
表 1 观测数据 Tab. 1 Observation data |
设A、B、P1、P2点的高程为未知参数
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{v_1}}\\ {{v_2}}\\ {{v_3}}\\ {{v_4}}\\ {{v_5}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - 1}&0&1&0\\ 0&0&{ - 1}&1\\ { - 1}&0&0&1\\ 0&{ - 1}&1&0\\ 0&{ - 1}&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\hat x}_1}}\\ {{{\hat x}_2}}\\ {{{\hat x}_3}}\\ {{{\hat x}_4}} \end{array}} \right] - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{r}} {3.782}\\ { - 9.640}\\ { - 5.835}\\ {7.384}\\ { - 2.270} \end{array}} \right] \Leftrightarrow \mathit{\boldsymbol{V}} = \mathit{\boldsymbol{B\hat X}} - \mathit{\boldsymbol{L}} \end{array} $ |
式中，未知参数的系数矩阵B为列秩亏，符号表示等价的矩阵形式。
A、B为已知点，可以组成限制条件方程：
| $ \begin{array}{*{20}{l}} {\left[ {\begin{array}{*{20}{l}} 1&0&0&0\\ 0&1&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{{\hat x}_1}}\\ {{{\hat x}_2}}\\ {{{\hat x}_3}}\\ {{{\hat x}_4}} \end{array}} \right] = }\\ {\left[ {\begin{array}{*{20}{l}} {237.483}\\ {233.868} \end{array}} \right] \Leftrightarrow \mathit{\boldsymbol{C\hat X}} = {\mathit{\boldsymbol{W}}_X}} \end{array} $ |
按观测距离定义观测值的权重，并令1 km的观测高差为单位权，则观测值的权阵为：
| $ \mathit{\boldsymbol{P}} = {\mathop{\rm diag}\nolimits} \left[ {\begin{array}{*{20}{l}} {1/2.0}&{1/1.0}&{1/2.0}&{1/2.0}&{1/2.0} \end{array}} \right] $ |
通过分析可知，上述误差方程式系数矩阵B秩亏数为1，限制条件方程系数C为行满秩，条件方程个数为2，大于秩亏数，满足存在性条件。
将已知参数B、P、L、C、WX代入本文推导的约束秩亏间接平差模型参数估计公式(30)，计算可得：
| $ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\left[ {\begin{array}{*{20}{l}} {{{\hat x}_1}}&{{{\hat x}_2}}&{{{\hat x}_3}}&{{{\hat x}_4}} \end{array}} \right]}^{\rm{T}}} = }\\ {{{\left[ {\begin{array}{*{20}{l}} {237.483}&{233.868}&{241.260}&{231.622} \end{array}} \right]}^{\rm{T}}}} \end{array} $ |
式中，
考虑A、B为已知点，设P1、P2点的高程为未知参数
| $ \begin{array}{c} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} {{v_1}}\\ {{v_2}}\\ {{v_3}}\\ {{v_4}}\\ {{v_5}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&0\\ { - 1}&1\\ 0&1\\ 1&0\\ 0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\hat x}_3}}\\ {{{\hat x}_4}} \end{array}} \right] - \\ \left[ {\begin{array}{*{20}{c}} {241.265}\\ { - 9.640}\\ {231.648}\\ {241.252}\\ {231.598} \end{array}} \right] \Leftrightarrow \mathit{\boldsymbol{V}} = \mathit{\boldsymbol{B\hat X}} - \mathit{\boldsymbol{L}} \end{array} $ |
同理，按观测距离定义观测值的权重。
根据最小二乘原则，将已知参数B、P、L代入，解算得：
| $ \left[ {\begin{array}{*{20}{l}} {{{\hat x}_3}}\\ {{{\hat x}_4}} \end{array}} \right] = {\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PB}}} \right)^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PL}} = \left[ {\begin{array}{*{20}{l}} {241.260}\\ {231.622} \end{array}} \right] $ |
由上述计算过程和结果可知，约束秩亏间接平差模型的分块矩阵求逆公式和间接平差模型对未知点P1、P2的参数估计
1) 本文对左上角子矩阵秩亏、右下角子矩阵为零的特殊四分块矩阵进行分析，在满足左下角子矩阵为行满秩及行数大于左上角子矩阵秩亏数的条件下，证明其存在凯利逆矩阵，该存在条件可为自由网附加条件法的平差提供理论依据。
2) 在通常的四分块矩阵求广义逆矩阵和凯利逆矩阵公式的基础上，利用广义逆矩阵法和矩阵变换法推导该类特殊四分块矩阵凯利逆矩阵的显性表达式。该公式可用于解算约束秩亏间接平差模型的参数估计，为约束秩亏间接平差模型的解算提供简单准确的方法，具有理论和应用价值。
参考文献
| [1] |
王新洲. 论经典测量平差模型的内在联系[J]. 测绘通报, 2004(2): 1-4 (Wang Xinzhou. On the Internal Relations of Classical Surveying Adjustment Models[J]. Bulletin of Surveying and Mapping, 2004(2): 1-4 DOI:10.3969/j.issn.0494-0911.2004.02.001)
(  0) |
| [2] |
於宗俦, 于正林. 测量平差原理[M]. 武汉: 武汉测绘科技大学出版社, 1990 (Yu Zongchou, Yu Zhenglin. Principle of Surveying Adjustment[M]. Wuhan: Wuhan Technical University of Surveying and Mapping Press, 1990)
( 0) |
| [3] |
张西光.地球参考框架的理论与方法[D].郑州: 信息工程大学, 2009 (Zhang Xiguang. Theory and Algorithms of Terrestrial Reference Frame[D]. Zhengzhou: Information Engineering University, 2009)
( 0) |
| [4] |
黄维彬. 近代平差理论及其应用[M]. 北京: 解放军出版社, 1992 (Huang Weibin. Modern Adjustment Theory and Its Application[M]. Beijing: PLA Press, 1992)
( 0) |
| [5] |
黄声享, 尹晖, 蒋征. 变形监测数据处理[M]. 武汉: 武汉大学出版社, 2003 (Huang Shengxiang, Yin Hui, Jiang Zheng. Deformation Monitoring Data Processing[M]. Wuhan: Wuhan University Press, 2003)
( 0) |
| [6] |
郭迎钢.工业摄影测量网形优化设计[D].郑州: 信息工程大学, 2017 (Guo Yinggang. Optimization Design for Industrial Photogrammetric Network[D]. Zhengzhou: Information Engineering University, 2017)
( 0) |
| [7] |
李征航, 黄劲松. GPS测量与数据处理[M]. 武汉: 武汉大学出版社, 2010 (Li Zhenghang, Huang Jinsong. GPS Surveying and Data Processing[M]. Wuhan: Wuhan University Press, 2010)
( 0) |
| [8] |
曾安敏.地球参考框架确定与维持的数据处理理论与算法研究[D].郑州: 信息工程大学, 2017 (Zeng Anmin. Research on Fusion Algorithm for Establishment and Maintenance of Terrestrial Reference Frame[D]. Zhengzhou: Information Engineering University, 2017)
( 0) |
| [9] |
秦永宽, 黄声享, 张书毕. 附有限制条件的间接平差秩亏时解法初探[J]. 海洋测绘, 2009, 29(1): 7-9 (Qin Yongkuan, Huang Shengxiang, Zhang Shubi. The New Solution of Rank-Defective Indirect Adjustment with Constraints[J]. Hydrographic Surveying and Charting, 2009, 29(1): 7-9)
( 0) |
| [10] |
赵海涛, 郭广礼, 查剑锋. 附有限制条件间接平差的虚拟观测算法[J]. 测绘科学, 2008, 33(2): 33-34 (Zhao Haitao, Guo Guangli, Zha Jianfeng. The Virtual Observation Algorithm with Restriction Condition Parameter Adjustment[J]. Science of Surveying and Mapping, 2008, 33(2): 33-34)
( 0) |
| [11] |
谢建, 朱建军. 约束秩亏自由网平差的一种新算法[J]. 测绘工程, 2009, 18(2): 9-11 (Xie Jian, Zhu Jianjun. A New Approach to Constrained Rank-Defective Free Network Adjustment[J]. Engineering of Surveying and Mapping, 2009, 18(2): 9-11)
( 0) |
| [12] |
陶本藻. 自由网平差与变形分析[M]. 武汉: 武汉测绘科技大学出版社, 2001 (Tao Benzao. Free Network Adjustment and Deformation Analysis[M]. Wuhan: Wuhan Technical University of Surveying and Mapping Press, 2001)
( 0) |
| [13] |
王松桂, 杨振海. 广义逆矩阵及其应用[M]. 北京: 北京工业大学出版社, 1996 (Wang Songgui, Yang Zhenhai. Generalized Inverse Matrix and Its Applications[M]. Beijing: Beijing University of Technology Press, 1996)
( 0) |
| [14] |
Rao C R. Linear Statistical Inference and Its Applications[M]. New Jersey: Wiley Interscience, 1973
( 0) |
| [15] |
杨明, 刘先忠. 矩阵论[M]. 武汉: 华中科技大学出版社, 2005 (Yang Ming, Liu Xianzhong. Matrix Theory[M]. Wuhan: Huazhong University of Science and Technology Press, 2005)
( 0) |
| [16] |
王松桂, 贾忠贞. 矩阵论中不等式[M]. 合肥: 安徽教育出版社, 1994 (Wang Songgui, Jia Zhongzhen. Inequalities in Matrix Theory[M]. Hefei: Anhui Education Press, 1994)
( 0) |
Calculation of Rank-Defective Indirect Adjustment Model with Constraint by Inverting Block Matrix
1. School of Civil Engineering and Architecture, Hefei Technology College, 1 South-Laoshan Road, Hefei 238000, China;
2. Bowen College of Management, Guilin University of Technology, 317 Yanshan Street, Guilin 541006, China
2. Bowen College of Management, Guilin University of Technology, 317 Yanshan Street, Guilin 541006, China
Abstract: Based on the general formula of generalized inverse matrix and Kelly inverse four block matrix, we analyze the existence conditions of a special kind of Kelly inverse four block matrix with a rank defective sub-block matrix in the upper left corner and a zero sub-block matrix in the lower right corner. The explicit expression formula of a Kelly inverse matrix of this kind is derived using the generalized inverting matrix method and the matrix transformation method, and is applied to the parameter estimation of rank-defective indirect adjustment model with constraints. The results show that when existence conditions are satisfied, the solution of rank-defective indirect adjustment model with constraints by inverting block matrix is consistent with that of the indirect adjustment model. This proves that the derived explicit expression formula is feasible.
Key words:
survey adjustment; block matrix; generalized inverse matrix; rank-defective indirect adjustment model with constraint