降雨的发生受多种气象变量、位置和季节的影响[1],近年来,基于GNSS技术反演PWV并研究其与降雨间的相关关系逐渐发展成为新的研究领域,一些学者根据降雨发生前PWV的异常变化特征,构建基于最小二乘法的简单短临降雨预测模型,以描述PWV与降雨间的相互关系[2-4]。
支持向量机(SVM)的相似版本——最小二乘支持向量机(LS-SVM)由Suykens等于1999年提出。SVM算法需要不敏感损失函数ε来解决特征空间中的凸二次规划问题,而LS-SVM仅需最小二乘损失函数以获取高维空间中一组线性等式,进而提高学习速率并降低SVM中凸规划的复杂度。此外,相比于SVM算法中惩罚参数、核参数sig2及不敏感损失函数ε等3种关键参数复杂的选取策略,LS-SVM仅需确定正则参数gam及径向基函数(RBF)参数sig2即可构建相应模型[5]。LS-SVM算法已成为一种解决非线性分类、函数估计及回归的重要理论,并被应用于多种学科[6-7]。
传统的简单降雨预测模型基于最小二乘原理拟合PWV/ZTD时变信息,以预测未来短期内发生的降雨事件。该类降雨预测模型普遍存在的缺陷是:1)降雨预测因子(PWV/ZTD)单一; 2)降雨预测精度较低,预测正确率仅为80%,错报率介于60~70%之间[2-4]。因此,本文首次将LS-SVM算法用于构建短临降雨预测模型,将多种与降雨相关的气象参数添加进训练样本,并分别从以上两个方面改进传统降雨预测模型。
1 理论和数据 1.1 GNSS获取PWVGNSS信号穿过对流层时会受中性大气延迟效应的影响,测站天顶总延迟(ZTD)可由信号倾斜路径总延迟(STD)通过映射函数投影至天顶方向得到。本文使用全球投影函数(GMF)将不同高度角的卫星信号投影至GNSS测站天顶方向,并忽略测站卫星信号弯曲的影响[8]。
ZTD主要由天顶静力延迟(ZHD)和天顶湿延迟(ZWD)组成[9],其中ZHD可通过saastamoinen模型求解。ZTD与ZHD之差即为ZWD,PWV与ZWD之间的转换公式为:
| $ \mathrm{PWV}=\frac{\xi \times \mathrm{ZWD}}{\rho} $ | (1) |
式中,ρ为液态水密度; ξ为PWV和ZWD之间的转换参数[10]:
| $ \begin{aligned} \xi=\left[-1 \times S_{\mathrm{GN}}(L) \times 1.7 \times 10^{-5}|L|^{H_{\mathrm{SN}}}-\right.\\ 0.0001] \times \cos \left(\frac{\mathrm{doy}-28}{365.25} \times 2 \pi\right)+\\ \left[\begin{array}{lll} 0.165-\left(1.7 \times 10^{-5}\right) & |L|^{1.65} \end{array}\right]+R \end{aligned} $ | (2) |
式中,L为测站纬度; doy为年积日。当GNSS测站位于南/北半球时,HSN分别为1.25和1.48,SGN(L)分别为-1和1。通过式(1)和式(2),可计算精度在±1 mm范围内的PWV时间序列[10]。
1.2 最小二乘支持向量机LS-SVM主要应用于解决非线性问题和分类及回归问题。假设样本数据集
| $ z(x)=\mathit{\boldsymbol{w}}^{\mathrm{T}} \vartheta(x)+b $ | (3) |
式中,w为权重向量;
| $ \min \left(\frac{1}{2} \boldsymbol{w}^{\mathrm{T}} \boldsymbol{w}+\frac{1}{2} \delta \sum\limits_{I=1}^{N} \xi_{I}^{2}\right) $ | (4) |
式中,δ为正则化参数,作用为平衡模型的复杂性和精度; ξI为输入向量xI的训练误差。式(4)对应的约束条件为:
| $ z_{I}= \mathit{\boldsymbol{w}}^{\mathrm{T}} \vartheta\left(x_{I}\right)+b+\xi_{I}, I=1, 2, \cdots, N $ | (5) |
与SVM不同的是,LS-SVM使用等式约束而非不等式约束。基于上述等式,拉格朗日函数可表示为:
| $\begin{array}{c} L\left(w, b, \xi_{I}, \alpha_{I}\right)=\frac{1}{2} \boldsymbol{w}^{\mathrm{T}} \boldsymbol{w}+\delta \sum\limits_{I=1}^{N} \xi_{I}^{2}- \\ \sum\limits_{I=1}^{N} \alpha_{I}\left(\boldsymbol{w}^{\mathrm{T}} \vartheta(x)+b-z_{I}+\xi_{I}\right) \end{array} $ | (6) |
式中,αI为拉格朗日乘子。函数逼近模型为:
| $z(x)=\sum\limits_{I=1}^{N} \alpha_{I} K\left(x, \mathit{\boldsymbol{x}}_{I}\right)+b $ | (7) |
式中,K(x, xI)为核函数,本文使用径向基函数。
1.3 数据简述选取南洋理工大学和新加坡国立大学2个GNSS并址气象站(NTUS和SNUS)2010~2012年的数据,其中GNSS数据经GIPSY/ OASIS Ⅱ处理得到ZTD数据[11],ZHD数据经saastamoinen经验模型计算得到,PWV数据经式(1)计算得到。NTUS站气象数据有温度(T)、相对湿度(RH)、露点温度(DPT),SNUS站气象数据有气压(P)、温度(T)、相对湿度(RH)。此外,新加坡地区的降雨主要受季节影响,大多发生在东北雨季及西南雨季期间,强对流型降雨出现在东北雨季的傍晚时段。因此,本文考虑将年积日(doy)和天积时(hod)作为与降雨相关的时间参数。
2 气象参数特征分析 2.1 参数时序分析降雨的发生受多种气象参数的影响,选择与降雨相关性高、易获取的气象参数对构建精度高、适用性强的LS-SVM降雨预测模型有很大帮助。图 1和2分别为NTUS站和SNUS站降雨及其相关气象参数的时变序列。由图可知,降雨发生前,PWV、RH、P及T都出现上升趋势; 降雨发生时都表现出下降的趋势,且T的下降速率及幅度均大于PWV; 而RH在降雨发生时表现出上升的趋势,DPT则表现出与之相反的变化趋势。
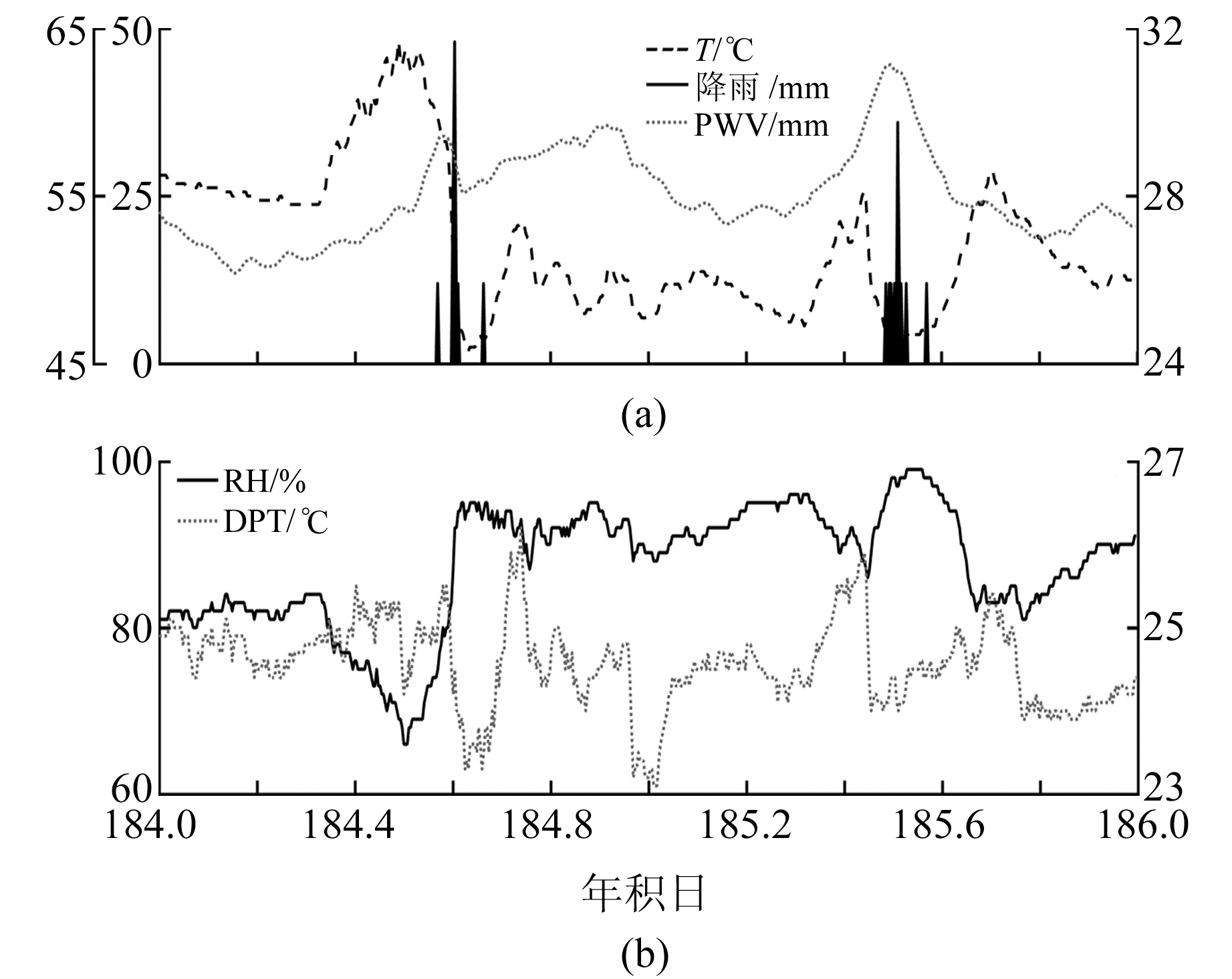
|
图 1 NTUS站2012年doy184~186降雨及其相关气象参数的时变序列 Fig. 1 The time series of rainfall and its correlated meteorological parameters at NTUS station over the period of doy 184-186 in 2012 |

|
图 2 SNUS站2011年doy237~239降雨及其相关气象参数的时变序列 Fig. 2 The time series of rainfall and its correlated meteorological parameters at SNUS station over the period of doy 237-239 in 2011 |
图 3为2010~2012年2个测站降雨及多种参数(doy、hod、T、DPT、RH、PWV)的相关系数示意图,可以看出,NTUS站中T和RH表现出强负相关特征,相关系数为-0.89;T和DPT的相关系数为0.5,表现出中等正相关特征; DPT和doy、RH和PWV及T和hod都表现出弱正相关特征,相关系数约为0.3。此外,降雨与气象参数间并无弱及以上相关性特征,表明降雨与本文所选气象参数相关性较弱,还可能与其他气象参数相关。同时PWV与降雨并未表现出强相关性特征,表明传统降雨预测模型仅依靠PWV不能达到构建高精度降雨预测模型的目的。
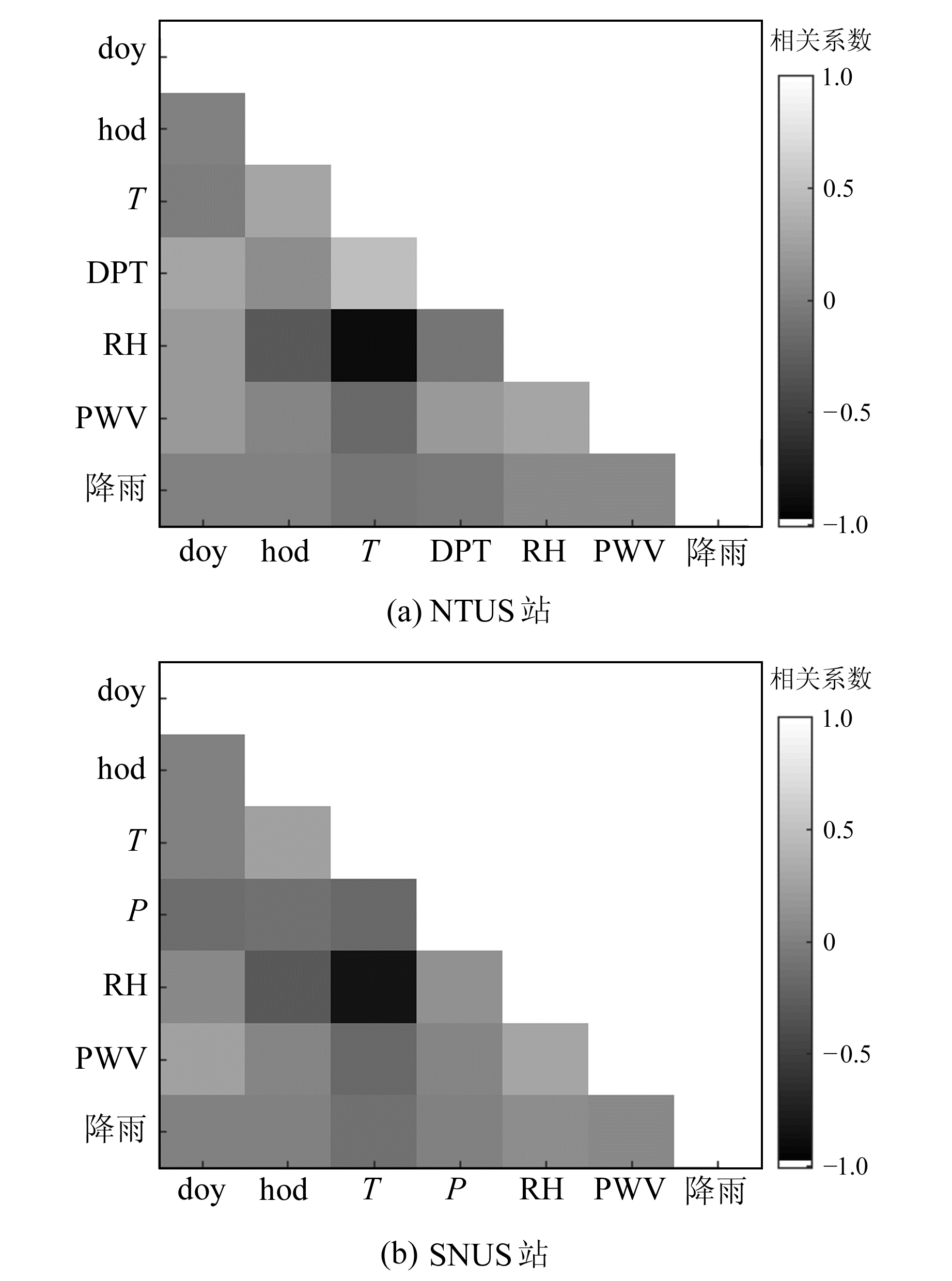
|
图 3 气象参数、时间参数与降雨间相关系数示意图 Fig. 3 Correlation coefficient between rainfall and meteorological parameters, time parameters |
LS-SVM降雨预测的实验流程主要分为模型构建、仿真实验和预测实验3个部分。1)模型构建:首先对训练数据进行均衡处理和归一化处理,同时对缺失数据进行删除。设置决定LS-SVM模型精度的正则化参数gam及RBF核参数sig2的范围,在将训练数据样本输入LS-SVM模型之前需要将降雨数据和PWV/气象数据分开并设置时差为55 min,目的是构建当前PWV/气象数据与未来55 min降雨事件间的高维非线性关系(基于LS-SVM模型)。由于大多数降雨持续时间超过35 min,因此降雨预测时间区间扩展为未来20~90 min。最后将训练样本输入LS-SVM模型进行训练,并基于网格搜索法和交叉验证法对参数进行寻优,得到基于LS-SVM的短临降雨预测模型。2)仿真实验:对训练数据进行归一化处理,并输入LS-SVM降雨预测模型得到仿真降雨数据,根据正确率(TFR)和错报率(FFR)评估仿真降雨数据与实际降雨数据间的吻合度。3)预测实验:将次年数据进行归一化处理后输入LS-SVM降雨预测模型,得到次年预测降雨数据,并根据TFR和FFR两个指标评估预测结果的精度。
3.2 数据预处理当多数类样本数据占样本数据的比例远大于少数类样本数据时,分类器可预测样本中多数类样本数据而完全忽略少数类样本数据[10]。图 4统计了NTUS站和SNUS站2010~2012年降雨类数据和非降雨类数据的数目后发现,二者的均值比例为1 :39,表明降雨类事件与非降雨类事件存在严重失衡的特征[12]。利用降采样方法得到相同数目的降雨类数据和非降雨类数据[13],并将二者组合为训练数据集。
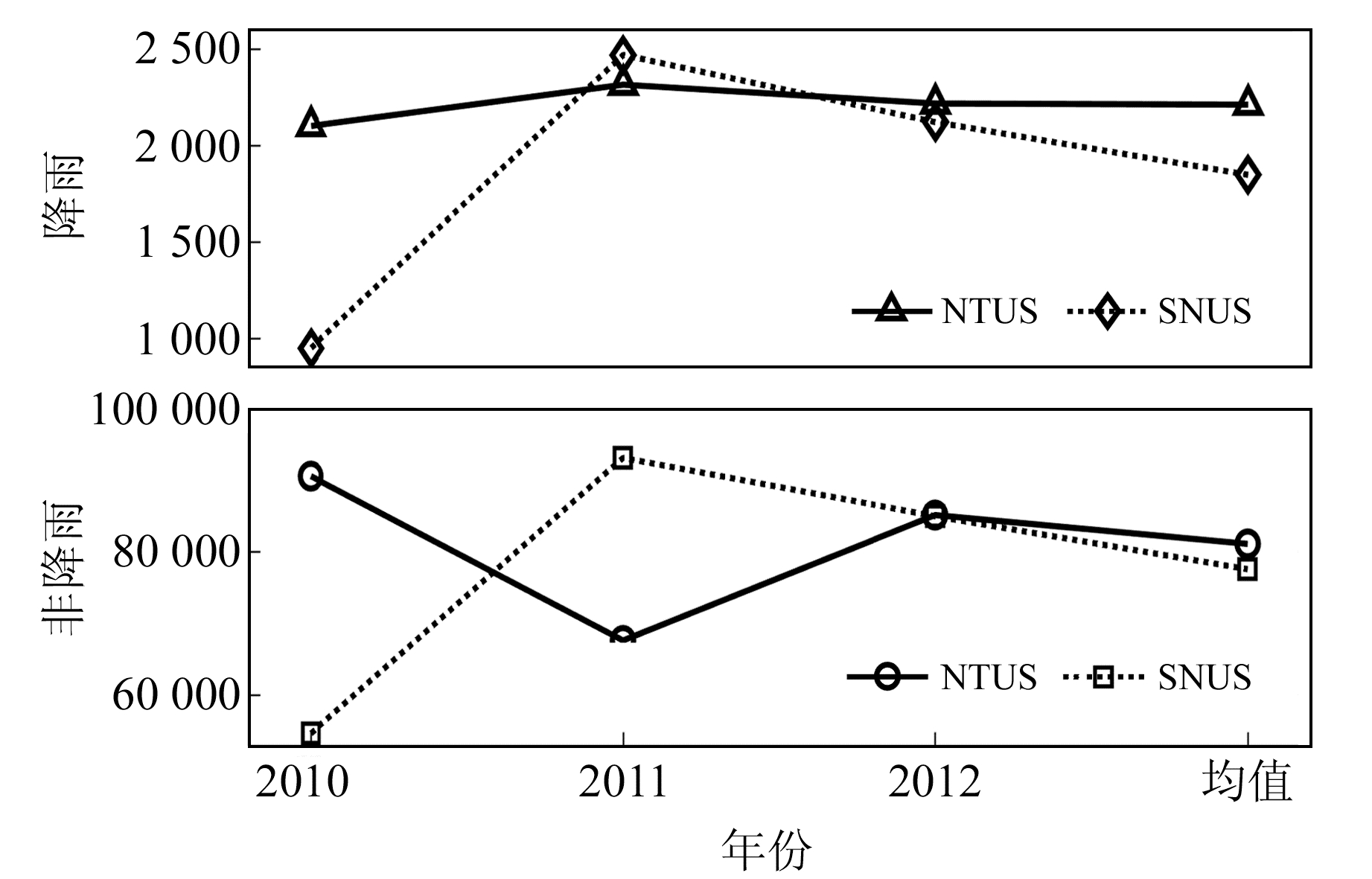
|
图 4 NTUS站和SNUS站降雨及非降雨数据 Fig. 4 The schematic diagram of rainfalland non-rainfall data at NTUS and SNUS stations |
以NTUS站2010年仿真实验为例,首先利用降采样方法对气象和时间参数进行均衡化及归一化处理。正则化参数δ/gam和RBF核函数
本文使用正确率(TFR)和错报率(FFR)来评估LS-SVM降雨预测模型的精度:
| $ \left\{\begin{array}{l} T_{\mathrm{FR}}=\frac{N_{t}}{N_{\text {real }}} \\ F_{\mathrm{FR}}=\frac{N_{f}}{N_{\text {real }}} \end{array}\right. $ | (8) |
式中,Nt为正确预报降雨次数,即预测降雨时段内实际发生的降雨次数; Nf为错误预报降雨次数,即预报时段内实际未发生降雨的次数; Nreal为实际发生的降雨次数。
图 5为SNUS站和NTUS站2010~2011年降雨仿真结果,由图可见,2个测站的降雨仿真TFR均接近100%,而SNUS站2010年和2011年的FFR均大约为44%,NTUS站2010年的FFR为53%,2011年的FFR为31%。综上所述,SNUS站和NTUS站在2010~2011年的降雨仿真TFR均值为99.94%,FFR均值为43%。结果表明,LS-SVM模型可仿真1 a中所有的降雨事件,且错报率低于传统降雨预测模型,可用于预测2011~2012年的降雨事件。
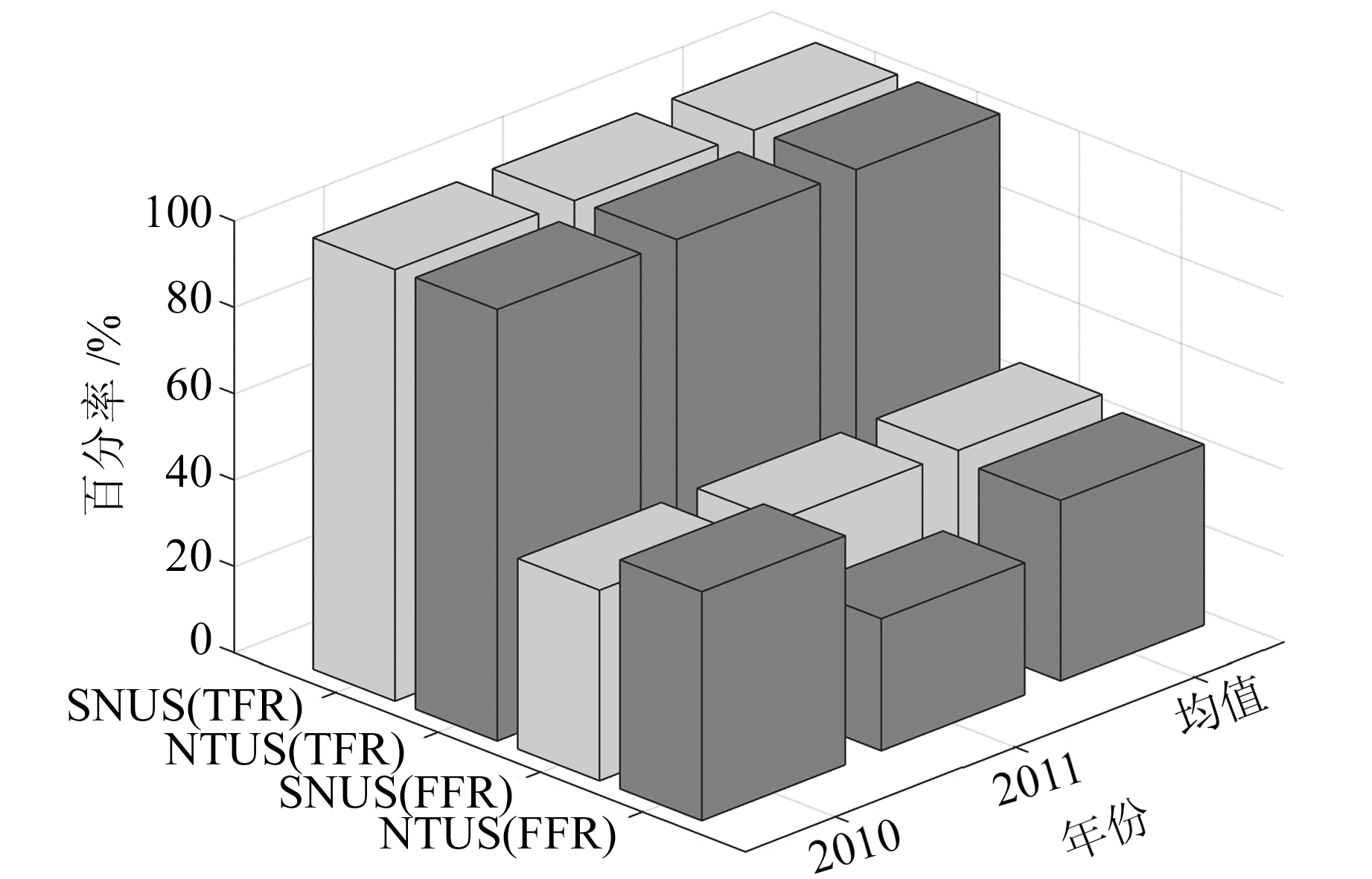
|
图 5 NTUS站和SNUS站2010~2011年降雨仿真实验结果 Fig. 5 The simulated experimental results of rainfall at NTUS and SNUS stations over the period of 2010-2011 |
以NTUS站2011年预测实验为例,首先对6种数据进行归一化处理,将数据输入仿真实验LS-SVM降雨预测模型中得到降雨预测数据,再根据TFR和FFR对数据精度进行评估。SNUS站的预测实验流程与该流程一致。
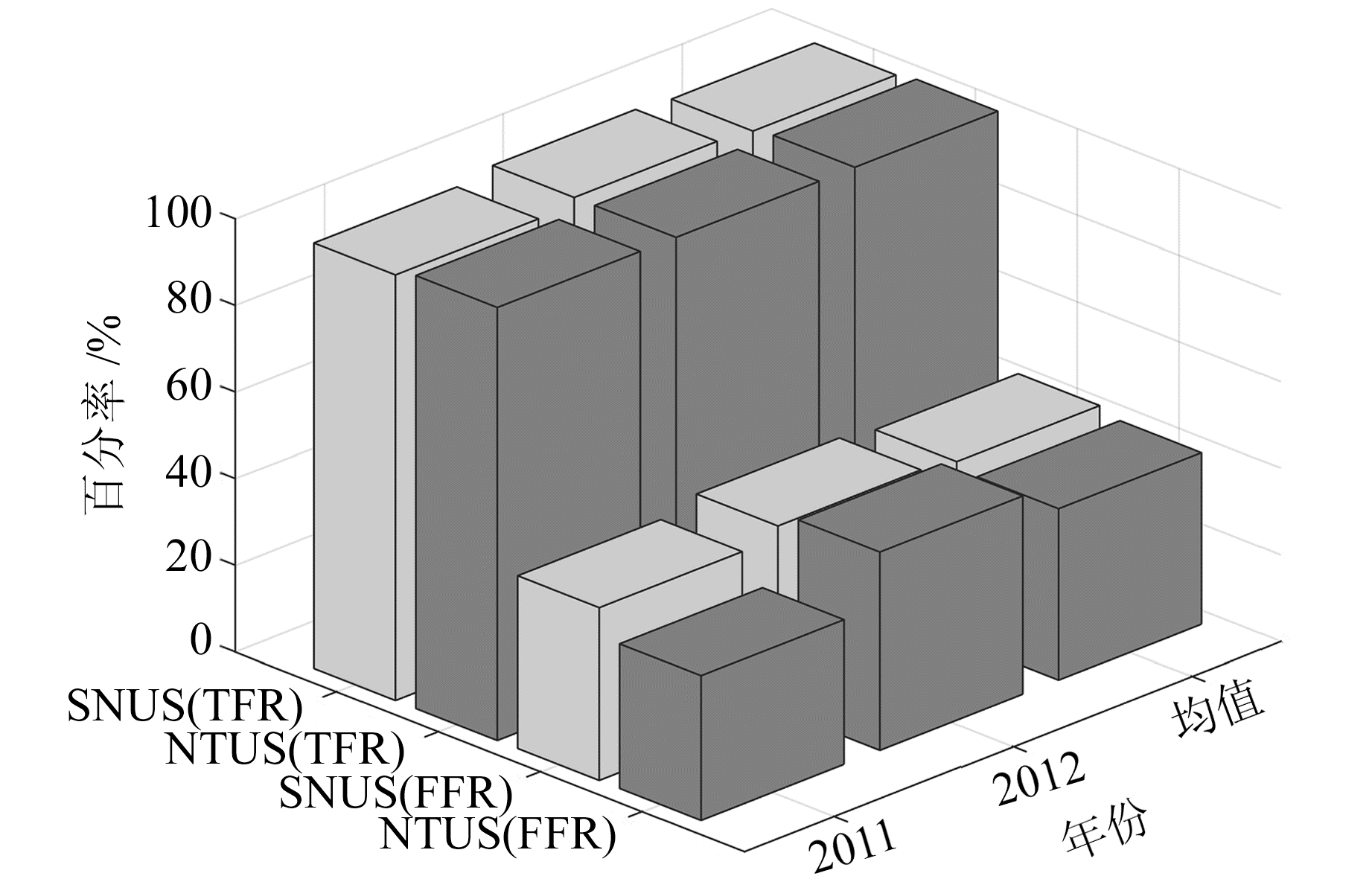
图 6为SNUS站和NTUS站2011~2012年降雨预测结果,由图可见,2个测站的降雨预测TFR相近,均接近100%;SNUS站与NTUS站2011年的FFR均小于40%,2012年FFR分别为42.58%和45.79%。综上可知,SNUS站与NTUS站在2011~2012年的降雨预测TFR均值为99.57%,FFR均值为40.42%。因此,本文基于LS-SVM的短临降雨预测模型可预测未来20~90 min内99%的降雨事件,且FFR为40%。与最小二乘线性降雨预测模型相比,本文模型预测结果的TFR提高近10%,FFR降低近20%。
|
图 6 NTUS站和SNUS站2011~2012年降雨预测实验结果 Fig. 6 The forecasted experimental results of rainfall at NTUS and SNUS stations over the period of 2011-2012 |
通过分析降雨及多种相关气象参数的时序信息发现,降雨期间多种气象参数均表现出明显的异常变化,表明气象参数与降雨间存在非线性关系。与PWV/ZTD描述的降雨事件相比,多种气象参数(T、RH、DPT、P)及时间参数(doy及hod)与降雨间的相互作用更强。结论如下:
1) 通过分析多种气象参数及时间参数与降雨的相关性特征发现,降雨与参数间均表现出弱相关性特征,表明降雨仍可能受其他气象参数的影响,因此传统降雨预测模型仅利用PWV不能达到高精度降雨预测的需求。
2) LS-SVM算法在解决函数估计及回归问题方面表现出良好的效果,基于该算法构建短临降雨预测模型仿真实验的结果表明,该模型可预测近99%的降雨事件,FFR为43%。
3) 预测实验结果表明,基于LS-SVM的短临降雨预测模型可预测未来20~90 min内99%的降雨事件,且FFR为40%。与最小二乘线性降雨预测模型相比,本文预测模型的TFR高出10%,FFR降低近20%。
本文在参数选取及算法方面对传统的基于最小二乘方法拟合PWV/ZTD的降雨预测模型进行了改进,结果表明,本文模型的精度高于传统模型。
致谢: 国际全球导航卫星系统服务(IGS)提供GNSS数据,南洋理工大学和新加坡国立大学提供免费公开的气象数据,在此一并表示感谢。
| [1] |
Manandhar S, Lee Y H, Meng Y S, et al. GPS-Derived PWV for Rainfall Nowcasting in Tropical Region[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(8): 4 835-4 844 DOI:10.1109/TGRS.2018.2839899
(  0) 0) |
| [2] |
Benevides P, Catalao J, Miranda P M A. On the Inclusion of GPS Precipitable Water Vapour in the Nowcasting of Rainfall[J]. Natural Hazards and Earth System Sciences, 2015, 15(12): 2 605-2 616 DOI:10.5194/nhess-15-2605-2015
(  0) 0) |
| [3] |
Yao Y B, Shan L L, Zhao Q Z. Establishing a Method of Short-Term Rainfall Forecasting Based on GNSS-Derived PWV and Its Application[J]. Scientific Reports, 2017, 7(1): 1-11 DOI:10.1038/s41598-016-0028-x
(  0) 0) |
| [4] |
Zhao Q Z, Yao Y B, Yao W Q. GPS-Based PWV for Precipitation Forecasting and Its Application to a Typhoon Event[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2018, 167: 124-133 DOI:10.1016/j.jastp.2017.11.013
(  0) 0) |
| [5] |
Ou P, Wang H S. Financial Volatility Forecasting by Least Square Support Vector Machine Based on GARCH, EGARCH and GJR Models: Evidence from ASEAN Stock Markets[J]. International Journal of Economics and Finance, 2010, 2(1): 51-64
(  0) 0) |
| [6] |
Kamari A, Nikookar M, Sahranavard L, et al. Efficient Screening of Enhanced Oil Recovery Methods and Predictive Economic Analysis[J]. Neural Computing and Applications, 2014, 25(3-4): 815-824 DOI:10.1007/s00521-014-1553-9
(  0) 0) |
| [7] |
Hwang S H, Ham D H, Kim J H. Forecasting Performance of LS-SVM for Nonlinear Hydrological Time Series[J]. KSCE Journal of Civil Engineering, 2012, 16(5): 870-882 DOI:10.1007/s12205-012-1519-3
(  0) 0) |
| [8] |
Hopfield H S. Two-Quartic Tropospheric Refractivity Profile for Correcting Satellite Data[J]. Journal of Geophysical Research Atmospheres, 1969, 74(18): 4 487-4 499 DOI:10.1029/JC074i018p04487
(  0) 0) |
| [9] |
Zhao Q Z, Yao Y B, Yao W Q, et al. Near-Global GPS-Derived PWV and Its Analysis in the El Niño Event of 2014-2016[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2018, 179: 69-80 DOI:10.1016/j.jastp.2018.06.016
(  0) 0) |
| [10] |
Manandhar S, Dev S, Lee Y H, et al. A Data-Driven Approach to Detecting Precipitation from Meteorological Sensor Data[C]. IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, 2018
(  0) 0) |
| [11] |
Desai S, Kuang D, Bertiger W. GIPSY/OASIS(GIPSY) Overview and under the Hood[R]. Lab, California Inst Technol, Pasadena, CA, USA, 2014
(  0) 0) |
| [12] |
Yen S J, Lee Y S. Cluster-Based under-Sampling Approaches for Imbalanced Data Distributions[J]. Expert Systems with Applications, 2009, 36(3): 5 718-5 727 DOI:10.1016/j.eswa.2008.06.108
(  0) 0) |
| [13] |
Laza R, Pavón R, Reboiro-Jato M, et al. Evaluating the Effect of Unbalanced Data in Biomedical Document Classification[J]. Journal of Integrative Bioinformatics, 2011, 8(3): 105-117 DOI:10.1515/jib-2011-177
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41

