2. 广西空间信息与测绘重点实验室,桂林市雁山街319号,541006
近年来,随着全球导航卫星系统(global navigation satellite system,GNSS)在气象学上的发展,GNSS水汽探测因相较于传统的水汽观测手段具有高时空分辨率、低成本、全天观测、高精度等优势,成为国内外专家学者研究的热点。在地基GNSS数据反演大气水汽(precipitable water vapor,PWV)的过程中,水汽转换系数K是将对流层天顶湿延迟(zenith wet delay,ZWD)转化为大气水汽的关键参数[1],主要受大气加权平均温度(Tm)的影响[2-3]。
目前,加权平均温度的计算模型可根据是否需要测站处的气象信息分为两类:第1类是需要地表气象参数的经验模型,这种模型一般需要实测的地表温度(Ts)等气象参数。其中,Bevis模型[4]是目前使用最广泛的模型之一,它首先探究Ts与Tm之间的线性关系,建立适合于中纬度地区(27°~65°N)的Bevis模型,但该模型应用到其他区域会存在明显的系统性偏差[5]。为此,不少学者对基于局部或全球多年Tm数据拟合的经验模型进行研究[6-8],并对Bevis经验模型进行改进,在地表气象参数可获得的情况下,这类Tm模型的效果最优。第2类是不需要气象参数的Tm模型[9-11],这类模型是基于局部或全球多年Tm数据拟合的经验模型,使用简单,但相比于采用实测地表气象信息的Tm模型,其精度不是很高。其中,Emardson模型[12]是直接利用测站纬度和年积日计算Tm的非气象参数模型,姚朝龙等[13]和刘立龙等[14]将Emardson模型分别在中国低纬度地区和新疆地区进行精化,并取得良好的效果。由于中国西部地区地形起伏大,Tm变化显著,现有模型在该地区的适用性较差[15]。实际大气中, 大气温湿廓线是千变万化的,在我国西部地区的GNSS水汽遥感中采用Bevis模型不能获得最优的计算效果,因此利用当地的气象资料对GNSS水汽反演中的Bevis模型进行修正是很有必要的。
本文在分析中国西部地区Tm与高程和地面温度相关性的基础上,利用探空数据对Bevis模型进行改进,建立一种与测站高程、地面温度和季节变化有关的Tm模型,并对其精度进行验证。
1 数据来源及计算原理选取中国西部地区45个探空站2014~2016共3 a的实测数据,数据采样间隔为12 h。数据可从美国怀俄明州立大学的网站免费下载(http//weather.uwyo.edu/upperair/sounding.html),各探空站的分布如图 1所示。

|
图 1 中国西部地区45个探空站点位分布 Fig. 1 Distribution of the 45 radiosonde stations in western China |
探空站资料分为大气分层数据和地表数据,其中分层数据包含气压、温度、露点温度、相对湿度等相关气象数据,地表数据包括大气可降水量和测站的位置等信息。根据不同的等压面,由数值积分法计算探空站Tm值是目前国内外学者公认的最为精确的方法,其具体计算过程见文献[3]。由于Tm是由测站上空水汽压和绝对温度沿天顶方向的积分求得的,对于缺乏探空资料的地区,Tm很难精确求得,所以通常是根据区域探空数据采用统计回归方法拟合出Tm与地面温度Ts的关系式。其中,较为经典、常用的是Bevis等[16]的Tm-Ts线性回归公式:
| $ {T_m} = 70.2 + 0.72{T_s} $ | (1) |
另外,Böhm等[10]提出的GPT2w模型是目前全球范围内较为先进的经验对流层格网模型,具有1°和5°格网分辨率,可提供包括Tm在内的多种对流层参数。GPT2w模型使用时只需输入目标点的位置和相应日期,就可以得到目标点处的Tm值。本文分别将1°分辨率和5°分辨率的GPT2w模型简称为GPT2w-1和GPT2w-5。
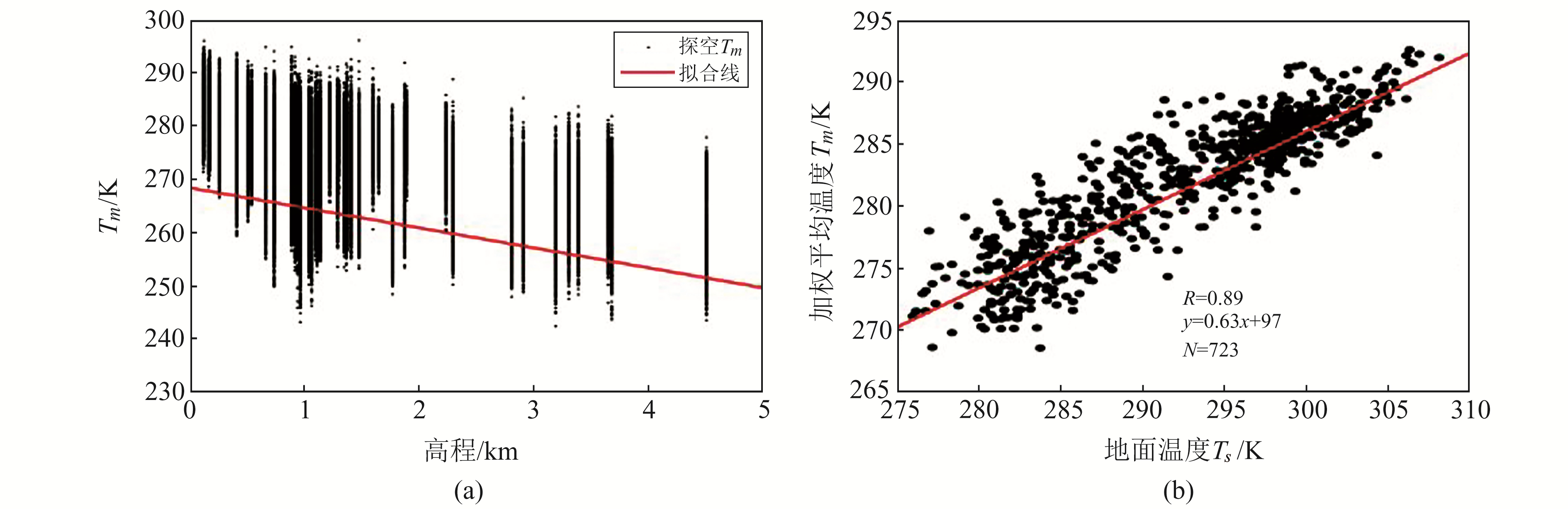
2 中国西部地区大气加权平均温度模型的建立 2.1 大气加权平均温度与高程、地面温度相关性分析中国西部地区经纬度范围广、地形起伏大,影响Tm的因素很多,其中Tm与高程[3]及Ts[4]有一定的相关性。为探究中国西部地区Tm与高程的关系,本文选取2015年该地区45个探空站数据,利用数值积分法计算出Tm值,并与相应测站高程的相关性进行探究,结果如图 2(a)所示;为探究中国西部地区Tm与Ts的关系,以2015年桂林探空站(25.33°N,110.3°E)数据为例,进行Tm和Ts的相关性分析,结果如图 2(b)所示。
|
图 2 Tm与相应测站的高程和Ts的相关性分析 Fig. 2 The correlations analysis between Tm and height, Tm and Ts in corresponding stations |
由图 2(a)可以看出,Tm与高程的变化呈相反趋势,即海拔越高,Tm越低,二者呈负相关关系。由此可见,考虑Tm的高程变化并对其进行改正是准确计算Tm的关键。由图 2(b)可以看出,Tm与Ts的变化呈相同趋势,即Ts越高,Tm越高,二者呈正相关关系,且具有较强的相关性。因此,在建立Tm模型时可以考虑加入Ts因素。
2.2 模型的建立研究表明,实测获取的Tm与模型计算的Tm的残差序列存在明显的周期性[17],对该残差序列进行建模,并对模型计算的Tm进行补偿,根据获取的Tm来源的不同,可建立不同的补偿模型。本文在对Tm进行建模时,考虑了Tm具有年周期和半年周期变化的特点,经过上述分析可知,Tm不仅与Ts呈线性正相关关系,而且与季节和高程也有密切关系,因此,本文在Bevis模型的基础上加入季节和高程因素,建立了一种新的Tm模型关系式:
| $ \begin{array}{*{20}{l}} {{T_m} = {a_1} + {a_2}{T_s} + {a_3}{\rm{sin}}\left( {\frac{{2{\rm{\pi }} \times {\rm{doy}}}}{{365.25}}} \right) + }\\ {{a_4}{\rm{cos}}\left( {\frac{{2{\rm{\pi }} \times {\rm{doy}}}}{{365.25}}} \right) + {a_5}{\rm{cos}}\left( {\frac{{4{\rm{\pi }} \times {\rm{doy}}}}{{365.25}}} \right) + }\\ {\;\;\;\;\;\;\;\;\;\;\;{a_6}{\rm{sin}}\left( {\frac{{4{\rm{\pi }} \times {\rm{doy}}}}{{365.25}}} \right) + {a_7}h} \end{array} $ | (2) |
式中,Ts为测站温度,doy为年积日,a1、a2、a3、a4、a5、a6和a7均为模型系数,h为测站高程。
本文利用中国西部地区45个探空站2014~2016年观测数据中各测站的大气加权平均温度Tm、地面温度Ts和测站高程来确立新模型的系数。首先利用数值积分法计算中国西部地区每个探空站的Tm值,然后通过代入相应的Tm、Ts和测站高程数据,利用式(2)拟合计算得到中国西部地区新Tm模型系数值,结果如表 1所示。
|
|
表 1 使用中国西部2014~2016年的探空数据计算的新Tm模型系数 Tab. 1 Model coefficients of new Tm model using radiosonde data from 2014 to 2016 over western China |
在应用该模型时,只需将目标处的地面温度Ts、年积日和高程(单位m)代入模型,就可得到所需的加权平均温度Tm。
3 新Tm模型精度验证为验证本文构建的新Tm模型精度,采用2017年探空站数据获得的Tm作为参考值对新模型进行精度分析。采用偏差(bias)和均方根误差(RMS)作为精度评价指标,其表达式为:
| $ {\rm{bias}} = \frac{1}{N}\mathop \sum \limits_{i = 1}^N (X_m^{{M_i}}X_m^{{R_i}}) $ | (3) |
| $ {\rm{RMS}} = \frac{1}{N}\mathop \sum \limits_{i = 1}^N {(X_m^{{M_i}}X_m^{{R_i}})^2} $ | (4) |
式中,N表示数据的样本数,XmMi表示第i个模型的计算值,XmRi表示第i个模型的参考值。
3.1 基于探空数据的模型精度分析利用中国西部地区45个探空站2017年数据资料获取的Tm作为参考值,验证新模型的精度,同时分别与广泛应用的Bevis模型和目前性能较优的GPT2w对流层模型进行对比分析,计算并统计bias和RMS,结果如表 2、图 3和4所示。
|
|
表 2 利用2017年探空站资料检验Bevis模型、GPT2w模型及新Tm模型的精度统计 Tab. 2 Statistical precision of Bevis model, GPT2w model and new Tm model tested using radiosonde data from 2017 |
|
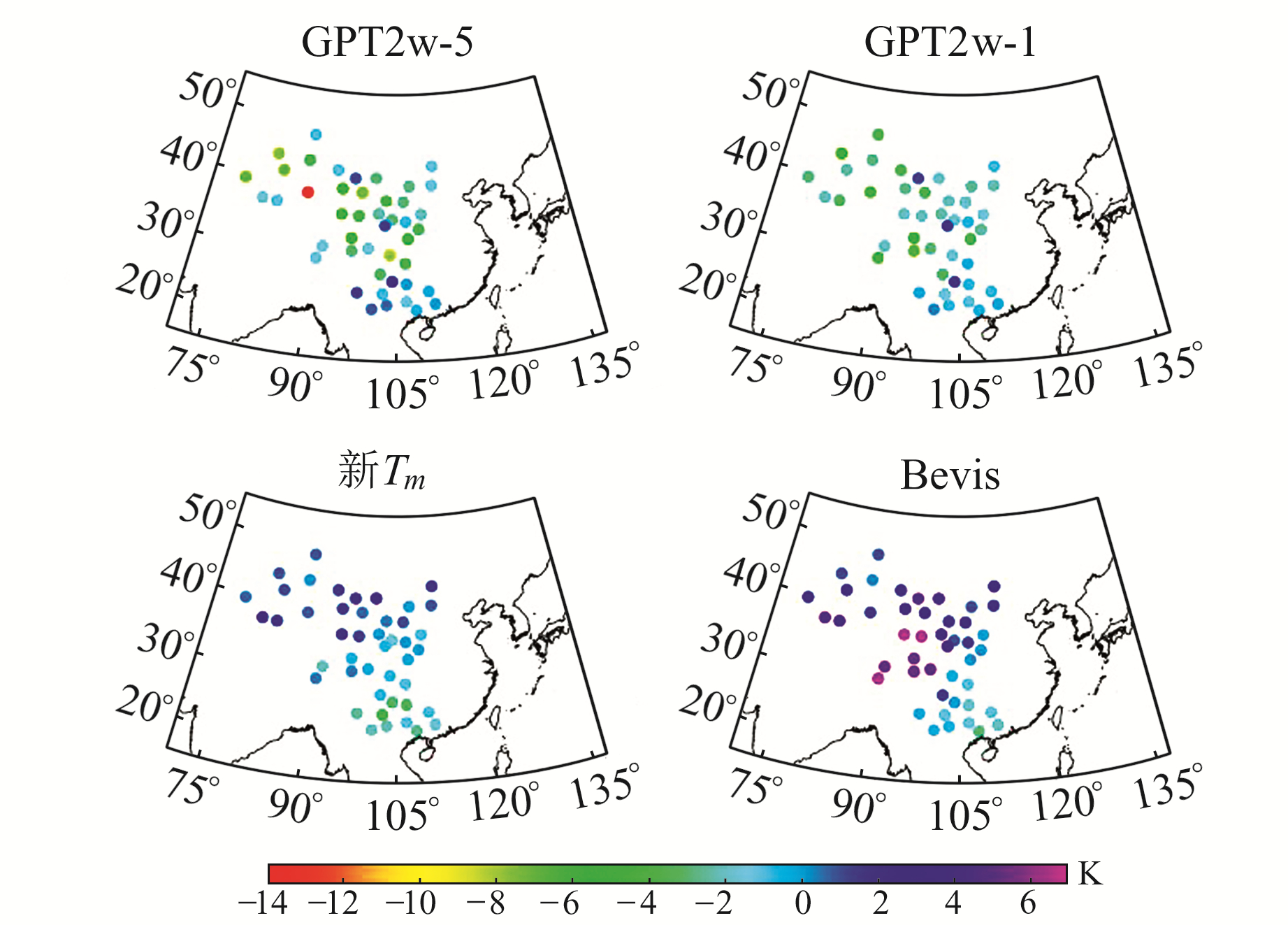
图 3 利用2017年探空资料评估中国西部地区新Tm模型、GPT2w模型及Bevis模型的年均bias分布 Fig. 3 Distribution of annual bias for new Tm model, GPT2w model and Bevis model assessed using radiosonde data from 2017 in western China |
|
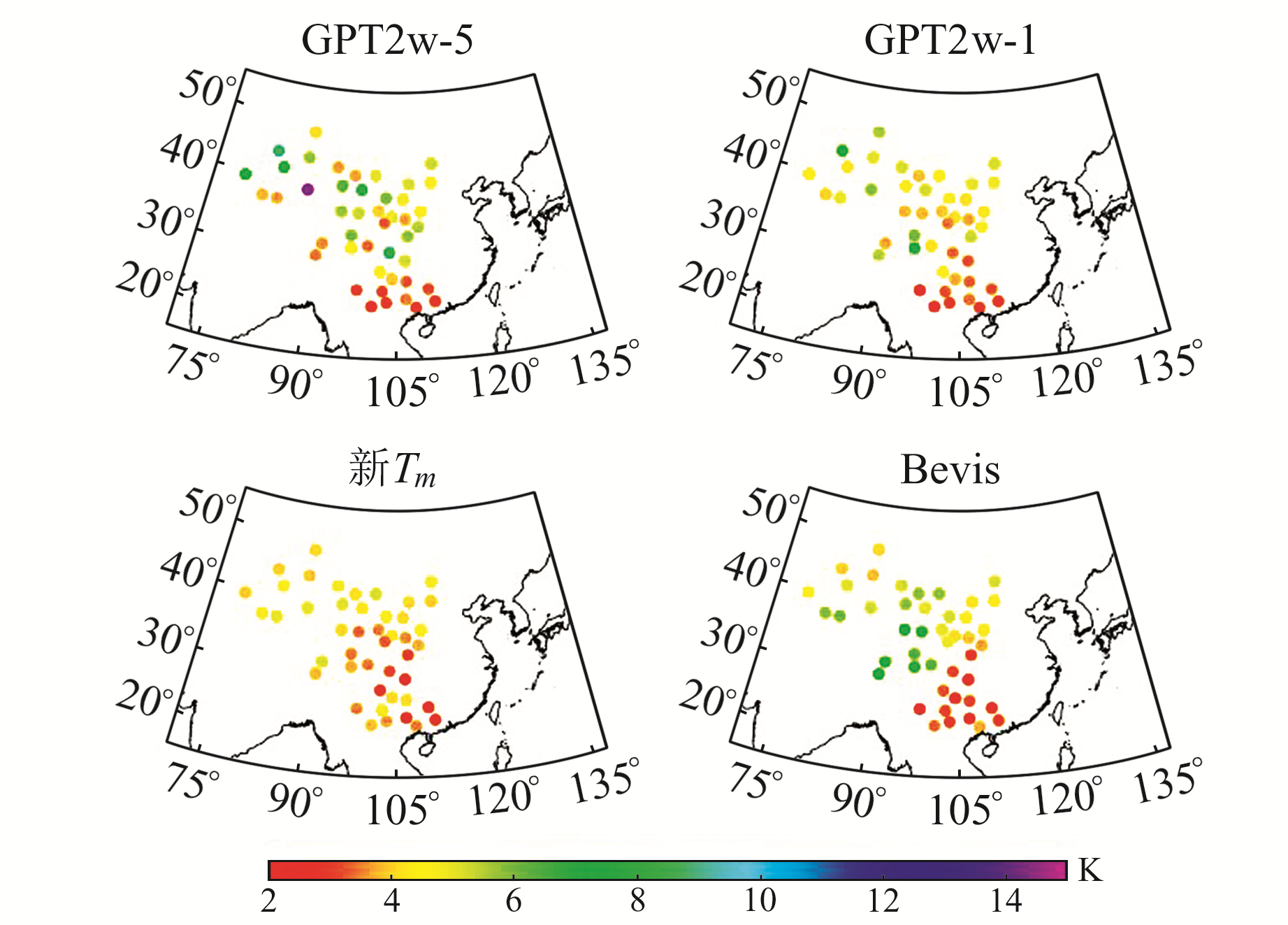
图 4 利用2017年探空资料评估中国西部地区新Tm模型、GPT2w模型及Bevis模型的年均RMS分布 Fig. 4 Distribution of annual RMS for new Tm model, GPT2w model and Bevis model assessed using radiosonde data from 2017 in western China |
由表 2可知,在中国西部地区Bevis模型表现出明显的正偏差,其年均值为1.87 K;GPT2w-1模型和GPT2w-5模型均表现出明显的负偏差,年均值分别为-2.06 K和-2.68 K,说明Bevis模型和GPT2w模型在中国西部地区计算Tm时均存在明显的系统偏差。而新Tm模型的最大、最小偏差分别为2.76 K和-3.94 K,平均偏差为-0.08 K,与另外3个模型相比偏差较小。同时,GPT2w-5模型表现出最大的RMS,其平均值为4.9 K,而GPT2w-1模型与Bevis模型精度相当,表明GPT2w-1模型的精度优于GPT2w-5模型。新Tm模型的平均RMS为3.89 K,其精度比Bevis模型提高了约0.65 K (14.3%),与GPT2w-5模型和GPT2w-1模型相比分别提高了1.01 K (20.6%)和0.4 K (9.3%),说明新Tm模型在中国西部地区相比于其他3个模型有较高的精度,且比其他模型稳定。
由图 3可知,Bevis模型在西部地区出现明显的正偏差,GPT2w-1模型和GPT2w-5模型则表现出明显的负偏差;而新Tm模型与Bevis模型相比,在青藏高原地区的偏差更趋稳定,这是由于青藏高原大部分地区的地表高程较大,Bevis模型的估计精度会随海拔的升高而逐渐降低[18],而新Tm模型则对这一误差进行了修正。在中国西部地区,新Tm模型的绝大部分bias绝对值小于4 K。总体而言,新Tm模型在中国西部地区有较小且稳定的偏差。
由图 4可知,在西部地区,Bevis模型、GPT2w-5模型和GPT2w-1模型均表现出较大的年均RMS,这是由于GPT2w模型在计算Tm时未考虑高程,而且未对日偏差进行改正,因此在地形起伏较大的中国西部地区表现出较大的偏差[3]。而新Tm模型在中国西部绝大部分地区的RMS小于5 K,相比于GPT2w模型和Bevis模型,其年均RMS更趋于稳定,进一步说明新Tm模型在计算中国西部地区Tm值时相较于其他模型有明显的改善,特别是在地形起伏较大的地区,具有较好的精度。由此可见,新Tm模型在中国西部地区表现出良好的精度和稳定性。为进一步验证新Tm模型、GPT2w-1模型、GPT2w-5模型和Bevis模型的精度,对中国西部地区45个探空站的年均bias和RMS进行统计,结果见图 5。
|
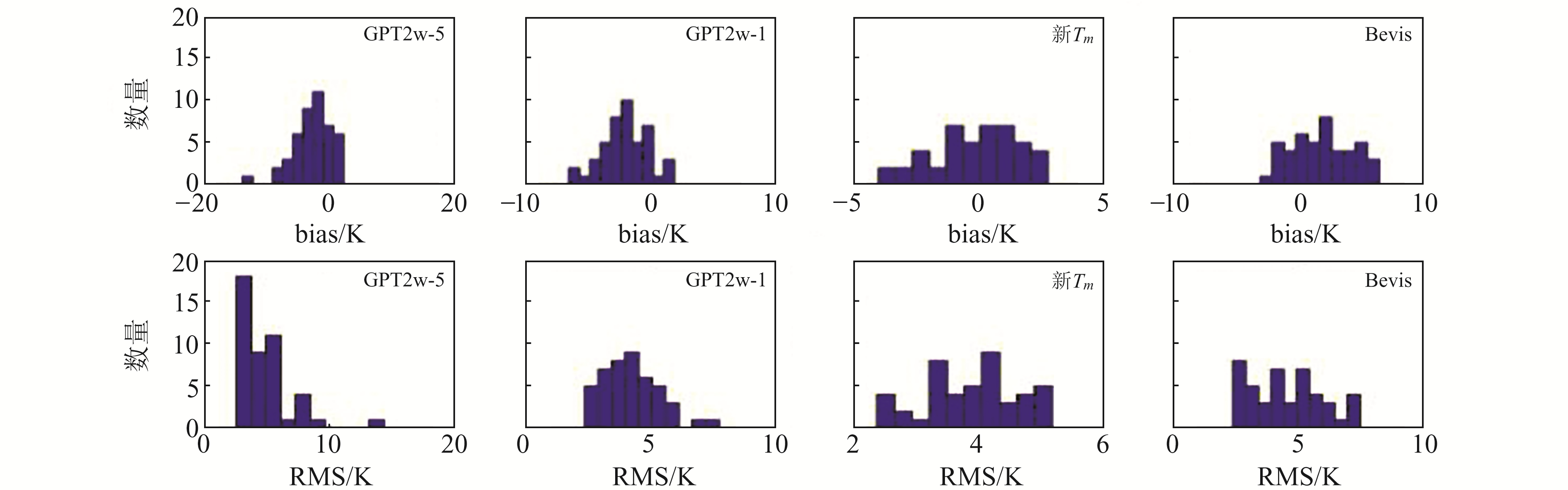
图 5 利用2017年探空资料评估中国西部地区不同模型的年均bias和RMS分布直方图 Fig. 5 Distribution histogram of annual bias and RMS for different models assessed using radiosonde data from 2017 in western China |
由图 5可知,新Tm模型的bias明显比其他3个模型的小且稳定;GPT2w-1模型和GPT2w-5模型与新Tm模型及Bevis模型相比表现出明显的负偏差,而新Tm模型的bias在零周围分布更均匀。新Tm模型及Bevis模型的RMS分布比GPT2w-1模型和GPT2w-5模型集中,而新Tm模型的RMS分布范围比Bevis模型小,进一步表明新Tm模型的性能比其他3种模型稳定。新Tm模型的精度比Bevis模型、GPT2w-1模型和GPT2w-5模型高,更适用于高低起伏大、地形复杂的中国西部地区。为检验不同模型的季节性表现,本文对每个模型进行日偏差检验,统计不同模型的bias和RMS,结果如图 6所示。

|
图 6 利用2017年探空资料评估中国西部地区不同模型的日均bias和RMS分布散点图 Fig. 6 Scatter diagram of daily bias and RMS for different models assessed using radiosonde data from 2017 in western China |
从图 6可以看出,新Tm模型受季节的影响要明显小于另外3种模型,在全年期间较为平稳。Bevis模型的偏差和变化幅度在夏季最低,春、冬季最高,而且在多天的精度检验中发现,新Tm模型的精度要高于Bevis模型,特别是在春、冬季,2种模型的精度对比较明显,进一步说明在同样受季节变化的影响下,新Tm模型要优于Bevis模型。在全年期间,虽然GPT2w模型考虑了Tm的季节性变化,但由于受系统误差的影响,GPT2w-5模型和GPT2w-1模型都表现出明显的负偏差,并且在春、冬季观察到较大的值。特别是GPT2w-5模型,由于空间分辨率比GPT2w-1模型低,其偏差和RMS变化较为明显;而在多数时间,新Tm模型均显示出较小的偏差,并且没有明显的季节性变化。就RMS而言,所有模型均显示出相对明显的季节性变化,春季和冬季的RMS相对较大,夏季的RMS较小。这是因为大多数选定的探空站位于中纬度地区,夏季Tm变化较小,冬季Tm变化较大, 影响了Tm的计算。此外,在大多数时间里,新Tm模型的RMS比其他模型小且稳定,显示出优越的季节性能。总之,与其他模型相比,考虑季节性变化的新Tm模型明显提高了Tm的计算精度。
大量研究表明,Tm的变化与高程具有较强的相关性。为分析Bevis模型、新Tm模型、GPT2w-1模型和GPT2w-5模型计算Tm的bias、RMS与高程的变化关系,本文对45个探空站进行分类,按高程小于500 m、500~1 000 m、1 000~1 500 m、1 500~2 000 m和大于2 000 m分别进行归类,结果见图 7。

|
图 7 利用2017年探空资料评估中国西部地区不同模型的bias和RMS随高程变化统计 Fig. 7 The statistics with height variations of daily bias and RMS for different models assessed using radiosonde data from 2017 in western China |
由图 7可知,GPT2w-1模型和GPT2w-5模型在每个高程范围内均表现出显著的负偏差,Bevis模型在大于500 m的高程范围内表现出显著的正偏差,而在小于500 m的高程范围内表现出负偏差,说明随着高程的增加,Bevis模型的系统误差越来越明显,不适用于高原地区Tm的计算。而新Tm模型在不同高程范围内均表现出相对较小甚至不显著的偏差。此外,GPT2w-1模型和GPT2w-5模型在500~1 000 m高程范围内表现出较大的RMS,Bevis模型在大于2 000 m的高程范围内也表现出较大的RMS,而新Tm模型在每个高程区间内的RMS都较小且较为均匀。由图 7还可以明显看出,4种模型都有较大的RMS,但总体来说,新Tm模型的RMS要小于其他3种模型,进一步说明新Tm模型的精度表现更好。
3.2 Tm对GNSS-PWV估计的影响建立中国西部地区新的Tm模型是为了提高Tm的计算精度,其最终目的是提高GNSS反演PWV的精度。但一般情况下,GNSS基准站与探空站不在同一地址,且大多数GNSS基准站主要用于大地测量研究,未安装气象传感器,所以难以全面、可靠地研究Tm对GNSS-PWV计算的影响。为此,本文采用Huang等[19]提出的计算Tm对GNSS-PWV影响的方法(式(5)),并对计算结果进行分析:
| $ \begin{array}{l} \frac{{{\rm{RM}}{{\rm{S}}_{{\rm{PWV}}}}}}{{{\rm{PWV}}}} = \frac{{{\rm{RM}}{{\rm{S}}_K}}}{K} = \frac{{{\rm{ }}{k_3} \times {\rm{RM}}{{\rm{S}}_{{T_m}}}}}{{\left( {k{'_2} + \frac{{{k_3}}}{{{T_m}}}} \right){T^2}_m}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{k_3}}}{{\left( {k{'_2} + \frac{{{k_3}}}{{{T_m}}}} \right){T_m}}} \times \frac{{{\rm{RM}}{{\rm{S}}_{{T_m}}}}}{{{T_m}}} \end{array} $ | (5) |
式中,RMSPWV为PWV的RMS,RMSK为转换系数K的RMS,RMSTm为Tm的RMS,RMSPWV/PWV为PWV的相对误差,其中Tm和PWV采用年均值计算。RMSPWV和RMSPWV/PWV用于评估模型计算Tm的误差对其计算GNSS-PWV的影响,各模型RMSPWV和RMSPWV/PWV的计算结果如表 3所示。
|
|
表 3 利用2017年探空站资料检验Bevis模型、GPT2w模型及新Tm模型计算PWV的理论RMS误差和相对误差统计 Tab. 3 Statistics of RMSPWV and RMSPWV/PWV resulted from the Bevis model, GPT2w model and new Tm model tested using radiosonde data from 2017 |
由表 3可知,GPT2w-5模型表现出较大的RMSPWV和RMSPWV/PWV,最大值分别为0.92 mm和5.22%。而新Tm模型的RMSPWV小于0.55 mm,平均值为0.22 mm;新Tm模型的RMSPWV/PWV平均值为1.43%,范围为0.85%~1.93%,比其他模型小且稳定。因此,用新Tm模型计算Tm带来的误差对GNSS-PWV的影响比其他模型小且较稳定,可以为中国西部地区GNSS-PWV估计提供更为准确的Tm。
4 结语1) 本文选用2014~2016年45个探空站数据,利用回归分析方法建立适用于中国西部地区的多因子加权平均温度模型(新Tm模型),并以2017年探空站获取的Tm作为参考值,计算的平均bias和平均RMS分别为-0.08 K和3.89 K。
2) 通过将新Tm模型与Bevis模型和GPT2w模型相比较可知,由于建模时顾及了Tm的季节性变化和高程变化,新Tm模型相比于Bevis模型和GPT2w模型在中国西部地区的平均偏差和RMS更小,精度更高,受高程及四季变迁的影响较小,对西部地区有着更好的适用性和稳定性。
3) 从理论上分析各模型计算的Tm误差对GNSS-PWV估计的影响,得到新Tm模型的RMSPWV和RMSPWV/PWV的平均值分别为0.22 mm和1.43%,比其他模型更小、更稳定。
总之,新Tm模型得到的Tm精度可靠,可以满足中国西部地区GNSS水汽探测的要求,能进一步改善中国西部地区GNSS大气水汽反演的精度,更好地服务于中国西部地区气象学研究工作。
| [1] |
黄良珂, 吴丕团, 王浩宇, 等. 中国西南地区GPS大气水汽转换系数模型精化研究[J]. 大地测量与地球动力学, 2019, 39(3): 256-261 (Huang Liangke, Wu Pituan, Wang Haoyu, et al. Refining the GPS Atmospheric Water Vapor Conversion Factor Model over Southwest China[J]. Journal of Geodesy and Geodynamics, 2019, 39(3): 256-261)
(  0) 0) |
| [2] |
刘立龙, 万庆同, 周威, 等. 基于傅里叶级数的中国沿海地区Tm模型精化研究[J]. 大地测量与地球动力学, 2019, 39(11): 1137-1141 (Liu Lilong, Wan Qingtong, Zhou Wei, et al. Research on Refinement of Tm Model in China's Coastal Area Based on Fourier Series[J]. Journal of Geodesy and Geodynamics, 2019, 39(11): 1137-1141)
(  0) 0) |
| [3] |
Huang L K, Liu L L, Chen H, et al. An Improved Atmospheric Weighted Mean Temperature Model and Its Impact on GNSS Precipitable Water Vapor Estimates for China[J]. GPS Solutions, 2019, 23
(  0) 0) |
| [4] |
Bevis M, Businger S, Chiswell S, et al. GPS Meteorology: Mapping Zenith Wet Delays onto Precipitable Water[J]. Journal of Applied Meteorology, 1994, 33(3): 379-386 DOI:10.1175/1520-0450(1994)033<0379:GMMZWD>2.0.CO;2
(  0) 0) |
| [5] |
于胜杰, 柳林涛. 水汽加权平均温度回归公式的验证与分析[J]. 武汉大学学报:信息科学版, 2009, 34(6): 741-744 (Yu Shengjie, Liu Lintao. Validation and Analysis of the Water-Vapor-Weighted Mean Temperature from Tm-Ts Relationship[J]. Geomatics and Information Science of Wuhan University, 2009, 34(6): 741-744)
(  0) 0) |
| [6] |
李建国, 毛节泰, 李成才. 使用全球定位系统遥感水汽分布原理和中国东部地区加权"平均温度"的回归分析[J]. 气象学报, 1999, 57(3): 283-292 (Li Jianguo, Mao Jietai, Li Chengcai. The Approach to Remote Sensing of Water Vapor Based on GPS Linear Regression Tm in Eastern Region of China[J]. Acta Meteorologica Sinica, 1999, 57(3): 283-292 DOI:10.3969/j.issn.1001-7313.1999.03.004)
(  0) 0) |
| [7] |
谢劭峰, 黎峻宇, 刘立龙, 等. 新疆地区GGOS Atmosphere加权平均温度的精化[J]. 大地测量与地球动力学, 2017, 37(5): 472-477 (Xie Shaofeng, Li Junyu, Liu Lilong, et al. Refinement of GGOS Atmosphere Weighted Mean Temperature in Xinjiang[J]. Journal of Geodesy and Geodynamics, 2017, 37(5): 472-477)
(  0) 0) |
| [8] |
姚宜斌, 张豹, 许超钤, 等. Tm-Ts的相关性分析及全球纬度相关的线性关系模型构建[J]. 科学通报, 2014, 59(9): 816-824 (Yao Yibin, Zhang Bao, Xu Chaoqian, et al. Analysis of the Global Tm-Ts Correlation and Establishment of the Latitude-Related Linear Model[J]. Chinese Science Bulletin, 2014, 59(9): 816-824)
(  0) 0) |
| [9] |
Yao Y B, Xu C Q, Zhang B, et al. GTm-Ⅲ: A New Global Empirical Model for Mapping Zenith Wet Delays onto Precipitable Water Vapour[J]. Geophysical Journal International, 2014, 197(1): 202-212 DOI:10.1093/gji/ggu008
(  0) 0) |
| [10] |
Böhm J, Möller G, Schindelegger M, et al. Development of an Improved Empirical Modelfor Slant Delays in the Troposphere(GPT2w)[J]. GPS Solutions, 2015, 19(3): 433-441 DOI:10.1007/s10291-014-0403-7
(  0) 0) |
| [11] |
黄良珂, 彭华, 刘立龙, 等. 顾及垂直递减率函数的中国区域大气加权平均温度模型[J]. 测绘学报, 2020, 49(4): 432-442 (Huang Liangke, Peng Hua, Liu Lilong, et al. An Empirical Atmospheric Weighted Mean Temperature Model Considering the Lapse Rate Function for China[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(4): 432-442)
(  0) 0) |
| [12] |
Emardson T R, Derks H J P. On the Relation between the Wet Delay and the Integrated Precipitable Water Vapour in the European Atmosphere[J]. Meteorological Applications, 2000, 7(1): 61-68 DOI:10.1017/S1350482700001377
(  0) 0) |
| [13] |
姚朝龙, 罗志才, 刘立龙, 等. 顾及地形起伏的中国低纬度地区湿延迟与可降水量转换关系研究[J]. 武汉大学学报:信息科学版, 2015, 40(7): 907-912 (Yao Chaolong, Luo Zhicai, Liu Lilong, et al. On the Relation between the Wet Delay and the Water Precipitable Vapor in Consideration of Topographic Relief in the Low-Latitude Region of China[J]. Geomatics and Information Science of Wuhan University, 2015, 40(7): 907-912)
(  0) 0) |
| [14] |
刘立龙, 陈香萍, 封海洋, 等. 新疆地区Emardson大气水汽转换系数的适用性分析[J]. 大地测量与地球动力学, 2016, 36(5): 434-437 (Liu Lilong, Chen Xiangping, Feng Haiyang, et al. Analysis of the Applicability of the Emardson Model for Transformation Coefficient of Water Vapor in the Region of Xinjiang[J]. Journal of Geodesy and Geodynamics, 2016, 36(5): 434-437)
(  0) 0) |
| [15] |
黄良珂, 李琛, 王浩宇, 等. 基于GPT2w模型计算中国地区对流层加权平均温度的精度分析[J]. 大地测量与地球动力学, 2019, 39(5): 496-501 (Huang Liangke, Li Chen, Wang Haoyu, et al. Precision Analysis of the Tropospheric Weighted Mean Temperature Derived from GPT2w Model over China[J]. Journal of Geodesy and Geodynamics, 2019, 39(5): 496-501)
(  0) 0) |
| [16] |
Bevis M, Businger S, Herring T A. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System[J]. Journal of Geophysical Research, 1992, 97(D14): 15787-15801 DOI:10.1029/92JD01517
(  0) 0) |
| [17] |
Yao Y B, Zhang B, Xu C Q, et al. Improved One/Multi-Parameter Models that Consider Seasonal and Geographic Variations for Estimating Weighted Mean Temperature in Ground-Based GPS Meteorology[J]. Journal of Geodesy, 2014, 88(3): 273-282 DOI:10.1007/s00190-013-0684-6
(  0) 0) |
| [18] |
姚宜斌, 孙章宇, 许超钤. Bevis公式在不同高度面的适用性以及基于近地大气温度的全球加权平均温度模型[J]. 测绘学报, 2019, 48(3): 276-285 (Yao Yibin, Sun Zhangyu, Xu Chaoqian. Applicability of Bevis Formula at Different Height Level and Global Weighted Mean Temperature Model Based on Near-Earth Atmospheric Temperature[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(3): 276-285)
(  0) 0) |
| [19] |
Huang L K, Jiang W P, Liu L L, et al. A New Global Grid Model for the Determination of Atmospheric Weighted Mean Temperature in GPS Precipitable Water Vapor[J]. Journal of Geodesy, 2019, 93(2): 159-176 DOI:10.1007/s00190-018-1148-9
(  0) 0) |
2. Guangxi Key Laboratory of Spatial Information and Geomatics, 319 Yanshan Street, Guilin 541004, China
 2021, Vol. 41
2021, Vol. 41


