2. 西安航天天绘数据技术有限公司,西安市航天大道59号,710054
电离层延迟误差是卫星导航系统误差的重要来源[1-3],误差影响可达几米甚至几十米,会对卫星的精度、连续性、可用性、完好性等性能造成影响。目前,GPS采用Klobuchar模型描述全球电离层变化[4],Galileo播发NeQucikG电离层模型参数[5],GLONASS不播发电离层参数,未来码分多址信号电文将播发3个电离层参数[6]。北斗区域导航系统播发区域电离层模型参数,每2 h更新一次[3],其在中国区域的修正精度优于GPS电离层模型,北斗三号系统使用BDGIM模型对全球范围内的电离层延迟进行改正[4-5]。同时,北斗导航系统可提供广域差分服务,播发广域差分格网电离层信息参数,为用户提供高更新频率及高精度的格网电离层信息[3]。
随着我国北斗导航系统的建设与完善,有学者[1-3, 7-9]对北斗各电离层模型的算法及性能进行了大量研究,但大部分只是对单个模型的某一项指标进行分析,未对北斗基本导航和星基增强电离层模型的多个指标进行全面的综合分析。本文将从模型参数、时间、空间、评估精度、定位精度等方面对BDSKlob模型及BDGIM模型进行详细分析,同时基于CODE格网电离层模型对北斗广域差分格网电离层模型进行研究。
1 北斗电离层模型 1.1 北斗区域电离层模型Klobuchar模型是基于三角余弦函数建立的电离层模型[1],已考虑电离层周日振幅与周期变化特性,基本可反映电离层的变化特征。该模型同时考虑了纬度差异性,默认最大电离层延迟出现时间为地方时14:00,默认夜间电离层延迟为5 ns,白天电离层延迟建模为本地时的余弦函数[10-13]。而BDSKlob模型分为8参数和14参数2种模型,本文采用较常使用的8参数模型,其表达式为:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{I_{{\rm{ion}}}}\left( t \right) = \\ \left\{ \begin{array}{l} {A_1} + {A_2}{\rm{cos}}\frac{{2{\rm{ \mathsf{ π} }}}}{{{A_4}}}(t-{A_3})|t-{A_3}| < {A_4}/4\\ {A_1}{\rm{ }},t为其他值 \end{array} \right.{\rm{ }} \end{array} $ | (1) |
式中,Iion为垂直方向电离层延迟(单位s);t为电离层穿刺点处的地方时(单位s);A1为夜晚电离层延迟平均值;A2为余弦函数幅值,可用式(2)表示;A3为初始相位,对应余弦曲线极点的地方时,一般取50 400 s,对应地方时14:00;A4为余弦函数的周期,可用式(3)表示。
| $ {A_2} = \left\{ {\begin{array}{*{20}{l}} {\sum\limits_{n = 0}^3 {{\alpha _n}} {{\left| {\frac{{{\varphi _M}}}{{\rm{ \mathsf{ π} }}}} \right|}^n}, {A_2} \ge 0}\\ {0, {A_2} \le 0} \end{array}} \right. $ | (2) |
| $ {A_4} = \left\{ {\begin{array}{*{20}{l}} {172800, {A_4} \ge 172800}\\ {\sum\limits_{n = 0}^3 {{\beta _n}} {{\left| {\frac{{{\varphi _M}}}{\pi }} \right|}^n}, 172800 > {A_4} \ge 72000}\\ {72000, {A_4} < 72000} \end{array}} \right. $ | (3) |
式中,参数αn、βn由导航电文给出,φM为电离层穿刺点的地理纬度。BDSKlob模型借鉴GPSKlob模型并对其进行改进,BDSKlob模型采用日固地理坐标系[11],地球半径为6 378 km,电离层高度为375 km,参数更新间隔为2 h[14]。
1.2 北斗全球电离层模型北斗全球系统采用BDGIM模型对单频电离层延迟进行改正,该模型以改进的球谐函数为基础[15],用户根据BDGIM模型计算电离层延迟改正值的过程为:
| $ {I_{{\rm{ion}}}} = {M_F} \times \frac{{40.28 \times {{10}^{16}}}}{{{f^2}}} \times \left[ {{A_0} + \mathop \sum \limits_{i = 1}^9 {\alpha _i}{A_i}} \right] $ | (4) |
式中,Iion为卫星与接收机视线方向的电离层延迟改正值(单位m);MF为投影函数,用于转换垂向与斜向的电离层总电子含量;f为当前信号的载波频率(单位Hz);αi为电离层模型参数(单位TECu);A0为根据固化于用户接收机的非播发电离层参数、用户穿刺点位置及观测时刻计算得到的电离层延迟预报值(单位TECu)。Ai为根据用户穿刺点位置及观测时刻计算的函数值,计算公式为:
| $ {A_i} = \left\{ {\begin{array}{*{20}{l}} {{N_{{n_i},{m_i}}} \times {P_{{n_i},{m_i}}}({\rm{sin}}\varphi ') \times }\\ {\;\;\;{\rm{cos}}({m_i} \times \lambda '),{m_i} \ge 0}\\ {{N_{{n_i},{m_i}}} \times {P_{{n_i},{m_i}}}({\rm{sin}}\varphi ') \times }\\ {\;\;\;{\rm{sin}}( - {m_i} \times \lambda '),{m_i}{\rm{ < }}0} \end{array},} \right.i = 1, \cdots ,9 $ | (5) |
式中,φ′与λ′为日固地磁坐标系下电离层交叉点的纬度和经度;ni、mi对应的取值为:
| $ \left\{ {\begin{array}{*{20}{l}} {{n_i} = 0,1,1,1,2,2,2,2,2}\\ {{m_i} = 0,0,1, - 1,0,1, - 1,2, - 2} \end{array}} \right.,i = 1, \cdots ,9 $ | (6) |
Pn, m为标准勒让德函数,Nn, m为正则化函数,可由式(7)确定:
| $ \begin{array}{l} {N_{n, m}} = \sqrt {\frac{{\left( {nm} \right)! \times \left( {2n + 1} \right) \times (2{\delta _{0, m}})}}{{{\rm{ }}\left( {n + m} \right)!}}} \\ {\delta _{0, m}} = \left\{ \begin{array}{l} 1, {\rm{ }}m = 0{\rm{ }}\\ 0, {\rm{ }}m > 0 \end{array} \right.{\rm{ }} \end{array} $ | (7) |
电离层延迟预报值A0由基于存储于用户接收机中的模型预报系数βi及电离层交叉点的位置(φ′, λ′)计算得到,具体计算公式为:
| $ \left\{ {\begin{array}{*{20}{l}} {{A_0} = \sum\limits_{j = 1}^{17} {{\beta _j}} {B_j}}\\ {{B_j} = \left\{ {\begin{array}{*{20}{l}} {{N_{{n_j},{m_j}}} \times {P_{{n_j},{m_j}}}({\rm{sin}}\varphi ') \times }\\ {\;\;{\rm{cos}}({m_j} \times \lambda '),{m_j} \ge 0}\\ {{N_{{n_j},{m_j}}} \times {P_{{n_j},{m_j}}}({\rm{sin}}\varphi ') \times }\\ {{\rm{sin}}( - {m_j} \times \lambda '),{m_j}{\rm{ < }}0} \end{array}} \right.} \end{array}} \right. $ | (8) |
式中,Bj的计算公式可参考Ai,βj根据非播发系数计算得到,具体计算方法参考北斗卫星导航接口控制文件。
1.3 北斗广域差分格网电离层模型北斗广域差分格网电离层垂直延迟参数为B1I频点的电离层垂直延迟(VTEC),可用距离表示,比例因子为0.125,单位m,范围为0~63.625 m,其中63.750 m表示格网点未被监测,63.875 m表示格网点不可用。格网点电离层信息的更新频率为6 min/次,电离层格网覆盖范围为70°~145°E、7.5°~55°N,按5°×2.5°划分成320个格网点,具体格网点编号参考北斗卫星导航接口控制文件[16-17]。
2 电离层模型精度评估方法本文以CODE格网电离层模型计算值为参考值,以北斗基本导航的BDSKlob模型、BDGIM模型及北斗广域差分格网电离层模型的计算值为待估值,分别计算各模型的均方根误差及改正比例,并评估北斗各电离层模型的性能。均方根计算公式为[18-22]:
| $ {\rm{RMS}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{({\rm{Ion}}{D_{{\rm{mod}}}}{\rm{ - Ion}}{D_{{\rm{ref}}}})}^2}} } $ | (9) |
改正比例计算公式为:
| $ {\rm{Per}} = \frac{1}{n}\sum\limits_{i = 1}^n {(1 - |{\rm{Ion}}{D_{{\rm{mod}}}}{\rm{ - Ion}}{D_{{\rm{ref}}}}|/{\rm{Ion}}{D_{{\rm{ref}}}})} $ | (10) |
式中,IonDmod为基于单频模型计算的垂直电离层延迟值,IonDref为基于CODE格网电离层模型计算的垂直电离层延迟值。
电离层延迟值为使用各电离层模型计算得到的实际值,电离层延迟误差是基于电离层模型计算的改正值与使用CODE格网电离层模型计算的电离层延迟值的差值。差值的均方根可反映模型的准确度,电离层延迟改正比例可反映模型的总体改正效果。
3 北斗基本导航电离层模型精度分析从模型参数的一致性、时间、空间、长时间评估结果、定位影响等方面比较分析BDGIM模型与BDSKlob模型的性能,其中电离层数据来自iGMAS监测评估中心综合预处理后的产品文件,CODE格网电离层模型文件可从IGS官网(ftp://cddis.nasa.gov/)下载。
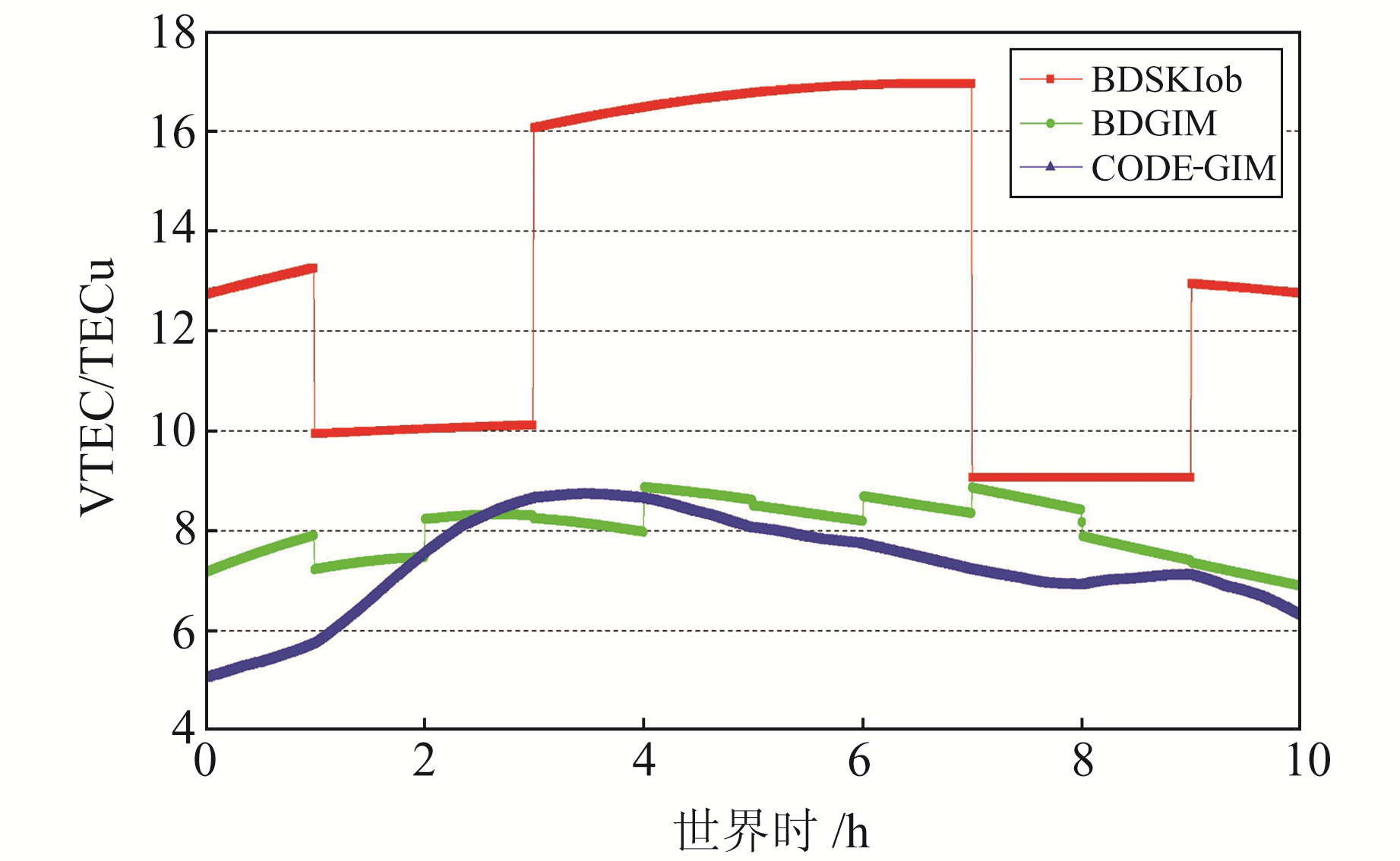
3.1 电离层模型参数一致性分析BDSKlob模型和BDGIM模型的参数每2 h更新一组,采用2个模型的电离层参数和CODE格网电离层模型计算垂直方向电离层延迟。图 1为2019-03-06部分时间段内各模型在110°E、60°N穿刺点处电离层垂直延迟变化。
|
图 1 BDSKlob/BDGIM/CODE-GIM垂直电离层延迟 Fig. 1 VTEC of BDSKlob/BDGIM/CODE-GIM |
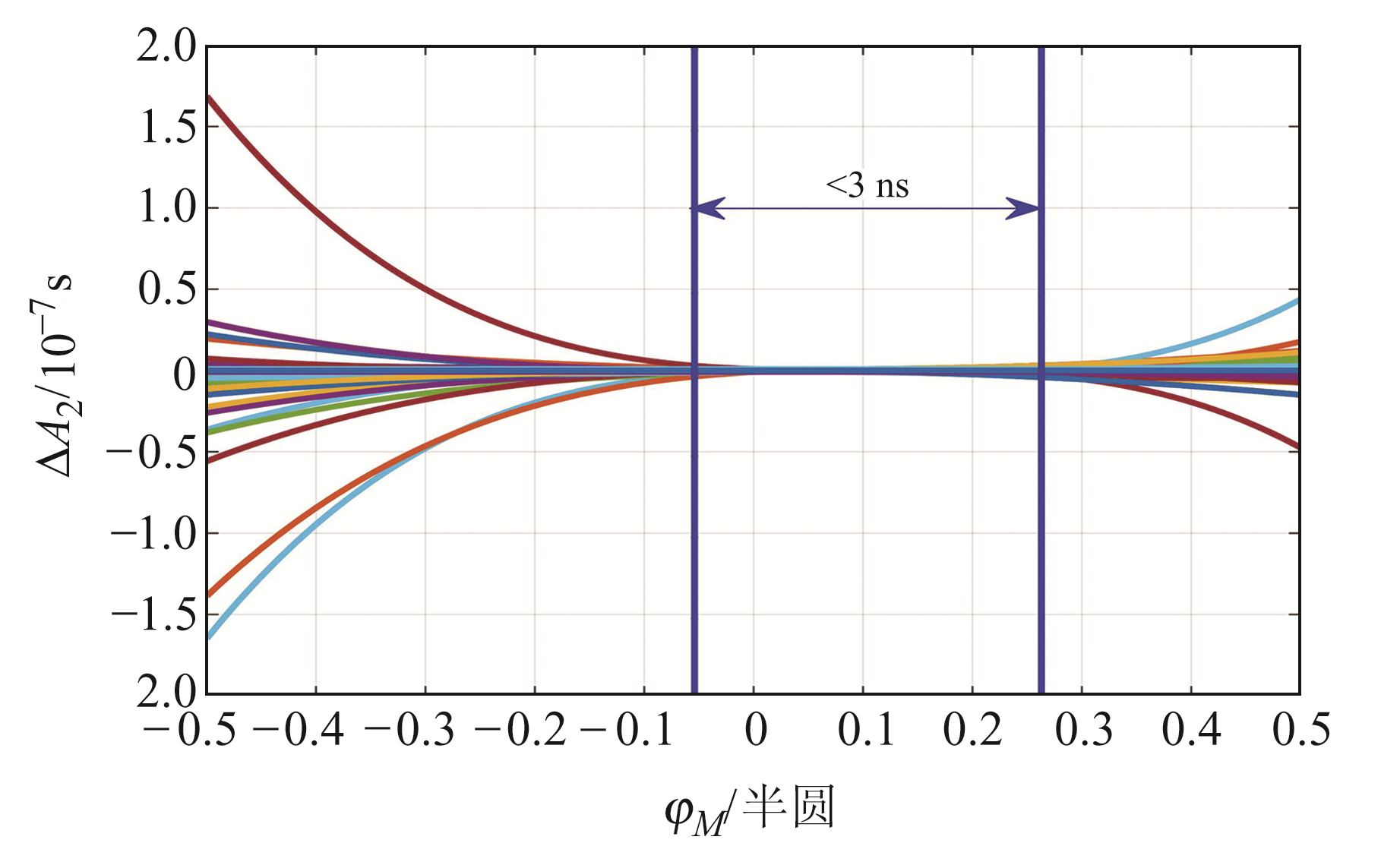
从图 1可以看出,BDSKlob模型在相邻电离层参数更新时明显存在延迟跳变现象,最大跳变量可达8 TECu。导致该现象的原因与BDSKlob模型中描述余弦函数幅值的A2参数有关,而A2值取决于BDSKlob模型中的4个α参数(见式(2))。为深入分析相邻2组α参数更新所引起的A2跳变,令ΔA2, i=A2(αi+1)-A2(αi),并绘制多条ΔA2, i曲线(图 2)。
|
图 2 相邻2组BDSKlob模型参数更新引起的ΔA2变化量 Fig. 2 Variation of ΔA2 with adjacent BDSKlob parameters updating |
从图 2可以看出,若以跳变量不超过3 ns为约束条件,即要求|ΔA2|不超3 ns,对应要求为北半球穿刺点纬度小于45°,南半球小于10°。由于余弦函数值不超过1,所以实际满足要求的穿刺点范围更大。BDGIM模型在参数更新时也存在跳变,但跳变量较小,垂直方向不超过1 ns,且与纬度变化无关,这是由于BDGIM模型与BDSKlob模型采用的建模方法不同。从用户的角度分析,BDSKlob模型出现8 ns的跳变是由A2变化直接引起的,但实际是由BDSKlob模型采用分段模型建模造成的。
3.2 电离层模型精度的空间变化为分析各电离层模型精度的空间变化情况,将纬度—87°~87°,经度—180°~180°的范围划分为5°×5°网格点,计算每个网格点2种电离层模型及CODE格网电离层模型的垂直电离层延迟改正值。此外,以CODE格网电离层模型为参考,计算2种模型的垂直电离层延迟误差的绝对值。
图 3为UTC 2019-03-09 06:00垂直电离层延迟值与延迟误差的空间分布,从图中可以直观看出,在北京时间14:00(UTC+8 h),东八区上空电离层较为活跃,电子含量较高,电离层延迟值较大。根据各模型计算的VTEC值虽存在差异,但基本都反映了总电子含量的分布情况,即处于夜晚的区域电离层较为平静,电离层延迟相对较小。BDGIM模型与CODE格网电离层模型较为接近,可在全球尺度上描述总电子含量的变化。BDSKlob模型采用地理坐标,南北半球电离层延迟值呈现对称特点,大部分高纬度区域计算的电离层延迟值较大,这与实际总电子含量的空间分布明显不符。这是由于在纬度较高区域αn|φM|n会随纬度的升高而快速增大,从而放大了BDSKlob模型中余弦函数的幅值A2,最终导致计算的电离层延迟值迅速变大。上述分析表明,BDSKlob模型不适用于高纬度地区的电离层延迟计算。

|
图 3 BDGIM模型、BDSKlob模型与CODE格网电离层模型VTEC之差绝对值 Fig. 3 VTEC difference between BDGIM、BDSKlob and CODE grid ionospheric models |
综合分析图 3可以得出以下结论:
1) BDSKlob模型在中国及周边亚太区域与CODE格网电离层模型较为接近,精度最高,而在高纬度地区延迟误差较大。这是因为高纬度地区BDSKlob模型中的振幅参数较大,且未实施限制,而GPS限制穿刺点纬度不超过74.88°[15]。
2) BDGIM模型在全球范围内与CODE格网电离层模型的差异较小,分布均匀,且南北半球无明显差异,在高纬度地区与CODE格网电离层模型的一致性较好。相对于BDSKlob模型,BDGIM模型在全球大部分范围都有明显提升。
3) 从BDGIM模型的电离层延迟误差可以看出,在70°S、30°W附近BDGIM模型与CODE格网电离层模型的垂直电离层延迟误差明显比其他区域大,这主要是受CODE格网电离层模型数据质量的影响,导致计算的VTEC结果出现异常,这一点从图 3(c)也能看出。
图 4为北斗2种模型电离层延迟误差随纬度的变化情况,从图中可以看出,在60°以上的高纬度地区,BDSKlob模型的精度快速下降,误差远大于BDGIM模型。从整体上看,BDGIM模型的VTEC在大部分纬度区域精度都较好,北半球精度高于南半球。这是因为BDGIM模型目前仍利用位于中国境内的观测数据生成,而南半球参与电离层模型解算的数据较少,所以南半球电离层精度较差。随着越来越多的数据参与生成BDGIM模型参数,南北半球的精度分布将会更加均匀。

|
图 4 北斗电离层模型电离层延迟误差随纬度变化情况 Fig. 4 Variation of ionospheric delay error of BDS ionospheric models with latitudes |
为分析不同电离层模型精度随时间的变化,选取低纬度(20°N, 110°E)、中纬度(40°N, 110°E)和高纬度(60°N, 110°E)3个点,按照30 s间隔分析3种电离层模型在2019-04-30的VTEC变化情况, 结果见图 5。从图中可以看出:

|
图 5 各模型电离层VTEC变化 Fig. 5 VTECs of different ionospheric models |
1) 各电离层模型的VTEC值白天变化剧烈,晚上变化较为平缓;低纬度地区变化剧烈,高纬度地区变化平缓。这与白天及赤道附近太阳辐射较高、电离层活跃相符。
2) 在低纬度区域,BDGIM模型与CODE格网电离层模型最为接近,尤其白天的符合程度较好;在中高纬度区域,BDSKlob模型明显变差,这会导致白天时段的电离层延迟值估计过高;
3) BDGIM模型整体上与CODE格网电离层模型最为接近,在高纬度区域明显优于BDSKlob模型。
3.4 电离层模型长期性能评估按照南、北半球(高、中、低纬度)、中国区域(70°~145°E, 7.5°~55°N)和全球范围,以5°×2.5°间隔划分网格,并计算每个格网点在白天(地方时8:00~20:00)和夜晚(地方时20:00~次日8:00)时段的模型改正比例及均方根,统计结果见表 1。
|
|
表 1 BDGIM与BDSKlob模型性能统计 Tab. 1 Performance statistics of BDGIM and BDSKlob models |
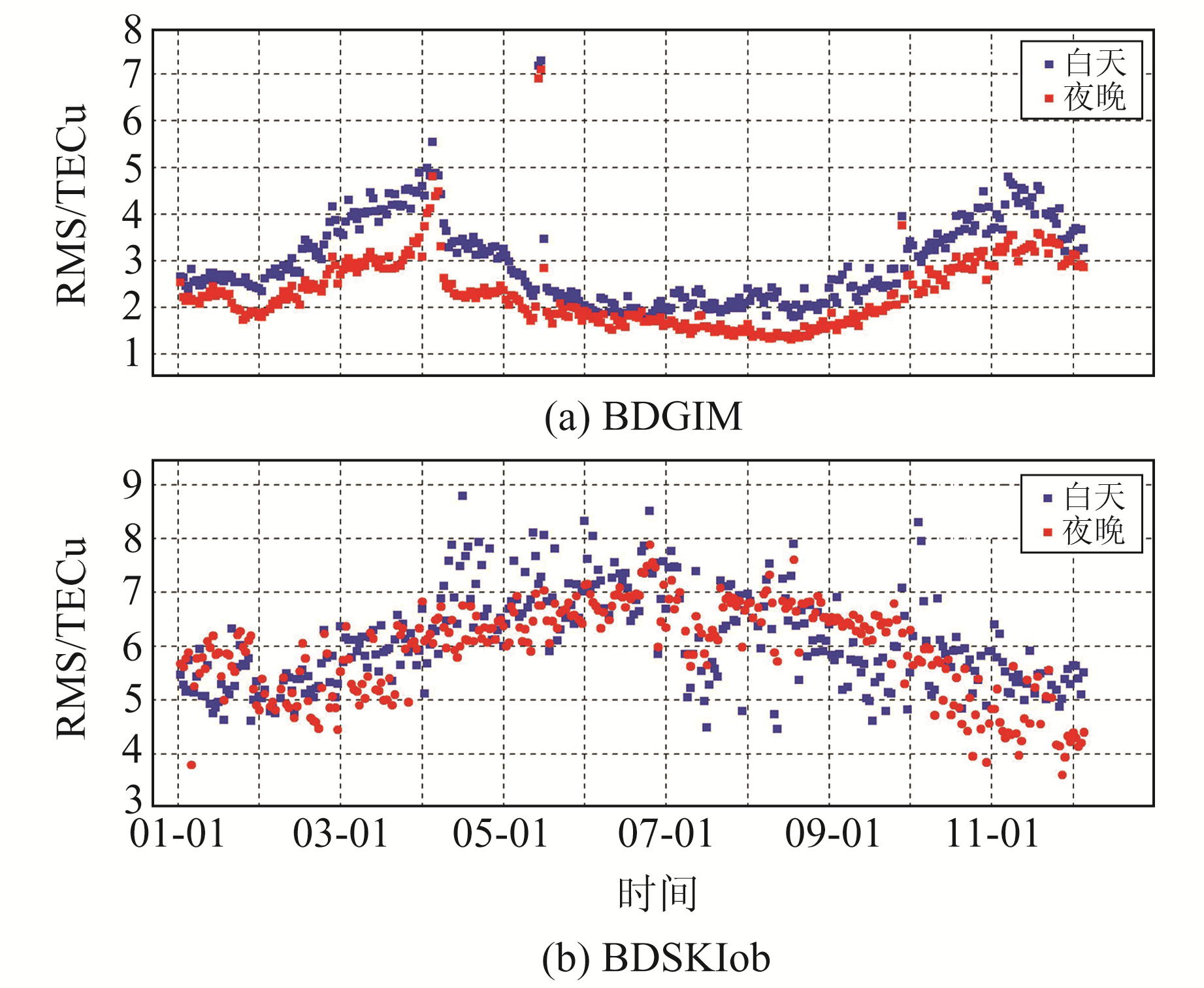
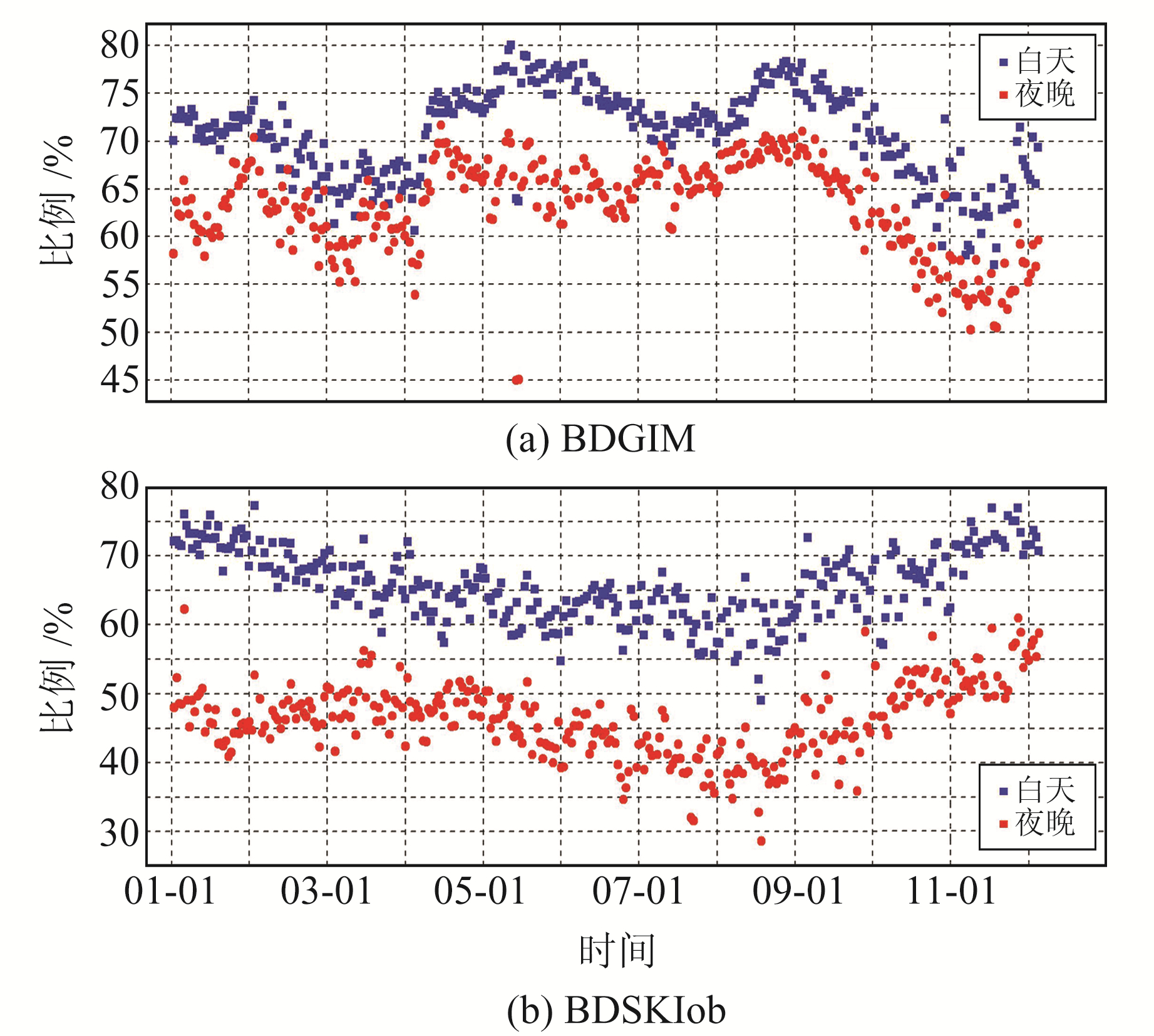
图 6为BDGIM模型和BDSKlob模型2019年白天和夜晚时段全球范围内电离层模型精度的变化情况,图 7为BDGIM模型和BDSKlob模型2019年白天和夜晚时段全球范围内电离层改正比例变化情况。从表 1和图 6可以看出:1)南半球高纬度地区BDGIM模型精度稍差,其他地区BDGIM模型精度较优,整体RMS值小于4 TECu;2)BDSKlob模型精度在白天和夜晚基本相当,夜晚时段BDGIM模型精度优于BDSKlob模型;3)BDGIM模型精度白天比夜晚高,春秋季较高,夏冬季较低。从图 7电离层模型的改正比例可以看出:1)BDGIM模型在中国区域的改正比例超过78%,优于BDSKlob模型,全球范围的改正比例优于62%;2)BDSKlob模型在中国区域的改正比例约为71%,全球范围内约为57%,白天时段改正比例比夜晚整体提高25%;3)BDGIM模型在春秋季的改正比例优于夏冬季,BDSKlob模型的改正比例夏季较低,春冬季较高;4)BDGIM模型的精度白天比夜晚低,但改正比例白天高于夜晚,这主要是由于夜间电离层活动较白天更为平静,量级较小。
|
图 6 2019年BDGIM/BDSKlob昼夜全球平均RMS Fig. 6 Global mean RMS of BDGIM/BDSKlob models in 2019 |
|
图 7 2019年BDGIM/BDSKlob昼夜全球平均改正比例 Fig. 7 Global mean correction ratio of BDGIM/BDSKlob models in 2019 |
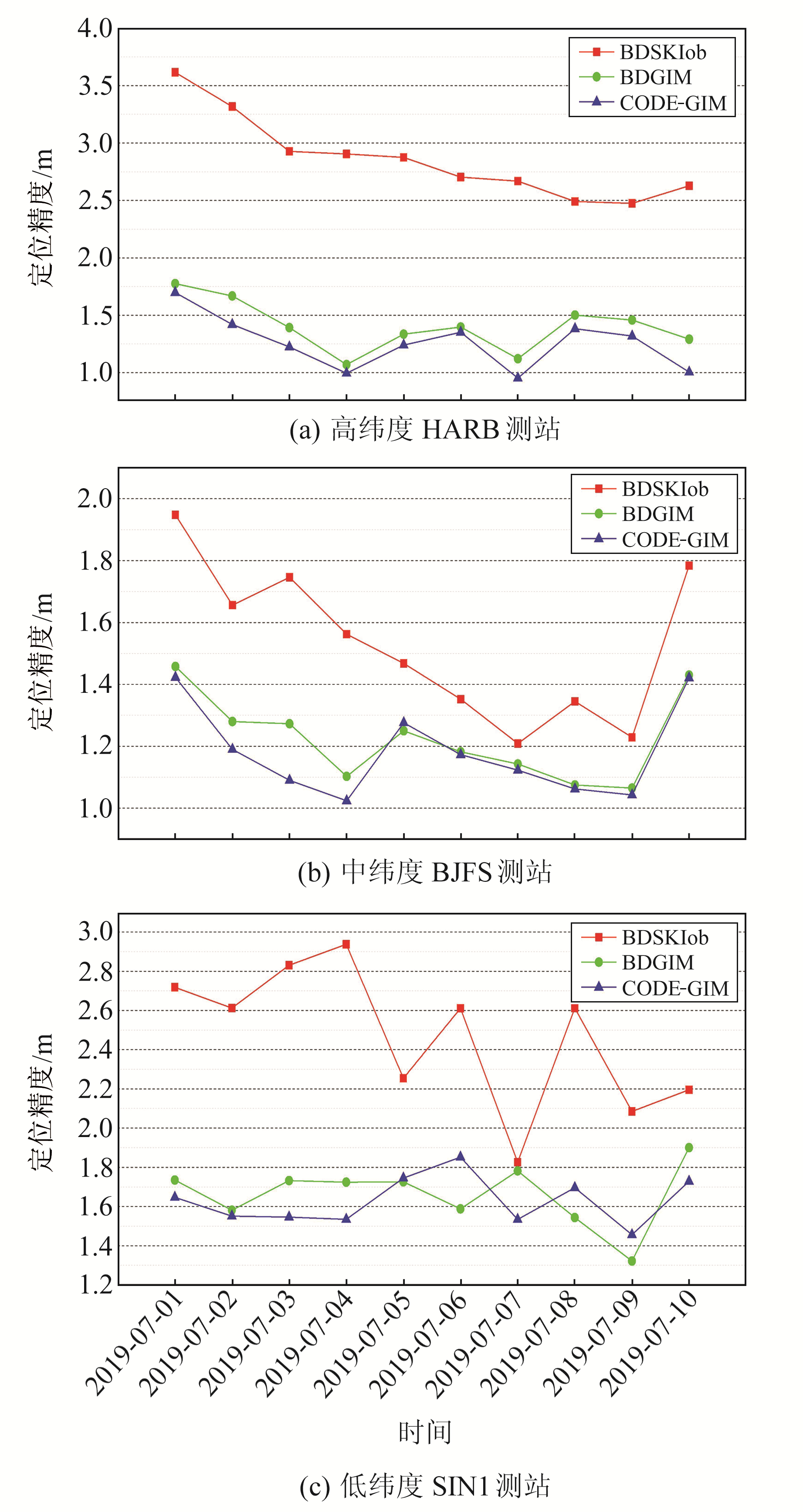
为分析北斗电离层模型对伪距单点定位的影响,从北半球的高、中、低纬度地区分别选取1个IGS测站2019-07-01~07-10的观测数据,固定其他传输路径误差改正方法,分别统计采用BDGIM模型、BDSKlob模型及CODE格网电离层模型改正电离层延迟情况下定位误差的RMS值。表 2为2019-07-06不同测站三种电离层模型E、N、U三方向及三维定位结果的准确度统计,图 8为不同测站10 d内定位精度的变化情况。
|
|
表 2 基于不同电离层模型的不同纬度带测站三维定位精度比较 Tab. 2 Comparisons of three dimensional positioning accuracy of stations in different latitudes ofdifferent ionospheric models |
|
图 8 电离层定位结果 Fig. 8 Ionospheric positioning results |
从图 8可以看出,北半球不同纬度地区BDGIM模型的定位精度均优于BDSKlob模型,高纬度的HARB测站更为明显。在高纬度地区,CODE格网电离层模型的精度比BDGIM模型优,中低纬度地区2个模型的精度基本相当。
从表 2可以看出,BDGIM模型在北半球的三维定位精度优于1.6 m,CODE格网电离层模型的定位精度优于1.9 m,BDGIM模型和CODE格网电离层模型在中纬度地区的定位精度最优,两者均优于1.2 m。BDSKlob模型在高纬度地区性能下降,HARB测站使用该模型的定位精度为2.7m;位于赤道附近的SIN1测站定位精度比中高纬度地区测站差,这可能与赤道地区电离层较为活跃有关。相比于BDSKlob模型,BDGIM模型在高、中、低纬度地区的定位精度分别提升48%、12%和39%。
4 北斗广域差分格网电离层模型精度分析以CODE格网电离层模型为基准,以2018年全年北斗广域差分格网电离层模型信息为待评估值,评估差分格网电离层模型的偏差精度、改正率及覆盖范围。北斗广域差分格网电离层模型待评估值为iGMAS监测评估中心提供的各测站预处理综合后的数据,CODE格网基准电离层模型文件可从IGS网站下载。
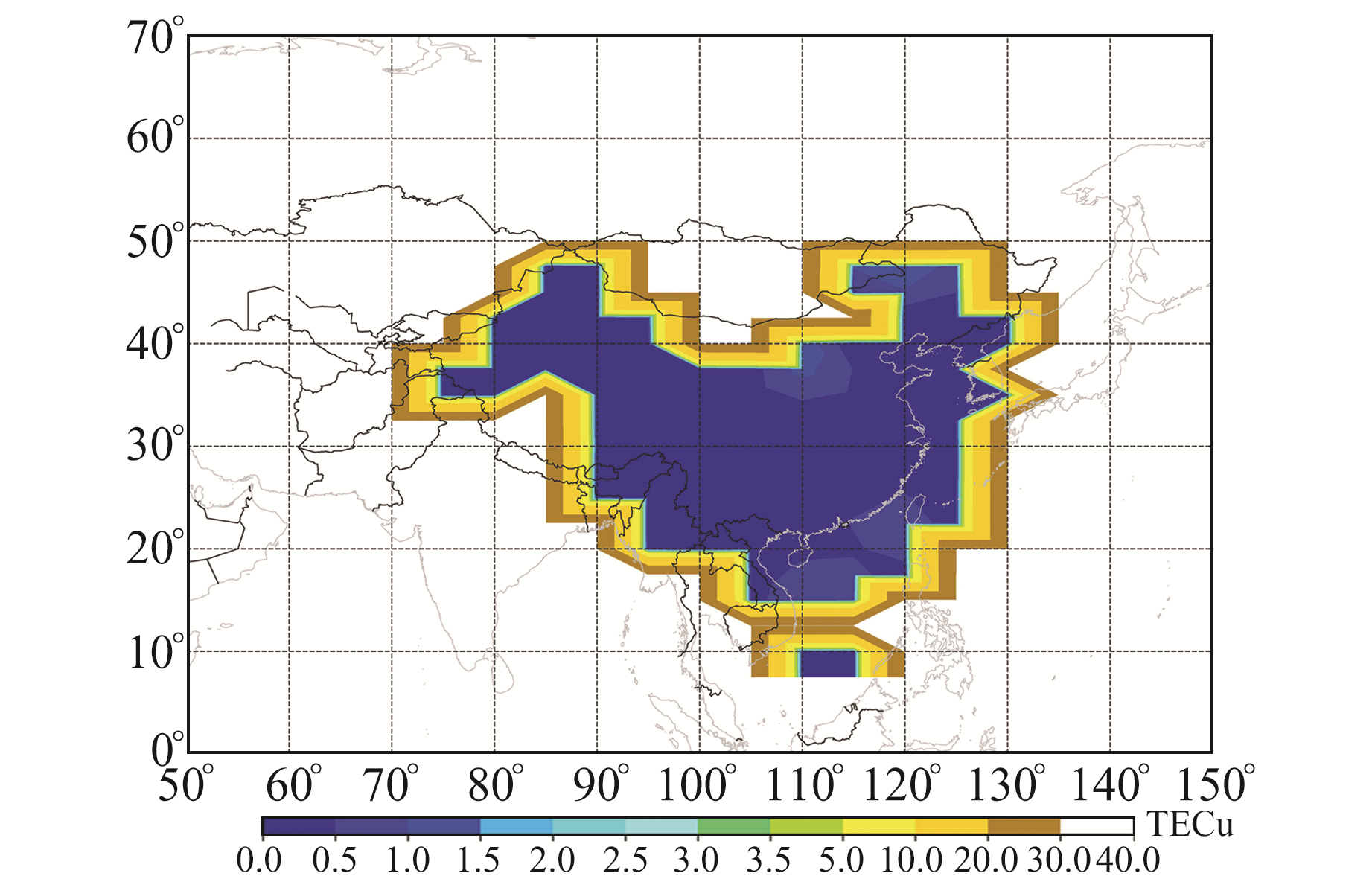
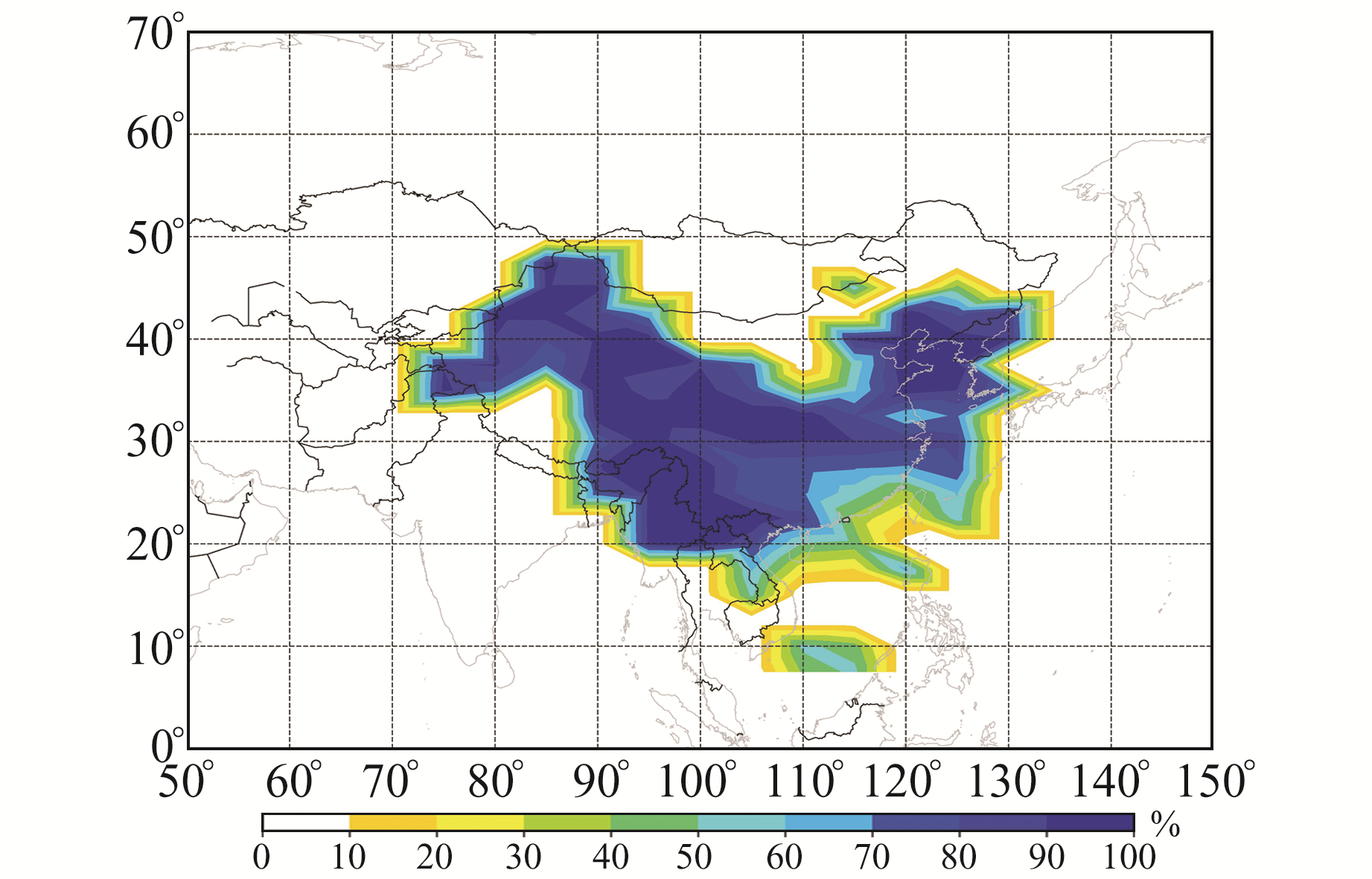
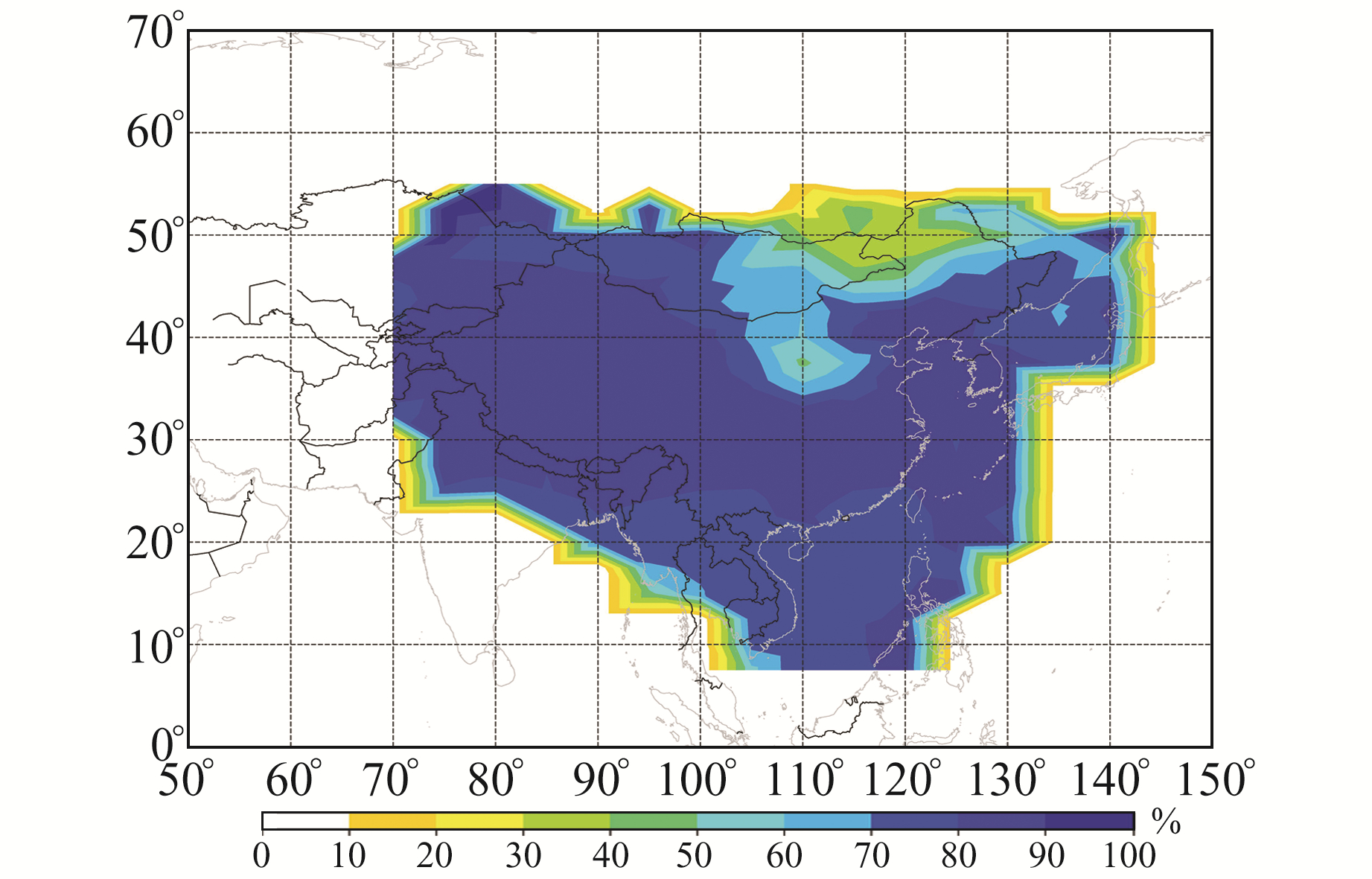
4.1 电离层模型服务性能覆盖性分析图 9和10为2018-12-30 18:00北斗广域差分格网电离层模型的电离层延迟误差和改正比例的瞬时结果,图 11和12为2018年北斗广域差分格网电离层模型的电离层延迟误差和改正比例的年评估结果。
|
图 9 北斗广域差分格网电离层模型电离层延迟误差 Fig. 9 Ionosphere delay error of Beidou wide area differential grid ionosphere modle |
|
图 10 北斗广域差分格网电离层模型改正比例 Fig. 10 Correction ratio of Beidou wide area differential grid ionosphere modle |

|
图 11 北斗广域差分格网电离层模型电离层延迟误差年评估结果 Fig. 11 Annual evaluation results of ionospheric delay error of Beidou wide area differential grid ionospheric modle |
|
图 12 北斗广域差分格网电离层模型改正比例年评估结果 Fig. 12 Annual evaluation results of correction ratio of Beidou wide area differential grid ionospheric modle |
从图 9和10可以看出,有效覆盖区域约占格网点电离层信息覆盖区域的2/3,基本覆盖了中国陆地区域,精度优于3 TECu,改正比例在70%以上,南海地区电离层延迟误差精度较差,约为12 TECu,改正比例约为50%。这主要是受测站分布的影响,导致该地区数据质量较差。
从图 11和12可以看出,北斗广域差分格网电离层模型的电离层延迟误差和改正比例可覆盖中国全域,电离层延迟误差精度优于3 TECu,且大部分地区小于2 TECu。除东北和内蒙古少部分区域外,其余大部分陆地区域的改正比例大于80%,南海区域的改正比例基本在70%左右。
4.2 电离层修正精度长短期变化分析 4.2.1 短期变化趋势分析图 13为北斗广域差分格网电离层模型中所有格网点的电离层延迟误差和改正比例平均值每小时的变化情况,共计24组。从图中可以看出,格网点电离层延迟误差白天(UTC 00:00~12:00)高于夜间(UTC 12:00~24:00),白天最高约为3.2 TECu,夜间变化平缓,约为1.0 TECu。格网电离层模型改正比例在白天和晚上呈周期变化,最高为88%,最低为72%。
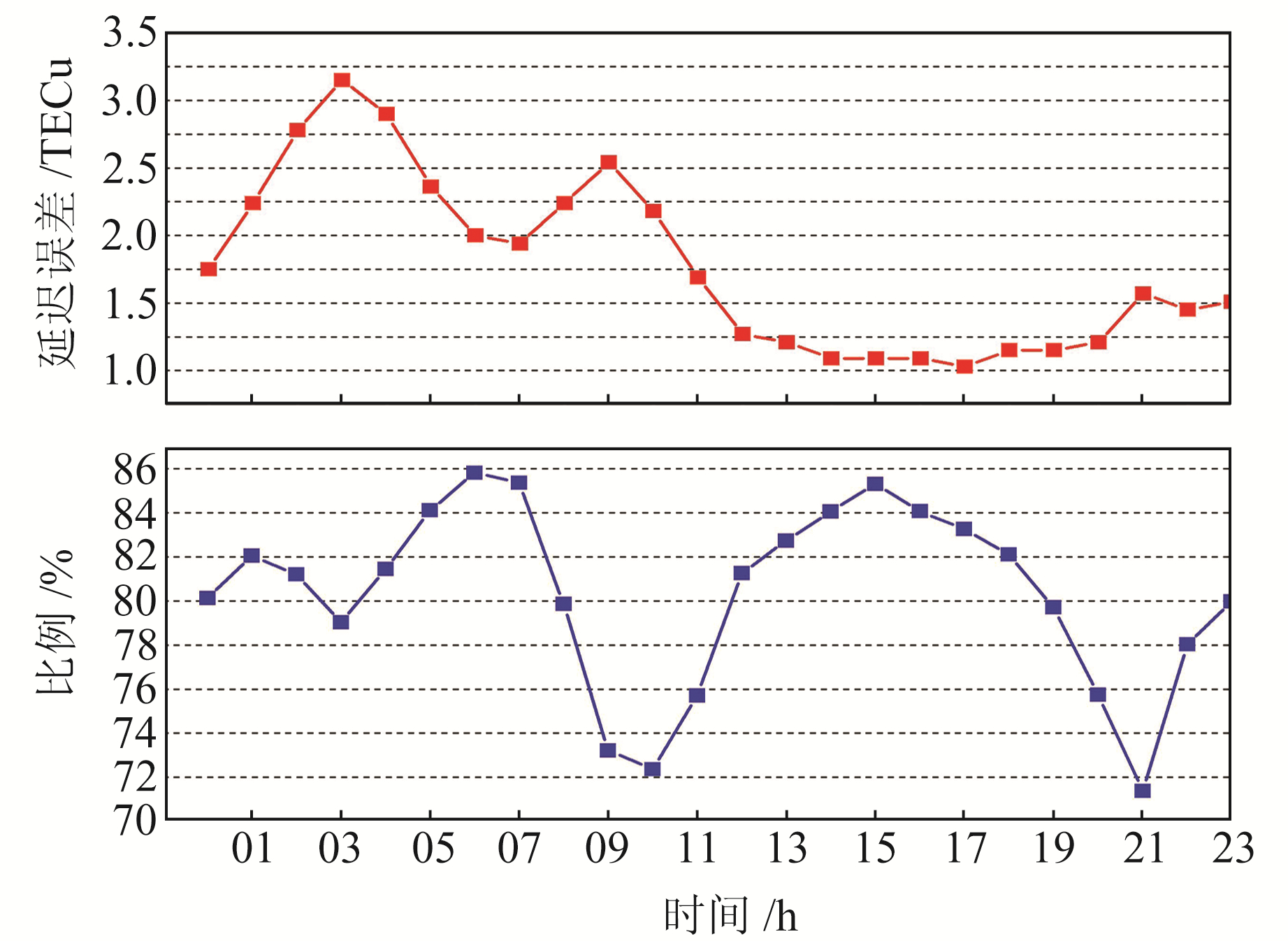
|
图 13 北斗广域差分格网电离层模型的电离层延迟误差和改正比例每小时变化 Fig. 13 Hourly variation of ionospheric delay error and correction ratio of Beidou wide area differential grid ionospheric modle |
图 14为2018年北斗广域差分格网电离层模型的电离层延迟误差和改正比例均值变化趋势,从图中可以看出,电离层延迟误差精度在春秋季较高,夏冬季较低,这与春秋季太阳活动剧烈有关,全年总体变化优于2.3 TECu,冬季最优达到1.8 TECu。改正比例特征为夏季较高、春冬季较低,全年大部分时间的改正比例优于80%,夏季最高可达83%。
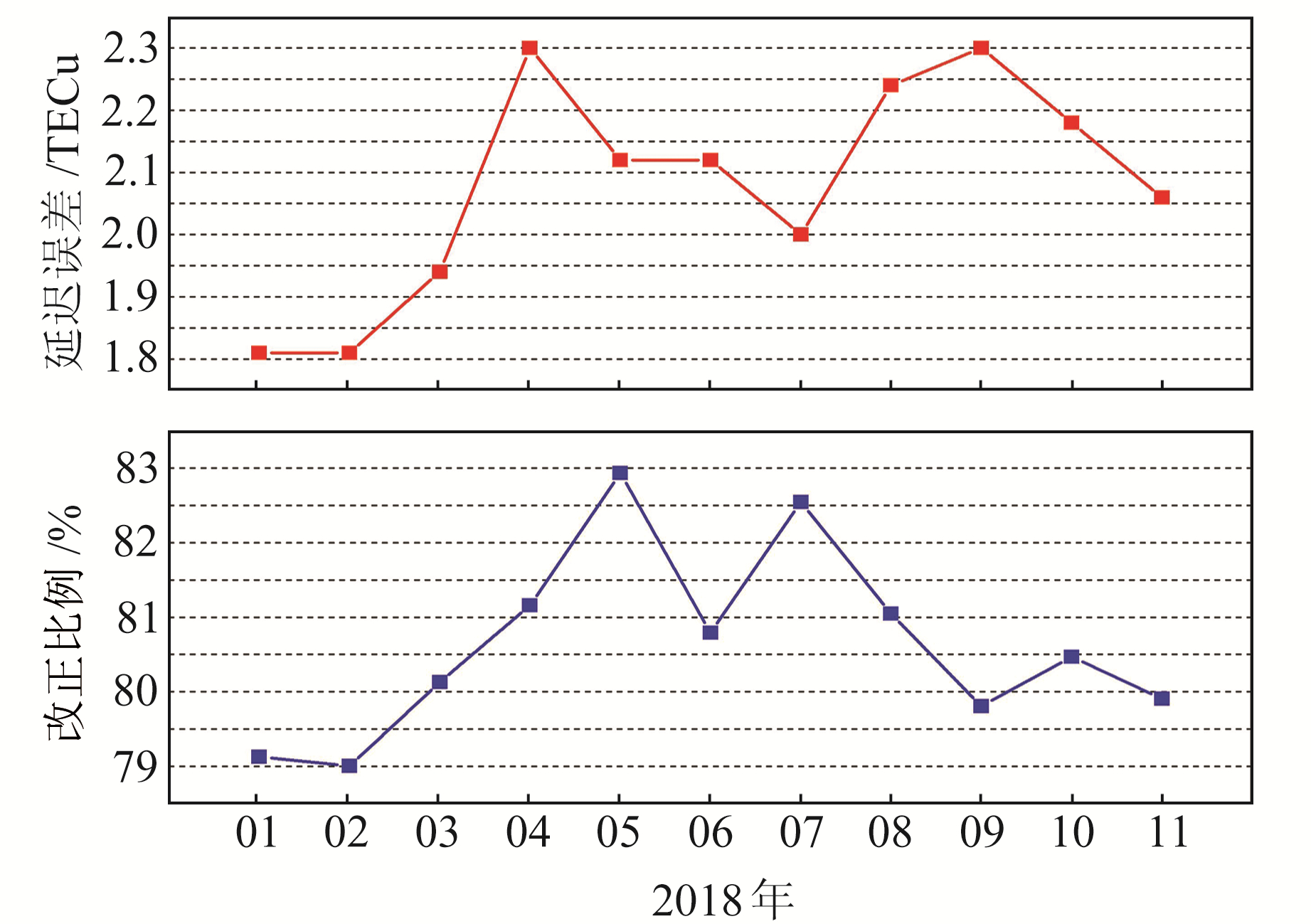
|
图 14 北斗广域差分格网电离层模型的电离层延迟误差和改正比例月变化 Fig. 14 Monthly variation of ionospheric delay error and correction ratio of Beidou wide area differential grid ionospheric modle |
相比于BDSKlob模型,BDGIM模型在覆盖范围和定位性能等方面均有所提升,在高纬度区域提升效果更明显。BDGIM模型在中国区域的改正比例达78%,全球范围可达63%。北斗广域差分格网电离层模型基本可覆盖中国陆地大部分区域,电离层延迟误差大部分优于3 TECu,改正比例优于80%。BDGIM模型的精度与北斗广域差分格网电离层模型相当,两者均远优于BDSKlob模型。
目前我国BDGIM模型和北斗广域差分格网电离层模型主要由中国区域测站数据计算获得,因此BDGIM模型在南半球高纬度地区及差分格网电离层模型在南海区域的精度相对较差。随着北斗三号基本导航系统的进一步完善及BDSBAS的建设,BDGIM模型和北斗广域差分格网电离层模型的精度将得到进一步提升。
本文主要运用CODE发布的GIM产品对北斗各电离层模型的精度进行分析,由于在中国区域所用测站较少,模型在中国区域的精度较差,仅用该模型评估北斗电离层模型的精度不够充分。下一步将增加GNSS实测数据并结合前人验证TEC模型精度的方法对GNSS电离层模型的精度进行评估。
致谢: 感谢IGS全球服务组织CODE中心和iGMAS监测评估中心提供精密电离层产品、广播电离层数据及北斗广域差分格网电离层数据。
| [1] |
刘帅, 贾小林. GNSS电离层模型改正精度评估与分析[J]. 空间科学学报, 2016, 36(3): 297-304 (Liu Shuai, Jia Xiaolin. Correction Accuracy Evaluation and Analysis for GNSS Ionosphere Model[J]. Chinese Journal of Space Science, 2016, 36(3): 297-304)
(  0) 0) |
| [2] |
陈秀德.电离层延迟改正模型算法的研究与探讨[D].西安: 长安大学, 2017 (Cheng Xiude. Research and Discussion on Algorithm of Ionospheric Delay Correction Model[D]. Xi'an: Chang'an University, 2017)
(  0) 0) |
| [3] |
程娜. GNSS广播电离层精度监测评估方法研究[D].西安: 长安大学, 2015 (Cheng Na. Study on Methods of Precision Monitoring and Assessment of Broadcast Ionospheric Model of GNSS[D]. Xi'an: Chang'an University, 2015)
(  0) 0) |
| [4] |
Klobuchar J A. Ionospheric Time-Delay Algorithm for Single-Frequency GPS Users[J]. IEEE Transactions on Aerospace and Electronic Systems, 1987, 23(3): 325-331
(  0) 0) |
| [5] |
GSA. Ionospheric Correction Algorithm for Galileo Single Frequency Users[EB/OL]. https://www.gsc-europa.eu/system/files/galileo_documents/Galileo_Ionospheric_Model.pdf, 2016
(  0) 0) |
| [6] |
JSC. GLONASS Interface Control Document——General Description of Code Division Multiple Access Signal System(Edition1.0)[Z]. 2016
(  0) 0) |
| [7] |
Yuan Y B, Wang N B, Li Z S, et al. The Beidou Global Broadcast Ionospheric Delay Correction Model(BDGIM) and Its Preliminary Performance Evaluation Results[J]. Navigation, 2019, 66(1): 55-69 DOI:10.1002/navi.292
(  0) 0) |
| [8] |
刘宸, 王威, 姜意, 等. BDS格网点电离层信息性能评估[J]. 全球定位系统, 2019, 44(5): 85-90 (Liu Chen, Wang Wei, Jiang Yi, et al. A Study on Performance of Ionospheric Grid Information of BDS[J]. GNSS World of China, 2019, 44(5): 85-90)
(  0) 0) |
| [9] |
张清华, 王源, 曾京, 等. 北斗系统广播电离层参数精度的评估[J]. 导航定位学报, 2015, 3(2): 16-18 (Zhang Qinghua, Wang Yuan, Zeng Jing, et al. Initial Assessment of BDS Broadcast Ionospheric Parameters Accuracy[J]. Journal of Navigation and Positioning, 2015, 3(2): 16-18)
(  0) 0) |
| [10] |
中国卫星导航系统管理办公室.北斗卫星导航系统空间信号接口控制文件: 公开服务信号(2.1)[Z]. 2016 (China Satellite Navigation Office. Beidou Navigation Satellite System Signal in Space Interface Control Document for Open Service Signal(2.1)[Z]. 2016)
(  0) 0) |
| [11] |
中国卫星导航系统管理办公室.北斗卫星导航系统空间信号接口控制文件: 公开服务信号B1C(1.0)[Z]. 2017 (China Satellite Navigation Office. Beidou Navigation Satellite System Signal in Space Interface Control Document for Open Service Signal BIC(1.0)[Z]. 2017)
(  0) 0) |
| [12] |
中国卫星导航系统管理办公室.北斗卫星导航系统空间信号接口控制文件: 公开服务信号B2a(1.0)[Z]. 2017 (China Satellite Navigation Office. Beidou Navigation Satellite System Signal in Space Interface Control Document for Open Service Signal B2a(1.0)[Z]. 2017)
(  0) 0) |
| [13] |
张强, 赵齐乐, 章红平, 等. 北斗卫星导航系统Klobuchar模型精度评估[J]. 武汉大学学报:信息科学版, 2014, 39(2): 142-146 (Zhang Qiang, Zhao Qile, Zhang Hongping, et al. Evaluation on the Precision of Klobuchar Model for Beidou Navigation Satellite System[J]. Geomatics and Information Science of Wuhan University, 2014, 39(2): 142-146)
(  0) 0) |
| [14] |
Wu X L, Hu X G, Wang G, et al. Evaluation of COMPASS Ionospheric Model in GNSS Positioning[J]. Advances in Space Research, 2013, 51(6): 959-968 DOI:10.1016/j.asr.2012.09.039
(  0) 0) |
| [15] |
周仁宇.北斗试验卫星系统服务性能初步分析[D].武汉: 武汉大学, 2018 (Zhou Renyu. Preliminary Analysis of the Service Performance of Beidou Experimental Satellite System[D]. Wuhan: Wuhan University, 2018)
(  0) 0) |
| [16] |
崔莹莹, 孟诏, 贾为民, 等. BD2系统广域差分格网电离层模型研究与应用[J]. 航天控制, 2014, 32(6): 12-15 (Cui Yingying, Meng Zhao, Jia Weimin, et al. The Research and Application of Wide Area Differential Grid Ionospheric Model in BD2 System[J]. Aerospace Control, 2014, 32(6): 12-15)
(  0) 0) |
| [17] |
于耕, 彭沫. BD星基增强系统格网电离层延迟算法[J]. 科学技术与工程, 2017, 17(22): 323-327 (Yu Geng, Peng Mo. Grid Ionospheric Delay Algorithm of BD Satellite-Based Augementation System[J]. Science Technology and Engineering, 2017, 17(22): 323-327 DOI:10.3969/j.issn.1671-1815.2017.22.053)
(  0) 0) |
| [18] |
张强, 赵齐乐, 章红平, 等.北斗卫星导航系统电离层模型精度的研究[C].第四届中国卫星导航学术年会, 武汉, 2013 (Zhang Qiang, Zhao Qile, Zhang Hongping, et al. Research on Beidou Navigation Satellite System Ionospheric Model Accuracy[C]. The 4th China Satellite Navigation Conference, Wuhan, 2013)
(  0) 0) |
| [19] |
程娜, 贾小林.基于改进CODE模型的北斗广播电离层模型精度评估[C].第五届中国卫星导航学术年会, 南京, 2014 (Cheng Na, Jia Xiaolin. Precision Assessment of Broadcast Ionospheric Model of COMPASS System Based on Improved CODE Model[C]. The 5th China Satellite Navigation Conference, Nanjing, 2014)
(  0) 0) |
| [20] |
李大武. BD-SBAS电离层与保护级算法研究[D].沈阳: 沈阳航空航天大学, 2018 (Li Dawu. Research on BD-SBAS Ionosphere and Protection Level Algorithm[D]. Shengyang: Shenyang Aerospace University, 2018)
(  0) 0) |
| [21] |
冯来平, 朱永兴. 北斗区域卫星导航系统电离层建模精度分析[J]. 海洋测绘, 2016, 36(5): 47-50 (Feng Laiping, Zhu Yongxing. Precision Analysis of Regional Ionosphere Model Based on Beidou Navigation Satellite System[J]. Hydrographic Surveying and Charting, 2016, 36(5): 47-50)
(  0) 0) |
| [22] |
Li Z S, Yuan Y B, Wang N B, et al. SHPTS: Towards a New Method for Generating Precise Global Ionospheric TEC Map Based on Spherical Harmonic and Generalized Trigonometric Series Functions[J]. Journal of Geodesy, 2015, 89(4): 331-345
(  0) 0) |
2. Xi'an Aerospace Data Technology Co Ltd, 59 Hangtian Road, Xi'an 710054, China
 2021, Vol. 41
2021, Vol. 41

