2. 华东交通大学土木建筑学院,南昌市双港东大街808号,330013;
3. 中铁第一勘察设计院集团有限公司轨道交通工程信息化国家重点实验室, 西安市西影路2号, 710043
近年来,不断累积的IGS基准站坐标数据为大地测量学和地球动力学研究提供了丰富的数据基础,也为GNSS坐标时间序列的研究提供了坚实的数据支撑[1]。GNSS坐标时间序列的精确预测对建筑物的变形监测、气候气象的预测及区域内地壳形变等研究具有重要意义。有研究指出,GNSS坐标时间序列在3个方向都有明显的周期性运动,其中高程方向的季节性变化最为显著[2-3]。另外,由于高程方向的噪声分量往往大于水平方向,且噪声模型的组成并不单一,使得建立高精度GNSS高程坐标时间序列预测模型的难度较大[4]。
诸多学者在GNSS坐标时间序列的拟合与预测领域进行了广泛研究[5-8],促进了GNSS坐标时间序列的研究进展,但针对高程坐标长期预测模型的研究仍存在一些不足:1)现阶段时间序列模型多存在建模复杂、稳定性差、无法动态调整模型参数等缺陷;2)模型对坐标数据的要求较高,建模精度容易受粗差影响,且未顾及数据缺失等不利影响;3)构建的模型缺乏长期预测能力,在预测时需要滚动预测才能保持模型的精度,增加了模型的操作难度与运行时间。
针对这些问题,本文提出将Prophet模型应用于GNSS高程坐标时间序列中,该模型对数据有良好的适应能力,在长期预测中有较高的可靠性与精度,且无需太多关于时间序列的先验知识。本文首先检验了Prophet模型在高程坐标时间序列中的适用性;再针对Prophet模型对非线性部分预测能力较弱的缺陷,引入随机森林(RF)模型,得到Prophet-RF组合预测模型;最后根据2种模型的特性设计多种组合方案, 并利用BJFS站的实测高程坐标数据检验不同组合方案的精度与适用性。
1 基本原理与评价指标 1.1 Prophet模型Prophet模型由Taylor等[9]于2017年提出并发布了相关的开源软件包,是一种可以分析时间序列的新模型,包括处理时间序列数据中的异常值和缺失值及对时间序列进行长短期预测并研究其变化规律。该模型在电离层异常探测[10]、市场销量研究[11]、空气质量分析[12-13]等领域都有成功案例,但在GNSS坐标时间序列方面几乎没有涉及。
Prophet模型在预测时的循环分析共分为4个部分:建立模型、预测评估、表现问题、可视化检测预测结果。使用Prophet模型分析数据时将4个部分构成一个循环体,根据不同专业及数据的具体要求对模型进行人工调整,并结合模型的自动预测功能,使Prophet模型较传统的时间序列模型有更好的灵活性与适用性[9]。
Prophet模型是一个广义加法模型,并且使用基于贝叶斯的曲线拟合方法对时间序列进行平滑和预测[9-10]。模型由趋势项、周期项及假日项组成,其加法模型的基本分解形式为:
| $ y\left( t \right) = g\left( t \right) + s\left( t \right) + h\left( t \right) + \varepsilon \left( t \right) $ | (1) |
其中,g(t)为趋势项,表示时间序列中非周期部分的变化函数,包含不同程度的假设与可调节光滑度的参数[11];s(t)为周期项,在Prophet模型中使用傅里叶级数对其进行构造,常以周、月、季度或年作为单位;h(t)为假日项,表示因假期或特殊原因造成的不规则影响,在GNSS坐标时间序列中通常不存在此类情况,故在分解数据时可不必对假日项进行建模;ε(t)为残差项,服从正态分布,表示模型中未预测到的随机趋势。具体描述见文献[9]。
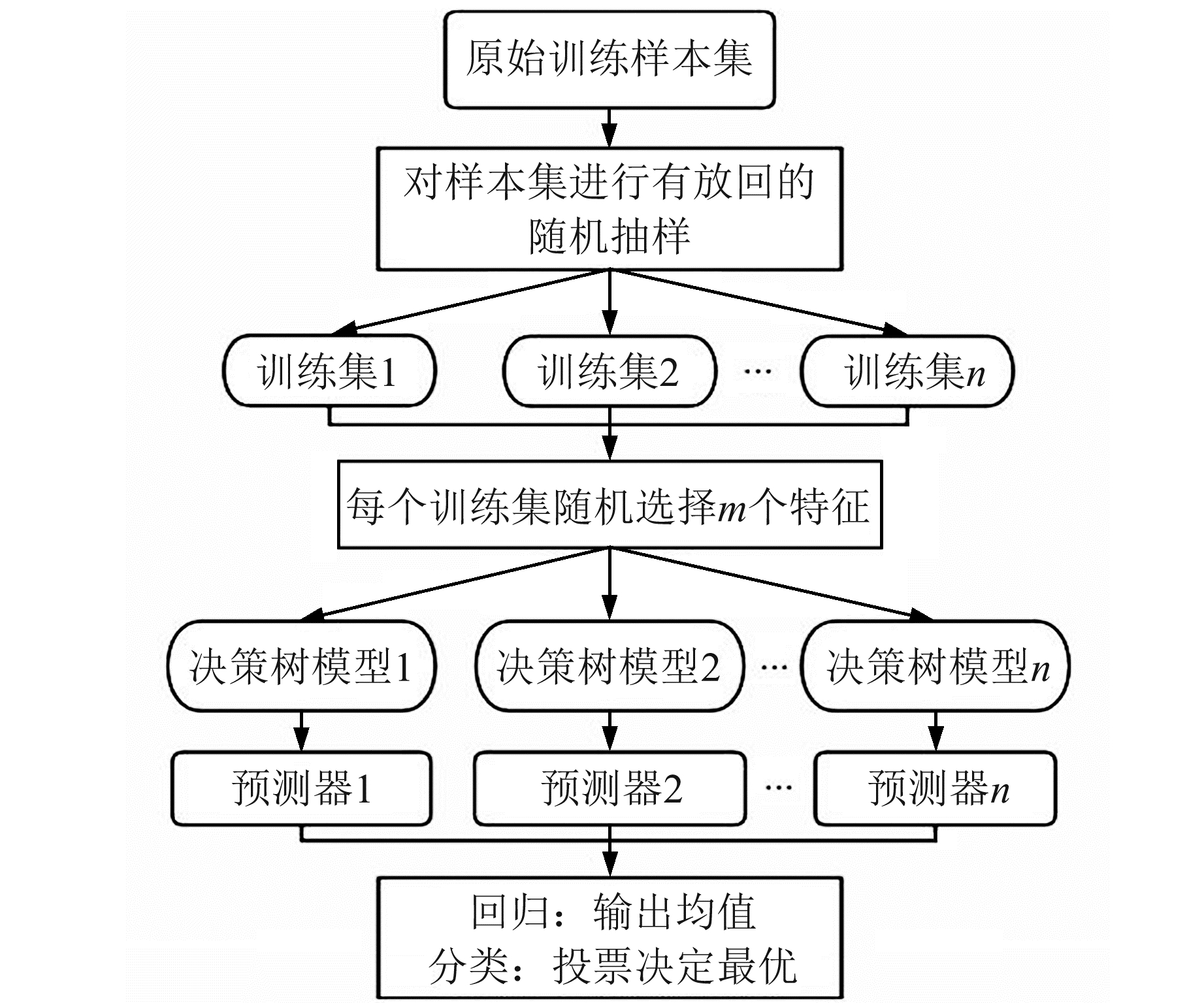
1.2 随机森林模型随机森林(random forest,RF)模型是一种具备集成思想的机器学习模型,是由一定数量的弱学习器决策回归树(classification and regression tree,CART)结合bagging集成学习理论和随机特征子空间构成的强学习器[14-15]。RF模型的随机性表现在随机选择样本及随机选择特征,在选择样本时采用的是bootstrap重抽样方法,其特点是既能保证每个样本在每次抽取时都有相同的概率被抽中,又能在不降低样本训练规模的同时留出验证集[16];而在特征选择上,CART使用基尼系数进行选择,基尼系数越小表示特征越好。构建RF模型的步骤如图 1所示。
|
图 1 随机森林算法流程 Fig. 1 Random forest algorithm flow |
RF模型的构建流程为:
1) 采用bootstrap重抽样方法从原始数据集N中抽取ntree个训练样本集,每个训练样本集的大小约为原始数据集的三分之二。
2) 对每个训练样本集分别建立CART,并从全部M个特征中随机抽取mtry个特征作为CART的特征变量,再根据基尼系数最小原则选择最佳方案对节点进行分裂。
3) 每棵决策树在生长期间都按照步骤2)进行,并保持mtry的大小不变;且每棵决策树都要进行完全的生长,不对其进行任何剪枝操作。
4) 由前3步生成的ntree棵决策树组成一个随机森林。在分类问题中,RF模型对检验集进行投票并根据少数服从多数的原则进行分类预测;而在回归问题中,将每棵树的结果等权相加,求得的均值作为最终预测值。
1.3 模型评价指标本文使用均方根误差(RMSE)与平均绝对误差(MAE)作为各个模型拟合与预测精度的评判标准。RMSE与MAE的定义为:
| $ {\rm{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{({g_i} - {h_i})}^2}} } $ | (2) |
| $ {\rm{MAE}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^n |{g_i} - {h_i}| $ | (3) |
式中,g为预测值,h为原始值。RMSE和MAE的值越小,表示模型的精度越高;反之,则表示模型的精度越低。
通过引入皮尔森相关系数(Pearson correlation coefficient)和斯皮尔曼相关系数(Spearman correlation coefficient)来检验各模型预测数据与原始数据的相关性。通常皮尔森相关系数对数据的要求较高,需要2个变量为线性关系且符合正态分布,而斯皮尔曼相关系数对数据没有过多限制。根据表 1可对数据的相关性强弱进行判断[17],相关系数的绝对值越接近1,表示其相关程度越强。
|
|
表 1 相关性强弱判定表 Tab. 1 Correlation strength judgment table |
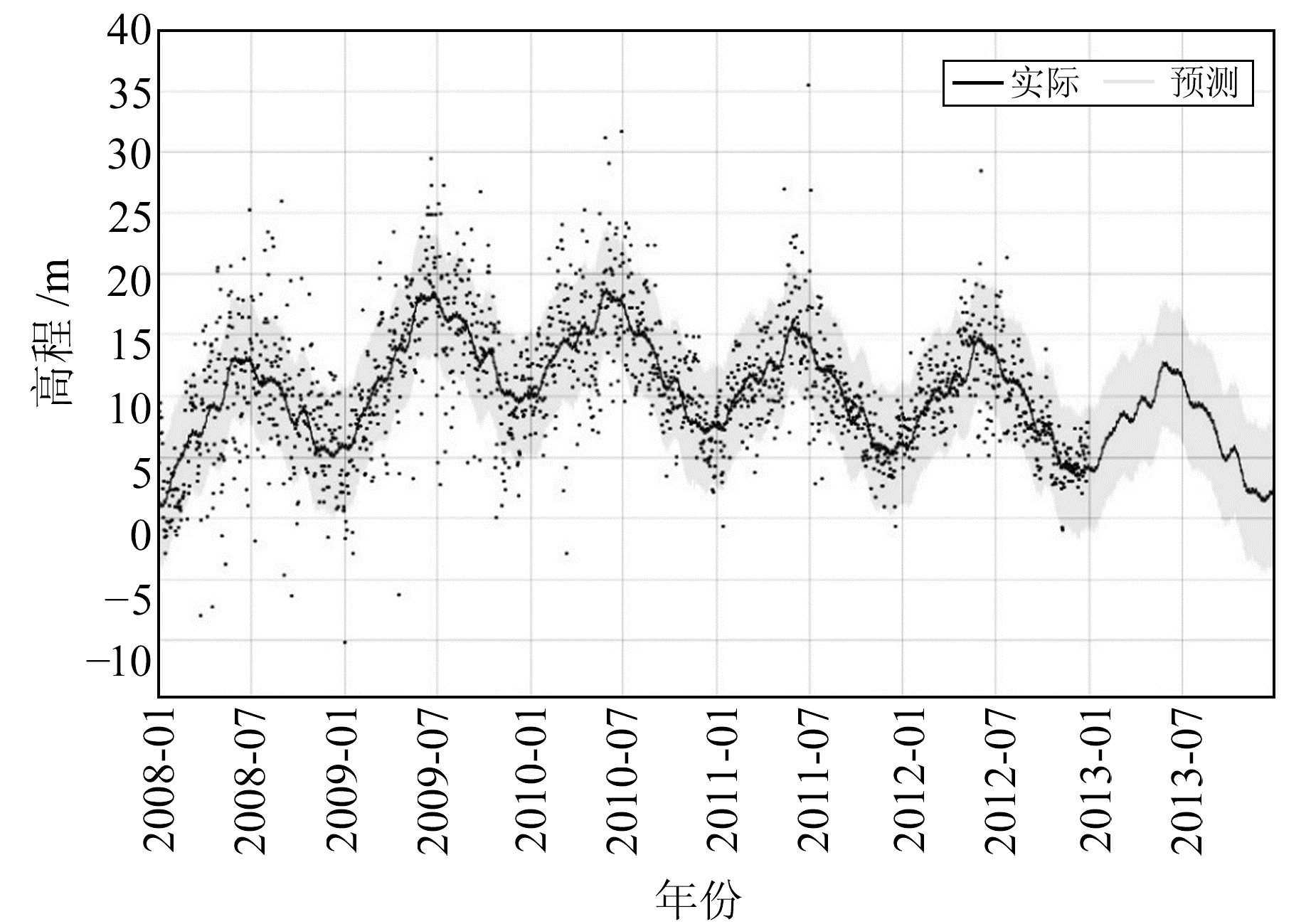
选用BJFS站2008~2013年的高程坐标数据作为实验数据,数据来源于中国地震局GNSS数据产品服务平台(http://www.cgps.ac.cn/), 采样间隔为1/365.25 a,最大采样频率为365.25 Hz。本文所有实验方案都保持相同的样本集划分:2008-01-01~2012-12-31的每日数据作为训练样本集,2013-01-01~12-31的数据作为测试样本集。图 2为由Prophet模型得到的预测结果,可以看出,Prophet模型能够较好地拟合原始数据中的周期性变化,且具有较好的抗粗差能力。
|
图 2 Prophet模型对BJFS站高程坐标的预测 Fig. 2 Prediction of elevation coordinate of BJFS station by Prophet model |
通过分析Prophet模型与RF模型的特性构建不同的组合方案:方案1是基于Prophet模型自带的分解功能,将数据分解为周期部分与非线性部分;方案2是假设在数据噪声量级较大的情况下,使用Prophet模型对原始数据进行拟合;方案3是假设在数据噪声量级较小的情况下,使用RF模型对原始数据进行拟合。
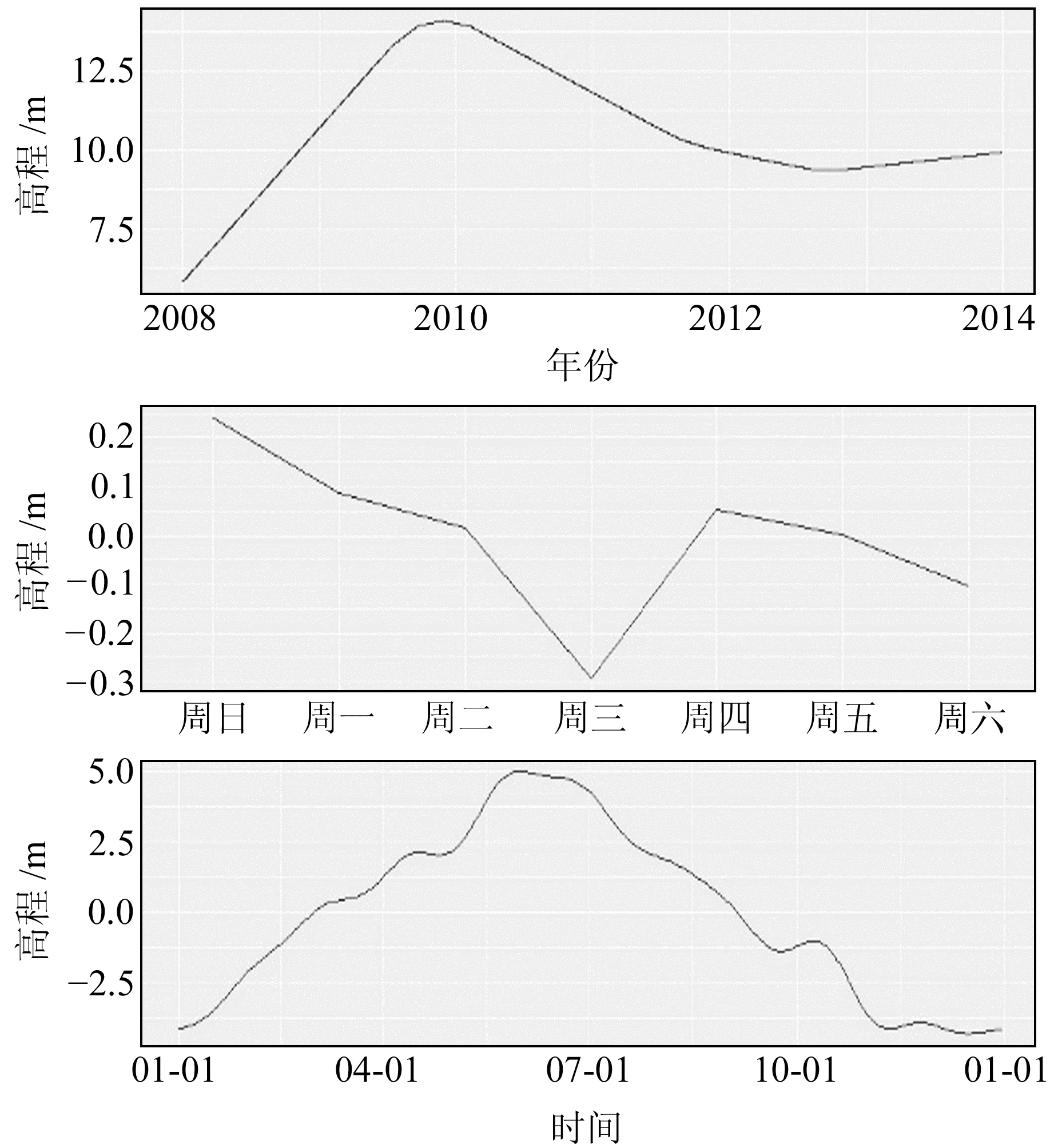
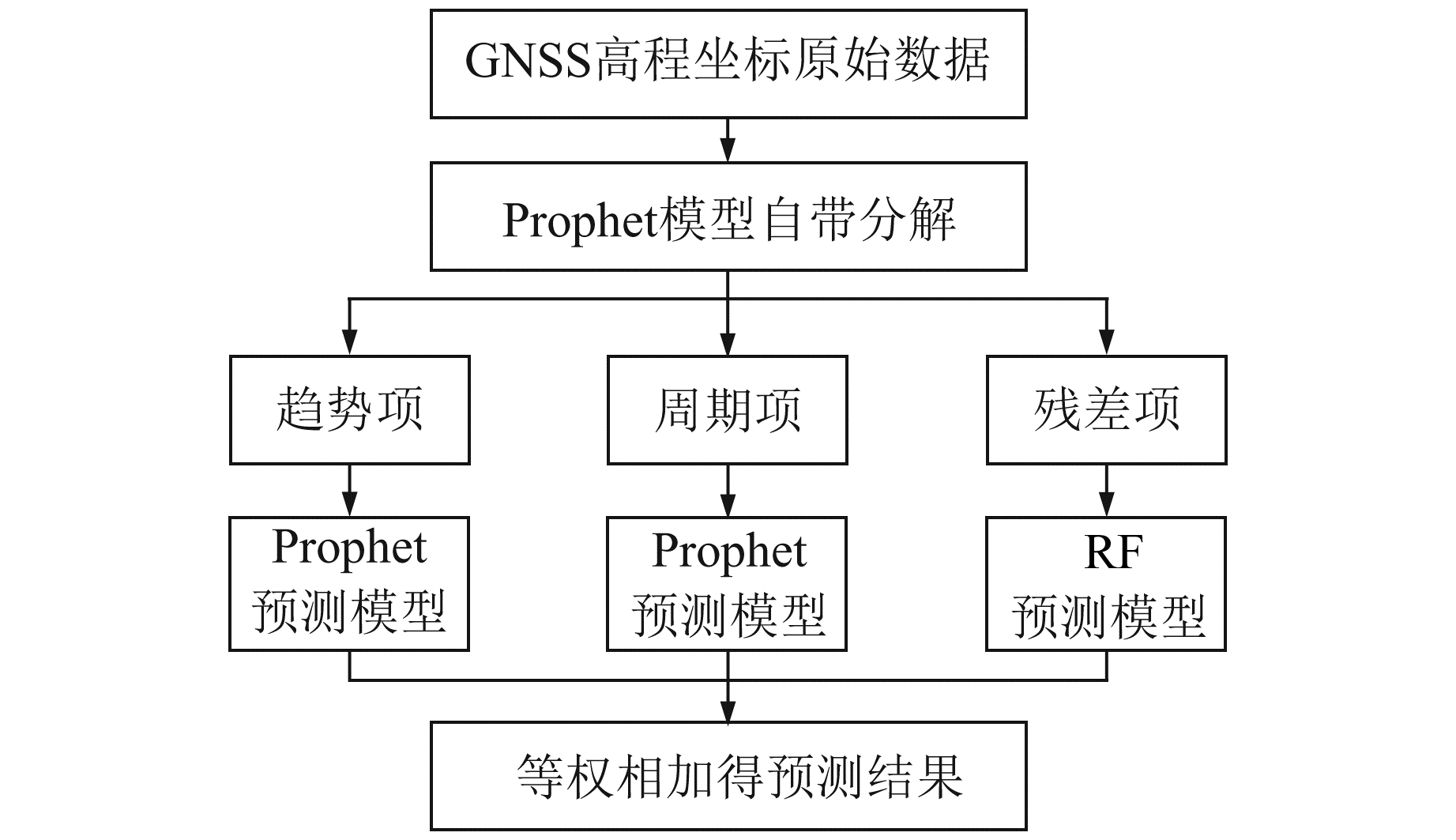
2.1 Prophet-RF组合模型方案1Prophet模型对线性趋势有较好的拟合与预测效果,对于非线性部分的预测效果较差。根据这一特性,使用Prophet模型自带的分解功能将高程坐标时间序列分解为趋势项与周期项,其他部分看作残差项。图 3中Prophet模型将BJFS站高程坐标时间序列分解为3个主要成分:1)由逻辑回归函数或分段线性函数拟合的趋势项;2)基于傅立叶级数构建的以a为周期的季节项;3)由虚拟变量表示的以周为周期的季节项[13]。假日项可单独添加,当数据中不存在此类情况时,采用默认分解即可。图 4为Prophet-RF组合模型方案1的流程。
|
图 3 Prophet模型分解坐标数据 Fig. 3 Prophet model decomposition coordinate data |
|
图 4 Prophet-RF模型方案1流程 Fig. 4 Flow of scheme 1 of Prophet-RF model |
Prophet-RF模型方案1的实现流程如下:
1) 使用Prophet模型自带的分解功能,将时间跨度为n天的坐标时间序列Sn分解为趋势项trendn、以周为周期的季节项weeklyn、以a为周期的季节项yearlyn及残差项errorn。
2) 趋势项、以周为周期的季节项及以a为周期的季节项分别使用Prophet模型建立预测模型,残差项则使用RF模型建立预测模型。将每个分量模型的前t天作为训练集,后k天作为测试集,且t+k=n。
3) 将各分量模型得到的拟合结果与预测结果等权相加,得到Prophet-RF组合模型方案1的拟合值与预测值:
| $ \begin{array}{*{20}{l}} {{S_{拟合}} = {\rm{tren}}{{\rm{d}}_t} + {\rm{weekl}}{{\rm{y}}_t} + {\rm{yearl}}{{\rm{y}}_t} + {\rm{erro}}{{\rm{r}}_t}}\\ {{S_{预测}} = {\rm{tren}}{{\rm{d}}_k} + {\rm{weekl}}{{\rm{y}}_k} + {\rm{yearl}}{{\rm{y}}_k} + {\rm{erro}}{{\rm{r}}_k}} \end{array} $ | (4) |
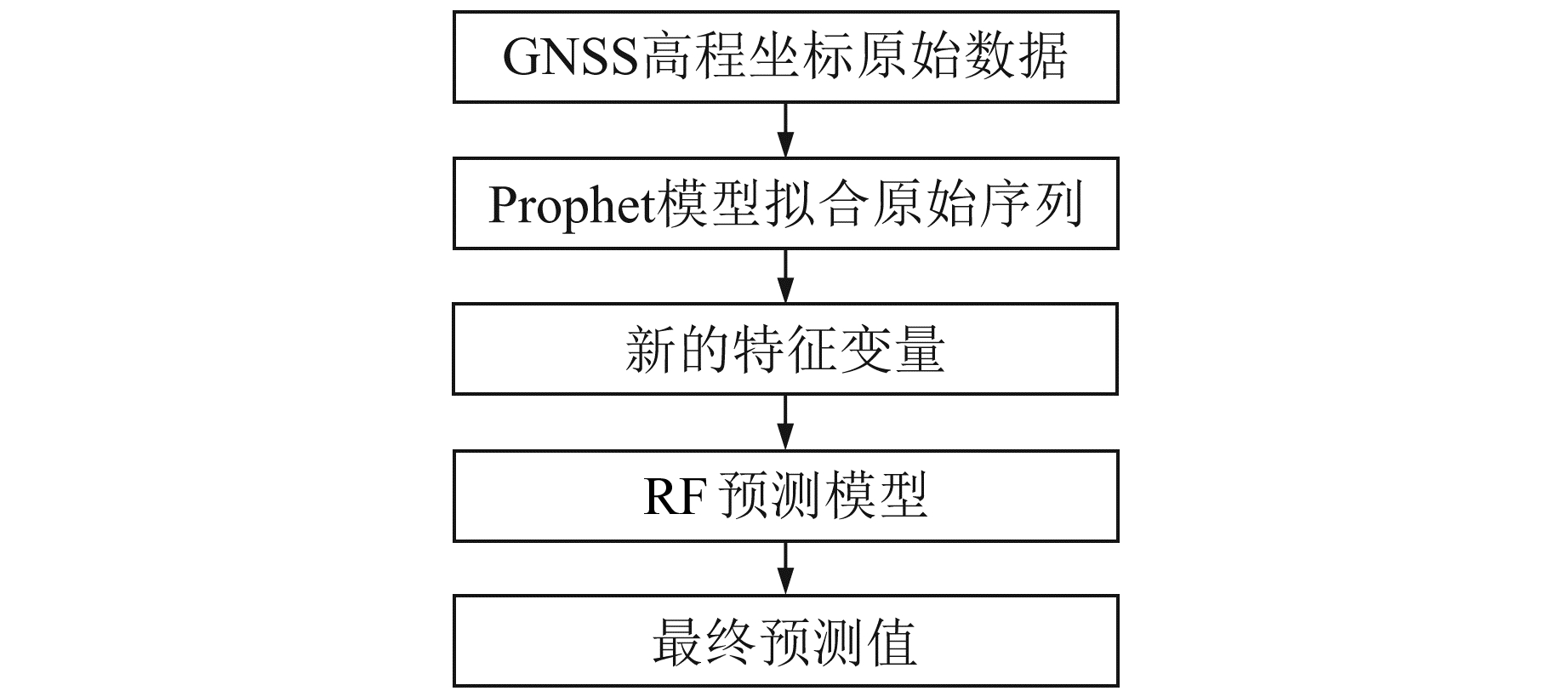
RF模型在某些噪声较大的分类或回归问题中可能会出现过拟合的情况,且数据中的噪声量级往往难以判断,故方案2在不明确数据噪声量级的情况下,假设原始数据中噪声量级较大。首先选用Prophet模型拟合坐标原始数据,再对拟合数据建立RF预测模型,避免了在数据噪声量级较大时RF模型造成数据过拟合的缺点。图 5为Prophet-RF组合模型方案2的流程。
|
图 5 Prophet-RF模型方案2流程 Fig. 5 Flow of scheme 2 of Prophet-RF model |
Prophet-RF模型方案2的实现流程如下:
1) 将时间跨度为n天的原始坐标数据划分为训练样本集和测试样本集,前t天作为训练样本集,后k天作为测试样本集,且t+k=n。
2) 使用Prophet模型拟合训练样本集,并将得到的拟合数据看作新的特征变量。
3) 利用RF模型对Prophet模型产生的特征变量建立预测模型,得到最终的拟合数据与预测数据。
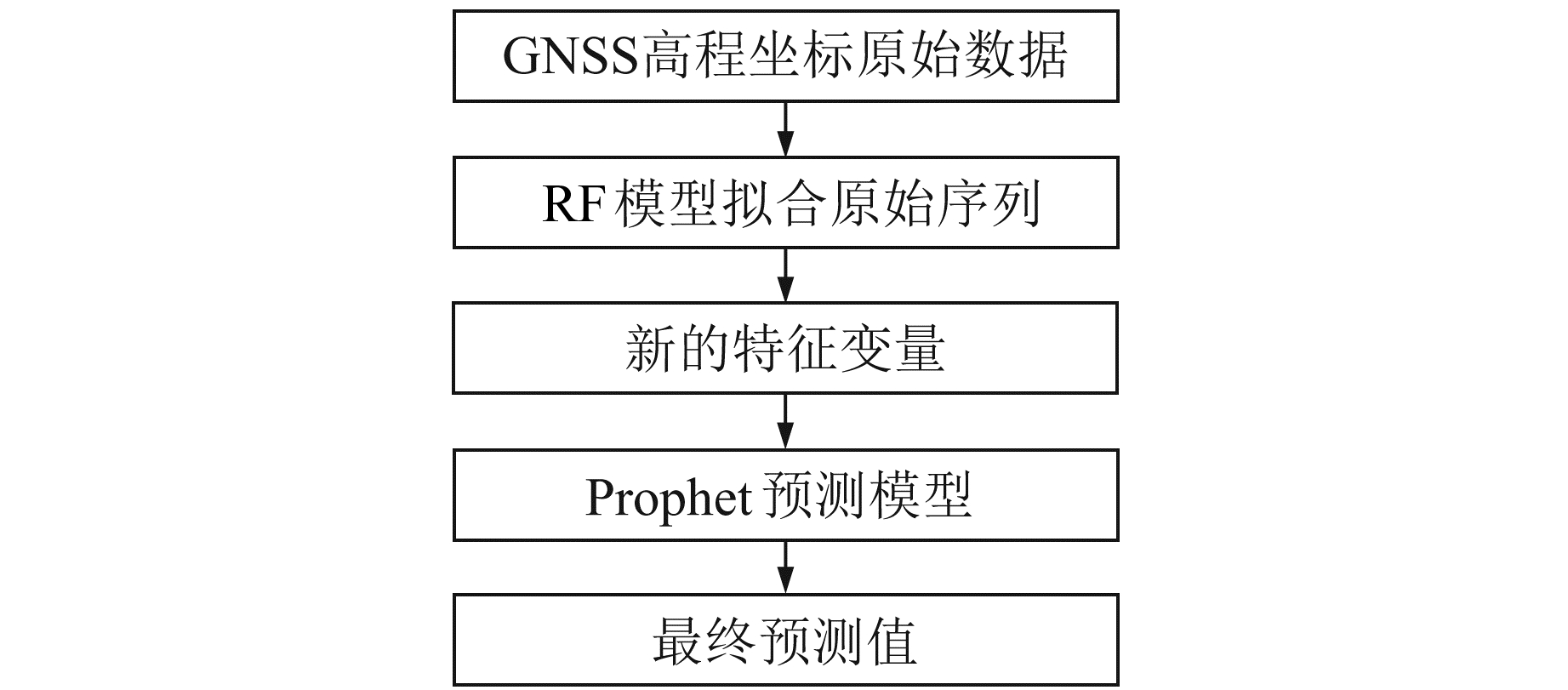
2.3 Prophet-RF组合模型方案3RF模型在数据噪声含量较少的情况下能够保持较好的独立性,即不易过度拟合数据,故方案3在假设原始数据噪声量级较小的情况下,使用RF模型拟合原始数据,避免了Prophet模型对非线性部分预测能力较弱的缺陷,从而能够充分发挥Prophet模型的预测优势。图 6为Prophet-RF组合模型方案3的流程。
|
图 6 Prophet-RF模型方案3流程 Fig. 6 Flow of scheme 3 of Prophet-RF model |
Prophet-RF模型方案3实现流程如下:
1) 将时间跨度为n天的坐标原始数据划分为训练样本集和测试样本集,前t天作为训练样本集,后k天作为测试样本集,且t+k=n。
2) 使用RF模型拟合训练样本集,并将得到的拟合数据看作新的特征变量。
3) 利用Prophet模型对RF模型产生的特征变量建立预测模型,并得到最终的拟合数据与预测数据。
2.4 方案对比与分析 2.4.1 精度对比本文选用BJFS站高程坐标时间序列作为实验数据,将Prophet模型及Prophet-RF组合模型方案1、方案2、方案3得到的拟合值与预测值分别与原始数据进行对比,同时引入经典ARMA模型作为参照,得到各模型相应的RMSE值与MAE值,结果见表 2。
|
|
表 2 不同模型的性能对比 Tab. 2 Performance comparison of different models |
由表 2可知,ARMA模型的拟合精度最高,但预测精度最低,这是由于经典ARMA模型容易出现过拟合现象, 且在长期预测中缺乏稳定性。而单一的Prophet模型也能得到较高的拟合精度,但预测精度却不如组合模型,表明模型的预测能力与拟合效果没有直接关系。Prophet-RF组合模型方案1、方案2、方案3预测数据的RMSE值较单一的Prophet模型分别提升0.7%、14.7%、16.1%,MAE值分别提升7.8%、23.4%、24.2%,其中方案1的预测精度提升较小,而方案2及方案3的预测精度都有较大提升。
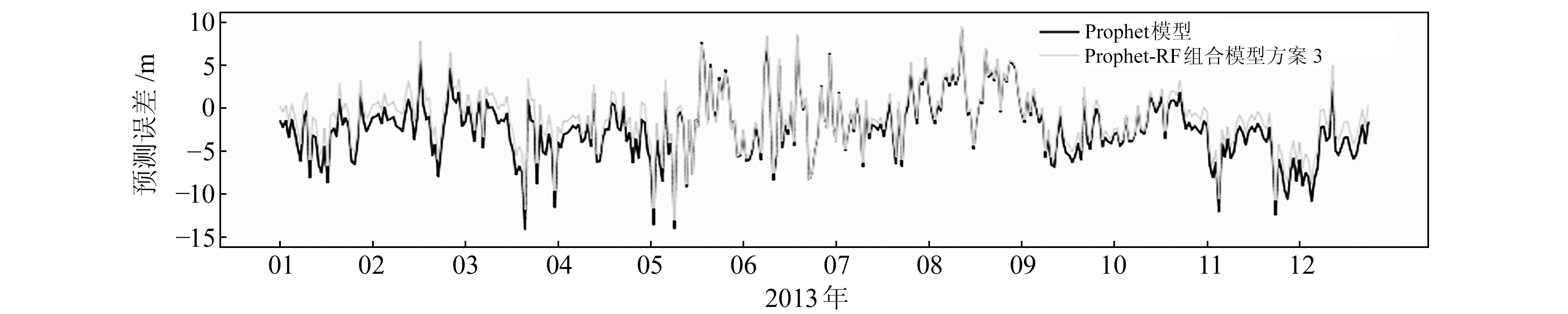
为检验各模型得到的拟合值、预测值与原始数据的关系,引入皮尔森相关系数和斯皮尔曼相关系数,由于ARMA模型在该数据中的适用性不强,故没有分析其相关性。由表 3可知,各模型的拟合值与原始数据具有强相关性,而预测值与原始数据具有中等强度相关性。通过对比分析表 2和3的指标认为,组合模型方案3在BJFS站高程方向的预测精度最高、适用性最强。图 7为Prophet模型与Prophet-RF组合模型方案3预测误差的对比,由预测值减去原始数据得到。
|
|
表 3 不同模型的相关性对比 Tab. 3 Correlation comparison of different models |
|
图 7 模型预测误差对比 Fig. 7 Model prediction error comparison |
在方案1中,通过分解原始数据的组成成分,并根据Prophet模型和RF模型的特点,针对不同组成成分选用合适的预测模型,但该方案较单一的Prophet模型性能几乎没有提升。这可能是由于实测数据中往往存在由于各种误差,如板块运动、电离层延迟、观测墩热胀冷缩等造成的非线性变化,还有季节性海洋、陆地及大气变化造成的地表水文负载等,这些都会对GNSS观测数据产生负面影响[1]。所以方案1在分解数据时受到误差的影响,无法较好地分离出各组成成分,从而导致模型精度提升较小。
方案2与方案3可看作一组对比实验,分别在数据噪声量级较大和较小的假设下进行。这2组方案较单一的Prophet模型预测精度都有较大提升,但方案3的预测精度更高,表明原始数据中的噪声量级相对较小。方案2由于使用Prophet模型拟合原始数据时对非线性部分的拟合效果较差,再使用RF模型进行预测时精度可能会受到Prophet模型拟合效果的影响。而方案3使用RF模型拟合原始数据,避免了过拟合并对非线性部分进行了修正,再使用Prophet模型进行预测时能够充分发挥模型优势,从而提高预测精度。
3 结语高精度的预测模型有助于研究GNSS坐标时间序列的长期变化与规律。本文将Prophet模型应用于GNSS坐标数据中,该模型能够分解坐标时间序列中的组成成分,且具有较强的可解释性;在Prophet模型的基础上引入RF模型,以解决Prophet模型对随机部分预测能力较弱的缺点。实验结果表明,Prophet-RF组合模型的预测精度相较于单一的Prophet模型,RMSE与MAE分别提升了16.1%与24.2%,并且对GNSS坐标时间序列有更好的长期预测能力。
由于数据往往受到噪声及其他未知成分的影响,本文在进行组合模型拟合时充分考虑了数据中可能存在的情况,并结合各模型的优缺点设计了多种组合方案,以保证实验结果的可靠性,最终得到BJFS站高程方向的最优组合方案。
本文对单个高程坐标时间序列进行了模型算法上的结合与研究,在今后的工作中应当结合更多的模型或引入更新的算法,以进一步提高预测精度。
| [1] |
姜卫平, 王锴华, 李昭, 等. GNSS坐标时间序列分析理论与方法及展望[J]. 武汉大学学报:信息科学版, 2018, 43(12): 2112-2123 (Jiang Weiping, Wang Kaihua, Li Zhao, et al. Prospect and Theory of GNSS Coordinate Time Series Analysis[J]. Geomatics and Information Science of Wuhan University, 2018, 43(12): 2112-2123)
(  0) 0) |
| [2] |
张鹏, 蒋志浩, 秘金钟, 等. 我国GPS跟踪站数据处理与时间序列特征分析[J]. 武汉大学学报:信息科学版, 2007, 32(3): 251-254 (Zhang Peng, Jiang Zhihao, Bei Jinzhong, et al. Data Processing and Time Series Analysis for GPS Fiducial Stations in China[J]. Geomatics and Information Science of Wuhan University, 2007, 32(3): 251-254)
(  0) 0) |
| [3] |
明锋, 杨元喜, 曾安敏, 等. 中国区域IGS站高程时间序列季节性信号及长期趋势分析[J]. 中国科学:地球科学, 2016, 46(6): 834-844 (Ming Feng, Yang Yuanxi, Zeng Anmin, et al. Analysis of Seasonal Signals and Long-Term Trends in the Height Time Series of IGS Sites in China[J]. Scientia Sinica Terrae, 2016, 46(6): 834-844)
(  0) 0) |
| [4] |
贺小星, 花向红, 鲁铁定, 等. 时间跨度对GPS坐标序列噪声模型及速度估计影响分析[J]. 国防科技大学学报, 2017, 39(6): 12-18 (He Xiaoxing, Hua Xianghong, Lu Tieding, et al. Effect of Time Span on GPS Time Series Noise Model and Velocity Estimation[J]. Journal of National University of Defense Technology, 2017, 39(6): 12-18)
(  0) 0) |
| [5] |
冯胜涛, 刘雪龙, 王友. 最小二乘拟合GNSS位置时间序列分析[J]. 测绘科学, 2015, 40(10): 157-160 (Feng Shengtao, Liu Xuelong, Wang You. Least-Squares Fit Used for Primary Analysis of Position Time Series of GNSS[J]. Science of Surveying and Mapping, 2015, 40(10): 157-160)
(  0) 0) |
| [6] |
李霞, 孙茂军, 黄永生. LSTM神经网络模型在GPS变形监测中的应用研究[J]. 甘肃科学学报, 2019, 31(3): 24-27 (Li Xia, Sun Maojun, Huang Yongsheng. Research on Application of LSTM Neural Network Model in GPS Deformation Monitoring[J]. Journal of Gansu Sciences, 2019, 31(3): 24-27)
(  0) 0) |
| [7] |
戴海亮, 孙付平, 肖凯, 等.小波多尺度分解和奇异谱分析在GNSS站坐标时间序列分析中的应用[EB/OL]. http://kns.cnki.net/kcms/detail/42.1676.tn.20190703.1838.001.html, 2019-07-05 (Dai Hailiang, Sun Fuping, Xiao Kai, et al. Application of Wavelet Decomposition and Singular Spectrum Analysis in GNSS Station Coordinate Time Series[EB/OL]. http://kns.cnki.net/kcms/detail/42.1676.tn.20190703.1838.001.html, 2019-07-05)
(  0) 0) |
| [8] |
张明敏, 刘盼, 周海龙, 等. 两种高程坐标预测模型的精度对比分析[J]. 测绘工程, 2019, 28(4): 13-18 (Zhang Mingmin, Liu Pan, Zhou Hailong, et al. Comparison and Analysis of the Accuracy of Two Elevation Coordinate Forecasting Models[J]. Engineering of Surveying and Mapping, 2019, 28(4): 13-18)
(  0) 0) |
| [9] |
Taylor S J, Letham B. Forecasting at Scale[J]. The American Statistician, 2018, 72(1): 37-45
(  0) 0) |
| [10] |
翟笃林, 张学民, 熊攀, 等. Prophet时序预测模型在电离层TEC异常探测中的应用[J]. 地震, 2019, 39(2): 46-62 (Zhai Dulin, Zhang Xuemin, Xiong Pan, et al. Detection of Ionospheric TEC Anomalies Based on Prophet Time-Series Forecasting Model[J]. Earthquake, 2019, 39(2): 46-62)
(  0) 0) |
| [11] |
葛娜, 孙连英, 石晓达, 等. Prophet-LSTM组合模型的销售量预测研究[J]. 计算机科学, 2019, 46(增1): 446-451 (Ge Na, Sun Lianying, Shi Xiaoda, et al. Research on Sales Forecast of Prophet-LSTM Combination Model[J]. Computer Science, 2019, 46(S1): 446-451)
(  0) 0) |
| [12] |
王晓飞, 王波, 陆玉玉, 等. 基于Prophet-LSTM模型的PM2.5浓度预测研究[J]. 软件导刊, 2020, 19(3): 133-136 (Wang Xiaofei, Wang Bo, Lu Yuyu, et al. Research of PM2.5 Concentration Forecasting Based on Prophet-LSTM Model[J]. Software Guide, 2020, 19(3): 133-136)
(  0) 0) |
| [13] |
常恬君, 过仲阳, 徐丽丽. 基于Prophet-随机森林优化模型的空气质量指数规模预测[J]. 环境污染与防治, 2019, 41(7): 758-761 (Chang Tianjun, Guo Zhongyang, Xu Lili. Scale Prediction of AQI Based on Prophet-Random Forest Optimization Model[J]. Environmental Pollution Control, 2019, 41(7): 758-761)
(  0) 0) |
| [14] |
Breiman L. Random Forests[J]. Machine Learning, 2001, 45(1): 5-32
(  0) 0) |
| [15] |
邓军, 雷昌奎, 曹凯, 等. 采空区煤自燃预测的随机森林方法[J]. 煤炭学报, 2018, 43(10): 2800-2808 (Deng Jun, Lei Changkui, Cao Kai, et al. Random Forest Method for Predicting Coal Spontaneous Combustion in Gob[J]. Journal of China Coal Society, 2018, 43(10): 2800-2808)
(  0) 0) |
| [16] |
方匡南, 吴见彬, 朱建平, 等. 随机森林方法研究综述[J]. 统计与信息论坛, 2011, 26(3): 32-38 (Fang Kuangnan, Wu Jianbin, Zhu Jianping, et al. A Review of Technologies on Random Forests[J]. Statistics and Information Forum, 2011, 26(3): 32-38)
(  0) 0) |
| [17] |
陈志方. 中国货币政策的有效性评估——基于皮尔森相关系数的分析[J]. 中国商论, 2020(6): 48-49 (Chen Zhifang. The Effectiveness Evaluation of China's Monetary Policy-Analysis Based on Pearson Correlation Coefficient[J]. Chinese Commerce, 2020(6): 48-49)
(  0) 0) |
2. School of Civil Engineering and Architecture, East China Jiaotong University, 808 East-Shuanggang Street, Nanchang 330013, China;
3. State Key Laboratory of Rail Transit Engineering Informatization, China Railway Survey and Design Institute Group Co Ltd, 2 Xiying Road, Xi'an 710043, China
 2021, Vol. 41
2021, Vol. 41


