重力异常向下延拓是物理大地测量的经典问题。长期以来,国内外开展了很多研究来解决向下延拓中的不适定问题,其中以求解球外Dirichlet问题的逆Poisson积分法应用最为广泛。迭代法是解算逆泊松积分的常用方法。Martine与Huang[1-2]利用迭代方式将加拿大落基山脉的航空重力值进行向下延拓;Kingdon、Ma与Zeng等[3-5]对迭代法进行了更深入的研究。正则化方法也是解决病态问题的常用方法。王兴涛等[6]采用Tikhonov正则化方法对5′×5′的航空重力异常进行向下延拓。蒋涛等[7]则将岭估计与广义岭估计应用于航空重力向下延拓。赵启龙等[8]使用半参数估计与最小二乘配置方法对台湾地区的航空重力进行向下延拓。在频率域进行重力延拓也是常用的方法。将重力异常从空间域利用FFT算法转换到频率域,在频率域进行向下延拓,最后将延拓后的重力异常从频率域转换回空间域[9]。宁津生等[10]使用小波分析研究了多尺度边缘约束的重力场向下延拓。黄谟涛等[11]提出基于向上延拓的向下解析延拓方法,利用向上延拓与垂直梯度进行航空重力向下延拓。Zhang也提出利用积分中值定理进行航空重力向下延拓的数值方法[12]。不同于逆Poisson积分法,还有一些方法是利用物理信息进行重力场延拓的研究,如直接代表法、虚拟点质量法、联合重力场模型与地形进行重力场向下延拓等。
本文结合拉格朗日中值定理以及重力异常垂直梯度在垂向上的分布特点,改进使用重力异常垂直梯度进行重力异常延拓的方法,回避了向下延拓的不适定性。针对经典积分求解重力异常垂直梯度的奇异性,本文使用差分的方式计算航空重力高度面上的垂直梯度,并在台湾地区进行模拟与实测航空重力异常向下延拓实验。
1 基本原理与方法 1.1 利用重力异常垂直梯度进行向下延拓重力异常向下延拓中,最直接的方法是利用垂直梯度进行向下延拓。根据拉格朗日中值定理,有:
| $\frac{\Delta g_{P^{\prime}}-\Delta g_{P}}{H}=\left.\frac{\partial \Delta g}{\partial r}\right|_{P^{\prime\prime}} $ | (1) |
式中,ΔgP′为P′点的重力异常,ΔgP为P点的重力异常,H为P′点与P点间的高差,
将式(1)变形得到:
| $\Delta g_{P}=\Delta g_{P^{\prime}}-\left.\frac{\partial \Delta g}{\partial r}\right|_{P^{\prime \prime}} H $ | (2) |
式中,ΔgP′与H为已知量,但是无法准确得到
重力异常垂直梯度(Δgr)在垂向上的变化较为缓慢,且呈现出与高度较强的线性关系。为了说明重力异常垂直梯度在垂向的分布特点,本文在台湾地区随机选取100个点,采用2 160阶次的EGM2008重力场模型模拟每个点从海平面到海平面以上10 000 m每隔100 m的重力异常,点位分布见图 1。图 2为各点位上每隔100 m模拟重力异常垂直梯度与高度的散点图。
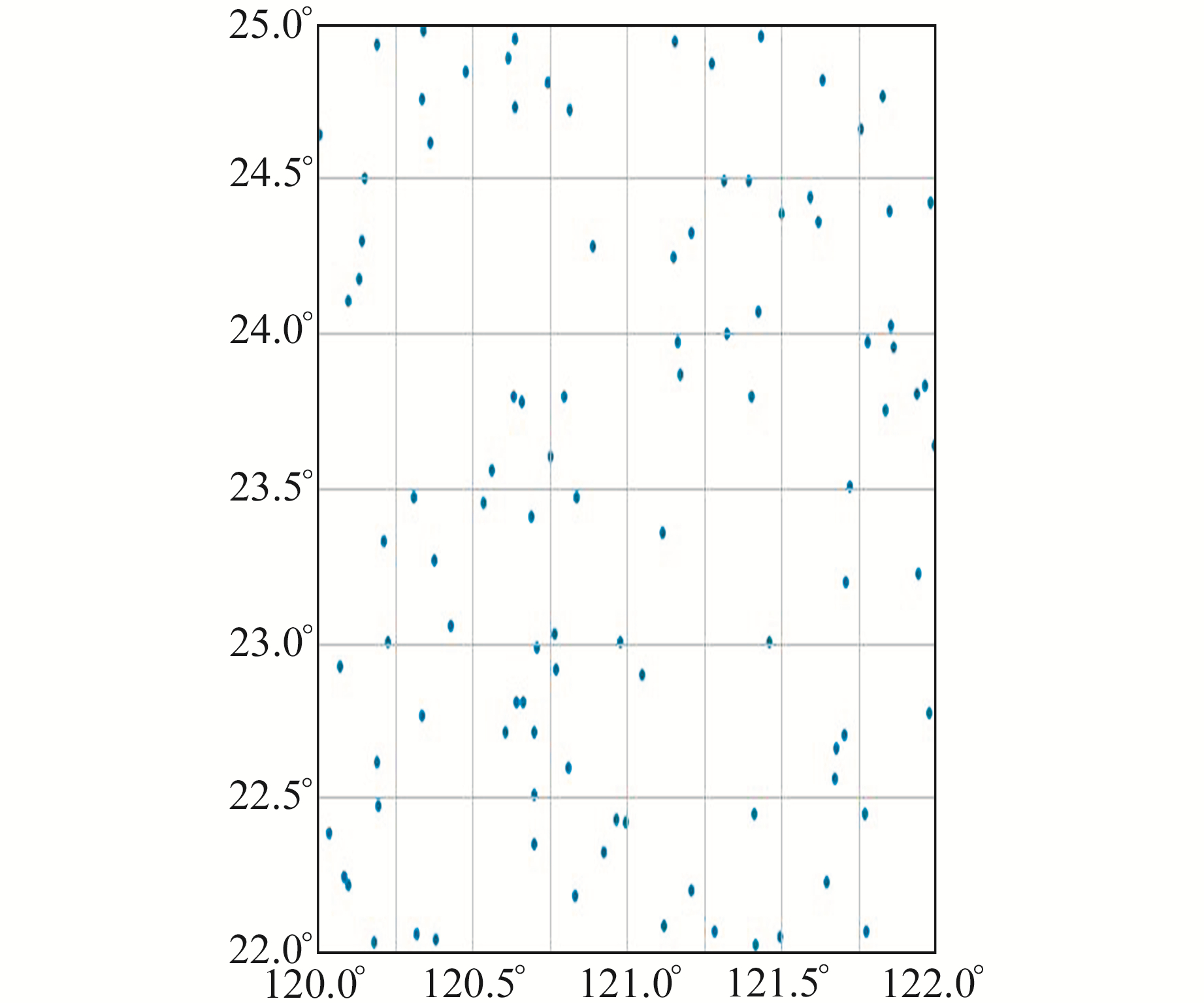
|
图 1 Δgr垂向分布实验的点位分布 Fig. 1 Distribution of points validating the radial pattern of Δgr |

|
图 2 各点位上Δgr与高度的散点图 Fig. 2 Scatter point plots of vertical gradients and height at each test point |
由图 2可以看出,多数点位上的模拟重力异常垂直梯度与高度呈现出强线性关系。为进一步说明这种线性关系,求得各点位上每隔100 m模拟重力异常垂直梯度与高度的线性相关系数(图 3)。在87个点位上,线性相关系数的绝对值大于0.85,重力异常垂直梯度在垂向上与高度呈现出极强的线性关系。

|
图 3 模拟点位上Δgr与高度的线性相关系数 Fig. 3 Linear correlation coefficients between Δgr and height at each test point |
在垂向上,Δgr的变化整体较为缓慢。表 1为各个点位上高度7 500 m与5 000 m、7 500 m与2 500 m以及5 000 m与2 500 m的Δgr差值统计。可以看出,三者Δgr差异的绝对值平均值分别为3.3 E、8.1 E、4.8 E。按5 000 m延拓高差计算,由梯度近似造成的相应的误差绝对值平均值分别为1.7 mGal、4.0 mGal以及2.4 mGal,对当前的航空重力观测精度以及向下延拓的精度而言,这个误差在可接受范围之内。
|
|
表 1 不同高度面Δgr模型值的差异 Tab. 1 Differences of Δgr on different heights |
为了进一步说明前文中重力异常垂直梯度呈强线性分布的结论,采用线性外推计算2 500 m高度处的Δgr:
| $\Delta g_{r_{-} 2500}^{e x}=2 \times \Delta g_{r_{-} 5000}-\Delta g_{r_{-} 7500} $ |
式中,Δgr_2500ex为2 500 m高度处外推值。Δgr_2500ex与Δgr_2500的差异统计见表 1的最后一行,此时Δgr_2500ex-Δgr_2500的绝对值平均值为1.8 E。同样按5 000 m的延拓高差计算,此时由梯度近似造成的误差仅为0.9 mGal。
利用图 4对式(2)中

|
图 4 Δgr线性外推示意图 Fig. 4 Demonstration of Δgr linear extrapolation |
| $\left.\frac{\partial \Delta g}{\partial r}\right|_{P^{\prime \prime}} \approx\left(2 \times\left.\frac{\partial \Delta g}{\partial r}\right|_{P^{\prime}}-\left.\frac{\partial \Delta g}{\partial r}\right|_{P_{M}^{2 H}}\right) $ | (3) |
式中,
球面上某一点重力异常的垂直梯度可以用该高度面上的重力异常表示:
| $\left.\frac{\partial \Delta g}{\partial r}\right|_{P}=-\frac{1}{R} \sum\limits_{n=0}^{\infty}(n+2) \Delta g_{n}=-\frac{1}{R} \sum\limits_{n=0}^{\infty} n \Delta g_{n}-\\ \frac{2}{R} \Delta g=\frac{R^{2}}{2 \pi} \iint\limits_{\sigma} \frac{\Delta g-\Delta g_{P}}{l_{0}^{3}} \mathrm{~d} \sigma-\frac{2}{R} \Delta g_{P} $ | (4) |
利用重力异常进行重力异常向上延拓的积分公式为:
| $\Delta g_{P^{\prime}}=\frac{R^{2}}{4 \pi r} \iint\limits_{\sigma} \frac{r^{2}-R^{2}}{l^{3}} \Delta g \mathrm{~d} \sigma $ | (5) |
式中,P′点为与式(4)中P点同一向径且高出P点H的点。式(5)与式(4)在数学上是等价的,证明如下。
| $\begin{array}{*{20}{c}} \left.\frac{\partial \Delta g}{\partial r}\right|_{P}=\lim\limits_{H \rightarrow 0} \frac{\Delta g_{P^{\prime}}-\Delta g_{P}}{H}=\lim\limits_{H \rightarrow 0} \frac{\frac{R^{2}}{4 \pi r} \iint \frac{r^{2}-R^{2}}{l^{3}} \Delta g \mathrm{~d} \sigma-\frac{R^{2}}{r^{2}} \Delta g_{P}+\frac{R^{2}}{r^{2}} \Delta g_{P}-\Delta g_{P}}{H}=\\ \lim\limits_{H \rightarrow 0} \frac{\frac{R^{2}}{4 \pi r} \iint \frac{r^{2}-R^{2}}{l^{3}}\left(\Delta g-\Delta g_{P}\right) \mathrm{d} \sigma+\left(\frac{R^{2}}{r^{2}}-1\right) \Delta g_{P}}{H}=\\ \lim\limits_{H \rightarrow 0} \frac{\frac{R^{2}}{4 \pi(R+H)} \iint \frac{(R+H)^{2}-R^{2}}{l^{3}}\left(\Delta g-\Delta g_{P}\right) \mathrm{d} \sigma+\left(\frac{R^{2}}{(R+H)^{2}}-1\right) \Delta g_{P}}{H}=\\ \lim\limits_{H \rightarrow 0} \frac{\frac{R^{2}}{4 \pi(R+H)} \iint \frac{2 R H+H^{2}}{l^{3}}\left(\Delta g-\Delta g_{P}\right) \mathrm{d} \sigma-\left(\frac{2 R H+H^{2}}{(R+H)^{2}}\right) \Delta g_{P}}{H}=\\ \lim\limits_{H \rightarrow 0} \frac{R^{2}}{4 \pi(R+H)} \iint \frac{2 R+H}{l^{3}}\left(\Delta g-\Delta g_{P}\right) \mathrm{d} \sigma-\left(\frac{2 R+H}{(R+H)^{2}}\right) \Delta g_{P}=\frac{R^{2}}{2 \pi} \iint \frac{\left(\Delta g-\Delta g_{P}\right)}{l^{3}} \mathrm{~d} \sigma-\frac{2}{R} \Delta g_{P} \end{array} $ |
在离散形式下通常使用式(6)进行重力异常向上延拓,以避免中心区域导致积分结果发散[14]:
| $\Delta g_{P^{\prime}}=\frac{R}{r} \Delta g_{P}+\frac{R}{4 \pi} \iint\limits_{\sigma} \frac{r^{2}-R^{2}}{l^{3}}\left(\frac{R}{r} \Delta g-\Delta g_{P}\right) \mathrm{d} \sigma $ | (6) |
在图 4中,由中值定理有:
| $\left.\frac{\partial \Delta g}{\partial r}\right|_{P_{M}^{2 H}}=\frac{\left(\Delta g_{P^{2 H}}-\Delta g_{P^{\prime}}\right)}{H} $ | (7) |
式中,ΔgP2H可由重力异常向上延拓稳定得到。
本文利用重力异常垂直梯度进行延拓的过程分为3步:
1) 根据向下延拓高度H,将航空重力异常向上延拓H,利用式(7)得到航空重力高度面上方某点的垂直梯度;
2) 近似计算航空重力高度面的垂直梯度。同样采用向上延拓后差分的方式,首先将重力异常向上延拓1/5 H(1/5 H为本文差分近似的经验值),然后差分得到垂直梯度近似值;
3) 利用式(3)外推航空重力高度面下方某点的垂直梯度,代入式(2)进行向下延拓。
2 台湾地区航空重力异常向下延拓本文在台湾地区进行航空重力向下延拓实验。为说明本文方法的有效性与实用性,首先采用EGM2008模型模拟观测值进行模拟实验[15],然后对实测航空重力数据进行处理。台湾地区有丰富的航空重力观测与地面重力测量数据,本文采用5 156 m高度的航空重力数据进行向下延拓,以及3 360个地面重力观测点进行检核[8]。图 5为台湾地区实测航空重力格网值,图 6为该地区地面重力值分布及相应重力异常。

|
图 5 台湾地区航空重力格网值 Fig. 5 Airborne gravity anomaly grid values in Taiwan area |
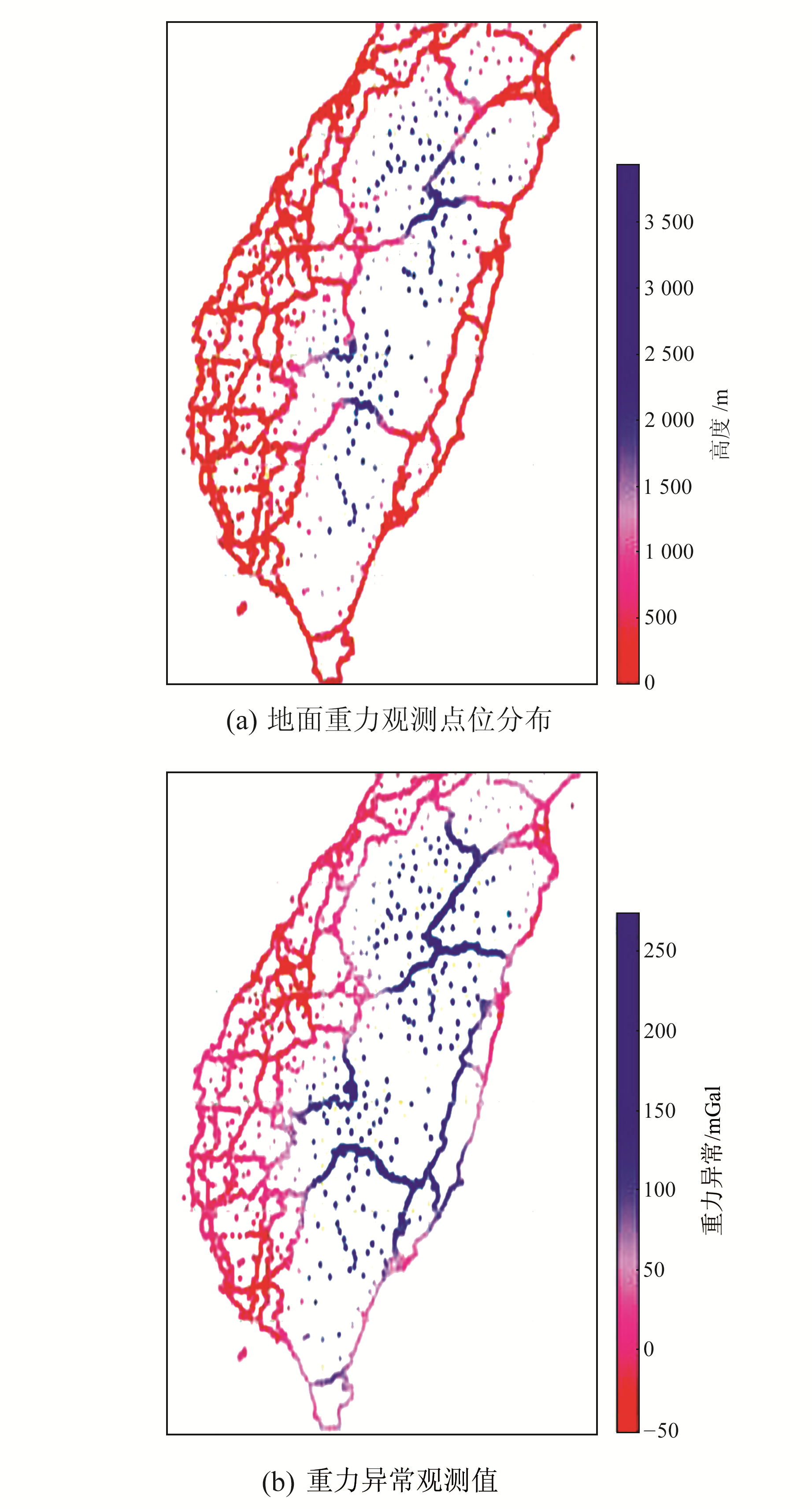
|
图 6 地面重力观测点位分布及观测值大小 Fig. 6 Ground gravity points and their gravity anomaly |
考虑到台湾地区地形复杂,使用GRAVSOFT软件对航空重力观测值及地面重力值进行以15′分辨率为平滑半径的残差地形改正[16-17]。考虑到边缘效应,将航空重力在22°~25°N、120°~122°E区域内进行格网化,然后向下延拓,格网分辨率为2′。航空重力异常最大值为253.72 mGal,最小值为-159 mGal。在该区域内有地面重力观测值3 360个。地面重力异常最低点高程为0,最高点高程为3 942.61 m;重力异常最小值为-52.54 mGal,最大值为271.95 mGal,标准差为78.50 mGal。在向下延拓实验中,将航空重力异常分别向下延拓至各地面重力点,再将延拓值与各点重力观测值进行比较。
为了说明本文方法的有效性,首先使用同样位置分布的EGM2008模型的模拟值进行延拓,向下延拓精度见表 2。
|
|
表 2 EGM2008模拟数据向下延拓精度统计 Tab. 2 Statistics of downward continuation results of EGM2008 simulated gravity anomaly |
在模拟实验中,仅利用向上延拓H后差分得到的梯度进行向下延拓的残差标准差为6.3 mGal。值得注意的是,该模拟实验的
上述结果中的
|
|
表 3 航空重力向下延拓精度统计 Tab. 3 Statistics of downward continuation results of airborne gravity observations |
表 3中,第1行的结果为使用模型值进行延拓的统计结果,第2行为实测航空重力向下延拓的结果。与表 2的模拟数据延拓结果相比较可以发现,仅使用
特别指出的是,使用外推梯度进行延拓具有更高的理论严密性,理应获得更高的延拓精度,这一点在表 2的结果中得到印证。而在实际计算中,计算误差的影响超过了理论严密的作用,仅使用
本文联合拉格朗日中值定理以及重力异常垂直梯度径向分布的特点,改进了利用重力异常垂直梯度进行航空重力异常向下延拓的方法,利用向上延拓后进行差分的方法获取重力异常垂直梯度,然后外推进行向下延拓。主要结论如下:
1) 与常用的泰勒级数一阶展开方式相比,使用拉格朗日中值定理进行垂直梯度外推然后进行向下延拓具有更高的理论严密性。
2) 重力异常垂直梯度在台湾地区在海平面到海平面以上10 000 m的空间范围内,在垂向分布上与高度具有强线性关系。在本文进行模拟实验随机选取的100个点位中,87个点位的重力异常垂直梯度与高度的线性相关系数绝对值超过了0.85。
3) 在使用EGM2008模拟实验中,直接模拟航空重力高度面上的垂直梯度,利用外推得到航空重力高度面以下的垂直梯度,然后进行向下延拓,精度达到2.3 mGal,较仅利用航空重力高度面垂直梯度或向上延拓差分梯度进行向下延拓精度有较大提升。
4) 在差分计算航空重力高度面垂直梯度中,航空重力高度面上垂直梯度计算的不准确会导致利用外推梯度延拓的结果精度反而下降,这是理论严密与数值精度之间的矛盾。将航空重力向上延拓相应点位处的向下延拓高差,将向上延拓前后重力异常与高度进行差分得到差分梯度值,仅利用该差分梯度进行向下延拓,精度达到10.1 mGal,该结果亦优于传统延拓结果[8, 19]。这也说明了使用垂直梯度进行向下延拓的优越性。
可以预期,在能得到航空重力高度面上较高精度垂直梯度的情况下,使用本文方法将进一步提升向下延拓的精度。下一步研究将集中在优化利用重力异常计算重力异常垂直梯度的方法上。
| [1] |
Martinec Z. Stability Investigations of a Discrete Downward Continuation Problem for Geoid Determination in the Canadian Rocky Mountains[J]. Journal of Geodesy, 1996, 70: 805-828 DOI:10.1007/BF00867158
(  0) 0) |
| [2] |
Huang J.Computational Methods for the Discrete Downward Continuation of the Earth Gravity and Effects of the Lateral Topographical Mass Density Variations on Gravity and the Geoid[D].Fredericton: The University of New Brunswick, 2002
(  0) 0) |
| [3] |
Kingdon R, Vaníĉek P. Poisson Downward Continuation Solution by the Jacobi Method[J]. Journal of Geodetic Science, 2010, 1(1): 74-81
(  0) 0) |
| [4] |
Ma G Q, Liu C. A Stable Iterative Downward Continuation of Potential Field Data[J]. Journal of Applied Geophysics, 2013, 98: 205-211 DOI:10.1016/j.jappgeo.2013.08.018
(  0) 0) |
| [5] |
Zeng X N, Li X H. An Adaptive Iterative Method for Downward Continuation of Potential-Field Data from a Horizontal Plane[J]. Geophysics, 2013, 78(4): 43-52
(  0) 0) |
| [6] |
Wang X T, Xia Z R, Shi P, et al. A Comparison of Different Downward Continuation Methods for Airborne Gravity Data[J]. Chinese Journal of Geophysics, 2004, 47(6): 1143-1149 DOI:10.1002/cjg2.599
(  0) 0) |
| [7] |
蒋涛, 李建成, 王正涛, 等. 航空重力向下延拓病态问题的求解[J]. 测绘学报, 2011, 40(6): 684-689 (Jiang Tao, Li Jiancheng, Wang Zhengtao, et al. Solution of Ill-Posed Problem in Downward Continuation of Airborne Gravity[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 684-689)
(  0) 0) |
| [8] |
Zhao Q L, Xu X Y, Forsberg R, et al. Improvement of Downward Continuation Values of Airborne Gravity Data[J]. Remote Sensing, 2018, 10(12): 1951 DOI:10.3390/rs10121951
(  0) 0) |
| [9] |
Fedi M, Florio G. A Stable Downward Continuation by Using the ISVD Method[J]. Geophysical Journal International, 2002, 151(1): 146-156 DOI:10.1046/j.1365-246X.2002.01767.x
(  0) 0) |
| [10] |
宁津生, 汪海洪, 罗志才. 基于多尺度边缘约束的重力场信号的向下延拓[J]. 地球物理学报, 2005, 48(1): 63-68 (Ning Jinsheng, Wang Haihong, Luo Zhicai. Downward Continuation of Gravity Signals Based on the Multiscale Edge Constraint[J]. Chinese Journal of Geophysics, 2005, 48(1): 63-68)
(  0) 0) |
| [11] |
黄谟涛, 刘敏, 邓凯亮, 等. 基于向上延拓的航空重力向下解析延拓解[J]. 地球物理学报, 2018, 61(12): 4746-4757 (Huang Motao, Liu Min, Deng Kailiang, et al. Analytical Solution of Downward Continuation for Airborne Gravimetry Based on Upward Continuation Method[J]. Chinese Journal of Geophysics, 2018, 61(12): 4746-4757 DOI:10.6038/cjg2018L0594)
(  0) 0) |
| [12] |
Zhang C, Lü Q T. Numerical Solutions of the Mean-Value Theorem:New Methods for Downward Continuation of Potential Fields[J]. Geophysical Research Letters, 2018, 45: 3461-3470 DOI:10.1002/2018GL076995
(  0) 0) |
| [13] |
张赤军, 边少峰. 地面扰动重力垂直梯度的确定[J]. 地球物理学进展, 2005, 20(4): 969-973 (Zhang Chijun, Bian Shaofeng. Determination of Disturbing Gravity Vertical Gradient in Earth's Surface[J]. Progress in Geophysics, 2005, 20(4): 969-973)
(  0) 0) |
| [14] |
管斌, 孙中苗, 刘晓刚. 重力异常向上延拓中Poisson积分离散化方法比较[J]. 测绘科学与工程, 2014, 34(6): 12-17 (Guan Bin, Sun Zhongmiao, Liu Xiaogang. Comparison of Discretization Methods of Poisson Integral in Upward Continuatioin of Gravity Anomaly[J]. Geomatics Science and Engineering, 2014, 34(6): 12-17)
(  0) 0) |
| [15] |
Pavlis N K, Holmes S A, Kenyon S C, et al. The Development and Evaluation of the Earth Gravitational Model 2008(EGM2008)[J]. Journal of Geophysical Research:Solid Earth, 2012, 117(B4)
(  0) 0) |
| [16] |
Forsberg R, Tscherning C C.An Overview Manual for the GRAVSOFT Geodetic Gravity Field Modelling Programs[M].DTU, 2008
(  0) 0) |
| [17] |
Forsberg R.Geoid Modelling with GRAVSOFT[R].Airborne Gravimetry for Geodesy Summer School, NOAA's National Geodetic Survey, 2016
(  0) 0) |
| [18] |
Brockmann J M, Norbert Z. EGM_TIM_RL05:An Independent Geoid with Centimeter Accuracy Purely Based on the GOCE Mission[J]. Geophysical Research Letters, 2014, 41(22): 8089-8099
(  0) 0) |
| [19] |
Huang C W, Hsiao Y S, Shih H C, et al. Geodetic and Geophysical Results from a Taiwan Airborne Gravity Survey:Data Reduction and Accuracy Assessment[J]. Journal of Geophysical Research:Solid Earth, 2007, 112(B4)
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41

