地磁低点位移法是一种使用地磁日变数据预报地震的方法。陈绍明[1]在研究1966-03邢台6.8级、7.2级地震余震的前兆时发现地磁异常现象,并于1972年提出“日变低点位移法”。丁鉴海等[2-3]在此基础上通过研究全国地磁台站日变低点位移的空间分布特点,于1975年提出“低点位移平面图”方法,并以此开展地震预报实践工作。1986年陈绍明[4]在研究华北地区地磁日变曲线的反相位现象时提出“日变反向”的概念。丁鉴海[3]研究发现,低点时间均出现在台站当地时间12时左右,于1988年提出低点时间的“经度效应”,并在1994年用数学归纳法推理低点位移法的判断标准,从而解决该方法有经验、无指标的缺点。2009年王亚丽等[5]通过建立地磁低点时间的期望值与地理经度的线性回归方程指出,低点时间标准差与纬度间具有正相关关系。2017年许康生等[6]在研究岷县-漳县M6.6地震前地磁低点位移现象时发现,单个台站的异常幅度与该台站的震源距有关。2018年郭增建等[7]提出地磁低点位移以磁暴倍九法作为补充预测的观点。贾昕晔等[8]使用“理论低点时间”与“实测低点时间”来区分地方时与世界时,并绘制低点时间垂直分量等值线图。2019马亮[9]提出随经度变化的地磁台站当地时的计算公式。戴勇等[10]使用克里格插值法求出岷县-漳县M6.6地震前的低点位移事件的突变界线,这是首次脱离手绘方式求取突变界线。本文将使用数学语言及MATLAB语言,对地磁低点位移法与其搭载软件进行改进,通过建立突变界线与台网地磁低点时间之间的几何解析关系来实现自动成图。
1 数据选取与问题提出中国地震台网中心调用全国124个地磁台站的数据来监测地磁低点位移现象,图 1为台站空间分布情况。东五区和东六区台站密度小,经向间距大;台湾省、上海市与港澳地区未建设地磁台站。该台网中观测仪包含FHD-2质子矢量磁力仪、FHDZ-M15自动化台站系统、GM4磁通门磁力仪、CTM-DI磁通门磁力仪、MINGEO磁通门磁力仪、Mag-01H磁通门地磁经纬仪、G856质子(旋进)磁力仪和GSM-19FD overhauser磁力仪,本文选用的数据均为该台网的地磁低点时间的垂直分量。由于地磁变化常受到空间磁暴的影响,本文对中国科学院国家空间科学中心空间环境预报中心(http://www.sepc.ac.cn/Kp3HPred_chn.php)提供的磁暴信息进行筛除,以排除磁暴干扰。
|
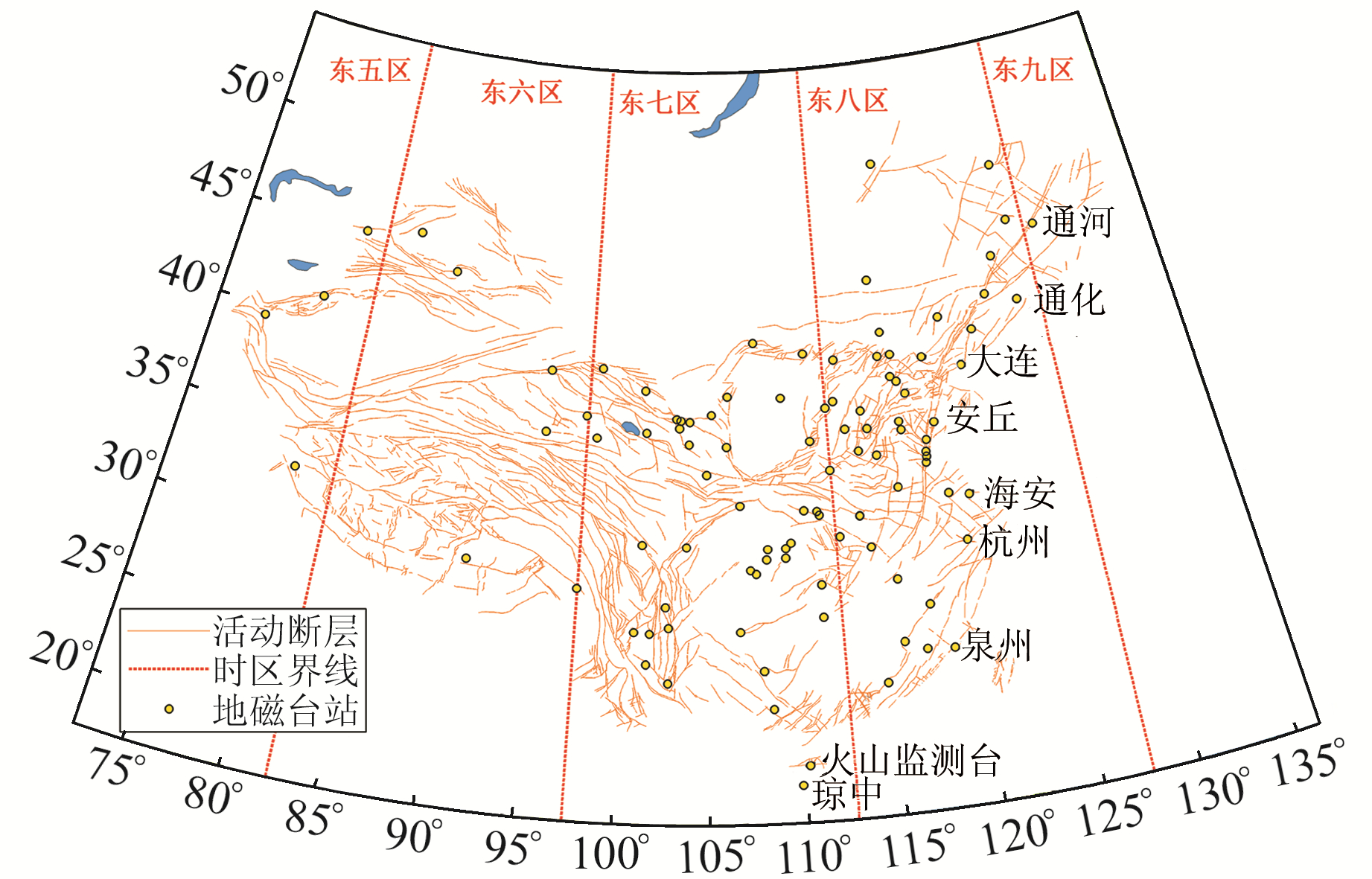
采用等距离圆锥投影以确保经向距离不变形 图 1 地磁台站空间分布 Fig. 1 Spatial distribution of geomagnetic stations |
王亚丽等[5]在研究低点时间的经度效应时发现,垂直分量的低点时间期望值与经度之间具有很强的负相关关系,这反映出低点时间具有显著的地方时依赖性。由于每个测点的低点时间约为测点地方时12:00,经度相差15°的两个地磁台站的世界时刚好相差1 h(图 1)。如果两个台站的经向间距超过一个时区,突变界线的走向会出现较大误差;如果两个台站的经向间距超过两个时区,在未出现地磁异常的情况下也可能存在地磁低点位移现象。为了消除经度效应带来的误差,需采用标准公式将世界时统一转化为地方时,再划分突变界线。
中国地震台网中心一般通过地震前兆信息处理与分析软件EIS2000调用地磁数据并绘制低点时间分布图。EIS2000中地磁低点时间采用格林威治时间,手绘突变界线并进行平滑处理,但该方法会产生两种误差。第一种误差由经度效应引起,同一时区内最西侧与最东侧的格林威治时间会自动产生1 h偏差(图 1),每个台站格林威治时间的时差随经度而不是随时区序数而变化,尤其是突变界线沿南北向延展时,格林威治时间对突变界限的走向会产生较大影响。第二种误差为手绘突变界线产生的随机误差,同时在平滑处理过程中又会产生二次误差。第一种误差较为简单,可用台站当地时间代替格林威治时间予以消除;第二种误差处理难度较大,本文将采用新思路进行处理。
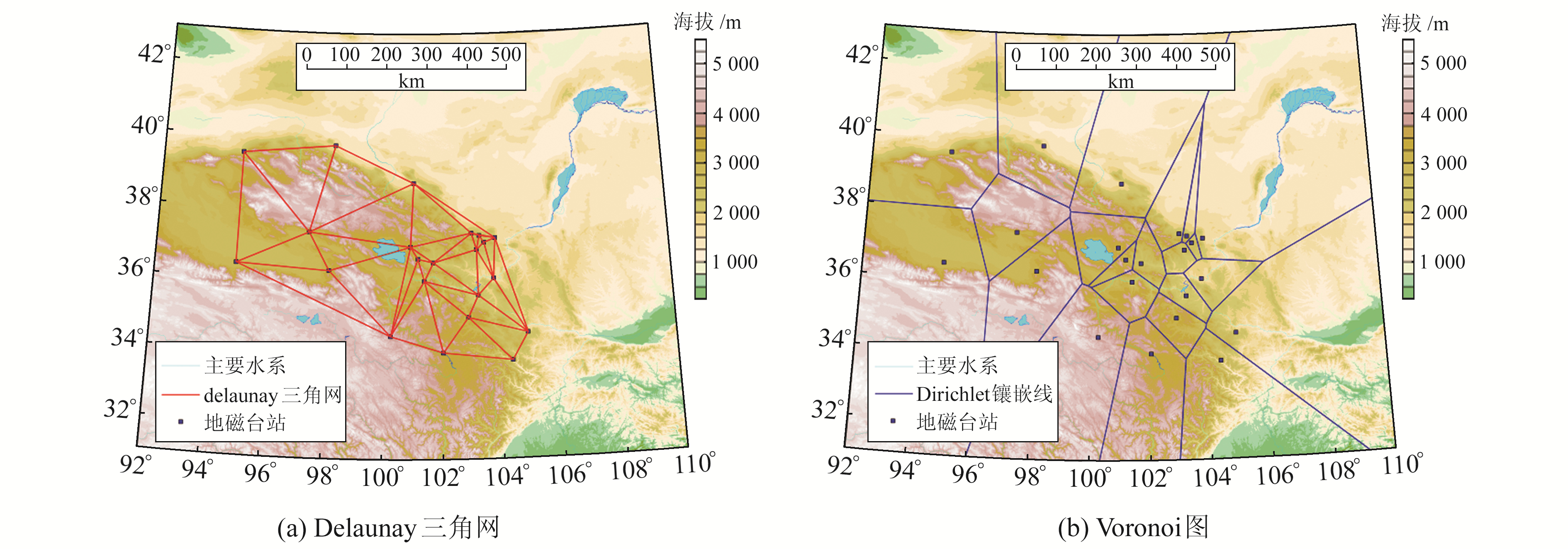
2 Voronoi剖分的应用从集合的观点来看,突变界线上任意一点到相邻两个台站的距离相等,因此突变界线一定沿这两个台站的垂直平分线延伸。为获取垂直平分线的坐标,本文引入Voronoi剖分技术,用Voronoi剖分线代替突变界线的可能走向线。Voronoi图(以下简称V图)与Delaunay三角剖分图互为偶图。以某一散点为核心的V图内部部分被称为该点的值守范围,V图中相邻两个散点之间的垂直平分线称为Dirichlet镶嵌线[11],图 2为甘肃-青海地磁台网的Delaunay三角剖分网和Dirichlet镶嵌线。按照地磁台站低点时间的大小对每个台站的值守范围进行涂色,如果Dirichlet镶嵌线两侧的色差超过2 h,地磁低点位移的突变界线便会沿该条Dirichlet镶嵌线延展。
|
图 2 甘肃-青海地磁台网的Delaunay三角网和Voronoi图 Fig. 2 Delaunay triangulation and Voronoi diagram of the Gansu-Qinghai geomagnetic station network |
从地磁日变曲线可以直观地看出,地磁低点时间大多位于当地时间12:00前后,且服从正态分布[9]。为消除采用格林威治时间对突变界线的走向造成的误差,本节地磁低点时间统一采用当地时间,与格林威治时间的转化关系为:
| $T_{\rm{l}}=T_{0}+N $ | (1) |
式中,Tl、T0分别为台站当地时间与格林威治时间,N为台站所在时区的序数。若将Tl表示为T0与台站经度的函数,则式(1)可写为[9]:
| $T_{\rm{l}}=T_{0}+\operatorname{lon} \cdot \frac{1}{15}\left(\mathrm{~h} /^\mathit{{\circ}}\right) $ | (2) |
式中,lon为地磁台站的经度。为避免低点时间随经度变化而对突变界线的走向产生影响,本节的地磁低点时间统一采用式(2)进行求解,并非采用当地时区时间。由于T0已知,因此只需知道台站经度便可计算地磁低点时间的当地时间,进而用集合思想计算出突变界线的坐标数组。
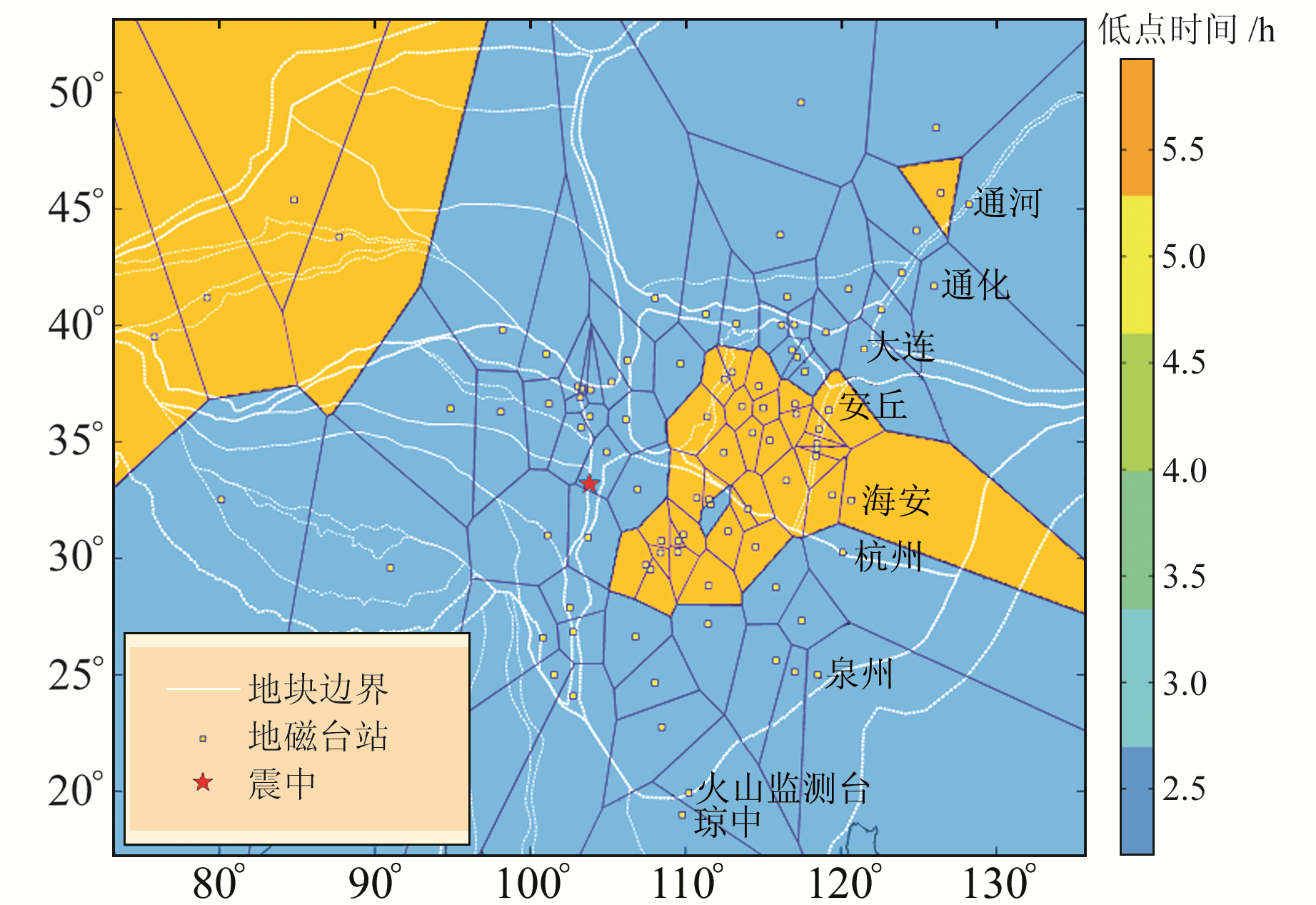
为评价使用式(2)的新算法相对于原算法的优势,本文以2017年九寨沟7.0级地震发生前07-20出现的地磁低点位移现象为例,分析时间格式的改进对地磁低点位移突变界线走向的影响。从图 1中可以看出,全国地磁台站的空间分布跨越5个时区,如果采用格林威治时间计算突变界线,东五区和东七区台站的地磁低点时间在正常情况下将会存在2 h偏差,为了直观地表现台站间的偏差,通过最近邻插值法将全国124个采用格林威治时间的地磁台的低点时间绘制成空间等值线分布图(图 3)。
|
图 3 采用格林威治时间的突变界线 Fig. 3 Abrupt boundaries based on GMT |
由于世界时会随经度而变化,在地磁数据无异常时,台站经向跨度较大的地区低点时间可能会相差2 h以上,从而产生“假异常”现象。图 3中新疆5个地磁台外边缘的突变界线就属于“假异常”突变界线,“假异常”是由世界时的固有性质而产生,与场地条件无关,采用本文方法中式(2)将世界时转化为当地时后即可消除。
各台站地质构造、地下电性结构存在差异,台站资料差异对突变界线的影响已体现在原始数据中。因此只要使用相同的数据,无论采用原始手绘方法还是本文方法,在去除手绘的随机误差后,突变界线走向一致。手绘的原始突变界线为折线,但经过后期平滑处理后可转化为平滑曲线。
新疆、西藏、青海、甘肃地区地磁台站稀疏,各台站经向跨度大,按照格林威治时间计算的突变界线的误差会被放大,为体现与式(2)地方时的差异,本节按式(2)将图 3中中国西部台站的原有低点时间转化为地方时,并求出两者的偏差值(表 1)。
|
|
表 1 西部地磁台网的格林威治时间与地方时的低点时间对比 Tab. 1 Comparison of low point-time between GMT and local time of western geomagnetic network |
从表 1可以看出,狮泉河台与喀什台的低点时间与背景值之差超过60 min,各台站格林威治地磁低点时间差异非常大,且经度跨度越大,地磁低点时间的差异越大。将格林威治时间转化为式(2)地方时后,各台站的低点时间约为12:00,与文献[3]研究结果一致,表明新方法可有效消除“经度效应”。但文献[3]未定义地方时的计算公式,该研究中“地方时”概念可能源于台站的时区时间,因此本文建议将各台站按式(2)计算的地方时的地磁低点时间长期观测的期望定义为地磁低点时间的背景值,以消除原有方法的“经度效应”。
4 突变界线的定位现虚拟一个由8个地磁台站组成的地磁台网,台站纬、经度分别用矩阵lat和lon表示,低点时间用矩阵data表示,突变界线在MATLAB中的坐标计算代码如下:
| $\begin{array}{l} {\bf{lat}} = \left[ {{y_1}, {y_2}, {y_3}, {y_4}, {y_5}, {y_6}, {y_7}, {y_8}} \right];\\ {\bf{lon}} = \left[ {{x_1}, {x_2}, {x_3}, {x_4}, {x_5}, {x_6}, {x_7}, {x_8}} \right];\\ {\bf{data}} = \left[ {{a_1}, {a_2}, {a_3}, {a_4}, {a_5}, {a_6}, {a_7}, {a_8}} \right];\\ [\mathit{\boldsymbol{X}}, \mathit{\boldsymbol{Y}}] = {\rm{meshgrid}}\left( {{\mathop{\rm linspace}\nolimits} \left( {{y_1}, {y_8}, n} \right)} \right., \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{\mathop{\rm linspace}\nolimits} \left( {{x_1}, {x_8}, n} \right)} \right); \end{array} $ |
| $\begin{array}{l} \mathit{\boldsymbol{Z = }}{\rm{griddata (}}{\bf{lat}}{\rm{, }}{\bf{lon}}{\rm{, }}{\bf{data}}{\rm{, }}\mathit{\boldsymbol{X}}, \mathit{\boldsymbol{Y}}, {\rm{'nearest'}});\\ \;\;\;\;\;\;[\mathit{\boldsymbol{C}}, \mathit{\boldsymbol{h}}, {\bf{CF}}]{\rm{ = }}{\mathop{\rm contourf}\nolimits} (\mathit{\boldsymbol{Y}}, \mathit{\boldsymbol{X}}, \mathit{\boldsymbol{Z}}, {\rm{2}}.{\rm{5}}); \end{array} $ |
其中,命令linspace(y1, y8, n)用来产生y1到y8之间等距离的n个点。[X, Y]=meshgrid(X, Y)(X=[x1, x2, x3], Y=[y1, y2, y3])函数用来产生网格矩阵,X为网格矩阵的横坐标范围,Y是网格矩阵的纵坐标范围;返回网格矩阵的坐标[X, Y]。Z=griddata(lat, lon, data, X, Y, ‘n’)为散点插值函数,用于在散点[lat, lon]之间进行插值[11],data为该点的色值,[X, Y]表示插值的网格(密度远大于[lat, lon]),n为插值类型;返回插值结果矩阵Z。函数[C, h, CF]=contourf(Y, X, Z, m)可用来绘制二维等值线图,Z为平面内网格点[Y, X]处的色值,m为梯度线的个数,添加色彩后会产生m+1种颜色。同时返回与命令contourc中相同的等高线矩阵C,C也可被命令clabel使用;返回包含patch图形对象的句柄向量h;返回填充色值的矩阵CF。
突变界线可通过设置参数m,将等值线阶数降为1阶来实现。将contourf命令中的m值设为[11]:
| $m=n-1 $ | (3) |
| $n=\frac{d}{L} $ | (4) |
式中,m为等值线条数,n为梯度数,d为总梯度差,L为步长。例如在某次地震事件中,低点时间等值线条数为m,所涂颜色共有n种,网内地磁低点时间的最早值与最晚值之差为d,两个区域之间的低点时间相差步长为L,且L≡2。例如网内低点时间的最早值与最晚值分别为08:00和15:00,此时d=7,将d和L≡2代入式(3)和式(4)中求出m值为2.5。执行contourf命令可输出以m为参数的地磁低点时间的等值线,突变界线为其中一条或一段。
式(3)中m并不是突变界线的条数,而是确定等值线的参数。在地磁台网中,所有台站的低点时间的相互差异程度决定m值的范围,当0<m < 1时,网内存在1个大区域,缺少等值线;当1≤m < 2时,网内存在2个大区域,有1条等值线;当2≤m < 3时,网内存在3个大区域,有2条等值线;当n≤m<n+1时,网内存在n+1个大区域,有n条等值线。通过合理地调节m值,可以使等值线的数量最少,一般控制成二阶等值线,从而将突变界线刻画出来;在n条等值线中,两侧低点时间差异最明显的那条等值线即为本文所求的突变界线。
在2015年皮山6.5级地震前06-21地磁低点位移事件中,m值为6,等值线有5条,突变界线有1条。在2016年门源6.4级地震前2015-12-23甘肃、青海地区出现的地磁低点位移现象中,m值为2,等值线有2条,突变界线有1条。在2016年甘肃金塔4.7级地震前02-28地磁低点位移事件中,m值为3,等值线有3条,突变界线有2条,本节案例参见文献[11]。
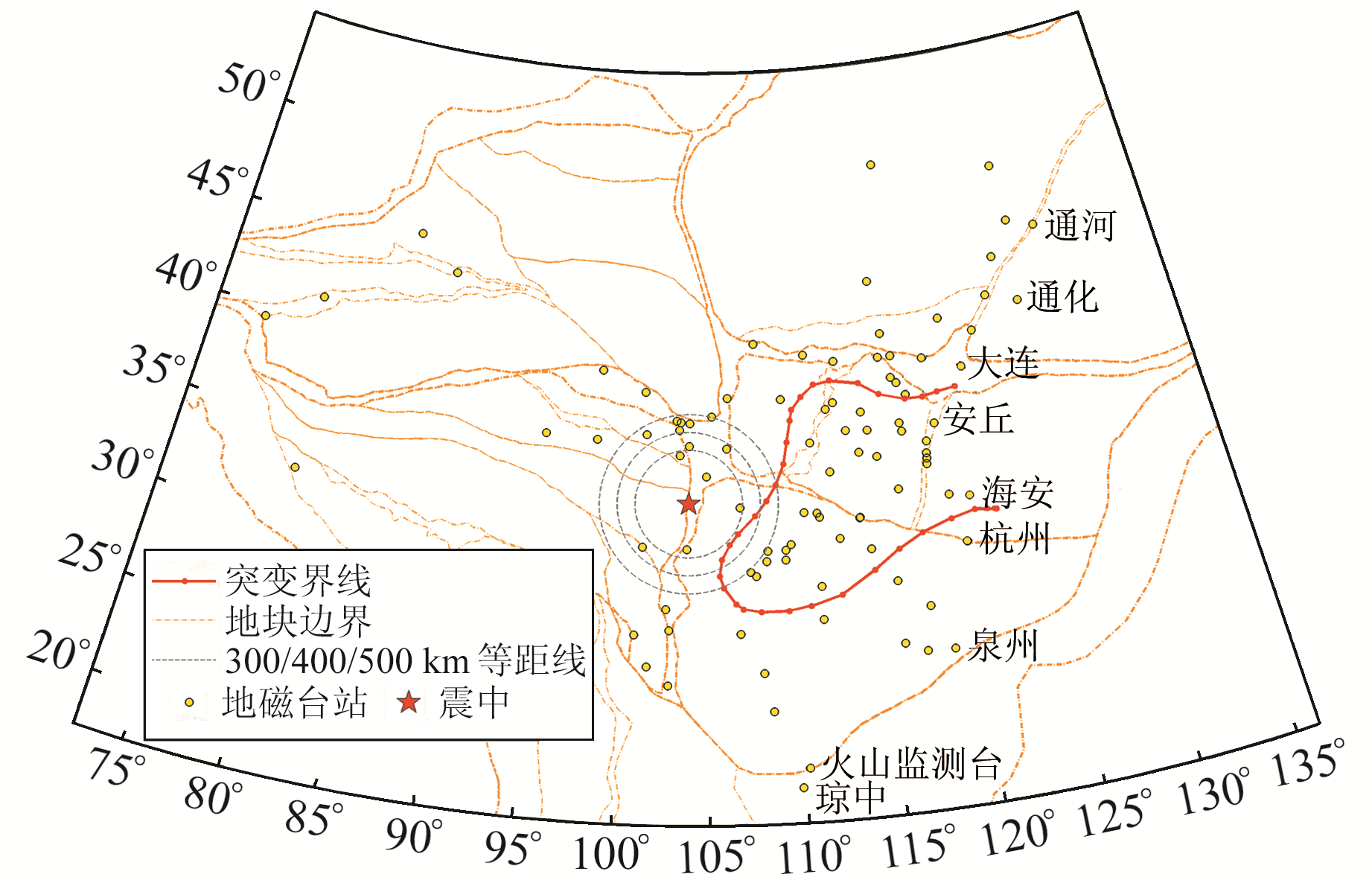
5 数据分析中国地震台网中心于2017-07-20在华北、长江中下游地区出现的地磁低点位移现象中发现,低点时间被分为内外两个区域,按原数据的格林威治时间统计的内区域平均低点时间为6.73时,外区域平均低点时间为3.84时,两者相差2.89 h;将格林威治时间转化为式(2)地方时后,内区域的平均低点时间为14.39时(表 2)。外区域的平均低点时间为11.01时,与内区域相差3.38 h。桃源台仪器出现故障,因此用邵阳台地磁数据代替。在地磁低点位移现象发生后的第19天,即北京时间2017-08-08 21:19,四川省阿坝州九寨沟县发生MS7.0地震,比文献[3]中统计的极可能发震区间的最小值小4 d,震中距突变界线约185 km。2017-08-08的K指数为2,未受到外空间磁暴干扰,地磁低点数据真实可靠,因此认为,07-20出现的地磁低点位移现象与此次地震具有较好的相关性,图 4为中国地震台网中心采用人工绘制的突变界线。
|
|
表 2 内区域全部台站的低点时间 Tab. 2 Low-point time of all stations in inner region |
|
图 4 2017-07-20出现的地磁低点位移现象(采用当地时间) Fig. 4 The geomagnetic low-point displacement phenomenon on July 20, 2017(use local time) |
突变界线由乳山、济南、红山、定襄、太原、临汾、万州、石柱、涪陵、重庆、桃源、九峰、高邮、海安台共同组成,外区域西端存在榆林、汉中、成都、美姑、贵阳、邵阳6个控制性台站,对突变界线的走向起决定性作用。为了直观地表现两种形式的低点时间在空间分布上的差异以及§4中自动定位技术提取与人工画线的差异,采用式(2)地方时结合§5方法求出全国124个台站的低点时间等值线图(图 5)。

|
图 5 采用当地时间绘制的突变界线 Fig. 5 Abrupt boundaries based on local time |
由图 5可见,最近邻插值结果中共有4条梯度线,第1条与人工绘制的突变界线形状相似,第2条在襄阳市、南阳市周围,第3条在山东省无棣大山地震台周围,第4条在新疆维吾尔自治区喀什市周围。由于单个地磁台站低点时间的偏移未形成大区域,因此认为,图 5中第2~4条梯度线不是地磁低点位移突变界线,只有第1条梯度线符合突变界线的定义。
图 5为使用式(2)地方时的结果,喀什台与都兰台的相对偏差减小为185 min,乌什台、红浅台、乌鲁木齐台与都兰台的低点时间色值相同。图 3为使用格林威治时间的结果,喀什台和都兰台低点时间色值不同,相对偏差为274 min,乌什台、红浅台、乌鲁木齐台和都兰台低点时间色值不同。上述分析表明,新方法可减小具有经向跨度的台站之间低点时间的偏差,可过滤掉新疆地区的“假异常”突变界线。
对比图 4与图 5可知,前者是平滑曲线,后者为折线。图 4中东北地区的第2条突变界线在人工绘制时未被发现,而图 5中已绘制东北地区的突变界线。在华北、华中地区,两个图的突变界线走向大体一致,在河北北部略有差异。图 5中的突变界线在内区域存在两个孤岛,由于单个地磁台站低点时间的偏移未形成大区域,因此本文未把孤岛外轮廓作为地磁低点位移突变界线。
6 结语本文提出的方法在不改变地磁低点位移法基本原理的情况下可有效排除干扰,减少误差。九寨沟地震前的地磁低点位移现象分析表明,本文提出的突变界线定位法与原有算法相比具有以下优点:
1) 原有方法会产生“经度效应”,新方法可很好地消除。
2) 原有方法的突变界线可以反映突变界线的大致走向,但无法获取突变界线内区域的孤岛;而新方法可以精确地绘制突变界线内区域中的孤岛。
3) 原有地磁低点时间的数据格式无法统计与地磁低点背景时间的偏差,并且使用概率统计法识别异常会受来自外空场的干扰所影响,从而较难识别真正的异常;而新方法中的低点时间采用式(2)地方时,可以更精确地识别异常和来自外空场的干扰,过滤“假异常”突变界线。
4) 如果将线条看作点的集合,且假定原方法手绘的突变界线足够精确,则原方法的突变界线为新方法的突变界线的非空真子集,后者包含前者,人工划线时容易遗漏一些隐藏的突变界线,而新方法不会遗漏隐藏的突变界线。
| [1] |
陈绍明. 地磁日变低点位移分界线的网络分布及其与地震关系的探讨[J]. 地震, 1987, 7(5): 33-39 (Chen Shaoming. Study on the Network Distribution of the Low Point Displacement Boundary of Geomagnetic Diurnal Variation and Its Relationship with Earthquakes[J]. Earthquake, 1987, 7(5): 33-39)
(  0) 0) |
| [2] |
丁鉴海, 卢振业, 黄雪香. 地震地磁学[M]. 北京: 地震出版社, 1994 (Ding Jianhai, Lu Zhenye, Huang Xuexiang. Seismomagnetism[M]. Beijing: Seismological Press, 1994)
(  0) 0) |
| [3] |
丁鉴海, 车时, 余素荣, 等. 地磁日变地震预报方法及其震例研究[M]. 北京: 地震出版社, 2009 (Ding Jianhai, Che Shi, Yu Surong, et al. The Earthquake Prediction Method of Geomagnetic Diurnal Variation and Cases Study[M]. Beijing: Seismological Press, 2009)
(  0) 0) |
| [4] |
陈绍明. 地磁垂直分量日变反向与华北地区中强震的关系[J]. 华北地震科学, 1986, 4(1): 96-100 (Chen Shaoming. The Relationship between the Diurnal Variation Reversal of Geomagnetic Vertical Component and Moderate Strong Earthquakes in North China[J]. North China Earthquake Sciences, 1986, 4(1): 96-100)
(  0) 0) |
| [5] |
王亚丽, 吴迎燕, 卢军, 等. 中国大陆地区地磁场Z分量日变化相位的空间分布特征研究[J]. 地球物理学报, 2009, 52(4): 1033-1040 (Wang Yali, Wu Yingyan, Lu Jun, et al. Spatial Distribution Characteristics of Geomagnetic Z Component Phase Variation in Chinese Mainland[J]. Chinese Journal of Geophysics, 2009, 52(4): 1033-1040 DOI:10.3969/j.issn.0001-5733.2009.04.020)
(  0) 0) |
| [6] |
许康生, 曾文浩. 地磁低点位移异常:岷县-漳县M6.6地震可能的震前反映[J]. 大地测量与地球动力学, 2017, 37(4): 425-428 (Xu Kangsheng, Zeng Wenhao. Abnormity of Geomagnitics Low-Point Shift:A Possible Seismogenic Reflection of the Minxian-Zhangxian M6.6 Earthquake[J]. Journal of Geodesy and Geodynamics, 2017, 37(4): 425-428)
(  0) 0) |
| [7] |
郭增建, 郭安宁, 贾源源, 等. 地磁低点位移以磁暴倍九法作为补充预测的讨论[J]. 地震工程学报, 2018, 40(5): 1131-1132 (Guo Zengjian, Guo Anning, Jia Yuanyuan, et al. Discussion on the Geomagnetic Low-Point Displacement Method with the Magnetic Storm Nine Days Multiplication Method as a Supplementary Prediction[J]. China Earthquake Engineering Journal, 2018, 40(5): 1131-1132 DOI:10.3969/j.issn.1000-0844.2018.05.1131)
(  0) 0) |
| [8] |
贾昕晔, 戴勇, 高立新, 等. 2010年山西河津4.8级地震地磁垂直分量日变化低点时间空间分布特征[J]. 地震工程学报, 2018, 40(增): 105-111 (Jia Xinye, Dai Yong, Gao Lixin, et al. Spatial Distribution Characteristics of Low-Point Time of Geomagnetic Vertical Component Diurnal Variation before the Hejin M4.8 Earthquake of 2010[J]. China Earthquake Engineering Journal, 2018, 40(S): 105-111)
(  0) 0) |
| [9] |
马亮. 地磁低点时间与经度的相关性分析[J]. 地震工程学报, 2019, 41(3): 763-769 (Ma Liang. Correlation Analysis of Geomagnetic Low-Point Time and Longitude[J]. China Earthquake Engineering Journal, 2019, 41(3): 763-769 DOI:10.3969/j.issn.1000-0844.2019.03.763)
(  0) 0) |
| [10] |
戴勇, 高立新, 姚丽, 等. 2013年岷县-漳县6.6级地震地磁垂直分量日变化低点时间空间分布特征[J]. 地震, 2019, 39(3): 106-114 (Dai Yong, Gao Lixin, Yao Li, et al. Low-Point Time Spatial Distribution Characteristics of Geomagnetic Vertical Component Diurnal Variation before the 2013 M6.6 Minxian-Zhangxian Earthquake[J]. Earthquake, 2019, 39(3): 106-114 DOI:10.3969/j.issn.1000-3274.2019.03.009)
(  0) 0) |
| [11] |
马亮, 孙三健. 地磁低点位移法的改进[J]. 地球物理学进展, 2020, 35(3): 59-67 (Ma Liang, Sun Sanjian. Improvement of Geomagnetic Low-Point Displacement Method[J]. Progress in Geophysics, 2020, 35(3): 59-67)
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41

