2. 武汉大学地球空间环境与大地测量教育部重点实验室,武汉市珞喻路129号,430079
卫星雷达测高已被广泛应用于海面高及其变化、海洋环流、海洋重力场、海底地形、冰盖消融、内陆水域变化等研究,在大地测量学、地球物理学、海洋学、水文学等领域发挥着重要作用。脉冲有限双频雷达高度计是卫星雷达测高的主要模式,但受限于沿轨迹空间分辨率和测距精度低,难以满足近岸、河流、海冰等区域以及中小尺度海洋现象监测的需求。为此,Ka波段雷达高度计、合成孔径雷达高度计、宽刈幅合成孔径雷达干涉高度计以及多星编队测高等模式被相继提出[1-2]。合成孔径雷达(synthetic aperture radar, SAR)测量模式相对于传统脉冲有限雷达测量模式具有较高的沿轨迹空间分辨率和测距精度[3],该技术已在Cryosat-2、Sentinel-3A、Sentinel-3B卫星中实现,并将用于Topex/Poseidon系列的后续卫星Jason-CS/Sentinel-6[4],为今后卫星测高的主要模式。
合成孔径雷达高度计具有较高的沿轨空间分辨率,但在近岸区域仍会受复杂地形海况影响,需要进行波形重跟踪处理。高度计对回波波束处理模式不同会使其回波波形存在较大差别,传统的脉冲有限雷达高度计回波后缘缓慢下降,而合成孔径雷达高度计回波后缘迅速下降,使得传统的布朗海恩模型无法适用,由此导致OCEAN算法、ALES算法[5]、BP算法[6]等基于布朗海恩模型的波形重跟踪算法无法用于合成孔径雷达高度计的数据处理。部分学者针对合成孔径雷达高度计回波问题提出一些基于函数模型的拟合算法,包括基于延迟多普勒原理[7]的SAMOSA(SAR altimetry mode studies and applications)重跟踪算法[8];利用一个五段函数模型拟合回波波形的IceSheet重跟踪算法,每段函数对应合成孔径雷达回波的一个区域[9]。此外,传统数学统计经验算法仍适用,包括OCOG算法[10]、阈值法[11]、ICE1算法[12]、多阈值法[13-14]等。
作为未来主要的卫星测高模式,合成孔径雷达高度计的波形重跟踪算法精度分析对其应用至关重要。目前基于模型的SAR重跟踪算法较少,SAMOSA和IceSheet为Sentinel-3A卫星官方采用的算法;而传统经验算法中,ICE1算法在获取内陆江河湖泊水面高时被证实具有较好的准确性[15],多阈值算法在近岸地区精度较好[13, 16-17]。本文将选取ICE1、多阈值、SAMOSA和IceSheet四种算法,利用全球验潮站观测数据分析其在近岸20 km范围内的重跟踪精度,为后续合成孔径雷达高度计观测数据处理提供参考。
1 数据与方法 1.1 采用数据本文选取Sentinel-3A卫星海洋数据的Level-2级非实时产品,该数据可提供仪器校正及各类地球物理和环境误差改正项。Sentinel-3A卫星海洋数据提供3种下载途径,其1 a内的观测数据由哥白尼在线数据访问平台(https://coda.eumetsat.int/)提供下载;长期历史数据存档可以在哥白尼数据中心(https://www.eumetsat.int/website/home/Data/DataDelivery/EUMETSATDataCentre/index.html)提交订单后获取;同时,考虑到后期算法升级,哥白尼在线数据再处理平台(https://codarep.eumetsat.int/)也提供再处理后的数据。Sentinel-3A卫星轨道高度为814 km,轨道倾角为98.56°,运行周期为27 d,每个周期共770个弧段,赤道处轨道间距约100 km,其星下点20 Hz采样间距约为330 m。
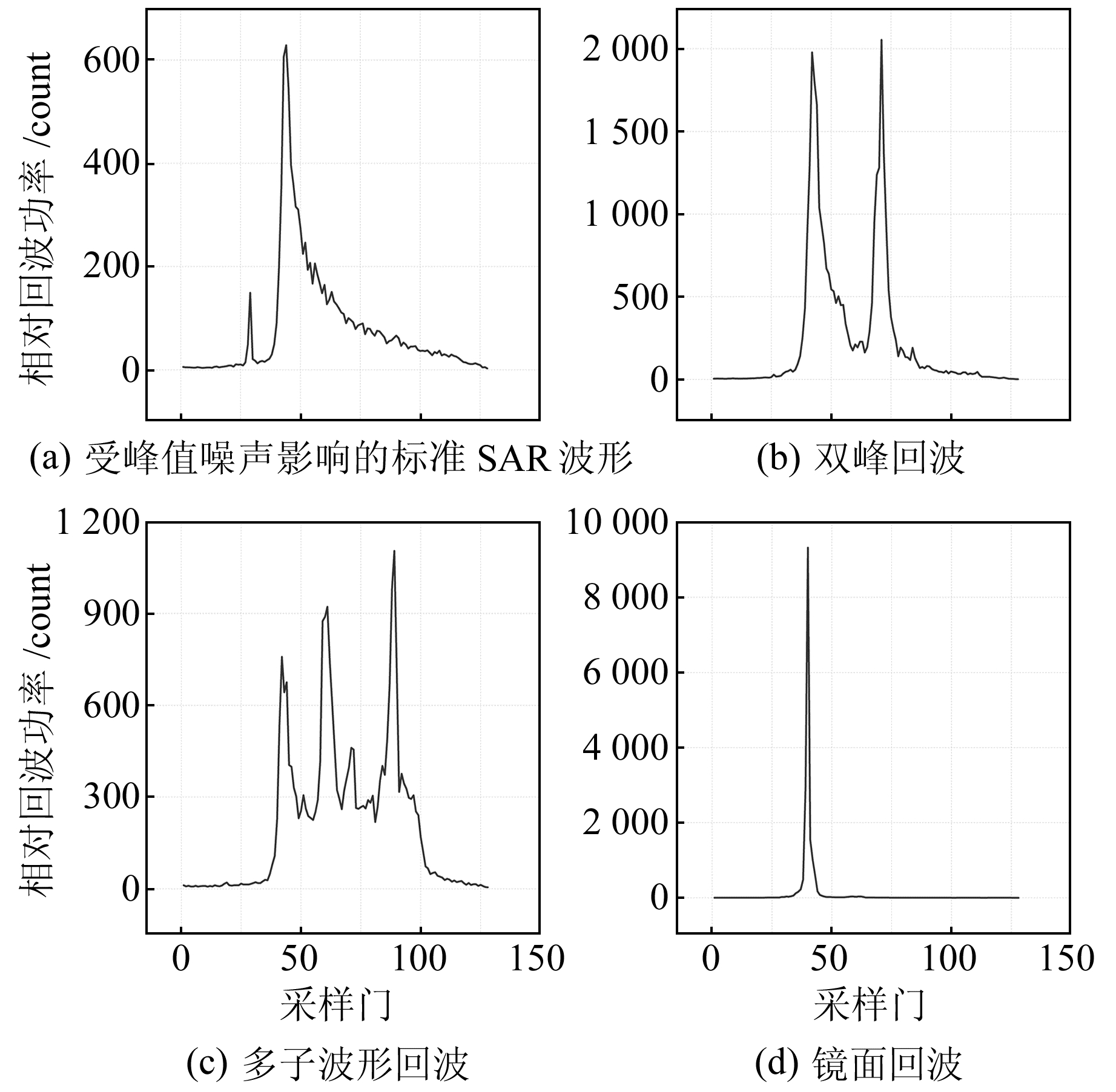
本文采用Sentinel-3A卫星海洋数据的SAR模式20 Hz多视平均回波数据,每个20 Hz波形包含128个采样门,每个距离门对应的时间延迟为3.125 ns,即46.84 cm的海面高改正值,其典型近岸波形如图 1所示。由于近岸微波辐射计对流层湿分量、双频电离层改正等依赖星载仪器的改正项精度相对较差,为便于比较算法的精度,在计算海面高时,需进行基于ECMWF模型的对流层干分量和湿分量改正、基于GIM模型的电离层改正、顾及高频大气响应的逆气压改正、基于GOT4.10c模型的海洋潮汐和海洋潮汐负荷改正、固体潮改正和极潮改正。海况偏差改正一般采用基于有效波高和风速的参数估计方法进行计算,或对其他所有误差改正后的残差进行非参数估计得到;而近岸波形受污染严重,导致有效波高计算误差较大,从而使近岸海况偏差改正精度较差。考虑到选取的验潮站附近测高弧段仅20 km,在小范围内可认为海况偏差改正为常数,且不同的重跟踪算法采用的海况偏差改正一致,为避免引入额外误差影响重跟踪算法精度,因此未添加海况偏差改正[6]。
|
图 1 Sentinel-3A卫星在近岸地区典型回波示意图 Fig. 1 Typical waveform of Sentinel-3A satellite in coastal area |
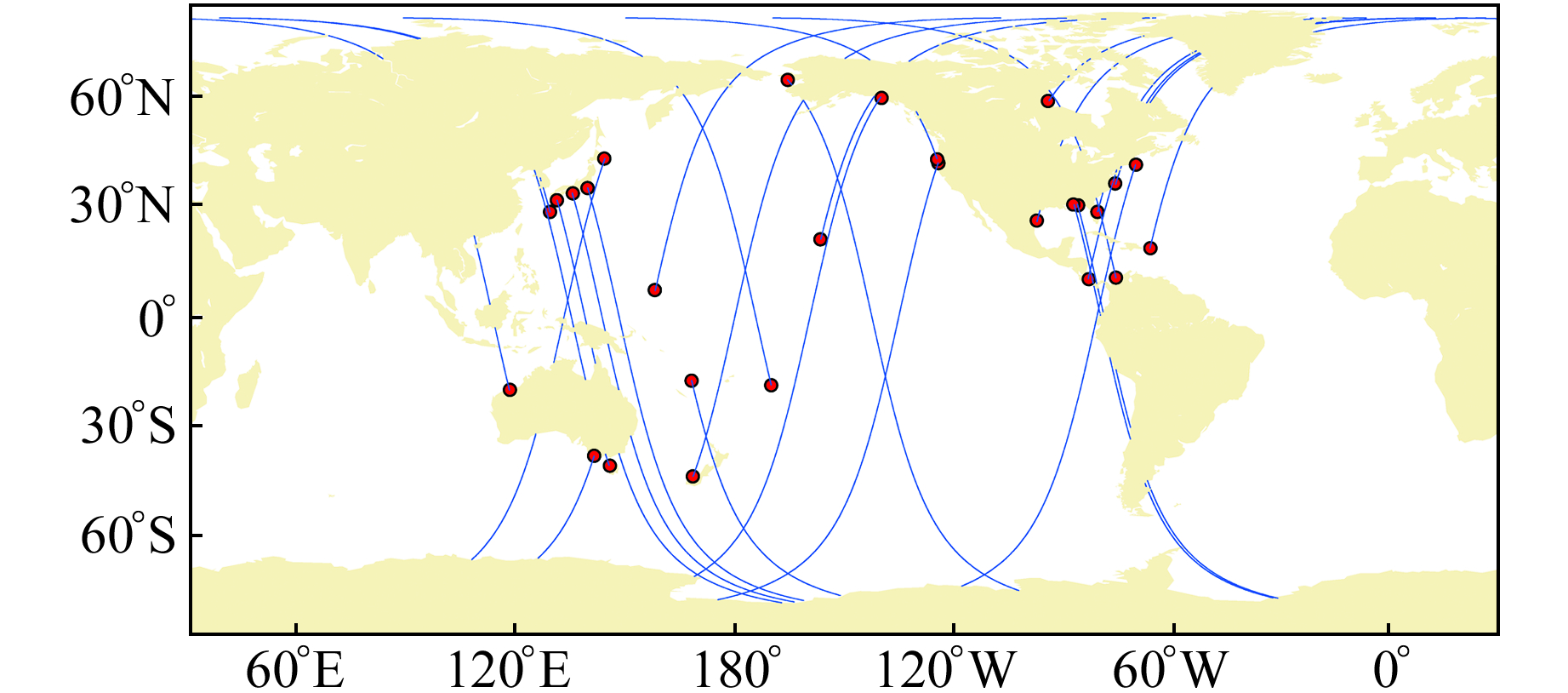
为验证测高数据的精度,选取美国夏威夷大学海平面研究中心发布的1 h采样。经过质量控制的验潮站观测数据(https://uhslc.soest.hawaii.edu/opendap/rqds/contents.html)用于外部验证,并进行逆气压改正达到与测高数据一致。首先,以Sentinel-3A卫星地面轨迹为参考,筛选出距离地面轨迹观测点小于20 km且重叠时间大于2.5 a的验潮站,并剔除最近星下点轨迹位于内陆或岛屿的验潮站;然后,在验潮站附近选取Sentinel-3A卫星观测弧度上距离海岸线1~20 km、以1 km为采样间隔的20个观测序列,分别计算与相邻验潮站海面高序列的相关性,剔除平均相关性小于0.5的验潮站及相应的测高弧段;最后,共选取27个验潮站及相应的Sentinel-3A有效弧段,站点分布如图 2所示,由于有效弧段长度仅20 km,在图中显示不明显,为此给出有效弧段从开始到结束的整个部分。此外,对验潮站数据进行滑动平均滤波去除高频信号和噪声,并利用线性插值方法将验潮站数据内插到测高时间历元。由于验潮站处的海平面数据是相对于站点基准面或其他自定义参考面,而卫星测高海面高的参考面为参考椭球面,为将两者进行比较,降低海面高粗差值的影响,分别在两种时间序列中移去各自的中值,进而消除基准差,同时重跟踪算法的系统偏差也会被消除。通过中值对齐,还可消除测高数据中未考虑海况偏差改正的影响。
|
图 2 选取的27个验潮站站点以及相应的Sentinel-3A有效弧段分布 Fig. 2 Distribution of 27 selected tide gauges and corresponding Sentinel-3A valid passes |
在近岸区域,传统的多阈值算法利用沿轨开放海域方向最近的重跟踪海面高作为参考高度,但必须保证从开放海域向沿岸方向搜索,然后将最接近该参考高度的子波形前缘作为有效前缘[16]。而卫星测高在开阔海域沿轨方向20 Hz的海面高噪声水平较高,如Jason-2数据可达到7.5 cm[18],该噪声在近岸区域更高。因此,如果以邻近的海面高作为参考,可能会引入较大不确定性,而通常沿轨星下点的海平面相对大地水准面的正高序列相对稳定,故本文采用正高序列的中值作为参考,以抑制沿轨噪声引入的不确定性。因此,对于SAR模式的多阈值算法,本文对其实施以下步骤进行修改:1)对所有波形采用Hwang等[16]的方法进行子波形搜索,并采用阈值重跟踪得到相应海面高;2)扣除所有子波形海面高所对应的EGM2008大地水准面高得到正高序列;3)当波形只有单个子波形前缘时,表明其受污染较小,可选择此类波形对应的正高序列的中值作为参考值;对于其他多前缘的子波形,选取相应正高值距离该参考值最近的子波形前缘所对应的海面高作为该波形的重跟踪海面高。
针对4种重跟踪算法,SAMOSA算法和IceSheet算法的重跟踪距离采用Sentinel-3A卫星数据产品提供的结果,ICE1算法和多阈值算法经测试后选择最优阈值用于获取重跟踪距离,然后对各算法采用相同的地球物理改正。利用4种重跟踪算法对近岸20 km内的观测数据进行处理得到所有海面高;将海面高以1 km为间隔进行平均,得到20个等间隔的平均海面高时间序列;利用EGM2008模型校正各点的大地水准面梯度;最后计算各点海面高序列与最邻近验潮站海面高序列的相关性和差值均方根误差。此外,本文对4种算法重跟踪后保留的有效波形个数相对原始波形的比例进行比较,并分析重跟踪后海面高序列相对EGM2008模型大地水准面高差值的标准差。
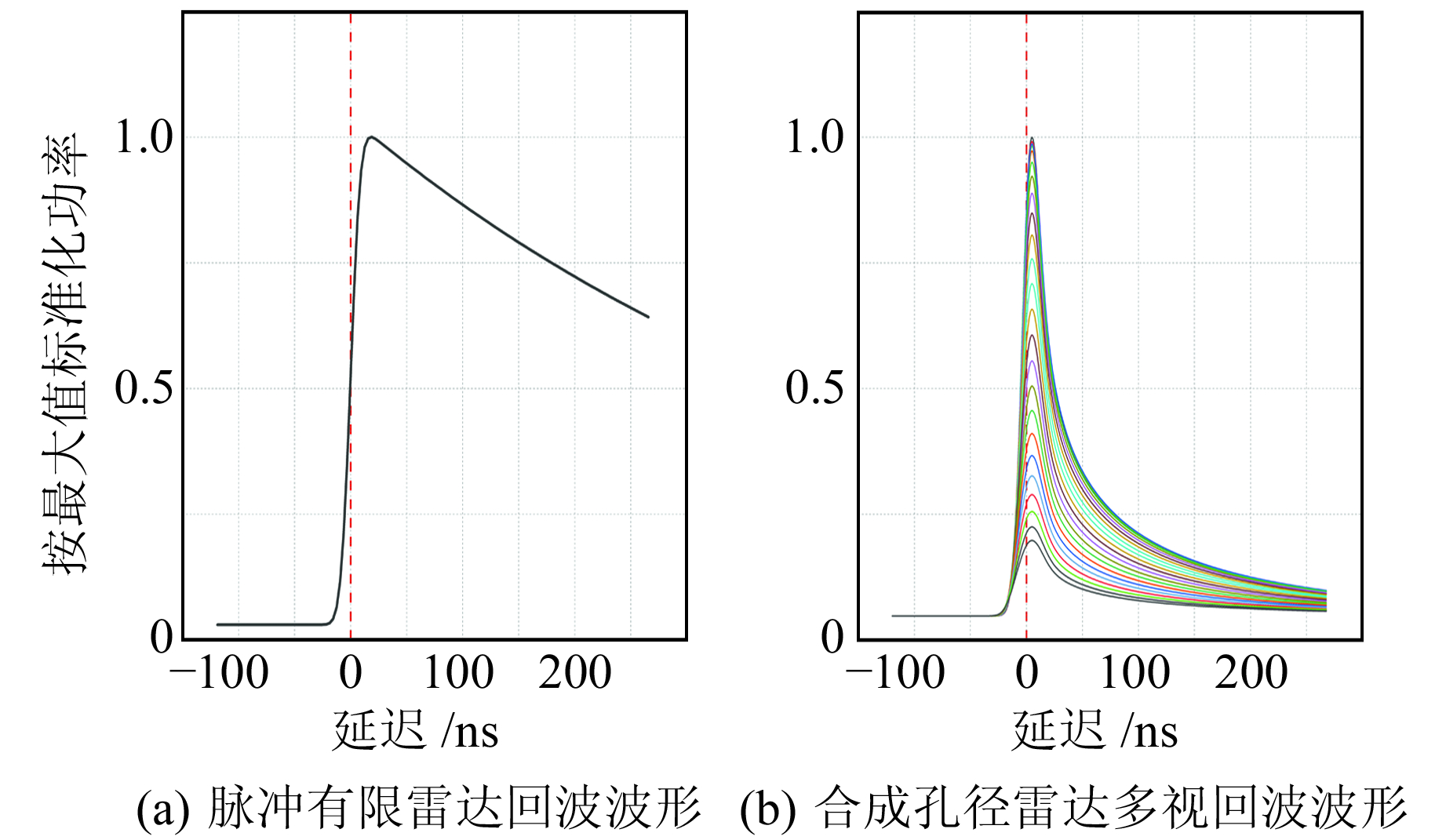
2 结果分析 2.1 多阈值和ICE1算法的最优阈值选取由于ICE1算法和多阈值算法涉及阈值的选取,为获得最佳阈值和最好的重跟踪效果,对阈值范围为0.3~1.0的两种算法的重跟踪海面高进行分析,并计算其与所选取的所有验潮站站点海面高序列的相关性和差值均方根误差(图 3),为更好地展示最优阈值的效果,未给出范围内所有阈值的重跟踪结果。从图 3可以看出,当ICE1阈值取0.85、多阈值算法阈值取0.75时,在近岸1~20 km范围内,两种海面高序列的相关性和差值均方根误差最优。由于回波波形存在差异,传统脉冲有限雷达高度计的星下点跟踪位置大致位于波形前缘中点,故一般阈值较小;而合成孔径雷达高度计的星下点跟踪位置更接近于峰值,故其阈值较大(图 4)。

|
图 3 不同阈值情况下验潮站海面高与重跟踪海面高序列的平均相关性和差值RMS Fig. 3 The mean correlation and RMS of difference between tide gauge sea levels and retracked sea levels under different thresholds |
|
图 4 有效波高4 m时脉冲有限雷达回波波形和合成孔径雷达多视回波波形 Fig. 4 The waveforms of pulse limited radar altimeter and synthetic aperture radar altimeter under 4 m significant wave height |
对4种算法重跟踪后的20个海面高时间序列进行分析,在每1 km处统计原始观测的回波波形个数,然后计算不同距离处重跟踪成功波形个数与原始波形个数之比,以分析不同离岸距离时各算法的重跟踪成功率[17],将明显偏离正常区间的重跟踪结果认定为重跟踪失败,本文采用3倍标准差准则进行判定。表 1为各算法统计结果,由表可见,除IceSheet算法在1 km处外,4种算法在所有距离段的重跟踪率均大于50%;多阈值算法在近岸9 km范围内成功率最高,且在3 km时已超过90%。在近岸9 km范围内,IceSheet算法的成功率始终低于其他算法,ICE1算法的成功率略高于SAMOSA算法;在近岸9~20 km范围内,SAMOSA算法成功率最高,表明在开阔海域该算法成功率较高。
|
|
表 1 不同离岸距离情况下4种重跟踪算法的有效波形比例 Tab. 1 The rates of effective waveform of four retrackers in different distances to the coast |
分别计算4种算法重跟踪后的20个海面高时间序列与最邻近验潮站海面高时间序列的相关性和差值均方根误差,并统计不同距离情况下4种算法的平均相关性和平均差值均方根误差(图 5)。由图可见,在近岸20 km范围内,SAMOSA算法相关性最低且均方根误差最大;在6 km范围内,多阈值算法平均相关性最高且差值均方根误差最小;在6 km范围外,多阈值和ICE1算法基本相当;IceSheet算法始终处于中等水平。

|
图 5 不同距离情况下4种算法重跟踪海面高与验潮站海面高时间序列的平均相关性和差值RMS Fig. 5 The mean correlation and RMS of difference between retracked sea levels and tide gauge sea levels of four retrackers in different distances to the coast |
由于平均海面高模型在近岸精度较差,且其主要采用传统卫星测高数据,而大地水准面模型在近岸具有较好的稳定性,故可通过计算重跟踪海面高序列与大地水准面的差值标准差来衡量算法自身的变异性[19]。将近岸20 km区域划分为若干个距离区间,分别统计每个验潮站在各距离区间的重跟踪海面高序列与EGM2008大地水准面模型的差值标准差,最后取区间内所有验潮站的平均标准差作为该区间的内部可靠性评价。为保证足够的沿轨迹采样数量,以5 km为间隔进行区间计算,结果见表 2。从表中可以看出,在近岸0~5 km范围内,IceSheet算法略优于其他算法;在近岸5~20 km范围内,SAMOSA算法显著优于其他算法,IceSheet、ICE1和多阈值算法效果相当,表明SAMOSA算法具有较高的稳定性(特别是在开阔海域),而在近岸近距离区域回波波形偏离标准海洋波形,导致基于回波模型的重跟踪算法出现偏差,与验潮站实测海面高的相关性和均方根误差偏差较大。此外,在离岸距离15~20 km范围内的均值略大于5~15 km区间的均值,其原因为个别弧段的大地水准面起伏异常,但其影响对各重跟踪算法基本一致,因此对各算法结果的比较不会造成影响。
|
|
表 2 不同离岸距离下4种算法重跟踪海面高与EGM2008大地水准面高差异的沿轨标准差 Tab. 2 The along-track STD of the difference between retracked sea surface height and EGM2008 geoid heights of four retrackers in different distances to the coast |
基于Sentinel-3A卫星合成孔径雷达高度计观测数据,利用全球范围内27个验潮站海面高数据,采用4种波形重跟踪算法对近岸20 km范围内邻近测高波形数据进行重跟踪,对各算法的精度进行分析。结果表明,ICE1和多阈值算法分别选取阈值0.85和0.75时精度最优,在此条件下多阈值算法在近岸6 km范围内可保留最多的有效波形个数,且与验潮站海面高序列的相关性最高和均方根误差最小;IceSheet算法具有较低的有效波形比例,但在近岸5 km范围内具有最好的稳定性;SAMOSA算法在近岸20 km范围内的重跟踪海面高与验潮站海面高相差最大,但在离岸距离大于5 km后算法稳定性最高,适用于开阔海域。总体而言,在近岸近距离海域,基于数学统计的多阈值重跟踪算法精度较好;在开阔海域,基于物理模型的SAMOSA重跟踪算法精度较好。
虽然现在已积累大量合成孔径雷达高度计实测数据,但相对脉冲有限雷达高度计,在波形数据处理及应用上的研究较少。新的高度计体系在理论上具有更高的沿轨分辨率和测距精度,但仍需进行更深入的验证和分析,以推进合成孔径雷达测高的应用,弥补脉冲有效雷达高度计的不足。
| [1] |
李建成, 金涛勇. 卫星测高技术及应用若干进展[J]. 测绘地理信息, 2013, 38(4): 1-8 (Li Jiancheng, Jin Taoyong. On the Main Progress of Satellite Altimetry and Its Applications[J]. Journal of Geomatics, 2013, 38(4): 1-8)
(  0) 0) |
| [2] |
汪海洪, 钟波, 王伟, 等. 卫星测高的局限与新技术发展[J]. 大地测量与地球动力学, 2009, 29(1): 91-95 (Wang Haihong, Zhong Bo, Wang Wei, et al. Limitations of Satellite Altimetry and Future Technology Improvements[J]. Journal of Geodesy and Geodynamics, 2009, 29(1): 91-95)
(  0) 0) |
| [3] |
McMillan M, Muir A, Shepherd A, et al. Sentinel-3 Delay-Doppler Altimetry over Antarctica[J]. The Cryosphere, 2019, 13(2): 709-722 DOI:10.5194/tc-13-709-2019
(  0) 0) |
| [4] |
Verrier S, le Traon P Y, Remy E, et al. Assessing the Impact of SAR Altimetry for Global Ocean Analysis and Forecasting[J]. Journal of Operational Oceanography, 2018, 11(2): 82-86 DOI:10.1080/1755876X.2018.1505028
(  0) 0) |
| [5] |
Passaro M, Cipollini P, Vignudelli S, et al. ALES: A Multi-Mission Adaptive Subwaveform Retracker for Coastal and Open Ocean Altimetry[J]. Remote Sensing of Environment, 2014, 145: 173-189 DOI:10.1016/j.rse.2014.02.008
(  0) 0) |
| [6] |
Peng F K, Deng X L. A New Retracking Technique for Brown Peaky Altimetric Waveforms[J]. Marine Geodesy, 2018, 41(2): 99-125 DOI:10.1080/01490419.2017.1381656
(  0) 0) |
| [7] |
Ray C, Martin-Puig C, Clarizia M P, et al. SAR Altimeter Backscattered Waveform Model[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(2): 911-919 DOI:10.1109/TGRS.2014.2330423
(  0) 0) |
| [8] |
Dinardo S, Lucas B, Benveniste J. Sentinel-3 STM SAR Ocean Retracking Algorithm and SAMOSA Model[C]. IEEE International Geoscience and Remote Sensing Symposium, Milan, 2015
(  0) 0) |
| [9] |
Shu S, Liu H X, Beck R A, et al. Analysis of Sentinel-3 SAR Altimetry Waveform Retracking Algorithms for Deriving Temporally Consistent Water Levels over Ice-Covered Lakes[J]. Remote Sensing of Environment, 2020, 239: 111 643 DOI:10.1016/j.rse.2020.111643
(  0) 0) |
| [10] |
Wingham D J, Rapley C G, Griffiths H D. New Techniques in Satellite Altimeter Tracking Systems[C]. IGARSS' 86 Symposium, Zurich, 1986
(  0) 0) |
| [11] |
Davis C H. Growth of the Greenland Ice Sheet: A Performance Assessment of Altimeter Retracking Algorithms[J]. IEEE Transactions on Geoscience and Remote Sensing, 1995, 33(5): 1 108-1 116 DOI:10.1109/36.469474
(  0) 0) |
| [12] |
Bamber J L. Ice Sheet Altimeter Processing Scheme[J]. International Journal of Remote Sensing, 1994, 15(4): 925-938 DOI:10.1080/01431169408954125
(  0) 0) |
| [13] |
常晓涛, 李建成, 郭金运, 等. 一种多前缘多阈值的波形重构算法[J]. 地球物理学报, 2006, 49(6): 1 629-1 634 (Chang Xiaotao, Li Jiancheng, Guo Jinyun, et al. A Multi-Leading Edge and Multi-Threshold Waveform Retracker[J]. Chinese Journal of Geophysics, 2006, 49(6): 1 629-1 634)
(  0) 0) |
| [14] |
Yang L, Lin M S, Liu Q H, et al. A Coastal Altimetry Retracking Strategy Based on Waveform Classification and Sub-Waveform Extraction[J]. International Journal of Remote Sensing, 2012, 33(24): 7 806-7 819 DOI:10.1080/01431161.2012.701350
(  0) 0) |
| [15] |
Frappart F, Legrésy B, Niño F, et al. An ERS-2 Altimetry Reprocessing Compatible with ENVISAT for Long-Term Land and Ice Sheets Studies[J]. Remote Sensing of Environment, 2016, 184: 558-581 DOI:10.1016/j.rse.2016.07.037
(  0) 0) |
| [16] |
Hwang C, Guo J Y, Deng X L, et al. Coastal Gravity Anomalies from Retracked Geosat/GM Altimetry: Improvement, Limitation and the Role of Airborne Gravity Data[J]. Journal of Geodesy, 2006, 80(4): 204-216 DOI:10.1007/s00190-006-0052-x
(  0) 0) |
| [17] |
郭金运, 高永刚, 常晓涛, 等. 近岸海域EnviSat卫星测高波形重定的Threshold优化算法[J]. 地球物理学报, 2010, 53(4): 807-814 (Guo Jinyun, Gao Yonggang, Chang Xiaotao, et al. Optimal Threshold Algorithm of EnviSat Waveform Retracking over Coastal Sea[J]. Chinese Journal of Geophysics, 2010, 53(4): 807-814 DOI:10.3969/j.issn.0001-5733.2010.04.005)
(  0) 0) |
| [18] |
Thibaut P, Poisson J C, Bronner E, et al. Relative Performance of the MLE3 and MLE4 Retracking Algorithms on Jason-2 Altimeter Waveforms[J]. Marine Geodesy, 2010, 33(S1): 317-335
(  0) 0) |
| [19] |
Huang Z K, Wang H H, Luo Z C, et al. Improving Jason-2 Sea Surface Heights within 10 km Offshore by Retracking Decontaminated Waveforms[J]. Remote Sensing, 2017, 9(10): 1 077 DOI:10.3390/rs9101077
(  0) 0) |
2. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, 129 Luoyu Road, Wuhan 430079, China
 2021, Vol. 41
2021, Vol. 41


