室外环境中的行人导航研究以卫星导航或全球导航卫星系统(GNSS)/惯性导航(INS)组合导航为主,近年取得了较好的成果[1]。对于行人定位导航技术的研究主要分为两类:一类是利用外部部署设备定位,主要基于室内超宽带(UWB)、Wi-Fi(wireless fidelity)及蓝牙等无线射频设备;另一类则是以惯性传感器定位,主要基于惯性导航技术等。目前,已有较多针对步数估计[2-9]、步长估计[10-12]及航向角估计[13-16]等方面的研究,并取得了不错的进展。
为提高行人在有磁场干扰环境中轨迹跟踪的准确性,本文在步数估计阶段采用双重阈值二值化算法提高计步的准确性;同时在航向估计阶段,利用自适应融合算法对加速度数据、角速度数据及磁力计数据融合得出更精准的航向;最后设计在有磁干扰和无磁干扰环境中进行对比实验,证明本文算法在航迹跟踪上的有效性。
1 行人位置推算行人航位推算时通过计步检测、步长估计、航向估计3个步骤完成用户位置的更新,并据此绘制出移动轨迹。在计步检测中,通常利用三轴加速度信息检测步数,当检测到用户移动1步时,步长估计和航向估计模块发生作用,开始进行位置的更新,其过程见图 1。假设初始时刻为t0,行人的初始位置为p0(e0,n0),沿北偏东α0的方向移动,在t1时刻行人的运动距离为S0(步长),此时行人的位置为p1(e1,n1)。同理可得,在t2时刻行人的位置为p2(e2,n2),距离为S1(步长)。

|
图 1 PDR位置更新 Fig. 1 PDR location update |
推广到一般情况,根据t时刻的步长St和行进方向αt,计算t+1时刻行人的位置为:
| $ \left\{ {\begin{array}{*{20}{l}} {{n_{t + 1}} = {n_t} + {S_t} \cdot \cos {{\alpha _t}} }\\ {{e_{t + 1}} = {e_t} + {S_t} \cdot \sin {{\alpha _t}} } \end{array}} \right. $ | (1) |
式中,nt为t时刻行人在全局坐标系中的横坐标,et为t时刻行人在全局坐标系中的纵坐标。
由于传统的计步检测过程中会出现伪峰谷值的影响,因此提出利用双重阈值二值化算法避免误判;传统的航向估计精度不高,本文采用自适应融合算法进行航向估计。
2 计步检测传统的波峰检测和阈值检测算法均无法处理行人在行走过程中出现的抖动情况,表现在加速度数据上的特征是出现伪波峰或伪波谷。本文提出利用双重阈值二值化算法进行计步检测,可精准计步,并处理出现伪波峰或伪波谷的情况。利用改进的步数算法进行计步检测的步骤为:
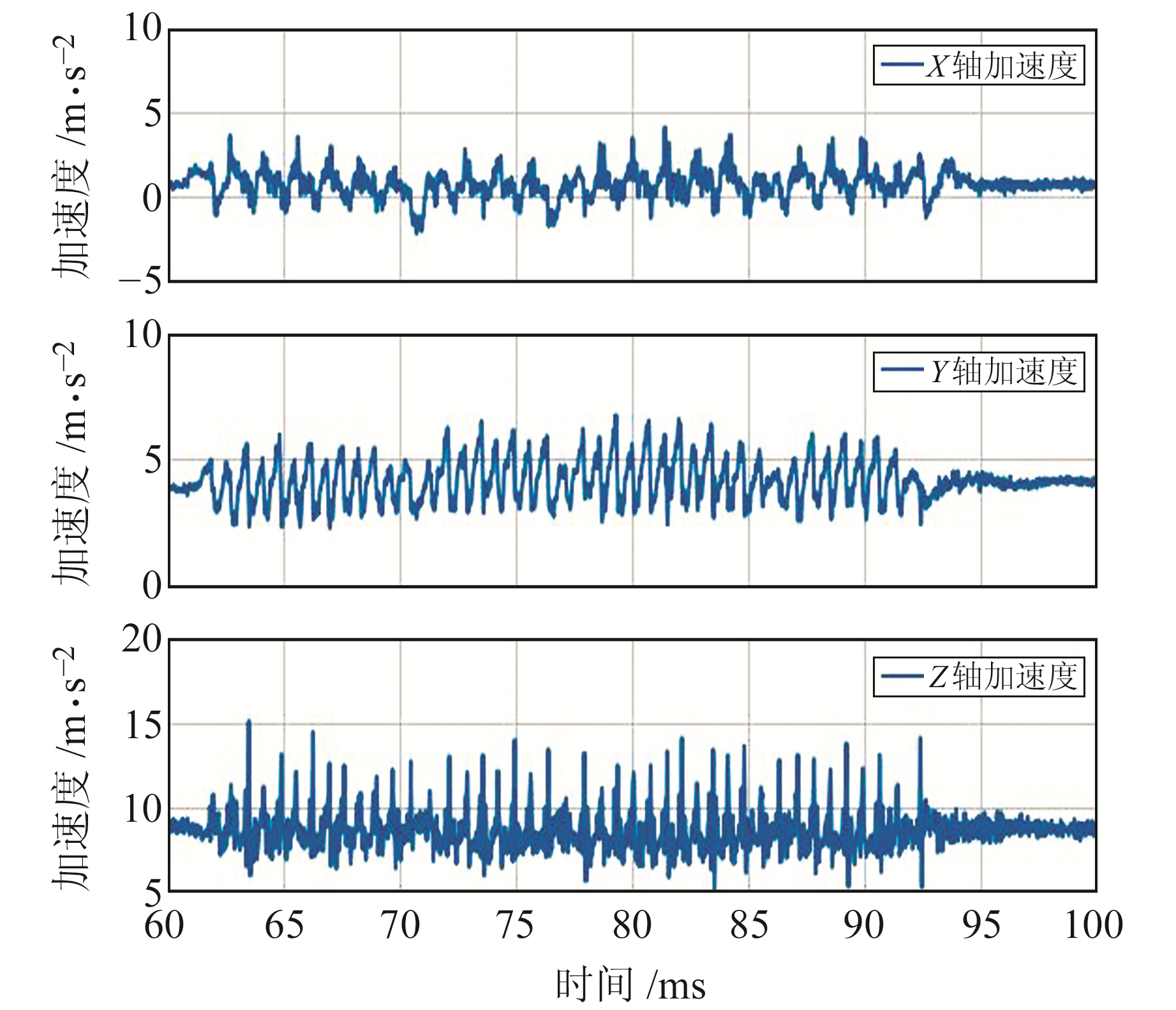
1) 求加速度模值。通过手机加速度传感器获取三轴加速度(图 2),再利用三轴加速度信息求加速度模值,其公式为:
| $ {\rm{acc\_mag}} = \sqrt {{a_x^2} + {a_y^2} + {a_z^2}} $ | (2) |
|
图 2 沿矩形路径行走的三轴加速度 Fig. 2 Triaxial acceleration along rectangular path |
式中,ax、ay、az为三轴加速度。
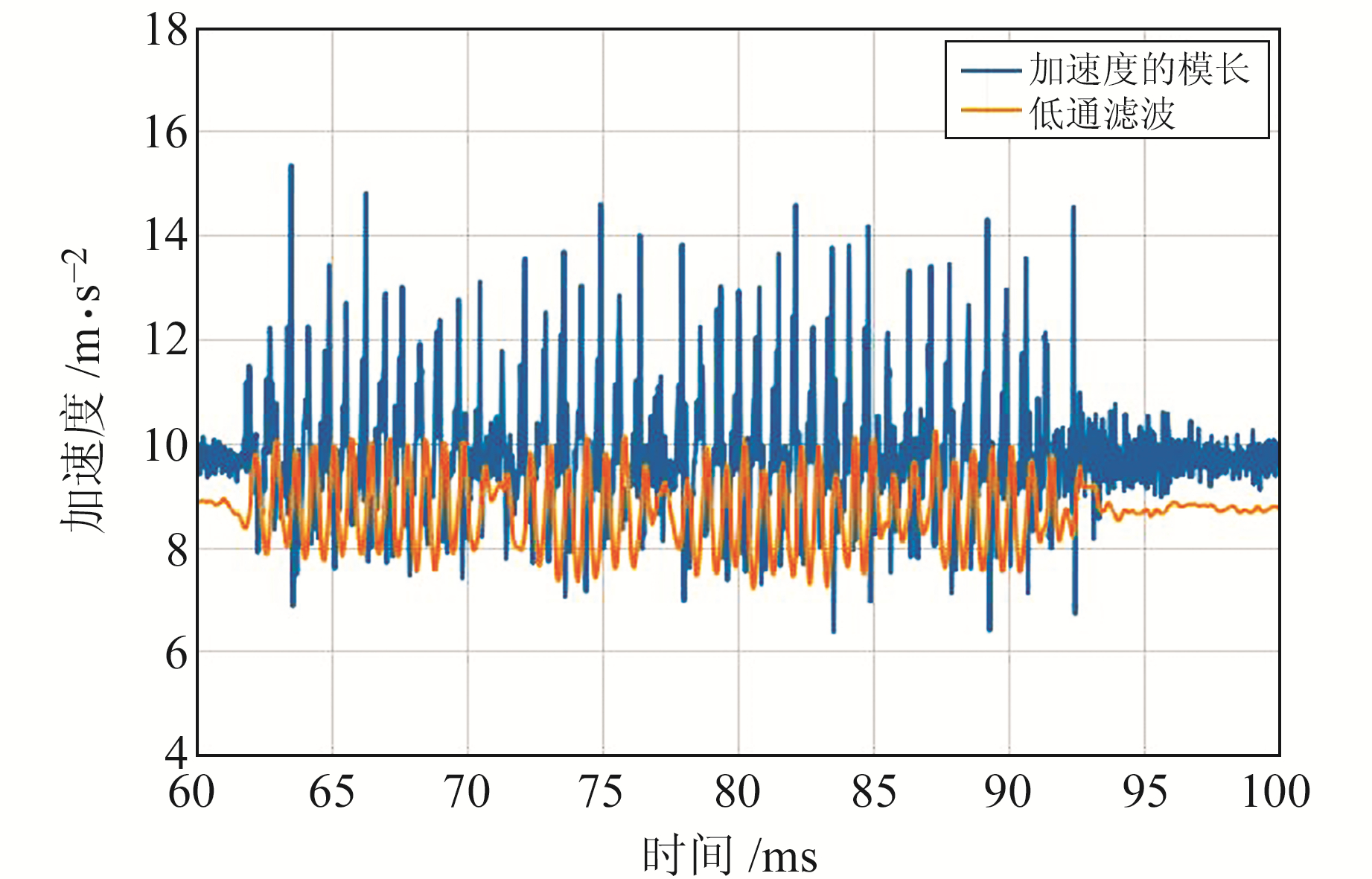
2) 低通滤波。利用四阶的低通滤波器对加速度模值进行滤波,正常人匀速行走的频率为每秒2步,变速行走平均为每秒3步,截止频率可设置为2 Hz或3 Hz,滤波前后的数据见图 3。
|
图 3 低通滤波后的加速度 Fig. 3 Low-pass filtered acceleration |
3) 去除重力。将滤波之后的加速度模值去除重力的影响:
| $ {\rm{acc\_detrend}} = {\rm{acc\_mag\_filt}} - g $ | (3) |
式中,acc_detrend为去除重力影响的加速度,acc_mag_filt为滤波后的加速度,g为重力加速度(取9.8 m/s2)。
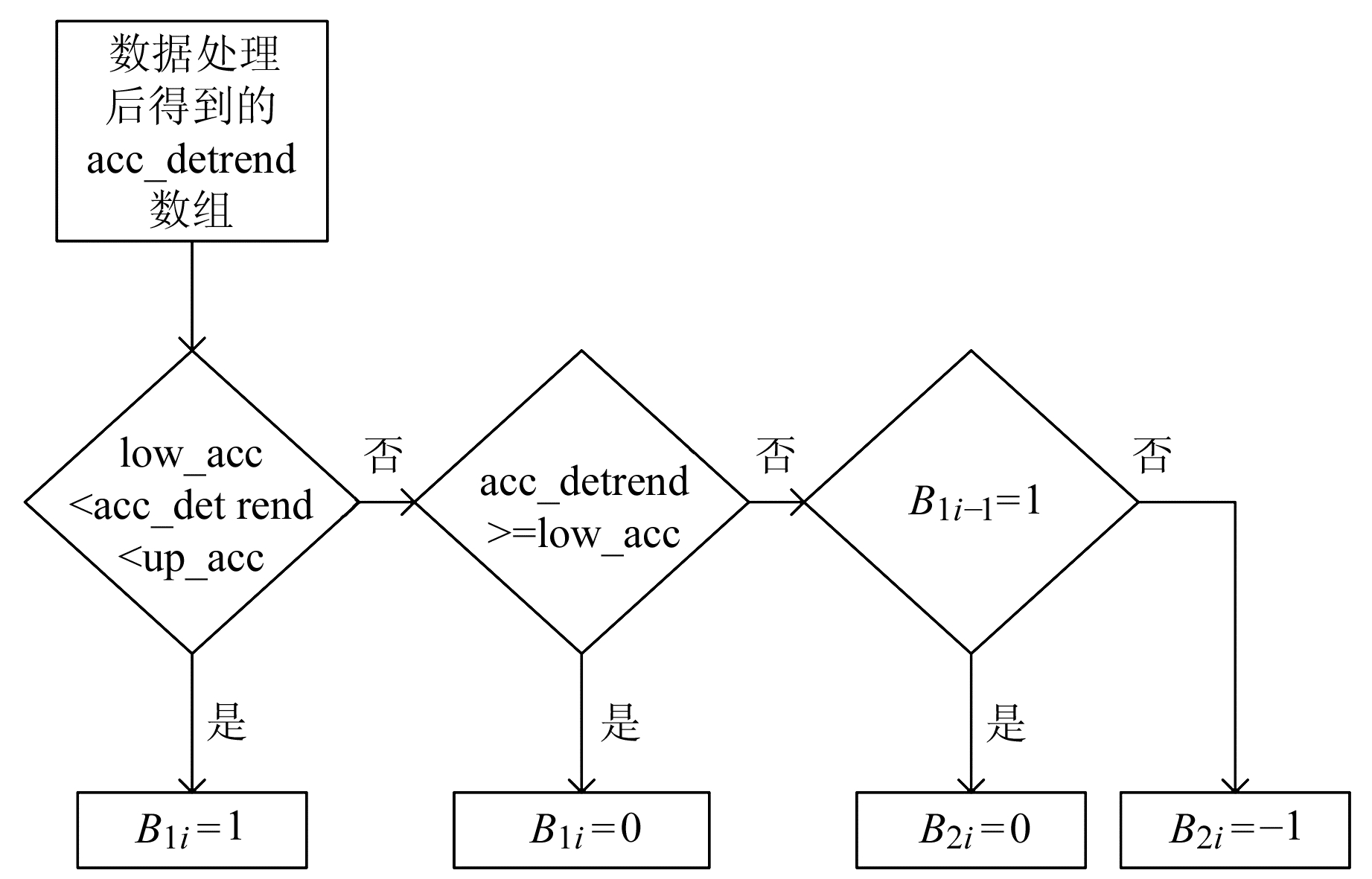
4) 双重阈值二值化。由于传统阈值方法对伪峰谷值的判断不准确,因此设计两重阈值细化加速度信息,其上限根据去除重力后加速度模值的最大值设置,下限根据行走多组实验取平均得出。同时,为从细化的加速度信息中提取峰谷值,采用二值化方法进行计算。双重阈值二值化流程见图 4,二值化后的加速度为:
| $ {B_{{\rm{1}}i}} = \left\{ {\begin{array}{*{20}{l}} 1&{{\rm{low\_acc}} < {\rm{acc\_detrend}} < {\rm{up\_acc}}}\\ 0&{{\rm{acc\_detrend}} \ge - {\rm{low\_acc }}} \end{array}} \right. $ | (4) |
| $ {B_{2i}} = \left\{ {\begin{array}{*{20}{l}} 0&{{B_{1i - 1}} = 1}\\ { - 1}&{{B_{1i - 1}} ≠ 1} \end{array}} \right. $ | (5) |
|
图 4 双重阈值二值化 Fig. 4 Double threshold binarization |
式中,low_acc和up_acc分别为阈值下限和上限,B1i、B2i分别为第i个样本在二值化后的加速度,B1i-1为前一个样本二值化后的值。
5) 计步。需同时满足从高加速度到低加速度,如B1i从1到0,且在1个时间窗口内加速度出现0,即可记为1步。
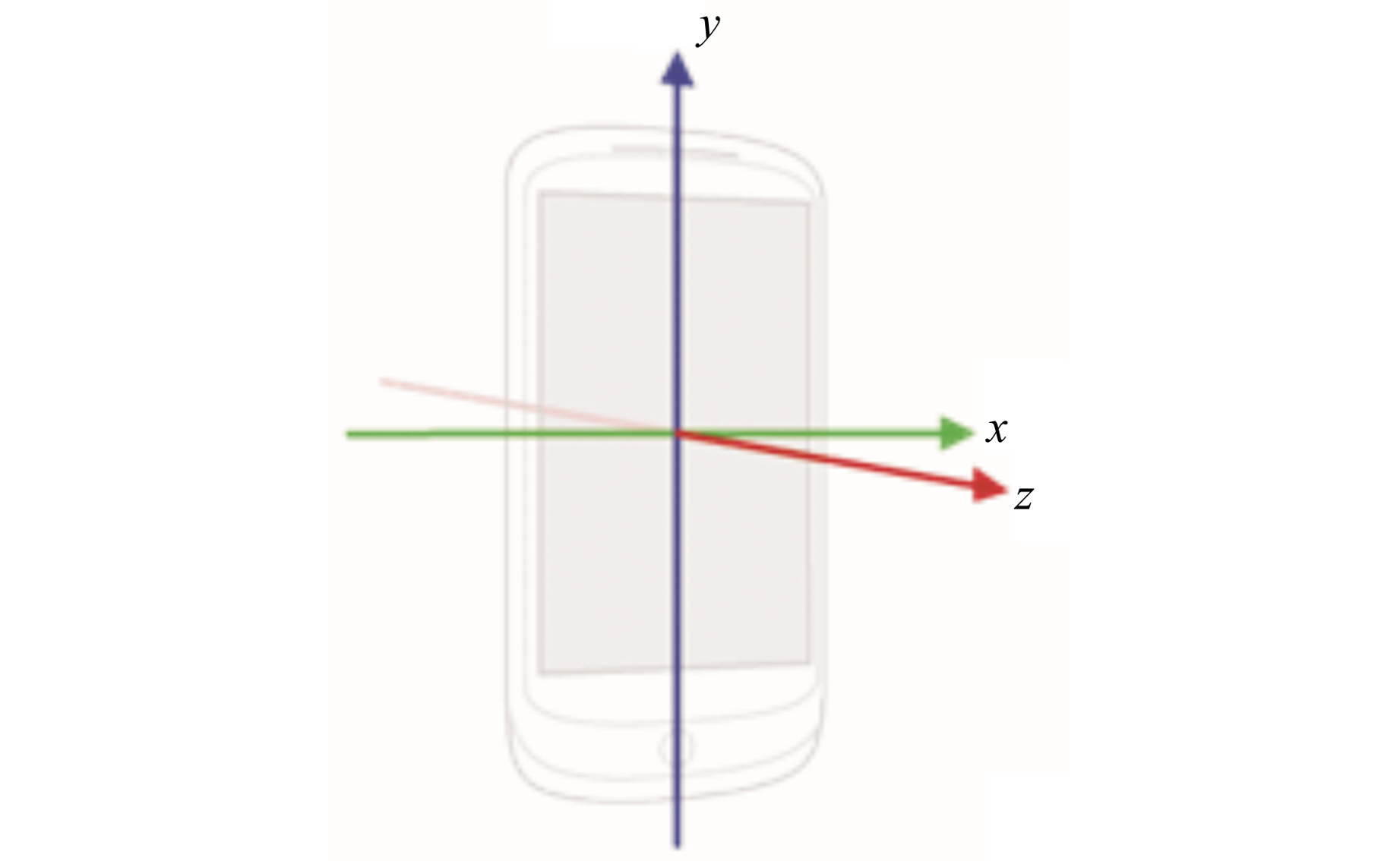
3 航向估计 3.1 基于欧拉角的坐标变换由于手机在行走过程中会不断发生移动,加速度传感器采集的数据因手机姿态的不断变化很难同前一时刻保持一致,因此采用空间坐标系转换的方法将数据从机体坐标系(body frame, b)映射至静态的导航坐标系(navigation frame,n)。机体坐标系如图 5所示。
|
图 5 机体坐标系 Fig. 5 Body frame |
在初始时刻,机体坐标系xbybzb与导航坐标系xnynzn是重合的,行走过程中设备载体的姿态会随行人的运动发生改变。导航坐标系可经过航向角(机体绕z轴旋转)、横滚角(机体绕y轴旋转)及俯仰角(机体绕x轴旋转)变化后得到机体坐标系,该旋转过程可表示为:
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{x_{\rm{n}}}}\\ {{y_{\rm{n}}}}\\ {{z_{\rm{n}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \theta }&{\sin \theta }&0\\ { - \sin \theta }&{\cos \theta }&0\\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&{\cos \varphi }&{\sin \varphi }\\ 0&{ - \sin \varphi }&{\cos \varphi } \end{array}} \right] \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {\cos \phi }&0&{ - \sin \phi }\\ 0&1&0\\ {\sin \phi }&0&{\cos \phi } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_{\rm{b}}}}\\ {{y_{\rm{b}}}}\\ {{z_{\rm{b}}}} \end{array}} \right] \end{array} $ | (6) |
式中,θ、φ、Ζ分别为航向角、横滚角及俯仰角。
3.2 改进的航迹推算算法描述针对航向估计准确性低的问题,传统算法利用陀螺仪积分得到角度,但积分会使角度误差随时间不断累积,导致航向错误,同时周围磁场也在发生变化,使得方向估计更加困难。因此,本文先将加速度计及陀螺仪数据进行融合,再根据磁感应强度阈值确定是否需要融合磁力计数据,具体流程见图 6。

|
图 6 融合框架 Fig. 6 Fusion framework |
具体算法步骤如下。
1) 根据加速度求取角度。根据加速度传感器采集的信息初始化手机的姿态信息,默认初始状态的yaw(航向角)为0°,roll(横滚角)和pitch(俯仰角)为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\rm{roll}} = \arctan \frac{{{a_y}}}{{{a_z}}}}\\ {{\rm{pitch}} = \arctan \frac{{ - {a_x}}}{{{a_z}}}} \end{array}} \right. $ | (7) |
2) 坐标转换。根据§3.1的描述,得出机体坐标系转换到导航坐标系下的初始旋转矩阵。
3) 由微分方程确定旋转矩阵,进行姿态解算。对姿态的解算本质上是求旋转矩阵,由于姿态随时间变化,在时间t处姿态的变化率为:
| $ \dot C(t) = \mathop {\lim }\limits_{\delta t \to 0} \frac{{C(t + \delta t) - C(t)}}{{\delta t}} $ | (8) |
式中,δt为陀螺仪的周期。式(8)可利用极限性质进行简化:
| $ \dot C(t) = C(t)\mathop {\lim }\limits_{\delta t \to 0} \frac{{\delta \mathit{\boldsymbol{ \boldsymbol{\varPsi} }}}}{{\delta t}} $ | (9) |
| $ \delta \mathit{\boldsymbol{ \boldsymbol{\varPsi} }} = \left( {\begin{array}{*{20}{c}} 0&{ - \delta \varphi }&{\delta \theta }\\ {\delta \varphi }&0&{ - \delta \phi }\\ { - \delta \theta }&{\delta \phi }&0 \end{array}} \right) $ | (10) |
式中,δΨ为t到t+δt时间段内的旋转矩阵,δθ为该时间段内微小的偏航角,δφ为该时间段内微小的横滚角,δϕ为该时间段内微小的俯仰角。
| $ \mathop {\lim }\limits_{\delta t \to 0} \frac{{\delta \mathit{\boldsymbol{ \boldsymbol{\varPsi} }}}}{{\delta t}} = \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}(t) $ | (11) |
| $ \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}(t) = \left( {\begin{array}{*{20}{c}} 0&{ - {\omega _{bz}}(t)}&{{\omega _{by}}(t)}\\ {{\omega _{bz}}(t)}&0&{ - {\omega _{bx}}(t)}\\ { - {\omega _{by}}(t)}&{{\omega _{bx}}(t)}&0 \end{array}} \right) $ | (12) |
式中,Ω(t)为陀螺仪角速率矩阵,t为陀螺仪周期开始时刻,ωbx(t)、ωby(t)、ωbz(t)分别为三轴角速率。由式(9)~(12)可得:
| $ \dot C(t) = C(t)\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}(t) $ | (13) |
陀螺仪实际上是不提供连续信号ωb(t)的,而是通常以固定频率提供角速度的样本,必须使用积分方案来积分采样信号。因此式(13)可改写为:
| $ \dot C(t) = C(t) \cdot \exp \left( {\int_t^{t + \delta t} \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} (t){\rm{d}}t} \right) $ | (14) |
由式(14)的微分方程可解得旋转矩阵为:
| $ \mathit{\boldsymbol{C}}(t) = \mathit{\boldsymbol{C}}(0) \cdot \exp \left( {\int_0^t \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} (t){\rm{d}}t} \right) $ | (15) |
式中,C(0)由步骤1)中加速度初始化的旋转矩阵确定,因此更新过程中融合了加速度信息。
4) 根据旋转矩阵求航向角。由步骤3)求得的旋转矩阵可以得出加速度融合陀螺仪的航向角为:
| $ \tan \theta = \frac{{{\mathit{\boldsymbol{C}}_{21}}}}{{{\mathit{\boldsymbol{C}}_{11}}}} $ | (16) |
式中,C21为旋转矩阵2行1列处的元素,同理C11为矩阵中1行1列处的元素。
5) 根据磁力计数据求航向角。由磁力计估计的航向角为:
| $ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\psi _{{\rm{mag}}}} = \\ \arctan \left( {\frac{{ - {h_y}\cos \phi + {h_z}\sin \phi }}{{{h_x}\cos \theta + {h_y}\sin \phi \sin \theta + {h_z}\cos \phi \sin \theta }}} \right) + D $ | (17) |
式中,hx、hy、hz为磁力计测得的三轴磁感应强度,D为当地磁偏角。
6) 融合策略。根据是否受磁场干扰确定加速度计、陀螺仪及磁力计的权重分配,其中有、无磁场干扰是根据传感器采集的磁感应强度模值决定的,大于阈值时认为有磁场干扰,反之则认为无磁场干扰。本文采取的策略为:如果受到磁场干扰,则磁力计的权重小,加速度计和陀螺仪融合结果权重大;如果没有受到磁场干扰,则磁力计权重大,加速度数据和陀螺仪融合结果权重小,以适应有磁场干扰的环境。
4 实验与结果分析 4.1 实验条件及数据采集为对本文提出的改进计步算法和航向估计算法在航迹跟踪上的效果进行验证,设计多组实验,并让行人按照标定好的矩形路径行走,比较航迹的误差。
实验的采集设备为华为P20手机,加速度计、陀螺仪和磁力计数据的采集利用LOPSI实验室(http://car.upm-csic.es/lopsi)开发的GetSensorData2.0应用程序,数据采集频率均为50 Hz,采集数据时右手持手机放在胸前。
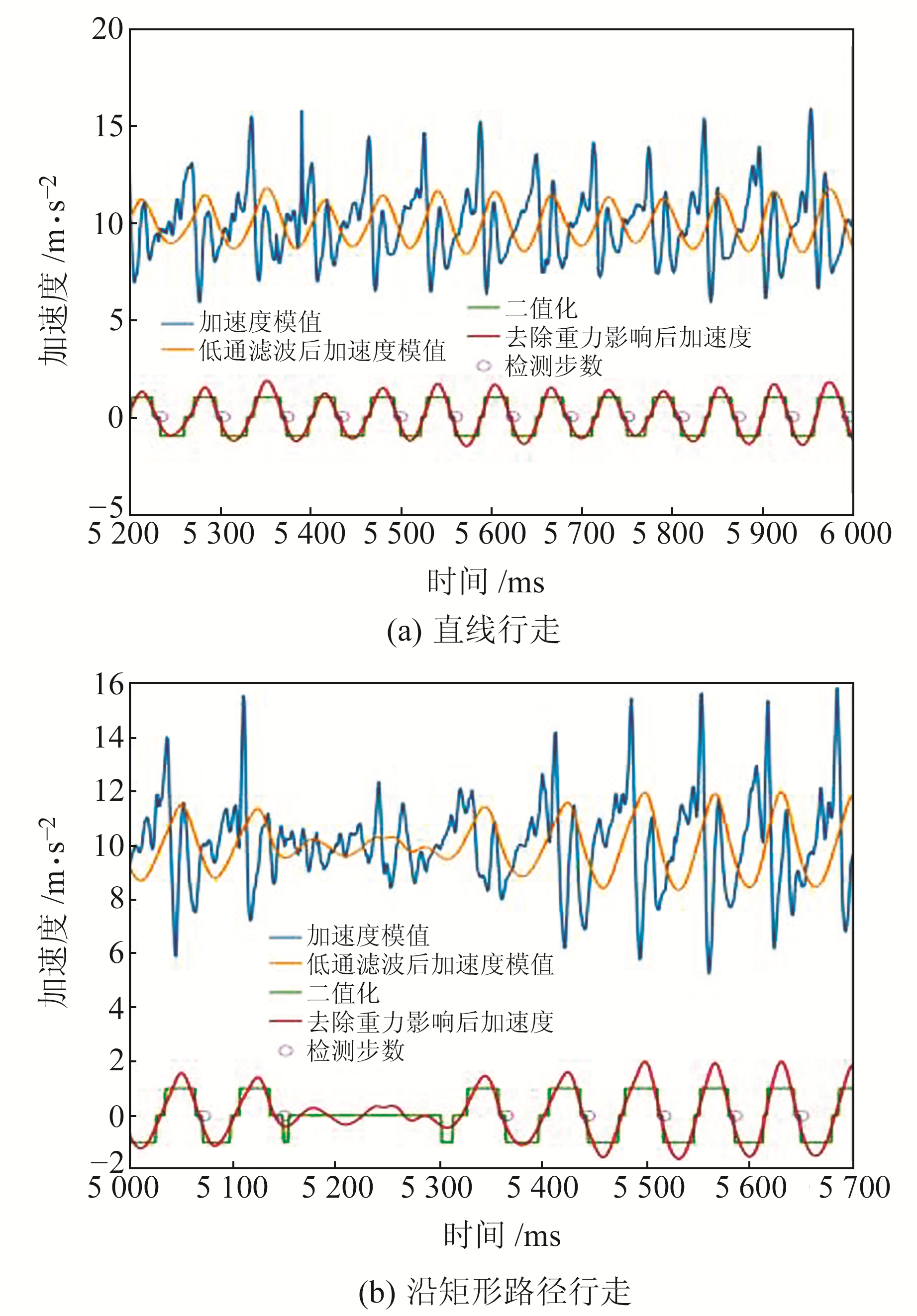
4.2 步数估计实验在计步检测实验中,采用本文提出的双重阈值二值化算法进行计步,阈值上限根据去除重力影响后加速度模值的最大值设置为2.2 m/s2,下限根据加速度模值的最小值设置为0.4 m/s2,实验过程中行人可以不同速度行走,以检验算法的鲁棒性。以直线行走和沿矩形路径行走为例,分析加速度变化特性并可视化,如图 7所示。可以看出,相邻的波峰与波谷之间为1步,但由于行人在运动过程中的摆动可能出现伪波峰或伪波谷,采用二值化的方式并结合时间约束可避免误判。从图 7(b)中可清晰地看出,在5 200~5 300 ms之间加速度模值出现伪波峰谷,二值化算法在该时段没有计步。
|
图 7 步数可视化 Fig. 7 Visualization of the number of steps |
为验证算法的有效性,通过计步准确性衡量指标分析本文算法与文献[8]中动态阈值算法在计步检测上的表现,结果见表 1。根据行人在行走过程中速度的变化将实验分为匀速运动和变速运动,行人在匀速行走时两种算法的计步准确率都在95%以上;行人在变速行走时,基于动态阈值波峰检测算法的计步准确率明显低于本文提出的双阈值二值化算法。由此可知,双阈值二值化算法可避免传统方法遇到的伪峰谷值的影响,进而提高计步的准确率,同时本文算法对行人的行走速度要求不高,更具有普适性。
|
|
表 1 步数判断结果 Tab. 1 Step judgment result |
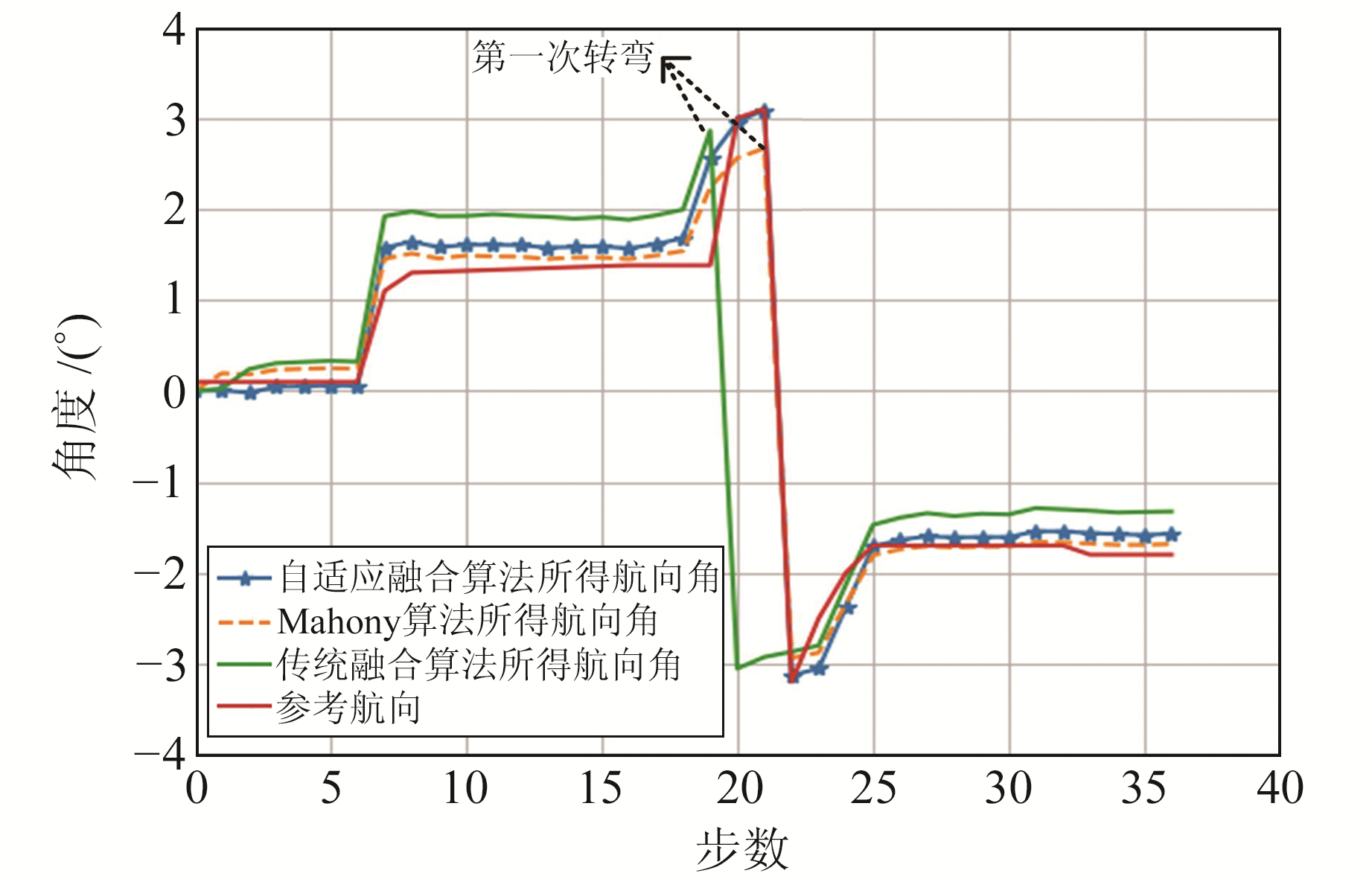
由于地球表面任一点的地球磁场强度矢量方向与水平面存在夹角,在航向估计中需要移除本地磁偏角(5°)。为验证自适应融合算法在航向估计中的准确性,设计行人沿着矩形路径行走,通过平均角度误差将本文改进的航向估计算法同传统算法以及文献[17]中的多传感器融合算法进行比对。图 8展示了行人沿矩形路径行走37步中角度的变化情况,其中自适应融合算法即为本文算法。由图可知,本文算法和文献[17]算法均在第20步时判断发生第1次转弯,但传统算法在行走到第18步时判断发生第1次转弯,从参考航向来看,第1次转弯发生在第20步,因此传统算法的转弯识别错误。在发生第1次转弯过程中3种算法的精度各不相同,本文算法在第1次转弯处与参考角度之间的误差为5.7°,文献[17]算法的误差为8.6°,传统算法的误差为11.4°;在第2次转弯时,传统算法判断在第20步时发生第2次转弯,而参考航向证明发生第2次转弯是在第21步,传统算法转弯识别错误,本文算法与文献[17]算法均在第21步时识别转弯,文献[17]算法与参考角度之间的误差为12.5°,本文算法的误差为5.4°。从图中还可看出,在行走到第24步时3种算法均判断发生第3次转弯,即3种算法在第3次转弯识别上的判断上是一致的,传统算法与参考角度之间的误差为5.7°,文献[17]算法的误差为2.5°,本文算法的误差为2.7°。为量化误差及衡量算法的准确性,利用平均角度误差衡量在3次转弯过程中的角度误差,由于传统算法未能正确识别第1次和第2次转弯,所以在平均角度误差衡量过程中不考虑传统算法。本文算法的平均角度误差为4.5°,文献[17]算法的平均角度误差为6.8°。综上所述,本文算法在航向估计中较文献[17]算法的角度误差更小,更有利于航迹跟踪时准确捕获航向变化。
|
图 8 航向估计结果 Fig. 8 Heading estimation result |
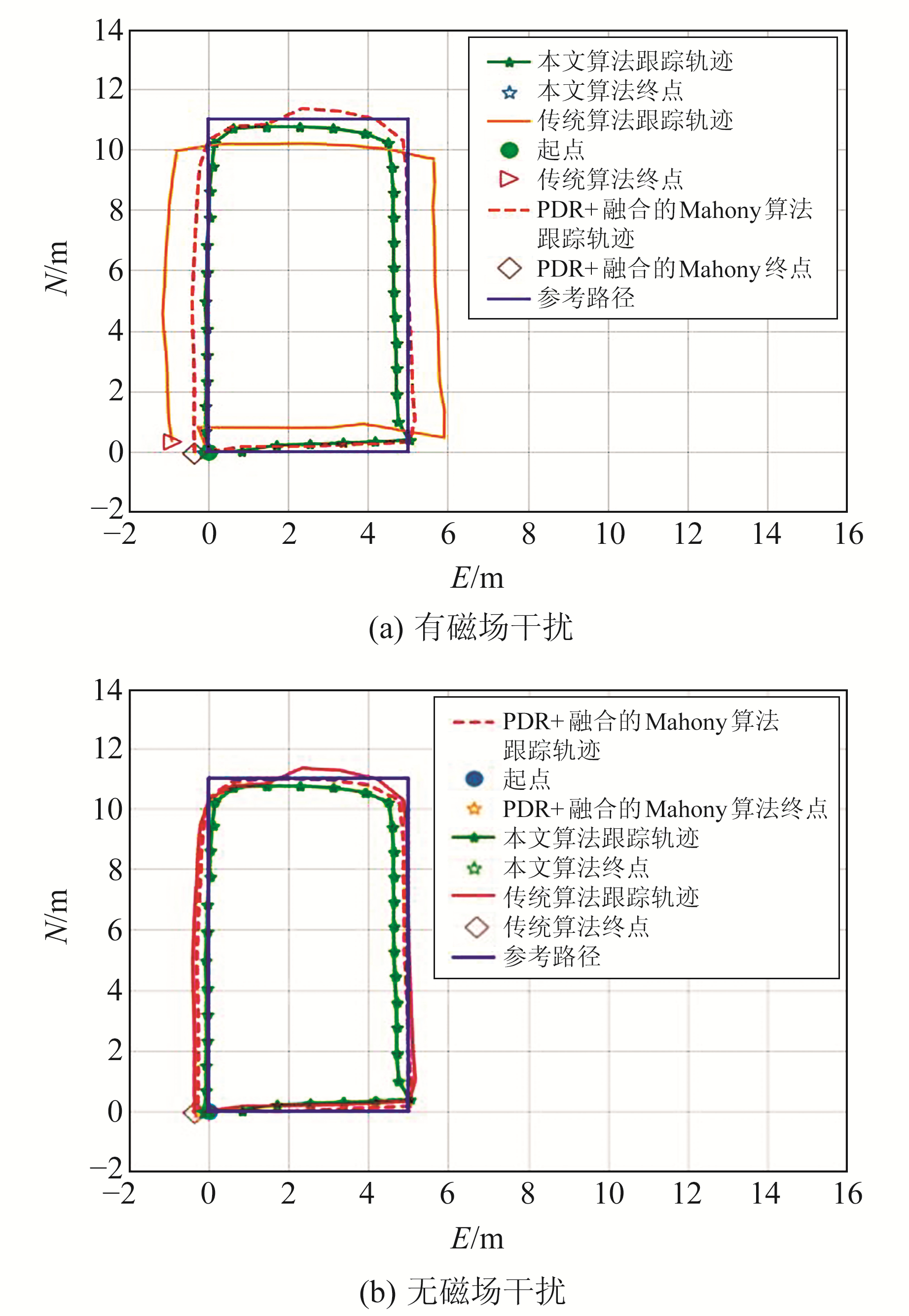
为得到更精确的位置和航向信息,实验通过计算最终定位结果与起始点之间的误差来比较算法的优劣。将磁感应强度阈值设置为30 μT,以鉴别是否存在磁场干扰;实验设计行人分别在有磁场干扰和无磁场干扰的环境中沿矩形路径行走,有磁场干扰的实验场地选在有铁质和钢质及无线通信设备的环境中,无磁场干扰实验场则是在空旷环境中,尽量屏蔽手机和钢铁带来的影响。矩形路径长为11 m,宽为5 m,其中步长估计采用文献[10]中的经典Weinberg步长模型,计步检测和航向轨迹利用本文的双重阈值二值化和自适应融合算法,并将本文算法与传统PDR算法及PDR+Mahony融合算法进行对比,图 9为在不同场景下对行人运动轨迹的跟踪情况。
|
图 9 行人轨迹跟踪 Fig. 9 Pedestrian tracking |
从图 9可以看出,在无磁场的环境下,传统算法和本文算法对行人轨迹的跟踪总体一致;但在有磁场环境中,传统算法未能对磁场干扰进行有效排除,因此最终的定位结果为(-0.88 m,0.22 m),与起始点的距离为0.91 m,对于32 m的行走距离而言误差为2.8%;PDR+Mahony融合算法在航迹上的跟踪结果为(-0.23 m, 0.12 m),与起始点的距离为0.26 m,误差为1.4%;而本文通过自适应融合算法,根据磁场强弱分配权重,最终的航迹跟踪定位结果为(-0.15 m, 0.14 m),与起始点的距离为0.21 m,误差为1.1%,精度分别提高了55%和25%。选取参考路径中的部分实验点作为误差分析参考点,将行人的二维定位坐标与对应参考点之间的欧氏距离定义为定位误差,其计算公式为:
| $ d_k^{{\rm{error }}} = \sqrt { {{{\left( {P_k^{{\rm{u, x }}} - P_k^{r, x}} \right)}^2} + {{\left( {P_k^{u, y} - P_k^{r, y}} \right)}^2}} } $ | (18) |
式中,(Pku, x, Pku, y)为第k步时行人的位置坐标,(Pkr, x, Pkr, y)为第k步时参考路径的位置坐标。
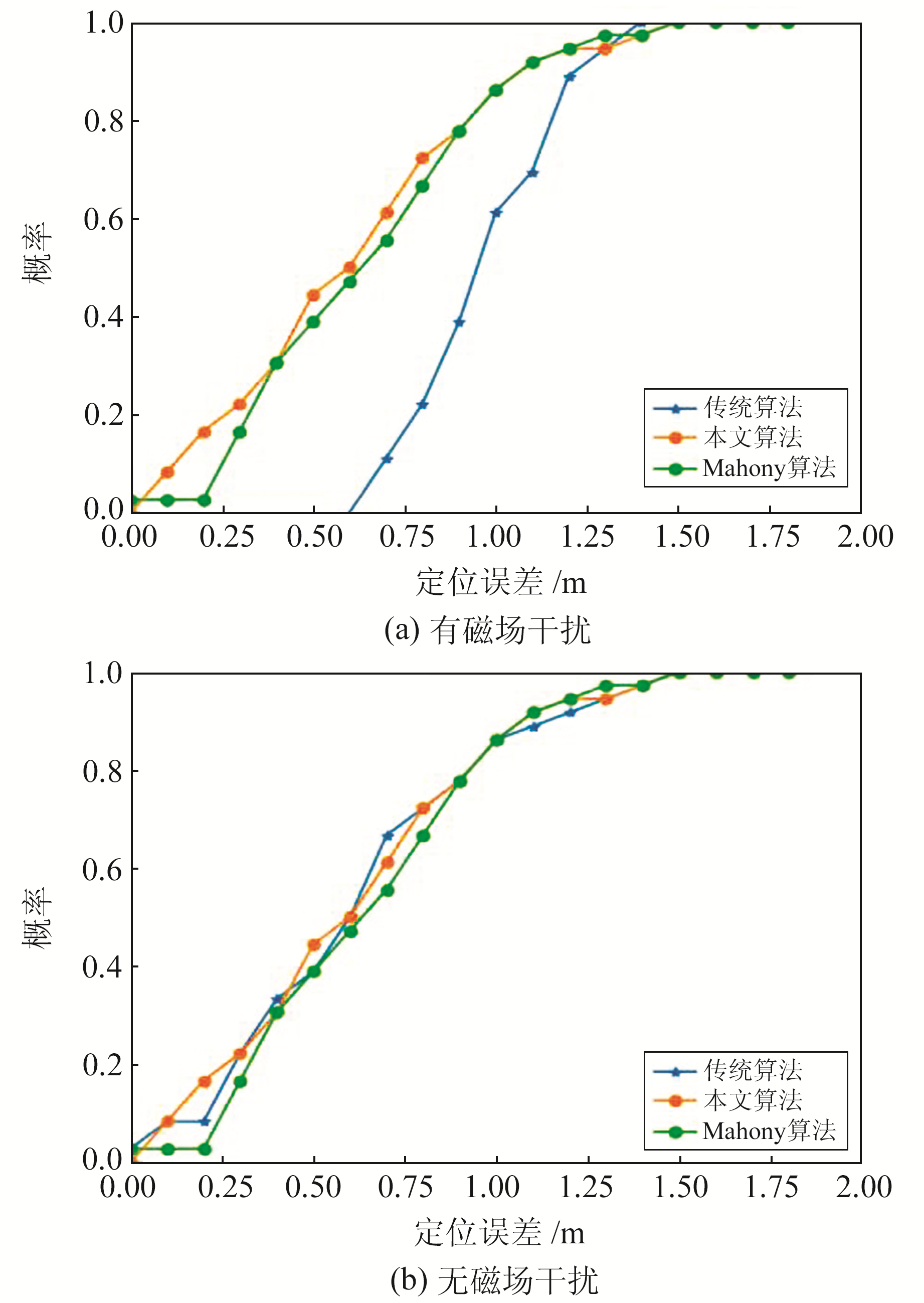
图 10为在有磁场干扰和无磁场干扰下根据定位误差绘制的累积概率分布,可以看出,本文算法定位误差小于0.75 m的概率为59%,PDR+Mahony融合算法定位误差小于0.75 m的概率为55%,传统算法定位误差小于0.75m的概率为22%;本文算法在定位误差小于0~1.0 m之间的概率均大于或等于PDR+Mahony融合算法;3种算法在无磁场干扰情况下的定位误差大致一致。
|
图 10 不同环境下的定位误差累积概率分布 Fig. 10 Probability distribution of positioning errors in different environments |
为了说明在不同环境下各算法的平均定位误差,分别让行人沿矩形路径行走32 m、64 m及96 m,其余实验变量与行走32 m的相同,表 2~4为在不同环境中的平均定位误差统计。从3个表中均可以看出,在有磁场干扰环境下,本文算法的定位误差更小;在无磁场干扰环境下,3种算法的性能大体一致。由此可知,本文算法对于航迹的跟踪更贴近真实轨迹,同时适应在有磁场干扰环境中的跟踪,并在定位精度方面有所提高。
|
|
表 2 行走32 m平均定位误差统计 Tab. 2 Statistics of average positioning error of 32 m walking |
|
|
表 3 行走64 m平均定位误差统计 Tab. 3 Statistics of average positioning error of 64 m walking |
|
|
表 4 行走96 m平均定位误差统计 Tab. 4 Statistics of average positioning error of 96 m walking |
本文提出一种基于行人航位推算的改进航迹跟踪算法,该算法利用双重阈值二值化算法对加速度数据进行处理,避免伪峰谷值的影响,并利用自适应融合算法对行人航向进行准确估计,最终推算出行人的运动轨迹。实验结果表明,本文算法在32 m矩形行走实验中定位误差为1.1%,能够有效减少误差积累,抑制航向发散,提高导航精度,使导航复现路线更加贴合真实行走轨迹。
| [1] |
Meng Q, Liu J Y, Zeng Q H, et al. Neumann-Hoffman Code Evasion and Stripping Method for Beidou Software-Defined Receiver[J]. Journal of Navigation, 2017, 70(1): 101-119
(  0) 0) |
| [2] |
陈帅, 王国英, 莫路锋. 基于角度补偿的手机多传感器数据融合测距算法[J]. 传感技术学报, 2017, 30(2): 253-259 (Chen Shuai, Wang Guoying, Mo Lufeng. Angle Data Compensated Ranging Using Multiple Sensors Data Fusion of Smart Phone[J]. Chinese Journal of Sensors and Actuators, 2017, 30(2): 253-259 DOI:10.3969/j.issn.1004-1699.2017.02.015)
(  0) 0) |
| [3] |
Poulose A, Eyobu O S, Han D S. An Indoor Position-Estimation Algorithm Using Smartphone IMU Sensor Data[J]. IEEE Access, 2019(7): 11 165-11 177
(  0) 0) |
| [4] |
Zhu Z S, Wang S B. A Novel Step Length Estimator Based on Foot-Mounted MEMS Sensors[J]. Sensors, 2018, 18(12)
(  0) 0) |
| [5] |
Cho S Y, Park C G. Threshold-Less Zero-Velocity Detection Algorithm for Pedestrian Dead Reckoning[C]. 2019 European Navigation Conference, Warsaw, 2019
(  0) 0) |
| [6] |
Hoshi H, Fujii M, Ito A, et al. A Study on Direction Estimation for Pedestrian Dead Reckoning[C]. Second International Symposium on Computing and Networking, Shizuoka, 2014
(  0) 0) |
| [7] |
Jimenez A R, Seco F, Prieto C, et al. A comparison of Pedestrian Dead-Reckoning Algorithms Using a Low-Cost MEMS IMU[C]. IEEE International Symposium on Intelligent Signal Processing, Budapest, 2009
(  0) 0) |
| [8] |
Zhang M, Shen W B, Yao Z F, et al. Multiple Information Fusion Indoor Location Algorithm Based on WIFI and Improved PDR[C]. 35th Chinese Control Conference, Chengdu, 2016
(  0) 0) |
| [9] |
Ruiz A R J, Granja F S, Honorato J C P, et al. Accurate Pedestrian Indoor Navigation by Tightly Coupling Foot-Mounted IMU and RFID Measurements[J]. IEEE Transactions on Instrumentation and Measurement, 2012, 61(1): 178-189 DOI:10.1109/TIM.2011.2159317
(  0) 0) |
| [10] |
Weinberg H. Using the ADXL202 in Pedometer and Personal Navigation Applications[J]. Analog Devices AN-602 Application Note, 2002, 2(2): 1-6
(  0) 0) |
| [11] |
Tian Q L, Salcic Z, Wang K I K, et al. A Multi-Mode Dead Reckoning System for Pedestrian Tracking Using Smartphones[J]. IEEE Sensors Journal, 2016, 16(7): 2 079-2 093 DOI:10.1109/JSEN.2015.2510364
(  0) 0) |
| [12] |
Renaudin V, Susi M, Lachapelle G. Step Length Estimation Using Handheld Inertial Sensors[J]. Sensors, 2012, 12(7): 8 507-8 525 DOI:10.3390/s120708507
(  0) 0) |
| [13] |
Afzal M H, Renaudin V, Lachapelle G. Magnetic Field Based Heading Estimation for Pedestrian Navigation Environments[C]. 2011 International Conference on Indoor Positioning and Indoor Navigation, Guimaraes, 2011
(  0) 0) |
| [14] |
Kang W, Han Y. SmartPDR: Smartphone-Based Pedestrian Dead Reckoning for Indoor Localization[J]. IEEE Sensors Journal, 2015, 15(5): 2 906-2 916 DOI:10.1109/JSEN.2014.2382568
(  0) 0) |
| [15] |
罗武胜, 徐涛, 杜列波. 基于加速度计和磁强计的定向钻进姿态测量及方位校正[J]. 国防科技大学学报, 2007, 29(1): 106-110 (Luo Wusheng, Xu Tao, Du Liebo. Directional Drilling Attitude Measurement and Azimuth Correction with Accelerometers and Magnetometers[J]. Journal of National University of Defense Technology, 2007, 29(1): 106-110 DOI:10.3969/j.issn.1001-2486.2007.01.022)
(  0) 0) |
| [16] |
Zhao H Y, Zhang L Y, Qiu S, et al. Pedestrian Dead Reckoning Using Pocket-Worn Smartphone[J]. IEEE Access, 2019, 12(7): 91 063-91 073
(  0) 0) |
| [17] |
Li X, Wang Y. Evaluation of AHRS Algorithms for Foot-Mounted Inertial-Based Indoor Navigation Systems[J]. Open Geosciences, 2019, 11(1): 48-63
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41


