2. 桂林理工大学测绘地理信息学院,桂林市雁山街319号,541006
陆态网自运行以来,为我国的地震趋势报告、地壳形变规律研究、边界勘查、测绘基准建设以及高精度的坐标框架维持提供了大量可靠的GNSS观测数据[1-4]。但是受外界各种因素的干扰,GNSS站点存在数据缺失、点位突变、粗差以及异常站点等现象[5],对观测站高精度坐标的提取具有较大影响。
此外,想要系统地研究基准站坐标时间序列的变化规律,更深层次地了解驱使基准站运动的内部机制,需要对GNSS基准站连续观测坐标时间序列的噪声特性及运动规律进行分析。基于主成分分析(principal component analysis, PCA)的GNSS时间序列研究已经很成熟,并取得了较理想的研究成果[6]。Dong等[7]充分考虑GNSS观测网的时空相关性因素,综合PCA和Karhunen-Loeve分解方法来扣除共模误差。袁林果等[8]利用主成分空间滤波方法有效提高了香港地区GPS坐标序列信号的信噪比。随着GNSS基准站坐标时间序列观测长度的不断增加,以及软硬件分析工具和方法的不断优化,对GNSS基准站坐标时间序列的研究也越来越方便。
本文利用主成分分析方法对陆态网224个GNSS基准站2010~2016年的坐标时间序列进行分析。首先分析各站点原始坐标序列,并进行突变项拟合、粗差剔除、缺失时间序列插值等预处理;然后对预处理后的结果分N、E、U方向组建坐标时间序列矩阵并进行主成分分析;最后对各主分量及其对应的空间特征向量进行分布特征、共模误差、站点响应区域等分析,并讨论异常站点对3个方向PCA结果的影响。
1 陆态网坐标时间序列预处理 1.1 数据选取GNSS基准站原始坐标时间序列中不仅包含由于观测设备改变、更换天线、板块位移、远场地震等引起的趋势变化,还包括地震引发的同震位移、点位突变以及数据缺失等造成的影响[5]。这些因素易导致主成分分析产生较大的负面影响,因此必须采取有效措施对原始坐标时间序列进行预处理。为了提升原始坐标序列的可靠性,本文将扣除缺失数据大于30%的基准站点,共剔除26个不达标的站点;选取剔除后的224个基准站时序坐标作为分析对象,截取这些站点2010~2016年的时序观测结果作为实验数据。
1.2 GNSS站点时间序列预处理本文首先对实验选取的GNSS坐标时间序列中的突变项进行消除,对突跳历元出现之后的数据统一进行突变变化值去除,依据GNSS观测文件联合各个方向的时序散点图来确定突跳时刻。假设站点N、E、U方向均有突变信号,在采用最小二乘法进行初始拟合时,尽量大范围地筛选出突跳的历元,然后比较拟合前后的时序散点图,对可能的突跳序列在N、E、U方向进行判别。
图 1为BJFS站在去除突跳项前后N、E、U方向的对比,可以看到,通过拟合处理后,突跳位置得到有效补充。此外对于因仪器设备更换而引起的突变,可以通过各个站点的log文件获取;对于其他未知原因造成的突变,为了确保该类突变的拟合效果,通过目视排查获取突变位置,从而提高突变探测的准确度。在本文数据获取时段内,发生过4次对观测数据产生较大影响的地震,分别为2011-03-11日本东北MW9.0地震、2013-04-20芦山MW7.0地震、2015-04-25和05-12尼泊尔MW7.9和MW7.3地震。参考各地震的发震时间及基准站站点的历史观测文件确定起始突变时刻。经过以上处理,本文在GNSS坐标时间序列预处理中设置了289个突跳历元,共拟合867个突跳项。

|
图 1 BJFS站突变项拟合前后对比 Fig. 1 Comparison of time series before and after fitting of mutations in N, E, and U directions at BJFS station |
除了突跳项以外,GNSS坐标序列中还会包含长时期趋势信息,并存在粗差及缺失数据等问题,因此还要对GNSS坐标时间序列进行去除趋势项、剔除粗差、缺失数据插值补齐等处理。本文利用四分位数粗差探测法对原始坐标时间序列进行粗差探测,将含有粗差的值从原始数据中剔除。对GNSS序列进行PCA分析时,须确保坐标序列是等时间间隔采样,因此需要根据缺失数据的实际情况选择合适的插值方法。三次样条插值方法对于缺失数据较小的时段,其插值效果比较好,但在缺失数据量较大时效果不佳。鉴于此,实验对缺失小于3 d的序列,利用三次样条插值法进行补齐;对于缺失3 d以上的序列,采用基于PCA迭代的方法予以补充。具体步骤如下:1)首先用全部有效基准站时间序列的平均值代替缺失部分的数据,组建GNSS坐标时间序列矩阵;2)对组建的矩阵进行PCA分析,选取前3个主分量来恢复缺失的时间序列;3)设置缺失时间序列两次迭代之差的阈值为10-6,直至全部的缺失时间序列的迭代之差均小于阈值为止。
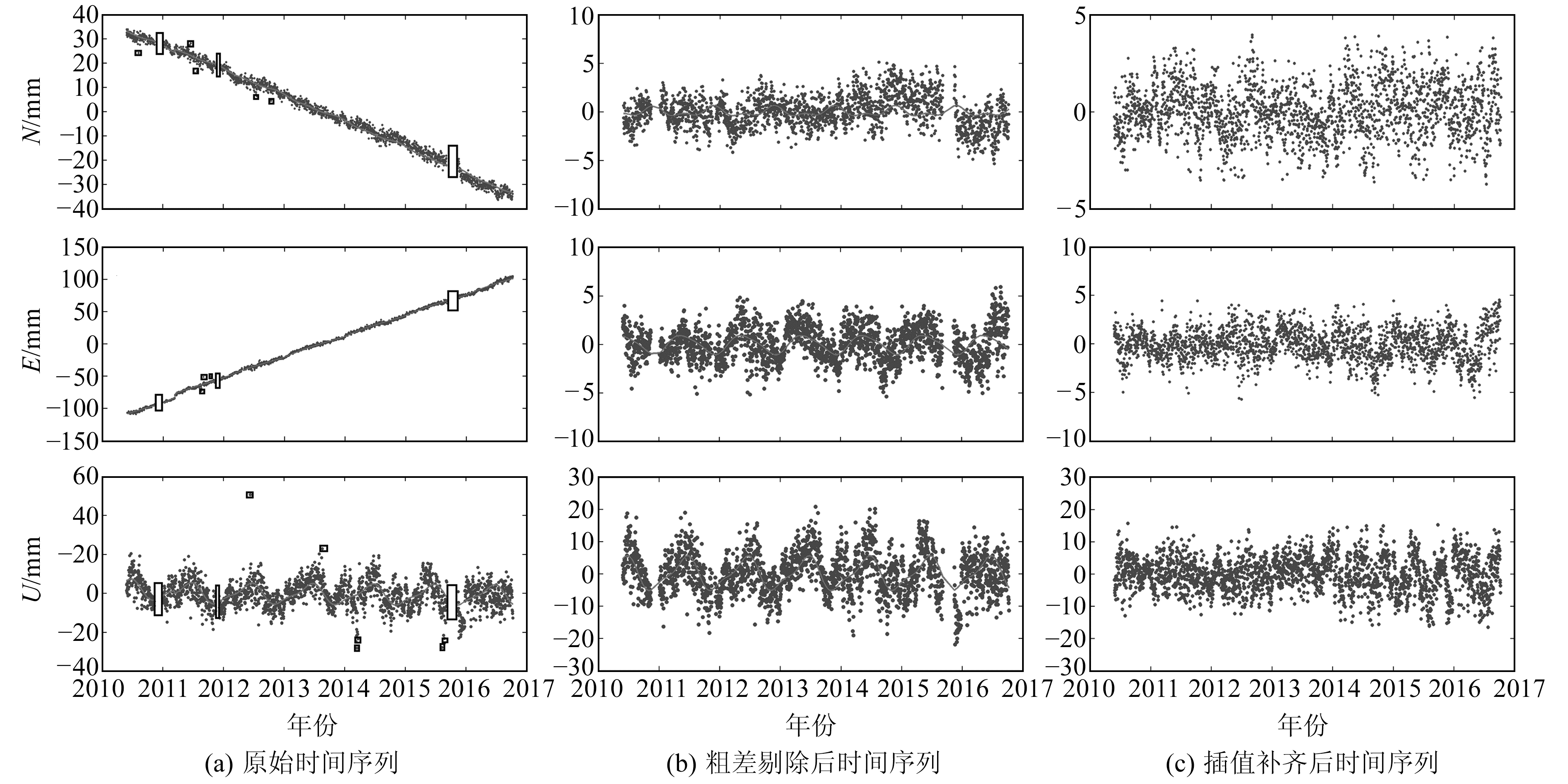
本文选取224个站点的坐标单日解共538 048个,剔除N、E、U方向粗差值4 925个,缺失数据共有65 759个。图 2为AHBB站N、E、U方向在粗差剔除及缺失时间序列补齐前后的对比,可以看到,未经过处理的序列中分布着较明显的粗差点和缺失点(矩形标记处),经过粗差剔除、数据插值等处理后的坐标序列得到明显改善。
|
图 2 AHBB站N、E、U方向原始数据、粗差剔除、缺失数据插值补齐时间序列 Fig. 2 Time series of original data, gross error elimination, and interpolation and completion of missing data in N, E and U directions at AHBB station |
对经过预处理后的陆态网GNSS站点分N、E、U方向组建坐标时间序列矩阵并进行PCA分析。图 3、4表示3个方向的主分量特征值分布情况及各方向主分量累积贡献率。由图 3可见,3个方向特征值的变化曲线相似,其中,N、E方向的特征值差别较小,U方向特征值明显比N、E方向大。

|
图 3 N、E、U方向特征值分布 Fig. 3 Distribution of eigenvalues in N, E and U directions |
|
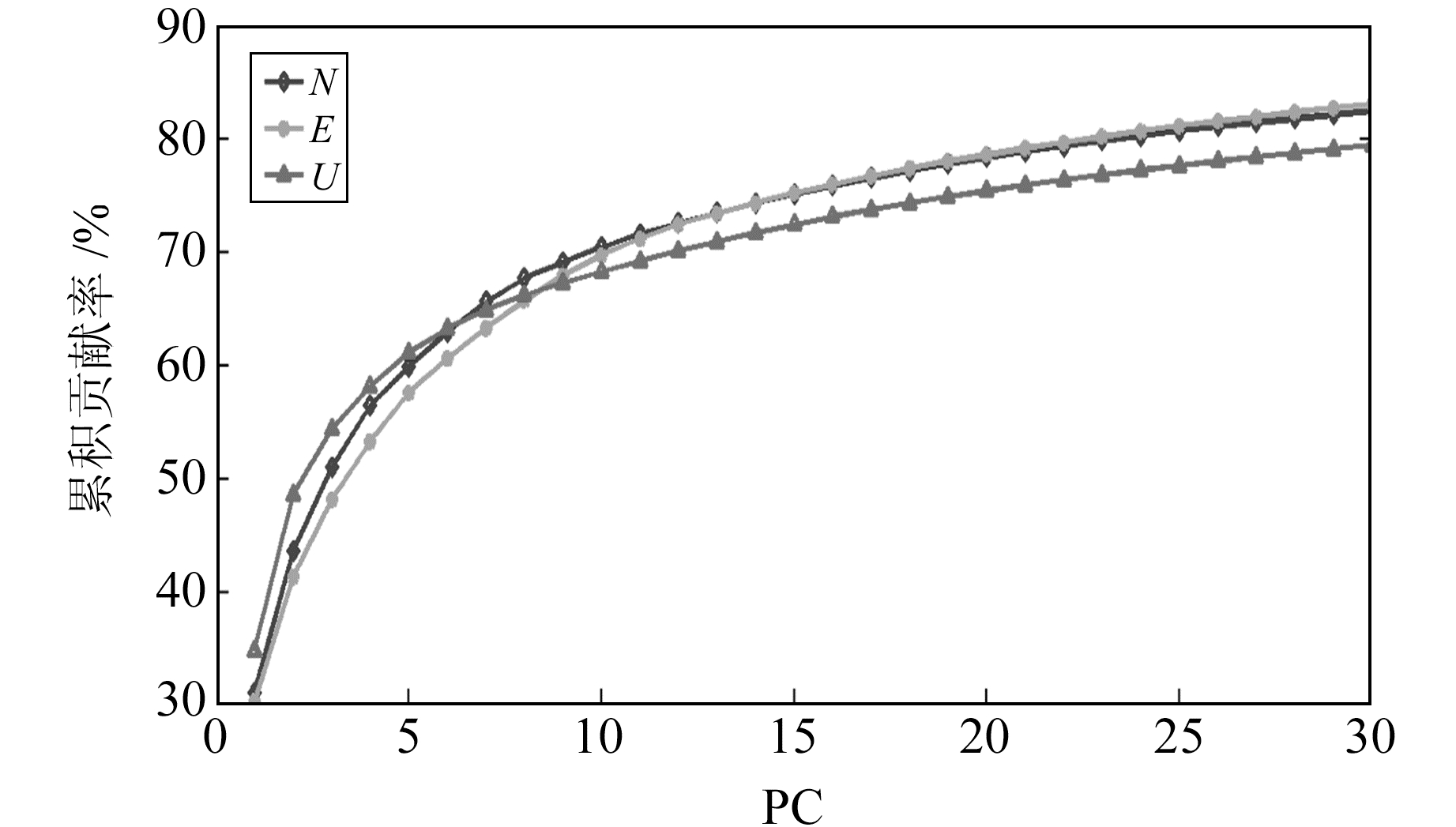
图 4 前30个主分量累积贡献率 Fig. 4 Cumulative contribution rate of the top 30 principal components in N, E, and U directions |
由图 4可见,N、E、U方向第1、2、3主分量贡献率分别为31.1%、30.3%、34.8%,12.4%、10.9%、13.7%,3%、6.8%、5.8%,前3个主分量累积贡献率分别为50.8%、48.0%、54.3%。除了前3个主分量外,其余主分量的贡献率逐步降低,N、E、U方向贡献率大于1%的主分量分别有11、12、9个。
主分量表示的是时间域上的变化,空间特征向量则表示各GNSS基准站的空间响应。为了对N、E、U方向各主分量的空间特征向量进行对比,本文分别对每个方向的前3个主分量对应的空间特征向量进行正则化处理,使每个站点的空间响应大小在-1~1之间(图 5)。

|
图 5 N、E、U方向第1、2、3主成分分析结果 Fig. 5 The first, second, and third principal components in N, E, and U directions |
N方向前3个主分量及其对应的空间特征向量如图 5(a)所示,箭头向上表示正响应,向下表示负响应。3个主分量在时域上没有表现出单纯的随机性或系统性变化,第1主分量波动较小,第2、3主分量则表现出较为显著的非线性变化趋势,第1、2主分量的振幅随时间推移显现出增大的趋势。第1主分量的空间响应分布较为一致,且为正响应,响应大小在区域分布上存在差异;第2、3主分量的空间响应则相对杂乱,响应大小在区域上不存在一致性分布的特征,且正、负响应均存在,正响应主要分布在内蒙和西北地区,负响应主要集中在华中、华南以及西南地区。
E方向前3个主分量及其对应的空间特征向量如图 5(b)所示,时域特征与N方向相似,没有表现出随机性或系统性变化。基准站点的第1主分量空间响应上与N方向类似,分布较为一致,西北和东北地区比其他地区的响应要小;第2主分量相比第1主分量要混乱许多,东部地区没有表现出明显的空间响应,西部地区的响应也比较弱,但分布较一致,少部分站点表现出较强的响应;第3主分量在西北地区表现出较强的负响应,而在华北、华南和华中地区则表现出正响应分布。
U方向前3个主分量及其对应的空间特征向量如图 5(c)所示,时域特征波动性变化相比N、E方向而言,变化的系统性和周期性较清晰。第1主分量的空间响应也表现出比较一致的空间分布;第2主分量的空间响应在西北和西南地区表现出一致的负响应分布,云南地区表现尤为显著,东北地区为正响应分布;第3主分量的空间特征向量在西北地区表现出较强的负响应分布,华南及东南沿海地区表现出较强的正响应分布。
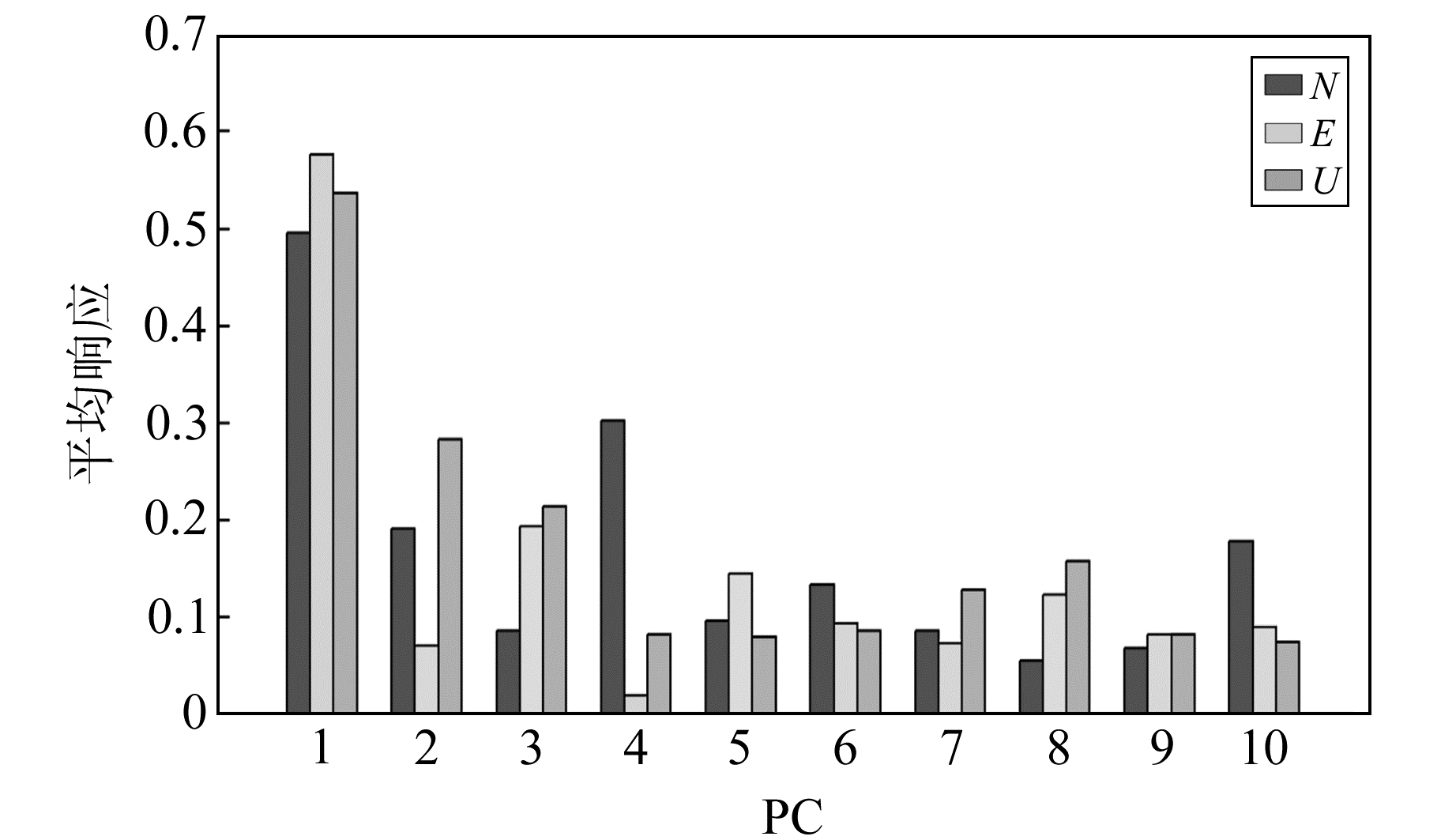
2.2 共模误差分析共模误差(common mode error, CME)是GNSS坐标时间序列的主要误差之一,严重影响GNSS的解算精度[9]。本文根据各主分量的贡献率、变化特征及其对应的绝对值化的平均空间响应对共模误差进行分析。N、E、U方向前10个主分量的贡献率及对应的平均空间响应情况如图 6、7所示,3个方向第1主分量的空间向量都表现出较为一致的空间响应,第1主分量的贡献率分别为31.1%、30.3%、34.8%,平均空间响应分别为0.495、0.576、0.537;第2、3主分量的空间响应在局部区域也表现出了一致性分布的特征,两者的贡献率也分别达到了12.4%、10.9%、13.7%和7.3%、6.8%、5.8%。从统计结果可以看出,如果仅将第1主分量当作共模误差或套用其他区域的研究标准不能准确地反映共模误差的时空特点。鉴于此,可对第1、2、3主分量共同进行共模误差分析。

|
图 6 N、E、U方向前10个主分量贡献率 Fig. 6 Distribution of the top ten principal components contribution rates in N, E, and U directions |
|
图 7 N、E、U方向前10个主分量正则化后平均空间响应对比 Fig. 7 Regularized spatial average response of the top ten principal components in N, E, and U directions |
空间响应分布一致的区域,有时候会存在少量异常站点,如华南沿海的GDST站、云南地区的XIAG站、海南的HISY站、江西的JXHK站等,这些站点在区域上会表现出更明显的空间响应,并且远大于该区域正常响应的大小,其时间序列也存在异常情况。对于这些异常站点,在没有剔除的情况下会对PCA的结果产生负面影响。本文剔除绝对值化的平均空间响应大于20%的站点,剔除后,对剩余的196个站点再次进行PCA计算,得到3个方向的主分量贡献率及站点绝对值化的平均空间响应情况(表 1)。
|
|
表 1 N、E、U方向异常站点剔除后站点绝对值平均空间响应及贡献率变化(“+”代表提高,“-”代表降低) Tab. 1 Changes in the average spatial response and contribution rate of the absolute value of the stations after removing abnormal sites in N, E, and U directions (+ means increase, -means decrease) |
由表 1可见,剔除异常站点后,N、E、U方向的第1主分量贡献率分别提升2.0%、3.9%、5.7%,而第2主分量分别下降1.1%、1.9%、6.7%。除前3个主分量以外,其他主分量贡献率总体变化不大。此外,N、E、U方向的平均空间响应也得到较为明显的提升,其中第1主分量最为显著,在3个方向分别提高0.22、0.10、0.24。N、E、U方向的前3个主分量累积空间响应分别提高0.35、0.22、0.34,累积贡献率分别为提升0.4%、3.2%和下降2.6%,说明异常站点的剔除有助于进一步研究区域站点的空间分布特征。
3 结语本文利用主成分分析法对陆态网GNSS坐标时间序进行分析。首先对各站点初始坐标序列进行突变项拟合、粗差剔除、缺失数据插值补齐等预处理,然后分N、E、U方向组建矩阵进行主成分分析。依据主分量时域上的变化特征、空间响应特征以及各个主分量贡献率等,建议将前3个主分量纳入共模误差分析;经过分析,水储量变化是引起华北、西北和云南地区空间响应在U方向一致性分布的主要原因;通过异常站点剔除前后的对比发现,异常站点对主成分分析结果影响显著,剔除异常站点后各方向的平均空间响应和贡献率在第1主分量上都有明显提高。
| [1] |
党亚民, 杨强, 薛树强, 等. GNSS监测的川滇地区地壳形变动态变化特征[J]. 大地测量与地球动力学, 2019, 39(2): 111-116 (Dang Yamin, Yang Qiang, Xue Shuqiang, et al. GNSS Monitoring Dynamic Variation Characteristics of Crustal Deformation in the Sichuan-Yunnan Region[J]. Journal of Geodesy and Geodynamics, 2019, 39(2): 111-116)
(  0) 0) |
| [2] |
贾路路, 王阅兵, 连尉平, 等. "陆态网"GPS与GRACE的中国大陆地表垂直形变对比分析[J]. 测绘学报, 2018, 47(7): 899-906 (Jia Lulu, Wang Yuebing, Lian Weiping, et al. Comparison and Analysis of Crustal Vertical Deformation in Mainland China Observed by GPS from CMONOC and GRACE[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(7): 899-906)
(  0) 0) |
| [3] |
李强, 宁百齐, 赵必强, 等. 基于陆态网络GPS数据的电离层空间天气监测与研究[J]. 地球物理学报, 2012, 55(7): 2 193-2 202 (Li Qiang, Ning Baiqi, Zhao Biqiang, et al. Applications of the CMONOC Based GNSS Data in Monitoring and Investigation of Ionospheric Space Weather[J]. Chinese Journal of Geophysics, 2012, 55(7): 2 193-2 202)
(  0) 0) |
| [4] |
邢乐林, 李辉, 李建国, 等. 陆态网络绝对重力基准的建立及应用[J]. 测绘学报, 2016, 45(5): 538-543 (Xing Lelin, Li Hui, Li Jianguo, et al. Establishment of Absolute Gravity Datum in CMONOC and Its Application[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(5): 538-543)
(  0) 0) |
| [5] |
姜卫平, 王锴华, 李昭, 等. GNSS坐标时间序列分析理论与方法及展望[J]. 武汉大学学报:信息科学版, 2018, 43(12): 2 112-2 123 (Jiang Weiping, Wang Kaihua, Li Zhao, et al. Prospect and Theory of GNSS Coordinate Time Series Analysis[J]. Geomatics and Information Science of Wuhan University, 2018, 43(12): 2 112-2 123)
(  0) 0) |
| [6] |
刘晓祥.中国陆态网GPS基准站坐标时间序列主成分分析[D].成都: 西南交通大学, 2017 (Liu Xiaoxiang. Analysis of Coordinate Time Series of CMONOC GPS Fiducial Stations Using Principal Component Analysis[D]. Chengdu: Southwest Jiaotong University, 2017)
(  0) 0) |
| [7] |
Dong D N, Fang P, Bock Y, et al. Spatiotemporal Filtering Using Principal Component Analysis and Karhunen-Loeve Expansion Approaches for Regional GPS Network Analysis[J]. Journal of Geophysical Research:Solid Earth, 2006, 111(B3): 1 581-1 600
(  0) 0) |
| [8] |
袁林果, 丁晓利, 陈武, 等. 香港GPS基准站坐标序列特征分析[J]. 地球物理学报, 2008, 51(5): 1 372-1 384 (Yuan Linguo, Ding Xiaoli, Chen Wu, et al. Characteristics of Daily Position Time Series from the Hong Kong GPS Fiducial Network[J]. Chinese Journal of Geophysics, 2008, 51(5): 1 372-1 384)
(  0) 0) |
| [9] |
田云锋. GPS坐标时间序列中的异常高频周期性噪声[J]. 测绘科学, 2011, 36(1): 26-28 (Tian Yunfeng. Anomalous High Frequency Seasonal Noises in GPS Positions Time Series[J]. Science of Surveying and Mapping, 2011, 36(1): 26-28)
(  0) 0) |
2. College of Geomatics and Geoinformation, Guilin University of Technology, 319 Yanshan Street, Guilin 541006, China
 2021, Vol. 41
2021, Vol. 41


