2. 武汉大学测绘学院,武汉市珞喻路129号,430079
GNSS成果归算时一般利用Helmert七参数转换将无基准约束解或松弛约束解转换到指定参考框架下。研究表明,GNSS技术类误差以及地表负载等地球物理效应均会影响七参数中的平移参数和尺度参数估值,进而影响GNSS测站坐标的计算[1]。以往多数研究针对平移参数(地心运动)进行,主要包括GNSS轨道误差、环境负载以及测站分布对地心运动的影响分析[1-3],而针对尺度参数的研究较少。在地球物理效应影响方面,文献[1]结果表明,地表负载及GPS测站的不均匀分布能够解释约30%的GPS尺度参数周年变化。在GNSS技术类误差影响方面,Springer[4]结果表明,GPS卫星天线相位中心Z方向(即星固坐标系中卫星至地心方向)偏差(z-PCOs)与尺度参数高度相关。在此基础上,Zhu等[5]研究给出GPS卫星z-PCOs的平均误差δz与尺度参数变化δs之间的近似关系为δs=7.8 δz;Ge等[6]研究表明,卫星星座的变化会导致z-PCOs模型的不完善,从而影响尺度参数。因此,如果GNSS原始数据处理过程中采用不同的卫星z-PCOs改正模型,将会影响成果归算时框架转换中尺度参数的估值。
自2017-01-29起,IGS采用天线相位中心改正模型igs14.atx取代先前的igs08.atx[7],igs08.atx和igs14.atx均为ANTEX(antenna exchange format)格式文件,提供各卫星以及不同型号接收机的天线相位中心改正信息。文献[7]研究了igs08.atx和igs14.atx的卫星z-PCOs对IGS第二次重新处理单天合并解与IGb08之间尺度参数的影响,结果表明,基于igs08.atx的尺度参数的残差比基于igs14.atx的结果更为离散,验证了igs14.atx中卫星z-PCOs改正模型的改善。除此之外,目前其他关于卫星z-PCOs对GNSS参考框架转换中尺度参数影响的研究还较少。
因此,本文分别基于igs08.atx和igs14.atx提供的卫星z-PCOs改正模型,计算了7个IGS分析中心(AC, analysis center)第二次重新处理单天解与IGS最新采用的参考框架(IGS14)之间的尺度参数序列,并比较分析两种卫星天线改正模型对尺度参数的噪声模型、平均偏移量、速度及季节性信号的影响。本文的主要目的是:1)对比igs08.atx和igs14.atx的卫星z-PCOs改正模型对尺度参数的影响;2)基于最优噪声模型,确定更为真实的尺度参数速度、季节性信号及其不确定度,从而详细了解7个AC单独解与IGS14之间的尺度参数现状。
1 数据与处理策略本文利用7个AC提供的单天解SINEX文件,分别计算各AC基于igs08.atx和igs14.atx的尺度参数序列。针对每个单天解SINEX文件,具体的计算方法为:1)检查并修正IGS基准站的相关信息,包括DOMES和阶跃信息等;2)将单天解SINEX文件中的卫星z-PCOs参数固定为igs08.atx或igs14.atx提供的相应值;3)去除原始法方程中的先验约束,恢复无约束法方程;4)对无约束法方程进行估计,其中,引入的坐标基准为测站先验坐标的参考框架;5)利用51个全球均匀分布的IGS14核心站,将步骤4)所得结果与IGS14结果进行Helmert七参数转换,从而得到基于igs08.atx或igs14.atx的尺度参数。表 1列出了计算的尺度参数序列的详细信息,包括名称、时间跨度、采样率以及SINEX文件来源。
|
|
表 1 尺度参数信息 Tab. 1 Summary of scale parameters |
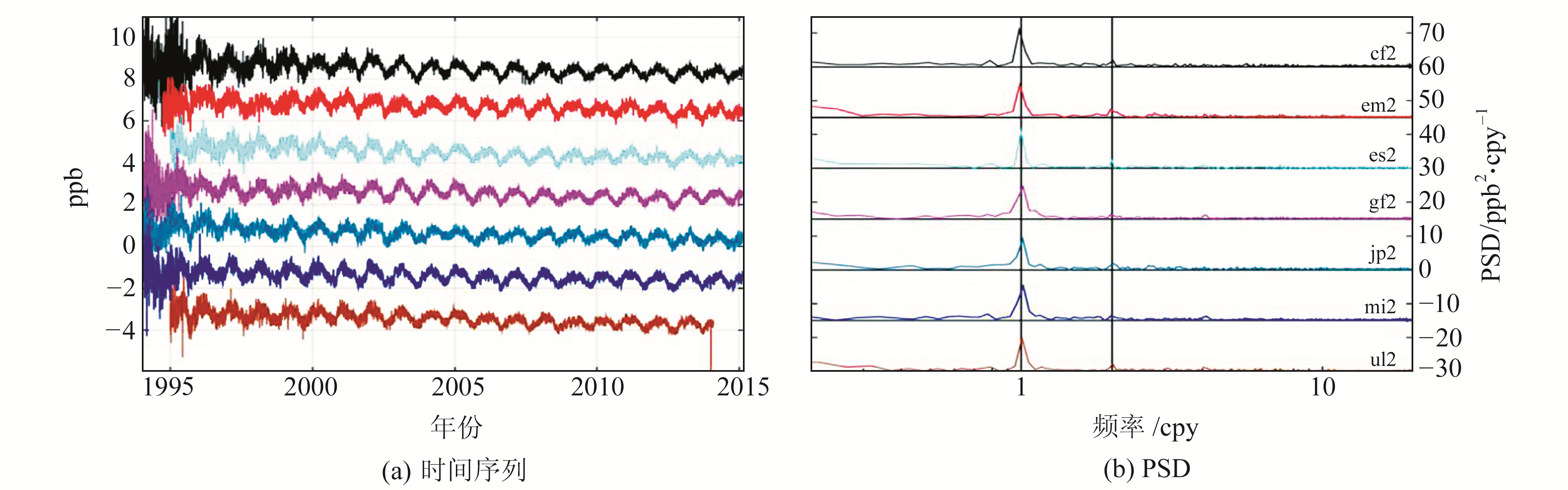
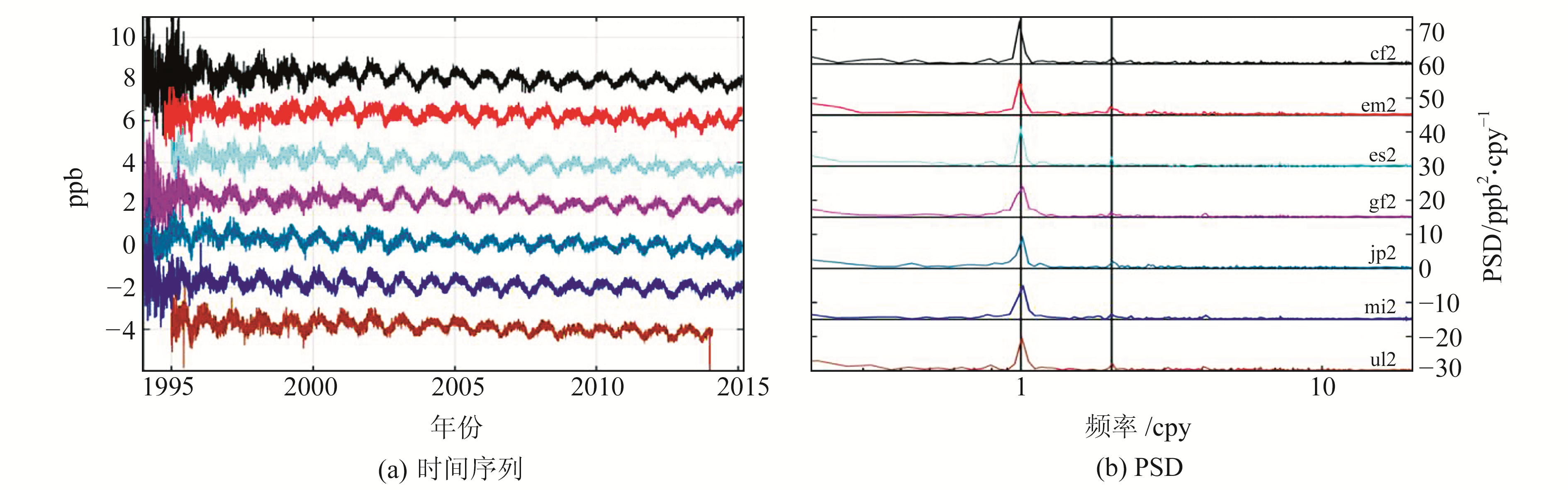
利用Lomb-Scargle周期图法[8]计算了各组尺度参数的功率谱密度(PSD,power spectrum density),图 1和图 2给出尺度参数时间序列及其PSD。其中,图 1和图 2中(a)、(b)两个图的同一颜色曲线代表相同的AC。为了更好地显示结果,图中序列进行了平移,图(a)的单位平移量为2 ppb,图(b)的单位平移量为15 ppb2/cpy。图(b)中黑色竖线表示1 cpy×n(n=1, 2),灰色竖线表示1.04 cpy×n(n=1, 2, …, 8)。由图可知,1996年以前,各组尺度参数均较为离散;不同AC的尺度参数表现出相似的变化,其中,周年信号最为显著,半周年信号相对较弱。
|
图 1 基于igs08.atx的尺度参数时间序列及其PSD Fig. 1 Scale parameters time series and their PSD based on igs08.atx |
|
图 2 基于igs14.atx的尺度参数时间序列及其PSD Fig. 2 Scale parameters time series and their PSD based on igs14.atx |
基于功率谱分析结果,本文选取了相应的参数模型和噪声模型进行后续分析。参数模型包括常数项、线性速度、周年及半周年信号;噪声模型共选取了5类:白噪声(wh)、白噪声加闪烁噪声(wh+fl)、白噪声加幂律噪声(wh+pl)、白噪声加广义高斯马尔可夫噪声(wh+GGM)及白噪声加一阶自回归噪声(wh+AR(1))。
2 分析与讨论 2.1 噪声模型为了分析尺度参数时间序列的随机特性,本文选取Hector软件[9],利用极大似然方法对所选的5种噪声模型进行测试,并采用贝叶斯信息量准则(BIC,Bayesian information criterion)进行噪声模型的评价,选取得到最小BIC值的噪声模型作为最优模型。表 2给出各组尺度参数基于igs08.atx和igs14.atx的随机特性统计结果。由表可知,基于igs08.atx的各组尺度参数的随机特性均可由白噪声加幂律噪声较好地描述,谱指数值约为-0.8;采用igs14.atx后,除em2的谱指数变化较大外,其他序列的随机特性并未发生明显改变。除em2和jp2外,其他5个AC基于igs14.atx获取的尺度参数WRMS略小于基于igs08.atx的结果,在一定程度上表明,igs14.atx较igs08.atx的卫星z-PCOs模型精度有所提高。需要说明的是,表 2中的WRMS单位为mm,在赤道上,1 ppb约为6.3 mm[10]。如无特殊说明,下文分析均基于表 2所列噪声模型。
|
|
表 2 尺度参数时间序列随机特性统计 Tab. 2 Stochastic characteristics of scale parameters |
图 3对比各AC尺度参数的线性部分(偏移量+速度),图中虚线和实线分别对应igs08.atx和igs14.atx的结果,单位平移量为1 ppb。由图可知,不同卫星天线相位中心改正模型对尺度参数的平均偏移影响较大,而对尺度参数的长期速度影响较小。表 3列出了各组尺度参数在2010.0历元处的偏移量、速度及其不确定度。在2010.0历元,基于igs08.atx的尺度参数偏移量最大值为3.53 mm,结合不确定度的大小,各组序列的偏移量较为相近;尺度参数速度范围处于-0.15~-0.22 mm/a之间,各组尺度参数速度整体一致。除em2和gf2外,基于igs14.atx的尺度参数序列在2010.0历元的偏移量值可近似为0;基于igs14.atx的尺度参数速度与基于igs08.atx的结果相比,两者变化趋势一致,整体相差较小,表明不同卫星天线相位中心改正模型对尺度参数的长期速度影响较小。

|
图 3 尺度参数的线性部分 Fig. 3 The linear parts of scale parameters |
|
|
表 3 尺度参数时间序列的偏移量(2010.0历元)及速度 Tab. 3 The offsets (at 2010.0 epoch) and rates of scale parameters |
由于GNSS轨道模型(地球辐射压模型和天线推力)的变化,从igs08.atx到igs14.atx,卫星z-PCOs的平均变化约为-6 cm[7],根据文献[5]中的公式δs=7.8δz,引起的尺度变化约为0.5 ppb(约3 mm)。在2010.0历元,本文基于两组卫星天线相位中心改正模型获得的尺度参数偏移量差异为2.41~3.24 mm,与利用文献[5]计算的尺度变化量相近,表明不同卫星天线相位中心改正模型会显著影响尺度参数的偏移量。
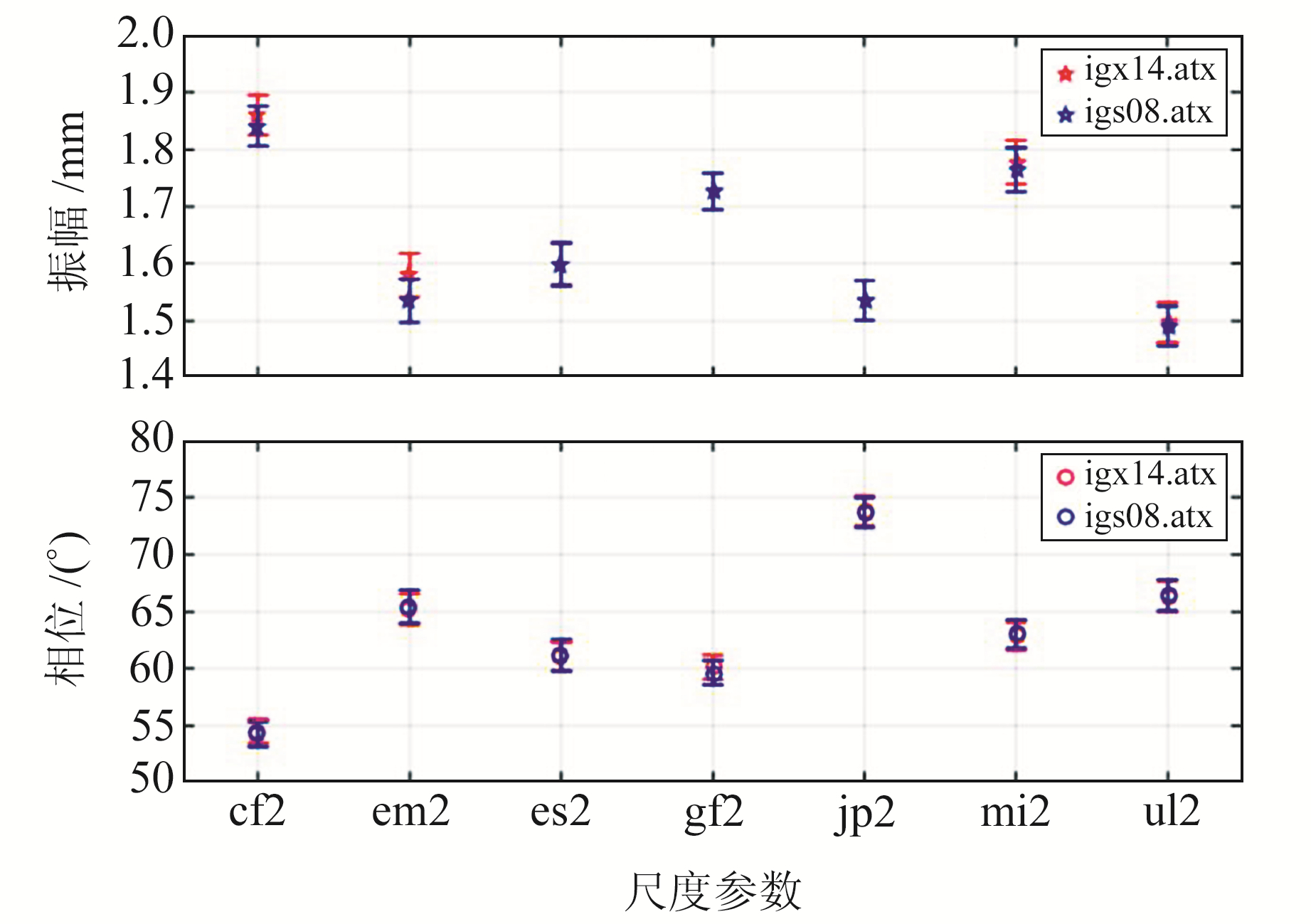
2.3 季节性信号由图 1和图 2可知,各组尺度参数序列中均存在非线性信号,主要表现为季节性信号。图 4和图 5给出了各组尺度参数的周年、半周年振幅和相位及其不确定度。由图 4和图 5可知,各组尺度参数的周年信号显著,半周年信号相对较弱;不同卫星天线相位中心模型对尺度参数的季节性信号的影响可以忽略。
|
图 4 尺度参数序列周年振幅和相位及其不确定度 Fig. 4 The annual amplitudes and phases and their uncertainties of scale parameters |

|
图 5 尺度参数半周年振幅和相位及其不确定度 Fig. 5 The semi-annual amplitudes and phases and their uncertainties of scale parameters |
GNSS测站坐标的单天解中包含地表质量重新分布引起的负载形变,而IGS14下的测站坐标中并不包含负载形变,因此,两者进行Helmert七参数转换时,部分负载形变会被转换参数吸收,该影响的大小与GNSS地面观测网的分布相关,通常称之为“网效应”[11-13]。尺度参数的非线性部分一般来源于两个方面[6, 12]:一是“网效应”的影响,二是GNSS卫星星座的变化使得卫星天线相位中心改正模型并不完善。尽管igs14.atx更新了卫星天线相位中心改正模型,其尺度参数的季节性信号仍与igs08.atx结果一致,表明各组尺度参数的季节性信号主要来源于“网效应”的影响。
3 结语本文得到的主要结论如下:1)各组尺度参数的随机特性均可由白噪声加幂律噪声较好地描述,不同卫星天线相位中心改正模型对其随机特性影响较小;2)不同卫星天线相位中心改正模型对尺度参数的平均偏移量影响较大,最大差值可达3.24 mm,约为0.5 ppb;3)不同AC的尺度参数速度值在-0.15~-0.22 mm/a之间变化,卫星天线相位中心改正模型的改变并未影响尺度参数速度;4)各组尺度参数周年信号显著,半周年信号相对较弱,季节性信号主要来源于与负载相关的“网效应”影响,而卫星天线相位中心改正模型的变化影响较小。
由于卫星钟差、天顶方向对流层延迟、测站高程与GNSS卫星z-PCOs之间的强相关性,利用GNSS观测值直接计算的卫星z-PCOs存在较大误差(最大可达m级)。卫星z-PCOs改正模型误差是GNSS定义地球参考框架尺度的主要误差来源之一。目前,利用GRACE、TOPEX/Poseidon等低轨卫星建立GNSS卫星天线相位中心改正模型可有效提高GNSS定义地球参考框架尺度的精度,具有较好的应用前景,这将是今后的重点研究方向。
| [1] |
魏娜, 施闯, 刘经南.地表负载及GPS测站分布对参考框架转换的影响分析[J].地球物理学报, 2016, 59(2): 484-493 (Wei Na, Shi Chuang, Liu Jingnan. Effects of Surface Loading and Heterogeneous GPS Network on Helmert Transformation[J]. Chinese Journal of Geophysics, 59(2): 484-493)
(  0) 0) |
| [2] |
Ma Y, Rebischung P, Altamimi Z, et al. Assessment of Geocenter Motion Estimates from the IGS Second Reprocessing[J]. GPS Solutions, 2020, 24
(  0) 0) |
| [3] |
Rodriguez-Solano C, Hugentobler U, Steigenberger P. Adjustable Box-Wing Model for Solar Radiation Pressure Impacting GPS Satellites[J]. Advances in Space Research, 2012, 49(7): 1 113-1 128
(  0) 0) |
| [4] |
Springer T. Modeling and Validating Orbits and Clocks Using the Global Positioning System[D]. Bern: University of Bern, 2000
(  0) 0) |
| [5] |
Zhu S, Massmann F, Yu Y, et al. Satellite Antenna Phase Center Offsets and Scale Errors in GPS Solutions[J]. Journal of Geodesy, 2003, 76(11-12): 668-672 DOI:10.1007/s00190-002-0294-1
(  0) 0) |
| [6] |
Ge M, Gendt G, Dick G, et al. Impact of GPS Satellite Antenna Offsets on Scale Changes in Global Network Solutions[J]. Geophysical Research Letters, 2005, 32(32): L06310
(  0) 0) |
| [7] |
Rebischung P, Schmid R. IGS14/igs14.atx: A New Framework for the IGS Products[C]. AGU Fall Meeting, San Francisco, 2016
(  0) 0) |
| [8] |
Scargle J. Studies in Astronomical Time Series Analysis. Ⅱ-Statistical Aspects of Spectral Analysis of Unevenly Spaced Data[J]. Astrophysical Journal, 1982, 263(2): 835-853
(  0) 0) |
| [9] |
Bos M, Fernandes R, Williams S, et al. Fast Error Analysis of Continuous GNSS Observations with Missing Data[J]. Journal of Geodesy, 2013, 87(4): 351-360
(  0) 0) |
| [10] |
Altamimi Z, Collilieux X, Legrand J, et al. ITRF2005: A New Release of the International Terrestrial Reference Frame Based on Time Series of Station Positions and Earth Orientation Parameters[J]. Journal of Geophysical Research Solid Earth, 2007, 112(B9)
(  0) 0) |
| [11] |
Rebischung P, Altamimi Z, Ray J, et al. The IGS contribution to ITRF2014[J]. Journal of Geodesy, 2016, 90(7): 611-630 DOI:10.1007/s00190-016-0897-6
(  0) 0) |
| [12] |
Collilieux X, Altamimi Z, Ray J, et al. Effect of the Satellite Laser Ranging Network Distribution on Geocenter Motion Estimation[J]. Journal of Geophysical Research Solid Earth, 2009, 114(B4)
(  0) 0) |
| [13] |
Collilieux X, Altamimi Z, Coulot D, et al. Impact of Loading Effects on Determination of the International Terrestrial Reference Frame[J]. Advances in Space Research, 2010, 45(1): 144-154
(  0) 0) |
2. School of Geodesy and Geomatics, Wuhan University, 129 Luoyu Road, Wuhan 430079, China
 2021, Vol. 41
2021, Vol. 41

