2. 中国科学院精密测量科学与技术创新研究院大地测量与地球动力学国家重点实验室,武汉市徐东大街340号,430077;
3. 中国科学院大学,北京市玉泉路甲19号,100049
目前GNSS测速方法主要包括位置中心差分法、多普勒频移法和动态PPP参数法,多普勒频移法分为原始多普勒频移法、导出多普勒频移法[1-2]。文献[3]提出一种结合多普勒频移和相位导出多普勒频移的测速法,能有效遏制传播误差,明显提高测速精度。位置中心差分法和导出多普勒频移法的测速精度取决于采样频率和载体运动状态,当载体处于匀速运动或静止情况下,载波相位导出多普勒频移法测速精度最高;在非匀速运动时,原始多普勒频移法测速精度最高[4]。SA政策取消后,GPS的各类误差对GPS测速存在一定影响,在静态模拟动态情况下原始多普勒频移法和载波相位导出多普勒频移法测速精度分别为cm/s和mm/s级[5]。文献[6]针对不同的采样频率和接收机型号对测速精度的影响因素进行分析,得到原始多普勒测速精度与采样间隔无关而与接收机类型有关的结论。对BDS而言,在静态仿动态和低动态情况下原始多普勒频移法和导出多普勒测速法分别达到cm/s、mm/s级的精度[7]。
然而,目前对于GNSS测速的研究多是针对位置差分法和多普勒频移法的研究,鲜有针对多普勒频移法(包括导出多普勒频移法)和动态PPP参数法测速精度的比较分析。北斗3号系统基本完成建设,已经向全球提供导航定位服务[8],针对北斗系统的多普勒频移法和动态PPP参数法的研究具有重要的现实意义。鉴于以上原因,本文旨在研究BDS2+3和GPS在静态模拟动态和动态情况下原始多普勒频移法、载波相位导出多普勒频移法和动态PPP参数法3种测速方法的精度以及影响测速精度的因素。
1 单点GNSS测速模型 1.1 原始多普勒频移测速法多普勒测速的原理是根据接收机到卫星之间的距离变化求解接收机运动速度。原始多普勒测速的数学模型可表示为[9]:
| $ D = {\mathit{\boldsymbol{e}}^i}\left( {{\mathit{\boldsymbol{v}}^i} - {\mathit{\boldsymbol{v}}_j}} \right) + b' + {\varepsilon ^i} $ | (1) |
式中,D为多普勒频移, D=di×λ,di为卫星i的多普勒频移观测量,λ为相应频率波长;vi为卫星i的运动速度,可根据导航文件和精密星历计算得出;vj为接收机速度,[vxj vyj vzj]T中的3个参数表示其3个方向;ei为接收机与卫星连线的方向余弦,[exi eyi ezi]中的3个参数表示如下:
| $ \begin{array}{l} {e^{xi}} = \frac{{{X_j} - {X^i}}}{{\sqrt {{{\left( {{X_j} - {X^i}} \right)}^2} + {{\left( {{Y_j} - {Y^i}} \right)}^2}} }} \cdot \\ \frac{{\sqrt {{{\left( {{X_j} - {X^i}} \right)}^2} + {{\left( {{Y_j} - {Y^i}} \right)}^2}} }}{{\sqrt {{{\left( {{X_j} - {X^i}} \right)}^2} + {{\left( {{Y_j} - {Y^i}} \right)}^2} + {{\left( {{Z_j} - {Z^i}} \right)}^2}} }} \end{array} $ | (2) |
| $ \begin{array}{l} {e^{yi}} = \frac{{{Y_j} - {Y^i}}}{{\sqrt {{{\left( {{X_j} - {X^i}} \right)}^2} + {{\left( {{Y_j} - {Y^i}} \right)}^2}} }} \cdot \\ \frac{{\sqrt {{{\left( {{X_j} - {X^i}} \right)}^2} + {{\left( {{Y_j} - {Y^i}} \right)}^2}} }}{{\sqrt {{{\left( {{X_j} - {X^i}} \right)}^2} + {{\left( {{Y_j} - {Y^i}} \right)}^2} + {{\left( {{Z_j} - {Z^i}} \right)}^2}} }} \end{array} $ | (3) |
| $ {e^{zi}} = \frac{{{Z_j} - {Z^i}}}{{\sqrt {{{\left( {{X_j} - {X^i}} \right)}^2} + {{\left( {{Y_j} - {Y^i}} \right)}^2} + {{\left( {{Z_j} - {Z^i}} \right)}^2}} }} $ | (4) |
式中,(Xj, Yj, Zj)、(Xi, Yi, Zi)分别为卫星和接收机的坐标;b′为接收机钟差变化率;εi为由卫星钟差、电离层误差、对流层误差等各种因素引起的误差项。利用最小二乘法求解[vxj vyj vzj b′]T中的4个参数。
1.2 载波相位导出多普勒测速多普勒频移还可以根据历元间的伪距观测值和载波相位观测值差分获得。本文分别利用BDS的B1、B3频率和GPS的L1、L2频率的载波相位观测值导出多普勒值。利用t-Δt和t+Δt历元的载波相位观测值φ1和φ3作差,求得历元t的多普勒频移观测值[10]:
| $ {d_2} = \frac{{{\varphi _3} - {\varphi _1}}}{{2\Delta t}} $ | (5) |
式中,Δt为观测值采样间隔,利用导出的多普勒观测值d2·λ代替式(1)中的D,以此来求解接收机的运动速度。
1.3 动态PPP参数法测速在动态PPP中,在X、Y、Z三个坐标分量的基础上增加了Vx、Vy、Vz三个速度参数和ax、ay、az三个加速度参数。
利用卡尔曼滤波处理动态数据建立状态方程和观测方程如下[11]:
| $ {\mathit{\boldsymbol{X}}_k} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k, k - 1}}{\mathit{\boldsymbol{X}}_{k - 1}} + {\mathit{\boldsymbol{\omega }}_{k - 1}}, {\mathit{\boldsymbol{\omega }}_{k - 1}} \sim N\left( {0, {\mathit{\boldsymbol{Q}}_{k - 1}}} \right) $ | (6) |
| $ {\mathit{\boldsymbol{z}}_k} = {\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{X}}_{k, k - 1}} + {\mathit{\boldsymbol{v}}_k}, {\mathit{\boldsymbol{v}}_k} \sim N\left( {0, {\mathit{\boldsymbol{R}}_k}} \right) $ | (7) |
考虑到接收机的复杂运动情况,实验采用动态加速模型,状态向量可表示为:
| $ {\mathit{\boldsymbol{X}}_k} = {\left[ {X\;Y\;Z\;{V_x}\;{V_y}\;{V_z}\;{a_x}\;{a_y}\;{a_z}\;{d_t}\;T{N_1} \cdots {N_n}} \right]^{\rm{T}}} $ | (8) |
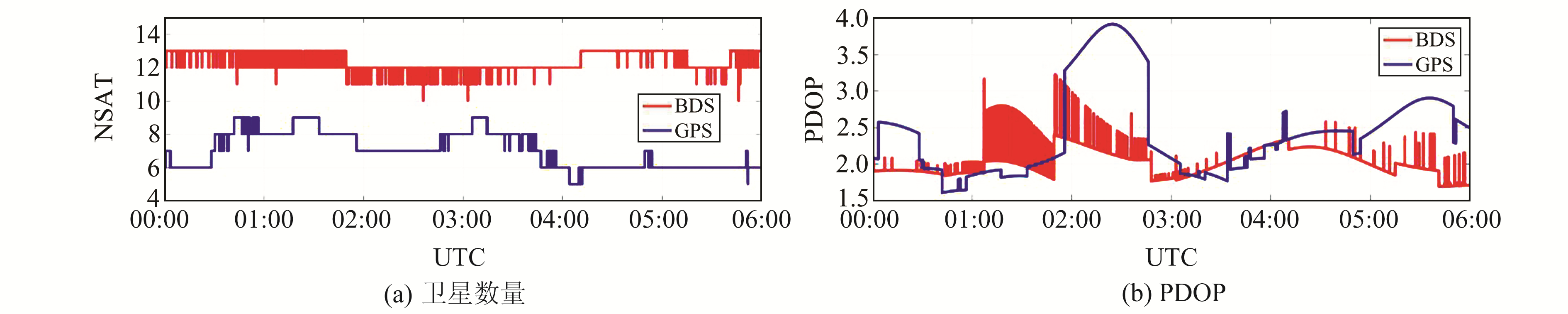
利用国际GNSS服务组织(International GNSS Service, IGS)提供的数据,选取分布在全球的JFNG、MAYG、SIN1、ZIM3、CUT0共5个IGS站BDS2+3和GPS两个系统的观测数据进行原始多普勒频移测速、载波相位导出多普勒频移测速和消电离层组合动态PPP参数法测速分析,观测时间为2019-10-01 00:00~10-02 00:00共24 h,把24 h的数据平均分为4个子时段,每个子时段6 h,数据采样间隔为1 s,精密产品采用武汉大学卫星导航定位技术研究中心提供的BDS、GPS精密星历和钟差产品。静态仿动态实验时,载体的速度真值为0,各方向解算出的速度值即为测速的真误差,以JFNG站第一个观测子时段为例,分别给出BDS、GPS系统3种测速方法E、N、U三个方向分量的误差序列。
由图 1可以看出,对BDS而言,原始多普勒测速法水平方向误差大多在3 cm/s以内,高程方向大部分在8 cm/s以内;动态PPP参数法水平方向和高程方向的误差大部分在1 cm/s以内;导出多普勒测速法E方向误差大部分在0.4 cm/s以内,N方向存在0.2 cm/s的系统误差(但大部分仍在0.8 cm/s以内),高程方向大部分在1.5 cm/s以内。对GPS而言,原始多普勒测速法水平方向误差大多在3 cm/s以内,高程方向在10 cm/s以内;动态PPP参数法各方向均在1.5 cm/s以内;导出多普勒测速法水平方向大多在0.6 cm/s以内,高程方向大多在1 cm/s以内。对比BDS/GPS系统不同测速方法的误差序列可知,原始多普勒测速法测速精度低于其他两种测速方法,误差最大为10 cm/s;导出多普勒测速在水平方向的测速精度高于动态PPP估计法,高程方向和动态PPP估计法测速精度相当。由图 2知,JFNG站的BDS可用卫星数一般在12颗上下,高于GPS的8颗左右。对GPS而言,在02:00~03:00时段可用卫星数量减少,PDOP值增大到3以上,导致原始多普勒测速和导出多普勒测速误差变大。

|
图 1 JFNG站第1时段BDS、GPS三种方法测速误差序列 Fig. 1 Velocity difference with three methods at station JFNG-1of BDS and GPS |
|
图 2 JFNG站第1时段BDS/GPS可见卫星数量和PDOP值 Fig. 2 Visible satellite number and PDOP value of BDS/GPS at station JFNG-1 |
由表 1(单位mm/s)可知,原始多普勒测速水平方向精度可达10 mm/s,高程方向约30 mm/s;导出多普勒测速法水平方向精度可达4 mm/s,高程方向约10 mm/s;动态PPP参数法水平方向精度可达5 mm/s,高程方向约5 mm/s。3种测速方法显示,水平方向的测速精度均要高于高程方向;导出多普勒测速精度最高,可达4 mm/s;整体而言,BDS测速精度略低于GPS。主要原因是BDS精密产品精度不足,在多普勒测速过程中,测速精度严重依赖卫星的轨道精度和卫星的速度精度。随着BDS地面监测站的增加,BDS精密产品精度会不断提高,测速精度也会得到相应提高。
|
|
表 1 BDS/GPS三种测速方法各方向的平均RMS Tab. 1 Average RMS of three methods in east/north/up component of BDS/GPS |
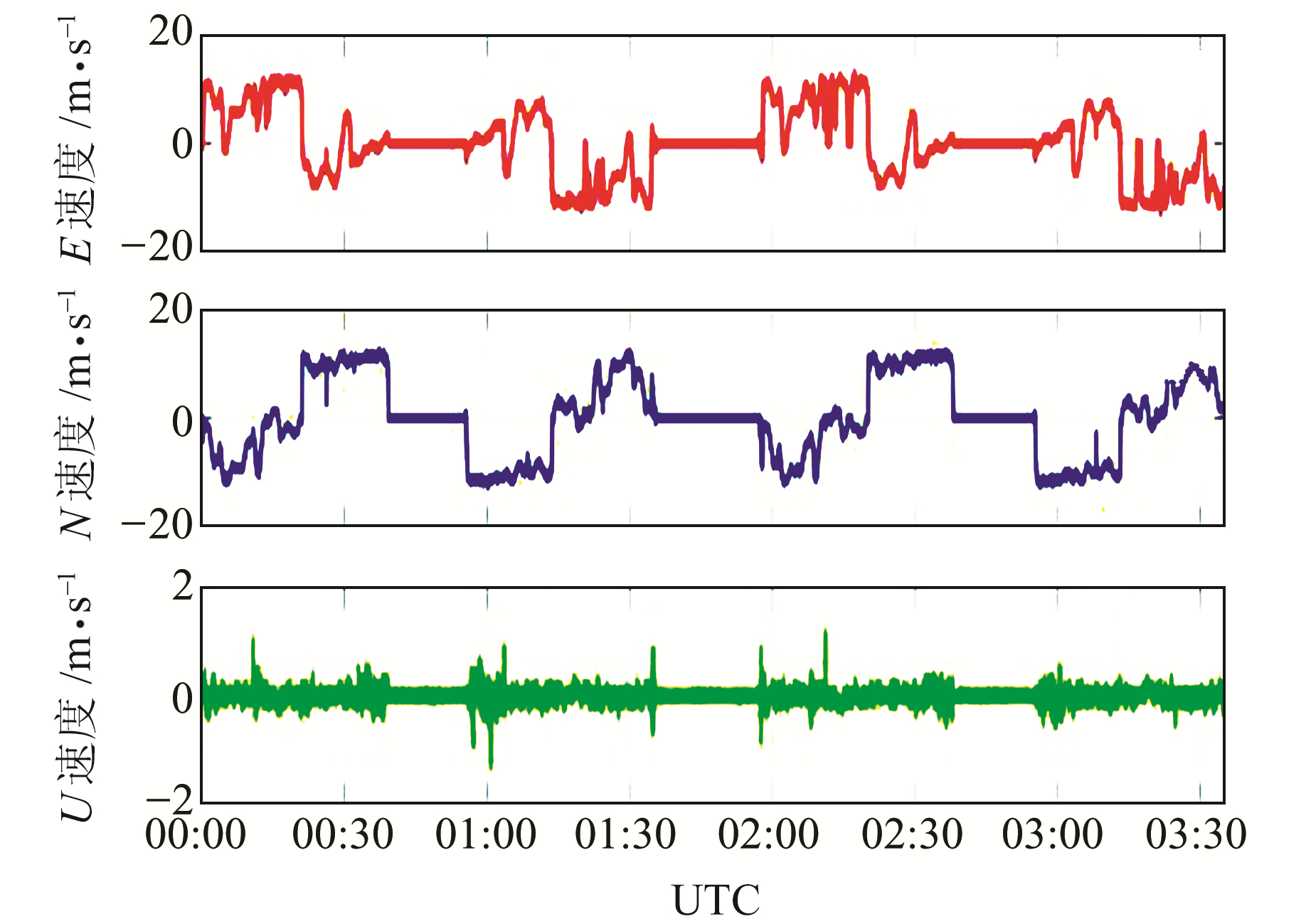
为了更好地比较动态PPP参数法和导出多普勒测速法在动态情况下的测速精度,本文还进行了车载动态实验。本次车载动态实验于UTC时间2019-05-16 05:33~09:08进行,约3 h 30 min,共得到约12 000个历元数据,全程约50 km。实验采用Novatel接收机,采样间隔为1 s, 截止高度角设置为10°。在汽车行驶过程中的真实速度值是未知的,鉴于原始多普勒测速法不受接收机运动速度变化的影响,且测速精度可达cm/s级, 因此,本次实验以原始多普勒测速法测得速度值作为参考真值,分析动态PPP参数法和导出多普勒测速法在真实运动中的测速精度。BDS和GPS两个系统动态PPP参数法和载波相位导出多普勒测速法测得的速度与原始多普勒测速法测得的速度差值见图 3,原始多普勒测速测得的速度值见图 4。

|
图 3 BDS、GPS动态PPP参数法与导出多普勒测速法的误差序列 Fig. 3 Kinematic PPP velocity difference and derivative Doppler velocity difference of BDS and GPS |
|
图 4 原始多普勒测速值 Fig. 4 Velocity value with Doppler measurement |
由表 2(单位cm/s)可知,动态情况下两种方法的速度差值的均方根均在cm/s级。由图 3和图 4可知,动态PPP参数法和导出多普勒测速法的速度差值大多在10 cm/s以内,最大差值为30 cm/s。BDS动态PPP参数法水平方向最大差值为30 cm/s,大部分在5cm/s以内;高程方向在20 cm/s以内,高于部分水平测速的精度。导出多普勒测速法水平方向误差最大为20 cm/s,大部分在5 cm/s以内,高程方向在20 cm/s以内。GPS两种测速方法的结果与BDS类似。在速度为零的情况下(如00:40~00:50时段),两种测速方法的差值均小于10 cm/s;在速度变化较大的情况下(如01:00~01:30时段),两种测速误差也会相应变大,动态PPP参数法均方根大于导出多普勒测速法。综上,当载体静止时,两种测速方法误差较小,当载体速度变化较大时,两种测速方法的测速误差会相应变大。在水平方向上,导出多普勒测速法的精度略高于动态PPP参数法,而动态PPP参数法测得的高程方向的测速精度高于其水平方向, 原因在于载体在行驶过程中道路坡度相对较小,高程方向的位置变化小。
|
|
表 2 BDS/GPS动态PPP参数法与导出多普勒测速法3个方向的RMS值 Tab. 2 RMS of kinematic PPP and derivative Doppler in east/north/up component of BDS/GPS |
本文采用精密星历和精密钟差产品,分析BDS、GPS两个系统使用原始多普勒测速法、动态PPP参数法和载波相位导出多普勒测速法3种测速方法的测速精度。结果表明:
1) 在静态模拟动态实验中,原始多普勒测速法、动态PPP参数法、载波相位导出多普勒测速法水平方向测速精度为10 mm/s、5 mm/s、4 mm/s。
2) 在动态实验中,载波相位导出多普勒测速法水平方向精度可达5 cm/s,动态PPP参数法可达8 cm/s,高程方向两种方法测速精度相当。导出多普勒测速法测速精度依赖于载波相位的观测值精度和采样间隔,采样间隔越小,载体速度变化越小,导出多普勒测速的精度越高。
| [1] |
Teunissen P J G, Odolinski R, Odijk D. Instantaneous Beidou+GPS RTK Positioning with High Cut-Off Elevation Angles[J]. Journal of Geodesy, 2014, 88(4): 335-350
(  0) 0) |
| [2] |
Schaffrin B, Wieser A. On Weighted Total Least-Squares Adjustment for Linear Regression[J]. Journal of Geodesy, 2008, 82(7): 415-421 DOI:10.1007/s00190-007-0190-9
(  0) 0) |
| [3] |
Wang Q X, Xu T H. Combining GPS Carrier Phase and Doppler Observations for Precise Velocity Determination[J]. Science China-Physics Mechanics and Astronomy, 2011, 54(6): 1 022-1 028 DOI:10.1007/s11433-011-4331-z
(  0) 0) |
| [4] |
何海波, 杨元喜, 孙中苗. 几种GPS测速方法的比较分析[J]. 测绘学报, 2002, 31(3): 217-221 (He Haibo, Yang Yuanxi, Sun Zhongmiao. A Comparison of Several Approaches for Velocity Determination with GPS[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(3): 217-221 DOI:10.3321/j.issn:1001-1595.2002.03.007)
(  0) 0) |
| [5] |
肖云, 夏哲仁. 利用相位率和多普勒确定载体速度的比较[J]. 武汉大学学报:信息科学版, 2003, 28(5): 581-584 (Xiao Yun, Xia Zheren. Comparison between Phase-Rate and Doppler to Determine Velocity[J]. Geomatics and Information Science of Wuhan University, 2003, 28(5): 581-584)
(  0) 0) |
| [6] |
单瑞, 赵铁虎, 于得水, 等. 单点GPS多普勒测速模型比较与精度分析[J]. 测绘通报, 2013(3): 7-9 (Shan Rui, Zhao Tiehu, Yu Deshui, et al. Model Comparison and Accuracy Analysis of Single-Stationed GPS Velocity Estimation Using GPS Doppler Measurements[J]. Bulletin of Surveying and Mapping, 2013(3): 7-9)
(  0) 0) |
| [7] |
刘朝英, 陈国, 赵齐乐, 等. BDS单点测速原理及精度分析[J]. 大地测量与地球动力学, 2014, 34(6): 114-118 (Liu Zhaoying, Chen Guo, Zhao Qile, et al. Principle and Precision Analysis of BDS Absolute Velocity Determination[J]. Journal of Geodesy and Geodynamics, 2014, 34(6): 114-118)
(  0) 0) |
| [8] |
中国卫星导航系统管理办公室.北斗卫星导航系统发展报告(4.0版)[R].北京, 2019 (Chinese Satellite Navigation System Management Office.Beidou Satellite Navigation System Development Report(4.0)[R].Beijing, 2019)
(  0) 0) |
| [9] |
李昕, 郭际明, 章迪, 等. 基于多普勒测速的GPS单历元动态定位算法[J]. 武汉大学学报:信息科学版, 2018, 43(7): 1 036-1 041 (Li Xin, Guo Jiming, Zhang Di, et al. An Algorithm of GPS Single-Epoch Kinematic Positioning Based on Doppler Velocimetry[J]. Geomatics and Information Science of Wuhan University, 2018, 43(7): 1 036-1 041)
(  0) 0) |
| [10] |
孙伟, 段顺利, 丁伟, 等. GPS单点测速方法的比较分析[J]. 导航定位学报, 2017, 5(1): 81-85 (Sun Wei, Duan Shunli, Ding Wei, et al. Comparative Analysis on Velocity Determination by GPS Single Point[J]. Journal of Navigation and Positioning, 2017, 5(1): 81-85)
(  0) 0) |
| [11] |
范磊.GPS/BDS精密单点定位算法及其应用研究[D].北京: 中国科学院大学, 2014 (Fan Lei.Study on the Algorithm and Applications of Precise Point Positioning Using GPS and BDS Data[D].Beijing: University of CAS, 2014)
(  0) 0) |
2. State Key Laboratory of Geodesy and Earth's Dynamics, Innovation Academy for Precision Measurement Science and Technology, CAS, 340 Xudong Street, Wuhan 430077, China;
3. University of Chinese Academy of Science, A19 Yuquan Road, Beijing 100049, China
 2021, Vol. 41
2021, Vol. 41


