2. 广西空间信息与测绘重点实验室,桂林市雁山街319号,541006
雾霾的主要成分是二氧化硫、氮氧化物以及细颗粒物(PM2.5、PM10)。雾霾的形成与大气可降水量(precipitable water vapor, PWV)、空气污染物排放以及气象条件等有着密切的关系。近年来,一些学者研究基于神经网络的PM2.5浓度时序预测方法[1-7],取得较好的预测结果,稳定性也较高。但这些预测方法只考虑了PWV(或天顶湿延迟ZWD、天顶总延迟ZTD)、空气污染物、气象条件这3类影响因子中的1类或2类,没有同时顾及这3类因子的影响;亦未见有利用鲸鱼优化算法(whale optimization algorithm, WOA)、狼群算法(wolf pack algorithm, WPA)优化神经网络预测PM2.5浓度的相关研究。为此,本文提出一种综合考虑ZTD、空气污染物以及气象条件3类因子影响,利用WOA和WPA混合优化BP神经网络的PM2.5浓度预测方法,将桂林市整体作为一个单点从时间维度上对其冬季和夏季的PM2.5浓度进行预测,并分析预测结果的精度。
1 WPA-WOA-BP神经网络 1.1 BP神经网络BP神经网络是一种多层前馈网络,按照误差逆向传播进行训练。这种网络可以在事先不知道映射关系的情况下,自主学习大量的输入和输出模式的映射关系,然后通过逆向传播不间断地修改网络的阈值与权值,从而使网络误差达到最小。BP神经网络的运算主要由3个部分组成,即由输入层途经隐含层到输出层的正向传播过程、网络预测输出与实际值的误差由输出层到输入层的反向修正过程、正向与反向过程交替进行的训练过程。然而传统BP神经网络收敛速度慢、容易陷入局部极值,并且初始权值和阈值不准确会影响预测效果。因此,可以运用具有全局搜索能力的算法对BP神经网络的初始权值和阈值进行优化。
1.2 WOA原理在鲸鱼捕食行为的启迪下,Seyedali等[14]提出一种新型优化算法——鲸鱼优化算法(WOA)。设鲸鱼优化算法中鲸鱼的种群规模是N,则第i头鲸鱼在D维空间中的位置可以表示为Xi=(xi1, xi2,…,xiD),i=1, 2, 3,…,N,最后鲸鱼捕食到的猎物的位置就是全局的最优解。其基本行为大致可分为包围捕食、气泡捕食、随机搜索猎物等,详细过程见文献[8-9]。
1.3 WPA原理狼群算法(WPA)[10]是根据狼群的捕食、进化等行为提出的一种优化算法,将狼群的行为抽象地分为游走、召唤以及围攻3种,还包括了狼群内部胜者为王的更新机制以及自然选择的优胜劣汰机制,可以解决函数最优化求解问题,具体过程见文献[10-11]。
1.4 WPA-WOA-BP神经网络原理WPA以及WOA优化BP神经网络主要是优化BP神经网络的权值和阈值,用个体狼、鲸鱼的最优状态代替BP神经网络的权值和阈值,通过不断地迭代寻优,把气味浓度值最小的人工狼或位置最佳的鲸鱼作为神经网络的初始权值和阈值。
WPA-WOA混合优化的核心步骤为:每次迭代用狼群的最优值替换鲸鱼群中适应度值最差的鲸鱼,进而实现WPA和WOA的混合,本质上是狼群算法不断为鲸鱼群提供新鲜血液。当WOA和WPA混合优化后,输出最优值当作BP神经网络的初始权值和阈值,然后进行网络训练,计算目标函数,输出最优解。基本步骤如下:
1) 读取数据,利用BP神经网络进行预测,得到预测误差。
2) 确定目标函数,然后基于目标函数,利用鲸鱼算法和狼群算法进行优化,使预测误差最小。
3) 根据目标函数确定鲸鱼的种群数X,随机产生鲸鱼群的位置,对各个参数进行初始化赋值。
4) 根据目标函数进行狼群的初始化,选出头狼,确定狼群中每匹狼的位置Xi、种群规模n、探狼最大游走次数Tmax、最大迭代次数Tsmax、步长因子S以及各种比例因子。
5) 在众多鲸鱼个体中选出一头适应度值最优的个体,并定义为X*。
6) 进入鲸鱼算法核心部分,更新鲸鱼个体的当前位置。
7) 对鲸鱼种群进行全面评价,选出全局最优鲸鱼位置。
8) 选取适应度较好的狼作为探狼,在d维空间中探狼根据气味寻找猎物;如果探狼i确定的猎物气味浓度Yi大于Ylead,则头狼进行更新,进入下个行为。
9) 探狼获取猎物的位置后,头狼会通过嚎叫的方式吸引种群中的猛狼,若猛狼i发现气味更浓的Yi,则头狼更新;若猛狼到头狼的距离di小于dnear,则猛狼对猎物展开围攻。
10) 对猎物展开进攻,获取猎物位置。
11) 头狼和狼群进行更新,更新的原则是大自然中的优胜劣汰。
12) 用头狼的最优状态代替最差的鲸鱼位置。
13) 判断算法是否达到最大迭代次数,如果未达到,则回到第3)步,继续迭代。
14) 结束循环以后,将替代后的鲸鱼最优位置作为BP神经网络的初始权值和阈值,网络训练后进行预测并输出结果。
具体流程如图 1所示。

|
图 1 WPA-WOA-BP神经网络流程 Fig. 1 The flow chart of WPA-WOA-BP neural network |
本次实验以桂林市为例,所用数据有空气主要污染物(含PM2.5、PM10、SO2、NO2、CO和O3)、GNSS ZTD以及气象因子(气压、温度、相对湿度)3种类型。空气污染物数据来源于广西生态环境数据中心,取桂林市4个空气质量监测站同小时数据的均值作为对应小时的数值;ZTD数据来源于中国地震局GNSS数据产品服务平台,采用陆态网桂林站的逐小时数据;气象数据来源于国家气象科学数据中心,采用桂林站的逐小时数据。为了确定合适的PM2.5浓度影响因子,首先基于SPSS软件研究PM2.5浓度与空气污染物、ZTD以及气象因子的相关性,结果如表 1和表 2所示。由表 1和表 2可知,PM2.5浓度与空气污染物之间基本上呈正相关,与ZTD之间呈负相关,与温度之间基本上呈正相关,与相对湿度之间呈负相关,与气压在夏季和秋季呈负相关、在春季和冬季呈正相关。PM2.5浓度与空气污染物、ZTD、温度、相对湿度以及气压的相关性较强,因此进行PM2.5浓度预测时选择这些因子作为预测输入。
|
|
表 1 不同季节PM2.5浓度与空气污染物的相关性 Tab. 1 Correlation of PM2.5 and air pollutants in different seasons |
|
|
表 2 不同季节PM2.5浓度与ZTD、温度、相对湿度以及气压的相关性 Tab. 2 Correlation of PM2.5 and ZTD, temperature, relative humidity and air pressure in different seasons |
分别应用BP神经网络、WPA-BP神经网络、WOA-BP神经网络和WPA-WOA-BP神经网络4种模型对冬季和夏季的PM2.5浓度进行预测,并对结果进行分析。选取2017-01、2017-07的数据进行实验,预测模型中每种输入数据的长度完全一致,分辨率为1 h。由于不同月份的有效数据量不同,所以各月份的建模数据也不相同。1月预测的输入数据长度为631 h,运用前583 h的数据进行建模;7月预测的输入数据长度为620 h,运用前572 h的数据进行建模。模型构建完成后,对未来48 h的PM2.5浓度进行预测输出。1月部分数据如表 3所示(7月数据略),表中PM2.5、PM10、SO2、NO2和O3的单位为μg/m3,CO的单位为mg/m3,ZTD单位为mm,气压单位为hPa,温度单位为℃,相对湿度单位为%。
|
|
表 3 1月样本数据 Tab. 3 Sample data in January |
为了更好地比较实验效果,对4种模型选取同样的隐含层节点数。在实际工作中,常用经验公式来确定隐含层节点数的估计值:
| $ m = \sqrt {n + l} + z $ | (1) |
式中,m为隐含层节点数,n、l分别为输入层、输出层节点数,z为1~10之间的整数。
然后采用试凑法确定准确的节点数,即先取一个较小的值,然后不断增加,选取使网络误差较小的值作为隐含层节点数。结合式(1)确定的估值,经试凑法不断调整,本实验确定的隐含层节点数为5。
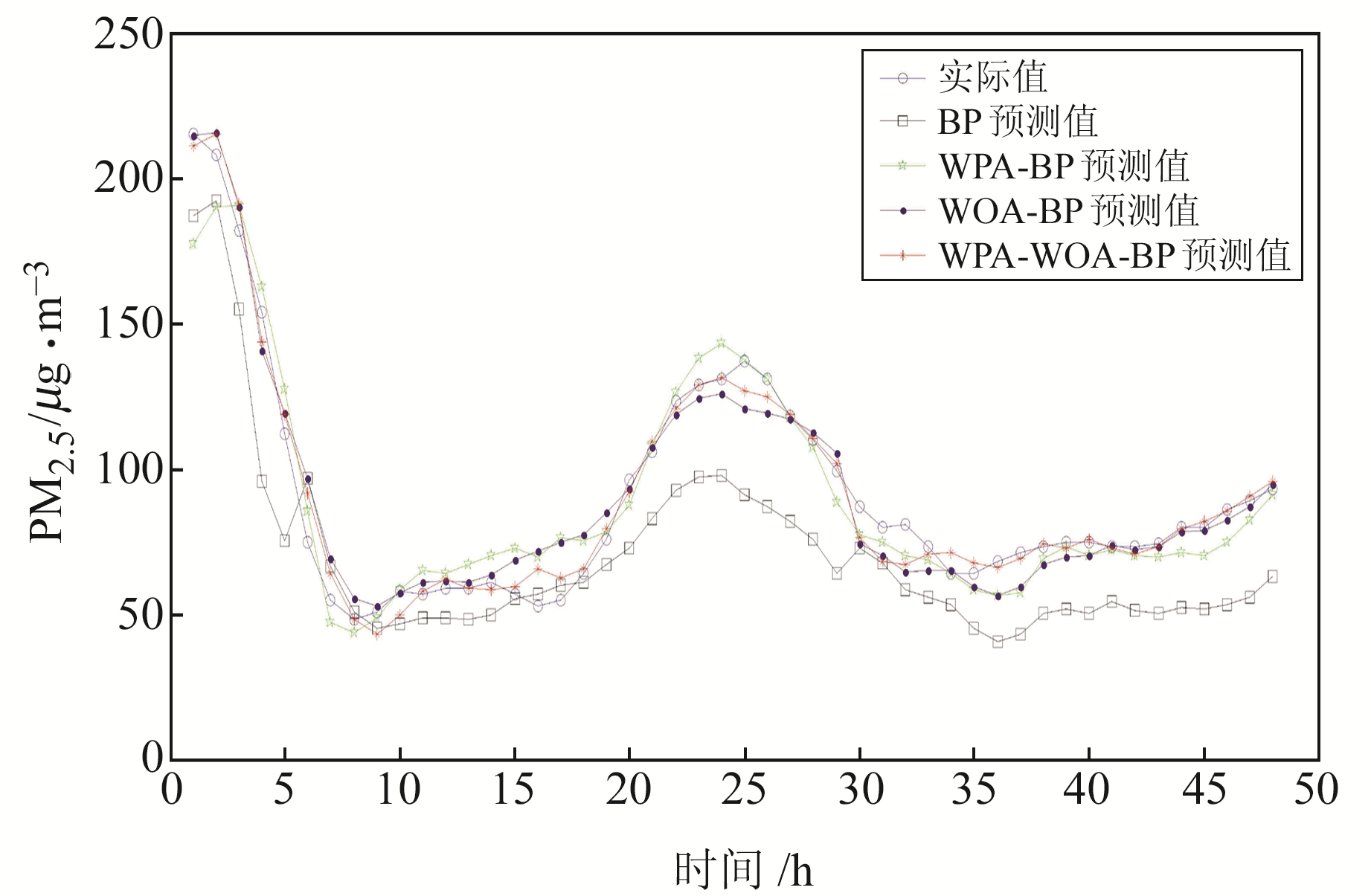
前期准备工作完成后,为了验证4种模型在不同季节的预测能力,选取1月样本数据中前583 h的空气污染物数据、ZTD数据和气象数据作为输入数据,预测未来48 h的PM2.5浓度,预测结果如图 2所示。图 3为各模型预测结果的相对误差,表 4为各模型的预测精度统计,表中MAPE(mean absolute percentage error)为平均绝对百分误差、MAE(mean absolute error)为平均绝对误差。
|
图 2 1月各模型预测结果 Fig. 2 The forecast results of each model in January |

|
图 3 1月各模型预测结果的相对误差 Fig. 3 The relative error of the forecast results of each model in January |
|
|
表 4 1月各模型预测精度 Tab. 4 Forecast precision of each model in January |
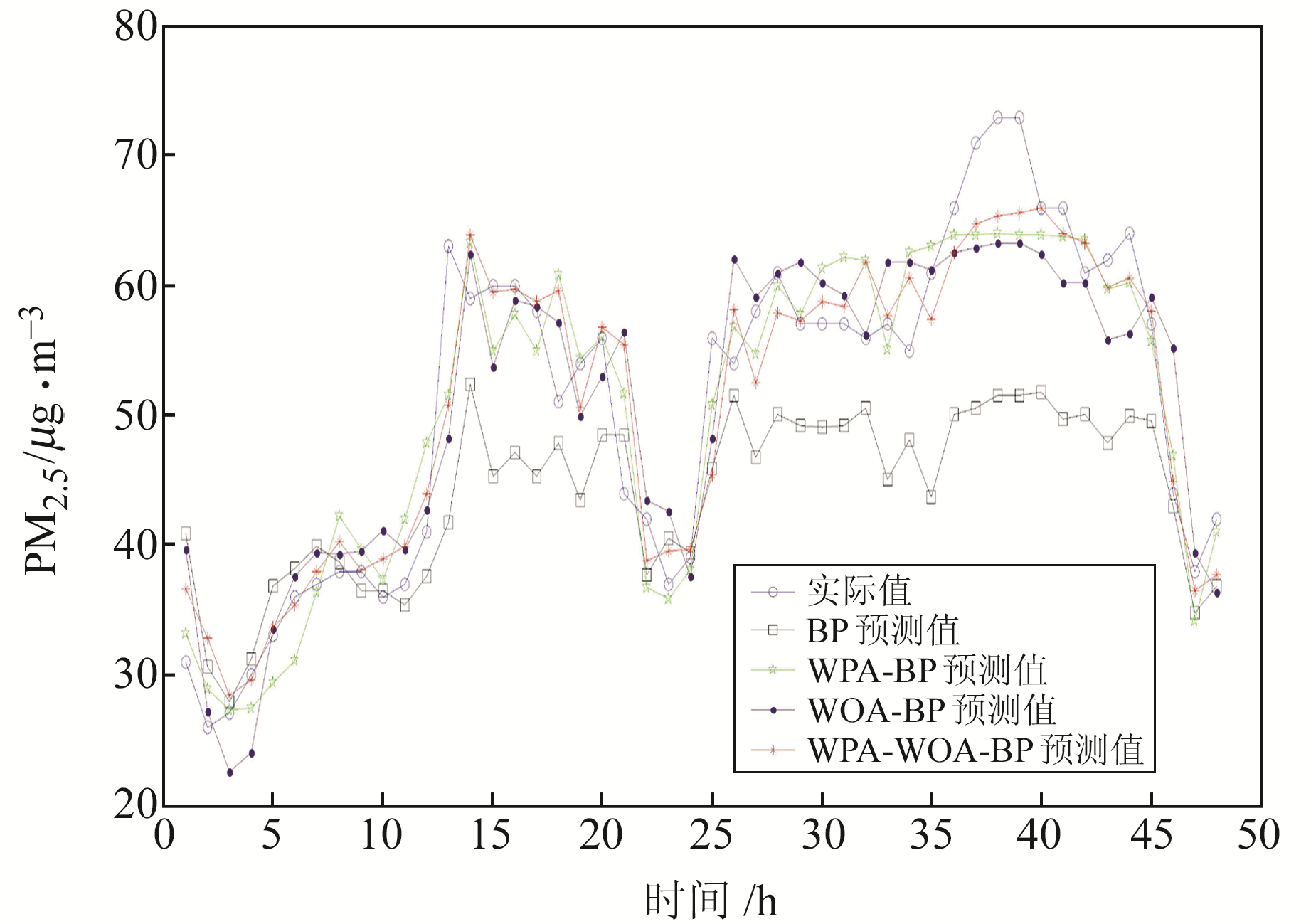
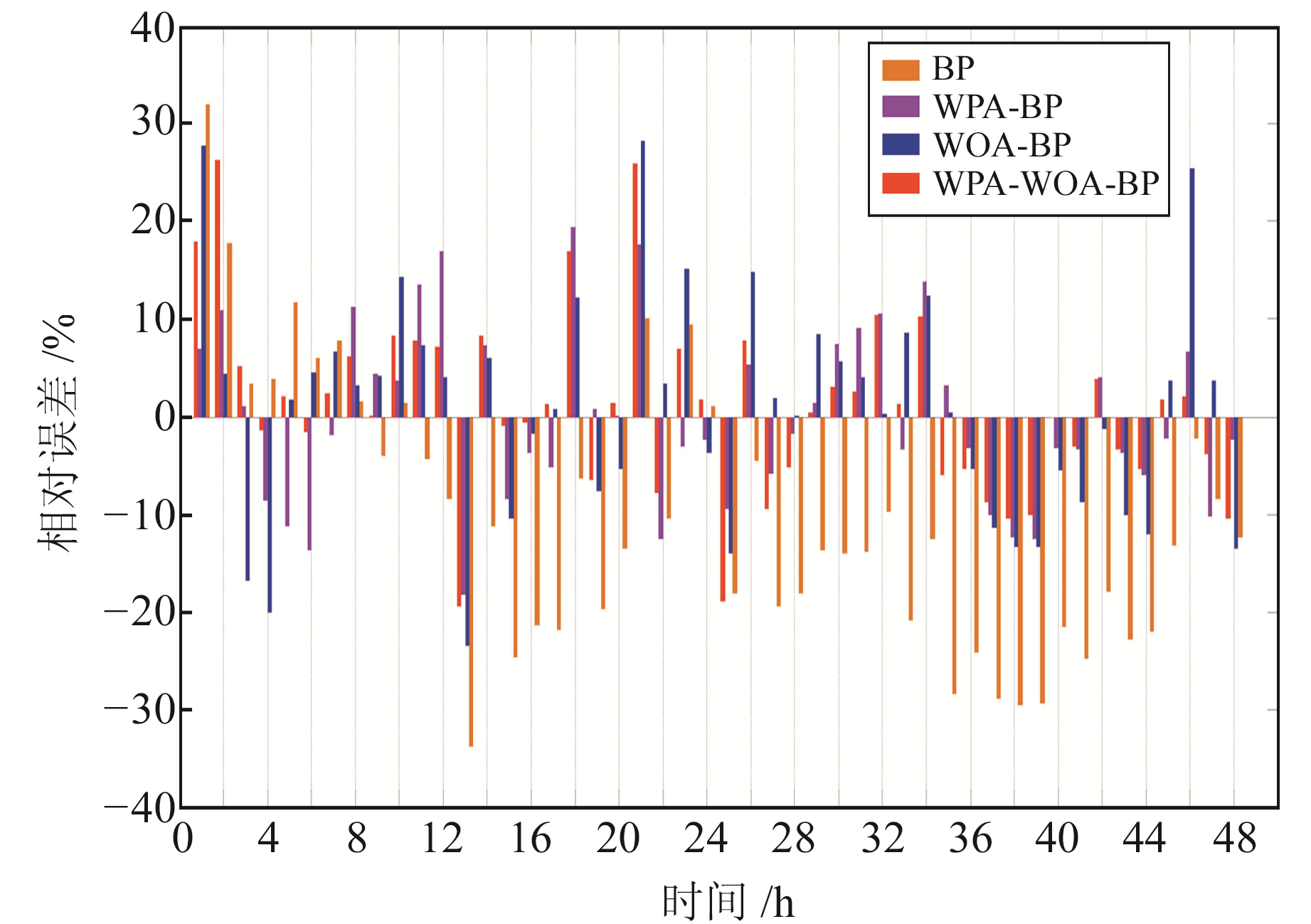
选取7月样本数据中前572 h的空气污染物数据、ZTD数据和气象数据作为输入数据,预测未来48 h的PM2.5浓度,预测结果如图 4。图 5为各模型预测结果的相对误差,表 5为各模型的预测精度统计。
|
图 4 7月各模型预测结果 Fig. 4 The forecast results of each model in July |
|
图 5 7月各模型预测结果的相对误差 Fig. 5 The relative error of the forecast results of each model in July |
|
|
表 5 7月各模型预测精度 Tab. 5 Forecast precision of each model in July |
为进一步验证各模型性能,采用桂林2017-02、2017-08的数据按同样方法再次进行实验,得到各模型的预测精度如表 6所示。
|
|
表 6 2月和8月各模型预测精度 Tab. 6 Forecast precision of each model in February and August |
由图 2、图 4可知,4种模型预测得到的结果与实际值具有很好的一致性,但优化后的BP神经网络预测精度显著高于优化前的预测精度。由图 3和图 5可以看出,BP神经网络相对误差较大,且随着预测时间的增加而增大;经优化后的3种BP神经网络相对误差明显降低,稳定性也有较大提高,其中以WPA-WOA-BP神经网络的相对误差降低最为明显。
由表 4、表 5可知,优化后的3种BP神经网络的RMSE值明显减小,说明优化后的BP神经网络预测的误差离散性较小,其中WPA-WOA-BP神经网络在1月和7月预测结果的RMSE分别为6.146 μg/m3、4.574 μg/m3,在4种预测模型中精度最高。从MAPE指标来看,BP神经网络、WPA-BP神经网络、WOA-BP神经网络以及WPA-WOA-BP神经网络1月预测结果分别为23.951%、9.572%、8.873%、5.523%,7月预测结果分别为14.876%、7.344%、8.944%、6.793%,说明WPA-BP神经网络、WOA-BP神经网络的预测值优于BP神经网络的预测值,并且WPA-WOA-BP神经网络的预测结果又优于单独优化的神经网络的预测结果。从MAE也可以进一步看出,优化后的3种BP神经网络预测精度均明显提升,其中同样以WPA-WOA-BP神经网络预测精度最高。另外,由表 6可知,WPA-WOA-BP神经网络预测的3种精度指标同样均为最优,且各模型2月、8月的预测精度分别与1月、7月的预测精度呈现相同的特点。综合表 4~6,比较桂林夏季和冬季的PM2.5浓度预测结果发现,优化后的BP神经网络预测精度均有极大提高,但是冬季预测精度提升幅度明显大于夏季。原因可能在于,冬季PM2.5浓度变化大,数据规律性较弱,而BP神经网络对数据的质量要求高,泛化能力弱,导致BP神经网络冬季预测精度较低。
4 结语本文运用WOA和WPA组合优化传统BP神经网络,构建了WPA-WOA-BP神经网络模型用于PM2.5浓度预测。实验结果表明,该模型精度优于BP神经网络、WPA-BP神经网络、WOA-BP神经网络。
| [1] |
Jin Liyang. The Prediction of Haze in Beijing Based on Temporal Variation of PWV[J]. Guilin: Guilin University of Technology, 2015
(  0) 0) |
| [2] |
Zhou Q P, Jiang H Y, Wang J Z, et al. A Hybrid Model for PM2.5 Forecasting Based on Ensemble Empirical Mode Decomposition and a General Regression Neural Network[J]. Science of the Total Environment, 2014, 496: 264-274 DOI:10.1016/j.scitotenv.2014.07.051
(  0) 0) |
| [3] |
周杉杉, 李文静, 乔俊飞. 基于自组织递归模糊神经网络的PM2.5浓度预测[J]. 智能系统学报, 2018, 13(4): 509-516 (Zhou Shanshan, Li Wenjing, Qiao Junfei. Prediction of PM2.5 Concentration Based on Self-Organizing Recurrent Fuzzy Neural Network[J]. CAAI Transactions on Intelligent Systems, 2018, 13(4): 509-516)
(  0) 0) |
| [4] |
白盛楠, 申晓留. 基于LSTM循环神经网络的PM2.5预测[J]. 计算机应用与软件, 2019, 36(1): 67-70 (Bai Shengnan, Shen Xiaoliu. PM2.5 Prediction Based on LSTM Recurrent Neural Network[J]. Computer Applications and Software, 2019, 36(1): 67-70)
(  0) 0) |
| [5] |
刘林波, 刘立龙, 黎峻宇, 等. 联合水汽因子的GA-BP神经网络PM2.5质量浓度预测[J]. 桂林理工大学学报, 2019, 39(2): 420-426 (Liu Linbo, Liu Lilong, Li Junyu, et al. Prediction of PM2.5 Mass Concentration Based on GA-BP Neural Network with Water Vapor[J]. Journal of Guilin University of Technology, 2019, 39(2): 420-426)
(  0) 0) |
| [6] |
任晓晨, 邹思琳, 唐娴, 等. 基于集合经验模态分解和BP神经网络的北京市PM2.5预报研究[J]. 北京大学学报:自然科学版, 2019, 55(4): 615-625 (Ren Xiaochen, Zou Silin, Tang Xian, et al. PM2.5 Forecast of Beijing Based on Ensemble Empirical Mode Decomposition and BP Neural Network[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2019, 55(4): 615-625)
(  0) 0) |
| [7] |
张旭, 杜景林. 改进PSO-GA-BP的PM2.5浓度预测[J]. 计算机工程与设计, 2019, 40(6): 1 718-1 723 (Zhang Xu, Du Jinglin. PM2.5 Concentration Prediction Based on Improved PSO-GA-BP[J]. Computer Engineering and Design, 2019, 40(6): 1 718-1 723)
(  0) 0) |
| [8] |
Mirjalili S, Lewis A. The Whale Optimization Algorithm[J]. Advances in Engineering Software, 2016, 95(95): 51-67
(  0) 0) |
| [9] |
牛培峰, 吴志良, 马云鹏, 等. 基于鲸鱼优化算法的汽轮机热耗率模型预测[J]. 化工学报, 2017, 68(3): 1 049-1 057 (Niu Peifeng, Wu Zhiliang, Ma Yunpeng, et al. Prediction of Steam Turbine Heat Consumption Rate Based on Whale Optimization Algorithm[J]. Journal of Chemical Industry and Engineering, 2017, 68(3): 1 049-1 057)
(  0) 0) |
| [10] |
吴虎胜, 张凤鸣, 吴庐山. 一种新的群体智能算法-狼群算法[J]. 系统工程与电子技术, 2013, 35(11): 2 430-2 438 (Wu Husheng, Zhang Fengming, Wu Lushan. New Swarm Intelligence Algorithm-Wolf Pack Algorithm[J]. Systems Engineering and Electronics, 2013, 35(11): 2 430-2 438)
(  0) 0) |
| [11] |
罗强, 饶运清, 刘泉辉, 等. 求解矩形件排样问题的十进制狼群算法[J]. 计算机集成制造系统, 2019, 25(5): 1 169-1 179 (Luo Qiang, Rao Yunqing, Liu Quanhui, et al. Decimal Wolf Pack Algorithm for Rectangular Packing Problem[J]. Computer Integrated Manufacturing Systems, 2019, 25(5): 1 169-1 179)
(  0) 0) |
2. Guangxi Key Laboratory of Spatial Information and Geomatics, 319 Yanshan Street, Guilin 541006, China
 2021, Vol. 41
2021, Vol. 41


