跨海大桥是人工与自然有机结合的整体,处在海洋这个复杂的环境中,运营后还需承受车载外力的作用,其各部分之间不断地进行能量、物质交换,通过系统信息熵的变化使桥梁整体走向有序[1-3]。因此,桥梁变形是一种非平衡态有序结构。由于我国跨海大桥建设也是近10 a的事情,运营后的跨海大桥变形特征及预测模型研究也处于起步阶段[4-5]。近几年建好的几座跨海大桥均建立了变形监测站,获得了桥梁变形数据,但在数据挖掘、建立动态非线性高精度的桥梁变形时空预测模型方面还远远不够[6-7]。因此,开展跨海大桥时空非线性变形模型研究是理论与实际结合、理论成果又反馈桥梁安全运营的实用课题[8-9]。
本文对青岛胶州湾跨海大桥开展了变形监测工作,桥梁特征点三维坐标数据采集使用的测量机器人为徕卡30全站仪,该仪器测角精度为0.5″, 测距精度为0.1 mm+10-6D。测量方法为:在稳定区域布设的D级GPS控制点上安置测量机器人,对桥墩、桥面、桥索塔的特征点自动进行三维坐标观测。由于桥梁处于海洋环境中,受海浪、飓风、船体撞击等因素的影响,使桥梁变形表现为动态非连续变形,并伴有混沌现象发生[10]。
目前用于混沌时间序列预测的数学模型主要有神经网络模型和支持向量机等,但由于支持向量机存在参数准确选取困难[11],并且局部优化能力差的缺点,因此本文根据桥梁变形监测数据,首先对桥梁变形系统混沌特征进行识别,并对桥梁水平位移单变量进行高精度RBF神经网络混沌预测的深入研究,这对揭示跨海大桥变形机理、实现桥梁安全运营具有重大意义。
1 桥梁水平位移观测数据混沌特征识别当桥梁系统受外界影响有扰动时,系统可能发生分岔并可能演变成混沌状态。为了判断桥梁变形是否有混沌状态,选取Verhulst生物模型拟合桥梁变形位移时间序列[1],即
| $ \frac{{{\rm{d}}x}}{{{\rm{d}}t}} = k(1 - x)x $ | (1) |
式中,x为变形位移值,t为时间,k为参数。其差分方程为:
| $ {x_{n + 1}} = k(1 - {x_n}){x_n} $ | (2) |
根据线性稳定分析桥梁系统随k变化的长期行为。变换后的位移监测数据系列中,若k取[0, 4]、x取[0, 1],对应的logistic映射结果表明,k值增加到kn时,表现为2n的周期加倍的分岔现象,即倍周期分岔;但当k≥k∞=3.57时,系统表现为
本文选取青岛胶州湾跨海大桥W1点3 a内的300期水平位移监测数据进行分析,取W1点后100期数据水平位移观测,其在x方向、y方向上的变形量无明显线性与周期性变化趋势,通过重构相空间寻找其内在规律。
1.1 最大Lyapunov指数Lyapunov指数表示多次迭代中平均每次迭代引起指数分离的度量。Lyapunov指数λ的表达式为:
| $ \lambda = \mathop {\lim }\limits_{n \to \infty } \frac{1}{n}\sum\limits_{i = 0}^{n - 1} {\ln } {\left| {\frac{{{\rm{d}}{F^n}(x)}}{{{\rm{d}}x}}} \right|_{x = {x_i}}} $ | (3) |
式中,λ为Lyapunov指数,F(x)为x的映射值。λ>0时,运动系统存在混沌状态。
基于最大Lyapunov指数的混沌时间序列预测,就是利用已经得到的最大Lyapunov指数(即轨道平均发散率),采用相空间重构技术,通过跟踪最邻近点的演化进行预测[12-14]。格里波基[15]证明,只要最大Lyapunov指数大于零,就可以肯定系统中存在混沌状态。
用小数据量法计算桥梁水平位移时间序列最大Lyapunov指数,x方向变形时间序列最大Lyapunov指数为0.015,证明x方向变形时间序列具有混沌性;同理,y方向变形时间序列最大Lyapunov指数为0.014,y方向变形时间序列也具有混沌性,此结果与Verhulst生物模型拟合的桥梁变形位移时间序列具有混沌状态相吻合。
1.2 时间延迟C-C法求取时间延迟的方法如下。将时间序列分成t个不相交的子序列,每个子序列可定义为:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} S(m,N,r,t) = \\ \frac{1}{t}\sum\limits_{s = 1}^t {\left[ {{C_s}\left( {m,\frac{N}{t},r,t} \right) - C_s^m\left( {1,\frac{N}{t},r,t} \right)} \right]} \end{array} $ | (4) |
式中,m为嵌入维数,N为点的个数,r为元素间相关半径,t为不相交子序列个数。
令N→∞,有:
| $ \begin{array}{l} S(m,r,t) = \frac{1}{t}\sum\limits_{s = 1}^t {\left[ {{C_s}(m,r,t) - } \right.} \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} C_s^m(1,r,t)],m = 2,3, \cdots \end{array} $ | (5) |
由于时间序列是有限的,且元素间也可能是相关的,故选择对应值中最大和最小的两个半径r,其差量为:
| $ \Delta S(m,t) = \max \left\{ {S\left( {m,{r_j},t} \right)} \right\} - \left\{ {S\left( {m,{r_j},t} \right)} \right\} $ | (6) |
取m=2, 3, 4, 5, ri=
| $ {\bar S(t) = \frac{1}{{16}}\sum\limits_{m = 2}^5 {\sum\limits_{j = 1}^4 S } \left( {m,{r_j},t} \right)} $ | (7) |
| $ {\Delta \bar S(t) = \frac{1}{4}\sum\limits_{m = 2}^5 \Delta S(m,t)} $ | (8) |
| $ {{S_{{\rm{cor }}}}(t) = \Delta \bar S(t) + |\bar S(t)|} $ | (9) |
在公式(7)~(9)中寻找S (t)的第一个零点或ΔS(t)的第一个极小值,得到序列独立的第一个局部最大值,此时的t即为空间延迟[16]。
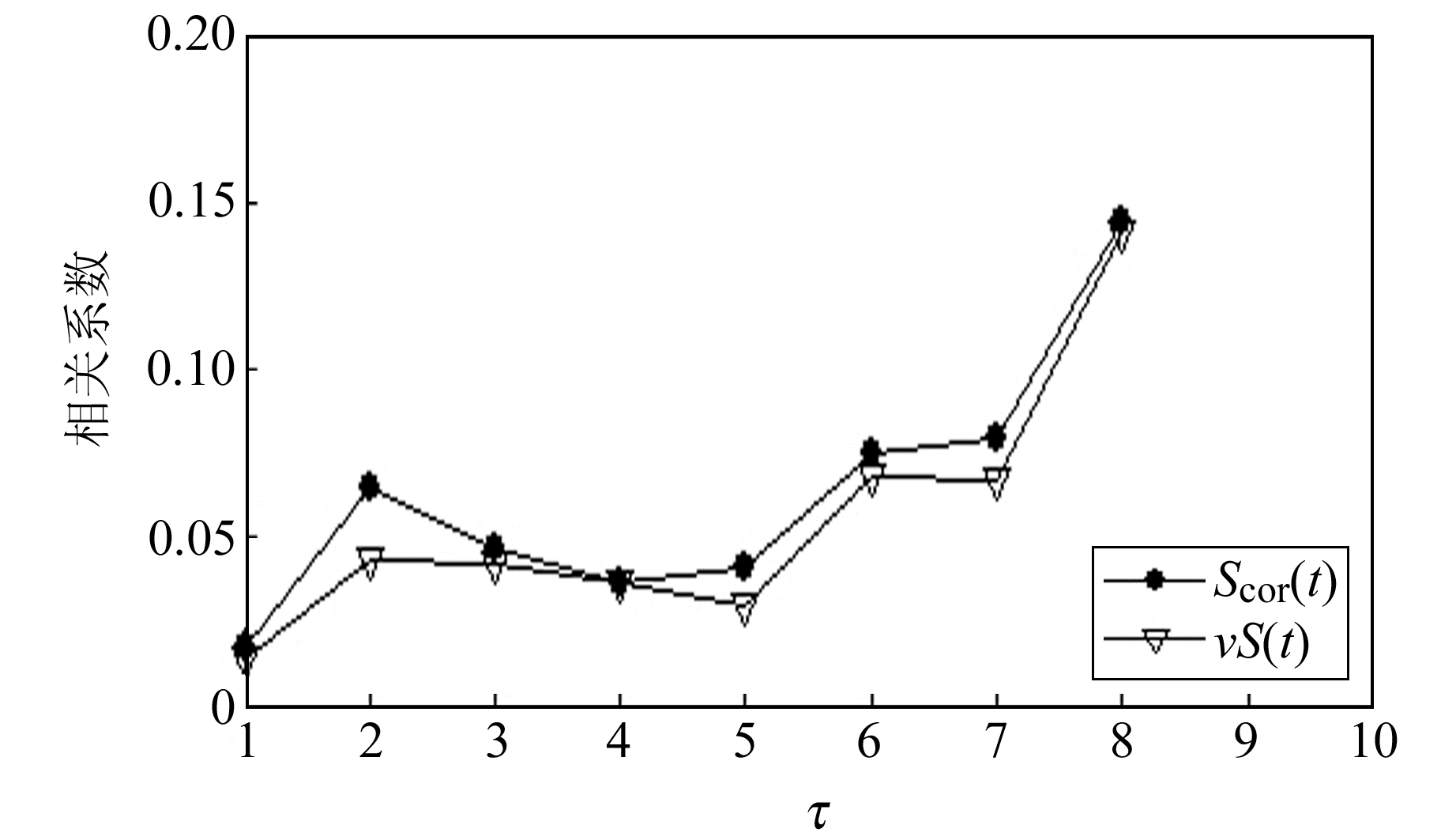
用C-C法求关于x方向变形时间序列的时间延迟如图 1所示。对于x方向变形时间序列,取ΔS(t)和Scor(t)到第一个近似极小值时τ为1,则由C-C法求得x方向变形时间序列的延迟时间τ=1;同理,求得y方向变形时间序列的延迟时间τ=1。
|
图 1 C-C法计算x方向变形时间序列的时间延迟 Fig. 1 Time delay of the deformation time series of x direction calculated by C-C method |
若{x1, x2, …, xi, …}为实测的一组等间隔变形数据,取{x1, x2, …, xi, …}中部分数据构成一个m维子空间,空间中N个点表达为:
| $ \left\{ {\begin{array}{*{20}{l}} {{r_1} = \left( {{x_1},{x_2}, \cdots ,{x_m}} \right)}\\ {{r_2} = \left( {{x_2},{x_3}, \cdots ,{x_{m + 1}}} \right)}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots }\\ {{r_N} = \left( {{x_N},{x_{N + 1}}, \cdots ,{x_{m + N - 1}}} \right)} \end{array}} \right. $ | (10) |
令
| $ C(r) = \frac{1}{{{N^2}}}\sum\limits_{i,j = 1,i \ne j}^N \theta (r - |{r_i} - {r_j}|) $ | (11) |
式中,θ(x)指Heaviside函数,N为点的个数。
吸引子的关联维数计算公式为:
| $ {d_c} = \mathop {\lim }\limits_{r \to 0} \frac{{\ln C(r)}}{{\ln r}} $ | (12) |
分别求出不同嵌入维数m所对应的dC值。取dC值第一个到达平稳时的m估值作为嵌入维数,此时dC值可作为吸引子维数的估值,则m=2[d]+1。这就是嵌入维数估计的G-P算法。
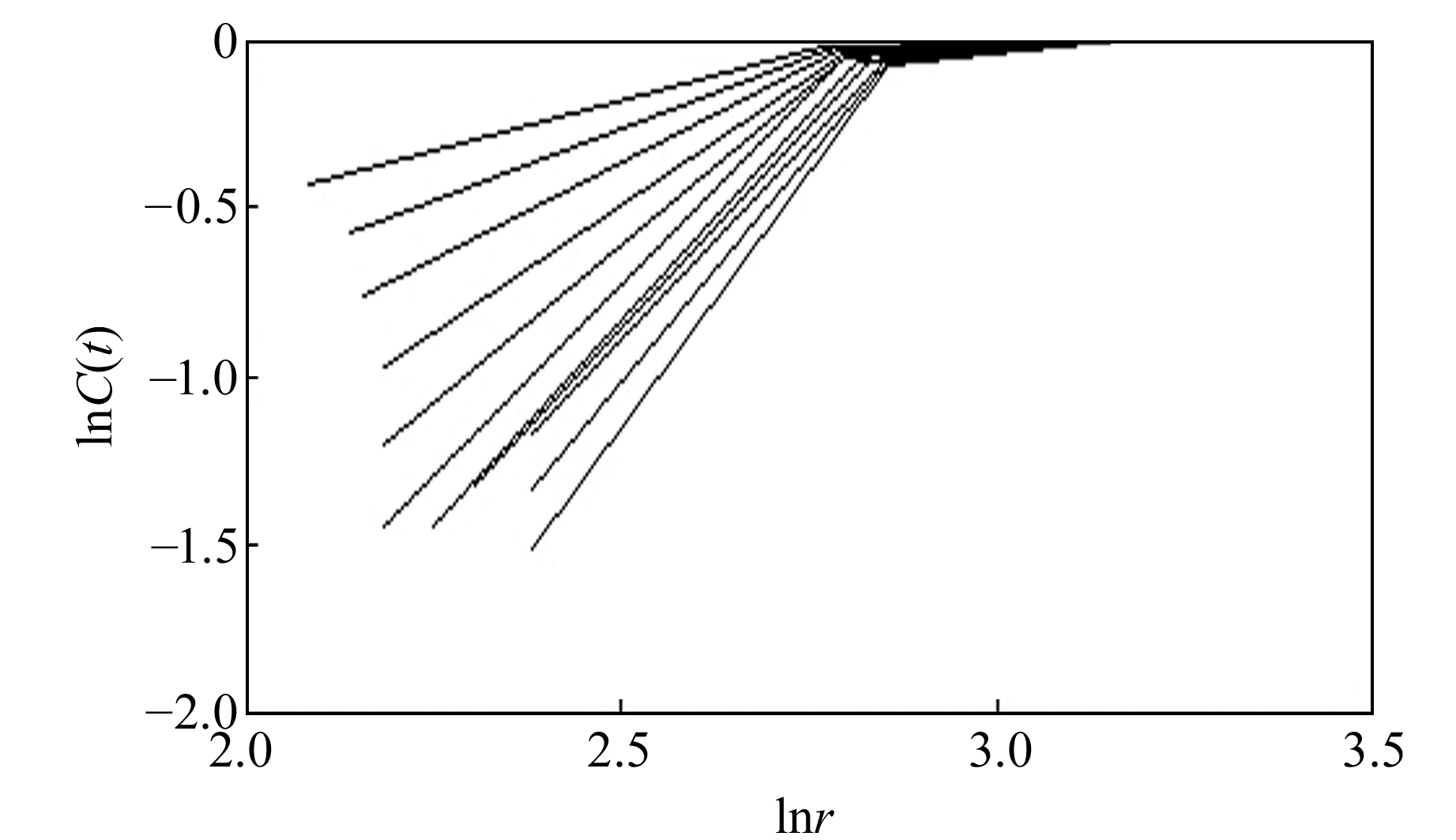
x方向时间延迟τ=1,设定维数m =2,3,…,12,分别绘制x方向变形时间序列饱和关联维数法(简称G-P法)的lnC(r)-lnr曲线(图 2),图中曲线自上而下对应于m=2,3,…,12。当维数增加到7时,lnC(r)与lnr的比值不再随m的增大发生变化,因此x方向嵌入维数为7。同理,求得y方向变形时间嵌入维数为7。
|
图 2 x方向变形时间序列lnC(r)-lnr图 Fig. 2 lnC(r)-lnr diagram of deformation time series of x direction |
重构相空间的目的是保持原先变形系统的几何结构,并与其具有等价的动力系统。相空间重构最重要的参数为时间延迟τ和嵌入维数m。延迟滞时重构的变形动力系统相空间简化模型[17-18]为:
| $ X(t) = (x(t),x(t - \tau ), \cdots ,x(t - (m - 1)\tau ) $ | (13) |
式中,m为嵌入维数,τ为时间延迟,t=1, 2, …, n。
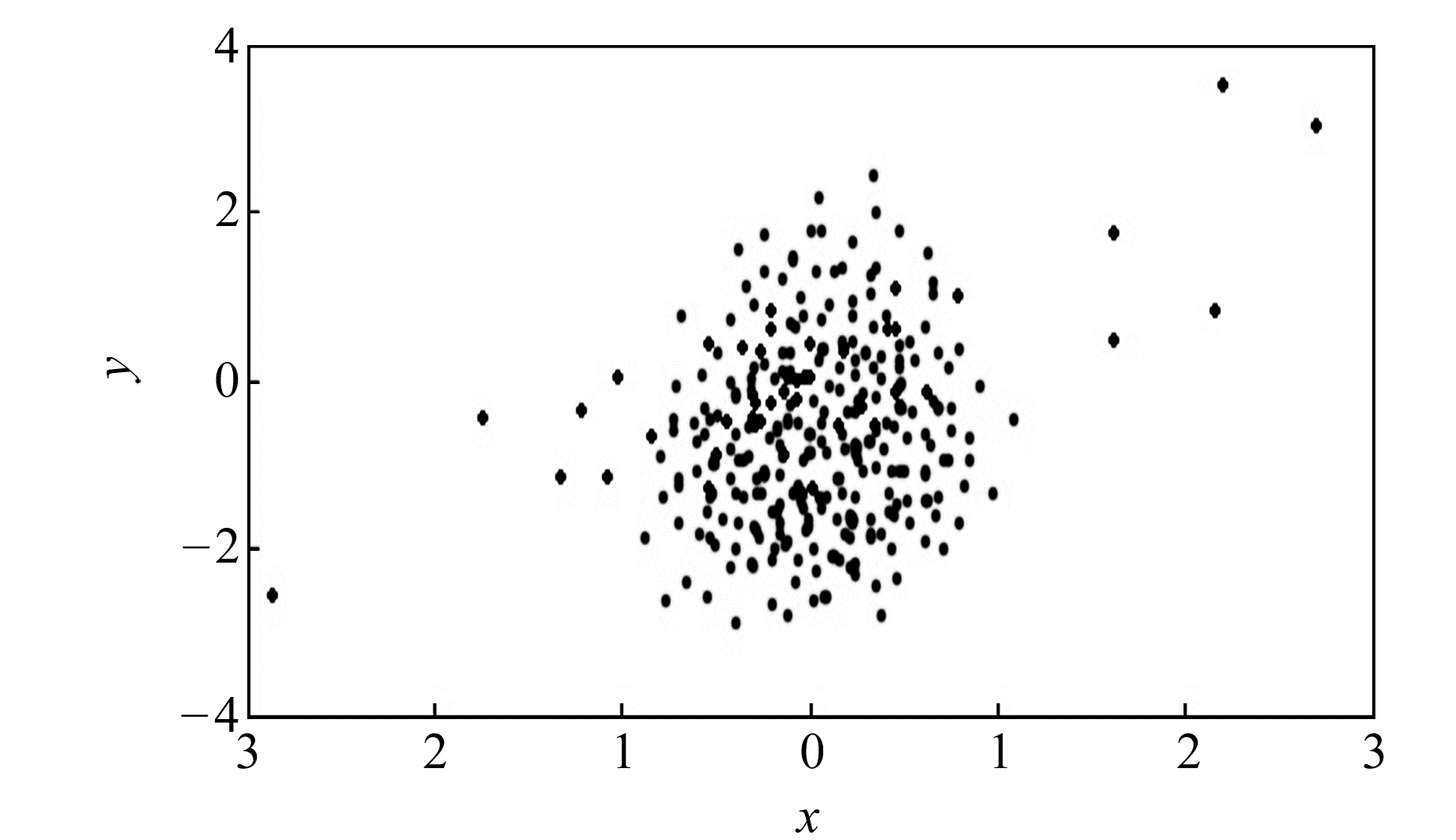
x方向和y方向最大Lyapunov指数之和为二维最大Lyapunov指数,即λ=λx+λy=0.029,故二维数据同样具有混沌特性。按时间延迟τ=1、m=7等参数对W1点水平位移时间序列进行二维相空间重构(图 3)。
|
图 3 水平位移二维相空间重构 Fig. 3 Two-dimensional phase space reconstruction of horizontal displacement |
RBF神经网络模型是一种3层前向网络,第1层为输入层,第2层为隐含层,第3层为输出层。其基本思想是通过隐含层将输入矢量转换到高维度空间,实现低维度空间内线性不可分问题在高维度空间内线性可分[6]。本文采用的RBF神经网络混沌预测模型的主要思想是通过混沌特征识别算法中得到的嵌入维数对输入数据进行相空间重构,得到一组输入样本,将其输入RBF神经网络模型,得到RBF神经网络的混沌预测值。用x(n)表示桥梁水平变形时间序列,X[i]为输入层第i个结点的输入,y为神经网络结点的输出,w为连接权重,f为非线性Sigmoidal函数,τ为时间延迟,则网络模型为:
| $ {X[i] = x(t + (i - 1)\tau )} $ | (14) |
| $ {y = \bar f\sum\limits_{i = 1}^m {(\omega [i]x[i])} } $ | (15) |
通过相空间重构得到输入层单元数为m、隐层单元数为k、输出单元数为1的网络拓扑结构m×k×1。
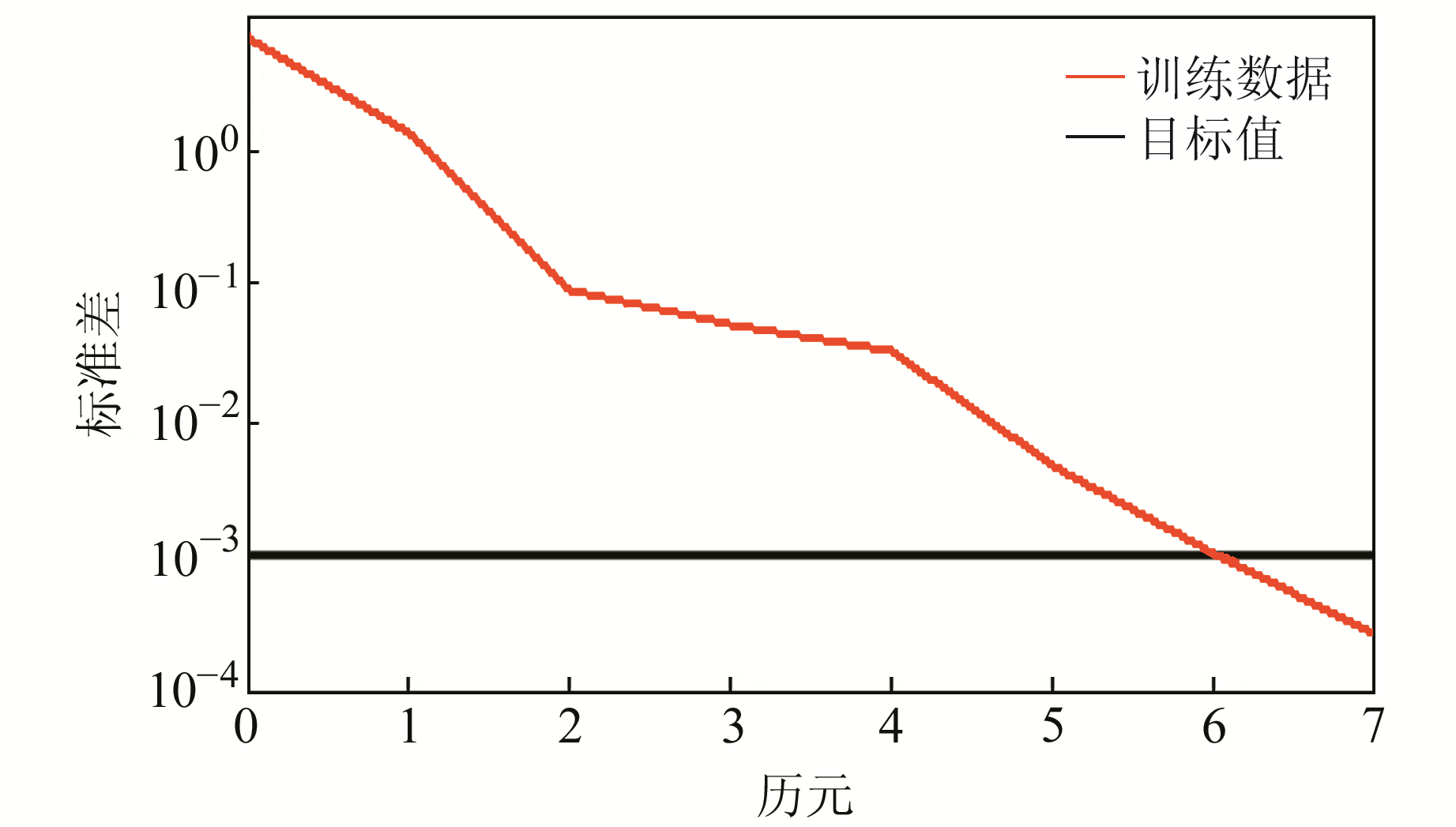
取W1点300期水平位移观测数据,前250期数据用来训练,后50期数据用来预测对比分析。对W1点x方向变形数据进行归一化处理,并将前250组数据作为训练样本,RBF神经网络误差曲线如图 4所示。由图可见,在网络训练过程中,只需6步就到达了目标标准差值0.001。
|
图 4 RBF神经网络误差曲线 Fig. 4 RBF neural network error curve |
对后输入的50个数据进行相空间重构,组成一个N-(m-1)τ样本输入,其中τ=1,m=7,输入样本点为44个,第t个输入样本为:
| $ \begin{array}{*{20}{c}} {X(t) = \{ x(t),x(t + 1),x(t + 2),}\\ {x(t + 3),x(t + 4),x(t + 5),x(t + 6)\} } \end{array} $ | (16) |
将44个输入样本输入RBF神经网络预测模型,计算得到RBF神经网络混沌预测值。
2.2 RBF神经网络混沌预测与最大Lyapunov指数混沌时间序列预测的比较将RBF神经网络混沌预测与基于最大Lyapunov指数的混沌时间序列预测的误差进行比较,分析两种预测模型的精度。
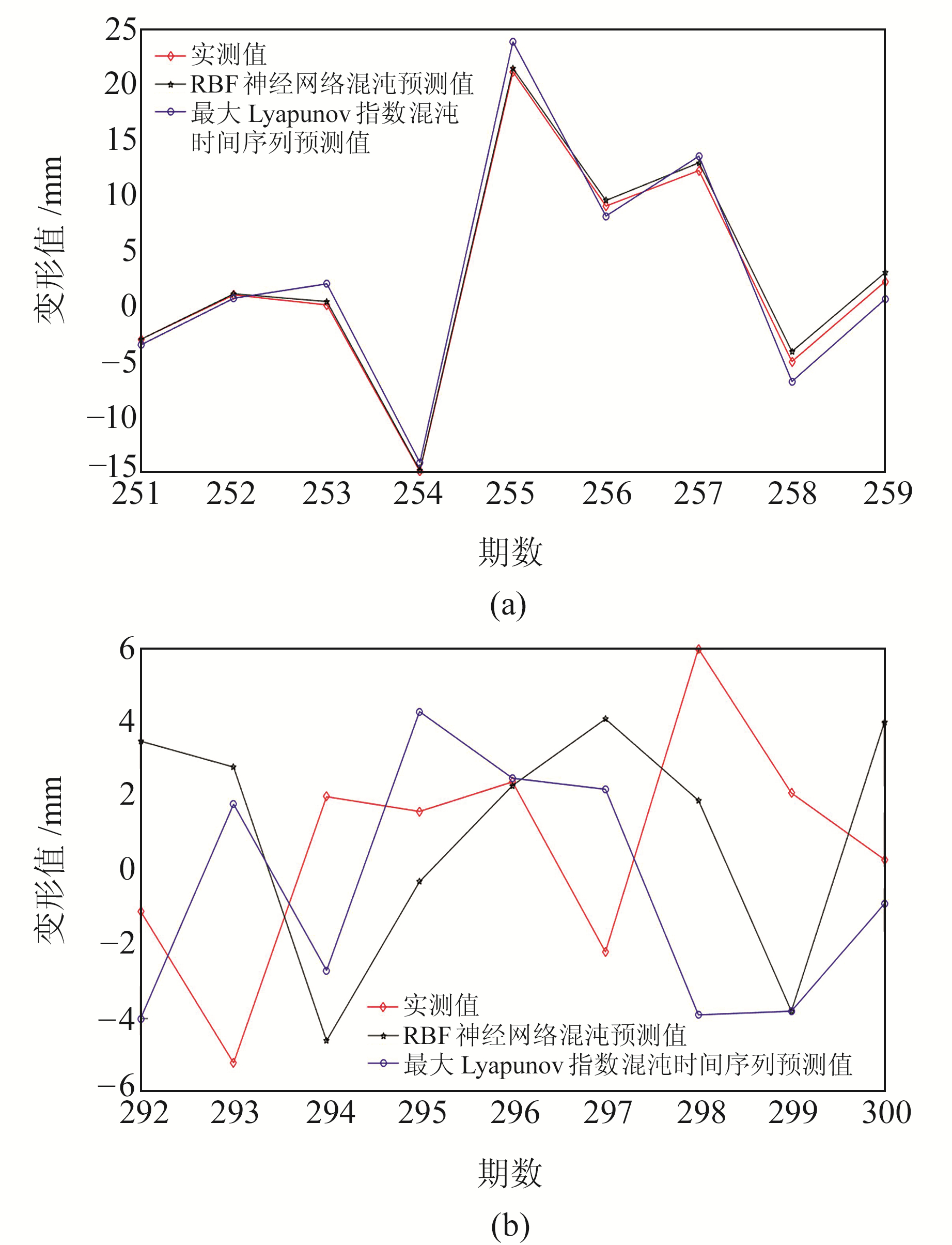
对于x方向的变形,对后50期数据进行预测,第251~259期数据预测结果如表 1所示,实测值与基于RBF神经网络的预测值和基于最大Lyapunov指数的混沌时间序列预测值对比如图 5(a)所示。
|
|
表 1 x方向预测值与实测值对比 Tab. 1 Comparison of the measured and predicted values of x direction |
|
图 5 x方向实测值与预测值对比 Fig. 5 Comparison of the measured and predicted values of x direction |
由表 1绝对差和RMSE对比分析可知,基于RBF神经网络混沌预测模型的预测值比基于最大Lyapunov指数混沌时间序列预测模型的预测值要更接近于实测值且精度明显提高。由图 5(b)可见,随着观测期数的增加,预测值逐渐偏离实测值,残差呈现逐渐变大的趋势。这证明本文基于RBF神经网络所建立的混沌预测模型在短期预测的情况下,比基于最大Lyapunov指数的混沌时间序列预测模型得到的预测结果更接近于真实值。这从一个方面证明混沌预测对时间序列只能进行短期预测。
3 结语1) 根据跨海大桥系统受外界影响扰动的特点,提出其变形伴有混沌现象。根据混沌理论,对桥梁变形时间序列进行混沌特性识别,确定青岛胶州湾跨海大桥监测数据表现为混沌性。
2) 运用C-C法计算时间序列的延迟时间τ,用G-P方法求得最佳嵌入维数m,通过求取的时间延迟和最佳嵌入维数对桥梁变形监测数据进行相空间重构,建立桥梁变形时间序列混沌性识别的理论模型与方法。
3) 基于RBF神经网络建立混沌时间序列预测模型,并通过MATLAB语言实现其算法。
4) 对基于RBF神经网络的混沌时间序列桥梁变形预测值与基于最大Lyapunov指数的混沌时间序列预测值以及实测数据进行对比分析,结果表明,基于RBF神经网络建立的混沌时间序列预测模型的预测结果比基于最大Lyapunov指数的混沌时间序列预测模型的预测结果要好,且短期预测效果好。
| [1] |
刘娜.基于混沌时间序列的桥梁变形预测分析[D].青岛: 山东科技大学, 2011 (Liu Na. The Analysis of Bridge Deformation Prediction Based on Chaotic Time Series[D]. Qingdao: Shandong University of Science and Technology, 2011)
(  0) 0) |
| [2] |
尹燕运.混沌时间序列预测在桥梁监测中的应用[D].青岛: 山东科技大学, 2014 (Yin Yanyun. The Applications of Chaotic Time Series Prediction in Bridge Monitoring[D]. Qingdao: Shandong University of Science and Technology, 2014)
(  0) 0) |
| [3] |
栾元重, 栾亨宣, 马德鹏, 等. 桥梁变形数据小波去噪与混沌预测[J]. 大地测量与地球动力学, 2013, 33(5): 133-135 (Luan Yuanzhong, Luan Hengxuan, Ma Depeng, et al. Wavelet Denoising and Chaos Prediction of Bridge Deformation Data[J]. Journal of Geodesy and Geodynamics, 2013, 33(5): 133-135)
(  0) 0) |
| [4] |
栾元重, 曹丁涛, 徐乐年, 等. 变形观测与动态预报[M]. 北京: 气象出版社, 2001 (Luan Yuanzhong, Cao Dingtao, Xu Lenian, et al. Dynamic Deformation Observation and Forecast[M]. Beijing: Meteorological Press, 2001)
(  0) 0) |
| [5] |
路明文, 贾凤君, 韦连波. 湖区开采观测技术[M]. 北京: 地震出版社, 2012 (Lu Mingwen, Jia Fengjun, Wei Lianbo. Lake District Mining Observation Technology[M]. Beijing: Seismological Press, 2012)
(  0) 0) |
| [6] |
徐耀群, 孙明. 混沌神经网络及其应用[M]. 哈尔滨: 黑龙江大学出版社, 2012 (Xu Yaoqun, Sun Ming. Chaotic Neural Network and Its Application[M]. Harbin: Heilongjiang University Press, 2012)
(  0) 0) |
| [7] |
张琪昌, 王洪礼, 竺致文, 等. 分岔与混沌理论及应用[M]. 天津: 天津大学出版社, 2005 (Zhang Qichang, Wang Hongli, Zhu Zhiwen, et al. Bifurcation and Chaotic Theory and Its Application[M]. Tianjin: Tianjin University Press, 2005)
(  0) 0) |
| [8] |
刘式达, 梁福明, 刘式适, 等. 自然科学中的混沌和分形[M]. 北京: 北京大学出版社, 2003 (Liu Shida, Liang Fuming, Liu Shishi, et al. Chaos and Fractal in Natural Science[M]. Beijing: Peking University Press, 2003)
(  0) 0) |
| [9] |
陈铿, 韩伯棠. 混沌时间序列分析中的相空间重构技术综述[J]. 计算机科学, 2005, 32(4): 67-70 (Chen Keng, Han Botang. A Survey of State Space Reconstruction of Chaotic Time Series Analysis[J]. Computer Science, 2005, 32(4): 67-70)
(  0) 0) |
| [10] |
李海波.混沌时间序列预测应用研究[D].合肥: 中国科学技术大学, 2009 (Li Haibo. Research on the Application of Chaotic Time Series Prediction[D].Hefei: University of Science and Technology of China, 2009)
(  0) 0) |
| [11] |
于国新.西康铁路秦岭隧道区岩体结构面分布规律的混沌特征及围岩分级预测[D].北京: 北京交通大学, 2009 (Yu Guoxin. The Chaotic Character on Distribution Prinple of Structural Surface of Rock Mass and Predicting to Classification of Wall Rock in Qinling Tunnel of Xikang Railway[D]. Beijing: Beijing Jiaotong University, 2009)
(  0) 0) |
| [12] |
侯媛彬, 杜京义, 汪梅. 神经网络[M]. 西安: 西安电子科技大学, 2007 (Hou Yuanbin, Du Jingyi, Wang Mei. Neural Network[M]. Xi'an: Xidian University, 2007)
(  0) 0) |
| [13] |
周金勇.混沌时间序列预测模型研究[D].武汉: 武汉理工大学, 2009 (Zhou Jinyong. Research on Predictive Model of Chaotic Time Series[D]. Wuhan: Wuhan University of Technology, 2009)
(  0) 0) |
| [14] |
孙明.基于小波和迟滞的混沌神经网络及其应用[D].哈尔滨: 哈尔滨工程大学, 2010 (Sun Ming. Chaotic Neural Networks Based on Wavelet and Hysteresis and Their Applications[D]. Harbin: Harbin Engineering University, 2010)
(  0) 0) |
| [15] |
魏海坤. 神经网络结构设计的理论与方法[M]. 北京: 国防工业出版社, 2005 (Wei Haikun. Theory and Method of Neural Network Structure Design[M]. Beijing: National Defense Industry Press, 2005)
(  0) 0) |
| [16] |
Grassberger P, Procaccia I. Estimation of the Kolmogorov Entropy from a Chaotic Signal[J]. Physics Review A, 1983, 28: 2 591-2 593 DOI:10.1103/PhysRevA.28.2591
(  0) 0) |
| [17] |
Cao L Y. Practical Method for Determining the Minimum Embedding Dimension of a Scalar Time Series[J]. Physica D: Nonlinear Phenomena, 1997, 110(1-2): 43-50 DOI:10.1016/S0167-2789(97)00118-8
(  0) 0) |
| [18] |
Abarbanel H D I, Brown R, Sidorowich J J, et al. The Analysis of Observed Chaotic Data in Physical Systems[J]. Reviews of Modern Physics, 1993, 65(4): 1 331-1 392
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41


