2. 东华理工大学江西省数字国土重点实验室,南昌市广兰大道418号,330013
变形监测数据包括真实数据和观测噪声,若直接利用原始监测数据进行建模预测难以获得满意结果。在工程应用中一般认为,噪声信号和干扰信号主要分布于高频信号中,而相对平稳的低频信号则被认为是有用的真实信号[1-2]。甘若等[3]运用改进小波阈值函数处理危岩变形沉降数据,能够有效去除噪声,提升信噪比;范千等[4]采用EMD方法降噪处理建筑物形变观测数据,从而获得其形变特征。但小波分析存在小波基选取及确定分解级数等问题,EMD方法存在端点效应与模式混叠等缺点[5]。Wu等[6]通过在原始信号中添加不同的高斯白噪声,提出整体经验模态分解(EEMD)方法,减弱了模式混叠现象的影响,但容易产生较大的重构误差;补充整体经验模态分解(CEEMD)[7]方法尽管提高了完备性和重构精度,但由于集成次数过多导致计算效率低下。
为解决上述问题,Dragomiretskiy等[8]提出一种新型自适应复杂信号分解方法——变分模态分解(VMD)方法,Ram等[9]验证该方法可缓解模态混叠和边界效应,且在鲁棒性、运算效率等方面具有明显优势。同时,根据样本熵(SE)能够反映时间序列复杂程度的特性,本文将其与VMD结合形成一种应用于变形监测数据的新降噪方法,并通过仿真算例和工程实例验证了VMD-SE方法的有效性。
1 算法原理 1.1 VMD算法不同于EMD方法对信号的剥离,VMD算法是通过设置模态数k、惩罚参数α和上升步长τ等参数将信号分解成k个中心频率为ωk的模态函数uk,其实质为变分问题的构造和求解。VMD算法构造的约束变分问题可表示为:
| $ \begin{array}{*{20}{c}} {\mathop {\min }\limits_{\left\{ {{u_k}} \right\},\left\{ {{\omega _k}} \right\}} \left\{ {\sum\limits_k {\left\| {\partial t\left[ {\left( {\delta (t) + \frac{{\rm{j}}}{{{\rm{ \mathsf{ π} }}t}}} \right){u_k}(t)} \right]{{\rm{e}}^{ - {\rm{j}}{\omega _k}t}}} \right\|_2^2} } \right\}}\\ {{\rm{ s}}{\rm{. t}}{\rm{. }}\sum\limits_k {{u_k}} = f} \end{array} $ | (1) |
式中,f为原始信号,uk为模态函数,ωk为各模态的实际中心频率,e-jωkt为每个解析信号的预估中心频率。
为求解该约束变分模型的最优解,引入拉格朗日乘子λ(t)和二次惩罚因子α,使其转变为无约束变分问题,得到增广拉格朗日表达式为:
| $ \begin{array}{*{20}{c}} {L\left( {\left\{ {{u_k}} \right\},\left\{ {{\omega _k}} \right\},\lambda } \right) = }\\ {\alpha \sum\limits_k {\left\| {\partial t\left[ {\left( {\delta (t) + \frac{{\rm{j}}}{{{\rm{ \mathsf{ π} }}t}}} \right){u_k}(t)} \right]{{\rm{e}}^{ - {\rm{j}}{\omega _k}t}}} \right\|_2^2} + }\\ {\left\| {f(t) - \sum\limits_k {{u_k}} (t)} \right\|_2^2 + \left\langle {\lambda (t),f(t) - \sum\limits_k {{u_k}} (t)} \right\rangle } \end{array} $ | (2) |
采用交替方向乘子算法,通过迭代更新求得增广拉格朗日表达式的鞍点,即为式(1)最优解。
1.2 样本熵针对VMD算法不能判定噪声主导的带限固有模态函数(BIMF)的问题,利用样本熵(SE)能够反映信号复杂程度的特性,将其作为判断噪声信号与监测数据有用信号的标准,有效识别形变监测数据有用成分与噪声成分的分界。样本熵的计算过程[10]为:
1) 对于长度为N的监测数据信号x(i),按顺序构建m维矢量Xi:
| $ \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{X}}_i} = [x(i)\quad x(i + 1) \cdots x(i + m - 1)],}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,2, \cdots ,N - m + 1} \end{array} $ | (3) |
2) 定义Dji为矢量Xi与Xj之间的距离,即两者对应元素差值绝对值的最大值,则:
| $ \begin{array}{*{20}{l}} {D_j^i = {\rm{max}}\{ |x(i + k) - x(j + k)|,}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\rm{ }} < {\rm{ }}k{\rm{ }} < {\rm{ }}m - 1\} } \end{array} $ | (4) |
3) 设定相似容限r,记Ci为Dji < r的数量,同时计算Ci与距离总数N-m-1的比值,即
| $ C_i^n(r) = \frac{{{C_i}}}{{N - m - 1}},i = 1,2, \cdots ,N - m $ | (5) |
4) 求Cim(r)的均值:
| $ {C^m}(r) = \frac{1}{{N - m}}\sum\limits_{i = 1}^{N - m} {C_i^m} $ | (6) |
5) 更新维数,令m=m+1,并重复上述步骤,即可得到Cm+1(r)。
6) 理论上,此时的样本熵为:
| $ {\rm{SE}}(m,r) = \mathop {\lim }\limits_{N \to m} \left[ { - \ln \frac{{{C^{m + 1}}(r)}}{{{C^m}(r)}}} \right] $ | (7) |
当N为有限数时,式(7)可表示为:
| $ \begin{array}{*{20}{c}} {{\rm{SE}}(m,r,N) = \mathop {\lim }\limits_{N \to m} \left[ { - \ln \frac{{{C^{m + 1}}(r)}}{{{C^m}(r)}}} \right] = }\\ {\ln {C^m}(r) - \ln {C^{m + 1}}(r)} \end{array} $ | (8) |
其中,参数m及r的设定会对样本熵(SE)的值产生较大影响,一般令m=2,r取原始数据标准差(SD)的0.1~0.25倍[11],本文取0.15倍。SE值越大反映信号的随机程度越高,包含的噪声成分越多;相反,SE值越小说明信号的规律性越强,包含的噪声成分越少[12]。
为能较为准确地判断出噪声分量与有用信号分量的界线,阈值的设定尤为重要。文献[12]中将SE阈值设定为0.2,用于区分微地震信号与噪声的分界,取得了不错的效果。但阈值设置得过小易将有效分量误判为噪声分量,导致过度降噪使信号失真;反之,若阈值设置过大也可能对降噪结果产生不利影响。考虑到不同变形体的变形规律差异较大,同时为提高方法的适用性,本文将SE阈值设定为0.5,以尽可能避免有用的非线性变形特征信号被划分为噪声信号而遭滤除。
1.3 基于VMD算法的变形监测数据降噪1) 设置VMD算法的相关参数,如模态数k、惩罚因子α及上升步长τ等;
2) 原始观测数据经VMD算法分解为k个BIMF,并计算各BIMF的样本熵;
3) 将样本熵大于设定阈值的高频BIMF作为随机噪声成分进行滤除;
4) 重构剩余的BIMF,获得降噪处理后的观测数据序列。
2 仿真模拟信号分析变形监测信号包含多种噪声,且频率分布范围较广,为保证与实际情况相符,构造复合仿真信号进行模拟实验。仿真信号的采样频率为1 Hz,采样个数为1 024,包括3个周期项和1个趋势项及随机噪声项(图 1),其表达式为:
| $ \begin{array}{*{20}{c}} {Y = 4\sin (2{\rm{ \mathsf{ π} }}t/500) + 3\sin (2{\rm{ \mathsf{ π} }}t/200) + }\\ {2\sin (2{\rm{ \mathsf{ π} }}t/40) + 0.001t + {\rm{ noise }}} \end{array} $ | (9) |

|
图 1 仿真信号 Fig. 1 Simulation signal |
为更好地展现本文方法的降噪效果,分别设置3组标准差噪声水平为0.5、1.0和1.5的高斯白噪声数据,并设置4种实验方案:方案1,未对噪声进行任何处理;方案2,采用EEMD方法降噪;方案3,采用CEEMD方法降噪;方案4,采用本文提出的VMD-SE方法降噪。为对比分析不同算法的处理效果,选用信噪比(SNR)和平滑度(r)[13]指标进行降噪质量评价:
| $ {\rm{SNR}} = 10{\rm{lg}}\left( {\frac{{{P_{\rm{s}}}}}{{{P_{\rm{n}}}}}} \right) $ | (10) |
| $ r = \frac{{\sum\limits_{t = 1}^{N - 1} {{{[\hat f(t + 1) - \hat f(t)]}^2}} }}{{\sum\limits_{t = 1}^{N - 1} {{{[f(t + 1) - f(t)]}^2}} }} $ | (11) |
式中,Ps为有效信号成分的功率,Pn为噪声成分的功率,f(t)为原始信号,
实际变形观测数据中有用成分和噪声的功率均未知,采用信噪比进行降噪质量评价是不合理的,因此引入降噪误差比(dnSNR)[14-15]评价降噪性能,其表达式为:
| $ {\rm{dnSNR}} = 10\lg \left( {\frac{{{P_{{\rm{s + n}}}}}}{{{P_{\rm{g}}}}}} \right) $ | (12) |
式中,Ps+n为含噪序列功率,Pg为滤除的噪声功率。
一般认为,SNR越高降噪质量越好,dnSNR及r的值越小降噪效果越显著。EEMD方法及CEEMD方法降噪的关键在于准确识别噪声分量与有效信号分量的分界,本文采用相关系数法[16-17]确定信噪分界。首先计算各阶IMF与原始信号的相关系数,然后寻找相关系数首个极小值出现的第k个IMF,将前k个IMF视为噪声IMF,最后从k+1个IMF开始重构,即可获得降噪后的信号序列。
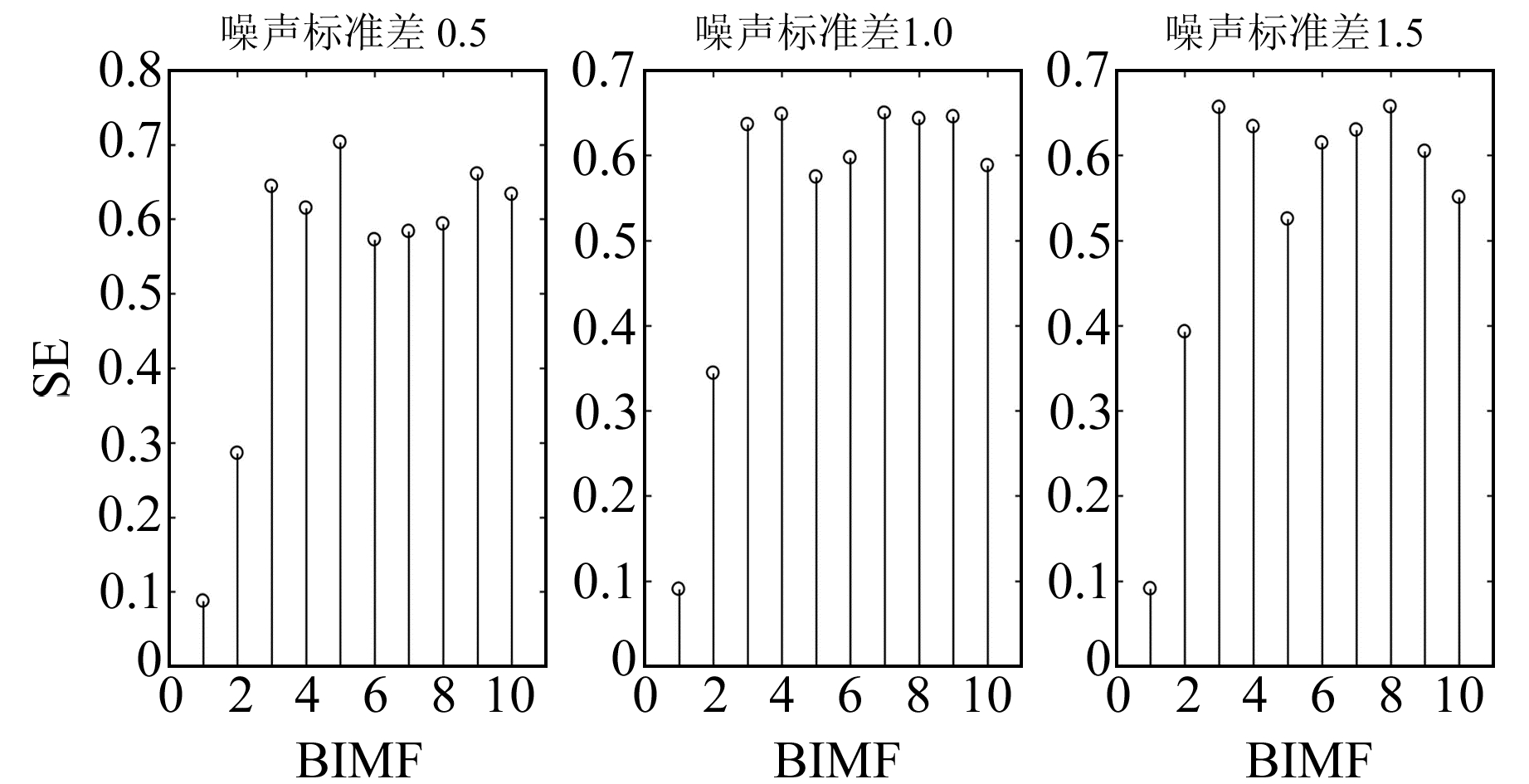
EEMD方法及CEEMD方法的基本参数设置参考文献[6],VMD算法中模态数k为10(与EEMD模态个数保持一致),惩罚参数α为3 000,上升步长τ为0。图 2为加入不同标准差噪声的仿真信号经VMD法分解后各BIMF的样本熵。
|
图 2 不同噪声标准差下各BIMF样本熵 Fig. 2 Sample entropy of each BIMF with different noise standard deviations |
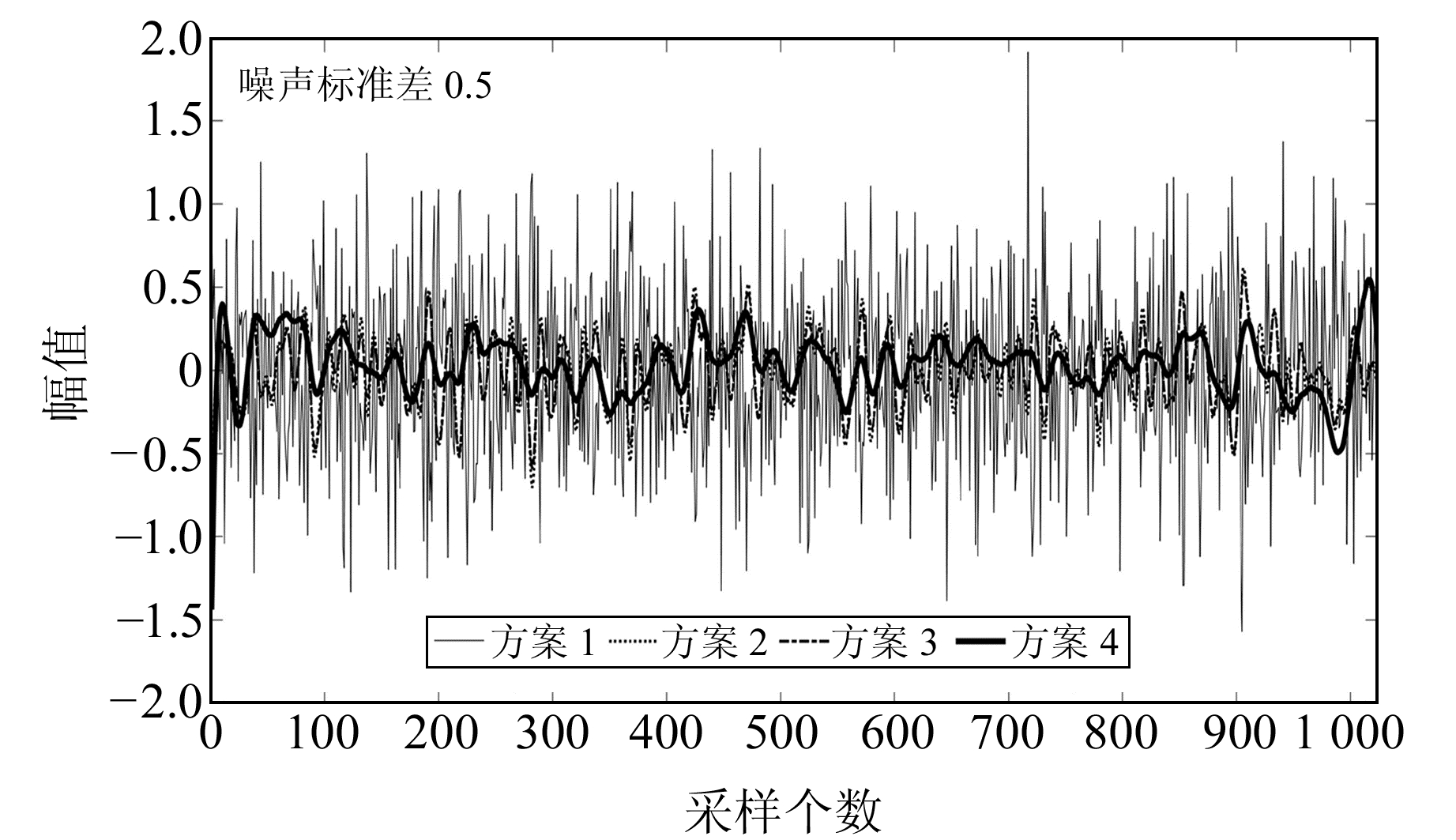
由图 2可以看出,在不同噪声水平下,BIMF1和BIMF2的样本熵值均小于0.5,对应为低频有用信号分量;而BIMF3~BIMF10的SE值均大于0.5,对应为高频噪声或虚假模态分量。限于篇幅,本文仅给出噪声标准差为0.5时采用4种方案处理后获得的结果与不含噪声的仿真信号残差,结果见图 3。表 1统计了不同噪声水平下EEMD、CEEMD及VMD-SE方法的SNR、r及dnSNR值。
|
图 3 4种方案降噪后信号与不含噪声的仿真信号的残差 Fig. 3 Residuals of the noise-reduced signals and simulated signals without noise of the four schemes |
|
|
表 1 3种方案降噪评价指标对比 Tab. 1 Comparison of noise reduction evaluation indexes of the three schemes |
由图 3可知,经EEMD与CEEMD降噪处理后的信号与原始参考信号相比存在一定偏差,CEEMD的整体降噪效果略优于EEMD,而采用VMD-SE处理后的信号与原始参考信号的偏差最小。从表 1可以看出,在相同噪声水平下,本文方法的SNR值高于EEMD方法和CEEMD方法,平滑度r和dnSNR值也均小于其他两种方法,说明在不同噪声水平下本文提出的新方法的降噪性能具有一定优势。
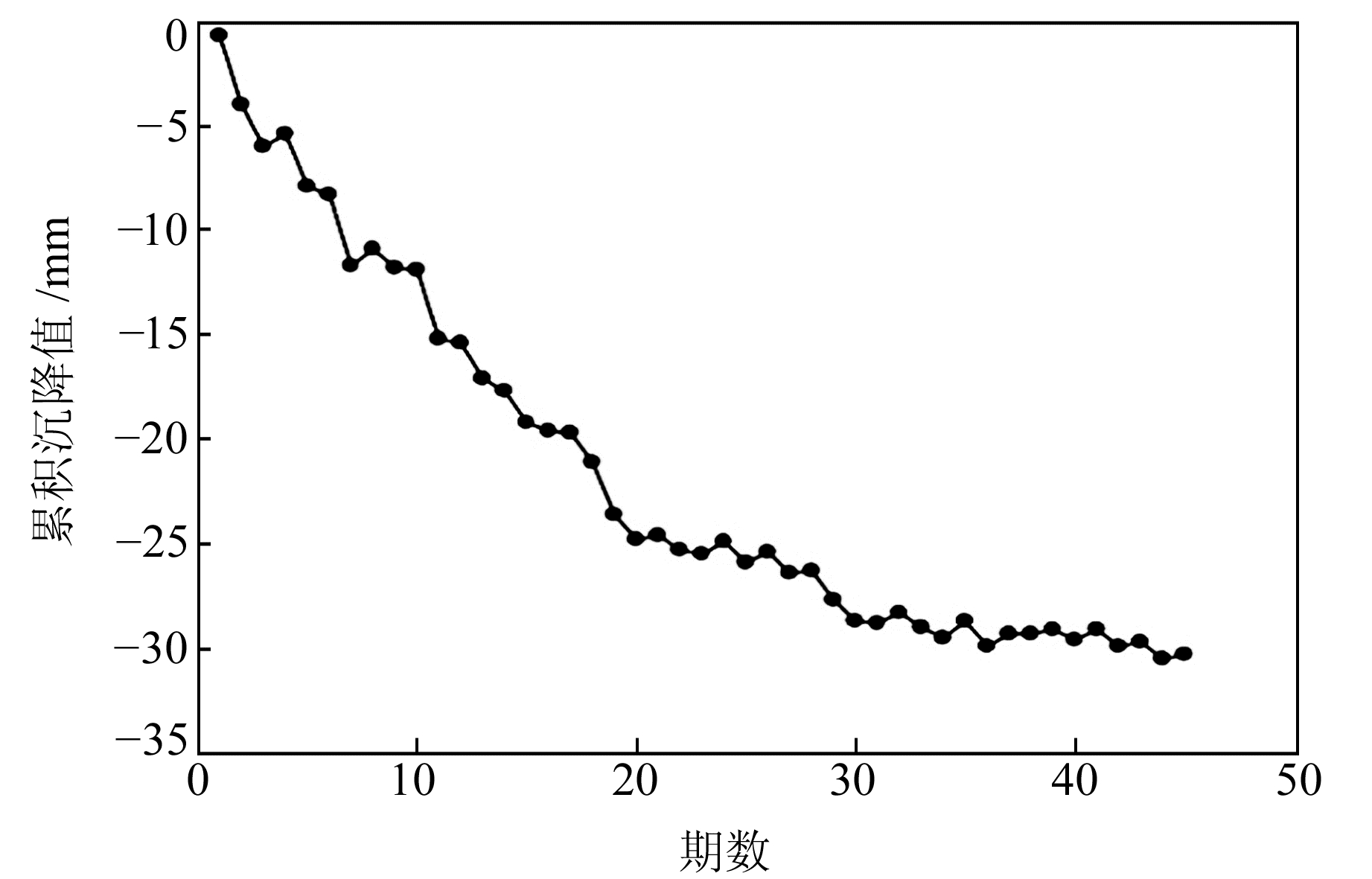
3 实例与分析某地铁车站基坑由于受到各种不确定因素的影响,如毗邻众多建筑物、场地属于不良地质及施工范围内的城市地下综合管线错综复杂等,施工安全问题非常突出,需随时掌握基坑的动态变化。选取2015-08~2019-04期间沉降监测点M17的45期观测数据进行实验[18],变形曲线见图 4。
|
图 4 监测点M17沉降变形曲线 Fig. 4 Settlement deformation curve of monitoring point M17 |
由图 4可知,该车站基坑沉降实测数据存在较为明显的随机性和不规则性。由于基坑在开挖过程受各种干扰因素的影响,观测数据中包含一定的随机噪声,若直接采用原始观测数据进行建模分析和预测,预测效果往往不佳。这是由于观测噪声会对建模和预测产生较大的干扰,因此需要对原始数据序列进行降噪处理,提高监测数据的质量,进而提高变形预测的精度。
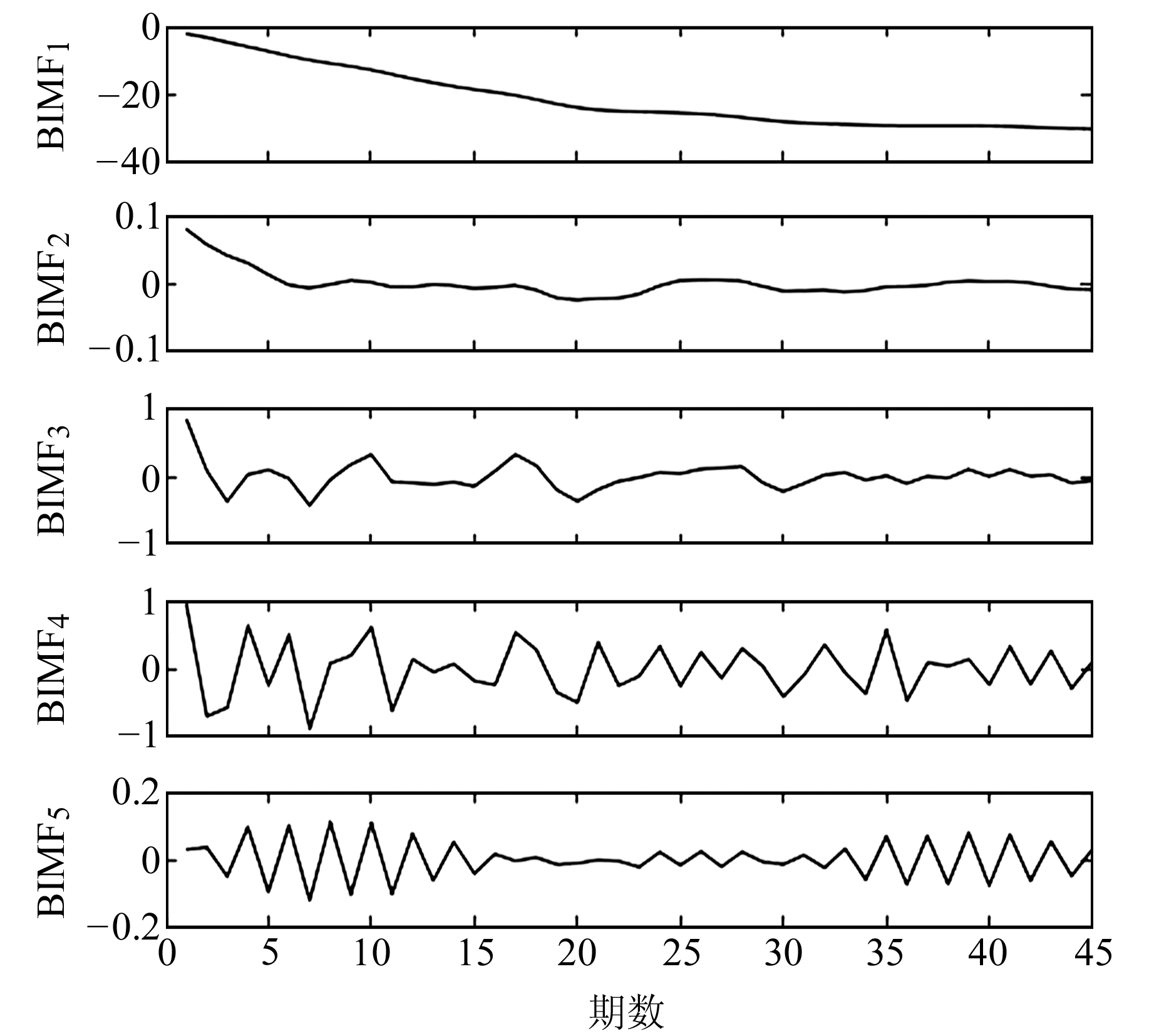
分别采用EEMD、CEEMD及VMD-SE方法对车站基坑沉降序列进行降噪处理,其中EEMD和CEEMD方法的相关参数设置与仿真实验一致。由于车站基坑沉降序列的信噪比较大,EMD法分解后得到的第1阶IMF就包含了绝大部分的噪声,从第2阶IMF开始重构获得降噪后序列[16]。同理,采用EEMD和CEEMD方法进行处理时,也均从第2阶IMF开始重构序列,获取降噪后序列。利用VMD法对观测数据进行分解时,设置模态数k为5(与EEMD分解模态个数保持一致);对于二次惩罚参数α,考虑到基坑序列的噪声水平,同时顾及分解之后序列的保真度[19],经过反复试算,最终确定为0.08,上升步长τ为0。VMD结果见图 5,各个BIMF的样本熵见图 6。
|
图 5 基坑沉降观测数据VMD结果 Fig. 5 VMD results of foundation pit settlement observation data |

|
图 6 各个BIMF的样本熵 Fig. 6 Sample entropy of each BIMF |
由图 5和图 6可以看出,VMD方法将基坑沉降时间序列分解成5个由低频至高频的BIMF分量,BIMF1的样本熵值为0.10,其整体趋势与原始监测数据基本保持一致;而BIMF2~BIMF5则表现出较强的随机性,对应的样本熵值均大于0.5,将其作为噪声剔除,以抑制随机噪声对真实数据的干扰。表 2为基于不同方法的降噪性能评价指标对比。
|
|
表 2 降噪性能评价指标 Tab. 2 Evaluation index of noise reduction performance |
由表 2可知,VMD-SE降噪方法的平滑度r和dnSNR值均小于另外两种方法,表明新方法的降噪效果最佳。为进一步反映各方法的降噪效果,分别将未经降噪和采用不同方法降噪后获得的前10期沉降观测数据利用高斯过程回归[20](GPR)建立滚动预测模型,以11~45期监测数据作为测试样本数据,用于验证各个预测模型的精度。各方法的预测结果见图 7,精度评定见表 3。

|
图 7 各方法的预测结果 Fig. 7 Forecast results of each method |
|
|
表 3 预测精度评定 Tab. 3 Evaluation of prediction accuracy |
由图 7可以看出,GPR模型采用未经降噪处理的原始数据进行训练及预测,预测结果的波动性较大;EEMD-GPR和CEEMD-GPR模型去除了一部分观测噪声,预测精度有一定的提高,且CEEMD-GPR模型的预测性能优于EEMD-GPR模型;VMD-SE-GPR模型的预测结果与实测数据最为接近,与表 3的统计结果一致,且与文献[18]的WEPM模型相比,预测结果的均方根误差(RMSE)仅为0.44 mm,减小了66.4%。同时与其他方法相比,VMD-SE-GPR模型的预测精度评定指标均为最优,RMSE分别减小了47.6%、38%和18.5%,表明该模型的整体预测精度最高,进一步验证了VMD-SE方法的降噪质量最好,在尽可能保证原始监测数据有用成分的基础上最大限度地滤除了噪声。
4 结语本文依据变分模态分解和样本熵各自的优势,提出VMD-SE变形监测数据降噪方法,并通过仿真算例对比分析其信噪比、平滑度、降噪误差比等指标,证实该方法降噪性能优于EEMD方法和CEEMD方法。同时,利用本文方法处理地铁车站基坑变形观测数据,降低了随机噪声信号的干扰影响,有效改善了数据质量,使预测精度得到较大提高,对形变分析具有一定的参考意义。但VMD中分解模态个数k和二次惩罚参数α的预设均会影响最终的分解结果,因此在实际工程应用中如何获取k和α的最佳参数组合,从而得到最优的分解结果,值得进一步深入研究。
| [1] |
梁桂兰, 徐卫亚, 谈小龙, 等. 岩石高边坡安全监测数据的小波变换去噪处理[J]. 岩石力学与工程学报, 2008, 27(9): 1 837-1 844 (Liang Guilan, Xu Weiya, Tan Xiaolong, et al. Denoising Processing of Safety Monitoring Data for High Rock Slope Based on Wavelet Transform[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(9): 1 837-1 844)
(  0) 0) |
| [2] |
戴吾蛟, 丁晓利, 朱建军, 等. 基于经验模式分解的滤波去噪法及其在GPS多路径效应中的应用[J]. 测绘学报, 2006, 35(4): 321-327 (Dai Wujiao, Ding Xiaoli, Zhu Jianjun, et al. EMD Filter Method and Its Application in GPS Multipath[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(4): 321-327 DOI:10.3321/j.issn:1001-1595.2006.04.005)
(  0) 0) |
| [3] |
甘若, 陈天伟, 郑旭东, 等. 改进的小波阈值函数对变形监测数据的去噪研究[J]. 大地测量与地球动力学, 2020, 40(1): 17-22 (Gan Ruo, Chen Tianwei, Zheng Xudong, et al. Research on Denoising of Deformation Monitoring Data by Improved Wavelet Threshold Function[J]. Journal of Geodesy and Geodynamics, 2020, 40(1): 17-22)
(  0) 0) |
| [4] |
范千, 方绪华. 基于经验模式分解消噪的高层建筑物变形监测数据处理方法[J]. 江南大学学报:自然科学版, 2010, 9(5): 555-558 (Fan Qian, Fang Xuhua. Method of Deformation Monitoring Data Processing for High-Rise Building Based on Empirical Mode Decomposition Denoising[J]. Journal of Jiangnan University: Natural Science Edition, 2010, 9(5): 555-558 DOI:10.3969/j.issn.1671-7147.2010.05.011)
(  0) 0) |
| [5] |
董振川.基于EMD的变形监测数据去噪与变形趋势提取研究[D].成都: 西南交通大学, 2018 (Dong Zhenchuan. Research on Denoising and Deformation Trend Extraction of Deformation Monitoring Data Based on Empirical Mode Decomposition[D]. Chengdu: Southwest Jiaotong University, 2018)
(  0) 0) |
| [6] |
Wu Z H, Huang N E, Chen X Y. The Multi-Dimensional Ensemble Empirical Mode Decomposition Method[J]. Advances in Adaptive Data Analysis, 2009, 1(3): 339-372 DOI:10.1142/S1793536909000187
(  0) 0) |
| [7] |
Yeh J R, Shieh J S, Huang N E. Complementary Ensemble Empirical Mode Decomposition: A Novel Noise Enhanced Data Analysis Method[J]. Advances in Adaptive Data Analysis, 2010, 2(2): 135-156 DOI:10.1142/S1793536910000422
(  0) 0) |
| [8] |
Dragomiretskiy K, Zosso D. Variational Mode Decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544
(  0) 0) |
| [9] |
Ram R, Mohanty M N. Comparative Analysis of EMD and VMD Algorithm in Speech Enhancement[J]. International Journal of Natural Computing Research, 2017, 6(1): 17-35
(  0) 0) |
| [10] |
Richman J S, Moorman J R. Physiological Time-Series Analysis Using Approximate Entropy and Sample Entropy[J]. American Journal of Physiology-Heart and Circulatory Physiology, 2000, 278(6): H2 039-H2 049 DOI:10.1152/ajpheart.2000.278.6.H2039
(  0) 0) |
| [11] |
张学清, 梁军, 张熙, 等. 基于样本熵和极端学习机的超短期风电功率组合预测模型[J]. 中国电机工程学报, 2013, 33(25): 33-40 (Zhang Xueqing, Liang Jun, Zhang Xi, et al. Combined Model for Ultra Short-Term Wind Power Prediction Based on Sample Entropy and Extreme Learning Machine[J]. Proceedings of the CSEE, 2013, 33(25): 33-40)
(  0) 0) |
| [12] |
王亚娟, 李怀良, 庹先国, 等. 一种集成经验模态分解的样本熵阈值微地震信号降噪方法[J]. 物探与化探, 2019, 43(5): 1 083-1 089 (Wang Yajuan, Li Huailiang, Tuo Xianguo, et al. A Denoising Method for Microseismic Signal Based on the Ensemble Empirical Mode Decomposition of Sample Entropy Threshold[J]. Geophysical and Geochemical Exploration, 2019, 43(5): 1 083-1 089)
(  0) 0) |
| [13] |
陈强, 黄声享, 王韦. 小波去噪效果评价的另一指标[J]. 测绘信息与工程, 2008, 33(5): 13-14 (Chen Qiang, Huang Shengxiang, Wang Wei. An Evaluation Indicator of Wavelet Denoising[J]. Journal of Geomatics, 2008, 33(5): 13-14)
(  0) 0) |
| [14] |
徐朗, 蔡德所. CEEMDAN与小波变换混合去噪方法在光纤陀螺监测系统信号去噪中的应用[J]. 水利水电技术, 2018, 49(9): 87-95 (Xu Lang, Cai Desuo. Application of De-Noising Method Mixed with CEEMDAN and Wavelet Transform to Signal De-Noising for Fiber Optic Gyro Monitoring System[J]. Water Resources and Hydropower Engineering, 2018, 49(9): 87-95)
(  0) 0) |
| [15] |
闫祥海, 周志立, 李忠利. 拖拉机动力输出轴载荷经验模态分解软阈值降噪研究[J]. 西安交通大学学报, 2019, 53(5): 67-72 (Yan Xianghai, Zhou Zhili, Li Zhongli. Study on the Noise Reduction of Tractor Power Take-off Load by Empirical Mode Decomposition Soft-Threshold Method[J]. Journal of Xi'an Jiaotong University, 2019, 53(5): 67-72)
(  0) 0) |
| [16] |
刘东瀛, 邓艾东, 刘振元, 等. 基于EMD与相关系数原理的故障声发射信号降噪研究[J]. 振动与冲击, 2017, 36(19): 71-77 (Liu Dongying, Deng Aidong, Liu Zhenyuan, et al. De-Noising Method for Fault Acoustic Emission Signals Based on the EMD and Correlation Coefficient[J]. Journal of Vibration and Shock, 2017, 36(19): 71-77)
(  0) 0) |
| [17] |
张宁. 基于CEEMD阈值和相关系数原理的MEMS陀螺信号去噪方法[J]. 传感技术学报, 2018, 31(9): 1 383-1 388 (Zhang Ning. Signal De-Noising Method for MEMS Gyroscope Based on CEEMD Threshold and Correlation Coefficient Principle[J]. Chinese Journal of Sensors and Actuators, 2018, 31(9): 1 383-1 388)
(  0) 0) |
| [18] |
郭健, 陈健, 胡杨. 基于小波智能模型的地铁车站基坑变形时序预测分析[J]. 岩土力学, 2020, 41(增1): 1-7 (Guo Jian, Chen Jian, Hu Yang. Time Series Prediction for Deformation of the Metro Foundation Pit Based on Wavelet Intelligence Model[J]. Rock and Soil Mechanics, 2020, 41(S1): 1-7)
(  0) 0) |
| [19] |
李麟玮, 吴益平, 苗发盛, 等. 基于变分模态分解与GWO-MIC-SVR模型的滑坡位移预测研究[J]. 岩石力学与工程学报, 2018, 37(6): 1 395-1 406 (Li Linwei, Wu Yiping, Miao Fasheng, et al. Displacement Prediction of Landslides Based on Variational Mode Decomposition and GWO-MIC-SVR Model[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(6): 1 395-1 406)
(  0) 0) |
| [20] |
罗亦泳. 基于高斯过程的大坝变形预测模型[J]. 浙江工业大学学报, 2016, 44(5): 543-546 (Luo Yiyong. A Gaussian Process Based Model for Predicting Deformations of Dams[J]. Journal of Zhejiang University of Technology, 2016, 44(5): 543-546 DOI:10.3969/j.issn.1006-4303.2016.05.015)
(  0) 0) |
2. Key Laboratory for Digital Land and Resources of Jiangxi Province, East China University of Technology, 418 Guanglan Road, Nanchang 330013, China
 2021, Vol. 41
2021, Vol. 41


