2. 四川建筑职业技术学院博士后创新实践基地,四川省德阳市嘉陵江西路4号,618000;
3. 信息工程大学地理空间信息学院,郑州市科学大道62号,450001
当扩展卡尔曼滤波(extend Kalman filter, EKF)随机模型不符合高斯白噪声假设时,估计精度会下降,严重时甚至引起发散。现实中不服从高斯白噪声分布的噪声序列表现为高斯有色噪声、非高斯白噪声和非高斯有色噪声3种形式。基于状态扩增、量测差分、时间序列分析和自适应因子调节技术的噪声建模法和自适应滤波理论可用于有色噪声处理[1]。孙清峰等[2]利用历元间的观测残差和状态残差建立有色噪声模型,提出一种基于有色噪声函数模型拟合的滤波方法。林旭等[3]研究多步相关EKF算法,先基于噪声的相关性构建多步相关的噪声协方差矩阵, 然后求解出状态协方差公式和增益矩阵。徐定杰等[4]提出基于变分贝叶斯学习的自适应EKF算法,对噪声方差与状态参数联合解算,削弱时变有色噪声对滤波估值的影响。上述算法较好地抵制了有色噪声的影响,但处理非高斯噪声污染问题时,它们均使用一个更大方差的高斯分布来涵盖真正的非高斯分布,这会使滤波状态估值的协方差过于保守。
高斯混合模型(Gaussian mixture model, GMM)的多模近似方法为解决非高斯噪声问题提供了可行途径,比简单采用膨大方差的高斯分布近似法具有更高的精度[5]。Terejanu等[6]利用GMM分解非高斯噪声,并结合非线性滤波技术提出GMEKF;George等[7]讨论依据协方差矩阵最大特征值和非线性程度2种方式的GMEKF建模理论;戴卿等[8]研究GMM优化的四元数约束容积卡尔曼滤波,改善了非理想高斯噪声环境中的四元数姿态估计性能。以上研究均对非高斯白噪声下的滤波随机模型起到了较好的建模效果,但却忽略了非高斯噪声中的有色噪声成分,不能有效应对更为普遍的非高斯有色噪声问题。
本文设计了一种顾及非高斯有色噪声影响的GMEKF优化算法,该算法基于GMEKF框架,通过GMM解决滤波中的非高斯噪声问题,融合状态扩增和量测组差技术白化处理高斯混合滤波中的有色噪声成分,削弱了非高斯有色噪声对滤波估值的影响。
1 非高斯有色噪声GMEKF优化算法 1.1 非高斯噪声的GMM近似GNSS/SINS紧组合定姿定位系统的信息融合常通过EKF来实现,设k时刻状态向量Xk为包含姿态四元数、速度、位置、陀螺漂移、加速度计漂移、GNSS时钟偏置和时钟漂移的18维状态列向量,其动力学模型和观测模型可概括为:
| $ {{\mathit{\boldsymbol{X}}_k} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k,k - 1}}{\mathit{\boldsymbol{X}}_{k - 1}} + {\mathit{\boldsymbol{W}}_k}} $ | (1) |
| $ {{\mathit{\boldsymbol{L}}_k} = {\mathit{\boldsymbol{A}}_k}{\mathit{\boldsymbol{X}}_k} + {\mathit{\boldsymbol{e}}_k}} $ | (2) |
式中,Wk为过程噪声;Lk=[ρk1, …, ρkm, k1, …, km]T为经卫星钟差、电离层延迟和对流层延迟改正后的GNSS伪距和伪距率观测向量,上标m为卫星个数;ek=[ek1, …, ekm,ėk1, …ėkm]T为接收机噪声、多路径效应和轨道预测残差等引起的观测误差向量;Φk, k-1为状态转移阵;Ak为观测设计阵。具体设置见文献[9]。
GMM是一种将多个高斯分量组合在一起的数学统计模型,随着高斯分量数目的增加,GMM能够以任意精度逼近真实非高斯模型[8]。由GMM将式(1)和式(2)中高斯混合分布的过程噪声Wk和量测噪声ek分别近似为:
| $ {p({\mathit{\boldsymbol{W}}_k}) \approx \sum\limits_{j = 1}^J {\alpha _{{W_k}}^j} N({\mathit{\boldsymbol{W}}_k};\mathit{\boldsymbol{\mu }}_{{W_k}}^j,\mathit{\boldsymbol{Q}}_k^j)} $ | (3) |
| $ {p({\mathit{\boldsymbol{e}}_k}) \approx \sum\limits_{l = 1}^L {\alpha _{{e_k}}^l} N({\mathit{\boldsymbol{e}}_k};\mathit{\boldsymbol{\mu }}_{{e_k}}^l,\mathit{\boldsymbol{R}}_k^l)} $ | (4) |
同理,有状态初始量X0的GMM近似形式为:
| $ p({\mathit{\boldsymbol{X}}_0}) \approx \sum\limits_{i = 1}^I {\alpha _{{X_0}}^i} N({\mathit{\boldsymbol{X}}_0};\mathit{\boldsymbol{\mu }}_{{X_0}}^i,\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{{X_0}}^i) $ | (5) |
式中,J、L和I分别为各GMM对应的高斯分量数目;0 < α < 1为分量权值;μ为分量均值;Q、R和Σ分别为过程噪声、量测噪声和状态初值所对应的协方差阵。这样,原先的非高斯模型就被分解成若干个呈高斯分布的分量。由于动态导航中的过程噪声和量测噪声属非高斯有色噪声序列,因此在使用GMEKF算法进行信息融合前,还需要先将其中的有色噪声部分进行白化处理。
1.2 非高斯有色噪声白化处理根据有色噪声特性,每个经GMM分解后的噪声分量满足:
| $ {\mathit{\boldsymbol{W}}_k^j = {\mathit{\boldsymbol{H}}_{k,k - 1}}\mathit{\boldsymbol{W}}_{k - 1}^j + \mathit{\boldsymbol{\xi }}_k^j} $ | (6) |
| $ {\mathit{\boldsymbol{e}}_k^l = {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{k,k - 1}}\mathit{\boldsymbol{e}}_{k - 1}^l + \mathit{\boldsymbol{\zeta }}_k^l} $ | (7) |
式中,ξkj和ζkl为互不相关的高斯白噪声序列;Hk, k-1和Ψk,k-1为设计矩阵。通过状态扩增对有色过程噪声Wkj进行白化处理,把过程噪声Wkj作为状态量的一部分:
| $ \mathit{\boldsymbol{X}}_k^{a(i,j)} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{X}}_k^i}\\ {\mathit{\boldsymbol{W}}_k^j} \end{array}} \right] $ | (8) |
将状态方程和量测方程进一步写成:
| $ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{X}}_k^i}\\ {\mathit{\boldsymbol{W}}_k^j} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k,k - 1}}}&\mathit{\boldsymbol{I}}\\ {\bf{0}}&{{\mathit{\boldsymbol{H}}_{k,k - 1}}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{X}}_{k - 1}^i}\\ {\mathit{\boldsymbol{W}}_{k - 1}^j} \end{array}} \right] + \left[ {\begin{array}{*{20}{l}} {\bf{0}}\\ \mathit{\boldsymbol{I}} \end{array}} \right]\mathit{\boldsymbol{\xi }}_k^j $ | (9) |
| $ \mathit{\boldsymbol{L}}_k^{i,j,l} = \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{A}}_k}}&{\bf{0}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{X}}_k^i}\\ {\mathit{\boldsymbol{W}}_k^j} \end{array}} \right] + \mathit{\boldsymbol{e}}_k^l $ | (10) |
或简写为:
| $ {\mathit{\boldsymbol{X}}_k^{a(i,j)} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k,k - 1}^a\mathit{\boldsymbol{X}}_{k - 1}^{a(i,j)} + \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_k^a\mathit{\boldsymbol{\xi }}_k^j} $ | (11) |
| $ {\mathit{\boldsymbol{L}}_k^{i,j,l} = \mathit{\boldsymbol{A}}_k^a\mathit{\boldsymbol{X}}_k^{a(i,j)} + \mathit{\boldsymbol{e}}_k^l} $ | (12) |
式中,ekl仍为有色噪声序列,进一步对其进行白化处理。由式(7)和式(12)有:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{L}}_{k + 1}^{i,j,l} = \mathit{\boldsymbol{A}}_{k + 1}^a\mathit{\boldsymbol{X}}_{k + 1}^{a(i,j)} + \mathit{\boldsymbol{e}}_{k + 1}^l = }\\ {\mathit{\boldsymbol{A}}_{k + 1}^a[\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k + 1,k}^a\mathit{\boldsymbol{X}}_k^{a(i,j)} + \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{k + 1}^a\mathit{\boldsymbol{\xi }}_{k + 1}^j] + {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{k + 1,k}}\mathit{\boldsymbol{e}}_k^l + \mathit{\boldsymbol{\zeta }}_{k + 1}^l = }\\ {[\mathit{\boldsymbol{A}}_{k + 1}^a\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k + 1,k}^a - {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{k + 1,k}}\mathit{\boldsymbol{A}}_k^a]\mathit{\boldsymbol{X}}_k^{a(i,j)} + {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{k + 1,k}}\mathit{\boldsymbol{L}}_k^{i,j,l} + }\\ {\mathit{\boldsymbol{A}}_{k + 1}^a\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{k + 1}^a\mathit{\boldsymbol{\xi }}_{k + 1}^j + \mathit{\boldsymbol{\zeta }}_{k + 1}^l} \end{array} $ | (13) |
即
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{L}}_{k + 1}^{i,j,l} - {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{k + 1,k}}\mathit{\boldsymbol{L}}_k^{i,j,l} = [\mathit{\boldsymbol{A}}_{k + 1}^a\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k + 1,k}^a - }\\ {{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{k + 1,k}}\mathit{\boldsymbol{A}}_k^a]\mathit{\boldsymbol{X}}_k^{a(i,j)} + \mathit{\boldsymbol{A}}_{k + 1}^a\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{k + 1}^a\mathit{\boldsymbol{\xi }}_{k + 1}^j + \mathit{\boldsymbol{\zeta }}_{k + 1}^l} \end{array} $ | (14) |
令
| $ {\mathit{\boldsymbol{L}}_k^{*(i,j,l)} = \mathit{\boldsymbol{L}}_{k + 1}^{i,j,l} - {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{k + 1,k}}\mathit{\boldsymbol{L}}_k^{i,j,l}} $ | (15) |
| $ {\mathit{\boldsymbol{A}}_k^* = \mathit{\boldsymbol{A}}_{k + 1}^a\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k + 1,k}^a - {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{k + 1,k}}\mathit{\boldsymbol{A}}_k^a} $ | (16) |
| $ {\mathit{\boldsymbol{e}}_k^{*(j,l)} = \mathit{\boldsymbol{A}}_{k + 1}^a\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{k + 1}^a\mathit{\boldsymbol{\xi }}_{k + 1}^j + \mathit{\boldsymbol{\zeta }}_{k + 1}^l} $ | (17) |
得新量测方程:
| $ \mathit{\boldsymbol{L}}_k^{*(i,j,l)} = \mathit{\boldsymbol{A}}_k^*\mathit{\boldsymbol{X}}_k^{a(i,j)} + \mathit{\boldsymbol{e}}_k^{*(j,l)} $ | (18) |
由此可见,新量测方程已不再含有色噪声,其新的组合量测误差ek*(j, l)的随机模型为:
| $ \begin{array}{*{20}{c}} {E[\mathit{\boldsymbol{e}}_k^{*(j,l)}] = E[\mathit{\boldsymbol{A}}_{k + 1}^a\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{k + 1}^a\mathit{\boldsymbol{\xi }}_{k + 1}^j + \mathit{\boldsymbol{\zeta }}_{k + 1}^l] = }\\ {\mathit{\boldsymbol{A}}_{k + 1}^a\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{k + 1}^aE[\mathit{\boldsymbol{\xi }}_{k + 1}^j] + E[\mathit{\boldsymbol{\zeta }}_{k + 1}^l]} \end{array} $ | (19) |
| $ \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{e_k^*}}(j,l) = \mathit{\boldsymbol{R}}_k^{*(j,l)} = }\\ {\mathit{\boldsymbol{A}}_{k + 1}^a\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{k + 1}^a\mathit{\boldsymbol{Q}}_{k + 1}^j{{(\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{k + 1}^a)}^{\rm{T}}}{{(\mathit{\boldsymbol{A}}_{k + 1}^a)}^{\rm{T}}} + \mathit{\boldsymbol{R}}_{k + 1}^l} \end{array} $ | (20) |
经上述步骤处理后,可按照GMEKF算法框架进行数据处理。
1.3 算法实现过程假设k-1时刻状态量为
| $ {\mathit{\boldsymbol{\bar X}}_k^{a(i,j,l)} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k,k - 1}^a\mathit{\boldsymbol{\hat X}}_{k - 1}^{a(i,j,l)}} $ | (21) |
| $ {{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{\bar X_k^{a(i,j,l)}}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k,k - 1}^a{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{\hat X_{k - 1}^{a(i,j,l)}}}{{(\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k,k - 1}^a)}^{\rm{T}}} + \mathit{\boldsymbol{Q}}_k^j} $ | (22) |
式(21)和式(22)为时间更新过程,然后进行量测更新分别求k时刻的状态估值
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat X}}_k^{a(i,j,l)} = }\\ {\mathit{\boldsymbol{\bar X}}_k^{a(i,j,l)} - \mathit{\boldsymbol{K}}_k^{i,j,l}(\mathit{\boldsymbol{A}}_k^*\mathit{\boldsymbol{\bar X}}_k^{a(i,j,l)} - \mathit{\boldsymbol{L}}_k^{*(i,j,l)})} \end{array} $ | (23) |
| $ \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{\hat X_k^{a(i,j,l})}} = (\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{K}}_k^{i,j,l}\mathit{\boldsymbol{A}}_k^*){\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{\bar X_k^{a(i,j,l}}}[\mathit{\boldsymbol{I}} - }\\ {{{(\mathit{\boldsymbol{A}}_k^*)}^{\rm{T}}}{{(\mathit{\boldsymbol{K}}_k^{i,j,l})}^{\rm{T}}}] + \mathit{\boldsymbol{K}}_k^{i,j,l}\mathit{\boldsymbol{R}}_k^{*(j,l)}{{(\mathit{\boldsymbol{K}}_k^{i,j,l})}^{\rm{T}}}} \end{array} $ | (24) |
| $ \mathit{\boldsymbol{K}}_k^{i,j,l} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k,k - 1}^a\mathit{\boldsymbol{A}}_k^*{[\mathit{\boldsymbol{A}}_k^*{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{\bar X_k^{a(i,j,l})}}{(\mathit{\boldsymbol{A}}_k^*)^{\rm{T}}} + \mathit{\boldsymbol{R}}_k^{*(j,l)}]^{ - 1}} $ | (25) |
最终,合并计算得到k时刻的状态估值
| $ {\mathit{\boldsymbol{\hat X}}_k^a = \sum\limits_{i = 1}^I {\sum\limits_{j = 1}^J {\sum\limits_{l = 1}^L {\alpha _k^{i,j,l}} } } \mathit{\boldsymbol{\hat X}}_k^{a(i,j,l)}} $ | (26) |
| $ {{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{\hat X_k^a}} = \sum\limits_{i = 1}^I {\sum\limits_{j = 1}^J {\sum\limits_{l = 1}^L {\alpha _k^{i,j,l}} } } {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{\hat X_k^{a(i,j,l)}}}} $ | (27) |
| $ \alpha _k^{i,j,l} = \frac{{\alpha _{{X_k}}^i\alpha _{{W_k}}^j\alpha _{{e_k}}^lN({\mathit{\boldsymbol{L}}_k};\mathit{\boldsymbol{L}}_k^{*(i,j,l)},\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{LL}^{i,j,l})}}{{\sum\limits_{i = 1}^I {\sum\limits_{j = 1}^J {\sum\limits_{l = 1}^L {\alpha _{{X_k}}^i} } } \alpha _{{W_k}}^j\alpha _{{e_k}}^lN({\mathit{\boldsymbol{L}}_k};\mathit{\boldsymbol{L}}_k^{*(i,j,l)},\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{LL}^{i,j,l})}} $ | (28) |
| $ \mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{LL}^{i,j,l} = \mathit{\boldsymbol{A}}_k^*{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{\hat X_k^{a(i,j,l)}}}{(\mathit{\boldsymbol{A}}_k^*)^{\rm{T}}} + \mathit{\boldsymbol{R}}_k^{*(j,l)} $ | (29) |
上述优化的GMEKF算法能够解决受非高斯有色噪声影响的状态估计问题。分析式(6)与式(7)发现,设计参数Hk, k-1和Ψk, k-1非零时,上述算法为顾及非高斯有色噪声影响的GMEKF算法;而当Hk, k-1和Ψk, k-1同为零时,即退化为非高斯白噪声下的GMEKF算法。由此可见,理论上本文推导的算法在处理非高斯噪声问题时更具一般性。
2 算法检校与分析 2.1 仿真检校为验证算法的有效性,采用GPSoft公司惯导工具箱和Siegen大学测姿工具箱编译的GNSS/SINS紧组合定姿定位平台。部分仿真参数设置如下:陀螺仪刻度系数0.2%,随机游走0.2°/ h,零偏0.1°/h;加速度计刻度系数0.3%,随机游走30 μg/ Hz,零偏0.1 mg;初始姿态标准差20″,初始速度标准差10 cm/s,初始位置由伪距单点定位确定(标准差为3 m)。基于2019-03-17的卫星星座分布和当前历元姿态仿真GNSS观测数据,接收机钟差和钟漂标准差分别为10 m和10 m/s。这里设置过程噪声Wk由2个高斯分量叠加构成:
| $ p({\mathit{\boldsymbol{W}}_k}) \approx 0.1N(\mathit{\boldsymbol{\mu }}_{{W_k}}^1,\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{{W_k}}^1) + 0.9N(\mathit{\boldsymbol{\mu }}_{{W_k}}^2,\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{{W_k}}^2) $ | (30) |
取Σ1Wk=diag(0.052…0.052),Σ2Wk=diag(0.22…0.22),μ1Wk=μ2Wk=0。同理设置观测噪声ek:
| $ p({\mathit{\boldsymbol{e}}_k}) \approx 0.1N(\mathit{\boldsymbol{\mu }}_{{e_k}}^1,\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{{e_k}}^1) + 0.9N(\mathit{\boldsymbol{\mu }}_{{e_k}}^2,\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{{e_k}}^2) $ | (31) |
取μ1ek=μ2ek= 0,Σ1ek=3Σ2ek=diag(0.32…0.32)。通过式(6)和式(7)模拟不同的非高斯有色噪声情形,分别采用GMEKF算法(方案1)和非高斯有色噪声GMEKF优化算法(方案2)进行数据处理。计算平台为:Inter Core i7-8550U 1.8 GHz,RAM 8 GB,MATLAB R2014a。
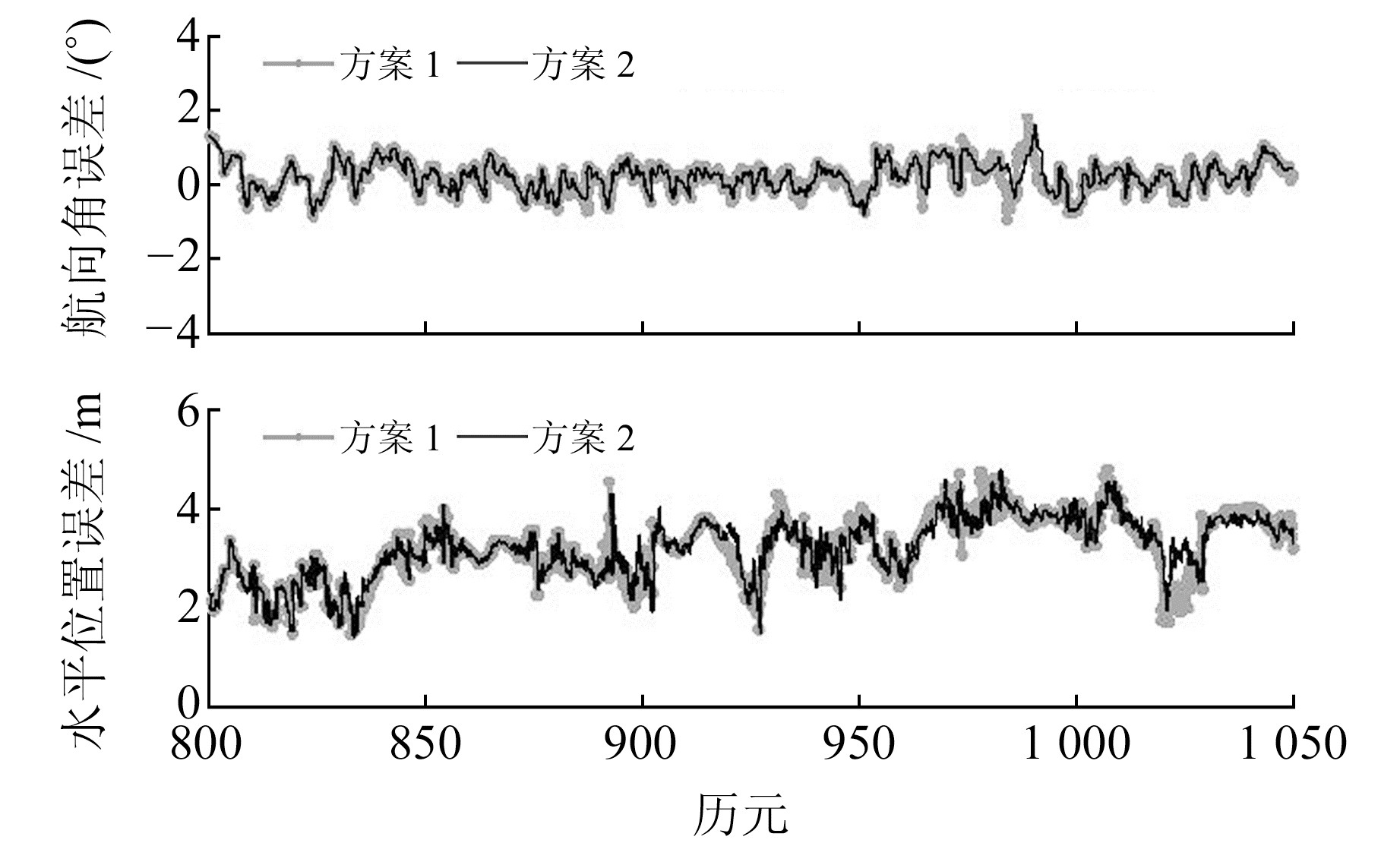
2.1.1 情形1当参数Hk, k-1、Ψk, k-1为零矩阵时, 图 1展示了仿真情景1下航向角和水平位置的误差变化曲线,表 1定量比较了50次蒙特卡洛仿真实验所得的均方根误差(RMSE)和单位历元计算耗时。
|
图 1 估计误差曲线(情形1) Fig. 1 Estimation error curve (scenario 1) |
|
|
表 1 均方根误差和耗时(情形1) Tab. 1 RMSE and time consumption (scenario 1) |
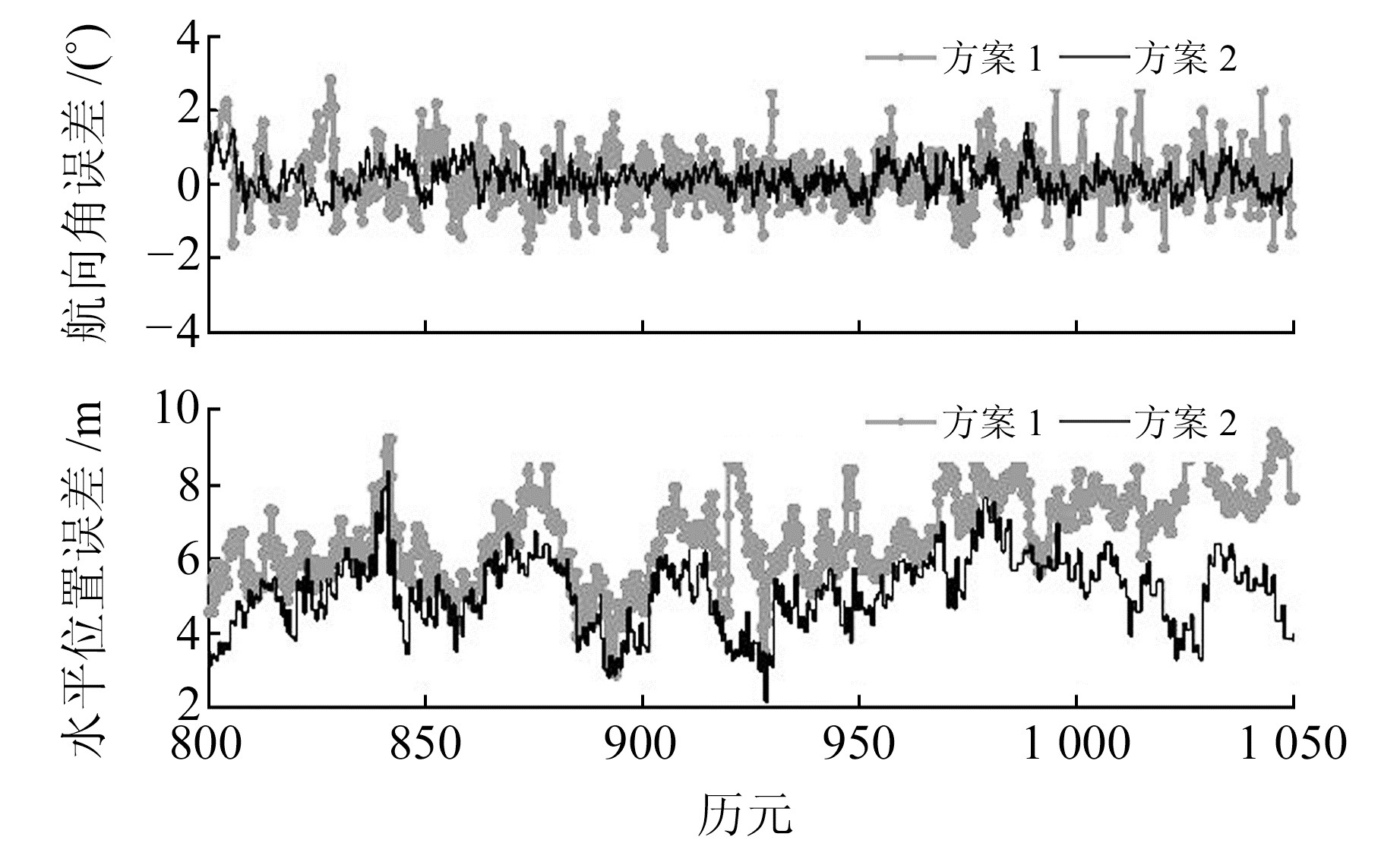
当参数Hk, k-1=Ψk, k-1=diag(1.2, 1.2, …, 1.2)时, 图 2展示了仿真情景2下航向角和水平位置的误差变化曲线,表 2定量比较了50次蒙特卡洛仿真实验所得的RMSE和单位历元计算耗时。
|
图 2 估计误差曲线(情形2) Fig. 2 Estimation error curve (scenario 2) |
|
|
表 2 均方根误差和耗时(情形2) Tab. 2 RMSE and time consumption (scenario 2) |
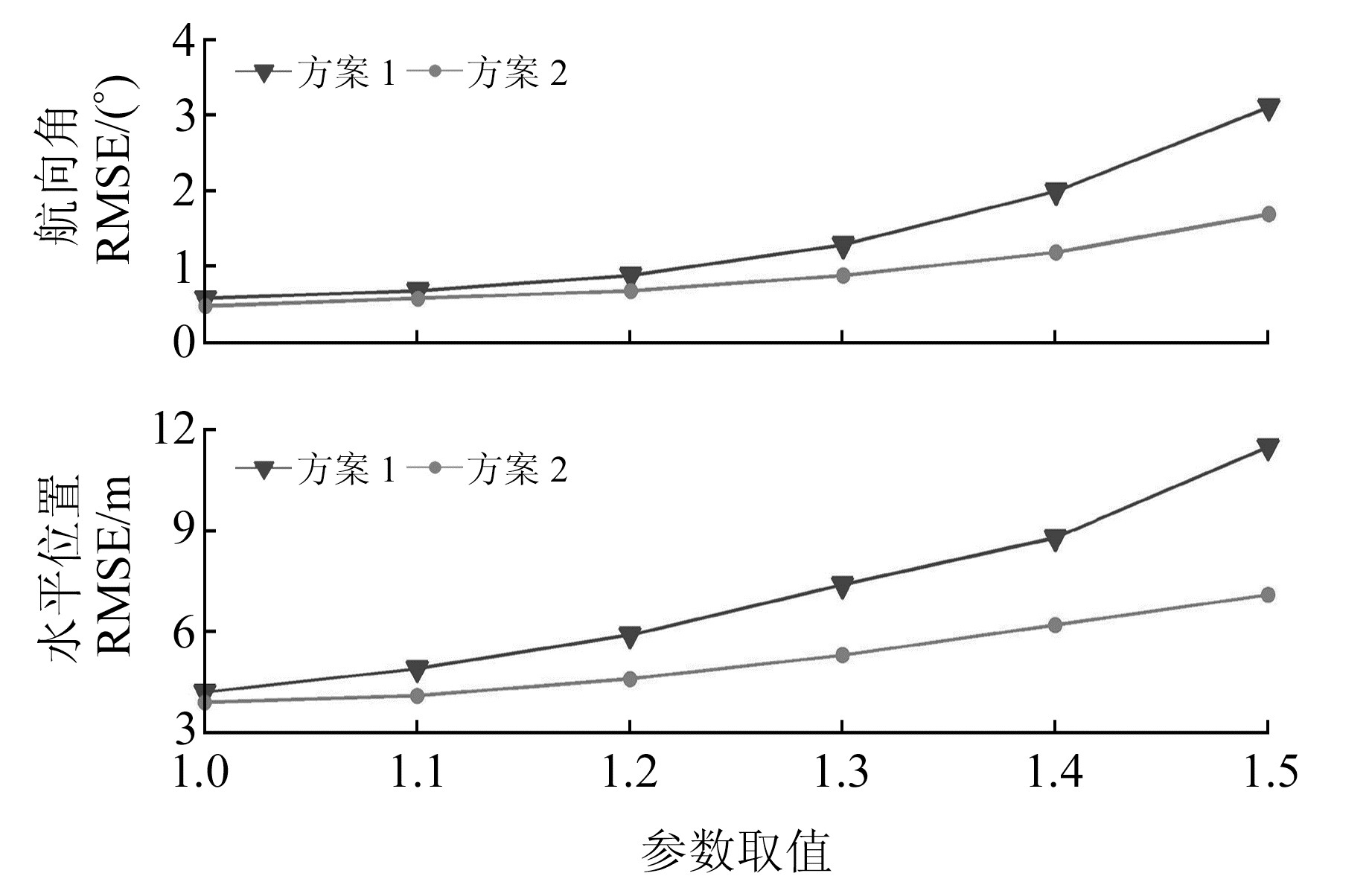
当参数Hk, k-1和Ψk, k-1中的元素为1.0, 1.1, …, 1.5时, 为验证算法的一般性,直观比较了ψ在不同取值情况下的数据处理结果,图 3给出了航向角和水平位置的RMSE均值变化曲线。
|
图 3 不同情形下的RMSE曲线 Fig. 3 RMSE curve in different scenarios |
情形1意味着噪声退化为非高斯白噪声的情况。不难看出,除个别历元外,方案1和方案2的航向角误差曲线和水平位置误差曲线几乎重合,估计精度接近,说明两者均能较好地解决非高斯白噪声的状态估计问题。
情形2意味着噪声表现为非高斯有色噪声的情况。可以看出,方案1的估计效果不佳,其航向角精度和水平位置精度明显恶化,说明算法性能受非高斯有色噪声的影响较大;方案2能较好地估计航向角和水平位置,证明了GMEKF优化算法解决非高斯有色噪声问题的有效性。
情形3中,当Hk, k-1和Ψk, k-1取某一特定值时,方案2的RMSE均小于方案1。特别地,随着设计参数取值的增大,方案2的RMSE均值增长速度明显低于方案1,进一步验证了情形2的推测,充分说明方案2能有效解决非高斯有色噪声影响的估计问题。
结合不同情形下的实验结果发现,方案2不仅能解决非高斯有色噪声问题,还能解决非高斯白噪声问题,比方案1具有更广阔的应用范围。由于方案2中子滤波器需进行有色噪声白化处理,增加了计算负担,故单位历元耗时相比于方案1略有增加。
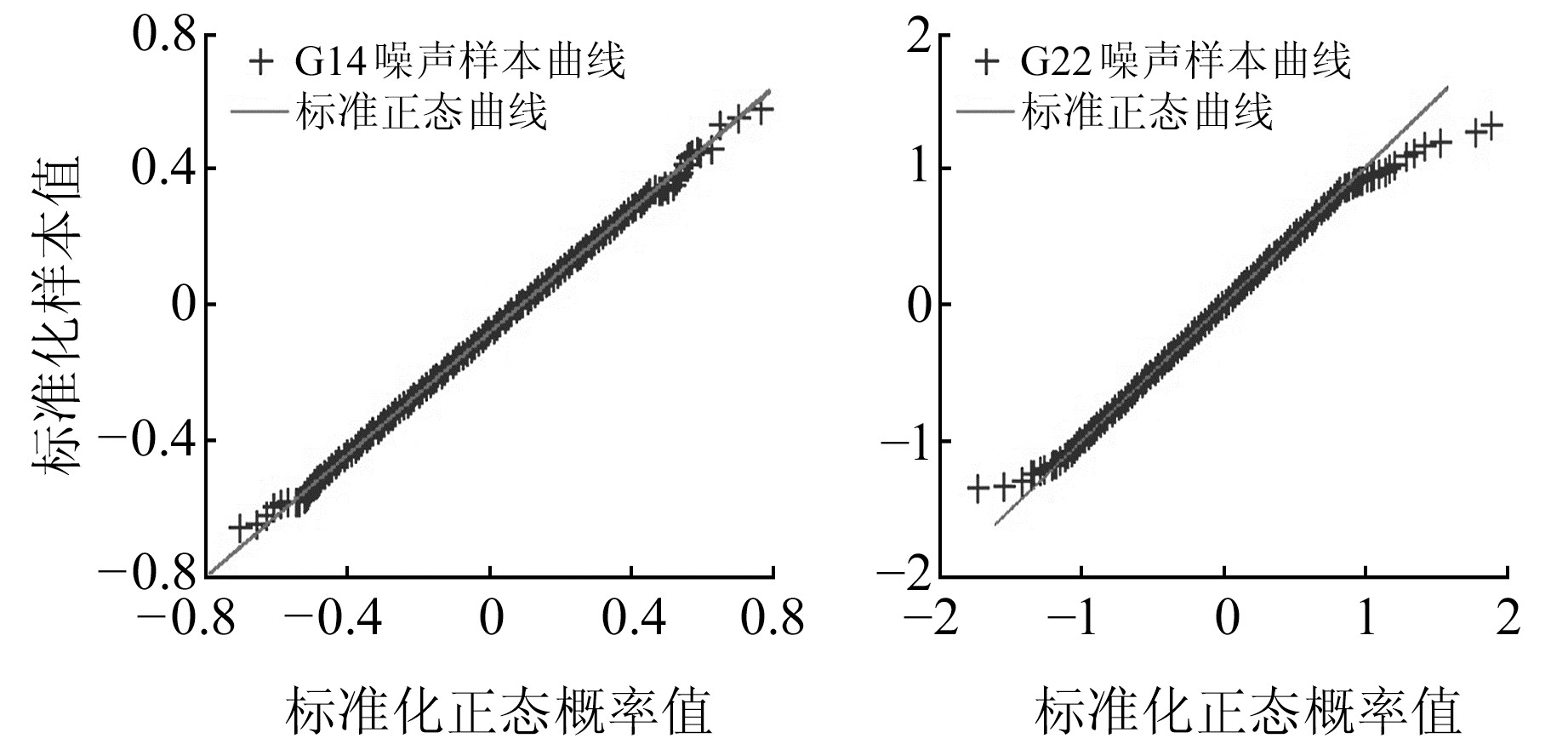
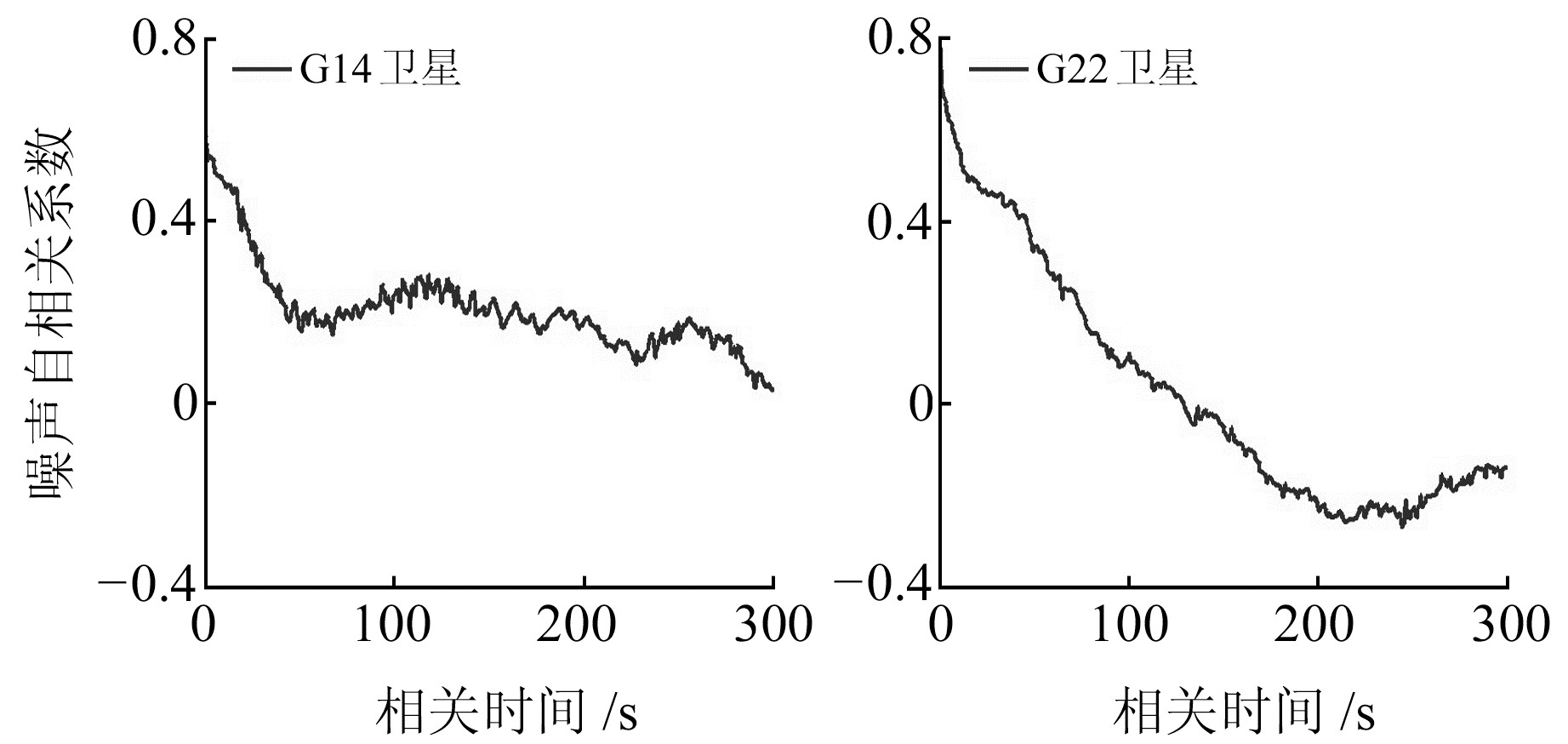
2.2 实验数据测试机动载体使用基于微机电系统(micro-electro mechanical systems, MEMS)的GNSS/SINS组合导航装置,其中GNSS接收机采样率为1 Hz;三轴陀螺零偏稳定性小于0.5°/h,采样率1 000 Hz,随机游走0.2°/ h;三轴加速度计灵敏度40±1 mV/g,温漂小于25 mg/℃。将基于光纤陀螺的GNSS/SINS高精度导航数据作为参考真值,并用于机动载体初始化。载体在2 000~3 500 s历元间途经建筑物、树林和水面,数据采集环境较为复杂,导致明显的多路径误差。选取截止角高度较低的G14卫星和G22卫星进行噪声统计特性分析。图 4为观测噪声的分位数-分位数图,可以发现,噪声样本曲线远离标准正态直线,呈现出明显的非高斯分布特性。图 5为观测噪声自相关系数,可以发现,其具有拖尾现象,有色噪声特性较明显。说明观测噪声不符合高斯白噪声分布,表现出非高斯有色噪声特性。采用§2.1中方案1和方案2进行数据处理并分析结果。
|
图 4 观测噪声分位数-分位数图 Fig. 4 Quantile-quantile plot of noise |
|
图 5 观测噪声的自相关系数 Fig. 5 Autocorrelation coefficient of noise |
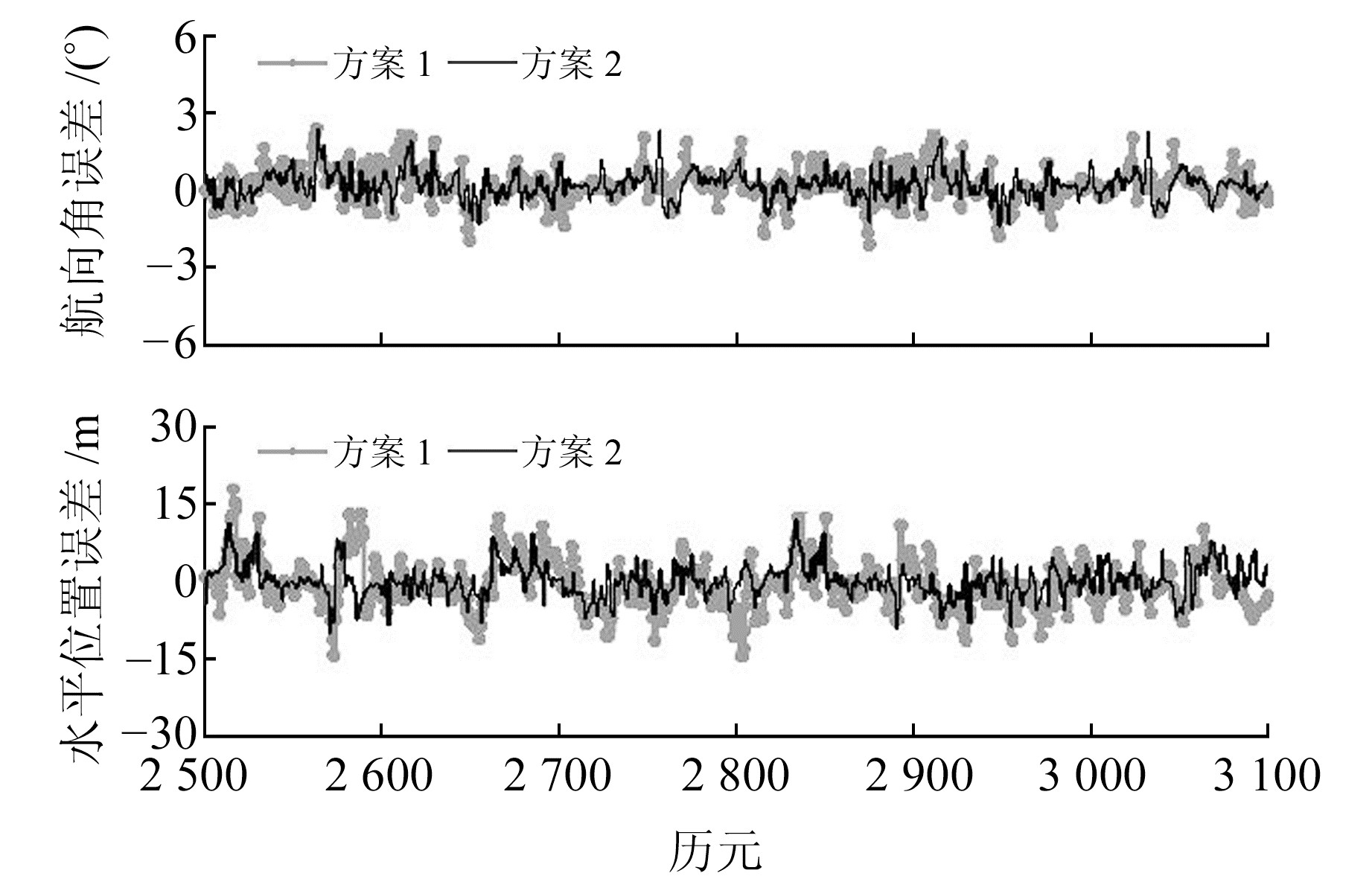
图 6为2 500~3 100历元间的滤波结果,可以看出,方案2航向角误差变化范围的最大值小于方案1,由于定位结果受姿态精度影响,相应的方案2水平位置精度也高于方案1。表 3统计了不同方案的航向角和水平位置RMSE结果,可以看出,方案2优势明显。说明当载体受非高斯有色噪声影响时,本文优化算法能精化随机模型,提高滤波精度。
|
图 6 估计误差曲线 Fig. 6 Estimation error curve |
|
|
表 3 不种方案RMSE的比较 Tab. 3 Comparison of RMSE using different schemes |
针对GNSS/SINS紧组合定姿定位系统在受非高斯有色噪声影响时直接使用GMEKF算法进行导航解算出现的估计精度下降的问题,设计了一种顾及非高斯有色噪声影响的GMEKF优化算法。该算法通过GMM对非高斯噪声进行多模近似,并结合状态扩增和量测组差白化处理其中的有色噪声成分,为复杂导航环境下实现高精度滤波解算提供了可能。实验结果表明,在更为普遍的非高斯有色噪声影响的环境下,本文优化算法能有效克服GMEKF的局限性。
| [1] |
杨元喜, 任夏, 许艳. 自适应抗差滤波理论及应用的主要进展[J]. 导航定位学报, 2013, 1(1): 9-15 (Yang Yuanxi, Ren Xia, Xu Yan. Main Progress of Adaptively Robust Filter with Applications in Navigation[J]. Journal of Navigation and Positioning, 2013, 1(1): 9-15)
(  0) 0) |
| [2] |
孙清峰, 蔡昌盛, 崔先强, 等. 一种顾及有色噪声的四星座GNSS动态导航滤波算法[J]. 大地测量与地球动力学, 2019, 39(6): 625-628 (Sun Qingfeng, Cai Changsheng, Cui Xianqiang, et al. A Filtering Algorithm for Quad-Constellation GNSS Kinematic Navigation with Consideration of Colored Noise[J]. Journal of Geodesy and Geodynamics, 2019, 39(6): 625-628)
(  0) 0) |
| [3] |
林旭, 刘俊钊. 有色噪声下的目标跟踪卡尔曼滤波新算法[J]. 中国惯性技术学报, 2018, 26(6): 830-834 (Lin Xu, Liu Junzhao. New Kalman Filtering Algorithm for Target Tracking with Colored Noise[J]. Journal of Chinese Inertial Technology, 2018, 26(6): 830-834)
(  0) 0) |
| [4] |
徐定杰, 沈忱, 沈锋. 时变有色观测噪声下基于变分贝叶斯学习的自适应卡尔曼滤波[J]. 电子与信息学报, 2013, 35(7): 1593-1 598 (Xu Dingjie, Shen Chen, Shen Feng. Adaptive Kalman Filtering with Time-Varying Colored Measurement Noise by Variational Bayesian Learning[J]. Journal of Electronics and Information Technology, 2013, 35(7): 1593-1 598)
(  0) 0) |
| [5] |
Xu H, Xie W C, Yuan H D, et al. Fixed-Point Iteration Gaussian Sum Filtering Estimator with Unknown Time-Varying Non-Gaussian Measurement Noise[J]. Signal Processing, 2018, 153(12): 132-142
(  0) 0) |
| [6] |
Terejanu G, Singla P, Singh T, et al. Adaptive Gaussian Sum Filter for Nonlinear Bayesian Estimation[J]. IEEE Transactions on Automatic Control, 2011, 56(9): 2 151-2 156 DOI:10.1109/TAC.2011.2141550
(  0) 0) |
| [7] |
George J, Terejanu G, Singla P. Spacecraft Attitude Estimation Using Adaptive Gaussian Sum Filter[J]. The Journal of the Astronautical Sciences, 2009, 57(1-2): 31-45 DOI:10.1007/BF03321492
(  0) 0) |
| [8] |
戴卿, 隋立芬, 田源, 等. 高斯混合模型优化的四元数约束CKF姿态估计[J]. 宇航学报, 2018, 39(8): 913-919 (Dai Qing, Sui Lifen, Tian Yuan, et al. Quaternion Constrained Cubature Kalman Filter Attitude Estimation Based on Gaussian Mixture Model[J]. Journal of Astronautics, 2018, 39(8): 913-919)
(  0) 0) |
| [9] |
Groves P D. Principles of GNSS, Inertial and Multisensor Integrated Navigation Systems[M]. London: Artech House, 2008
(  0) 0) |
2. Innovation and Practice Base for Postdoctors, Sichuan College of Architectural Technology, 4 West-Jialingjiang Road, Deyang 618000, China;
3. School of Surveying and Mapping, Information Engineering University, 62 Kexue Road, Zhengzhou 450001, China
 2020, Vol. 40
2020, Vol. 40

