2. 国家海洋环境预报中心,北京市大慧寺8号,100081
GNSS观测数据的高精度处理是获取可靠位置信息的前提,也是实现对极地冰川消融、海平面变化、大气水汽等进行动态监测的基础。鉴于南极地理位置的重要性,研究南极GNSS数据高精度处理具有重要意义。
影响极地GNSS定位精度的因素较多,如卫星星历、对流层映射函数、卫星截止高度角、海潮负荷等,学者们对上述影响因素进行过大量研究[1-6]。但截止高度角、映射函数、海潮负荷等因素对南极GNSS定位结果影响的研究较少,导致在处理GNSS数据时缺少方法选用的依据。受极地特殊的地理位置和自然环境的影响,南极GNSS数据质量相比中低纬度地区较差,处理难度更大。本文采用精密单点定位和双差模式,分析卫星截止高度角、映射函数模型、海潮模型对南极地区GNSS测站坐标精度的影响。
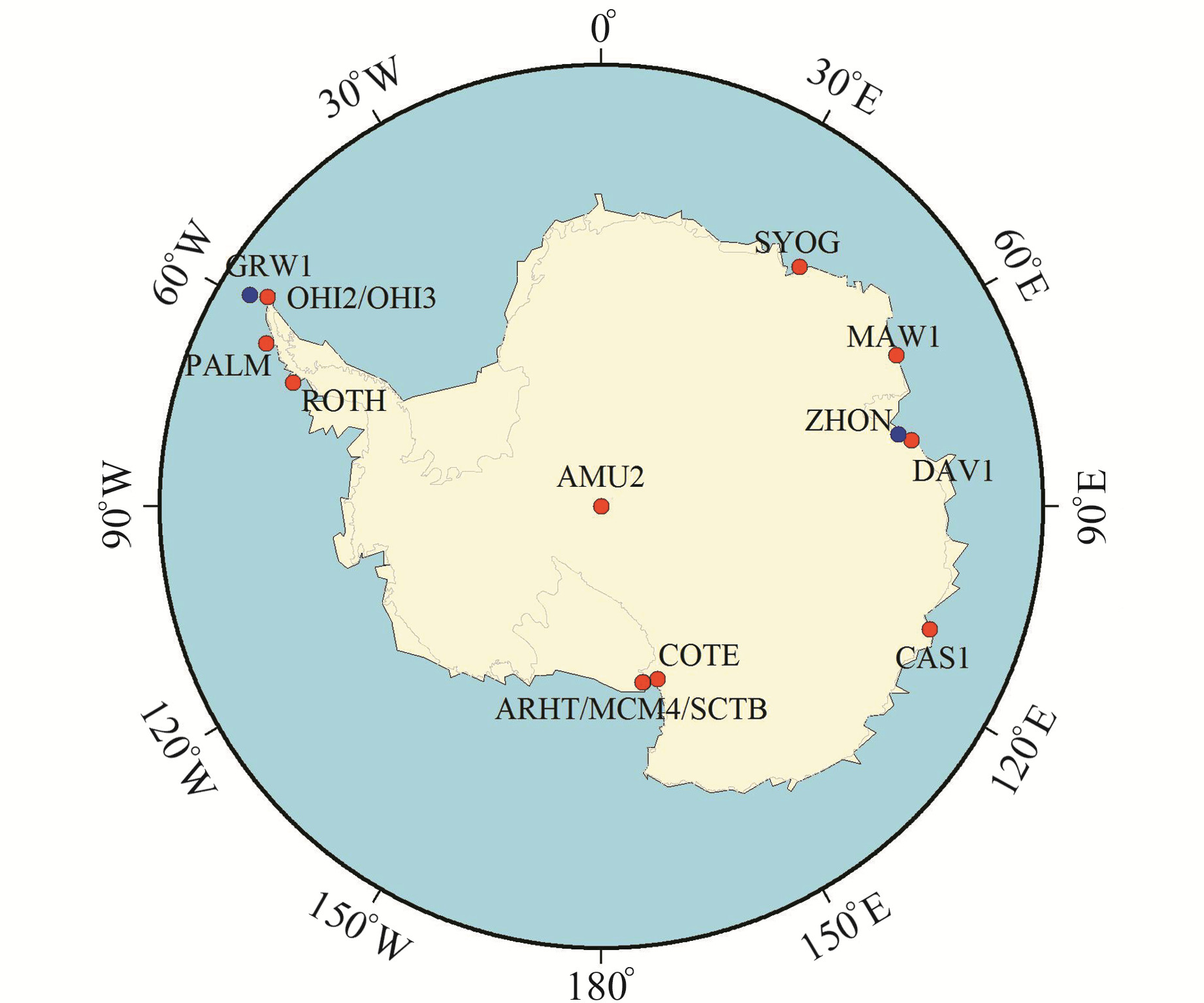
1 数据资料和方法 1.1 数据来源选取长城站(GRW1)、中山站(ZHON)、南极地区公开的13个IGS站2018年的观测数据为研究对象。图 1为GNSS站分布情况,其中OHI2和OHI3站,ARHT、MCM4和SCTB站位置非常接近,在图中位置重合。除GRW1和ZHON站仅能接收到GPS卫星信号外,其他观测站能同时接收到GPS和GLONASS卫星信号,各观测站接收机的截止高度角均为0°。IGS站观测数据的采样间隔为30 s,ZHON和GRW1站数据的采样间隔为15 s。为统一各站的采样间隔,将ZHON和GRW1站数据的采样间隔抽稀为30 s。
|
图 1 GNSS站点分布 Fig. 1 Distribution of GNSS stations |
由于南极观测环境复杂,卫星高度角较低,数据观测质量较差,且各测站间间距较远,从而对基线解算提出特殊要求。通过综合考虑,本文利用Bernese 5.2软件的精密单点定位(PPP)和双差(DD)模式对GPS/GLONASS数据进行处理,获得各测站的单日解坐标。在数据处理时,采用IGS欧洲定轨中心(CODE)提供的精密星历和地球定向参数等产品,整周模糊度采用QIF(无电离层组合模糊度固定)策略,基线组成方法采用OBS-MAX(以构成的单差观测值数量最多为原则),考虑到GNSS接收机为双频接收机,基线预处理采用COMBINED方法,其他参数设置见表 1。
|
|
表 1 GNSS数据处理主要参数设置 Tab. 1 The main parameters setting in GNSS data analysis |
本文分别采用PPP和DD模式,选取3°、5°、7°、10°和15°的截止高度角分别对南极GNSS数据进行处理,其他参数设置相同。在数据处理时,映射函数模型采用GMF模型,海潮模型采用FES2004模型。选用长期重复性作为评估坐标精度的指标,其计算公式见文献[7]。计算南极各GNSS站在不同截止高度角下的坐标精度,结果见图 2、3。

|
图 2 各GNSS测站在不同截止高度角下PPP精度 Fig. 2 PPP accuracy of each GNSS station under different cut-off elevation angles |
|
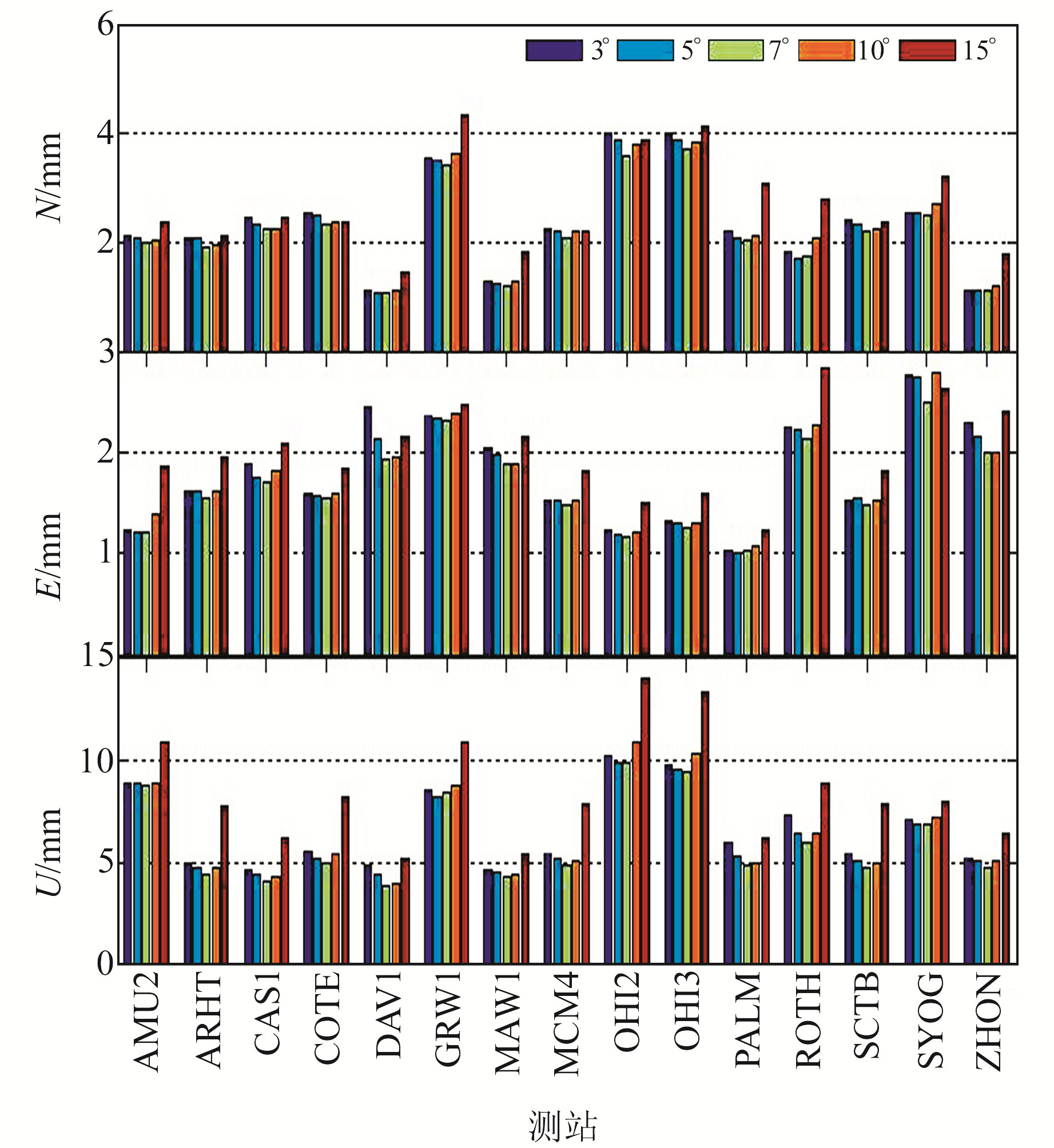
图 3 各GNSS测站在不同截止高度角下的双差定位精度 Fig. 3 Double difference positioning accuracy of each GNSS station under different cut-off elevation angles |
从图 2看出,采用精密单点定位时,不同截止高度角的坐标精度在N、E方向上差别较小,SYOG站在E方向上最大误差为5.6 mm,其他测站在水平方向上误差均小于4.0 mm;GNSS坐标精度在U方向上差别较大,截止高度角为7°或10°时大多数测站坐标精度最优,随着截止高度角的增大或减小,坐标精度逐渐降低。从图 3可知,采用双差定位时,不同截止高度角的坐标精度在N、E、U方向上差别较大,当截止高度角为5°或7°时,南极大多数GNSS测站坐标精度最高,随着截止高度角的增大或减小,坐标精度逐渐降低。表 2为不同截止高度角时南极GNSS测站坐标的平均精度,可以看出,当截止高度角为7°时,精密单点定位和双差定位GNSS测站坐标精度在E、N、U方向上均最优,随着截止高度角的增大或减小,坐标长期重复性逐渐降低。当截止高度角为15°时,坐标精度在水平方向下降不明显,而在高程方向呈明显下降趋势。从不同季节分析截止高度角对GNSS定位精度的影响发现,无论是精密单点定位还是双差定位,GNSS测站坐标在U方向的季节精度差异大于水平方向,且当截止高度角为7°时,不同季节的坐标精度均最优。
|
|
表 2 不同截止高度角下GNSS测站坐标结果的平均精度 Tab. 2 Average accuracy of GNSS station coordinates under different cut-off elevation angles |
南极各GNSS测站坐标在高程方向的精度明显比水平方向差,其原因与南极地区卫星高度角较低、极区电离层闪烁频繁、TEC日间波动较中纬度地区更剧烈有关[8]。李斐等[9]通过分析不同噪声模型下南极半岛GPS坐标时间序列也发现,高程方向受闪烁噪声的影响明显高于水平方向。
2.2 不同映射函数模型结果对比采用PPP和DD模式分析比较NMF、GMF、VMF1和VMF3映射函数模型对GNSS测站坐标精度的影响。GNSS数据处理时,卫星截止高度角设为7°,海潮模型采用FES2004。图 4、5分别为PPP和DD模式下不同映射函数模型的GNSS测站坐标精度。
|
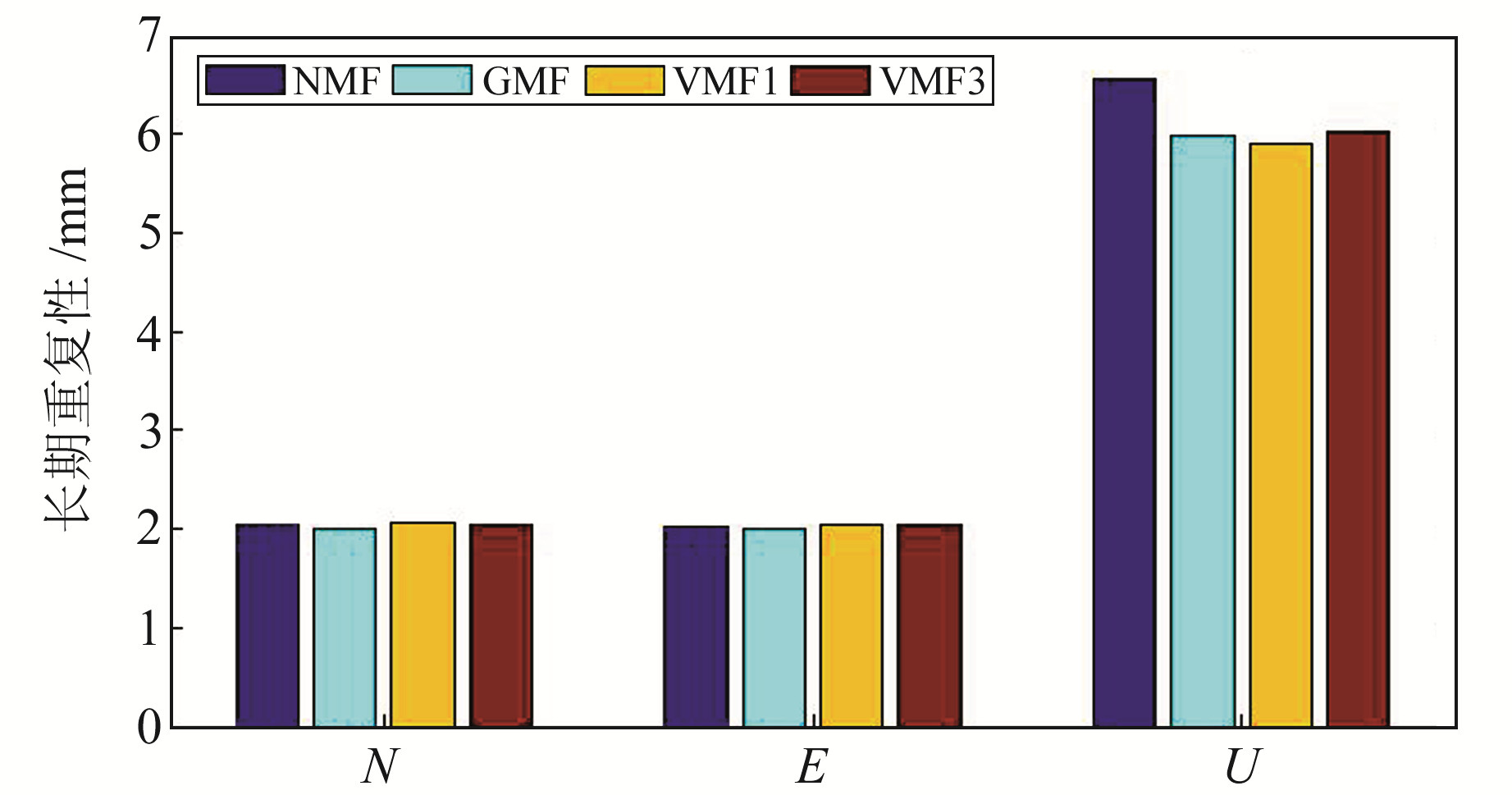
图 4 不同映射函数模型下GNSS测站精密单点定位坐标精度 Fig. 4 PPP coordinates accuracy of GNSS stations under different mapping function models |
|
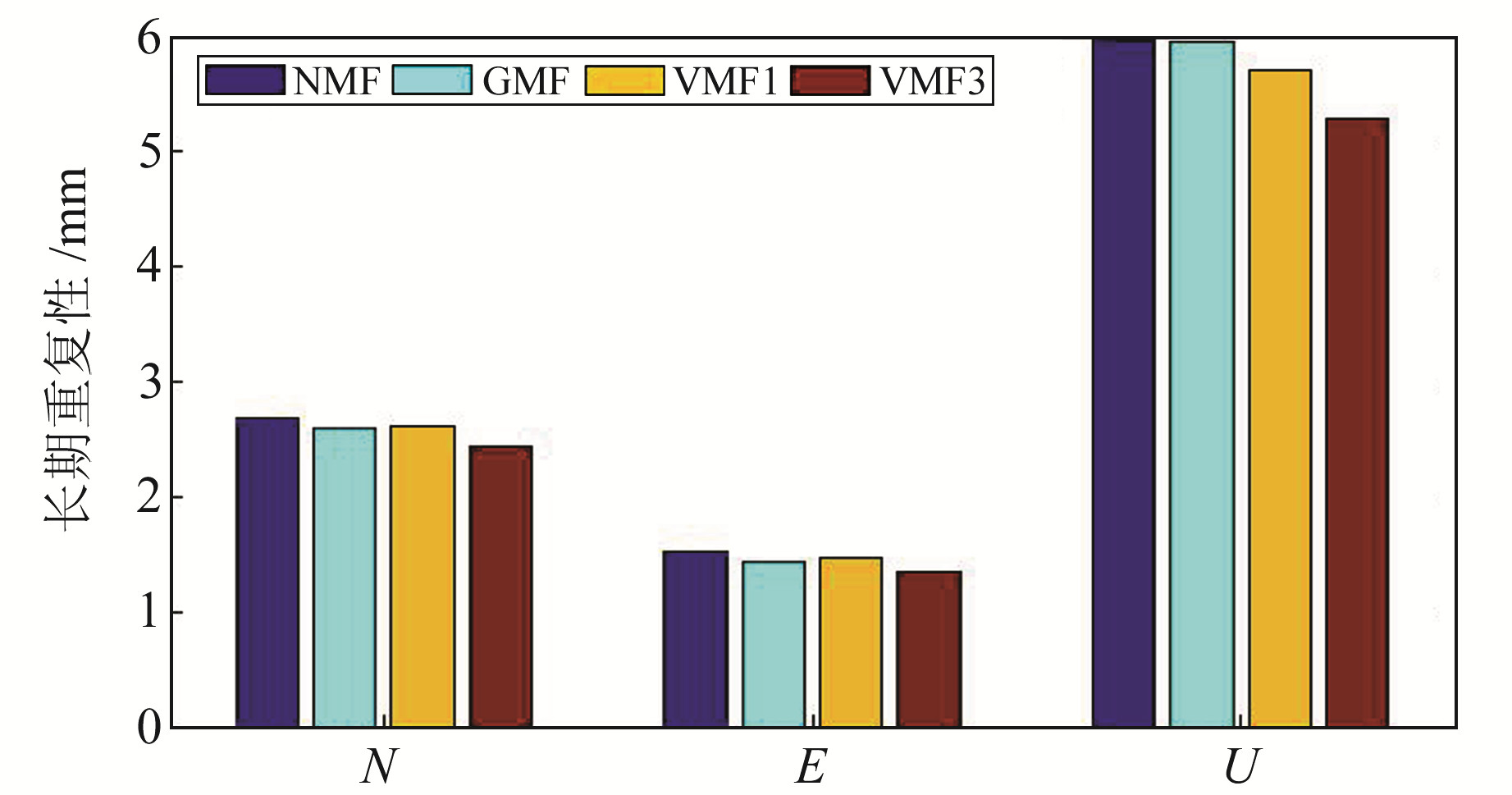
图 5 不同映射函数模型下GNSS测站双差定位的坐标精度 Fig. 5 Double difference positioning coordinates accuracy of GNSS stations under different mapping function models |
从图 4可以看出,在精密单点定位模式下,采用4种映射函数模型解算的GNSS测站坐标的平均精度在水平方向差异较小,其中GMF、VMF1和VMF3模型在高程方向的精度略优于NMF模型,表明映射函数模型主要改正GNSS坐标的高程方向,对水平方向的影响较小。由图 5可知,在双差定位模式下,采用VMF3模型解算的测站坐标精度在N、E和U方向均优于其他3种模型;采用VMF1模型解算的坐标精度在高程方向略优于NMF和GMF模型,但在水平方向上,3种模型解算的测站坐标精度差异较小。对比图 4、5可知,采用精密单点定位解算的测站坐标精度在E、N方向差异较小,而采用双差定位解算的坐标精度在E方向上优于N方向。统计PPP和DD模式下不同映射函数模型解算的GNSS坐标精度的季节变化可知,不同映射函数模型解算的坐标精度在U方向上季节差异较大,采用PPP模式解算的GNSS测站坐标精度的季节差异大于DD模式解算的结果。在水平方向上,各映射函数模型解算的坐标精度季节差异较小。
2.3 不同海潮模型结果对比选用FES2004、FES2014b、CSR4.0、GOT4.8、TPXO7.2等5种全球海潮模型和不添加海潮模型对南极15个测站的坐标解算进行海潮改正,比较分析不同方案的测站坐标精度。使用的海潮模型数据来自海潮负荷网站(http://holt.oso.chalmers.se/loading/),该网站计算得到的海潮模型包括4个半日分潮(M2、S2、N2、K2)、4个全日分潮(K1、O1、P1、Q1)以及3个长期分潮(Mf、Mm、Ssa),每个分潮给出3个方向的振幅和迟角。
目前国际数据处理中心在处理GNSS数据时多采用FES2004模型,因此以FES2004模型解算的坐标作为标准值,通过比较不添加海潮模型和采用FES2004模型解算的坐标差异,分析海潮负荷对GNSS坐标精度的影响。表 3为PPP和DD模式下采用FES2004模型和不添加海潮模型的各GNSS测站坐标差异的bias和RMS。分析南极15个测站坐标差异的平均bias和RMS可知,无论精密单点定位还是双差定位,不添加海潮模型与采用海潮模型解算结果的平均bias在水平方向和高程方向均小于0.5 mm,表明是否添加海潮模型不会对坐标的长期趋势造成影响。两者坐标差的RMS在U方向大于水平方向,即海潮负荷对坐标解的影响与坐标方向有关。精密单点定位结果RMS在E、N方向差异较小,而双差定位结果RMS在N方向上明显大于E方向。从表 3还可以看出,不同GNSS测站受海潮负荷影响存在差异,表明海潮负荷对坐标精度的影响也与测站所处地理位置有关。此外,统计不添加海潮模型和采用FES2004模型的单日解坐标在高程方向的最大差值,精密单点定位结果最大偏差为8.5 mm,双差定位结果最大偏差平均值达到18.2 mm。
|
|
表 3 不添加海潮模型和采用FES2004模型情况下坐标结果差异统计 Tab. 3 Statistic of coordinate differences between without adding ocean tide model and using FES2004 model |
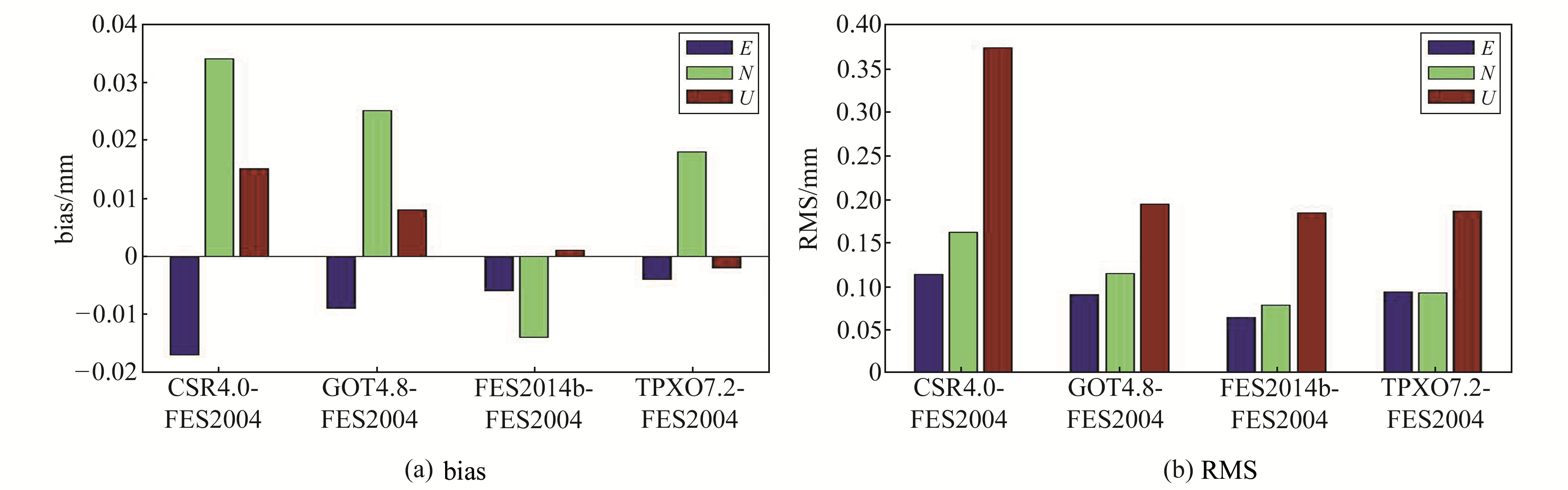
分别使用不同的海潮模型对南极GNSS数据进行处理,以FES2004模型解算的坐标作为标准值,对比分析不同海潮模型对GNSS坐标精度的影响。由于精密单点定位结果与双差定位结果基本一致,因此仅对比双差定位模式下不同海潮模型的解算结果。从图 6可以看出,采用不同海潮模型解算的坐标差异较小,不同坐标结果的平均bias在水平方向和高程方向均小于0.04 mm,RMS均小于0.4 mm,表明在南极地区不同海潮模型对GNSS坐标解算的差异较小。与其他全球海潮模型相比,采用CSR4.0模型解算的GNSS测站坐标与采用FES2004模型解算的结果差异最大,高程方向RMS约为0.4 mm,而其他海潮模型RMS在0.2 mm以内。采用不同海潮模型解算的GNSS坐标在U方向上差异最大,N方向次之,E方向最小,表明不同海潮模型间的差异也与方向有关。
|
图 6 不同海潮模型双差定位坐标差异比较 Fig. 6 Comparison of coordinate differences in double difference positioning between different ocean tide models |
1) 当截止高度角设为7°时,无论采用精密单点定位还是双差定位,南极各GNSS测站的平均坐标精度在E、N、U方向上均最优,随着截止高度角的增大或减小,坐标精度逐渐降低。
2) 当采用双差定位时,VMF3模型解算的GNSS测站坐标精度在高程方向明显优于NMF、GMF和VMF1模型;而采用精密单点定位时,VMF3模型解算出的GNSS测站坐标精度在高程方向与GMF和VMF1模型相当,且优于NMF模型解算结果。在水平方向上,4种模型的坐标精度差别在0.2 mm以内。
3) 在南极高精度GNSS数据处理中,需考虑海潮负荷的影响。海潮负荷对测站坐标U方向的影响大于水平方向。不同海潮模型在南极地区表现出较好的一致性,采用不同海潮模型解算的测站坐标差值的RMS均小于0.4 mm。
致谢: 感谢武汉大学中国南极测绘研究中心提供中国长城站、中山站的GPS观测数据。
| [1] |
Malkin Z. Influence of the Cut-Off Elevation Angle and Elevation-Dependent Weighting on Parameter Estimates: A Case of CONT05[C]. The 5th IVS General Meeting, St. Petersburg, 2008
(  0) 0) |
| [2] |
周润杨, 陈明剑. 高纬度BDS/GPS PPP中截止高度角最优选取[J]. 导航定位学报, 2017, 5(1): 75-80 (Zhou Runyang, Chen Mingjian. Optimal Selection of the Elevation Cutoff Angle in BDS/GPS PPP at High-Latitude Regions[J]. Journal of Navigation and Positioning, 2017, 5(1): 75-80)
(  0) 0) |
| [3] |
Urquhart L, Nievinski F G, Santos M C. Assessment of Troposphere Mapping Functions Using Three-Dimensional Ray-Tracing[J]. GPS Solutions, 2014, 18(3): 345-354 DOI:10.1007/s10291-013-0334-8
(  0) 0) |
| [4] |
谢劭峰, 张朋飞, 王新桥, 等. 对流层延迟模型映射函数研究[J]. 大地测量与地球动力学, 2016, 36(11): 941-945 (Xie Shaofeng, Zhang Pengfei, Wang Xinqiao, et al. Research on the Mapping Functions for Tropospheric Delay Model[J]. Journal of Geodesy and Geodynamics, 2016, 36(11): 941-945)
(  0) 0) |
| [5] |
Landskron D, Böhm J. VMF3/GPT3: Refined Discrete and Empirical Troposphere Mapping Functions[J]. Journal of Geodesy, 2018, 92(4): 349-360 DOI:10.1007/s00190-017-1066-2
(  0) 0) |
| [6] |
雷锦韬, 李斐, 张胜凯, 等. 不同海潮模型对东南极沿海地区GPS基线解算的影响[J]. 武汉大学学报:信息科学版, 2015, 40(11): 1 479-1 486 (Lei Jintao, Li Fei, Zhang Shengkai, et al. Effects of Different Ocean Tide Models on GPS Baseline Solutions in Coast Area, East Antarctica[J]. Geomatics and Information Science of Wuhan University, 2015, 40(11): 1 479-1 486)
(  0) 0) |
| [7] |
Larson K M, Agnew D C. Application of the Global Positioning System to Crustal Deformation Measurement: 1. Precision and Accuracy[J]. Journal of Geophysical Research Atmospheres, 1991, 96(B10): 16 547-16 565 DOI:10.1029/91JB01275
(  0) 0) |
| [8] |
杨元喜, 徐君毅. 北斗在极区导航定位性能分析[J]. 武汉大学学报:信息科学版, 2016, 41(1): 15-20 (Yang Yuanxi, Xu Junyi. Navigation Performance of Beidou in Polar Area[J]. Geomatics and Information Science of Wuhan University, 2016, 41(1): 15-20)
(  0) 0) |
| [9] |
李斐, 马超, 张胜凯, 等. 南极半岛地区GPS坐标时间序列噪声分析及形变模式初探[J]. 地球物理学报, 2016, 59(7): 2 402-2 412 (Li Fei, Ma Chao, Zhang Shengkai, et al. Noise Analysis of the Coordinate Time Series of the Continuous GPS Station and the Deformation Patterns in the Antarctic Peninsula[J]. Chinese Journal of Geophysics, 2016, 59(7): 2 402-2 412)
(  0) 0) |
2. National Marine Environmental Forecasting Center, 8 Dahuisi, Beijing 100081, China
 2020, Vol. 40
2020, Vol. 40

