北斗卫星导航系统(BDS)作为我国自主研发的导航系统,按照“三步走”指导方针已于2020年提供全球定位、导航、授时服务[1],是首个全星座播发三频的卫星导航系统,提供B1、B2和B3三频信号。传统精密单点定位(PPP)通常采用双频消电离层模型(IF-PPP)。前期BDS PPP多采用GPS模型,并未考虑BDS异构星座和星内多路径等特性[2]。近年来部分学者对三频信号组合及三频PPP进行了大量研究[3-6],但前期BDS PPP研究主要集中于静态或仿动态条件,缺乏对实际动态条件的验证。
本文首先分析BDS PPP三频消电离层模型(IF-BDS)原理,利用空间几何原理推导三频消电离层参数,并给出最小噪声直线的空间表达式,同时采用5组静态BDS三频观测量和1组实测跑车数据,对比分析三频与双频(IF-BDS)的定位精度和收敛速度。
1 北斗三频IF-PPP模型 1.1 观测模型单台接收机观测北斗卫星时可获取伪距观测值P和载波相位观测值L,观测方程可表示为:
| $ \left\{ \begin{array}{l} P_j^s = {\rho ^{\rm{s}}} + c{\rm{d}}{t_{\rm{r}}} - c{\rm{d}}{t^{\rm{s}}} + {T^{\rm{s}}} + {\gamma _j}{I^{\rm{s}}} + \\ {B_{{\rm{r}}, {P_j}}} - B_{{P_j}}^{\rm{s}} + \varepsilon _{{P_j}}^{\rm{s}}\\ L_j^{\rm{s}} = {\lambda _j}\Phi _j^{\rm{s}} = {\rho ^{\rm{s}}} + c{\rm{d}}{t_{\rm{r}}} - c{\rm{d}}{t^{\rm{s}}} + {T^{\rm{s}}} - \\ {\gamma _j}{I^{\rm{s}}} + {\lambda _j}N_j^{\rm{s}} + {B_{{\rm{r}}, {L_j}}} - B_{{L_j}}^{\rm{s}} + \varepsilon _{{L_j}}^{\rm{s}} \end{array} \right. $ | (1) |
式中,下标r和上标s分别为接收机和卫星;下标j为卫星载波频率(j=1, 2, 3);λj为j频率的波长(单位m);Φ为载波相位观测值(单位周);ρs为站星几何距离(单位m);c为光速(单位m/s); dtr和dts分别为卫星接收机钟差和卫星钟差;Ts为对流层延迟(单位m);γj=f12/fj2;Is为B1频率上的电离层延迟;N为整周模糊度浮点解(cycle);Br, Pj和BsPj分别为接收机和卫星伪距硬件延迟(单位m);Br, Lj和BsLj分别为接收机和卫星载波相位硬件延迟(单位m);εsPj和εsLj分别为伪距观测噪声和载波相位观测噪声(单位m)。
北斗三频IF-PPP模型可表示为[7]:
| $ \left\{ {\begin{array}{*{20}{l}} {P_{{\rm{IF}}}^{\rm{s}} = \alpha P_1^{\rm{s}} + \beta P_2^{\rm{s}} + \gamma P_3^{\rm{s}}}\\ {L_{{\rm{IF}}}^{\rm{s}} = \alpha L_1^{\rm{s}} + \beta L_2^{\rm{s}} + \gamma L_3^{\rm{s}}} \end{array}} \right. $ | (2) |
式中,PsIF和LIFs分别为消电离层伪距和载波相位(单位m);α、β、γ为消电离层系数。
为保持站星距离及钟差参数不变,须满足条件式(3),构成组合系数和为1的几何平面:
| $ \alpha + \beta + \gamma = 1 $ | (3) |
消电离层具体表达式为:
| $ \alpha + 1.672\;4\beta + 1.514\;5\gamma = 1 $ | (4) |
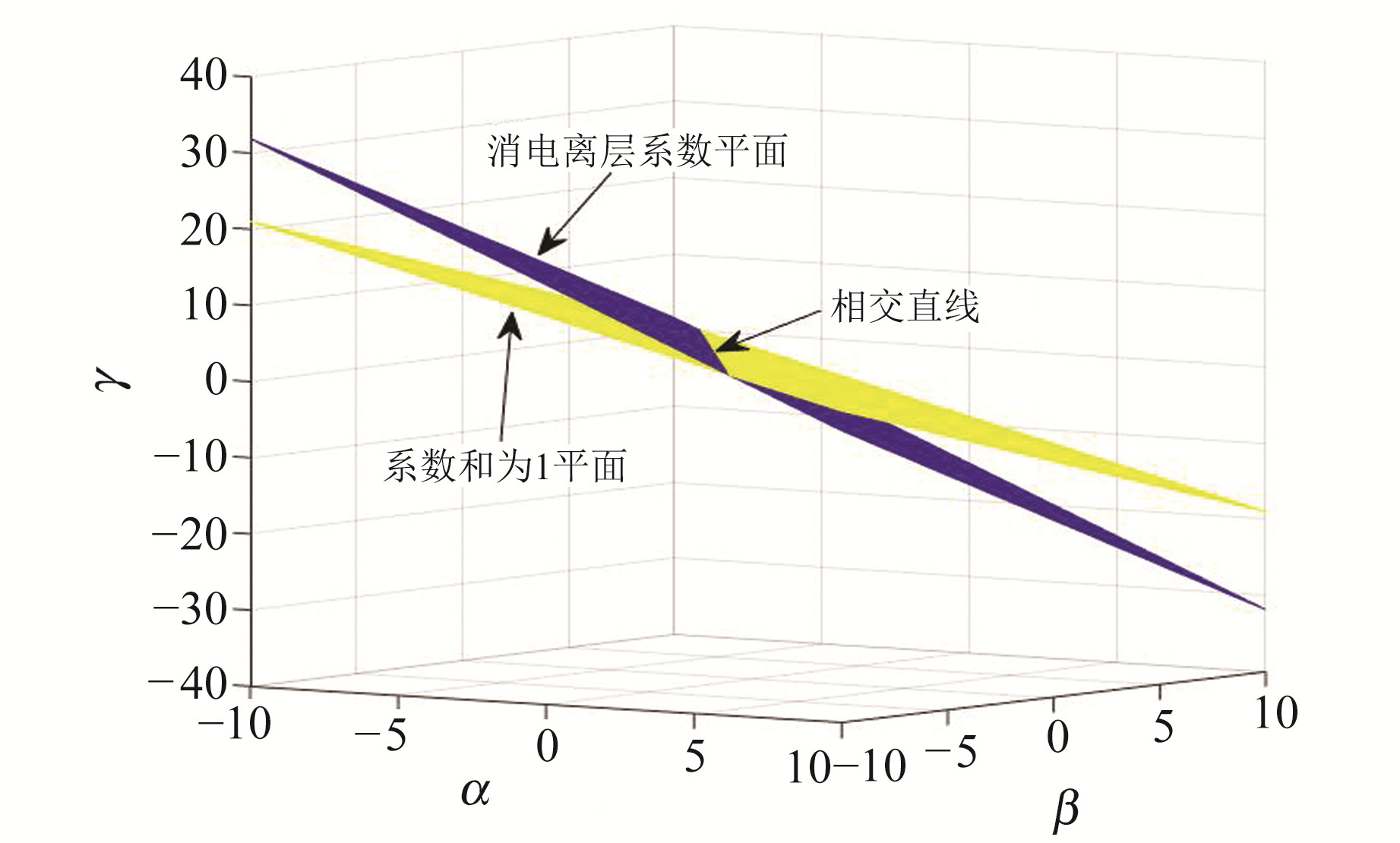
式(3)、(4)构成的平面在空间相交可得到一条直线,空间结构如图 1所示,即直线上的点满足无电离层及系数和为1。由于IF组合会扩大噪声作用,影响滤波稳定性,故本文选取最小噪声作为约束条件[8]。
|
图 1 消电离层系数平面及系数和为1平面 Fig. 1 Planes of ionospheric-free and coefficient sum is 1 |
伪距和载波相位观测噪声可分别表示为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma _{{P_{{\rm{IF}}}}}} = {\sigma _P}\;\;\;{\kern 1pt} \sqrt {{\alpha ^2} + {\beta ^2} + {\gamma ^2}} }\\ {{\sigma _{{L_{{\rm{IF}}}}}} = {\sigma _L}\sqrt {{\alpha ^2} + {\beta ^2} + {\gamma ^2}} } \end{array}} \right. $ | (5) |
最小噪声可表示为:
| $ \sqrt {{\alpha ^2} + {\beta ^2} + {\gamma ^2}} \to \min $ | (6) |
求得相交直线空间表达式为:
| $ \frac{x}{{ - 0.1579}} = \frac{{y + 9.5915}}{{ - 0.5145}} = \frac{{z - 10.5915}}{{0.6724}} $ | (7) |
则最小噪声的几何意义为所求空间直线上某坐标点到空间原点(0, 0, 0)的最短距离,表 1为三频消电离层系数。
|
|
表 1 IF-PPP参数及最小噪声 Tab. 1 IF-PPP parameters and minimum noise |
本文采用高度角模型进行量化[9]。顾及到北斗星座由GEO/IGSO/MEO不同轨道卫星组成,3种轨道卫星的伪距和载波相位观测精度不同,本文采用表 2中基准噪声进行研究。
|
|
表 2 伪距和载波相位观测精度 Tab. 2 Observation accuracy of pseudorange and carrier phase |
采用扩展卡尔曼滤波进行参数估计,PPP计算过程中对流层改正、潮汐改正、相对论效应、潮汐改正等与GPS模型相同,具体处理策略见表 3。
|
|
表 3 精密单点定位参数处理策略 Tab. 3 Processing strategy of precise point positioning parameters |
本文选取科廷大学5个静态观测站CUT0、CUT2、CUTA、CUTB、CUTC的BDS三频观测数据,时间为2019-12-01(doy335),采样间隔为30 s,数据预处理时使用无几何组合和MW组合进行周跳探测与标记。位置误差由计算坐标与官方公布的参考坐标作差得到。
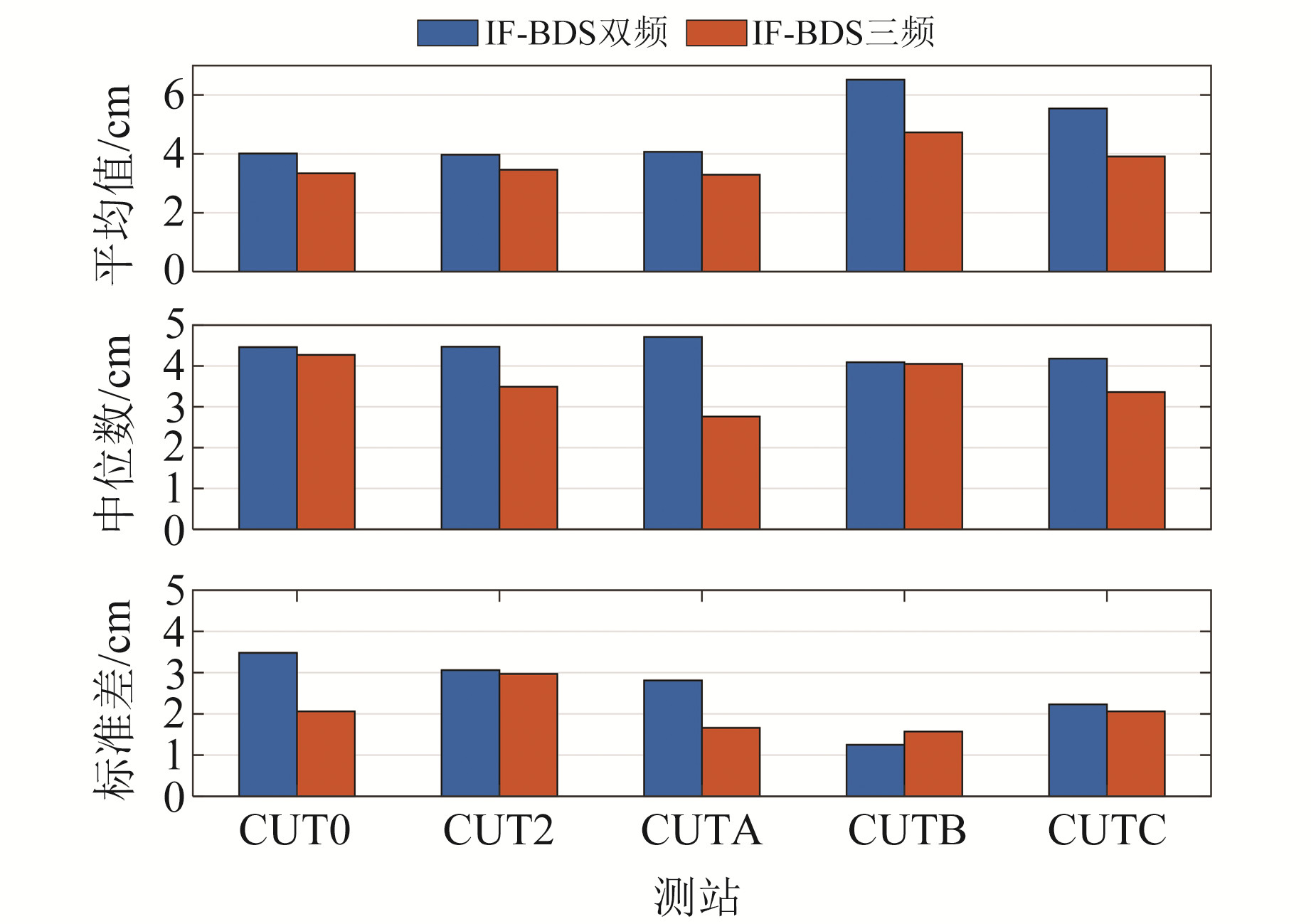
3.1.1 定位精度分析图 2为5个测站BDS双频PPP和三频PPP的3D位置误差平均值、中位数和标准差,表 4为统计结果。
|
图 2 测站位置误差统计 Fig. 2 Statistic of station position error |
|
|
表 4 测站位置误差统计 Tab. 4 Statistic of station position error |
从图 2和表 4可以看出,三频PPP定位精度和稳定性优于双频PPP,三频PPP位置误差平均值为3.75 cm,标准差为2.06 cm,比双频PPP减小22.3%和19.8%。其中CUTB站三频PPP的误差标准差高于双频,其原因可能为B3频率发生小周跳或钟跳。
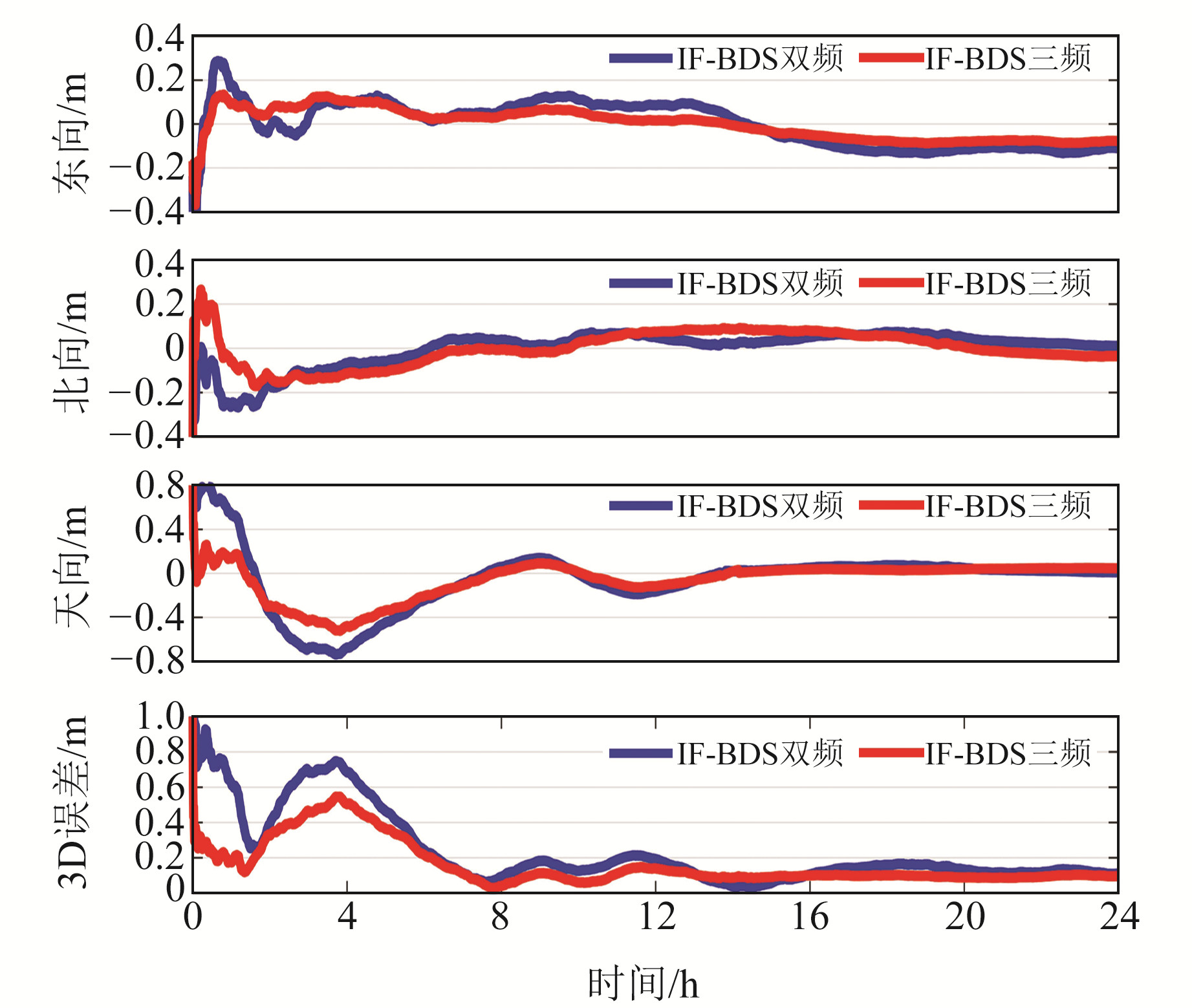
限于篇幅,本文仅给出CUTC站的位置误差序列图(图 3)。可以看出,三频PPP定位精度和收敛速度优于双频,但在4 h处三频PPP位置误差出现小幅增大,其原因为B3频点观测数据缺失或小周跳导致天向误差增大。
|
图 3 CUTC站位置误差序列 Fig. 3 Position error series of CUTC station |
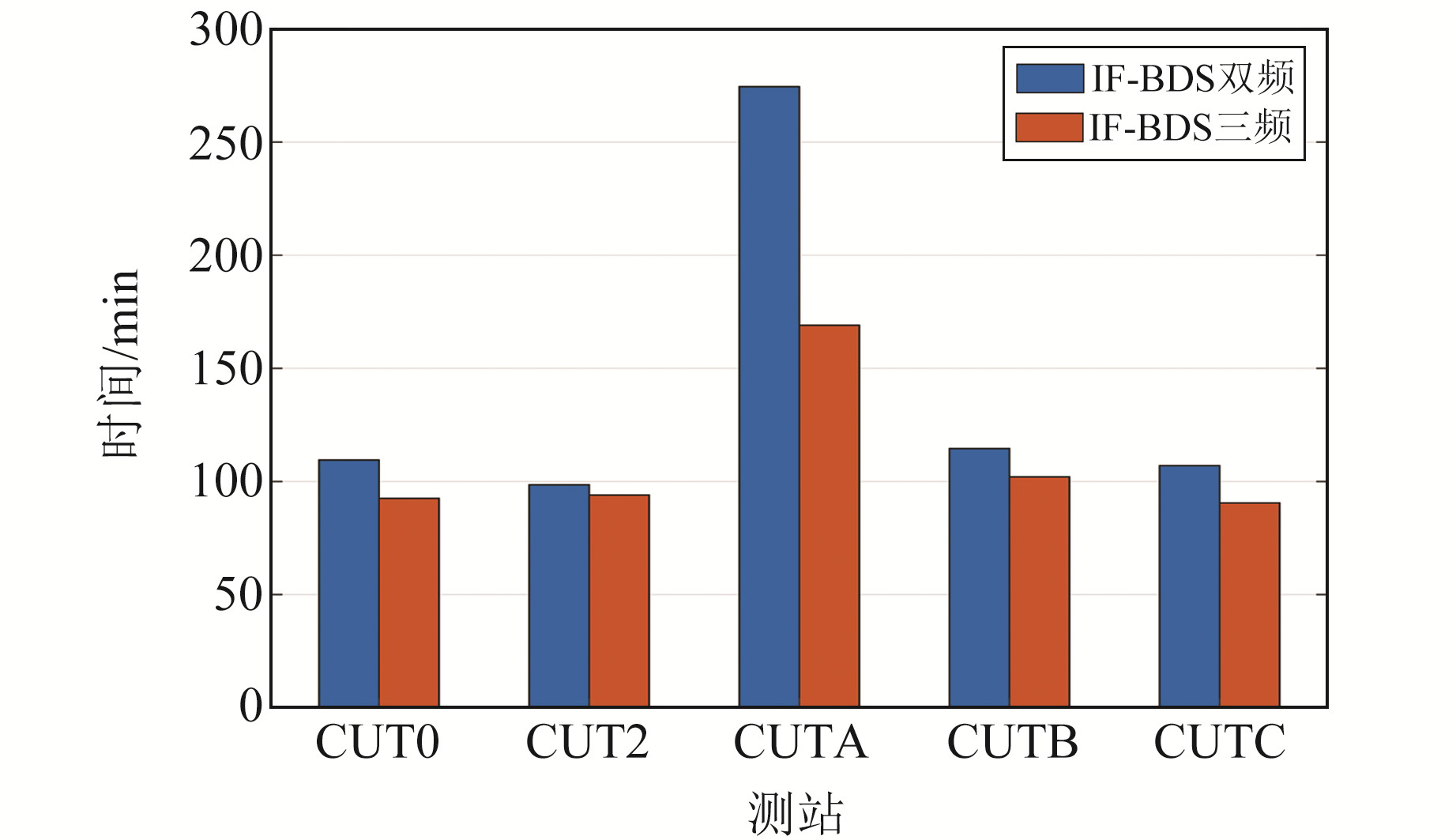
进一步分析三频观测量对收敛速度的影响,将收敛条件设置为三维位置误差连续5 min均小于10 cm。图 4为5个测站首次满足该条件的收敛时间,表 6为具体时间数值及统计结果。
|
图 4 测站收敛时间 Fig. 4 Convergence time of the stations |
|
|
表 6 动态PPP位置误差统计 Tab. 6 Statistic of position error of dynamic PPP |
从表 5可以看出,三频PPP平均收敛时间为109.6 min,较双频PPP缩短22.1%。其中CUTA站双频PPP收敛时间为274.5 min,明显高于平均时间,其原因为某一频率伪距出现异常,导致双频误差较大,收敛速度较慢,而三频模型可减少该频率粗差造成的影响,缩短收敛时间,体现出三频PPP具有一定优势。
|
|
表 5 收敛时间统计 Tab. 5 Statistic of convergence time |
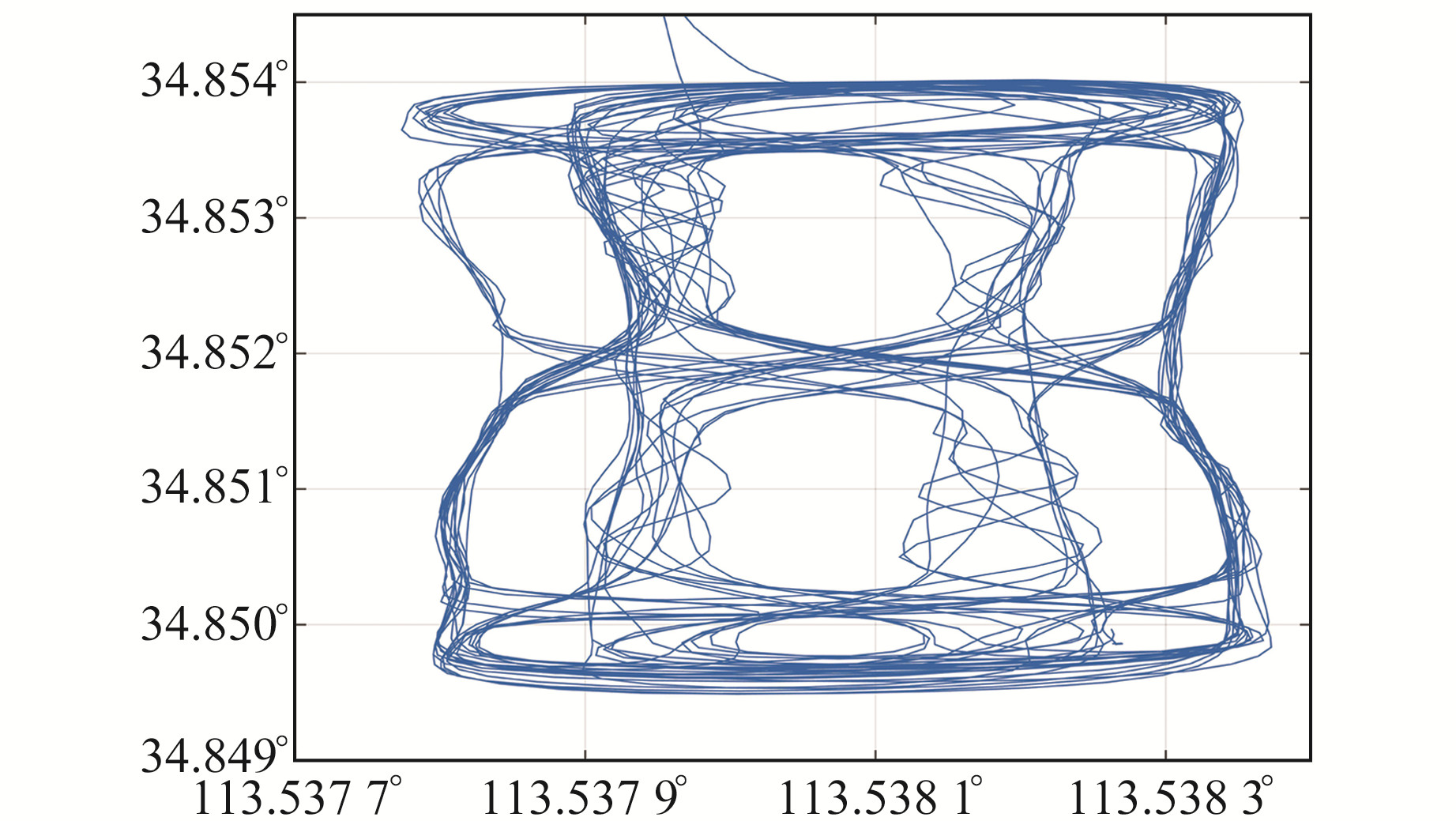
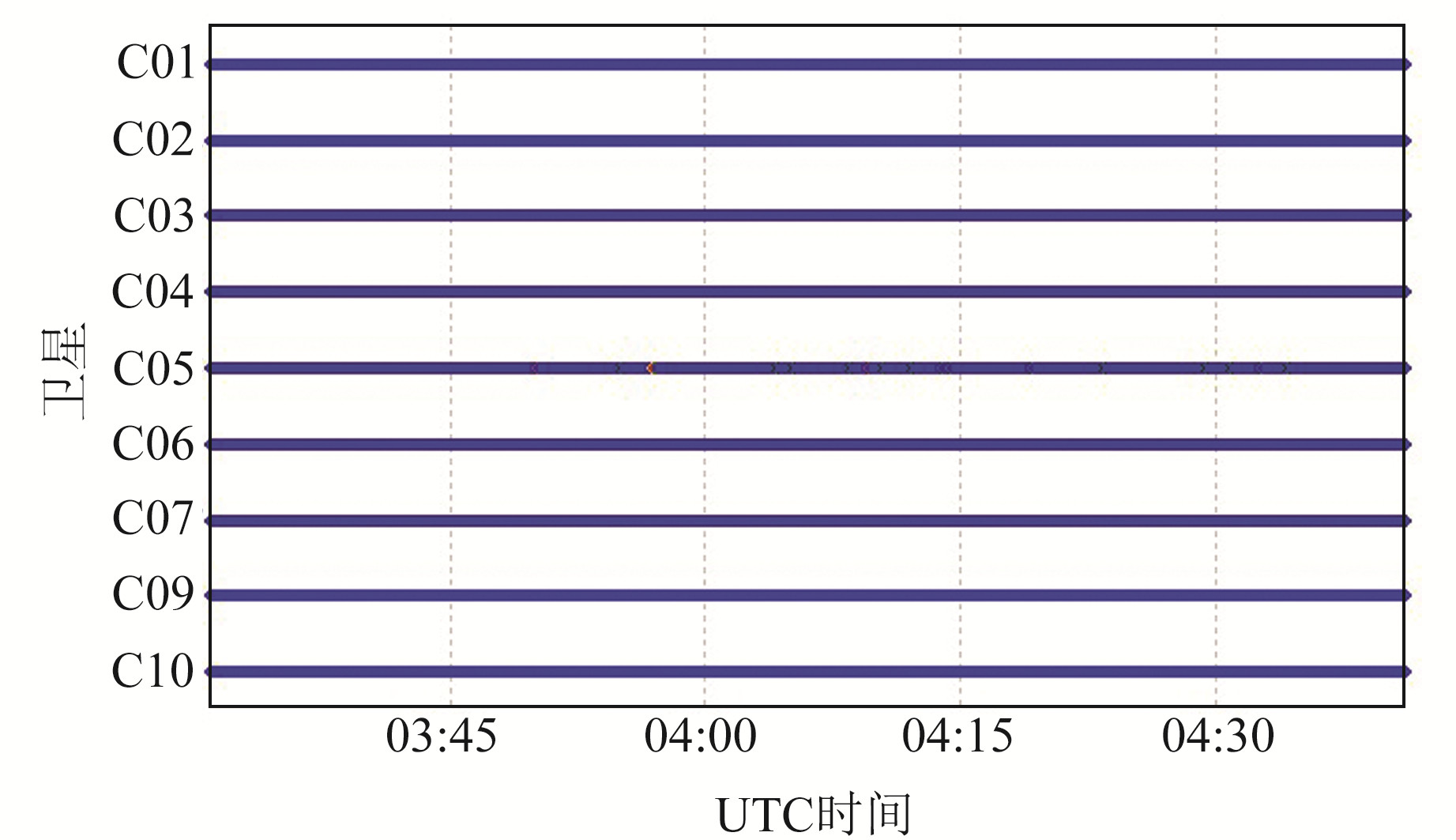
前期BDS PPP均基于静态数据进行仿动态研究,本文将采用1组实测跑车数据验证三频PPP在动态条件下的定位性能。实验GNSS接收机为司南M300 Pro,内置板卡可接收处理三系统八频(含BDS三频)信号,实验时长约75 min,采样间隔1 s,以三系统RTK解算坐标作为参考值。图 5、6为跑车轨迹以及卫星工作状态。
|
图 5 跑车轨迹 Fig. 5 Track of car |
|
图 6 观测卫星工作状态 Fig. 6 Working condition of observed satellites |
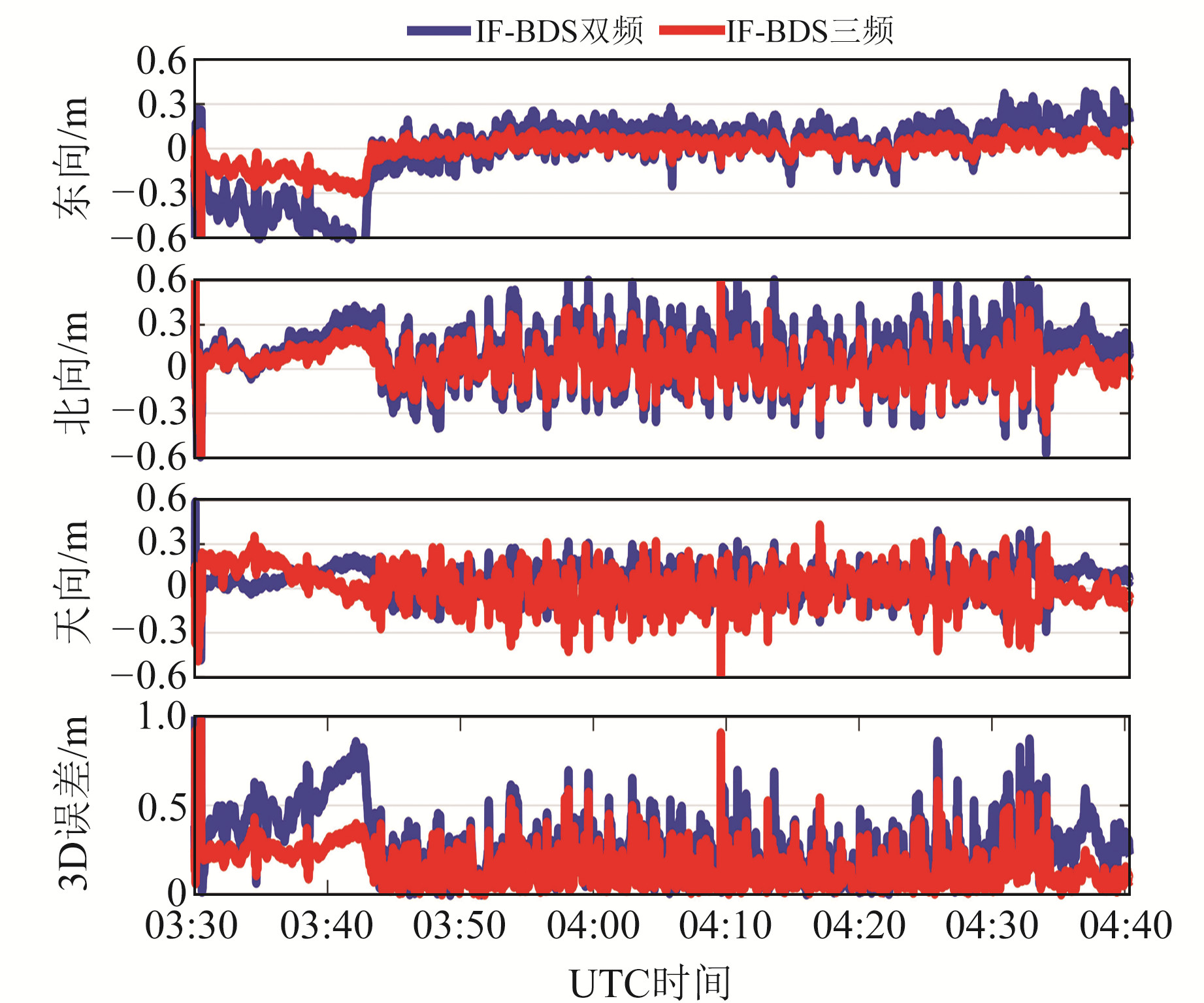
图 7为位置误差序列图,表 6为统计结果。分析可知,三频PPP位置误差为15.21 cm,标准差为12.89 cm,较双频PPP分别减小42.4%和26.8%,且收敛速度也优于双频PPP。
|
图 7 动态PPP位置误差序列 Fig. 7 Position error series of dynamic PPP |
基于空间几何原理计算得到三频消电离层模型参数,采用科廷大学5个静态观测站数据和1组实测动态跑车数据对比分析三频BDS PPP和双频BDS PPP的定位精度和收敛时间,得到以下结论:
1) 三频PPP的定位精度和收敛速度均明显优于双频PPP。静态条件下,三频PPP的位置误差为3.75 cm,标准差为2.06 cm,平均收敛时间为109.6 min,较双频PPP分别提升22.3%、19.8%、22.1%;动态条件下,三频PPP的位置误差为15.21 cm,标准差为12.89 cm,较双频PPP分别提升42.4%、26.8%,且收敛速度也更优。
2) 频率观测粗差会严重影响双频PPP的定位精度和收敛速度,三频PPP可有效减弱单频率粗差的影响,提高定位可靠性和稳定性。
3) 对比静态和动态实验可以看出,BDS PPP的位置误差较大,收敛速度慢而导致收敛时间较长,其原因为BDS卫星以GEO/IGSO为主,卫星几何结构变化较慢,伪距观测精度低,且GEO卫星精密星历精度比MEO卫星低。
| [1] |
杨元喜, 许扬胤, 李金龙, 等. 北斗三号系统进展及性能预测——试验验证数据分析[J]. 中国科学:地球科学, 2018, 48(5): 584-594 (Yang Yuanxi, Xu Yangyin, Li Jinlong, et al. Progress and Performance Evaluation of Beidou Global Navigation Satellite System: Data Analysis Based on BDS-3 Demonstration System[J]. Science China: Earth Sciences, 2018, 48(5): 584-594)
(  0) 0) |
| [2] |
张小红, 李星星, 李盼. GNSS精密单点定位技术及应用进展[J]. 测绘学报, 2017, 46(10): 1 399-1 407 (Zhang Xiaohong, Li Xingxing, Li Pan. Review of GNSS PPP and Its Application[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1 399-1 407)
(  0) 0) |
| [3] |
Deo M, El-Mowafy A. Triple-Frequency GNSS Models for PPP with Float Ambiguity Estimation: Performance Comparison Using GPS[J]. Survey Review, 2018, 50(360): 249-261 DOI:10.1080/00396265.2016.1263179
(  0) 0) |
| [4] |
张小红, 何锡扬. 北斗三频相位观测值线性组合模型及特性研究[J]. 中国科学:地球科学, 2015, 45(5): 601-610 (Zhang Xiaohong, He Xiyang. BDS Triple-Frequency Carrier-Phase Linear Combination Models and Their Characteristics[J]. Science China: Earth Sciences, 2015, 45(5): 601-610)
(  0) 0) |
| [5] |
Pan L, Zhang X H, Liu J N. A Comparison of Three Widely Used GPS Triple-Frequency Precise Point Positioning Models[J]. GPS Solutions, 2019, 23(4): 121 DOI:10.1007/s10291-019-0914-3
(  0) 0) |
| [6] |
张小红, 柳根, 郭斐, 等. 北斗三频精密单点定位模型比较及定位性能分析[J]. 武汉大学学报:信息科学版, 2018, 43(12): 2 124-2 130 (Zhang Xiaohong, Liu Gen, Guo Fei, et al. Model Comparison and Performance Analysis of Triple-Frequency BDS Precise Point Positioning[J]. Geomatics and Information Science of Wuhan University, 2018, 43(12): 2 124-2 130)
(  0) 0) |
| [7] |
彭利, 王玲, 黄文德, 等. 北斗双频/三频静态精密单点定位性能比较与分析[J]. 全球定位系统, 2017, 42(1): 53-58 (Peng Li, Wang Ling, Huang Wende, et al. Positioning Performance Comparison and Analysis on BDS Dual-and Triple Frequency Static Precise Point Positioning[J]. GNSS World of China, 2017, 42(1): 53-58)
(  0) 0) |
| [8] |
Guo F, Zhang X H, Wang J L. Timing Group Delay and Differential Code Bias Corrections for Beidou Positioning[J]. Journal of Geodesy, 2015, 89(5): 427-445 DOI:10.1007/s00190-015-0788-2
(  0) 0) |
| [9] |
李德伟.随机模型对GPS/BDS联合定位精度影响研究[D].淄博: 山东理工大学, 2016 (Li Dewei. The Improved Random Model in Combined GPS/BDS Positioning Precision[D]. Zibo: Shandong University of Technology, 2016)
(  0) 0) |
| [10] |
黄观文, 张睿, 张勤, 等. BDS卫星天线相位中心改正模型比较[J]. 大地测量与地球动力学, 2015, 35(4): 658-661 (Huang Guanwen, Zhang Rui, Zhang Qin, et al. Comparison and Analysis of Different Models of Antenna Phase Center Correction of BDS Satellites[J]. Journal of Geodesy and Geodynamics, 2015, 35(4): 658-661)
(  0) 0) |
| [11] |
Huang G W, Yan X Y, Zhang Q, et al. Estimation of Antenna Phase Center Offset for BDS IGSO and MEO Satellites[J]. GPS Solutions, 2018, 22(2): 49 DOI:10.1007/s10291-018-0716-z
(  0) 0) |
| [12] |
Wanninger L, Beer S. Beidou Satellite-Induced Code Pseudorange Variations: Diagnosis and Therapy[J]. GPS Solutions, 2015, 19(4): 639-648 DOI:10.1007/s10291-014-0423-3
(  0) 0) |
| [13] |
Lou Y D, Gong X P, Gu S F, et al. Assessment of Code Bias Variations of BDS Triple-Frequency Signals and Their Impacts on Ambiguity Resolution for Long Baselines[J]. GPS Solutions, 2017, 21(1): 177-186 DOI:10.1007/s10291-016-0514-4
(  0) 0) |
| [14] |
Zhang X H, Li X, Lu C X, et al. A Comprehensive Analysis of Satellite-Induced Code Bias for BDS-3 Satellites and Signals[J]. Advances in Space Research, 2019, 63(9): 2 822-2 835 DOI:10.1016/j.asr.2017.11.031
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40

