BDS-3卫星均搭载了Ka波段星间链路载荷,实现了星间距离测量和星间通讯功能,为BDS-3自主定轨核心功能的实现奠定了基础[1]。
不少学者给出了BDS-3自主定轨功能工程实现的理论方法和仿真分析结论[2-9],但尚未有结合BDS-3组网卫星开展自主定轨及实际性能的评估与分析。因此,本文主要开展基于实测星间测距数据的BDS-3基本系统的自主定轨处理,并重点评估可以实现的定轨和时间同步性能。
1 BDS-3星间链路距离测量情况BDS-3星间链路采用Ka频段,并基于相控阵天线的并发空分时分双工技术,在3.0 s内完成建链卫星之间的双向单程距离测量[9]。
对于自主定轨来说,星间链路距离测量的连续性情况、卫星之间的建链数目和建链所形成的几何构型都是影响定轨性能的重要因素,因此本文先对这3个方面进行分析。
本文的所有计算分析工作均针对BDS-3的基本系统展开,采用2019-06-01~30(MJD58 635~MJD58 664)期间分布在3个轨道面上正常在轨工作的18颗BDS-3 MEO卫星的星间链路观测数据。
1.1 星间链路的建链情况BDS-3 MEO卫星间存在持续可见、非持续可见、不可见3种可视关系,星间测量的连续性、建链数与卫星所在轨位、时隙路由规划等因素有关。
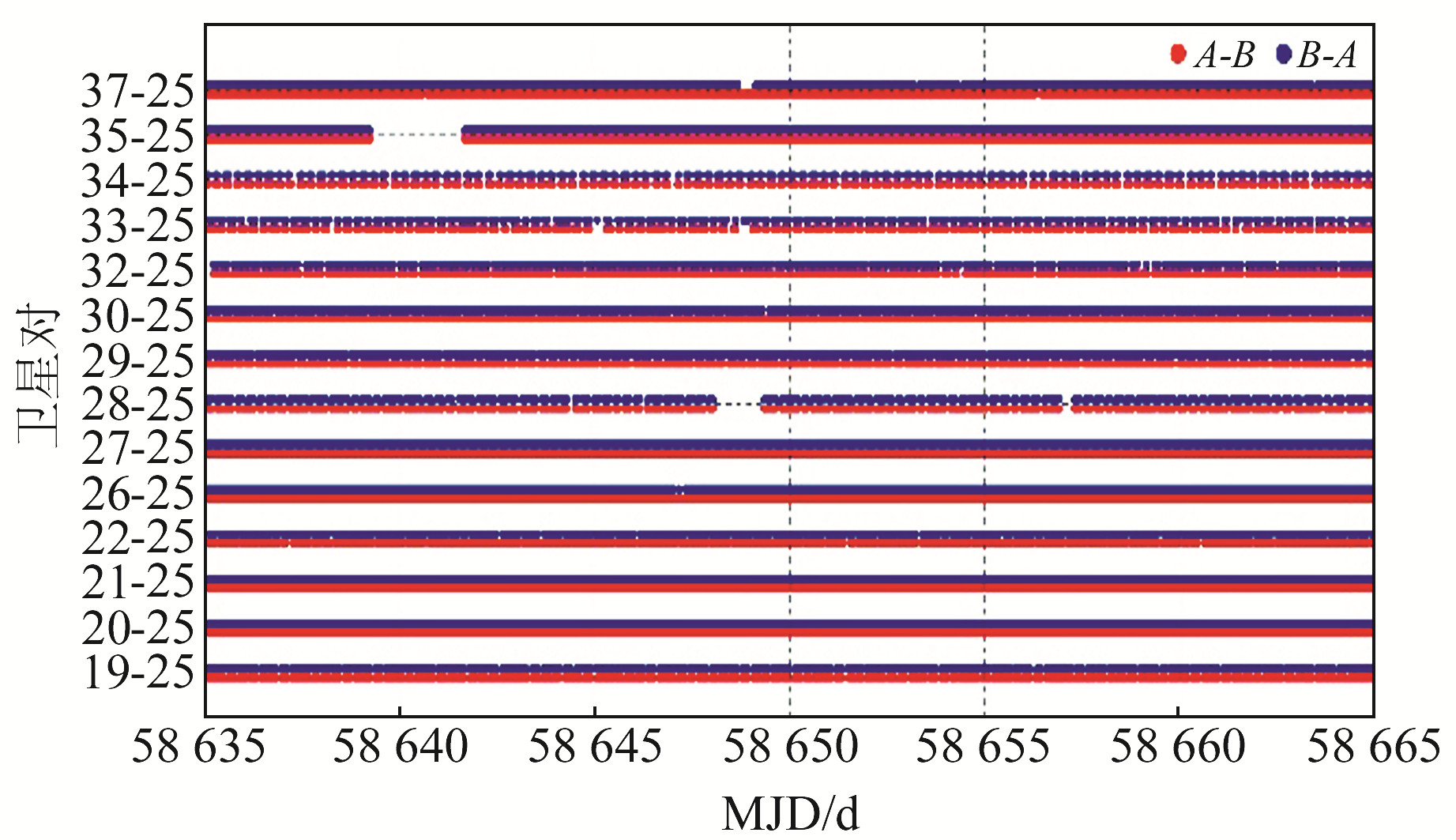
图 1给出了任意选取的C25卫星在连续30 d期间的星间测距工作状态,可以看出,在基本星座构型情况下,C25卫星总共与14颗卫星进行了建链测量,除了C28、C33、C34之外,与其他11颗卫星的跟踪测量较为连续。
|
图 1 BDS-3基本系统下C25卫星与其他卫星之间30 d的建链跟踪情况 Fig. 1 The 30-days tracking situation of ISL between the C25 and other satellites for the BDS-3 basic system |
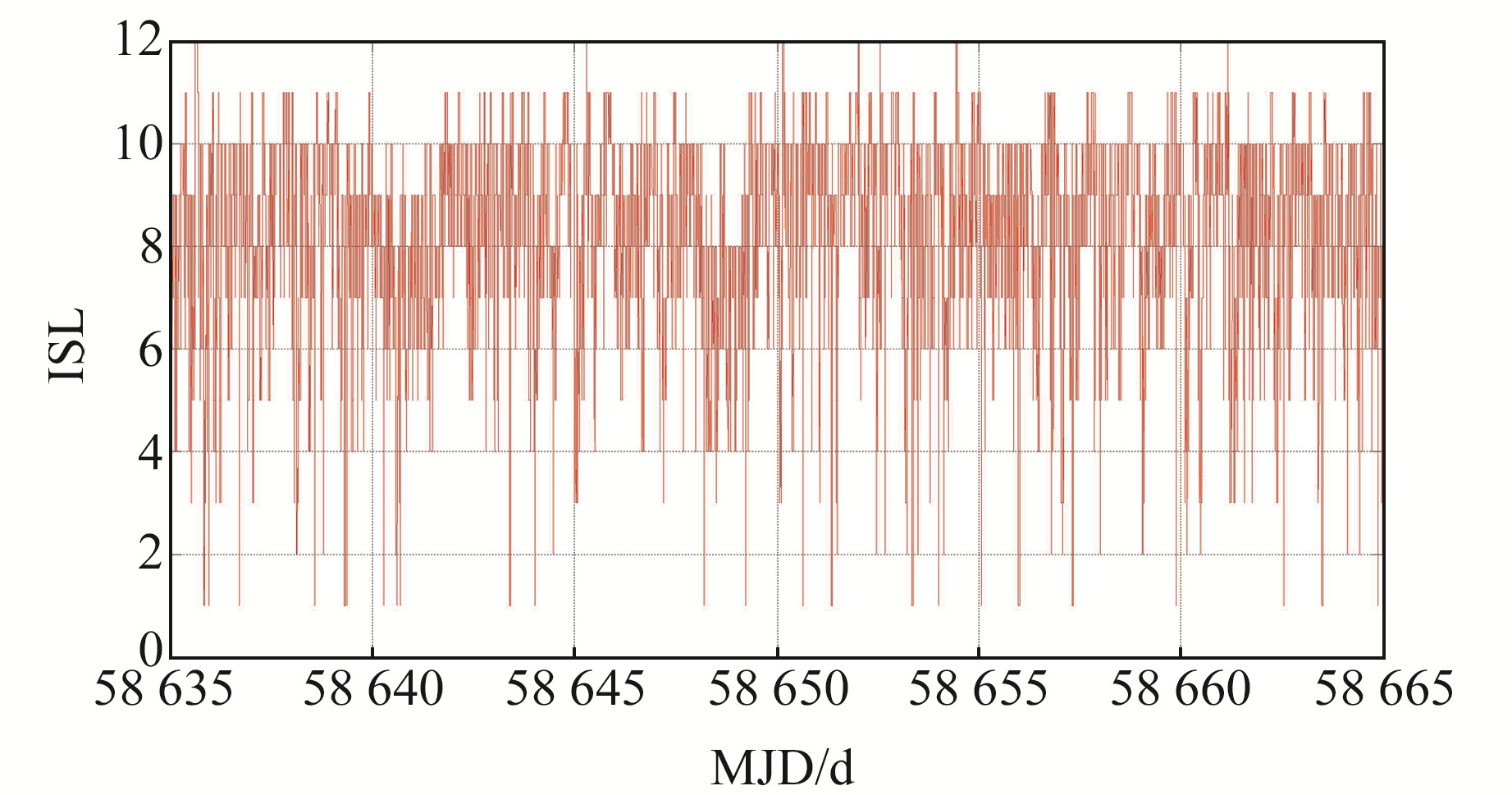
图 2给出了C25卫星在连续30 d期间的建链卫星数目的变化情况,可以看出,建链数目波动较大,最少为1条,最多时达到12条。表 1给出了基本系统MEO卫星的建链数统计情况,对所有卫星平均而言,最少建链数目为1条,最多为12.3条,平均建链数目为8.5条。
|
图 2 BDS-3基本系统下C25卫星30 d的链路跟踪数目 Fig. 2 The 30-day link tracking number of C25 satellite for BDS-3 basic system |
|
|
表 1 BDS-3基本系统下各卫星的建链数目统计 Tab. 1 The statistics of the number of ISL for each satellite for the BDS-3 basic system |
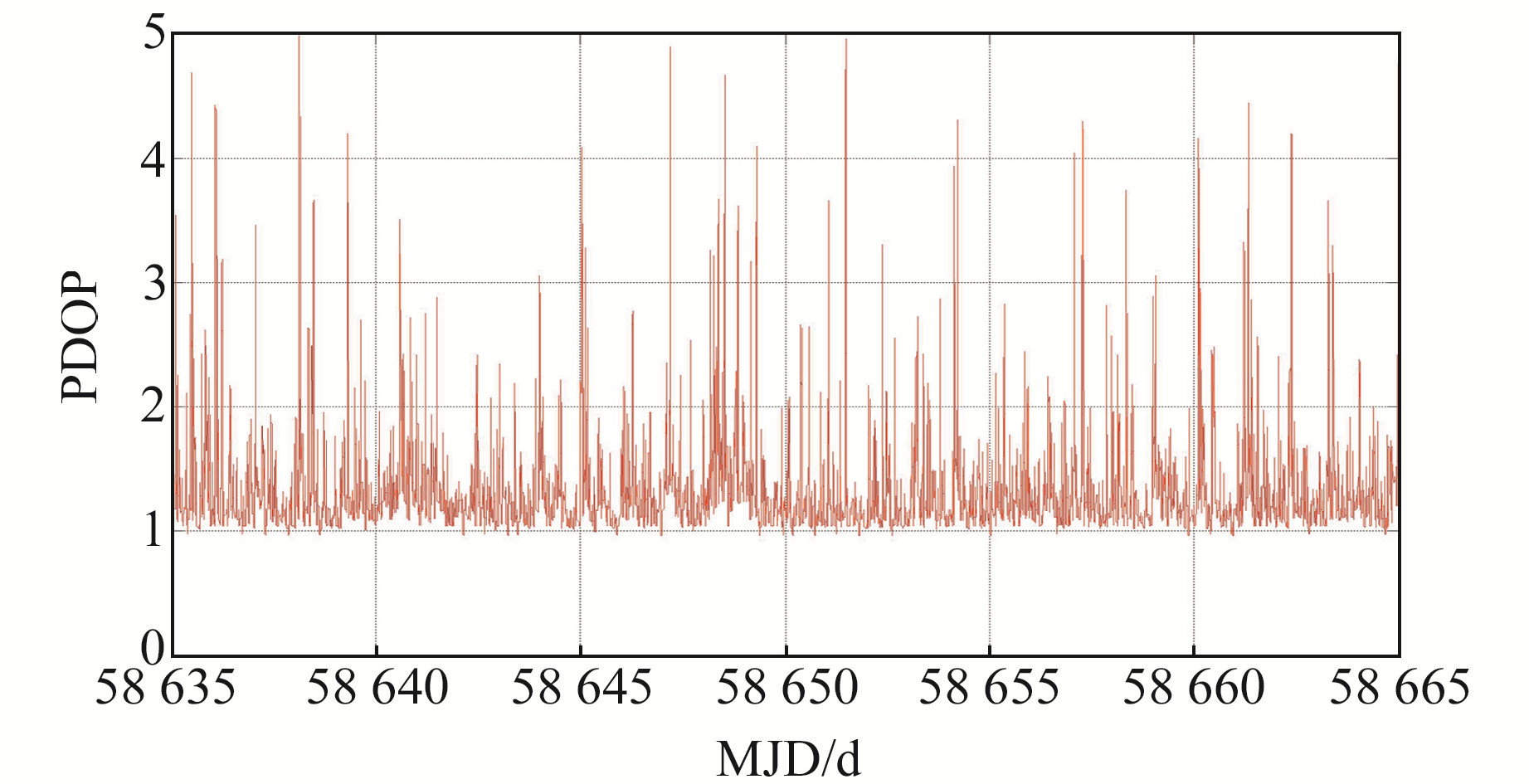
当与待评估卫星间的建链数目大于等于3条时,可以计算出相应的PDOP值以反映星间建链几何构型的好坏。图 3给出了C25卫星在连续30 d期间的PDOP值变化情况,表 2给出了所有基本星座18颗卫星的PDOP值统计情况。可以看出,所有卫星的平均最小PDOP值约为0.96,平均最大PDOP值约为4.99,平均PDOP值约为1.34,星间建链的几何图形结构整体较好,但在个别时间也会出现明显的PDOP值的跳跃,经分析,主要是星上时隙路由表切换导致的。
|
图 3 BDS-3基本系统下以C25卫星为定位对象的PDOP值变化情况 Fig. 3 The PDOP series of C25 satellite as a positioning object for BDS-3 basic system |
|
|
表 2 BDS-3基本系统下各卫星的PDOP值统计 Tab. 2 The statistics of PDOP for each satellite for the BDS-3 basic system |
卫星可以根据星间链路的时隙路由与视场中所有可见的卫星建立星间链路,在每个时隙内,多个卫星对会同时完成星间双向测量。
在3 s内的不同时刻,SVA和SVB卫星的观测方程可以表示为:
| $ \begin{array}{*{20}{c}} {{\rho _{AB}} = \left| {{R_B}\left( {{t_1}} \right) - {R_A}\left( {{t_1} - \Delta {t_1}} \right)} \right| + c \cdot {{{\mathop{\rm clk}\nolimits} }_B}\left( {{t_1}} \right) - }\\ {c \cdot {{{\mathop{\rm clk}\nolimits} }_A}\left( {{t_1} - \Delta {t_1}} \right) + c \cdot \tau _A^{{\rm{trans }}} + c \cdot \tau _B^{{\rm{rec }}} + \Delta \rho _{AB}^{{\rm{corr }}} + {\varepsilon _{AB}}} \end{array} $ | (1) |
| $ \begin{array}{*{20}{c}} {{\rho _{BA}} = \left| {{R_A}\left( {{t_2}} \right) - {R_B}\left( {{t_2} - \Delta {t_2}} \right)} \right| + c \cdot {{{\mathop{\rm clk}\nolimits} }_A}\left( {{t_2}} \right) - }\\ {c \cdot {{{\mathop{\rm clk}\nolimits} }_B}\left( {{t_2} - \Delta {t_2}} \right) + c \cdot \tau _B^{{\rm{trans }}} + c \cdot \tau _A^{{\rm{re }}} + \Delta \rho _{BA}^{{\rm{oorr }}} + {\varepsilon _{BA}}} \end{array} $ | (2) |
式中, RA、RB分别为SVA和SVB卫星的位置,c为光速,clkA和clkB分别为SVA和SVB卫星的钟差,Δt1和Δt2分别为ρAB和ρBA的传播时间,τtrans和τrec分别为卫星的发射时延和接收时延,ΔρABcorr和ΔρBAcorr为包括相对论效应、天线相位中心偏差等可以模型化的误差项,εAB和εBA分别为观测值的噪声。
在基于星间双向测距的导航星座自主定轨处理中,可以将相同时刻的双向星间链路观测值通过相加或相减形成定轨和时间同步,使得组合观测方程只包含轨道参数或钟差参数解耦,实现轨道参数和钟差参数的解耦,便于轨道确定和钟差计算。
首先,利用预报轨道和预报卫星钟差参数,将t1和t2时刻测量的观测值归算至最近的整3 s的t0时刻。考虑到双向观测值在非常短的时间内完成,轨道和钟差的预报误差可以忽略。
| $ \begin{array}{l} {\rho _{AB}}\left( {{t_0}} \right) = {\rho _{AB}} + \left| {{R_B}\left( {{t_0}} \right) - {R_A}\left( {{t_0}} \right)} \right| - \left| {{R_B}\left( {{t_1}} \right) - } \right.\\ \left. {{R_A}\left( {{t_1} - \Delta {t_1}} \right)} \right| + c \cdot \left( {{{{\mathop{\rm clk}\nolimits} }_B}\left( {{t_0}} \right) - {{{\mathop{\rm clk}\nolimits} }_A}\left( {{t_0}} \right)} \right) - \\ c \cdot \left( {{{{\mathop{\rm clk}\nolimits} }_B}\left( {{t_1}} \right) - {{{\mathop{\rm clk}\nolimits} }_A}\left( {{t_1} - \Delta {t_1}} \right)} \right) \end{array} $ | (3) |
| $ \begin{array}{l} {\rho _{BA}}\left( {{t_0}} \right) = {\rho _{BA}} + \left| {{R_A}\left( {{t_0}} \right) - {R_B}\left( {{t_0}} \right)} \right| - \left| {{R_A}\left( {{t_2}} \right) - } \right.\\ \left. {{R_B}\left( {{t_2} - \Delta {t_2}} \right)} \right| + c \cdot \left( {{{{\mathop{\rm clk}\nolimits} }_A}\left( {{t_0}} \right) - {{{\mathop{\rm clk}\nolimits} }_B}\left( {{t_0}} \right)} \right) - \\ c \cdot \left( {{{{\mathop{\rm clk}\nolimits} }_A}\left( {{t_2}} \right) - {{{\mathop{\rm clk}\nolimits} }_B}\left( {{t_2} - \Delta {t_2}} \right)} \right) \end{array} $ | (4) |
然后,将t0时刻双向伪距相加,整理可以得到只包含卫星轨道参数的观测方程:
| $ \begin{array}{*{20}{c}} {\frac{{{\rho _{AB}}\left( {{t_0}} \right) + {\rho _{BA}}\left( {{t_0}} \right)}}{2} = \left| {{R_B}\left( {{t_0}} \right) - {R_A}\left( {{t_0}} \right)} \right| + }\\ {\frac{{c \cdot \tau _A^ + }}{2} + \frac{{c \cdot \tau _B^ + }}{2} + {\varepsilon ^ + }} \end{array} $ | (5) |
式(5)即为自主定轨中的轨道确定观测方程,其中,τ+为卫星的发射时延与接收时延之和,在自主定轨中被称为时延和参数。
同时,将t0时刻双向伪距相减,整理可以得到星间相对钟差:
| $ \begin{array}{*{20}{c}} {\frac{{{\rho _{AB}}\left( {{t_0}} \right) - {\rho _{BA}}\left( {{t_0}} \right)}}{2} = c \cdot \left( {{{{\mathop{\rm clk}\nolimits} }_B}\left( {{t_0}} \right) - {{{\mathop{\rm clk}\nolimits} }_A}\left( {{t_0}} \right)} \right) + }\\ {\frac{{c \cdot \tau _A^ - }}{2} - \frac{{c \cdot \tau _B^ - }}{2} + {\varepsilon ^ - }} \end{array} $ | (6) |
式(6)即为自主定轨中的时间同步观测方程,其中,τ-为卫星的发射时延与接收时延之差,在自主定轨中被称为时延差参数。
对于仅利用星间链路测距数据的导航卫星自主定轨, 由于缺少外部基准,时延和参数及时延差参数是不可解的。经分析,BDS-3 MEO卫星的时延参数在时间上具有较好的稳定性[10],因此,在实际的数据处理中可以将先前精密标定的时延参数值直接代入自主定轨公式中。
同时,在仅利用星间链路测距观测值的导航星座自主定轨中也将不可避免地存在星座整体旋转误差问题[2-3],这在BDS-3自主定轨处理中必须考虑。本文采用宋小勇等[8]给出的一种整体约束补偿算法,在估计得到滤波解算轨道相对于参考轨道的星座旋转误差后,就可以对自主定轨中得到的轨道参数直接进行校正,实现对星座整体旋转误差的抑制。
3 BDS-3卫星自主定轨及结果分析 3.1 自主定轨处理方案及策略导航卫星自主定轨的处理模式主要分为集中式和分布式2种[3]。集中式算法可以有效使用所有观测信息,充分利用整网的约束条件,理论上能得到轨道的最优解,精度和可靠性高,但星上计算量较大;分布式算法可以有效减少星上的计算量,但结果并不是最优解,精度和可靠性较差。当前我国BDS-3卫星已搭配了星间链路载荷,其星上计算能力以及星上通讯能力有了很大提高,为集中式算法运用到未来的工程化实现中提供了一定的可行性,因此本文采用集中式算法进行自主定轨处理,以期评估BDS-3自主定轨有望实现的最优精度和整体性能。
在一般的精密定轨处理中,需要估计的参数包括卫星的轨道位置参数、速度参数、光压参数、钟差参数(钟差、钟速)以及其他附加参数。在本文的自主定轨处理中,考虑到自主定轨的精度需求、工程化实现以及目前星上处理器的性能限制,对自主定轨算法进行针对性的优化。表 3给出本文自主定轨解算所采用的具体模型及相关策略。其中,光压摄动采用ECOM模型,且使用较长弧段的BDS-3基本导航定轨产品对光压参数进行较为精细的建模,残余的模型误差在估计中不予考虑。这样可以减小参考轨道定向参数的预报误差,提高自主定轨中轨道面参数的精度,还可以保证较少的待估参数和较小的计算负荷。
|
|
表 3 自主定轨解算策略 Tab. 3 Processing strategy of the autonomous orbit determination(AOD) |
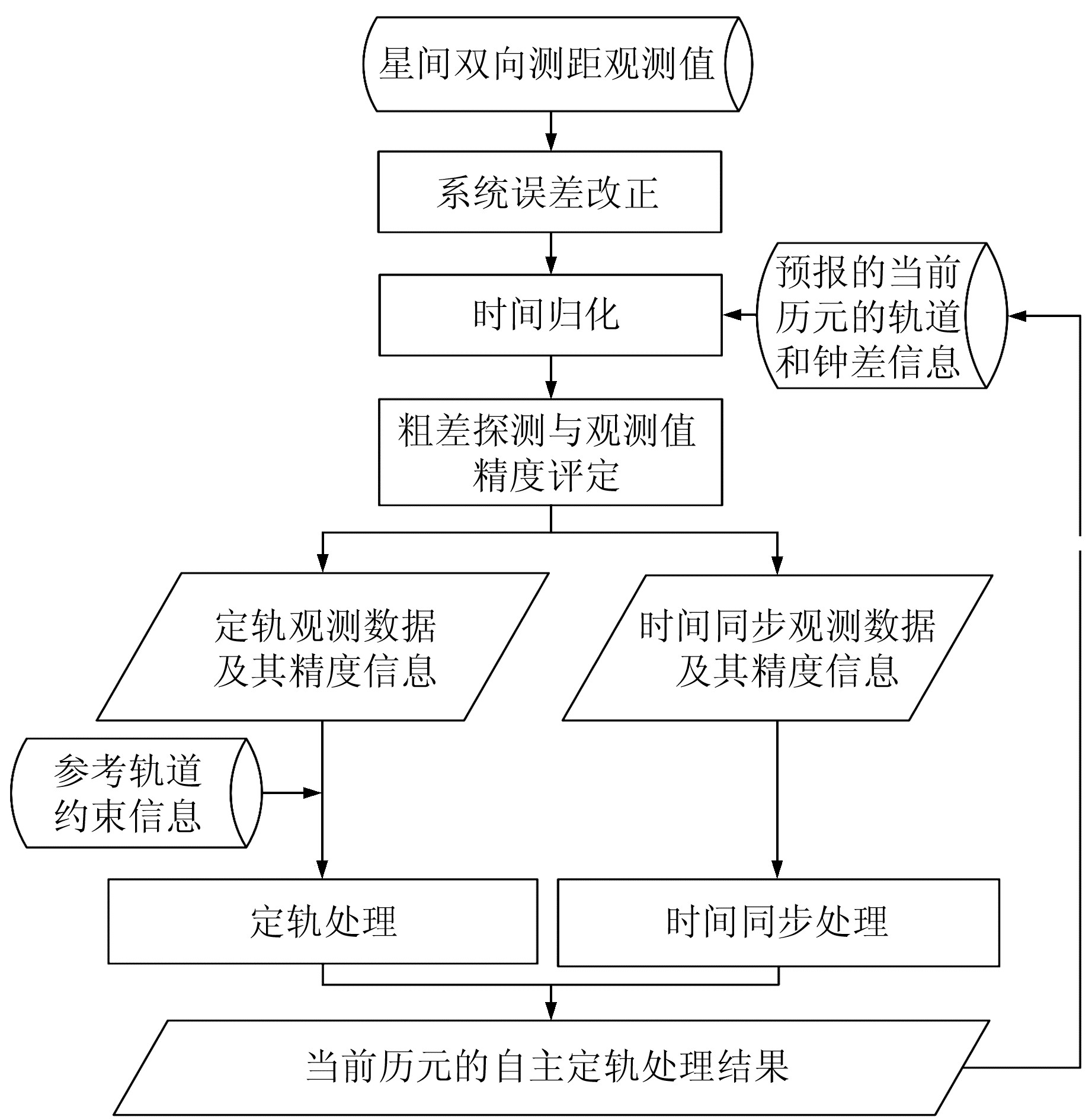
在本文的自主定轨数据处理中,首先进行必要的观测误差改正;然后根据预报的当前历元的轨道和钟差信息对观测数据进行时间归化处理;进而探测并剔除粗差观测数据,并导出不包含粗差数据的定轨观测数据和时间同步观测数据;最后采用轨道估计和时间同步估计2个独立的滤波器分别实现定轨和时间同步的处理解算(图 4)。
|
图 4 自主定轨数据处理流程 Fig. 4 Data process chart of AOD |
采用武汉大学IGS分析中心WUM发布的BDS-3卫星事后精密轨道和钟差产品对自主定轨所获得的轨道和钟差进行评估。
3.3.1 轨道评估方案将2种轨道求差,并转换为径向R、切向A和法向C方向上的误差,同时统计轨道综合误差URE。对于MEO卫星来说,卫星的地心距离约为28 000 km。若不考虑钟差带来的误差,则MEO卫星的轨道URE计算方法可表述为[11]:
| $ {\rm{URE}} = \sqrt {0.96{\rm{d}}{R^2} + 0.04\left( {{\rm{d}}{A^2}{\rm{ + d}}{C^2}} \right)} $ | (7) |
式中,dR、dA和dC分别为径向R、切向A和法向C的定轨误差。
3.3.2 钟差评估方案采用双差评估方法进行钟差评估,重点考察的是星座内的自主时间同步能力。该方法可以简述如下[12]。
在选择一个时钟产品作为比较的基准后,不同卫星钟误差在单个历元的钟差单差为:
| $ {\Delta ^j}(i) = \delta {t^j}(i) - \delta t_{{\rm{ref}}}^i(i) $ | (8) |
式中,Δj(i)为钟差单差,δtj(i)和δtrefi(i)分别为卫星j的待评估钟差和基准钟差。由上述公式得到的钟差单差包含了卫星钟初始时钟偏差的影响,不能真实反映时钟的精度。因此,有必要消除初始时钟偏差的影响。在一个连续弧段中,可以选择一颗卫星作为参考卫星,任意卫星j的钟差偏差扣除参考卫星的钟差偏差表示为:
| $ \nabla {\Delta ^j}\left( i \right) = {\Delta ^j}\left( i \right) - {\Delta ^{{\rm{ref}}}}\left( i \right) $ | (9) |
式中,∇Δj(i)为扣除参考卫星的钟差偏差后得到的相对钟差偏差,Δj(i)和Δref(i)分别为卫星j的钟差偏差与参考卫星的钟差偏差。最后,用∇Δj(i)的标准差(STD)来反映待评估钟差的精度。
需要说明的是,武汉大学WUM所发布的BDS-3精密钟差是采用B1I和B3I组合观测值计算获得的,而本文自主定轨中的钟差参数实际上与北斗广播钟差采用的频点相关,均为B3I频点。因此,在进行具体的钟差比较时,还需要考虑这2种钟差参数之前的硬件时延偏差的影响。
3.4 定轨精度分析本文使用作者自研的北斗卫星自主定轨处理软件,按照上述方案和策略,对2019-06-01~30(MJD58 635~MJD58 664)期间BDS-3基本系统的18颗MEO卫星的星间链路测距数据进行连续30 d的自主定轨处理,程序运行正常、稳定。
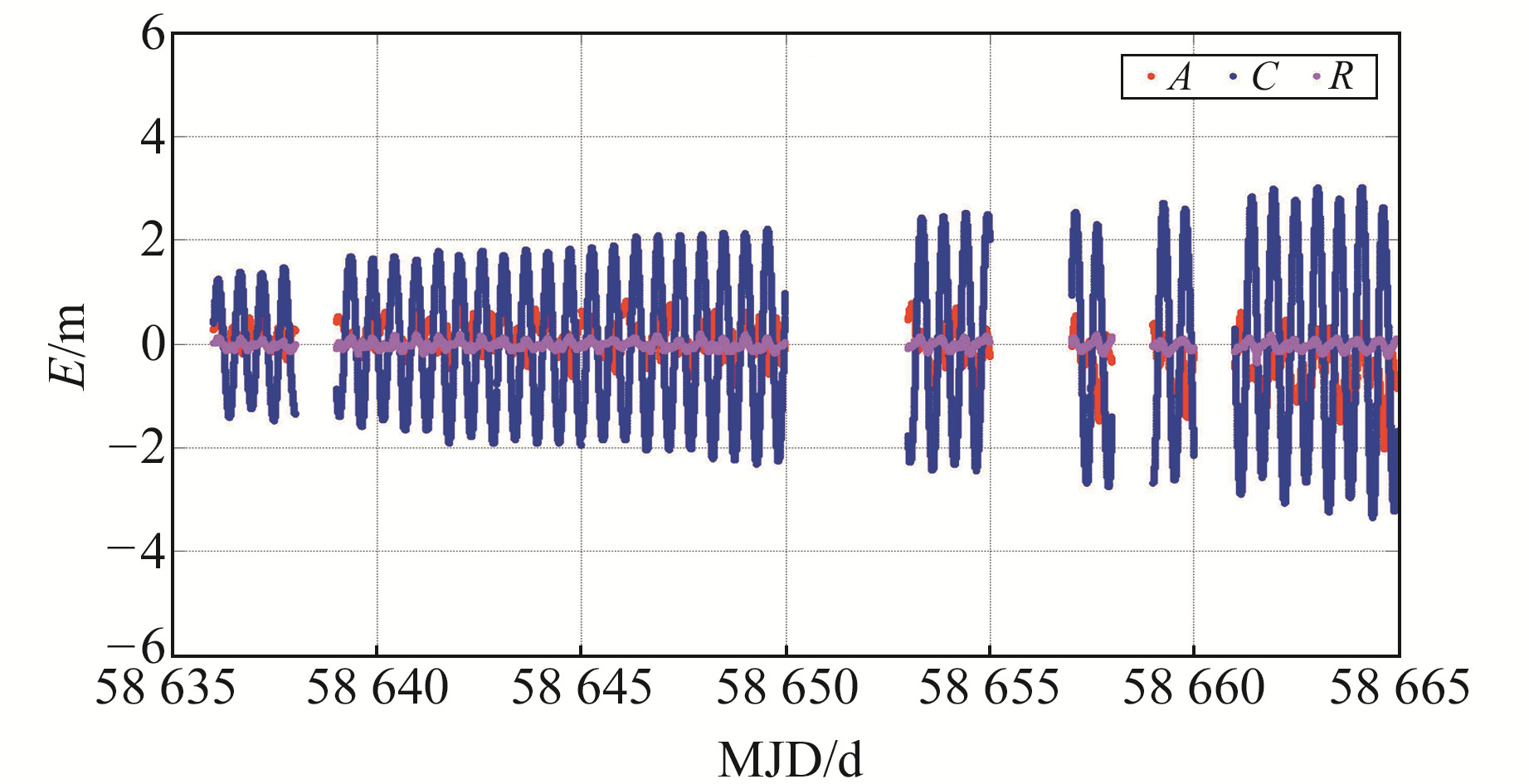
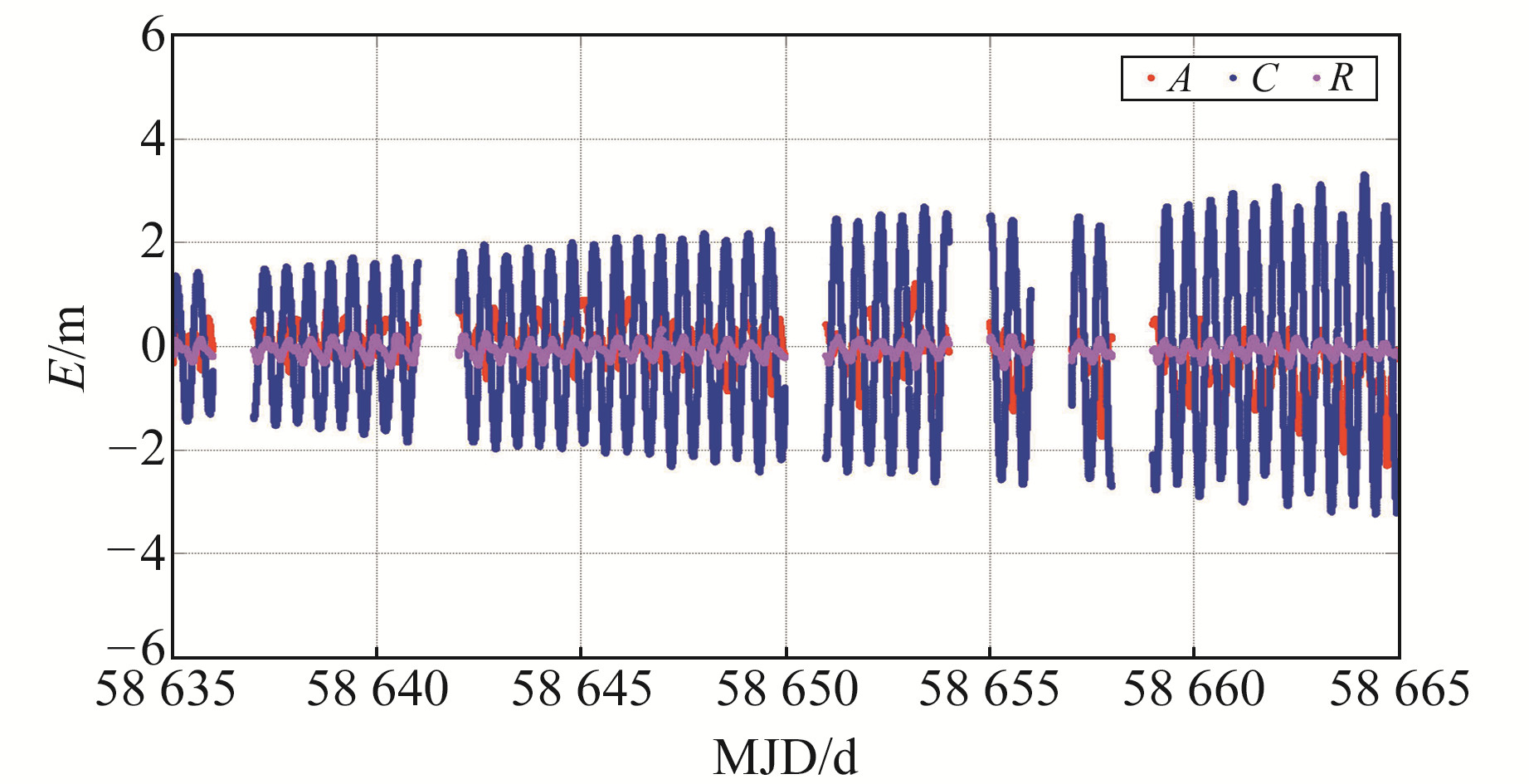
对自主定轨结果,按照§3.3的轨道评估方案进行定轨结果分析。图 5、6给出任意选取的C24和C25卫星连续30 d的自主定轨的误差序列,图中结果中断部分的原因是缺少用作参考的精密轨道。从单颗卫星的自主定轨结果来看,卫星的径向误差很小,法向误差的波动范围明显大于其他2个方向。这是因为,在自主定轨中,由于缺少轨道面的方向基准,不得不使用预报的轨道面法向参数对自主定轨结果进行约束或校正,而光压参数不准导致轨道面法向预报精度不高,从而使自主定轨的轨道法向误差较大。
|
图 5 BDS-3基本系统下C24卫星的自主定轨轨道误差序列 Fig. 5 Orbit error series of AOD of C24 satellite for BDS-3 basic system |
|
图 6 BDS-3基本系统下C25卫星的自主定轨轨道误差序列 Fig. 6 Orbit error series of AOD of C25 satellite for BDS-3 basic system |
表 4(单位m)给出基本星座18颗MEO卫星自主定轨30 d的平均精度统计情况。同时,考虑到自主定轨的总体误差随自主定轨时间增加而逐渐增大的特点,所以表 5(单位m)给出第30天的自主定轨精度统计情况。可以看出,所有卫星的三维位置误差和URE量级基本一致,除C23和C32卫星之外,其他卫星的径向能够保持0.2 m的精度,切向和法向呈现出精度慢慢变大的趋势。对于所有18颗卫星来说,30 d的轨道平均三维误差为2.04 m,轨道URE的平均RMS为0.47 m;第30天的轨道平均三维误差为2.71 m,轨道URE的RMS为0.59 m。此外,C23和C32卫星的径向、URE误差明显大于其他16颗卫星,经初步分析,与两者相关的观测值验后残差明显大于其他卫星,这可能与其观测噪声较大、时延参数标定不够准确有关,深层次的原因有待进一步分析。
|
|
表 4 BDS-3基本系统所有卫星自主定轨30 d的轨道平均精度 Tab. 4 The 30-days average orbit accuracy of AOD of all satellites for BDS-3 basic system |
|
|
表 5 BDS-3基本系统所有卫星自主定轨第30天的轨道精度 Tab. 5 The orbit accuracy of the 30th day of AOD of all satellites for BDS-3 basic system |
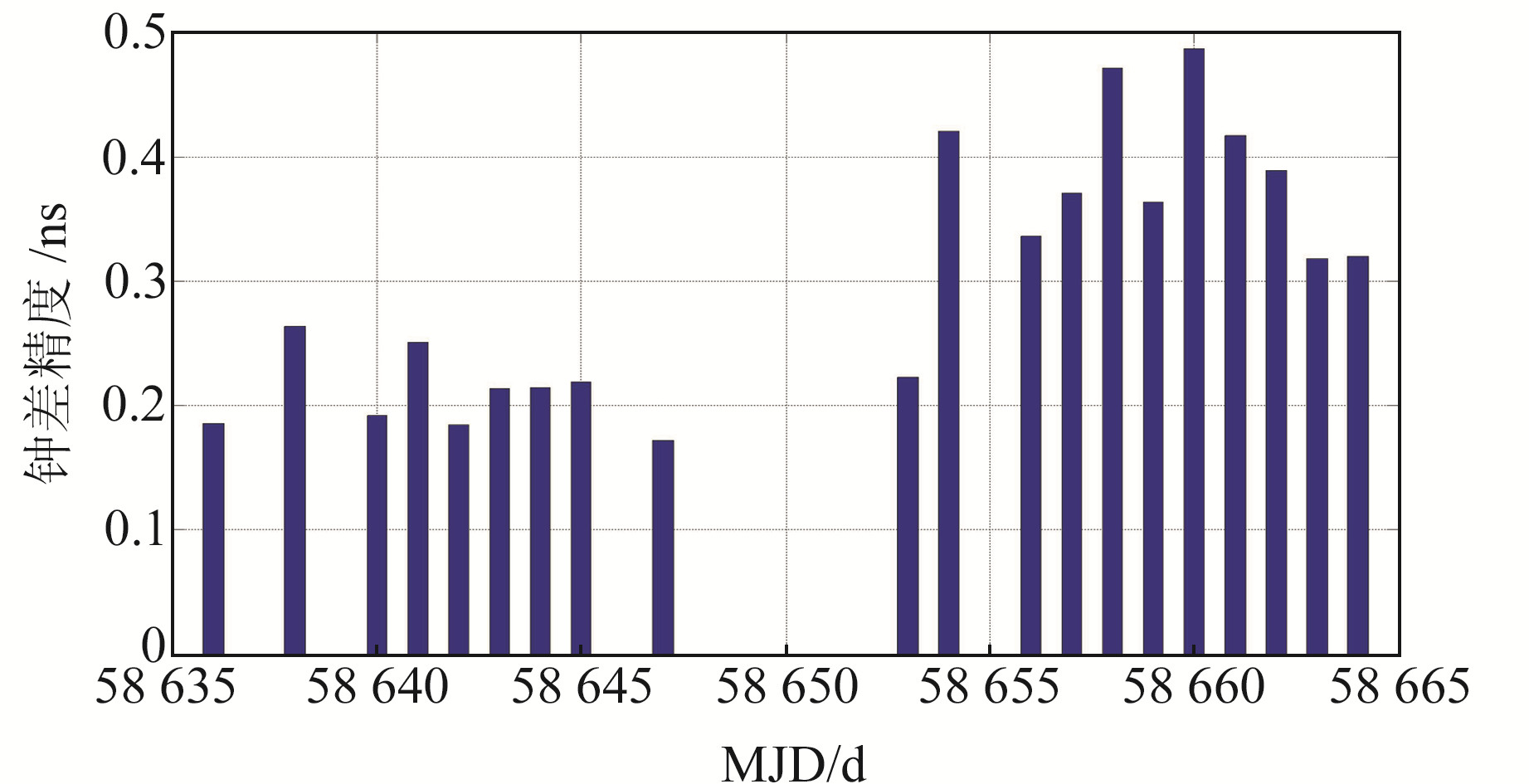
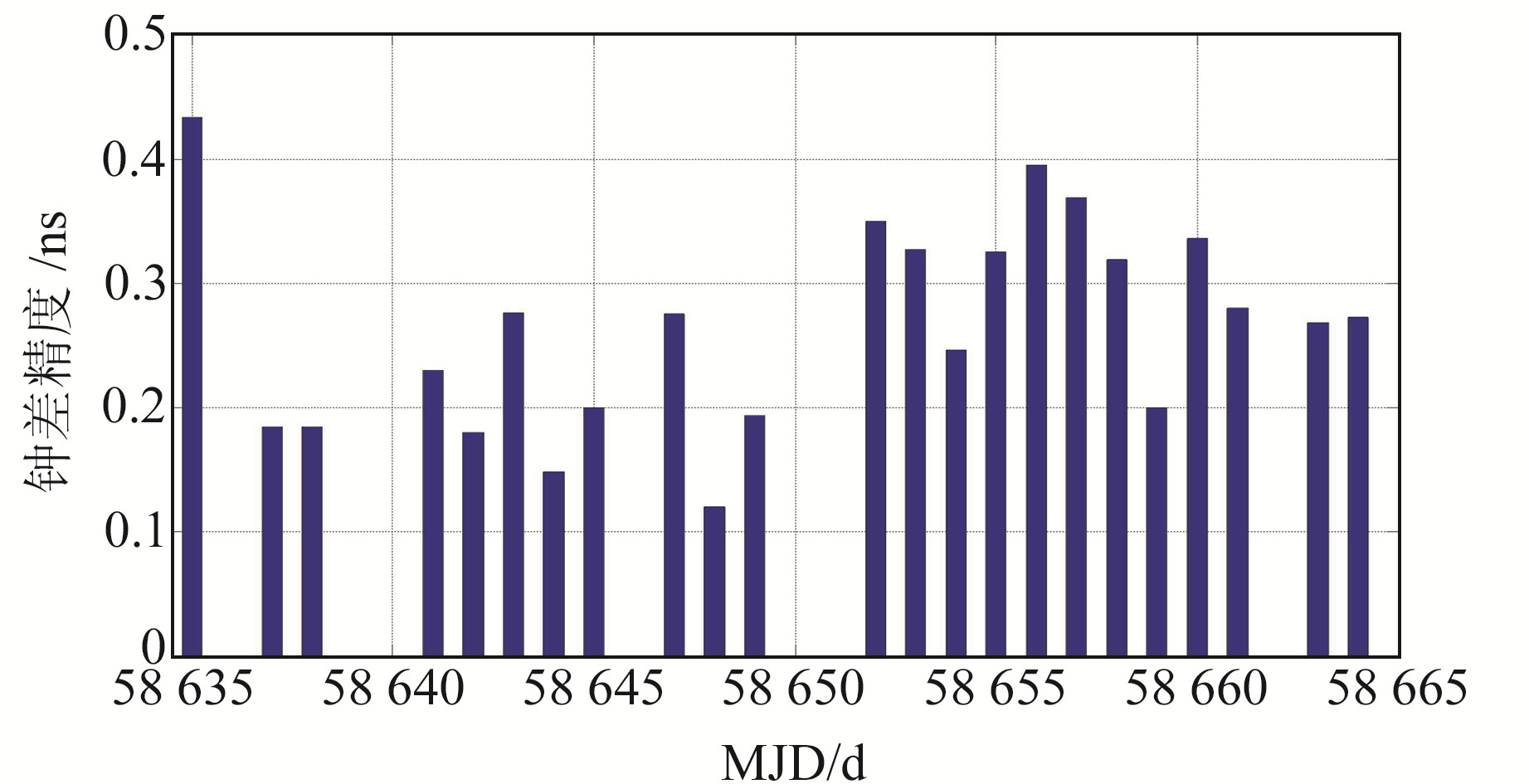
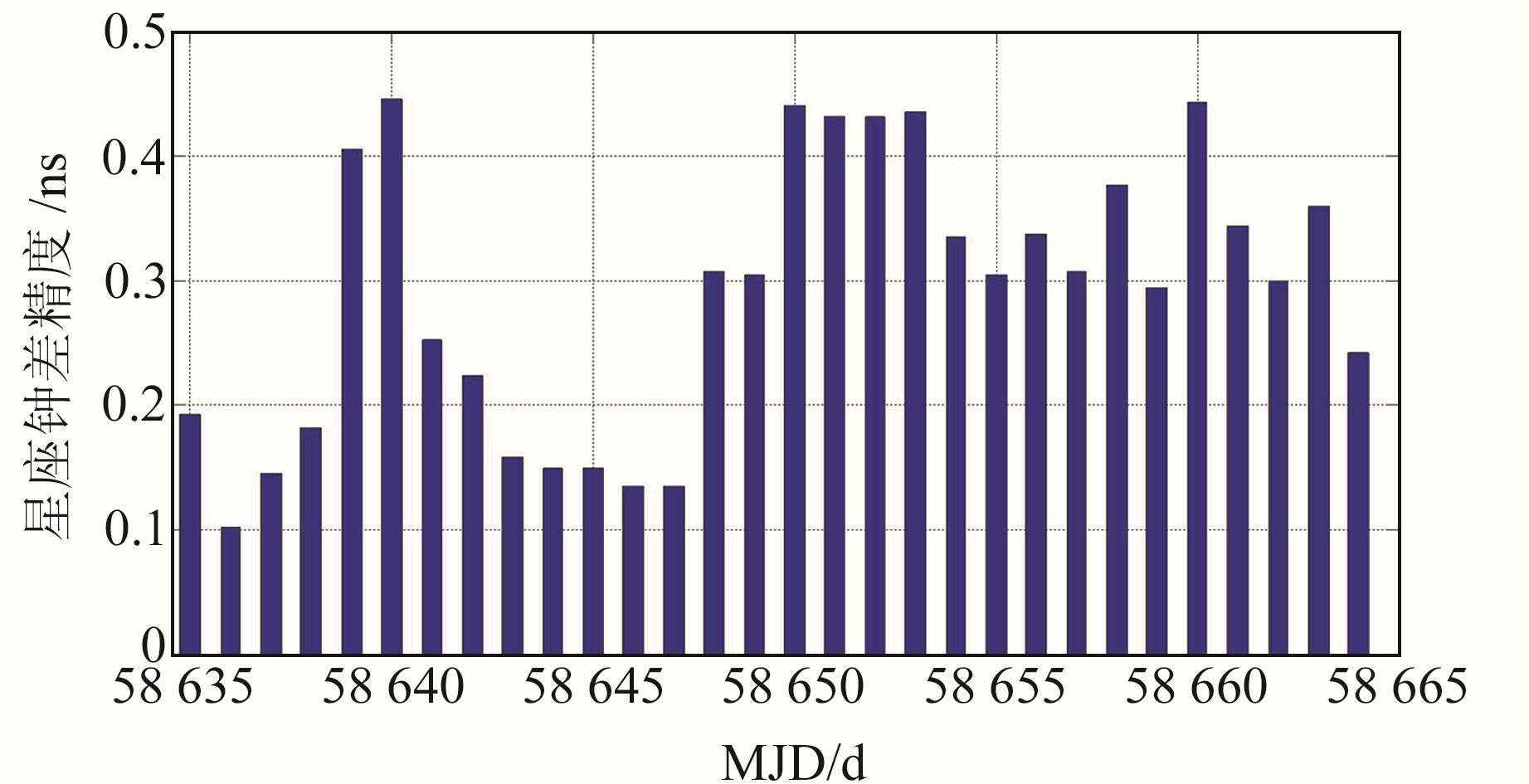
将C19卫星作为参考卫星,按照上述钟差评估方案对30 d的自主时间同步结果进行评估分析。图 7、8为任意选取的C24和C25卫星连续运行30 d的日钟差精度RMS,30 d的钟差平均RMS分别为0.29 ns和0.28 ns,图中间断的原因是缺少作为参考的精密钟差,导致不能进行该段时间的评估。图 9为整网卫星的钟差评估精度,结果表明,虽然卫星钟差相对参考星包含有初始的偏差,但整网卫星的钟差精度在30 d基本一致,所有卫星的平均钟差RMS约为0.31 ns。
|
图 7 BDS-3 C24卫星自主时间同步30 d的钟差精度 Fig. 7 The clock accuracy of autonomous time synchronization of BDS-3 C24 satellite for 30 days |
|
图 8 BDS-3 C25卫星自主时间同步30 d的钟差精度 Fig. 8 The clock accuracy of autonomous time synchronization of BDS-3 C25 satellite for 30 days |
|
图 9 BDS-3基本系统自主时间同步30 d的星座整体钟差精度 Fig. 9 The constellation overall clock accuracy of the BDS-3 basic system autonomous time synchronization for 30 days |
本文简要给出BDS-3卫星自主定轨的模型和处理方案,并针对BDS-3基本系统,分析18颗正常在轨工作的MEO的星间链路跟踪性能,开展基于实测星间链路数据的BDS-3自主定轨处理及性能分析。结果表明:
1) BDS-3星间链路测距功能工作状态正常,测距数据连续性较好,单星平均建链数目较多,约为8.5条;星间建链几何构型好,平均PDOP值约为1.34。
2) 连续30 d的集中式自主定轨运行处理正常稳定,与武汉大学WUM发布的事后精密产品比较表明,所有卫星轨道URE的30 d平均三维误差为2.04 m,平均RMS为0.47 m,星座相对时间同步误差的平均RMS约为0.31 ns,自主定轨整体结果稳定可靠。
本文完成的工作和获得的相关结论可为后续我国BDS-3自主定轨功能的工程化实现提供一定的参考。然而,在缺少地面参考基准的情况下,利用星间链路测距数据进行导航星座自主定轨是无法彻底消除自主定轨星座旋转误差的,后续有待进一步开展基于锚固支持下的导航星座自主定轨技术的研究及性能分析。
| [1] |
谭述森. 北斗卫星导航系统的发展与思考[J]. 宇航学报, 2008, 29(2): 391-396 (Tan Shusen. Development and Thought of Compass Navigation Satellite System[J]. Journal of Astronautics, 2008, 29(2): 391-396)
(  0) 0) |
| [2] |
张艳.基于星间观测的星座自主导航方法研究[D].长沙: 国防科学技术大学, 2005 (Zhang Yan. Study on Autonomous Navigation of Constellation Using Inter-Satellite Measurement[D]. Changsha: National University of Defense Technology, 2005)
(  0) 0) |
| [3] |
刘万科.导航卫星自主定轨及星地联合定轨的方法研究和模拟计算[D].武汉: 武汉大学, 2008 (Liu Wanke.Research and Simulation of Autonomous Orbit Determination of Navigation Satellite and Joint Orbit Determination of Satellite and Earth[D].Wuhan: Wuhan University, 2008)
(  0) 0) |
| [4] |
王甫红, 刘万科, 林晓静.分布式导航卫星自主定轨滤波算法与模拟分析[C].中国卫星导航学术年会, 上海, 2011 (Wang Fuhong, Liu Wanke, Lin Xiaojing.Distributed Autonomous Orbit Determination of Global Navigation Constellation Via Inter-Satellite Pseudo-Ranging Measurements[C].China Satellite Navigation Conference, Shanghai, 2011)
(  0) 0) |
| [5] |
郑晋军, 林益明, 陈忠贵, 等. GPS星间链路技术及自主导航算法分析[J]. 航天器工程, 2009, 18(2): 28-35 (Zheng Jinjun, Lin Yiming, Chen Zhonggui, et al. GPS Crosslink Technology and Autonomous Navigation Algorithm Analysis[J]. Spacecraft Engineering, 2009, 18(2): 28-35)
(  0) 0) |
| [6] |
陈艳玲, 胡小工, 周善石, 等. 基于星间测距的导航卫星自主定轨新算法[J]. 中国科学:物理学力学天文学, 2015, 45(7) (Chen Yanling, Hu Xiaogong, Zhou Shanshi, et al. A New Autonomous Orbit Determination Algorithm Based on Inter-Satellite Ranging Measurements[J]. Scientia Sinica Physica, Mechanica and Astronomica, 2015, 45(7))
(  0) 0) |
| [7] |
杜玉军.分布式导航卫星自主定轨星座整体旋转及抑制方法研究[D].武汉: 武汉大学, 2015 (Du Yujun.Study on the Whole Rotation and Suppression Method of Autonomous Orbit Constellation of Distributed Navigation Satellite[D].Wuhan: Wuhan University, 2015)
(  0) 0) |
| [8] |
宋小勇, 毛悦, 冯来平, 等. BD卫星星间链路定轨结果及分析[J]. 测绘学报, 2017, 46(5): 547-553 (Song Xiaoyong, Mao Yue, Feng Laiping, et al. The Preliminary Result and Analysis for BD Orbit Determination with Inter-Satellite Link Data[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(5): 547-553)
(  0) 0) |
| [9] |
唐成盼, 胡小工, 周善石, 等. 利用星间双向测距数据进行北斗卫星集中式自主定轨的初步结果分析[J]. 中国科学:物理学力学天文学, 2017, 47(2) (Tang Chengpan, Hu Xiaogong, Zhou Shanshi, et al. Centralized Autonomous Orbit Determination of Beidou Navigation Satellites with Inter-Satellite Link Measurements: Preliminary Results[J]. Scientia Sinica Physica, Mechanica and Astronomica, 2017, 47(2))
(  0) 0) |
| [10] |
Xie X, Geng T, Zhao Q L, et al. Precise Orbit Determination for BDS-3 Satellites Using Satellite-Ground and Inter-Satellite Link Observations[J]. GPS Solutions, 2019, 23: 40 DOI:10.1007/s10291-019-0823-5
(  0) 0) |
| [11] |
刘帅.卫星导航系统空间信号精度评估理论与算法研究[D].郑州: 信息工程大学, 2016 (Liu Shuai.Research on Space Signal Accuracy Evaluation Theory and Algorithm of Satellite Navigation System[D].Zhengzhou: Information Engineering University, 2016)
(  0) 0) |
| [12] |
楼益栋, 施闯, 周小青, 等. GPS精密卫星钟差估计与分析[J]. 武汉大学学报:信息科学版, 2009, 34(1): 88-91 (Lou Yidong, Shi Chuang, Zhou Xiaoqing, et al. Realization and Analysis of GPS Precise Clock Products[J]. Geomatics and Information Science of Wuhan University, 2009, 34(1): 88-91)
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40


