2. 中国科学院大学,北京市玉泉路19号甲,100049
不同类型的GNSS导航信号在卫星和接收机不同通道产生的时间延迟(或硬件延迟)并不完全一致,由此产生的两类导航信号之间的时延差异称为差分码偏差(differential code bias, DCB)[1]。不同频率不同类型测距信号之间的DCB称为频间偏差,比如GPS的P1-P2码信号的硬件延迟之差;而同一频率不同类型测距信号之间的DCB称为频内偏差,比如GPS的P1-C1码信号的硬件延迟之差。GPS导航电文中的广播钟差参数基准定义在P1-P2码双频无电离层组合观测量上,GPS导航用户在使用不同于这一基准的观测量进行数据处理时,需要对卫星硬件延迟进行修正[2]。GPS在广播电文中实时播发时间群延迟(timing group delay, TGD)参数对P1码和P2码的导航用户进行硬件延迟修正。对于C1码用户,除了进行TGD修正外,还应对P1码和C1码之间的频内偏差进行改正。虽然有研究表明,修正P1-C1频内差后,C1码和C1-P2码用户的伪距单点定位精度都有提升[3-4],但由于仅利用广播电文中播发的TGD参数对相应频点的卫星硬件延迟进行修正基本就可以满足GPS基本导航服务精度的需求,因此,P1-C1频内差修正往往在数据处理中被忽略。但对于高精度应用,这一偏差不容忽视。Kouba等[5]认为,在PPP定位时,必须考虑不同伪距观测值之间的DCB差异;黄健等[6]和赵磊等[7]认为,修正P1-C1频内差对GPS静态PPP的定位精度和动态PPP的收敛速度均有一定程度的提升。在星基增强系统(satellite-based augmentation system, SBAS)数据处理过程中,P1-C1频内差也是重要的误差源。星基增强系统通常由广域分布的几十个坐标精确已知的监测站对导航卫星进行观测,利用双频无电离层组合的伪距观测数据通过几何法(倒单点定位)估计卫星广播钟差和广播星历改正数。当选取GPS的C1-P2码双频组合的伪距观测数据进行GPS SBAS改正数计算时,如果忽略P1-C1频内偏差,则该偏差经双频组合系数放大后被吸收至卫星钟差改正数中,从而影响SBAS的服务精度。
中国的北斗星基增强系统BDSBAS目前正处在实验建设阶段,建成后,其将通过GEO卫星向服务区域内包括BDS、GPS、Galileo、GLONASS等多个GNSS系统的用户播发增强改正数和完好性信息,进一步提升卫星导航系统的服务性能[8-9]。如何依靠中国地区广域分布的监测站观测数据计算生成各卫星导航系统高精度的星基增强改正数是BDSBAS面临的重要挑战。本文利用中国地区广域分布监测站的GPS C1-P2双频载波相位平滑伪距观测数据计算GPS卫星钟差和星历改正数,基于CODE分析中心每月发布的P1-C1频内偏差产品探讨P1-C1码间偏差对星基增强改正数计算的影响,将P1-C1频内偏差修正前后计算得到的SBAS改正数分别用于GPS星基增强定位,并对定位精度进行评估和分析。
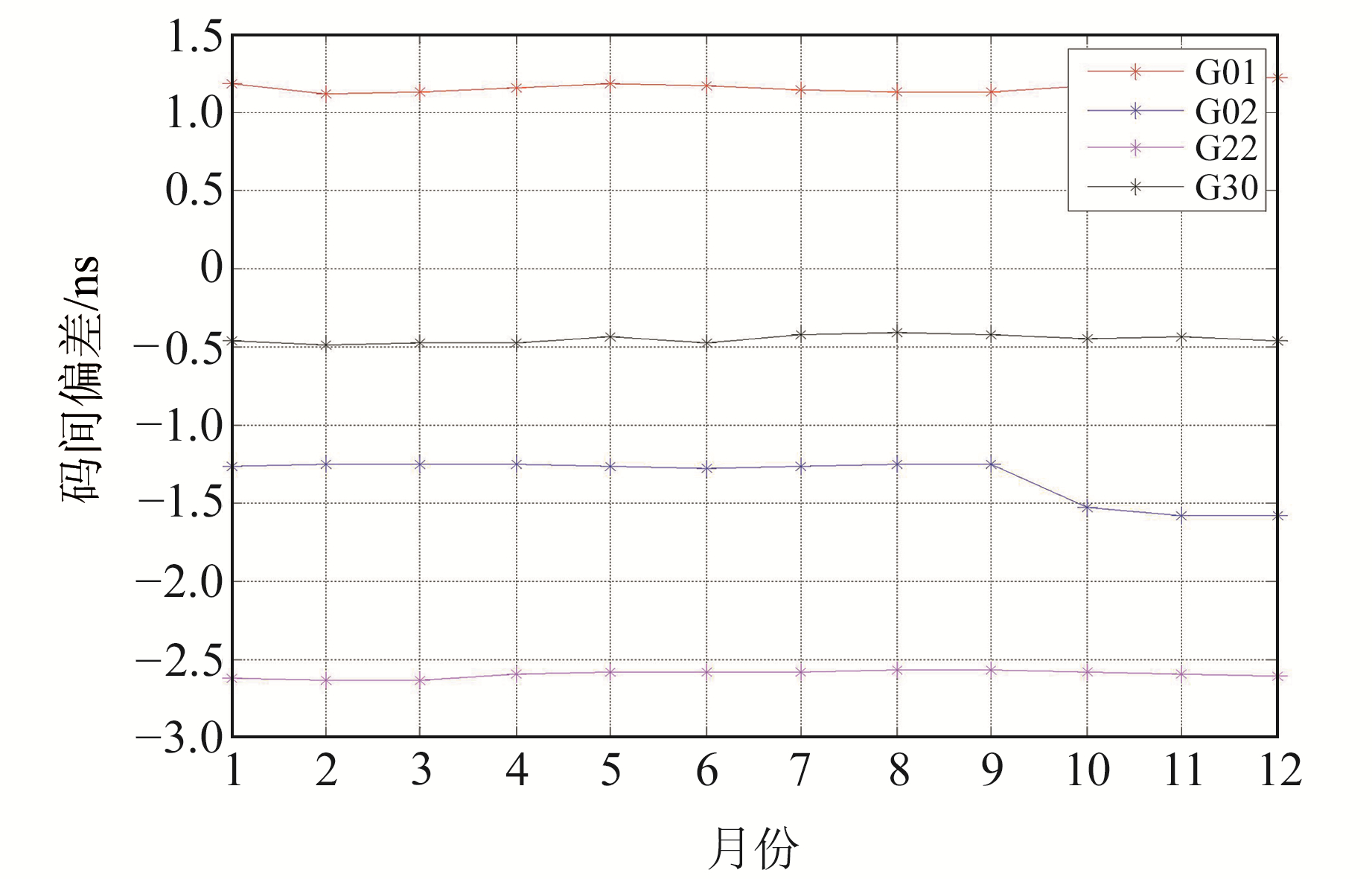
1 P1-C1码间偏差修正对GPS基本导航定位精度的提升CODE基于全球分布的IGS基准站,采用电离层TEC建模的方法解算得到GPS P1-C1码间偏差参数[10],该参数产品每月发布,用户可在CODE官网下载。从CODE发布的产品来看,GPS不同卫星的P1-C1码间偏差值差异较为明显,最大可达3~4 ns;但同一卫星的P1-C1码间偏差较为稳定,不同月份之间差异较小。图 1是CODE发布的部分GPS卫星2019年的P1-C1码间偏差值。
|
图 1 2019年CODE P1-C1码间偏差值序列 Fig. 1 CODE's P1-C1 DCB series in 2019 |
研究P1-C1码间偏差对星基增强服务精度的影响,首先应明确其对基本导航定位精度的影响。选取中国境内的7个测站,站上均装有国产GPS接收机,将其作为用户接收机,采用CODE发布的产品进行P1-C1码间偏差修正,验证该修正对GPS C1码单频用户和C1-P2码双频用户伪距单点定位精度的提升作用。实验时间段为2020-01-01~07,卫星轨道与钟差由GPS广播电文播发的参数计算,对流层延迟误差由Saastamoinen模型计算,对于C1码单频用户,电离层延迟误差由广播电文中的Klobuchar 8参数计算,截止高度角为15°,观测数据采样间隔30 s。以GPS静态精密单点定位的结果作为坐标参考真值,图 2、3分别是修正P1-C1码间偏差前后C1码单频用户和C1-P2码双频用户的95%三维定位误差。可以看出,修正P1-C1码间偏差后,C1码单频伪距用户定位精度略有提升,而C1-P2码双频用户定位精度提升较为明显。根据表 1,P1-C1修正后,单频用户水平定位误差由1.82 m降为1.78 m,高程定位误差由3.72 m降为3.41 m;双频用户水平定位误差由2.58 m减小至1.69 m,高程定位误差由4.46 m减小至2.82 m。这说明P1-C1码间偏差在基本导航服务中对双频用户影响更大,原因是定位计算时该偏差经过了双频组合系数倍的放大。

|
图 2 P1-C1码间偏差修正前后的C1码单频三维定位误差(95%) Fig. 2 C1-code 3D positioning error (95%) before/after P1-C1 DCB correcting |

|
图 3 P1-C1码间偏差修正前后的C1-P2码双频三维定位误差(95%) Fig. 3 C1-P2-code 3D positioning error (95%) before/after P1-C1 DCB correcting |
|
|
表 1 修正P1-C1频内差前后GPS基本导航单、双频定位精度(95%定位误差) Tab. 1 GPS C1-code single-frequency and C1-P2-code dual-frequency positioning error(95%) before/after P1-C1 DCB correcting |
获取高精度的改正数信息,是保证星基增强系统服务性能的关键。SBAS系统通常采用几何法计算改正数,几何法不依赖于卫星轨道动力学模型,利用广域分布的监测站伪距观测数据(辅以载波相位观测数据)即可解算可视卫星的钟差和轨道改正数,然后通过GEO卫星将改正数播发给地面用户,用户可综合利用卫星导航电文和SBAS改正信息进行定位,以获得更高精度的导航定位服务。
本节采用几何法(倒单点定位)计算GPS卫星钟差改正数和星历改正数,并分析P1-C1码间偏差对改正数计算的影响。
2.1 改正数计算方法GPS SBAS改正数计算的几何法观测方程可以表示为:
| $ P_i^j = \rho _i^j - \delta {t^j} + \delta {t_i} + {\delta _{{\rm{trop}}}} + {\delta _{{\rm{pco}}}} + {\delta _{{\rm{rel}}}} + \varepsilon $ | (1) |
式中,Pij为P1码和P2码伪距的双频无电离层组合观测值,由于监测站坐标精确已知,卫星位置可用导航电文计算得到,因此卫星与地面接收机的几何距离ρij可直接计算;δtj和δti分别为卫星钟差与接收机钟差,其中卫星钟差也可由导航电文计算得到;δtrop、δpco、δrel分别为对流层延迟、接收机天线相位中心偏差和相对论延迟等系统误差;ε为多路径误差和噪声。
从双频伪距观测量中扣除星地几何距离、卫星钟差以及其他各项系统误差后,得到伪距残差,记为ocij。由于导航电文中的卫星轨道和钟差信息存在一定误差,因此伪距残差中除包含测站接收机钟差和多径噪声外,还包括导航电文的钟差误差和星历误差。伪距残差计算公式可以表示为:
| $ {\rm{oc}}_i^j = \delta {t_i} - \delta B + \varepsilon $ | (2) |
式中,δti和ε与式(1)中含义一致;δB为卫星钟差改正数,统一修正卫星钟差误差和卫星星历误差在全部监测站视线方向投影的平均值。利用广域分布的监测站对所有可视GPS卫星的观测数据采用倒单点定位方法,固定主控站接收机钟差,利用最小二乘法实时求解其他监测站接收机钟差与卫星钟差改正数。
虽然δB已经修正了卫星星历误差在全部监测站视线方向投影的平均值,但由于星历误差在不同视线方向的投影存在差异,因此仍然存在残余的星历误差。由于测站钟差、卫星钟差误差与星历径向误差强相关,同时求解星历误差与钟差误差会导致法方程严重病态,影响解算结果的正确性。因此在解算得到卫星钟差改正数和接收机钟差的基础上,在式(2)的伪距残差中先将二者扣除,然后解算X、Y、Z方向残余的卫星轨道改正数。这样,在伪距测距残差中仅剩下星历投影误差和观测噪声,此时的伪距残差可以表示为:
| $ {\rm{o\tilde c}}_i^j = {a_{x,iij}}{\rm{d}}x_i^j + {b_{y,ij}}{\rm{d}}y_i^j + {c_{z,ij}}{\rm{d}}z_i^j + \varepsilon _i^j $ | (3) |
式中,
PS卫星钟差改正数和轨道改正数可以由上述方法计算生成,这些改正信息由GEO卫星播发给BDSBAS服务区域的GPS SBAS用户,通过改正GPS导航电文的误差实现对用户定位精度的增强。
2.2 P1-C1码间偏差对改正数计算的影响如果参与SBAS改正数计算的监测站均采用C1-P2码双频组合代替P1-P2码双频组合,则由于P1码与C1码之间存在码间偏差,双频伪距观测方程由式(1)变为:
| $ P_i^j = \rho _i^j - \delta {t^j} + \delta {t_i} + {\delta _{{\rm{trop}}}} + {\delta _{{\rm{pco}}}} + {\delta _{{\rm{rel}}}} + m * {\rm{DC}}{{\rm{B}}_{{\rm{P1 - C1}}}} + \varepsilon $ | (4) |
式中,
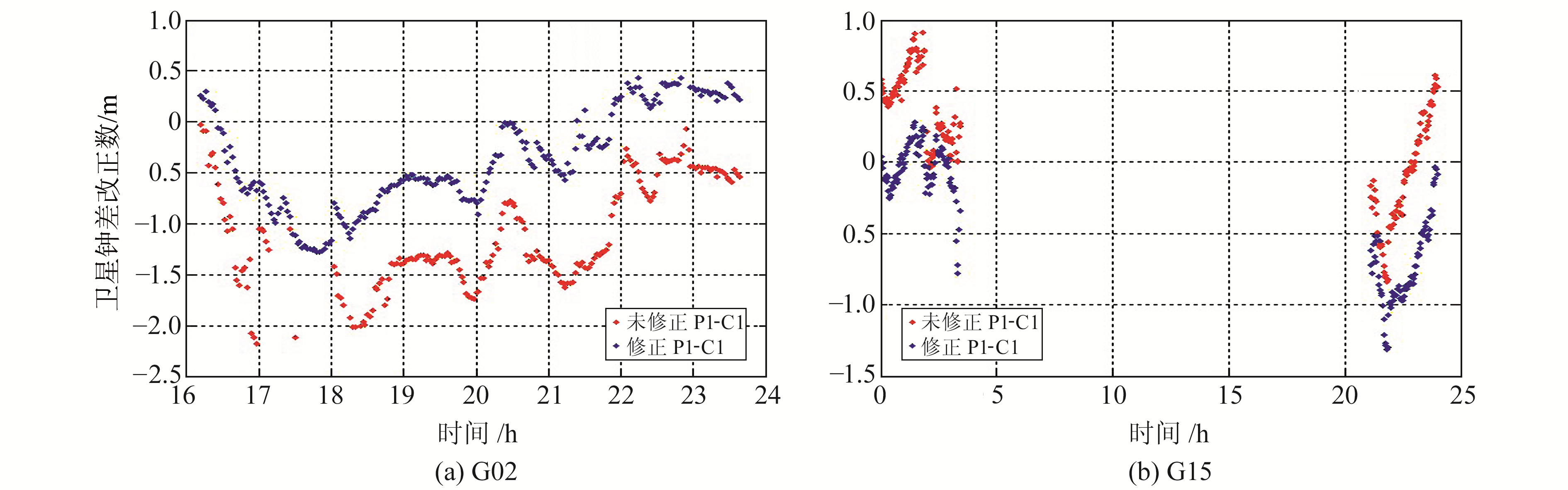
利用中国地区广域分布的20个监测站经平滑后的GPS C1-P2双频伪距观测数据,采用§2.1方法计算GPS卫星钟差改正数与轨道改正数,P1-C1码间偏差将主要影响各向同性的卫星钟差改正数的计算。采用CODE发布的DCB产品对P1-C1码间偏差进行修正,修正P1-C1码间偏差前后计算得到的卫星钟差改正数序列(以G02和G15星为例),如图 4所示。由图可见,修正码间偏差后,钟差改正数均值变化较为明显。
|
图 4 P1-C1码间偏差修正前后的GPS卫星钟差改正数序列 Fig. 4 GPS satellite clock corrections series before and after P1-C1 DCB correcting |
本节重点研究星基增强用户定位,将§2.2生成的SBAS改正数用于GPS单、双频用户的定位,评估增强后的定位精度。
3.1 实验方案利用由中国地区广域分布的地面监测站经过平滑后的GPS C1-P2双频伪距观测数据计算得到的卫星钟差与轨道改正数对服务区域内的GPS地面用户进行增强定位实验,选取与§1相同的7个测站(不同于SBAS改正数计算所用的站)作为SBAS用户,站上接收机均能接收GPS C1码和P2码伪距观测数据,时间跨度为2020-01-01~07。为研究P1-C1码间偏差对SBAS定位的影响,分析定位精度,针对C1码单频用户和C1-P2双频用户分别设计不同的实验方案,如表 2、3。在定位处理中,对流层、电离层等误差的计算、P1-C1码间偏差修正所用的DCB产品、截止高度角和观测数据采样间隔等均与§1相同。
|
|
表 2 GPS单频定位实验方案 Tab. 2 Experimental schemes of GPS single-frequency positioning |
|
|
表 3 GPS双频定位实验方案 Tab. 3 Experimental schemes of GPS dual-frequency positioning |
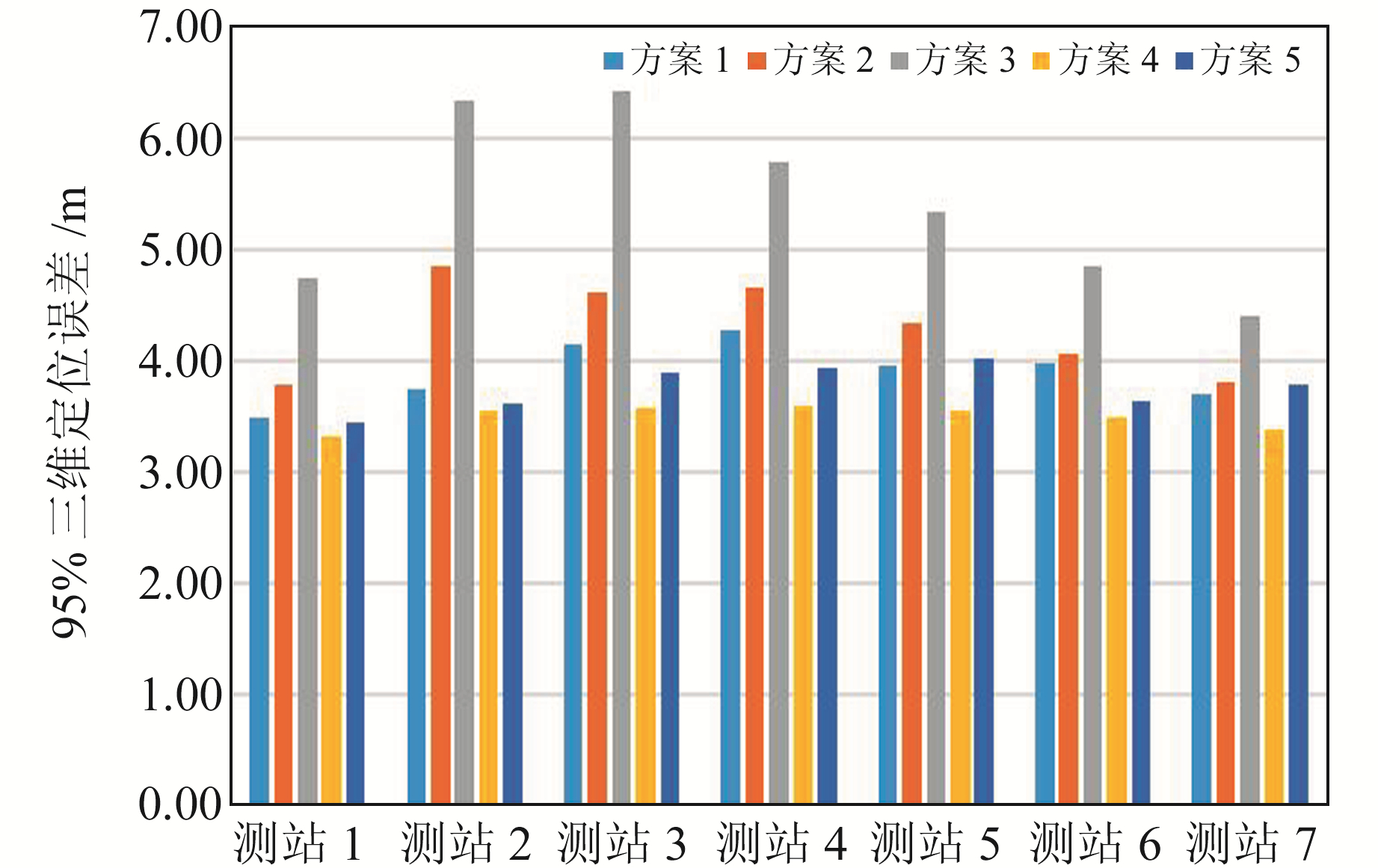
图 5给出7个测站单频定位实验中各方案的95%三维定位误差。由图可见,方案3的定位结果最差,这是因为SBAS用户端在C1码伪距定位时修正了P1-C1码间偏差,但是由于计算SBAS改正数时未对该偏差进行修正,导致卫星钟差改正数中包含了双频系数放大后的P1-C1偏差,放大后的偏差成为定位中极大的误差源;方案2中SBAS用户并未修正P1-C1,其定位误差小于方案3,大于方案1和方案4,这是由于SBAS钟差改正数中包含双频系数倍的P1-C1偏差,但是用户端仅存在1倍的P1-C1偏差,并不完全自洽,所以相比方案1(基本导航)定位精度不仅没有提升,反而下降;方案4的定位精度最高,因为在SBAS改正数计算的过程中扣除了P1-C1频内差的影响,而用户端定位时也对C1码伪距作了修正;方案5虽然在SBAS改正数计算的过程中扣除了P1-C1频内差,但用户端并未对该频内差进行修正,该偏差也导致方案5的定位精度差于方案4。
|
图 5 各站不同方案单频定位95%三维定位误差 Fig. 5 GPS single-frequency 3D positioning error (95%) of different schemes |
表 4是单频实验中各方案7个测站水平、高程和三维的平均95%定位误差。由表可见,方案2和方案3相比方案1(基本导航),均不能实现定位精度增强;方案4彻底扣除P1-C1的影响,相比方案2(用户端定位和SBAS改正数计算时都不修正P1-C1偏差),水平误差由1.94 m降低至1.45 m,高程误差由3.82 m降低至3.14 m,三维定位精度提升约19%;相比于方案1,方案4的三维定位精度提升约10%;方案5用户端并未对P1-C1频内差进行修正,但在SBAS改正数计算时扣除了频内差影响,在用户定位时该频内差的存在使得其定位精度差于方案4。
|
|
表 4 GPS单频定位实验各方案95%定位误差统计 Tab. 4 GPS single-frequency positioning error statistics (95%) of different schemes |
以上实验结果表明,SBAS改正数计算时若不修正P1-C1码间偏差,会严重影响SBAS单频用户的定位精度,只有扣除P1-C1偏差的影响,才能相较基本导航实现定位精度的增强。
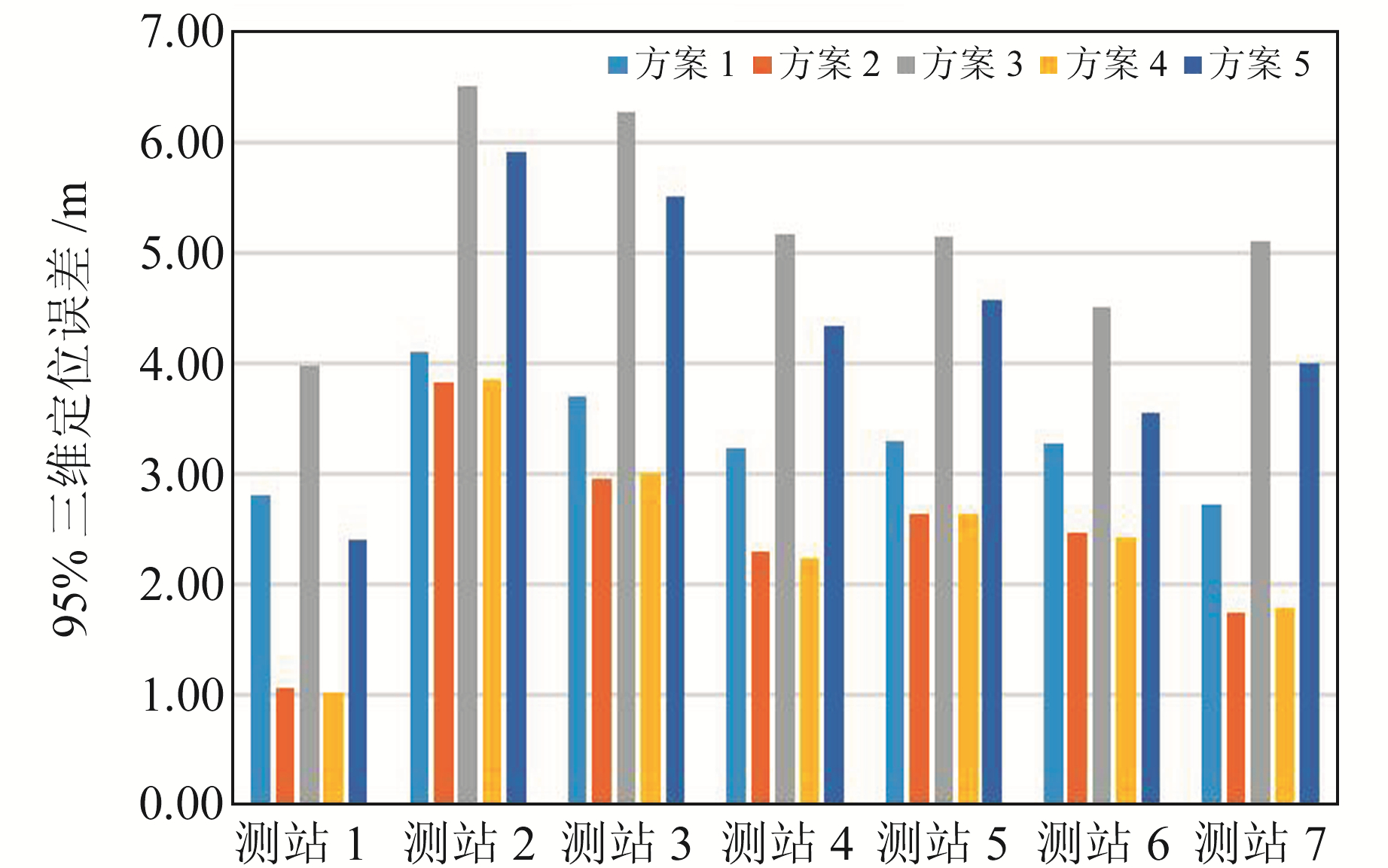
图 6给出7个测站双频定位实验中各方案的95%三维定位误差。由图看见,方案3的定位误差最大,这一点与单频实验的情况一致;方案2中SBAS双频用户并未修正P1-C1偏差,SBAS改正数计算时也未扣除该偏差,用户端和卫星钟差改正数中的P1-C1偏差均为放大双频系数倍,完全自洽,因此定位精度较高;方案4在用户定位与SBAS改正数计算时均扣除P1-C1影响,与方案2的定位精度基本一致;方案5中SBAS改正数已扣除P1-C1频内差的影响,但用户端并未进行修正,因此该偏差对定位精度依然有较大影响,也导致其定位误差明显大于方案4。这里也可以看出,相比于单频用户,双频用户端的P1-C1频内差对定位精度的影响更大,这一点与前文的基本导航实验结果一致。
|
图 6 各站不同方案双频定位95%三维定位误差 Fig. 6 GPS dual-frequency 3D positioning error (95%) of different schemes |
表 5是双频实验中各方案7个测站水平、高程和三维的平均95%定位误差。由表可见,方案3由于SBAS改正数中包含P1-C1影响,因此其定位结果最差;方案2和方案4的定位精度一致,相比方案1(基本导航),均实现了明显的精度增强,其中水平误差由1.69 m降低至1.15 m,高程误差由2.82 m降低至2.10 m左右,三维定位精度提升约27%;方案5用户端的P1-C1影响最终的定位精度,使其整体定位误差高于方案4。
|
|
表 5 GPS双频定位实验各方案95%定位误差统计 Tab. 5 GPS dual-frequency positioning error statistics (95%) of different schemes |
以上实验结果表明,只需要保证在SBAS双频用户定位时对观测量中卫星P1-C1码间偏差的处理与SBAS改正数计算时一致,就可消除卫星P1-C1码间偏差的影响,得到理想的定位效果。
4 结语本文基于CODE提供的GPS卫星P1-C1码间偏差产品,首先验证了GPS P1-C1码间偏差修正对基本导航伪距单点定位精度的提升作用,然后利用中国地区广域分布监测站的GPS C1-P2双频载波相位平滑伪距观测数据,计算GPS星基增强改正数,分析P1-C1码间偏差对改正数计算与SBAS定位精度的影响,得到结论如下:
1) 修正GPS卫星P1-C1码间偏差对基本导航C1-P2码双频用户伪距单点定位精度提升尤其明显,其中95%水平定位误差由2.58 m减小至1.69 m,高程定位误差由4.46 m减小至2.82 m。
2) 卫星P1-C1码间偏差是SBAS数据处理的重要误差源,修正P1-C1频内差前后得到的卫星钟差改正数差异十分明显。
3) 在SBAS改正数计算时修正P1-C1码间偏差,对C1码单频用户SBAS定位精度提升十分明显,修正该偏差后,95%水平误差由1.94 m降低至1.45 m,高程误差由3.82 m降低至3.14 m。
4) 对于GPS C1-P2码双频SBAS用户,原则上只要保证在定位时对观测量中卫星P1-C1码间偏差的处理与SBAS改正数计算时一致,就可消除卫星P1-C1码间偏差的影响,得到较高的增强定位精度。
5) 建议我国的星基增强系统BDSBAS在计算GPS星基增强改正数时对P1-C1码间偏差进行修正,同时要求C1码和C1-P2码的GPS用户在使用SBAS改正数进行定位时修正P1-C1偏差,从而保证GPS C1码单频用户和C1-P2码双频用户均可实现较高的SBAS定位精度。
| [1] |
袁运斌, 欧吉坤. GPS观测数据中的仪器偏差对确定电离层延迟的影响及处理方法[J]. 测绘学报, 1999, 28(2): 110-114 (Yuan Yunbin, Ou Jikun. The Effects of Instrumental Bias in GPS Observations on Determining Ionospheric Delays and the Methods of Its Calibration[J]. Acta Geodaetica et Cartographica Sinica, 1999, 28(2): 110-114)
(  0) 0) |
| [2] |
El-Mowafy A, Deo M, Rizos C. On Biases in Precise Point Positioning with Multi-Constellation and Multi-Frequency GNSS Data[J]. Measurement Science and Technology, 2016, 27(3)
(  0) 0) |
| [3] |
王宁波, 袁运斌, 张宝成, 等. GPS民用广播星历中ISC参数精度分析及其对导航定位的影响[J]. 测绘学报, 2016, 45(8): 41-50 (Wang Ningbo, Yuan Yunbin, Zhang Baocheng, et al. Accuracy Evaluation of GPS Broadcast Inter-Signal Correction(ISC) Parameters and Their Impacts on GPS Standard Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(8): 41-50)
(  0) 0) |
| [4] |
潘宇明, 丁乐乐, 王珍, 等.北斗和GPS差分码偏差改正及其对导航定位的影响[C].中国卫星导航学术年会, 上海, 2017 (Pan Yuming, Ding Lele, Wang Zhen, et al. The DCB Correction of BDS and GPS and Its Influence on Navigation and Positioning[C]. China Satellite Navigation Conference, Shanghai, 2017)
(  0) 0) |
| [5] |
Kouba J, Héroux P. Precise Point Positioning Using IGS Orbit and Clock Products[J]. GPS Solutions, 2001, 5(2): 12-28
(  0) 0) |
| [6] |
黄健, 汪平, 阮仁贵, 等. DCB对精密单点定位精度影响研究[J]. 大地测量与地球动力学, 2010, 30(3): 110-112 (Huang Jian, Wang Ping, Ruan Rengui, et al. Study on Precise Point Positioning Accuracy Affected by DCB[J]. Journal of Geodesy and Geodynamics, 2010, 30(3): 110-112)
(  0) 0) |
| [7] |
赵磊, 张守建. GPS卫星P1-C1码间偏差对动态PPP影响分析[J]. 大地测量与地球动力学, 2016, 36(2): 143-145 (Zhao Lei, Zhang Shoujian. Impact Analysis of P1-C1 Differential Code Biases of GPS Satellites on the Kinematic Precise Point Positioning[J]. Journal of Geodesy and Geodynamics, 2016, 36(2): 143-145)
(  0) 0) |
| [8] |
Yang Y X, Gao W G, Guo S R, et al. Introduction to Beidou-3 Navigation Satellite System[J]. Navigation, 2019, 66(1): 7-18
(  0) 0) |
| [9] |
Chen S S, Jin B, Li D J, et al. Study on the Prediction Method of Single and Dual Frequency Service Area for BD SBAS[C].China Satellite Navigation Conference, Beijing, 2019
(  0) 0) |
| [10] |
Montenbruck O, Hauschild A, Steigenberger P. Differential Code Bias Estimation Using Multi-GNSS Observations and Global Ionosphere Maps[J]. Navigation, 2014, 61(3): 191-201 DOI:10.1002/navi.64
(  0) 0) |
2. University of Chinese Academy of Sciences, A19 Yuquan Road, Beijing 100049, China
 2020, Vol. 40
2020, Vol. 40

