在星载InSAR系统中，卫星定轨精度不高会使轨道状态矢量存在误差，从而导致基线不准确，并对InSAR数据处理造成影响^[1-2]。轨道误差的存在会降低InSAR地表高程测量中DEM的精度和形变监测的可靠性^[3-5]。基于干涉相位的轨道误差改正算法，尤其是多项式方法，由于操作简单而得到广泛应用^[5-6]。但实际估计轨道误差时，常混合轨道误差、形变、地形残差、大气误差等，在残余相位中还存在基线误差和DEM残差^[7]。本文提出一种基于小波多尺度分析的星载InSAR轨道误差估计方法，直接对干涉图中轨道误差进行估计并去除，最后通过模拟数据和实测数据对算法的有效性进行分析验证。

1 小波稳健最小二乘估计的轨道误差校正算法 1.1 基于小波理论的InSAR差分干涉相位误差分析

在不考虑地表形变及电离层延迟的影响时，差分干涉相位成分可表示为：

$ {\varphi _{{\rm{diff}}}} = {\varphi _{{\rm{topo}}}} + {\varphi _{{\rm{orbit}}}} + {\varphi _{{\rm{atm}}}} + {\varphi _{{\rm{noi}}}} $

(1)

式中，φ_topo为地形误差相位，φ_orbit为轨道误差，φ_atm为对流层延迟误差相位, φ_noi为失相关噪声相位。轨道误差φ_orbit是在利用轨道参数估计平地相位并去除平地相位过程中由于轨道参数误差而导致干涉图中存在的相位趋势误差，在干涉图中表现为长条纹的系统性误差，波长比噪声相位更长，在频域表现为低频。失相关噪声相位φ_noi在频域表现为高频，可通过干涉图滤波^[8]，如采用Goldstein法对噪声进行压制。地形误差相位φ_topo通常以短波长成分为主，但也会出现与轨道误差相位混叠的现象。对流层延迟误差相位φ_atm波长可从几十m到几十km，会与其他相位出现混叠现象，但φ_atm在空间分布上不具有线性关系。从式(1)可知，为估计轨道误差相位，需要降低地形误差相位、噪声相位等的干扰，否则会影响多项式模型的拟合效果。研究表明，离散小波变换可较好地对干涉图中不同的相位成分进行分析，可在不同分辨率条件下分析差分干涉相位的空间分布^[9]。差分干涉相位经过小波多尺度分解后可分离出轨道误差所在的低频频带，然后再对低频相位进行加权最小二乘估计，从而确定轨道误差趋势面。

1.2 算法实现

差分干涉相位经过二维多尺度小波分解后，可滤除部分地形误差相位、对流层延迟误差相位、噪声相位，再利用多项式模型对差分干涉图中的轨道误差进行拟合。

设二次多项式模型为：

$ {\phi ^{{\rm{orbit}}}}\left( {x, y} \right) = a + bx + cy + dxy + e{x^2} + f{y^2} $

(2)

式中，Φ^orbit为小波分解后的低频部分，(x, y)为SAR坐标系下轨道误差距离向和方位向的坐标，a、b、c、d、e、f为待求的二次多项式模型参数。用矩阵表示为：

$ \mathit{\boldsymbol{L}} = \mathit{\boldsymbol{BX}} + \mathit{\boldsymbol{\Delta }} $

(3)

式中，$\mathit{\boldsymbol{L}} = {\left[ {{L_1}, {L_2}, \cdots , {L_n}} \right]^{\rm{T}}}$为低频部分提取的n个点，$\mathit{\boldsymbol{X}} = {\left[ {a, b, c, d, e, f} \right]^{\rm{T}}}$为待求模型参数，$\mathit{\boldsymbol{\Delta }} = {\left[ {{\Delta _1}, {\Delta _2}, \cdots , {\Delta _n}} \right]^{\rm{T}}}$为误差相位，$\mathit{\boldsymbol{B}} = \left[ \begin{array}{l} 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {x_1}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {y_1}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {x_1}{y_1}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x_1^2{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} y_1^2\\ 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {x_2}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {y_2}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {x_2}{y_2}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x_2^2{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} y_2^2\\ \vdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots \\ 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {x_n}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {y_n}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {x_n}{y_n}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x_n^2{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} y_n^2 \end{array} \right], \left( {{x_n}, {y_n}} \right)$为SAR坐标系下轨道误差距离向和方位向的坐标。则误差方程为：

$ \mathit{\boldsymbol{\Delta }} = \mathit{\boldsymbol{BX}} - \mathit{\boldsymbol{L}} $

(4)

为降低残余的地形误差相位和噪声相位对多项式拟合的干扰，采用稳健最小二乘估计对二次多项式模型参数进行估计。

$ \mathit{\boldsymbol{X}} = {\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PB}}} \right)^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PL}} $

(5)

式中，P为观测向量L的权阵。假定观测向量L之间相互独立，P为一个N×N的对角阵，对角上每个元素对应观测量的权重。由于受噪声和解缠误差的影响，L存在误差，P在平差前无法确定，为消除误差的影响，采用迭代法对参数X进行求解。通过平差得到的残差来调整权重，调整权重的比例因子为：

$ \omega _k^j = \frac{1}{{\left| {{\bf{\Delta }}_k^j} \right| + u}}, k = 1, 2, \cdots , n;j = 1, 2, \cdots , m $

(6)

式中，j为迭代次数，Δ_k为第k个观测量的残差值，u为一个很小的常数。迭代更新权重及参数平差的过程可表示为：

$ \begin{array}{l} \mathit{\boldsymbol{P}}_{ii}^j = \mathit{\boldsymbol{P}}_{ii}^{j - 1} \cdot \omega _i^j\\ {\mathit{\boldsymbol{P}}^j} = {\rm{diag}}\left[ {P_1^j{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} P_2^j{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \cdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} P_n^i} \right]\\ {{\mathit{\boldsymbol{\hat X}}}^j} = {\left( {{\mathit{\boldsymbol{B}}^\rm{T}}{\mathit{\boldsymbol{P}}^j}\mathit{\boldsymbol{B}}} \right)^{ - 1}}{\mathit{\boldsymbol{B}}^\rm{T}}{\mathit{\boldsymbol{P}}^j}\mathit{\boldsymbol{L}}\\ {\mathit{\boldsymbol{\Delta }}^j} = \mathit{\boldsymbol{B}}{{\mathit{\boldsymbol{\hat X}}}^j} - \mathit{\boldsymbol{L}} \end{array} $

(7)

初始权阵P⁰可通过干涉相位相干值来确定，迭代中止条件可表示为：

$ \max \left\{ {\left| {\frac{{{\mathit{\boldsymbol{X}}^j} - {\mathit{\boldsymbol{X}}^{j - 1}}}}{{{\mathit{\boldsymbol{X}}^{j - 1}}}}} \right|} \right\} ＜ \delta $

(8)

式中，δ是一个很小的常数，当参数的相对变化率小于某一常数时将不再变化，则迭代中止，即可确定最小二乘加权迭代估计的模型参数X。

2 实验结果与分析 2.1 模拟数据实验结果与分析

图 1(a)、1(b)分别为模拟轨道误差相位和地形残差、噪声相位，图 1(c)为模拟差分干涉图。

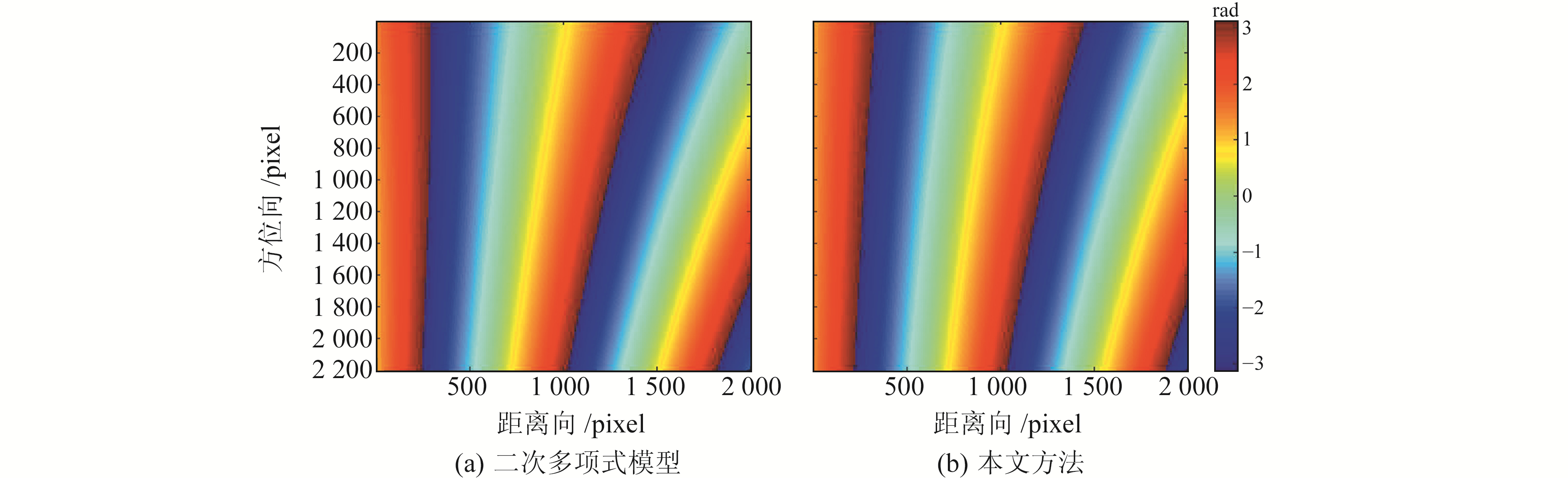
分别采用二次多项式模型和本文方法进行实验，图 2为估计的轨道误差。从图中可以看出，2种方法都能获得轨道误差的趋势向，二次多项式模型、本文方法的轨道误差与真值的均方根误差分别为0.25 rad和0.13 rad，本文方法的轨道误差细节信息更接近于真实的轨道误差，表明通过小波分解可有效抑制波长短于轨道误差的成分。

2.2 实测数据验证

采用覆盖河南义马实验区的2景ASAR数据进行研究，获取时间分别为2006-11-19和2007-01-28。为显示条纹的变化情况，将差分干涉相位缠绕到[－π, π]。从图 3(a)可以看出，差分干涉图中含有明显的趋势性轨道误差。采用本文方法对数据进行处理时，通过小波多尺度分解确定分解层数，图 3(b)为分解结果，当小波分解层数为6时，均方根误差变化率趋于1~1.1^[10]，因此本文选择分解层数为6。图 3(c)是分解尺度为6时提取的低频部分，其低频部分趋势与差分相位图轨道误差趋势基本一致。

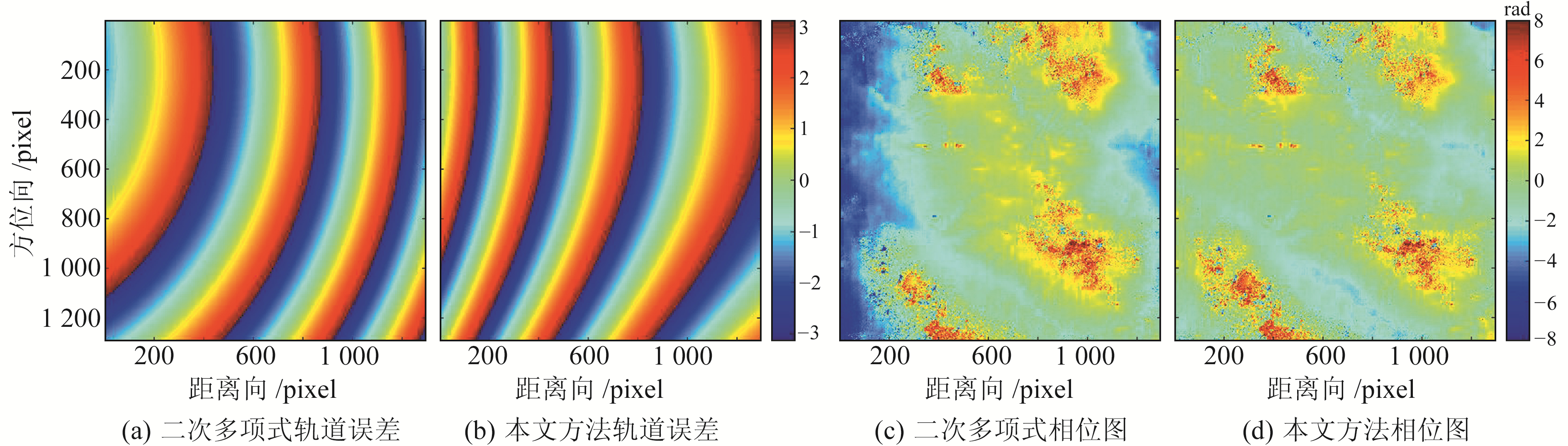
图 4(a)、4(b)分别为二次多项式模型、本文方法估计的轨道误差，图 4(c)、4(d)为改正后的差分相位图。从图 4可以看出，二次多项式模型虽然能估计出大部分轨道误差，但在干涉图西部区域还存在明显的趋势性轨道误差；而本文方法改正后的干涉图中含有的趋势性轨道误差更少，尤其是在二次多项式模型无法改正的区域，如干涉图西部的趋势向，本文方法的去除效果更优。

为进一步验证本文算法的有效性，将上述轨道误差的改正结果用于DEM估计。以ASTER GDEM数据作为参考值，对重建的DEM的精度进行评价。轨道误差校正前生成的DEM与ASTER GDEM的均方根误差为77.83 m，校正后的二次多项式模型和本文方法的均方根误差分别为28.47 m和23.05 m，精度提高19.04%。为进一步显示获取DEM的细节效果，选取局部区域进行放大分析。图 5(a)~5(c)分别为改正前和二次多项式模型、本文方法改正后局部范围的地形地貌图，图 5(d)为局部地区ASTER GDEM结果。从图中可以看出，本文方法生成的DEM在高程细节信息上优于二次多项式模型，其更接近于ASTER GDEM结果。图 5(e)为轨道误差去除前和二次多项式模型、本文方法改正后的干涉图生成的DEM与ASTER GDEM的差异对比。

3 结语

针对二次多项式模型去除干涉相位轨道误差时，须对干涉相位其他项的分布性质作假设等问题，提出一种新方法对轨道误差相位进行处理。首先采用小波多尺度分析滤除波长比轨道误差相位短的地形误差相位、对流层延迟误差及噪声相位部分；然后对轨道误差所在的频带相位采用稳健最小二乘估计多项式模型参数；最后通过模型进行轨道误差提取并去除。结果表明，差分干涉相位通过小波分解可以有效抑制波长短于轨道误差相位的成分，改正后的干涉图中含有的趋势性轨道误差更少，尤其是在二次多项式模型无法改正的区域，本文方法的去除效果更优，可提升多项式拟合结果的可靠性。将轨道误差改正后的干涉图用于DEM高程估计，结果显示，二次多项式模型和本文方法重建的DEM与ASTER GDEM的标准差分别为28.47 m和23.05 m，本文方法的估计精度高于二次多项式模型，可以有效改善干涉系统的测高精度。