在实际数据处理过程中，InSAR干涉图受各类误差相位的影响，且它们对干涉相位的影响方式和量级各不相同^[1]。可以将受各种误差影响明显以至不能真实反映地表形变的InSAR观测值视为粗差。如果多源InSAR观测值中包含粗差时，仍按最小二乘估计方法处理，得到的不是最优无偏估值，而是被严重歪曲的估值，影响三维地表形变解算结果的质量。

目前有2种处理粗差的方式，一种是把粗差归入函数模型来实现粗差的处理；另一种是把粗差归入随机模型进行粗差处理，即抗差估计^[2-3]。本文考虑通过抗差估计的方式处理多视线向D-InSAR数据中的粗差。抗差估计中的选权迭代法是处理测量数据粗差的常用方法，一般是通过最小二乘估计来确定第一次平差的残差值，其前提是获取可靠的先验方差。但在没有其他测量手段获取形变观测结果的情况下，往往难以准确获取多视线向D-InSAR技术观测值的先验方差，而方差分量估计定权方法不需要精确确定先验方差。本文提出通过Helmert方差分量估计求出观测值的验后方差，将粗差视为来自期望为零、方差很大的正态母体的子样，再利用方差检验可找出方差异常大(即含粗差)的观测值；然后基于等价权原理给予它一个相应小的权，通过多次迭代，使含粗差的观测值的权逐步趋近于0，实现抗差估计。

1 多视线向D-InSAR三维地表形变抗差解算方法

设$\mathit{\boldsymbol{d}} = {\left( {{d_{\rm{U}}}, {d_{\rm{E}}}, {d_{\rm{N}}}} \right)^{\rm{T}}}$为三维地表形变信息，$\mathit{\boldsymbol{R = }}{\left[ {R_{{\rm{LOS}}}^1, R_{{\rm{LOS}}}^2, \cdots , R_{{\rm{LOS}}}^n} \right]^{\rm{T}}}$为雷达坐标系中不同视线向形变信息，建立如下形变模型：

$ \mathit{\boldsymbol{R}} = \mathit{\boldsymbol{Bd}} $

(1)

式中，B为三维形变模型系数矩阵，可由文献[4]建立。根据最小二乘原理，解算出三维形变信息：

$ \mathit{\boldsymbol{d}} = {\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PB}}} \right)^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PR}} $

(2)

式中，P=diag((1/σ_LOS¹)², (1/σ_LOS²)², (1/σ_LOS³)², (1/σ_LOS⁴)²)表示权阵，diag(·)为对角阵，σ_LOS¹、σ_LOS²、σ_LOS³和σ_LOS⁴分别为R_LOS¹、R_LOS²、R_LOS³和R_LOS⁴的标准差。

如果观测值中包含粗差，导致观测误差不服从正态分布，而平差时没有考虑粗差的存在，仍按最小二乘估计方法处理，则得到的不是最优无偏估值，而是被严重歪曲的估值，影响三维地表形变解算结果的质量。为此，本文提出一种InSAR三维地表形变抗差解算方法。然而，多种InSAR技术观测值的先验方差往往难以准确获取。这里采用Helmert方差分量估计的简化公式进行定权。首先，按照观测量的精度对观测量进行分组。一般而言，采用2种传感器升、降轨SAR影像便可以实现三维地表形变解算，因此可将观测量分为2组，即${\mathit{\boldsymbol{R}}_1} = {\left[ {R_{{\rm{LOS}}}^1, R_{{\rm{LOS}}}^2} \right]^{\rm{T}}}$和${\mathit{\boldsymbol{R}}_2} = {\left[ {R_{{\rm{LOS}}}^3, R_{{\rm{LOS}}}^4} \right]^{\rm{T}}}$，相应的权阵为$\mathit{\boldsymbol{P}} = {\left[ {{P_1}, {P_2}} \right]^{\rm{T}}}$。按照间接平差列出如下误差方程：

$ \left\{ \begin{array}{l} {\mathit{\boldsymbol{V}}_1} = {\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{d}} - {\mathit{\boldsymbol{R}}_1}\\ {\mathit{\boldsymbol{V}}_2} = {\mathit{\boldsymbol{B}}_2}\mathit{\boldsymbol{d}} - {\mathit{\boldsymbol{R}}_2} \end{array} \right. $

(3)

式中，${\mathit{\boldsymbol{V}}_1} = {\left[ {V_{{\rm{LOS}}}^1, V_{{\rm{LOS}}}^2} \right]^{\rm{T}}}$和${\mathit{\boldsymbol{V}}_2} = {\left[ {V_{{\rm{AZ}}}^1, V_{{\rm{AZ}}}^2} \right]^{\rm{T}}}$分别为两类观测量对应的误差向量，B₁和B₂分别为相应的系数矩阵。值得注意的是，在InSAR三维地表形变的解算过程中，同一个区域多源SAR影像的数量有限(通常采用4个轨道SAR影像)，很难有更多的多余观测数据。为了保证观测值的方差因子验后估计的可靠性，这里采用Helmert方差分量估计简易公式：

$ \left\{ \begin{array}{l} \sigma _{0i}^2 = \mathit{\boldsymbol{V}}_i^T{\mathit{\boldsymbol{P}}_i}{\mathit{\boldsymbol{V}}_i}/{z_i}\\ {z_i} = {n_i} - {\rm{tr}}\left( {{\mathit{\boldsymbol{P}}_i}{\mathit{\boldsymbol{N}}_i}{\mathit{\boldsymbol{N}}^{ - 1}}\mathit{\boldsymbol{N}}_i^T} \right)\\ \mathit{\boldsymbol{N}} = {\mathit{\boldsymbol{B}}^T}\mathit{\boldsymbol{PB}}, {\mathit{\boldsymbol{N}}_i} = \mathit{\boldsymbol{B}}_i^T{\mathit{\boldsymbol{P}}_i}{\mathit{\boldsymbol{B}}_i}, i = 1, 2 \end{array} \right. $

(4)

式中，σ_0i²为两类观测量的单位权中误差，n_i为第i类观测量中观测量的个数。

如果某一像元对应第i类观测量中第j个形变量R_ij受到的粗差污染，则参数估值就会被扭曲。基于等价权原理有：

$ \mathop \sum \limits_{i = 1}^r \left( {\mathit{\boldsymbol{B}}_i^T{{\mathit{\boldsymbol{\bar P}}}_i}{\mathit{\boldsymbol{B}}_i}\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{B}}_i^T{{\mathit{\boldsymbol{\bar P}}}_i}{\mathit{\boldsymbol{R}}_i}} \right) = 0 $

(5)

式中，P为R_i的等价权矩阵，${\mathit{\boldsymbol{\bar P}}_{ij}} = {\mathit{\boldsymbol{P}}_{ij}}{w_{ij}}, {w_{ij}}$为降权因子，以此赋予受粗差污染观测量较小的权重，实现削弱甚至消除粗差影响的目的。选择IGGⅢ权函数确定相应的等价权矩阵P，具体形式可参照文献[5]。计算出单位权方差后重新计算权阵：

$ \mathit{\boldsymbol{\bar P}} = {\mathit{\boldsymbol{P}}_1}, \mathit{\boldsymbol{\bar P}} = \frac{{\sigma _{01}^2}}{{\sigma _{02}^2}}{\mathit{\boldsymbol{P}}_2} $

(6)

令, ${\mathit{\boldsymbol{P}}_1} = {\mathit{\boldsymbol{\bar P}}_1}, {\mathit{\boldsymbol{P}}_2} = {\mathit{\boldsymbol{\bar P}}_2}$, 再次进行迭代计算，直到σ₀₁²≈σ₀₂²，按照式(6)计算出P，进而按照式(2)计算出三维形变信息。

2 拉奎拉地震三维地表形变解算及结果分析 2.1 实验区与数据源

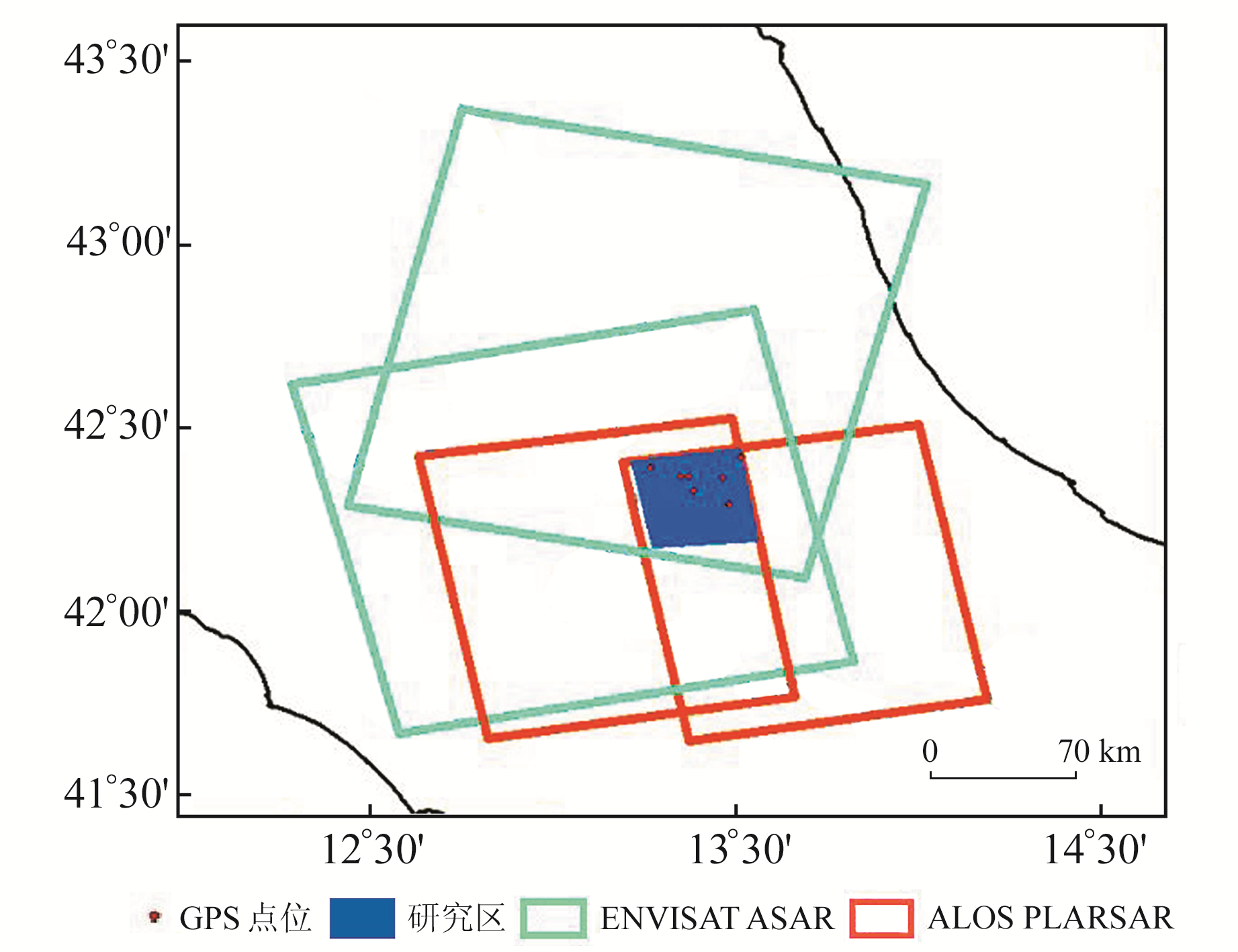
2009-04-06意大利拉奎拉市发生M_W6.3地震，地震发生后，欧空局公布了ENVISAT ASAR数据以及日本的ALOS PALSAR数据，包括地震前和地震后升、降轨数据^[6]等。本文以该地震震中区域为研究区来验证所提出三维地表形变抗差解算方法的有效性，所选取的4个干涉像对SAR影像覆盖范围如图 1所示，基本参数如表 1所示。

2.2 数据处理

以震前获取的数据为主影像，将震后获取的数据与主影像进行配准和干涉处理，获取干涉相位图。采用30 m分辨率的SRTM DEM作为外部DEM模拟出地形相位并从干涉相位中去除，从而获取原始差分干涉相位图。进一步采用Goldstein滤波方法对噪声进行滤波处理，按照最小费用流法^[7]对滤除噪声后缠绕的相位图进行解缠。最终，解缠后的干涉图中只包含形变相位和大气延迟相位。其中，大气延迟相位对干涉图的影响主要体现在对流层延迟方面，往往跟地形高程有一定的相关性，通过GAMMA软件的相关算法可以在一定程度上去除大气延迟误差。之后便可以获取由地表形变导致的干涉相位，如图 2所示。

由图可见，4个干涉像对在震中和断裂带周边形成了比较明显的干涉条纹，并且在形变位置和大致影响范围上基本一致，这说明该区域是本次地震的主要形变区。但2种不同传感器SAR影像获取的形变相位也存在一定的差异，这些差异及其原因主要体现在2个方面：1)ENVISAT ASAR数据监测出的干涉条纹相对于ALOS PALSAR数据监测出的干涉条纹多而密集；2)ENVISAT ASAR数据监测出的干涉条纹的覆盖范围比ALOS PALSAR数据监测出的干涉条纹覆盖范围大，其原因是2种SAR影像波长不同，导致对地表形变监测能力以及小量级形变的敏感程度均有所不同^[8]。

2.3 三维地表形变解算

将上述干涉图经过相位解缠、地理编码等处理后，获取雷达坐标系中4个不同视线向的地表形变信息，建立三维地表形变解算模型并进行解算。值得注意的是，2种数据形变监测结果具有不同的空间分辨率，这里将ASAR数据监测结果重采样至ALOS数据分辨率。入射角和方位角信息如表 1所示。根据式(5)建立三维解算模型后便可以进行三维形变抗差估算。为了研究粗差对三维地表形变解算的影响以及本文提出的抗差方法的有效性，设计2种解算方案：1)加权最小二乘三维地表形变解算；2)Helmert方差分量估计抗差最小二乘三维地表形变解算。

使用本文提出的解算方法进行三维地表形变解算。首先，按照观测量所采用的SAR影像传感器的不同(ENVISAT ASAR传感器和ALOS PALSAR传感器)，将4个观测量分为2组；其次，按照间接平差进行三维地表形变初次解算，获取并建立最小二乘残差与观测量单位权方差的函数关系，按照式(4)进行定权；最后，根据IGGⅢ权函数方案，通过对观测量进行保权、降权和淘汰处理来实现参数抗差解算。其中，初始权阵根据SAR影像相干性系数来确定，即计算窗口大小为5×5像元相干性系数平均值的倒数。在加权最小二乘三维地表形变解算中，假设权矩阵为单位矩阵。

图 3(a)、3(b)和3(c)分别是采用加权最小二乘解算方法获取的东西、南北和垂直向形变解算结果，形变主要集中在研究区中部的震中地区。其中，南北向的最大形变量为1.221 m，东西向的最大形变量为-0.308 m，垂直向的最大形变量为-0.389 m。图 3(d)、3(e)和3(f)分别是采用本文提出的抗差最小二乘解算方法获取的东西、南北和垂直向形变解算结果。其中，南北向的最大形变量为0.987 m，东西向的最大形变量为-0.287 m，垂直向的最大形变量为-0.352 m。东西向和南北向在震中区域表现出了明显的水平错动，将形变区域分为上半区域和下半区域，并且东西向和南北向水平错动位置基本吻合，表明错动位置即为本次地震断层所在的位置，这与USGS网站上发布的断层位置(图中黑线所示)完全吻合，综合三维形变场的特征与地质调查的结果基本一致。

2.4 精度验证

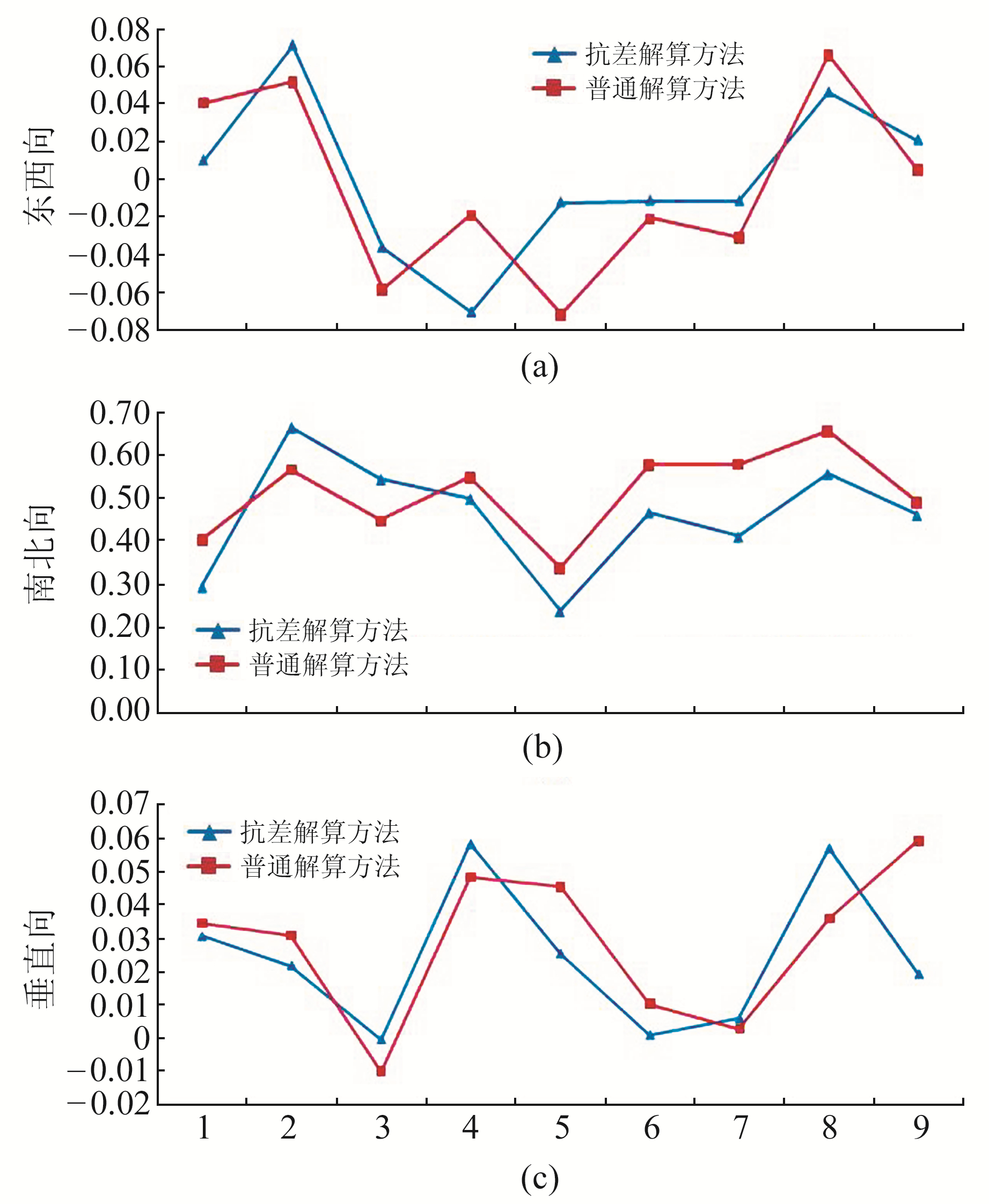
为了验证本文提出的抗差解算方法的有效性，将2种方案解算出的三维地表形变结果与真实GPS数据进行对比。同期的GPS数据来源于文献[9]，其点位分布如图 1圆点所示。这里直接将解算结果与GPS地表形变监测数据作差进行对比，图 4给出了对比结果，曲线越接近于0，说明解算结果越准确。

由图 4可见，东西向和垂直向与GPS观测值的对比结果(纵坐标取值)范围要比南北向小，说明这2个方向的解算精度要比南北向高。其主要原因是，SAR卫星通常是沿近南北方向飞行，导致雷达视线向对南北方向的形变不敏感，在解算过程中观测值中的噪声被放大，使南北向精度较差。因此，在利用InSAR技术实现三维地表形变监测时，还需要通过增加其他观测量作为约束，如方位向形变量等。表 2进一步统计了2种解算方法得出的三维地表形变与GPS观测量对比的均方根误差(RMSE)。从定量统计结果中也可以看出，本文所采用的三维地表形变抗差解算方法获取的3个方向的RMSE值均比普通解算方法获取的RMSE值小，说明其解算精度更高。

3 结语

本文针对采用多视线向D-InSAR技术进行三维地表形变解算时容易受到粗差影响的问题，提出一种抗差解算方法，并以2009年意大利拉奎拉地震为例，采用升、降轨ENVISAT ASAR以及ALOS PALSAR共4个轨道的SAR影像进行可行性验证，得出以下结论：

1) 2种传感器SAR影像都获取了具有明显干涉条纹的差分干涉图并且干涉条纹位置基本一致，但干涉条纹在具体覆盖区域大小以及疏密程度等方面略有不同。采用不同传感器SAR影像进行地表形变监测可以获取更丰富的地表形变监测结果。

2) 采用多视线向D-InSAR三维地表形变抗差解算方法可以有效获取研究区内三维地表形变场。从形变分布图中可以明显看出本次地震断裂带所在的位置，为研究地震断层滑动分布提供更直接的地表形变监测结果。

3) 相对于普通加权最小二乘获取的三维地表形变解算结果而言，本文所提出的抗差最小二乘解算方法在3个方向上的精度都有所改善，证明了其有效性。