UBGM(1, 1)-Markov模型广泛应用于沉降预测^[1]。该模型利用UBGM(1, 1)模型消除GM(1, 1)-Markov模型中的灰色固有偏差，提高预测精度。然而，UBGM(1, 1)-Markov预测模型存在2个邻近值可能被归属到不同状态、导致预测值产生偏差的问题。针对该问题，本文引入模糊分类理论，构建了FC-UBGM(1, 1)-Markov预测模型。

1 方法 1.1 模糊分类

模糊分类以模糊集合理论为基础，利用数学模型建立事物所属模糊类别的隶属度函数，并根据隶属度大小确定其归属，是一种用于沉降预测的新方法。图 1为利用三角法构建的模糊空间^[2]，其中E₁、E₂、E₃为3个模糊类别，属于该3个模糊类别的特征值隶属度之和为1。

1.2 构建FC-UBGM(1, 1)-Markov预测模型

基于传统GM(1, 1)模型构建的无偏灰色预测模型UBGM(1, 1)为：

$ {\hat x^{\left( 0 \right)}}\left( k \right) = \left\{ \begin{array}{l} {x^{\left( 0 \right)}}\left( 1 \right), k = 1\\ A{{\rm{e}}^{E\left( {k - 1} \right)}}, k = 2, 3, \cdots , n \end{array} \right. $

(1)

式中，$A = \frac{{2b}}{{2 + a}}, E = \ln \left( {\frac{{2 - a}}{{2 + a}}} \right)$，a、b分别为GM(1, 1)模型的发展系数和灰色作用量，${\hat x^{\left( 0 \right)}}\left( k \right)$为UBGM(1, 1)的拟合值。

在拟合值的残差ε⁽⁰⁾中，找到满足以下条件的可建模残差尾端序列ε^(1)[3]：1)$\forall k \ge {k_0}, {\varepsilon ^{\left( 0 \right)}}\left( k \right)$的符号一致；2)$n - {k_0} \ge 4$，其表达式为${\varepsilon ^{\left( 1 \right)}} = \left( {\left| {{\varepsilon ^{\left( 0 \right)}}\left( {{k_0}} \right)} \right|, \left| {{\varepsilon ^{\left( 0 \right)}}\left( {{k_0} + 1} \right)} \right|, \cdots , \left| {{\varepsilon ^{\left( 0 \right)}}\left( n \right)} \right|} \right)$。对ε⁽¹⁾重建GM(1, 1)模型，并利用最小二乘原理计算参数序列${\mathit{\boldsymbol{\hat a}}_\varepsilon } = {\left[ {{a_\varepsilon }, {b_\varepsilon }} \right]^{\rm{T}}}$，得到残差修正值：

$ \hat \varepsilon \left( {k + 1} \right) = \left( { - {a_\varepsilon }} \right)\left( {{\varepsilon ^{\left( 0 \right)}}\left( {{k_0}} \right) - \frac{{{b_\varepsilon }}}{{{a_\varepsilon }}}} \right){{\rm{e}}^{ - {a_ \in }\left( {k - {k_0}} \right)}} $

(2)

结合式(1)和(2)，构建残差修正后的UBGM(1, 1)模型：

$ {\hat x^{\left( 0 \right)}}\left( {k + 1} \right) = \left\{ \begin{array}{l} {{\hat x}^{\left( 0 \right)}}, k = 0\\ A{{\rm{e}}^{Ek}}, 0 ＜ k ＜ {k_0}\\ A{{\rm{e}}^{Ek}} \pm \hat \varepsilon \left( {k + 1} \right), k \ge {k_0} \end{array} \right. $

(3)

将式(3)拟合值的相对残差序列作为马尔科夫链，划分出n个区间[δ_i-1, δ_i](i=1, 2, …, n, n+1)，每个区间对应一种状态E_i(i=1, 2, …, n)。把[δ_i-1, δ_i]代入模糊分类的隶属度函数^[2]，计算出模糊向量，向量中的每个分量即是隶属度，根据隶属度最大原则确定其所属状态E_i。通过统计状态E_i之间的一步转移情况，得到一步Markov状态转移概率矩阵p¹。

记第k+1期的模糊向量为V⁽⁰⁾，该向量V⁽⁰⁾经过l步转移后的模糊向量为V^(l)，即

$ {\mathit{\boldsymbol{V}}^{\left( l \right)}} = {\mathit{\boldsymbol{V}}^{\left( 0 \right)}}{\left( {{\mathit{\boldsymbol{p}}^1}} \right)^l} $

(4)

利用V^(l)确定预测值所属状态E_i，再根据E_i判断该预测值相对残差的区间[δ_i-1, δ_i]，计算预测值的取值范围[Y_i1, Y_i2](i=1, 2, …, n)，其中,

$ {Y_{i1}} = \frac{{{{\hat x}^{\left( 0 \right)}}\left( k \right)}}{{1 - {\delta _{i - 1}}}}, {Y_{i2}} = \frac{{{{\hat x}^{\left( 0 \right)}}\left( k \right)}}{{1 - {\delta _i}}} $

(5)

那么，经过残差修正后的UBGM(1, 1)-Markov预测值为[Y_i1, Y_i2]的加权平均值，即

$ \hat x\left( l \right) = \frac{{{Y_{i1}} + {Y_{i2}}}}{2} $

(6)

最后，利用新陈代谢方法将经过残差修正后的UBGM(1, 1)-Markov模型的最新预测值加入到原始序列中，同时剔除最早期的观测数据，再次构建残差修正的UBGM(1, 1)-Markov预测模型，最终得到FC-UBGM(1, 1)-Markov预测值。

2 案例分析 2.1 研究区概况与数据源

某露天矿的原最高峰经过露天开采，边坡深切、陡峭，多次发生塌陷。在北边坡变形敏感部位上布设监测点，在南边坡变形范围外稳定的建筑物顶上布设基准点，形成一个长边控制网。采用双频GNSS接收机进行静态相对定位观测，并利用内业数据处理软件对静态观测数据进行基线解算和平差处理，得到沉降观测数据。

以Q3监测点累积沉降观测数据为例，每5 d为一个观测周期, 原始累积沉降量如表 1所示。选取前25期为实验数据，后5期为验证数据。

2.2 算法验证

露天矿边坡沉降速率会随时间变缓，利用弱化缓冲算子对前25期数据进行光滑处理，得到：

$ d\left( i \right) = \frac{{\mathop \sum \limits_{i = k}^n x\left( i \right)}}{{n - k - 1}}, k = 1, 2, \cdots , n $

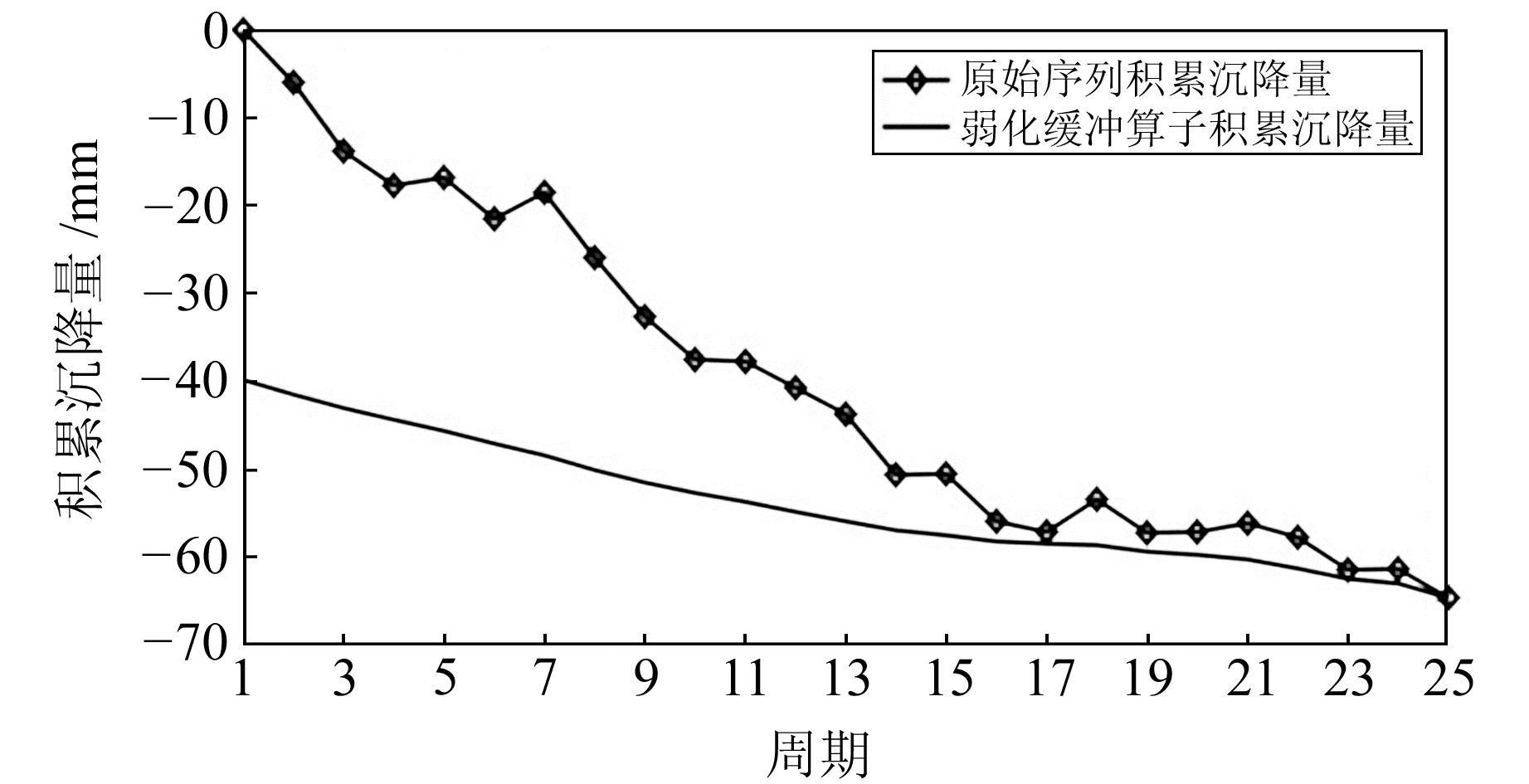
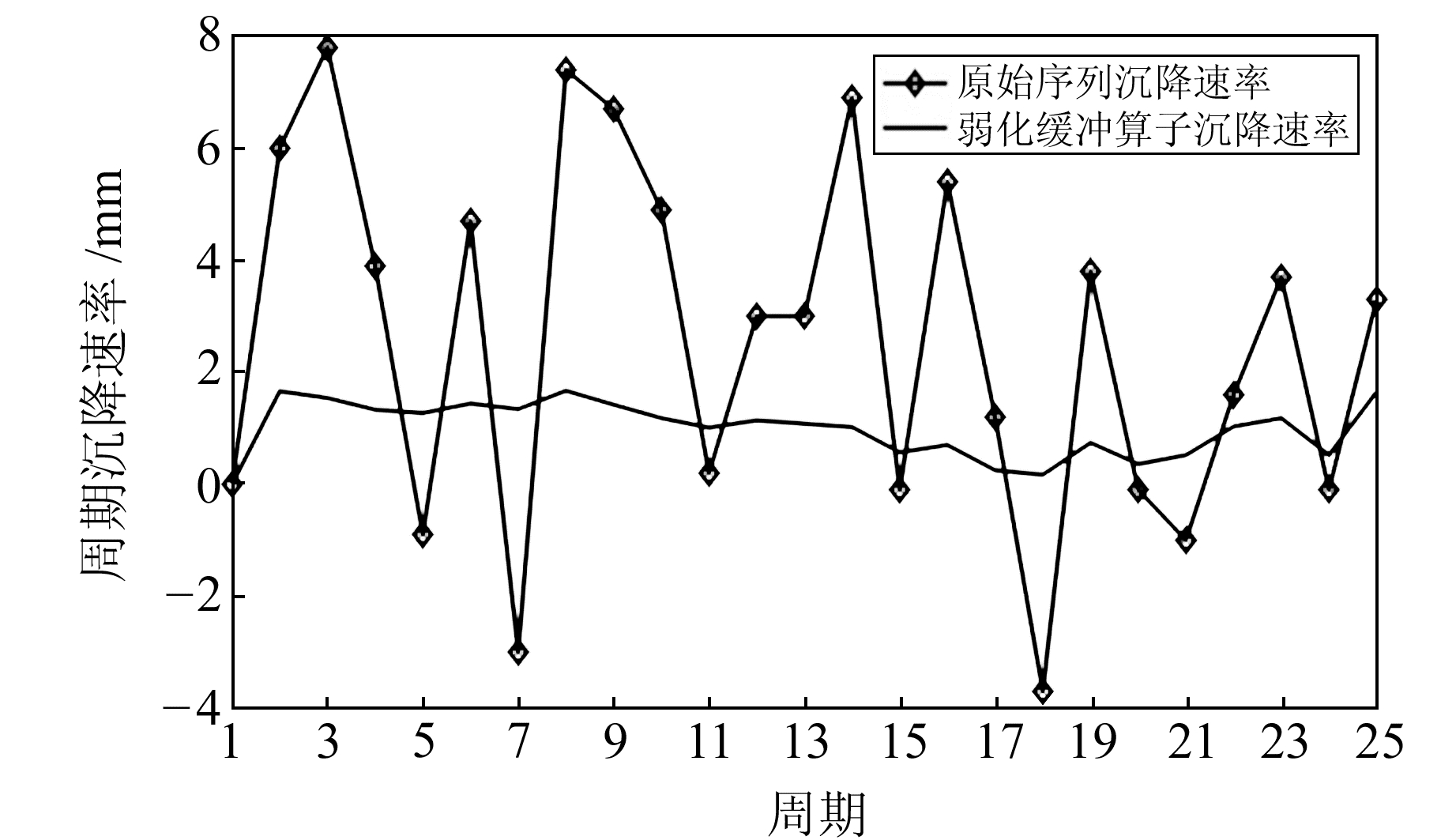
图 2、3分别为弱化缓冲算子处理前后累积沉降量和周期沉降速率对比。分析图 2可知，原始累积沉降量曲线表明后一期的累积沉降量小于前一期，可能是周围荷载被运走、土质膨胀所致；经过弱化缓冲算子处理后的累积沉降曲线变得平缓，减小了扰动因子的干扰，有利于提高预测精度^[4]。分析图 3可知，原始沉降速率曲线表明在监测初期沉降速率较大，但随着监测周期的不断推移，沉降速率逐渐变缓；经过弱化缓冲算子处理后的沉降速率曲线变得平缓。

通过计算UBGM(1, 1)模型的拟合值可知，其19~25期拟合值的残差符号一致。选取k₀=19，n=25，并且n-k₀=6>4，满足残差修正条件，构建残差修正后的UBGM(1, 1)预测函数为：

$ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\hat x}^{\left( 0 \right)}}\left( {k + 1} \right) = \\ \left\{ \begin{array}{l} 39.81, k = 0\\ 44.020{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 9{{\rm{e}}^{0.016{\kern 1pt} {\kern 1pt} {\kern 1pt} 7\left( k \right)}}, 0 ＜ k ＜ 19\\ 44.020{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 9{{\rm{e}}^{0.016{\kern 1pt} {\kern 1pt} {\kern 1pt} 7\left( k \right)}} - 0.990{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2{{\rm{e}}^{0.063{\kern 1pt} {\kern 1pt} {\kern 1pt} 7\left( {k - 19} \right)}}, k \ge 19 \end{array} \right. \end{array} $

残差修正后的UBGM(1, 1)拟合值结果见表 2。根据拟合值的相对残差波动范围将其划分为3个区间：[-8, -1]、(-1, -3]、(-3, 5]。将该3个区间分别代入隶属度函数^[2]中，再根据隶属度函数计算每个相对残差的模糊向量，结果见表 2。在模糊向量中，根据其分量的大小(即隶属度)确定每个相对残差所属的状态E_i。那么，根据表 2可得到状态E_i间的一步转移情况，进而得到状态E_i间的一步转移概率矩阵。

由表 2可知，第25期拟合值相对残差的模糊向量为(0.115, 0.885, 0)。然后，利用式(4)分别计算第26~30期预测值相对残差的模糊向量，并根据隶属度最大原则确定其所隶属的状态E_i。最后，通过式(6)计算第26~30期预测值。

利用新陈代谢方法，去掉原始累积沉降序列中的第1期数据，并加入第26期的预测数据。再次进行残差修正的UBGM(1, 1)-Markov过程，最终得到基于FC-UBGM(1, 1)-Markov的第26~30期预测结果，见表 3。

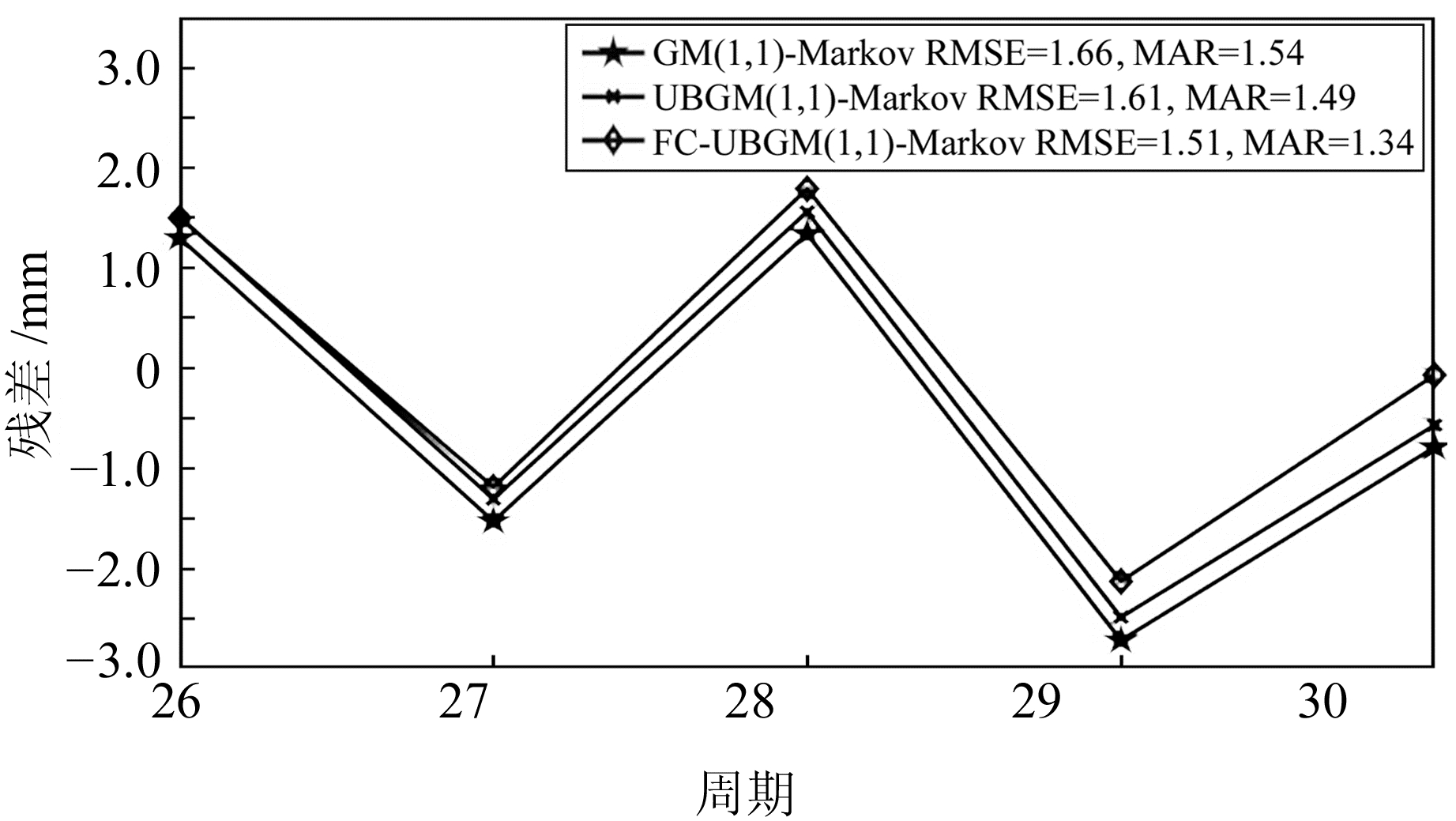
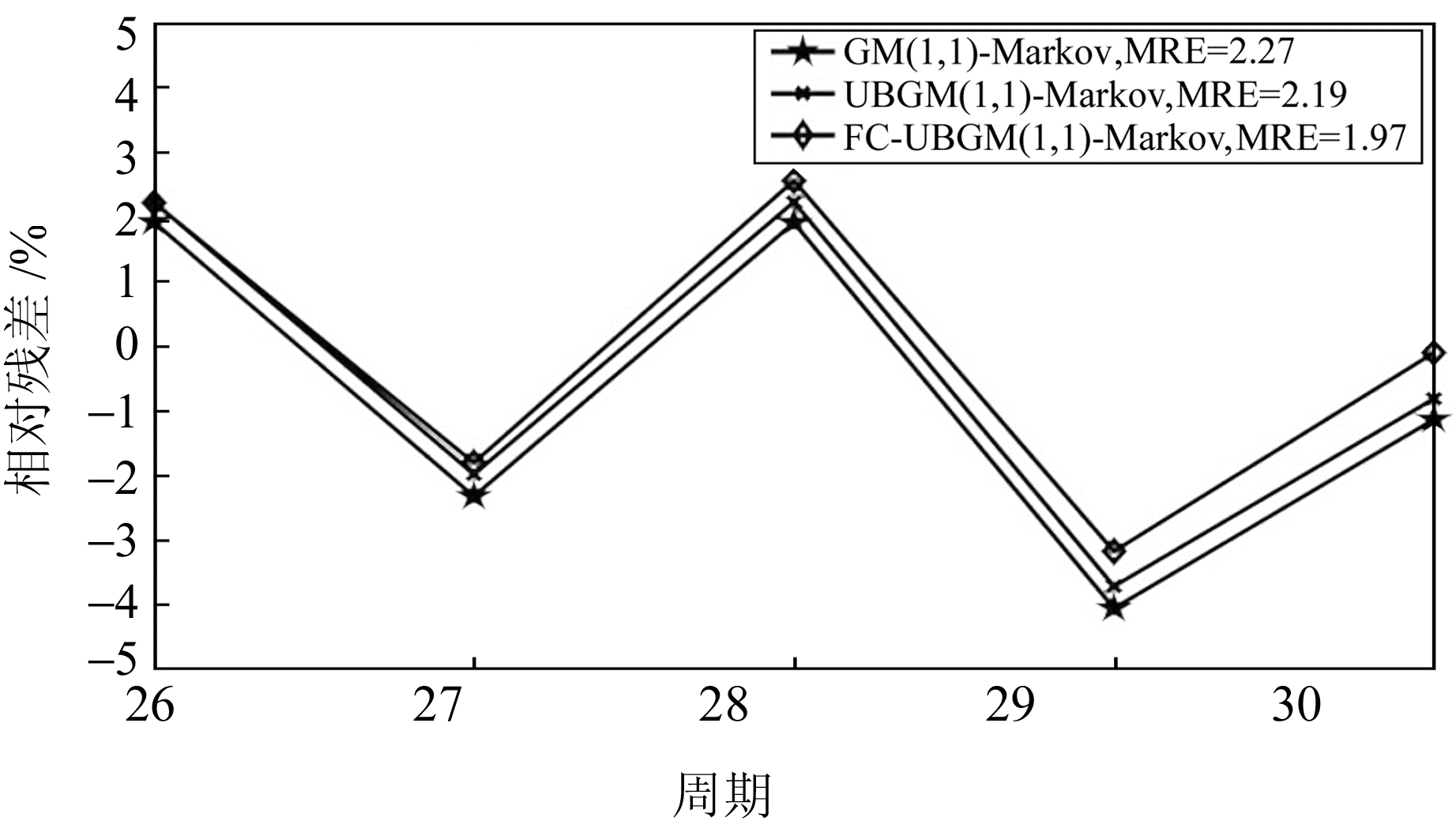
为了更加直观地比较本文模型与其他传统预测模型的精度，分别计算预测值的残差和相对残差，如图 4、5所示。分析图 4可知，本文模型的残差较其他2种模型的残差更趋近于0，其平均绝对误差(MAR)和均方根误差(RMSE)分别为1.34和1.51。其中，MAR较另外2种模型分别降低12.99%、10.07%；RMSE较另外2种模型分别降低9.04%、6.21%。分析图 5可知，本文模型的相对残差较其他2种模型更趋近于0，其平均相对误差(MRE)为1.97，较另外2种模型分别降低13.22%和10.05%。通过以上分析可知，本文模型的预测效果优于传统模型。

3 结语

针对传统UGM(1, 1)-Markov模型中存在2个邻近值可能被归属到不同状态的问题，引入模糊分类理论，构建了基于模糊分类的UBGM(1, 1)-Morkov模型。通过露天矿边坡沉降观测数据对该预测模型进行案例分析，结果表明，本文方法的各项精度评价指标均小于传统模型，并且相对于UBGM(1, 1)-Markov模型的RMSE、MAE、MRE分别提高6.21%、10.07%、10.05%，预测效果有一定程度的提高，可用于短期的露天矿边坡沉降预测。

本文不足之处在于，由于监测点位于高陡边坡上，不便于采用精密水准测量的方法进行沉降观测。因此，本实验采用双频GNSS接收机对监测点的沉降进行静态相对定位观测，其观测精度不高，对模型的预测精度分析有一定影响。

未来工作内容：1)克服观测环境因素的影响，选择更加合适的设备和观测方法，提高沉降观测数据的精度；2)不断完善本模型，进一步提高预测精度，并使其可适用于中、长期的沉降预测。