2. 中国地震局地质研究所地震动力学国家重点实验室,北京市华严里甲1号,100029
在研究地震前兆的各类方法中,GPS时间序列空间测地技术具有高精度、低成本和多尺度直接观测的特点[1],其时间序列解算的绝对精度可以达到mm级[2],是深入探讨地壳形变的优良手段。本文以2016-01-21门源地震为例,采用深度神经网络预测GPS时间序列的方法,研究地震的前兆信息。
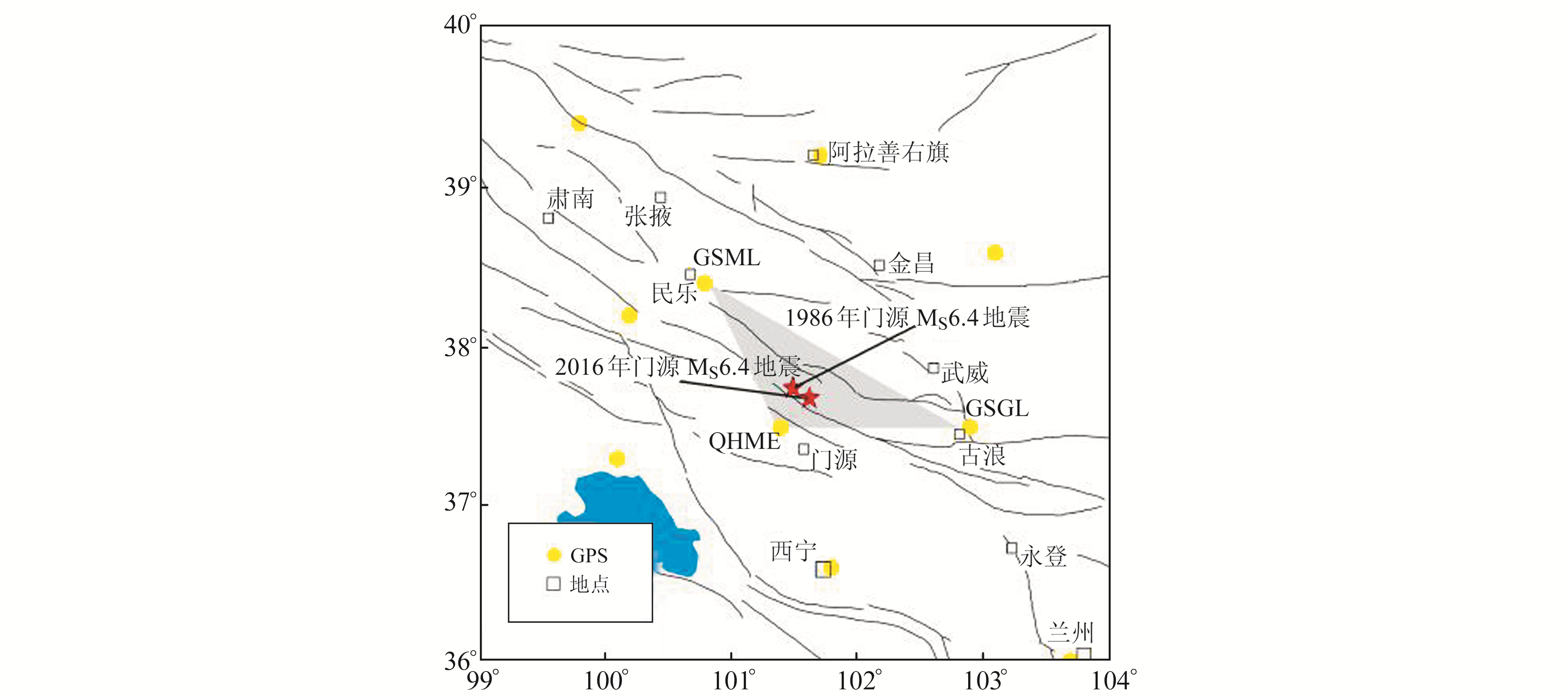
1 门源地震构造背景2016-01-21位于门源北部的祁连山冷龙岭地区发生MS6.4地震,震中所处的青藏高原东北缘区域布设有较为密集的GPS观测网[3-4],区域构造背景及周边GPS观测台站分布见图 1,图中黄色圆点为连续GPS观测站。
|
图 1 2016年门源MS6.4地震构造背景及周边GPS观测站分布 Fig. 1 Tectonic background of the 2016 Menyuan MS6.4 earthquake and distribution of GPS observation stations nearby |
震中附近的冷龙岭断裂带是一条全新世活断层,位于青藏高原东北缘隆起区域,是北祁连活动断裂带的重要组成部分,具有非均匀性的特点,其北侧长期受印度板块东向挤压运动的影响[5]。震源附近的门源台(QHME)、民乐台(GSML)及古浪台(GSGL)较好地覆盖了发震区域(图 1中灰色三角形区域),对这3个台站的GPS时间序列进行分析可以捕捉到地震前兆信息。
2 方法步骤设计总概本文资料来源于中国地震局GNSS数据产品服务平台,由于深度学习对资料有一定的要求,需要对获取的数据进行适当的预处理。训练LSTM时序预测模型是获取后续分析数据的关键,也是整个设计总概的核心;训练出的模型用来预测指定的时间序列;再用指定时间段的预测时间序列与真实时间序列进行定性的相似性分析和定量的异常检测来分析地震前的数据变化特征,以期从中发现地震的前兆信息。
2.1 LSTM时间序列预测模型GPS时间序列属于非平稳时间序列,传统的循环神经网络RNN不能处理长时间的时间序列。LSTM神经网络具有强辨别力和学习能力,可以学习时间序列数据包含的非线性关系,且LSTM网络解决了RNN网络出现的梯度消失问题[6]。本文设计的LSTM神经网络时序预测模型框架见图 2,预测模型主要由输入层、隐藏层、输出层及模型训练构成。

|
图 2 LSTM神经网络时序预测模型框架 Fig. 2 Time series prediction model framework of LSTM neural network |
GPS时间序列首先进入输入层,利用经典的LagFeatures方式[7]作补全处理,重构为以ts(t-lag)~ts(t-1)为输入特征、ts(t)为输出特征的序列,并将其转换为监督式学习问题,再进行数据的划分、数据归一化等处理;时间序列转换成LSTM输入格式后进入隐藏层,并逐次通过3个门(输入门、遗忘门、输出门)进行计算,最终得到隐藏层输出;输出层对LSTM神经网络预测输出的结果进行反归一化处理,计算损失函数均方误差(MSE),以损失函数最小为优化目标,使用BPPT算法更新模型中的权重直到损失函数收敛。训练选用适应性动量估计算法Adam(adaptive moment estimation)作为优化器,采用批量训练方式[8]。
2.2 时间序列相似性分析 2.2.1 Pearson相关系数时间序列{xt}、{yt}(t=1, 2, …, T)的Pearson相关系数为[9]:
| $ \rho = \frac{{\mathop \sum \limits_{t = 1}^T \left( {{x_t} - {{\bar X}_T}} \right)\left( {{y_t} - {{\bar Y}_T}} \right)}}{{\sqrt {\mathop \sum \limits_{t = 1}^T {{\left( {{x_t} - {{\bar X}_T}} \right)}^2}} \sqrt {\mathop \sum \limits_{t = 1}^T {{\left( {{y_t} - {{\bar Y}_T}} \right)}^2}} }} $ | (1) |
式中,XT和YT分别为{xt}和{yt}的平均值,且0≤|ρ|≤|1|。当|ρ|值靠近1时,表示2条时间序列的相关程度较高;当|ρ|值靠近0时,表示2条时间序列的相关程度较低。ρ为正值时,2条时间序列正相关;ρ为负值时,2条时间序列负相关。基于Pearson相关系数计算2个时间序列之间的距离关系
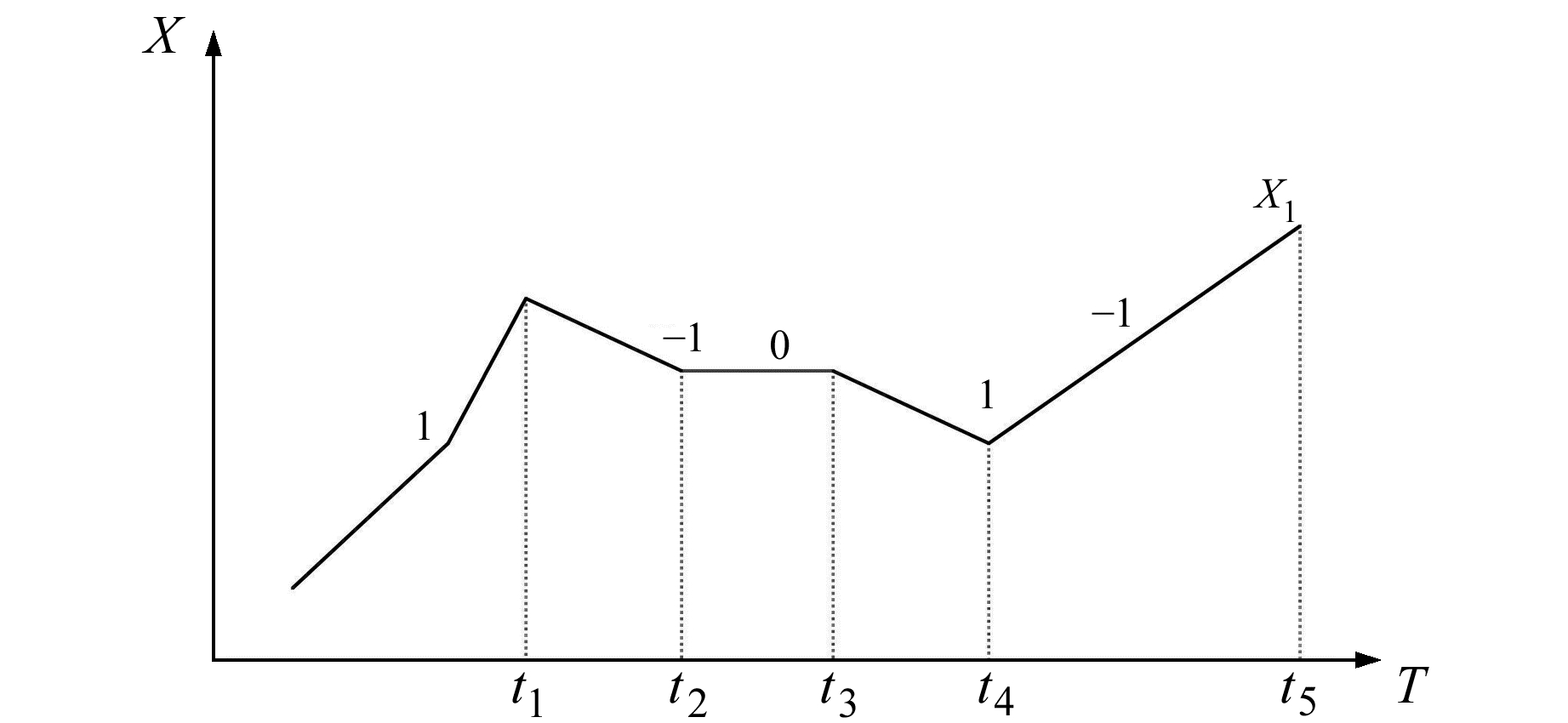
形状距离能够较好地衡量2条时间序列走势的相似性。首先利用重要点的方式对时间序列进行分段,每段标记为上升、不变或下降,将时间序列的极值点作为重要点计算每段的斜率,若斜率为正值设成1,为0设成0,为负值则设成-1。如图 3的时间序列可表示为X1={1, -1, 0, -1, 1}。
|
图 3 时间序列线性分段 Fig. 3 Time series piecewise linear representation |
分别将2条时间序列进行线性分段,再利用重要点的并集对其进行等模式化,使得2条时间序列有相同的分割点,可表示为:
| $ {S_1} = \left\{ {\left( {{m_{11}}, {t_1}} \right), \left( {{m_{12}}, {t_2}} \right), \cdots , \left( {{m_{1i}}, {t_i}} \right)} \right\} $ | (2) |
| $ {S_2} = \left\{ {\left( {{m_{21}}, {t_1}} \right), \left( {{m_{22}}, {t_2}} \right), \cdots , \left( {{m_{2i}}, {t_i}} \right)} \right\} $ | (3) |
令每个分割区间端点对应序列值的差值为
| $ {A_1} = \left\{ {\left( {\Delta {y_{11}}, {t_1}} \right), \left( {\Delta {y_{12}}, {t_2}} \right), \cdots \left( {\Delta {y_{1i}}, {t_i}} \right)} \right\} $ | (4) |
| $ {A_2} = \left\{ {\left( {\Delta {y_{21}}, {t_1}} \right), \left( {\Delta {y_{22}}, {t_2}} \right), \cdots \left( {\Delta {y_{2i}}, {t_i}} \right)} \right\} $ | (5) |
式中,Δy1i为时序S1的第i个区间端点对应序列值的差值。
定义形状距离D为:
| $ {D_{{s_1},{s_2}}} = \sum\limits_{i = 1}^n {{t_{{w_i}}}} \cdot \left| {{m_{1i}} - {m_{2i}}} \right| \cdot \left| {{A_{1I}} - {A_{2I}}} \right| $ | (6) |
式中,twi=ti/tn, ti为第i个模式所跨越的时间,tn为总的时间长度。
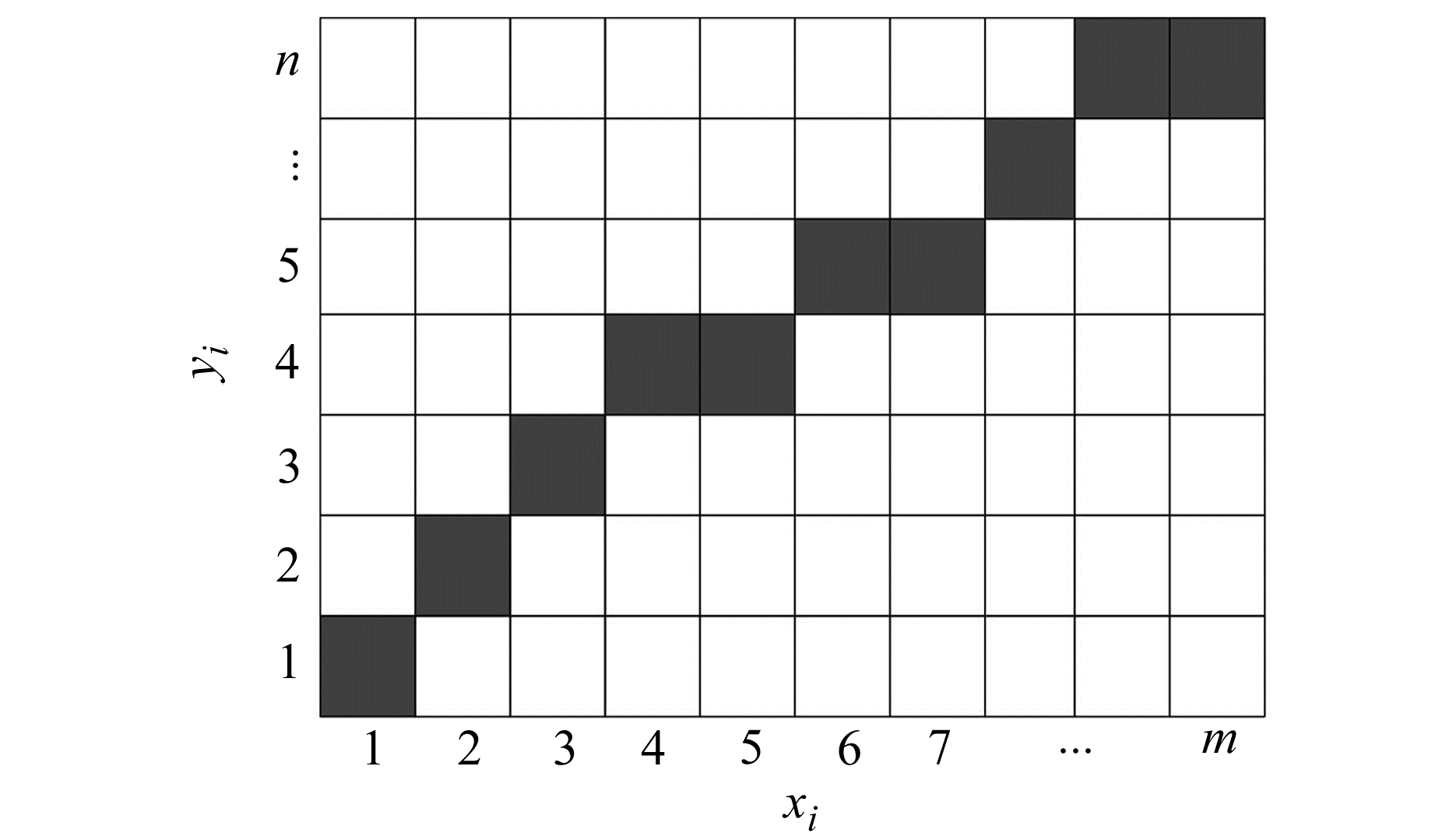
2.2.3 动态时间弯曲距离动态时间弯曲(dynamic time warping,DTW)是通过弯曲时间轴来对时间序列进行匹配映射的相似性度量。首先计算2条时间序
|
图 4 动态时间弯曲路径图 Fig. 4 Dynamic time warping path diagram |
| $ r\left( {i, j} \right) = d\left( {i, j} \right) + \min \left\{ \begin{array}{l} r\left( {i, j - 1} \right)\\ r\left( {i - 1, j - 1} \right)\\ r\left( {i - 1, j} \right) \end{array} \right. $ | (7) |
且r(0, 0)=0,r(i, 0)=r(0, j)=∞。
最优路径需要满足边界限制、连续性和单调性等3个条件,2条时间序列的动态时间弯曲距离则由最优路径条件下的累计矩阵表示,即L(X, Y)=r(m, n)。
3 实验结果与分析 3.1 实验数据选用中国地震局GNSS数据产品服务平台GAMIT解算的2010-08-23~2016-01-20门源台、民乐台和古浪台的E、N、U方向的GPS时间序列,解算精度均在mm级。考虑到研究区域在2013-06-21发生3.1级地震,2013-09-20发生5.1级地震,2013-09-22发生3.0级地震,为准确训练出无震时的LSTM时间序列预测模型,删除2013-03-21~12-22的数据。
本文选取的GPS时间序列均为震前历史数据,不使用震时和震后数据。由于获取的GPS时间序列会存在部分数据缺失的情况,采用邻近点线性趋势的方法对缺失的时间序列进行补全,再将数据划分成训练集、验证集及测试集,其中训练集和验证集作为无震时的历史数据用于学习无震时GPS时间序列变化规则及验证模型精准度,最终将训练得到的LSTM时间序列预测模型应用到测试集。实验中将2010-08-23~2015-10-20中删除2013-03-21~12-22后剩下的1 607 d的数据用于模型的训练与验证,将数据以9 :1的比例划分为训练集与验证集,选择2015-10-23~2016-01-20共90 d数据作为真实环境中的测试集进行前兆异常的检测。
3.2 模型评价选用均方根误差(RMSE)对预测模型输出结果的精度进行评价[10],其表达式为:
| $ {\rm{RMSE = }}\sqrt {\frac{1}{n}\sum\limits_{t = 1}^n {{{\left( {{t_{{\rm{obs}}}} - {t_{{\rm{pre}}}}} \right)}^2}} } $ | (8) |
式中,n为预测的总天数,tobs为实际观察的第t天真实值,tpre为第t天的预测值。
预测精度见表 1,由于模型训练时用的数据不同,不同LSTM时间序列预测模型的精度有所差别,但都在mm级,满足GPS时间序列预测的要求。
|
|
表 1 模型预测精度 Tab. 1 Prediction accuracy of the model |
本文选取需要预测的历史无震时和震前(测试集时区)数据时间分别为2015-04-01~06-30和2015-10-23~2016-01-20,利用LSTM时间序列预测模型分别预测GPS时间序列,并计算其与真实时间序列的相似性指标,分析是否有震前异常。
3.3.1 相似性对比1) Pearson相关系数对比。分别计算无震时和震前3个台站3个方向的真实时序与预测时序的ρ值和d值,结果见表 2、3。由表 2可知,总体上,无震时各台站的ρ值比震前要大,说明无震时的真实时序与预测时序的相似性比震前好,表明震前3个月内真实的时间序列相对于以往无震时在一定程度上出现了异常。由表 3也可以看出,总体上,震前各台站的d值大于无震时的d值,进一步说明震前的真实时序发生了异常变化。
|
|
表 2 真实时序与预测时序的ρ值 Tab. 2 ρ values of real time series and predicted time series |
|
|
表 3 真实时序与预测时序间距离 Tab. 3 Distance between real time series and predicted time series |
2) 形状距离对比。形状距离是时间序列经过模式化后定义的距离,可以较好地反映2条时间序列是否相似地上升或下降。对无震时90 d内时序与震前90 d内时序的时间序列作形状距离的分析,结果见表 4。可以看出,除U向的门源台和古浪台外,总体上,无震时的真实时序与预测时序的形状距离低于震前,进一步说明真实时序与预测时序的相似性在无震时优于震前,表明震前的时间序列出现了异常,可能是地震前兆。
|
|
表 4 真实时序与预测时序间形状距离 Tab. 4 Shape distance between real time series and predicted time series |
3) 动态时间弯曲距离对比。表 5为无震时90 d内时序与震前90 d内时序的DTW距离。可以看出,无震时真实时序与预测时序的DTW距离比震前小,表明无震时真实时序与预测时序的相似性明显优于震前,进一步说明震前90 d内3个台站3个方向所测的时间序列出现了异常,可能是地震前兆。
|
|
表 5 无震时及震前的DTW距离 Tab. 5 DTW distance during non-earthquake and before earthquake |
以上3个相似性指标结果表明,总体上,震前真实时序与预测时序的相似性低于无震时,说明地震前兆异常的存在性较大。
3.3.2 时间序列的趋势异常和异常日期分析分别对3个台站E、N、U方向在门源MS6.4地震前90 d、60 d及30 d的GPS时间序列进行预测,并计算预测精度,结果见表 6。可以看出,精度均在mm级,符合要求。
|
|
表 6 时间序列预测精确度 Tab. 6 Prediction accuracy of time series |
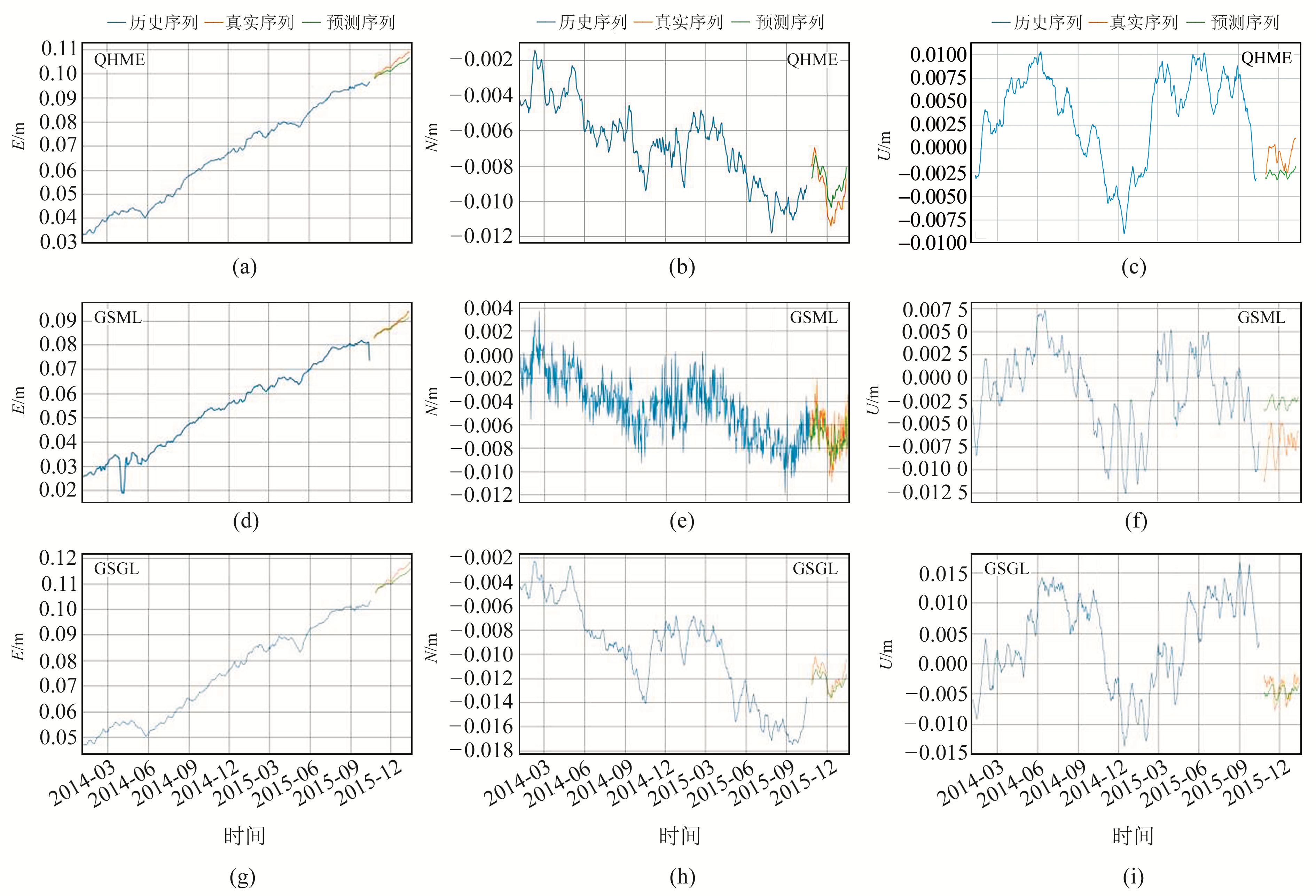
GPS时间序列记录了地壳形变等信息,其变化幅度反映了地壳的变形程度,依据GPS时间序列的整体变化趋势可判断是否出现异常。本文通过高精度的LSTM神经网络时序预测模型对地震前3个月的GPS时间序列进行回溯预测,并将预测时间序列同真实时间序列进行对比分析,图 5为各台站3个方向上GPS时间序列趋势。如图 5(a)、5(d)及5(g)所示,E方向上3个台站的预测时间序列与真实时间序列的变化趋势相近,但存在差值较大的情况,统计两者差值超过95%置信区间的异常日期发现,古浪台及民乐台均含有2015-12-22的异常日期,3个台站均含有2016-01-09的异常日期。由图 5(b)、5(e)及5(h)可知,N方向上3个台站的预测时间序列与真实时间序列的曲线斜率有明显差值。如图 5(c)、5(f)及5(i)所示,U方向上3个台站的预测时间序列与真实时间序列的曲线斜率有明显差异。综上所述,由高精度LSTM时间序列预测模型学习出来的时间序列曲线与真实时间序列曲线对比发现,2016-01-21门源地震前有前兆异常。
|
图 5 各台站在3个方向上的GPS时间序列趋势图 Fig. 5 Trend chart of GPS time series of each station in three directions |
本文利用LSTM神经网络学习无震时GPS时间序列变化规律,得到LSTM时间序列预测模型,再利用其分别预测无震时和震前GPS时间序列,并通过Pearson相关系数、形状距离、DTW距离等3种数学方法分别分析无震时和震前真实时间序列与预测时间序列之间的相似性。结果发现,无震时真实时间序列与预测时间序列之间的相似性好于震前,表明震前出现了异常时段。另外,通过对GPS时间序列和异常日期进行分析发现,震前预测时间序列与真实时间序列有差异,且多个台站在同一方向有相同的异常日期,说明震前有存在地震前兆的可能。
综上所述,用深度学习预测GPS时间序列探索门源6.4级地震前兆的方法是可行的,该方法的应用达到了预期目的,但对于实验出现的异常时段和异常日期反映的前兆异常程度不够显著,可能是地震前兆本身异常强度较弱。目前仅针对门源地震进行了实验检测,后续将会对其他中强震进行处理分析,以进一步验证用深度学习预测GPS时间序列探索地震前兆方法的可行性。
| [1] |
陈光. 小波分析在GPS位移时间序列特征中的应用[J]. 地震地磁观测与研究, 2010, 31(5): 95-99 (Chen Guang. Wavelet Analysis in GPS Displacement Time Series Analysis[J]. Seismological and Geomagnetic Observation and Research, 2010, 31(5): 95-99)
(  0) 0) |
| [2] |
何月帆.高精度GPS数据处理及时间序列分析[D].西安: 长安大学, 2019 (He Yuefan. High Precision GPS Data Processing and Time Series Analysis[D]. Xi'an: Chang'an University, 2019)
(  0) 0) |
| [3] |
甘卫军, 张锐, 张勇, 等. 中国地壳运动观测网络的建设及应用[J]. 国际地震动态, 2007(7): 43-52 (Gan Weijun, Zhang Rui, Zhang Yong, et al. Development of the Crustal Movement Observation Network in China and Its Applications[J]. Recent Developments in World Seismology, 2007(7): 43-52)
(  0) 0) |
| [4] |
陈为涛, 甘卫军, 肖根如, 等. 2016年青海门源MS6.4地震前的区域地壳形变特征[J]. 大地测量与地球动力学, 2017, 37(8): 777-781 (Chen Weitao, Gan Weijun, Xiao Genru, et al. The Regional Crustal Deformation before the 2016 Menyuan MS6.4 Earthquake[J]. Journal of Geodesy and Geodynamics, 2017, 37(8): 777-781)
(  0) 0) |
| [5] |
赵强, 王双绪, 蒋锋云, 等. 利用InSAR技术研究2016年青海门源MW5.9地震同震形变场及断层滑动分布[J]. 地震, 2017, 37(2): 95-105 (Zhao Qiang, Wang Shuangxu, Jiang Fengyun, et al. Coseismic Deformation Field and Fault Slip Distribution of the 2016 Qinghai Menyuan MW5.9 Earthquake from InSAR Measurement[J]. Earthquake, 2017, 37(2): 95-105)
(  0) 0) |
| [6] |
Graves A. Supervised Sequence Labelling with Recurrent Neural Networks[J]. Computational Intelligence, 2012, 385: 1-141
(  0) 0) |
| [7] |
Brownlee J. Long Short-Term Memory Networks with Python: Develop Sequence Prediction Models with Deep Learning[M]. Machine Learning Mastery, 2017
(  0) 0) |
| [8] |
Ioffe S, Szegedy C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift[C]. International Conference on Machine Learning, Lille, France, 2015
(  0) 0) |
| [9] |
何海江. 带时延的长时间序列线性相关挖掘研究[J]. 计算机工程与应用, 2006, 42(16): 180-183 (He Haijiang. Research on Mining Linear Correlation of Long Time Series with Time Delay[J]. Computer Engineering and Applications, 2006, 42(16): 180-183)
(  0) 0) |
| [10] |
Willmott C J, Matsuura K. Advantages of the Mean Absolute Error(MAE) over the Root Mean Square Error(RMSE) in Assessing Average Model Performance[J]. Climate Research, 2005, 30(1): 79-82
(  0) 0) |
2. State Key Laboratory of Earthquake Dynamics, Institute of Geology, CEA, A1 Huayanli, Beijing 100029, China
 2020, Vol. 40
2020, Vol. 40


