2. 中国地震台网中心,北京市三里河南横街5号,100045
地震监测数据序列的趋势转折变化是地震前兆异常的一个重要信息,也是出现频率较高的一类[1-2]。目前对该类异常的识别提取主要依靠形态分析和经验判定,缺少数学上的定量方法,异常认定的标准不统一。针对时间序列模式的表示方式有多种[3-4],其中分段线性的表示方法(piecewise linear representation,PLR)最常用[5],其具有形式直观、距离度量灵活及计算简单等特点,常被应用到时间序列的信息挖掘中。时间序列分段描述的核心思想是用线性拟合的直线近似代替原有的观测曲线,其难点在于准确求取分段点的位置[6]。通过对时间序列分段点规律的深入分析发现,这些点可归结为两类,即达到一定幅度的极值点和单调区间内速率改变较快的点,这些特征点对时间序列的变化特征起到主要的控制作用。一些学者利用给定窗口长度的平均值代替原有时间序列的PAA分段表示算法[7-8]; 也有学者针对分段点的特征进行研究,提出基于时间序列重要点或者特征点的直线分段方法[8-10],在求出分段点以后,采用最小二乘算法拟合分段点两侧的直线段[11]。当前对PLR算法的应用主要是以整体拟合误差最小作为约束条件,但在这种约束条件下,转折点可能未被准确求取或者提取出过多的虚假转折点[12-13]。
针对以上问题,为减少主观判断带来的偏差,科学、快速、及时地提取该类型地震的异常信息,本文提出一种基于极值点和矢量转角相结合的方法,研究定量提取时间序列的趋势转折点,并通过矢量转角的大小定义异常幅度,根据震例对应规则(结合区域构造特征、断层分布及以往震例对应情况,确定测点可预测的地震空间范围与震级下限)深入挖掘观测数据所蕴藏的地震异常信息,并对提取结果进行预报效能评估。
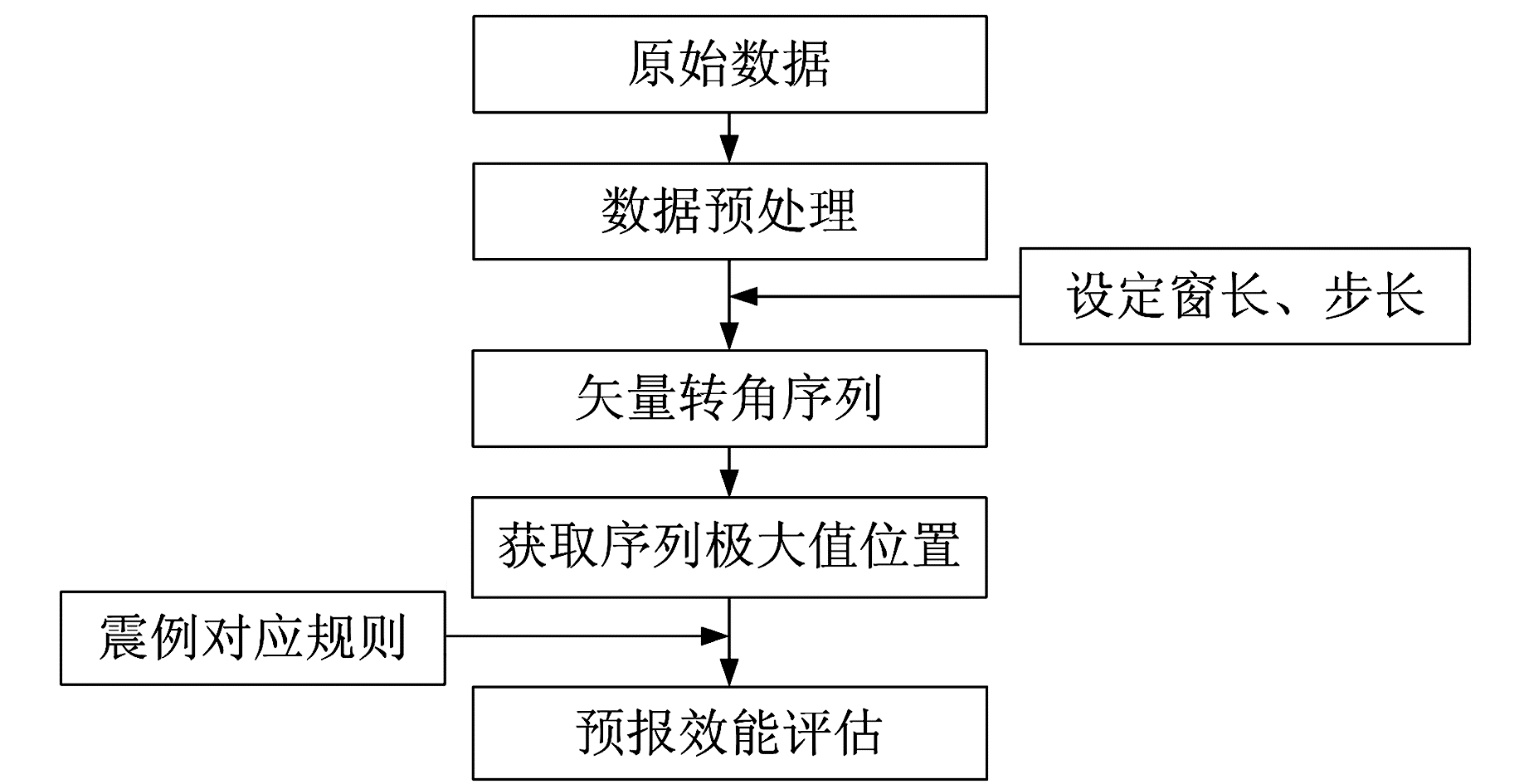
1 方法和模型本文方法的主要计算流程为:在获取观测数据的基础上进行数据预处理,包括去除突跳点,去趋势、低通滤波及数据的归一化处理; 根据研究的问题设定转折点前后拟合窗长及计算的滑动步长,基于矢量转角滑动进行直线拟合,并计算转折角度; 在此基础上对矢量转角的时间序列进行极大值的提取,实现时间序列转折点的准确提取,结合震例对应规则对提取的趋势转折异常进行地震预测效能评估(图 1)。
|
图 1 计算流程 Fig. 1 Calculation procedure |
首先,通过查看观测日志表,剔除原始观测数据中因人为、环境等干扰造成的数据变化,并进行数据插值,保证数据的完整性和连续性; 其次,将原始观测曲线去除稳定的线性变化,凸显偏离背景基值的趋势转折变化,这样有利于异常信息的获取; 最后,考虑到时间序列来自于不同的观测仪器及研究时段,为使不同观测曲线矢量转角的量值具有可比性,在计算之前将不同观测曲线的时间序列坐标统一设定在一个固定时段内,之后将观测资料的时间序列与观测值序列归一化到[0, 1]之间。
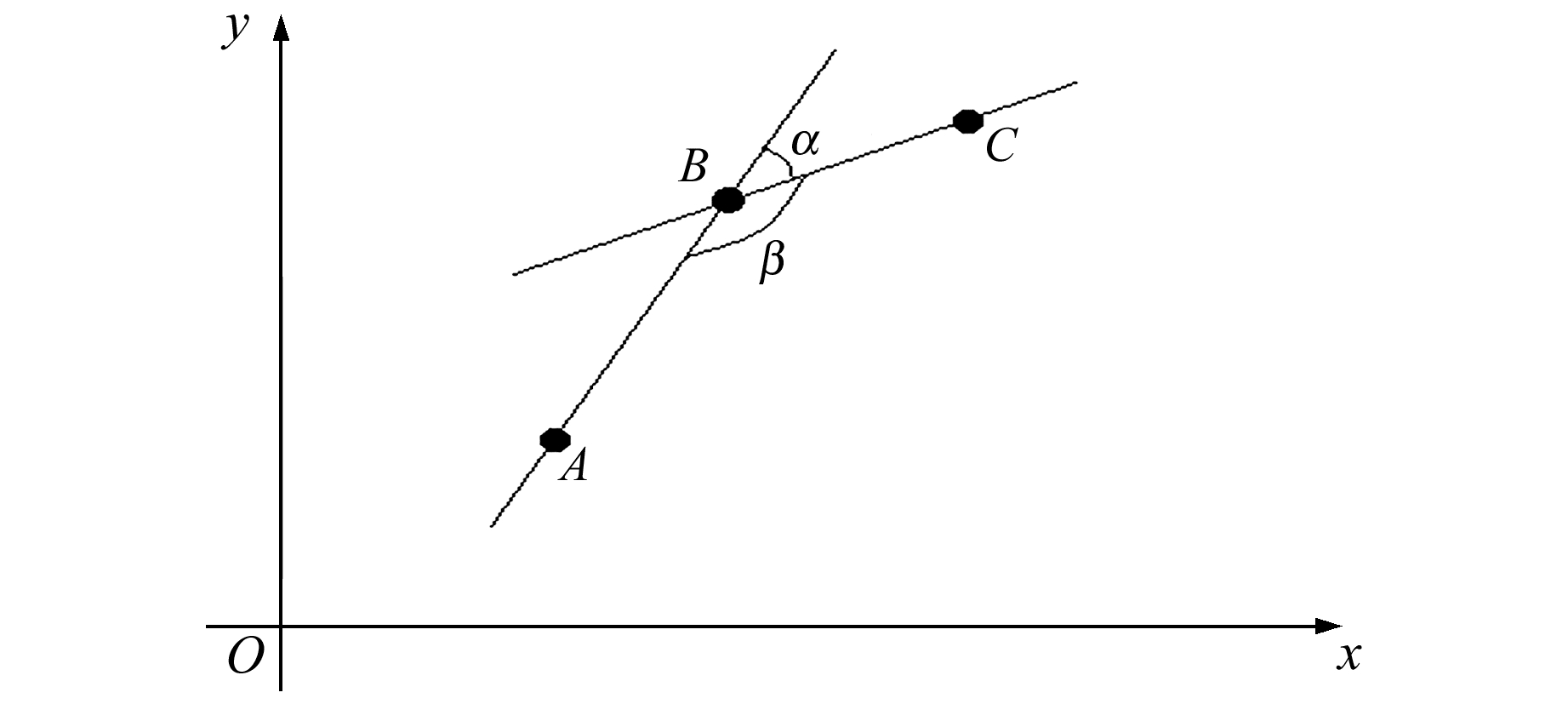
1.2 趋势转折幅度的量化跨断层水准观测是研究地震前兆的重要手段之一,正常情况下,跨断层基线的时间序列呈速率稳定的线性变化,当断层活动偏离背景出现非线性变化时,可能反映了构造应力场的变化信息。为了量化观测曲线的“异常”变化幅度,可用偏离背景的速率来近似表达,本文选用矢量转角方法来定量分析其异常幅度,具体描述见图 2。如果观测曲线在出现转折前数据变化为AB,转折后观测数据为BC,那么根据式(1)可得到表征异常幅度的指标α,另外异常幅度的量值与观测曲线顺时针转折还是逆时针转折无关。
|
图 2 矢量转角示意图 Fig. 2 Vector angle schematic diagram |
| $ \alpha = a\cos \frac{{\overline {\mathit{\boldsymbol{AB}}} \cdot \overline {\mathit{\boldsymbol{BC}}} }}{{|\overline {\mathit{\boldsymbol{AB}}} | \cdot |\overline {\mathit{\boldsymbol{BC}}} |}} $ | (1) |
向量AB和向量BC是根据给定的最小周期窗口进行线性拟合得到的,如果拟合误差偏大就不能较为真实地反映趋势转折的幅度,因此需要对拟合误差进行判断。若向量AB是由时间序列y=[y1, y2…yn]进行线性拟合所得,利用线性插值的方法对向量AB进行填充,得到衍生的拟合时间序列记为y1=[y11, y21…yn1],则拟合序列与原始序列的拟合误差公式为:
| $ E = \sqrt {\sum\limits_{i = 1}^n {{{({y_i} - y_i^1)}^2}} } $ | (2) |
拟合误差是衡量拟合时间序列与原始时间序列差异的一个重要指标,在相同的最小周期窗口下,拟合误差越小,能反映的趋势转折幅度越真实。
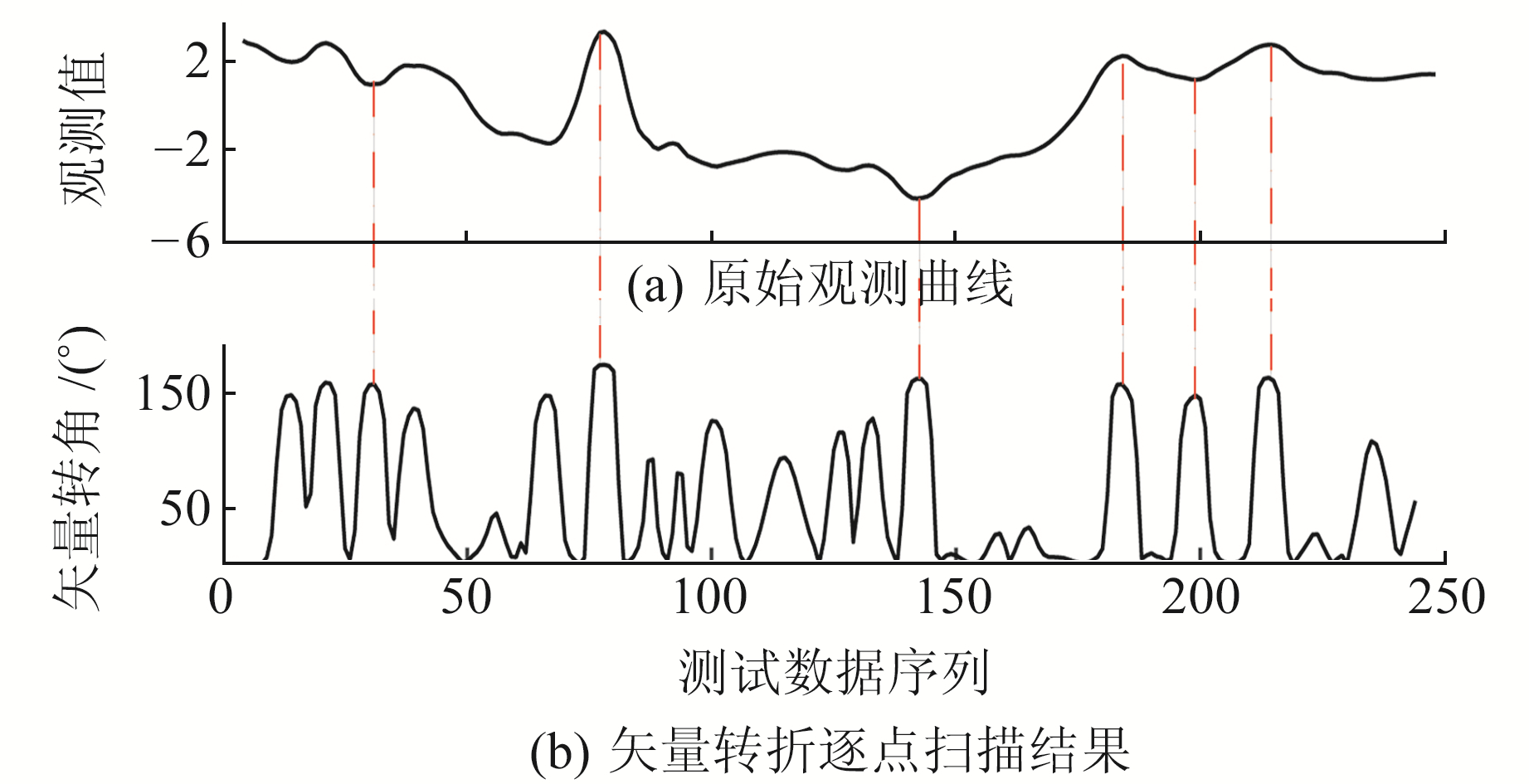
1.3 趋势转折点自动提取直接在原始观测曲线上进行趋势转折点的提取,其计算复杂度高且易受噪声影响,因此有必要对原始时间序列进行初步的筛选和转换。而现有的PLR分段线性表示方法大多存在对转折点的筛选准确度不高及转折点附近过多提取的问题。选取一段测试数据,采用矢量转角的方法对观测曲线进行逐点计算扫描,得到矢量转角时间序列(图 3(b))。研究发现,该时间序列的极大值点对应原始观测曲线(图 3(a))的极值点及速率改变较大点的位置,即观测曲线偏离背景变化的转折点,因此在求得矢量转角时间序列的基础上求该时间序列的极大值,即可准确求取原始观测序列趋势转折点的位置。由图 3可知,时间序列的转折点包含了极值点和单调区间内速率变化较大的点,此时位于异常点前后的时间序列变化趋势完全不同,可用该方法有效提取时间序列趋势转折的自然分割点。
|
图 3 观测曲线时间序列 Fig. 3 Observation curve time series |
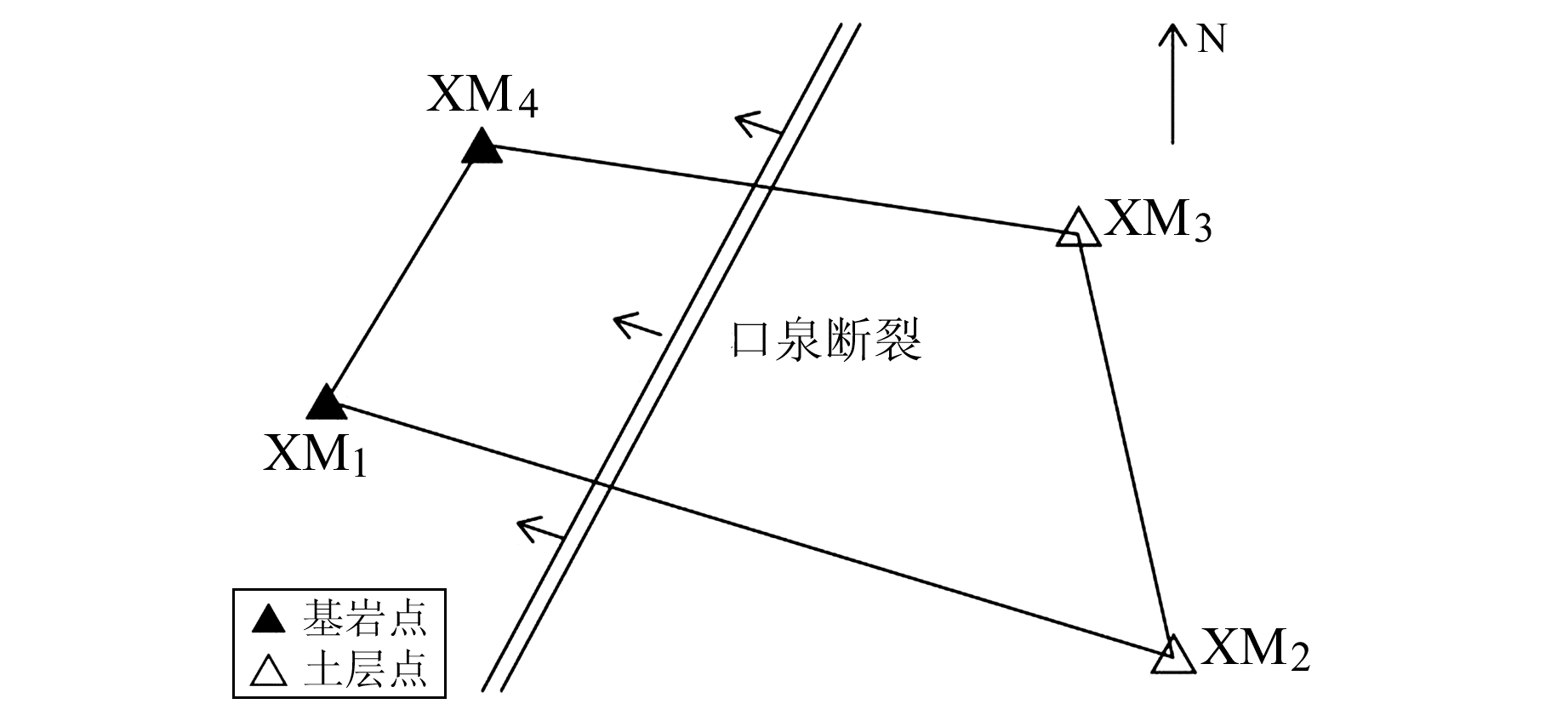
为验证矢量转角和极值点相结合的方法在实际数据分析工作中的效果,本文以山西断陷带北部映震性能较好的小磨流动水准XM1-XM2测线为例进行分析。该测线位于山西省朔州市怀仁县云中镇小磨村,监测大同盆地西侧边界的口泉断裂活动,断裂走向为NNE,倾角为80°,破碎带宽度为35 m,4条测线全长约1 270 m,其中XM1为基岩点,XM2为土层点,XM1-XM2测线始测于1984年,至今已积累近35 a的连续观测数据。多年的观测实践表明,该测线数据稳定、连续可靠、观测精度较高,为研究口泉断裂活动积累了较丰富的震例资料。
XM1-XM2测线始测以来,在口泉断裂及附近发生了1989年大同-阳高M5.9、1991年忻州M5.1、1991年大同-阳高M5.8、1998年张北M6.2及1999年大同-阳高M5.6地震,几次现代中强地震震前出现过不同程度的趋势转折变化,表明该测线对附近区域的中强地震比较敏感。
根据以往震例总结及区域构造特点,以小磨测线为中心,选取200 km范围内M4.5以上地震(扣除余震序列)前的观测数据进行实例分析,共选出满足条件的地震7个,具体见表 1。
|
图 4 小磨流动水准测线分布 Fig. 4 Xiaomo mobile level survey line distribution |
|
|
表 1 按照对应规则筛选的震例 Tab. 1 The earthquakes selected by corresponding rules |
转折点的提取结果主要与给定的窗口长度和滑动步长有关,针对同一观测曲线选择不同的参数会有不同的分析结果,在实际应用中要结合不同观测场地的具体情况设定计算参数。计算的窗口长度与所要提取异常信息的最小周期有关,针对跨断层资料一般取180~360 d,滑动步长依据观测周期设定,针对跨断层资料选取观测周期即可。小磨XM1-XM2测线的观测周期为2个月,以往震例研究该测线异常持续时间均在1 a以上,因此选取计算窗口长度为360 d,设定滑动步长为60 d。
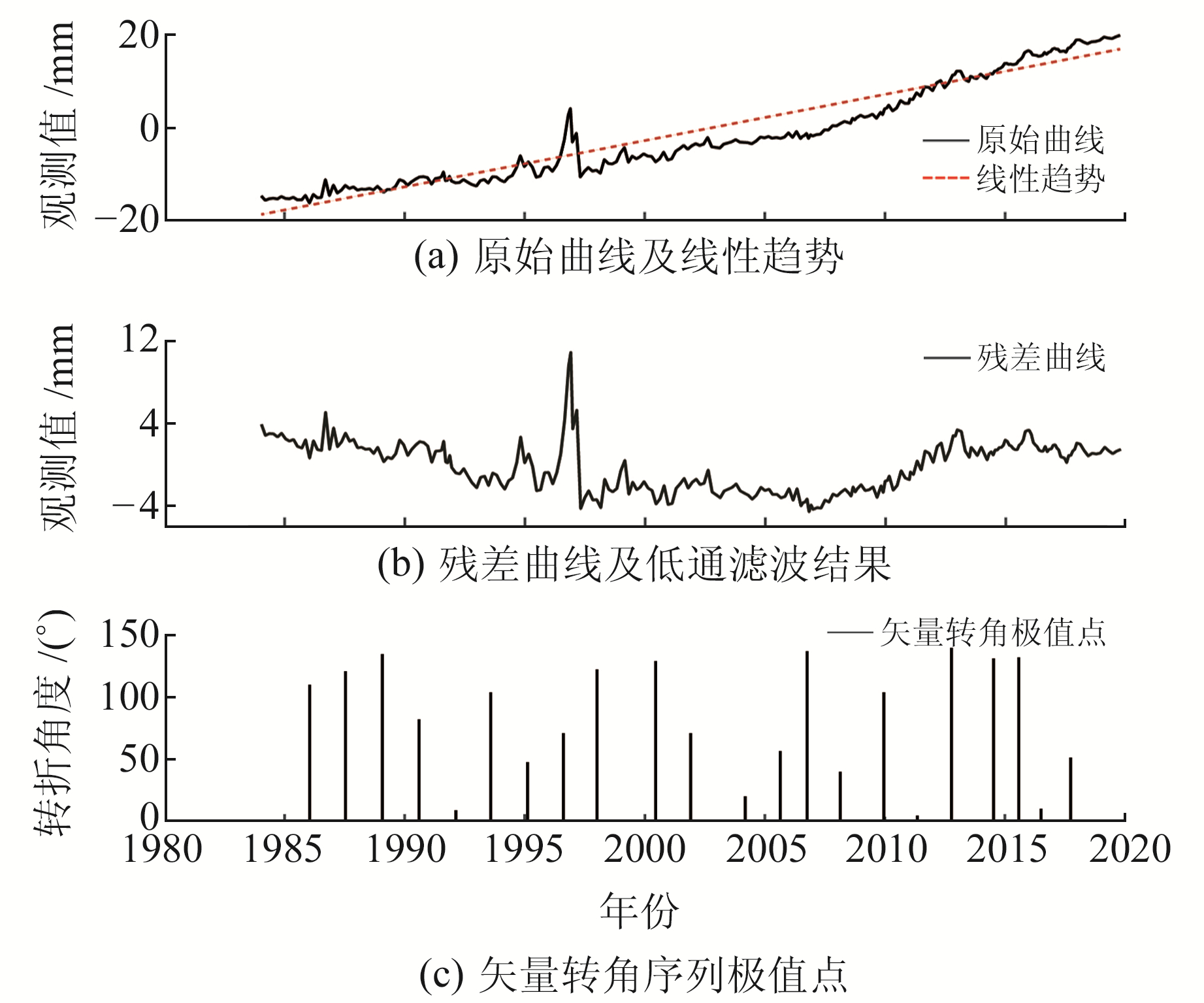
在经过前期数据整理后得到的预处理时间序列如图 5(a)黑色实线所示,红色虚线为线性拟合的趋势线。可以看出,XM1-XM2测线自观测以来整体呈继承性张性活动(曲线向上为张性,向下为压性),期间也出现过偏离背景的波动变化; 扣除稳定的线性趋势后得到的残差序列如图 5(b)黑色实线,反映了断层活动的细节信息。根据所选的窗长和步长,逐点扫描得到矢量转角的时间序列,并求取其极大值点位置(图 5(c))。由扫描结果可知,矢量转角时间序列的极大值点对应于观测曲线的趋势转折点位置,转折点前后的时间序列变化趋势可表征断层的活动状态。
|
图 5 趋势转折点提取实例 Fig. 5 An example of trend turning point extraction |
以往研究及相关理论模型均证实,当应力应变积累到一定程度时,地震观测时间序列在震前可能会出现趋势性转折现象,这些趋势性转折点对地震预测可能具有一定的指示意义,本文将此类趋势性转折点暂定为可能与地震有关的异常点。
2.3 地震预测效能评估地震预报效能R值评分方法的核心思想是同时考虑地震的报准率和预报地震所占用的时间[14]。取0°~180°作为趋势性转折阈值的搜索范围,60~720 d为预报期搜索范围,趋势性转折点前后直线拟合窗口长度为360 d,根据震例对应规则循环迭代,计算出最优R值及最优R值下的阈值,计算公式为:
| $ R = \frac{{{N_R}}}{{{N_A}}} - \frac{{{T_R}}}{{{T_A}}} $ | (3) |
式中,NR为报对地震次数,NA为应预报地震总次数,TR为预报占用时间,TA为预报研究的总时间。
异常点的提取是以趋势转折点为基础,在给定的震例对应规则下依据式(3)计算最优R值下的转折角度阈值,最终确定异常点。因此,异常点的识别不仅与所选定的窗口长度和滑动步长有关,也与给定的震例对应规则有很大的关系,在实际应用中需注意其科学性与合理性。
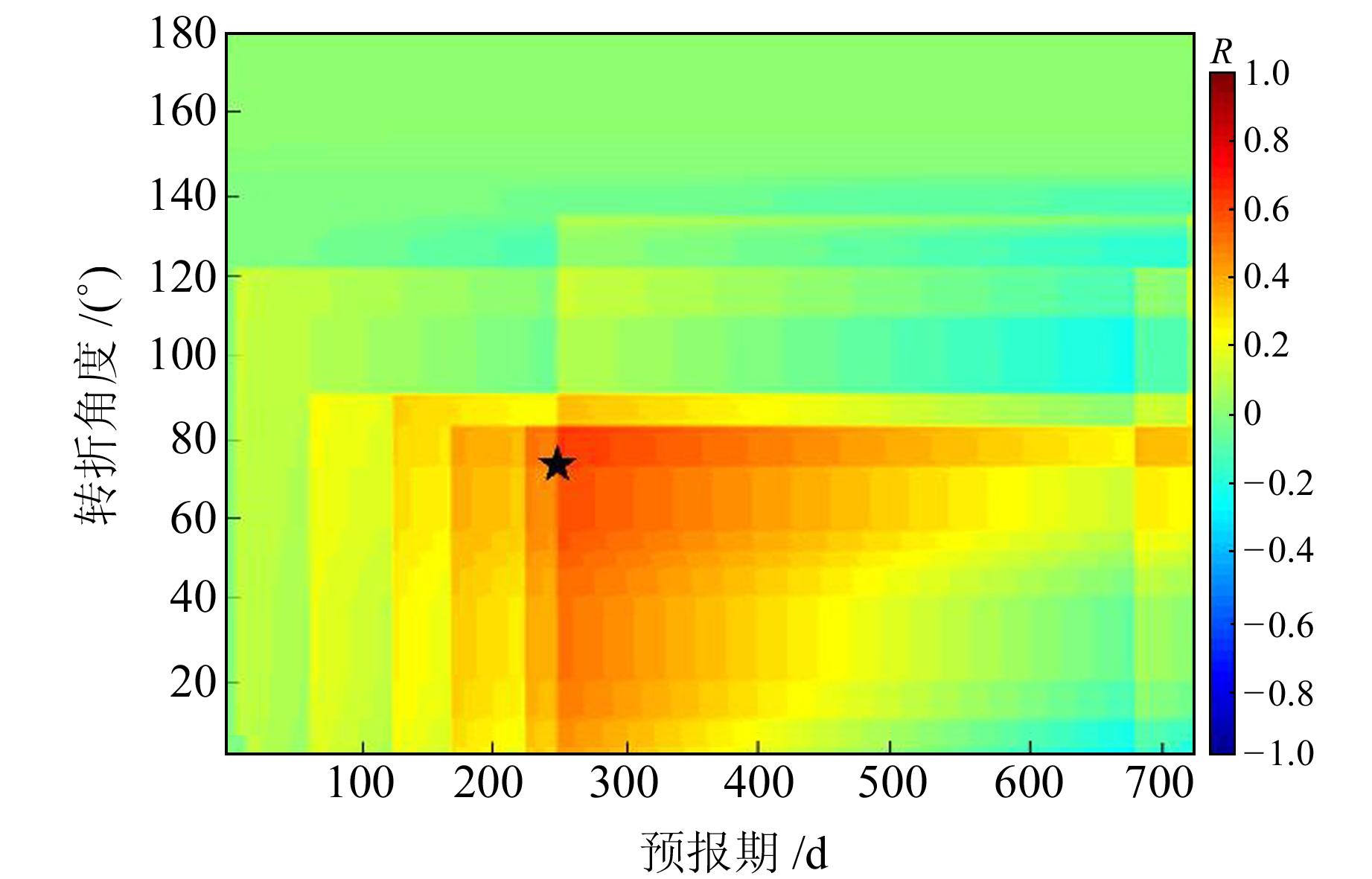
图 6为小磨流动水准XM1-XM2测线预报效能R图谱在预报期-阈值坐标系下的空间分布,其中黑色五角星位置为最佳阈值及最优预测期下的R值,表 2为该测线趋势性转折异常及效能评估统计。结果显示,小磨XM1-XM2测线预测指标的最佳阈值为矢量转角75°,最优预测期为247 d,R值为0.63(R0=0.43),R图谱较为直观地展现了该测线的预测效能评估结果。根据实际回溯结果,预测期内发生的6次地震在震前原始观测序列上均存在不同程度的趋势性转折现象。
|
图 6 预报效能R图谱分布 Fig. 6 Distribution of predictable efficiency R map |
|
|
表 2 小磨流动水准XM1-XM2测线趋势转折异常及效能评估 Tab. 2 Trend break anomalies and effectiveness evaluation of Xiaomo mobile level XM1-XM2 line |
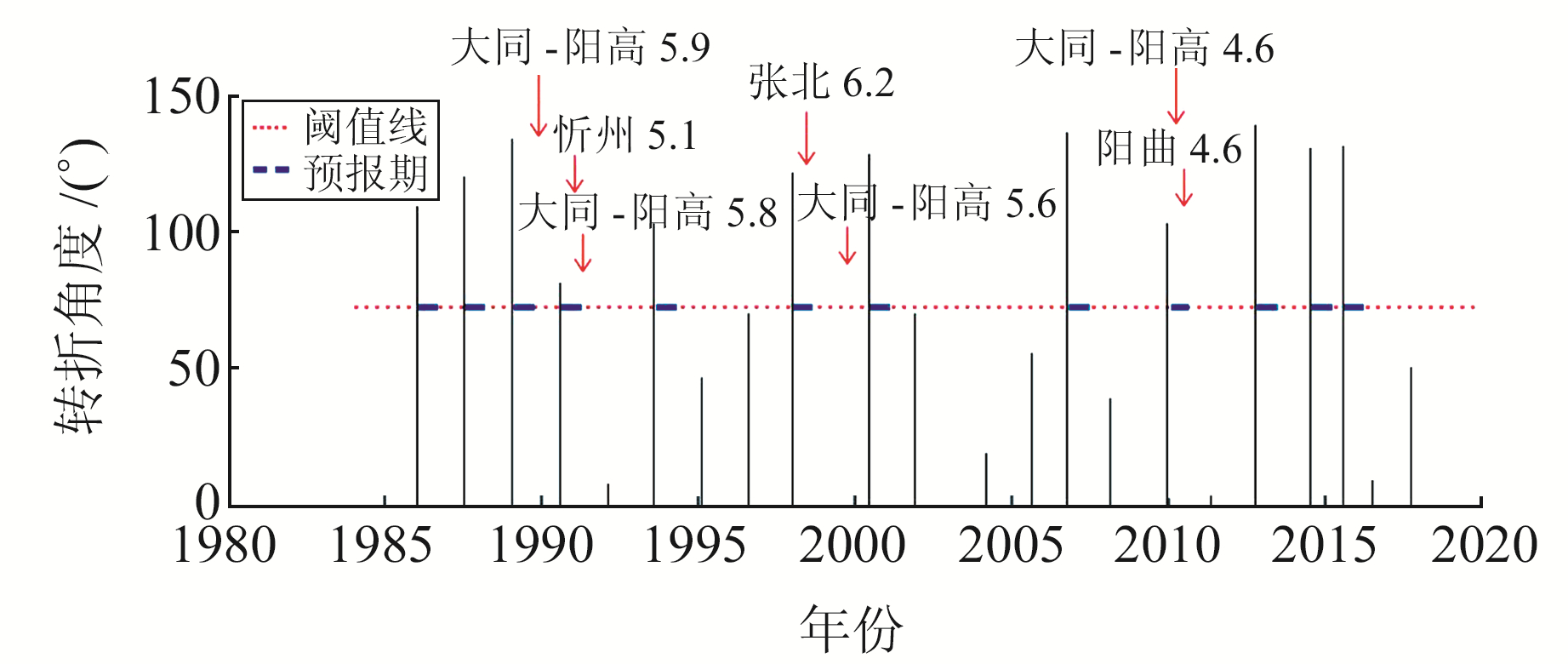
图 7为小磨流动水准XM1-XM2测线逐点扫描矢量转角时间序列极大值及最优阈值下地震对应情况,其中红色虚线为最优阈值线,蓝色虚线为最优预报期,箭头指示地震发生时刻,红色代表在最佳预测期内发生的地震,黑色代表发生在最优预测期外的地震。表 3给出在最优阈值下小磨流动水准XM1-XM2测线趋势转折出现的时间、是否报准地震及距地震发生的时间间隔。结果显示,2000年以前数据趋势转折比较频繁,且幅度较大,该时段内超过阈值线的转折点共出现6次,发生5次M5.0以上地震,其中4次地震发生在最优预测期内,相关研究也证实了1989~2000年间山西北部的流动水准测线多次出现张性速率减缓的趋势性转折变化[15]。2000年之后,流动水准数据变化较为缓慢,该时段预测区内共发生2次M4.6地震,而超过阈值线的转折点共出现5次,虚报次数较多,但该时段预测区外发生了2008年汶川8.0级和2011年日本9.0级强震,一些研究表明,在这2次地震前后山西断陷带形变场发生了不同程度的趋势转折变化[16-21]。刘峡等[16]依据GPS观测结果,利用有限元方法对2008年汶川8.0级地震前后山西断陷带的地壳形变进行了数值模拟,结果显示,山西断陷带形变场与构造应力场出现显著变化,由相对均匀的构造拉张转为强烈的构造挤压。张希等[18]利用约30 a的鄂尔多斯周缘跨断层短水准资料,借助灰色关联度垂向综合指标方法分析了远场大震孕育-发生对该区的影响,结果显示,2011年日本9.0级地震后,山西断陷带的北段和南段出现短暂的加速或转折变化。因此,该时段形变场多次超过阈值的趋势性转折变化可能与远场强震引起的应力变化有关。
|
图 7 矢量转角时间序列极大值及最优阈值下地震对应情况 Fig. 7 Vector angle time series maximum value and earthquake corresponding under optimal threshold |
|
|
表 3 小磨流动水准XM1-XM2趋势转折出现时间以及对应地震情况 Tab. 3 Anomaly time and earthquake corresponding of Xiaomo mobile level XM1-XM2 line |
图 8为在震例对应规则下预测地震的空间分布情况,其中红色为报准地震,蓝色为未报准地震。从空间分布来看,小磨XM1-XM2测线对山西断陷带中北部的地震有很好的指示意义。

|
图 8 震例对应规则下预测地震的空间分布情况 Fig. 8 The spatial distribution of predicted earthquakes under the corresponding rules of the earthquake case |
本文在总结归纳前人对分段直线表示方法的基础上,提出了一种极值点与矢量转角相结合的趋势转折型异常自动识别方法,利用矢量转角计算公式滑动扫描原始观测序列,得到矢量转角的一维时间序列,并在此基础上提取该序列的极大值点,从而准确获得原始观测序列的趋势转折点。利用小磨流动水准XM1-XM2测线对该方法进行验证,结果显示,提取的结果与震例总结、人工判读的结果基本一致,预测效能评估结果R=0.63(R0=0.43),对山西中北部M4.5以上地震具有较好的对应关系。
根据《地震分析会商技术方法测试评估细则》,2019年中国地震局监测预报司主持开展了地震分析会商技术方法测试评估工作,本文使用的方法属于通过评估的23种技术方法之一,被列入了《地震分析会商技术方法列装清单(2019版)》(震台网函(2019)112号); 全国146项符合要求的观测测项使用该方法提取异常的地震预测效能高于随机预测(R>0)的测项比例为100%,能通过置信度97.5%的显著性检验(R≥R0)的测项比例为54%,说明该方法的计算结果是可靠的,可用于时间序列趋势转折型异常的自动识别。本文的研究重点是对时间序列趋势性转折点提取算法进行改进,提出了震前观测异常定量化研究的自动识别算法,并用具体的实例展示了该方法的可行性。
对比前人的研究成果,本文提出的算法可以较准确地提取出趋势性转折点及速率变化较大的点,简单易行且适应范围广,可为定量化提取地震异常信息提供客观的基础信息。下一步尝试将其应用于地球物理场观测数据类似异常的提取,以提高在地震观测大数据信息化背景下分析预报人员的工作效率及分析预报工作的科学性。
| [1] |
刘冠中, 马瑾, 杨永林, 等. 川西地区长周期气温变化对跨断层位移观测的影响及芦山地震前的异常断层活动[J]. 地球物理学报, 2014, 57(7): 2150-2164 (Liu Guanzhong, Ma Jin, Yang Yonglin, et al. Effect of Long-Term Surface Temperature Variation on Fault Displacement Observation and Anomalous Fault Movement in Western Sichuan before the Lushan MS7.0 Earthquake[J]. Chinese Journal of Geophysics, 2014, 57(7): 2150-2164)
(  0) 0) |
| [2] |
孔庆敏, 王广才, 史浙明. 云南地区震前地下流体异常特征统计分析[J]. 地震学报, 2018, 40(5): 632-645 (Kong Qingmin, Wang Guangcai, Shi Zheming. Statistical Analysis of Pre-Seismic Anomalous Characteristics of Subsurface Fluids in Yunnan Region[J]. Acta Seismologica Sinica, 2018, 40(5): 632-645)
(  0) 0) |
| [3] |
Lin J, Keogh E, Lonardi S, et al. A Symbolic Representation of Time Series, with Implications for Streaming Algorithms[C]. ACM SIGMOD Workshop on Research Issues in Data Mining and Knowledge Discovery, California, 2003
(  0) 0) |
| [4] |
林意, 朱志静. 基于趋势的时间序列分段线性化算法[J]. 重庆大学学报, 2019, 42(3): 92-98 (Lin Yi, Zhu Zhijing. A Method of Time Series Piecewise Linearization Based on Tendency[J]. Journal of Chongqing University, 2019, 42(3): 92-98)
(  0) 0) |
| [5] |
Krawczak M, Sikatuła G. An Approach to Dimensionality Reduction in Time Series[J]. Information Sciences, 2014, 260: 15-36 DOI:10.1016/j.ins.2013.10.037
(  0) 0) |
| [6] |
Li L, Su X N, Zhang Y, et al. Trend Modeling for Traffic Time Series Analysis: An Integrated Study[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(6): 3430-3439 DOI:10.1109/TITS.2015.2457240
(  0) 0) |
| [7] |
Yi B, Faloustsos C. Fast Time Sequence Indexing for Arbitrary Lp Norms[C]. The 26th International Conference on Very Large Data Bases, San Francisco, 2000
(  0) 0) |
| [8] |
Keogh E, Chakrabarti K, Pazzant M, et al. Dimensionality Reduction for Fast Similarity Search in Large Time Series Databases[J]. Knowledge and Information Systems, 2001, 3(3): 263-286 DOI:10.1007/PL00011669
(  0) 0) |
| [9] |
Pratt K B, Fink E. Search for Patterns in Compressed Time Series[J]. International Journal of Image and Graphics, 2002, 2(1): 89-106
(  0) 0) |
| [10] |
Park S, Kim S W, Chu W W. Segment-Based Approach for Subsequence Searches in Sequence Databases[C]. The 16th ACM Symposium on Applied Computing, New York, 2001
(  0) 0) |
| [11] |
Fuentes J, Poncela P, Rodríguez J. Sparse Partial Least Squares in Time Series for Macroeconomic Forecasting[J]. Journal of Applied Econometrics, 2015, 30(4): 576-595 DOI:10.1002/jae.2384
(  0) 0) |
| [12] |
孙达辰.基于DTW的时间序列相似性搜索的研究[D].大庆: 大庆石油学院, 2010 (Sun Dachen. The Research of Similarity Match Based on DTW in TSDM[D]. Daqing: Daqing Petroleum Institute, 2010)
(  0) 0) |
| [13] |
尚福华, 孙达辰. 基于时间序列趋势转折点的分段线性表示[J]. 计算机应用研究, 2010, 27(6): 2075-2077 (Shang Fuhua, Sun Dachen. PLR Based on Time Series Tendency Turning Point[J]. Application Research of Computers, 2010, 27(6): 2075-2077)
(  0) 0) |
| [14] |
张帆, 韩晓明, 李娟, 等. 内蒙古乌拉特后旗-临河地区地震活动的预测效能评估[J]. 华北地震科学, 2018, 36(3): 35-39 (Zhang Fan, Han Xiaoming, Li Juan, et al. The Prediction Efficiency Evaluation of Seismicity in Wulatehouqi-Linhe Area[J]. North China Earthquake Sciences, 2018, 36(3): 35-39)
(  0) 0) |
| [15] |
贾晓东, 武艳强, 闫伟, 等. 山西断裂带跨断层形变观测资料动态特征分析[J]. 大地测量与地球动力学, 2012, 32(3): 31-35 (Jia Xiaodong, Wu Yanqiang, Yan Wei, et al. Dynamic Analysis of Shanxi Fault Zone Cross-Fault Deformation Observational Data[J]. Journal of Geodesy and Geodynamics, 2012, 32(3): 31-35)
(  0) 0) |
| [16] |
刘峡, 马瑾, 占伟, 等. 汶川地震前后山西断陷带的地壳运动[J]. 大地测量与地球动力学, 2013, 33(3): 5-10 (Liu Xia, Ma Jin, Zhan Wei, et al. Crustal Motion of Shanxi Rift Zone before and after Wenchuan Earthquake[J]. Journal of Geodesy and Geodynamics, 2013, 33(3): 5-10)
(  0) 0) |
| [17] |
张希, 贾鹏, 张四新, 等. 鄂尔多斯地块周缘地区构造活动与应变积累特性研究[J]. 大地测量与地球动力学, 2018, 38(4): 331-337 (Zhang Xi, Jia Peng, Zhang Sixin, et al. Study on the Characteristics of Tectonic Activities and Strain Accumulation at the Surroundings of Ordos Block[J]. Journal of Geodesy and Geodynamics, 2018, 38(4): 331-337)
(  0) 0) |
| [18] |
张希, 蒋锋云, 唐红涛, 等. 汾渭断裂带近10年GPS观测获得的剖面变形与应变积累分析[J]. 地震研究, 2011, 34(4): 504-510 (Zhang Xi, Jiang Fengyun, Tang Hongtao, et al. Analysis on the Section Deformation and Strain Accumulation of the Fen-Wei Fracture Belt Observed by GPS in Recent 10 Years[J]. Journal of Seismological Research, 2011, 34(4): 504-510)
(  0) 0) |
| [19] |
陈阜超, 塔拉, 陈聚忠. 基于水准剖面的山西断陷带现今活动性研究[J]. 大地测量与地球动力学, 2015, 35(4): 576-580 (Chen Fuchao, Ta La, Chen Juzhong. Study of Recent Activity in the Shanxi Rift Zone Based on Leveling Profile[J]. Journal of Geodesy and Geodynamics, 2015, 35(4): 576-580)
(  0) 0) |
| [20] |
李宏伟, 刘瑞春, 陈永前. 山西南部区域应变场演化与地震关系的数值模拟[J]. 山西地震, 2018(4): 7-10 (Li Hongwei, Liu Ruichun, Chen Yongqian. Numerical Simulation of the Relationship between Regional Strain Field Evolution and Earthquake in Southern Shanxi Province[J]. Earthquake Research in Shanxi, 2018(4): 7-10)
(  0) 0) |
| [21] |
刘瑞春, 沈晓松, 王翾潞. 利用陆态网络基准站资料研究山西断陷带近期地壳形变特征[J]. 高原地震, 2015, 27(1): 8-13 (Liu Ruichun, Shen Xiaosong, Wang Xuanlu. Research on Recent Deformation Characteristics of Shanxi Fault Subsidence Zone Using CMONOC GPS Reference Station Data[J]. Plateau Earthquake Research, 2015, 27(1): 8-13)
(  0) 0) |
2. China Earthquake Networks Center, 5 Nanheng Street, Sanlihe, Beijing 100045, China
 2020, Vol. 40
2020, Vol. 40

