2. 防灾科技学院河北省地震动力学重点实验室,河北省三河市学院街465号,065201
2015-09-16安第斯俯冲带中部发生强烈的逆冲型大地震,为该区1943年MW7.9地震后发生的最大地震。美国地质调查局地震信息中心(USGS-NEIC)测定此次地震矩震级为MW8.3,发震时刻为22:54:32(UTC),震中位置为31.573°S、71.674°W,深度为22.4 km,位于智利Illapel西部约47 km处。许多学者[1-11]对该次地震的震源机制、破裂过程、强地面运动以及发震构造进行了研究,但得到的标量地震矩存在较大差别,范围在(2.5~4.42)×1021 Nm,对应的矩震级范围为MW8.2~8.4(表 1),表明对于特大地震,根据不同观测资料反演得到的震源机制解具有一定程度的不确定性。
|
|
表 1 基于不同数据反演得到的本次地震的震源机制解 Tab. 1 The focal mechanism solutions obtained by different data |
自由振荡能量的大小与震源的破裂方式和破裂程度密切相关,可反映地震整体破裂形态[12-13],因此利用大地震后的自由振荡信号可对震源机制解进行总体检验和约束。超导重力仪(superconducting gravimeter, SG)为目前监测地表形变和重力场变化最精密的仪器,可为检测地球自由振荡信号及约束震源机制解提供很好的数据基础。大地震破裂过程的计算、震后库仑应力变化及对周边地区的影响、强地面运动模拟以及震后周边地区重力场变化的研究均需要准确的震级作为约束。利用地震学方法计算地震震级通常基于宽频带地震波数据,而利用连续的重力观测数据也可对大地震震级进行约束与研究。本文以2015-09-15智利Illapel MW8.3地震为例,利用超导重力仪观测数据研究其震源参数,基于最佳震源机制解,通过对比分析观测值与模拟值,计算此次地震更为准确的标量地震矩和断层倾角。
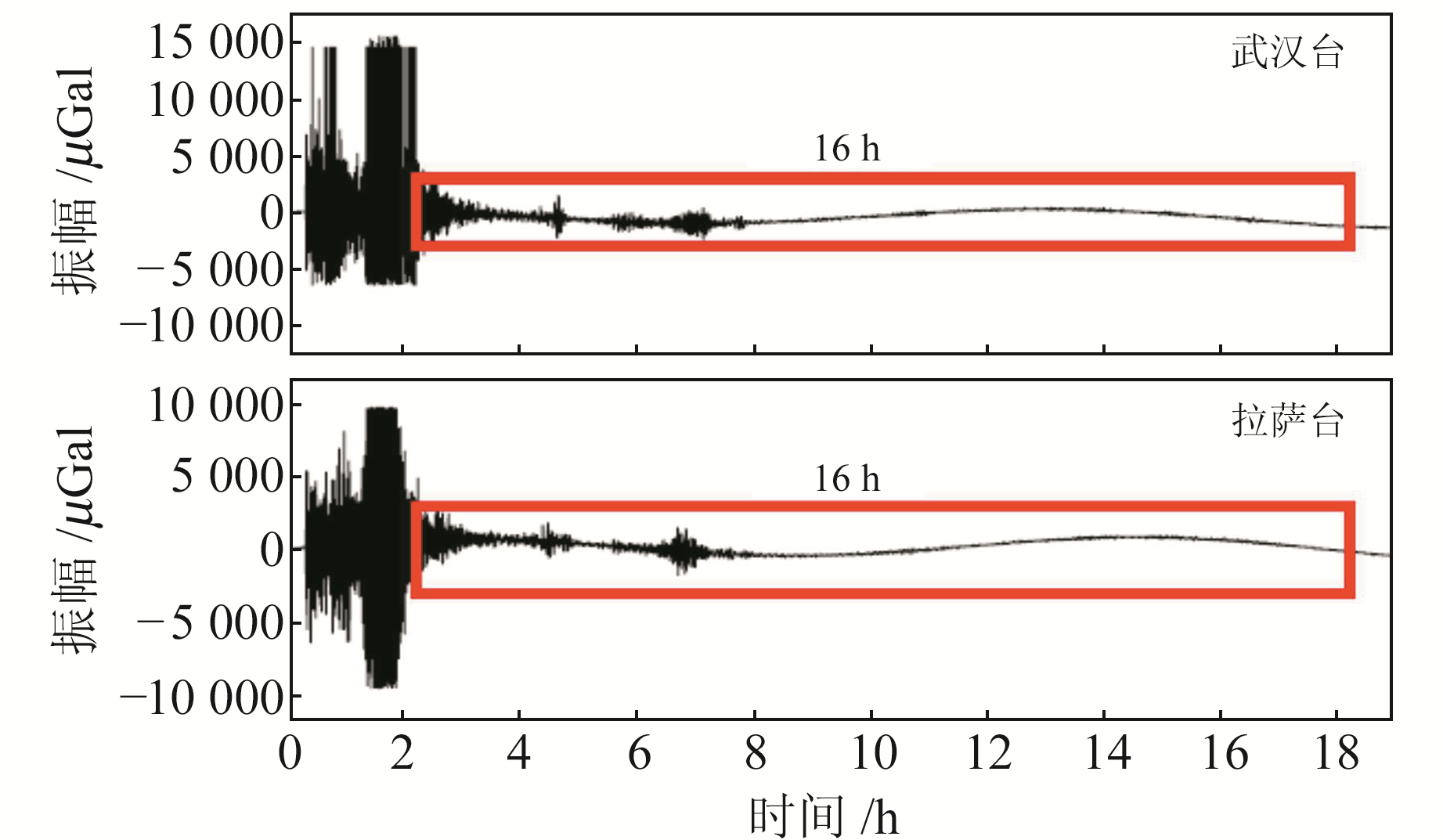
1 数据和方法武汉站和拉萨站超导重力仪在Illapel地震发生后清晰记录到相应的重力变化(图 1),由于此次地震震级较大,同震重力信号出现限幅现象,因此本文选取信噪比较高的观测数据进行研究。在提取自由振荡信号前,首先对各台站的观测资料进行预处理,利用TSoft重力潮汐数据预处理程序去除突跳、间断等; 采用ETERNA调和分析软件计算大气导纳因子,并在重力观测中扣除大气影响; 利用标准地球模型和地震震源机制解计算台站接收到的地震激发的自由振荡信号。在计算自由振荡振幅时,将震中位置视为点源,模拟计算台站自由振荡需要的参数有:震源位置、发震断层走向(strike)、倾角(dip)、滑动角(rake)、矩张量标量(M0)、台站位置等。地震的震源机制模型将震源等效为双力偶点源,根据双力偶地震矩心矩张量理论,得到6个独立的地震矩张量,由地球格林函数对矩张量加权求和,矩张量源激发产生的地球自由振荡位移为[14]:
| $ {u_n}\left( {x, t} \right) = \sum\limits_{i = 1}^6 {{M_i}{G_{in}}} $ | (1) |
式中,Mi为矩张量分量,由标量地震矩M0、走向、倾角、滑动角组合而成; Gin为每个地震矩张量分量对应的格林函数。基于PREM地球模型,结合震源机制解,对地球格林函数加权矩张量进行求和,得到由矩张量源激发产生的地球自由振荡位移,从而模拟自由振荡信号[15]。通过对比观测值与模拟值,搜索最符合实际的标量地震矩,并进一步计算更为准确的地震震级,矩震级MW可由标量地震矩求得[14]:
| $ {M_W} = \frac{2}{3}{\rm{lg}}{M_0} - 6.033 $ | (2) |
式中,M0为标量地震矩。
|
红框表示所用的数据长度 图 1 武汉台和拉萨台超导重力仪的观测数据 Fig. 1 Observation data of Wuhan and Lhasa SG stations |
利用Mineos软件包(http://www.geodynamics.org/cig/software/mineos),基于PREM地球模型和震源机制解,对格林函数矩张量进行加权求和,得到接收台站的理论地震图。为避免环境噪声对简正模振幅造成影响,选取武汉站和拉萨站采样间隔为1 s、时间长度为16 h的重力观测数据(图 1)。由于震级较高会造成超导重力仪限幅,因此从地震发生后8 000 s开始选取数据,观测数据和模拟数据在经过汉宁窗处理和离散傅里叶变换后可获得线性振幅谱。为确定最符合实际地震能量释放的震源机制解,选取1.5~5.3 mHz频段内信噪比较高的振型进行分析。
图 2、3为武汉站和拉萨站超导重力仪的自由振荡观测值和基于不同震源机制解计算的模拟值在1.5~5.3 mHz频段的结果。由于部分结果比较接近,故仅列出8个震源机制解的理论模拟结果与实测结果的对比图。从2个台站的理论值与观测值的对比结果来看,利用震源机制解1和6计算得到的理论值振幅明显高于观测值振幅,而基于震源机制解9和10计算得到的理论振幅明显低于观测值振幅,其他震源机制解得到的模拟值与观测值相当。基于震源机制解14得到的理论值与观测值最为接近,表明震源机制解14最能反映此次地震的真实震级,同时也说明基于长周期地震波信号或联合多种观测资料反演得到的震级最为可靠。

|
图 2 1.5~5.3 mHz频段内武汉台超导重力仪观测数据与基于不同地震矩计算的理论值对比 Fig. 2 Comparison between observation data of Wuhan SG station and theoretical value based on different seismic moments with frequency band of 1.5~5.3 mHz |

|
图 3 1.5~5.3 mHz频段内拉萨台超导重力仪观测数据与基于不同地震矩计算的理论值对比 Fig. 3 Comparison between observation data of Lhasa SG station and theoretical value based on different seismic moments with frequency band of 1.5~5.3 mHz |
为更加详细地反映对比结果,选用1.5~5.3 mHz频段中信噪比较高的球型自由振荡的模拟值和观测值进行比较,以残余方差F(不符合度)和比例因子S(符合度)作为判断标准:
| $ F = \sum\limits_{i = 1}^n {{{({O_i} - {S_i})}^2}} /\sum\limits_{i = 1}^n {O_i^2} $ | (3) |
| $ S = \sum\limits_{i = 1}^n {{O_i}{S_i}} /\sum\limits_{i = 1}^n {O_i^2} $ | (4) |
式中,Oi和Si分别为观测值振幅和模拟值振幅; n为所有振型的数量。当S接近1时,震源机制解对应的M0可靠,可描述震源的大小和强度。
表 2为基于14个震源机制解计算的2个台站模拟值和观测值的残余方差平均值F和比例因子平均值S。可以看出,基于震源机制解14计算的自由振荡模拟结果与实测结果最为接近,F为0.077,S为1.022,最接近1,最能反映地震释放能量的大小,表明震源机制解14的结果最准确。基于震源机制解1计算的模拟值与观测值的符合度最差,F为0.399,S为1.486,远高于地震的真实震级。基于震源机制解10计算的模拟值与观测值相差也较大,F为0.077,S为0.840。理论上讲,震源机制解对1.5~5.3 mHz频段内振型振幅的影响相同,为更加直观地比较不同机制解的差异,给出武汉站和拉萨站超导重力仪自由振荡信号的观测值与震源机制解1、10、14的理论模拟值的对比结果(图 4(a)、4(b)),同时选取2个模态0S14和0S27进行放大对比(图 4(c)、4(d))。可以看出,震源机制解1的自由振荡振幅明显偏离观测值,不符合度F高达0.399,震源机制解14的拟合度最高。基于最接近实际的震源机制解14的结果,本文进一步分析此次地震的震级和断层倾角。
|
|
表 2 基于14个震源机制解计算的残余方差和比例因子 Tab. 2 Residual variance and scaling factor calculated by the 14 seismic moments |

|
图 4 1.5~5.3 mHz频段内武汉台与拉萨台超导重力仪观测数据与基于3个不同地震矩计算的理论值对比 Fig. 4 Comparison between observation data of Wuhan and Lhasa SG station and theoretical values based on three different seismic moments with frequency band of 1.5~5.3 mHz |
地震的标量地震矩M0是影响自由振荡振幅的最大因素,而断层走向、倾角、滑动方向角和震源深度对自由振荡振幅的影响较小[15]。震源机制解4、7和11标量地震矩相同,同时基于震源机制解得到的残余方差F和比例因子S也相同。地震激发的长周期自由振荡数据仅能约束震源机制解中滑动角和地震矩的综合影响,却无法分别对其进行约束。考虑到这种折中关系,本文以理论值和观测值的最小拟合误差为基准,同时对地震矩和断层倾角进行网格搜索。其中,地震矩的搜索范围参考表 1数据,范围为(2.5~ 4.42)×1021 Nm,间隔为0.2×1021 Nm; 断层倾角的搜索范围为16°~22°,间隔为1°。图 5为搜索结果,可以看出,本次地震最优的标量地震矩为(3.0±0.2)×1021 Nm,相应的矩震级为MW8.3,最佳断层倾角为19°。

|
“+”大小表示误差大小,五角星位置为最优解 图 5 基于不同断层倾角和地震矩计算的误差分布 Fig. 5 Distribution of error calculated by different dip angle and seismic moment |
本文选取武汉站和拉萨站的超导重力观测数据,利用自由振荡信号约束2015-09-16智利MW8.3地震的标量地震矩和断层倾角,对比分析14个震源机制解和地震矩,有效评估最符合地震实际释放能量的震源机制解。基于最佳震源机制解,通过对比分析观测值与模拟值计算更为准确的震级和断层倾角。结果表明,利用超导重力仪记录的1.5~5.3 mHz球型简正模观测可有效评估智利MW8.3地震的震源机制解。基于多种观测资料(体波、强震数据、高频GPS、同震GPS位移)联合反演得到的震源参数确定的自由振荡模拟值与观测值符合最好,不符合度F为0.077,比例因子S为1.022,最接近1,表明其反演的标量地震矩可较好地反映此次地震释放的能量。通常情况下,对于特大地震(M>8),由于震级的饱和效应,仅用体波数据或面波数据反演的标量地震矩会偏小,而联合近远场观测数据反演可显著改善震源机制解和地震矩M0。
本文以理论值和观测数据的最小拟合误差为基准,对地震矩和断层倾角进行联合搜索。计算结果表明,2015年Illapel地震的标量地震矩为(3.0±0.2)×1021 Nm,相应的矩震级为MW8.3,搜索的最佳断层倾角为19°。今后研究中将尝试联合利用大地测量数据和地震波数据约束地震断层倾角,再结合地球自由振荡的观测和模拟约束地震矩。
致谢: 感谢武汉大地测量国家野外科学观测研究站提供武汉站和拉萨站超导重力观测数据。
| [1] |
Heidarzadeh M, Murotani S, Satake K, et al. Source Model of the 16 September 2015 Illapel, Chile, MW8.4 Earthquake Based on Teleseismic and Tsunami Data[J]. Geophysical Research Letters, 2016, 43(2): 643-650 DOI:10.1002/2015GL067297
(  0) 0) |
| [2] |
Li L Y, Lay T, Cheung K F, et al. Joint Modeling of Teleseismic and Tsunami Wave Observations to Constrain the 16 September 2015 Illapel, Chile, MW8.3 Earthquake Rupture Process[J]. Geophysical Research Letters, 2016, 43(9): 4303-4312 DOI:10.1002/2016GL068674
(  0) 0) |
| [3] |
Shrivastava M N, González G, Moreno M, et al. Coseismic Slip and Afterslip of the 2015 MW8.3 Illapel(Chile) Earthquake Determined from Continuous GPS Data[J]. Geophysical Research Letters, 2016, 43(20): 10710-10719 DOI:10.1002/2016GL070684
(  0) 0) |
| [4] |
Zhang Y F, Zhang G H, Hetland E A, et al. Coseismic Fault Slip of the September 16, 2015 MW8.3 Illapel, Chile Earthquake Estimated from InSAR Data[J]. Pure and Applied Geophysics, 2016, 173(4): 1029-1038 DOI:10.1007/s00024-016-1266-3
(  0) 0) |
| [5] |
Okuwaki R, Yagi Y, Aránguiz R, et al. Rupture Process during the 2015 Illapel, Chile Earthquake: Zigzag-Along-Dip Rupture Episodes[J]. Pure and Applied Geophysics, 2016, 173(4): 1011-1020 DOI:10.1007/s00024-016-1271-6
(  0) 0) |
| [6] |
Ruiz S, Klein E, Campo F D, et al. The Seismic Sequence of the 16 September 2015 MW8.3 Illapel, Chile, Earthquake[J]. Seismological Research Letters, 2016, 87(4): 789-799 DOI:10.1785/0220150281
(  0) 0) |
| [7] |
Herman M W, Nealy J L, Yeck W L, et al. Integrated Geophysical Characteristics of the 2015 Illapel, Chile, Earthquake[J]. Journal of Geophysical Research: Solid Earth, 2017, 122(6): 4691-4711 DOI:10.1002/2016JB013617
(  0) 0) |
| [8] |
Klein E, Vigny C, Fleitout L, et al. A Comprehensive Analysis of the Illapel 2015 MW8.3 Earthquake from GPS and InSAR Data[J]. Earth and Planetary Science Letters, 2017, 469: 123-134 DOI:10.1016/j.epsl.2017.04.010
(  0) 0) |
| [9] |
Feng W P, Samsonov S, Tian Y F, et al. Surface Deformation Associated with the 2015 MW8.3 Illapel Earthquake Revealed by Satellite-Based Geodetic Observations and Its Implications for the Seismic Cycle[J]. Earth and Planetary Science Letters, 2017, 460: 222-233 DOI:10.1016/j.epsl.2016.11.018
(  0) 0) |
| [10] |
An C, Yue H, Sun J B, et al. The 2015 MW8.3 Illapel, Chile, Earthquake: Direction-Reversed Along-Dip Rupture with Localized Water Reverberation[J]. Bulletin of the Seismological Society of America, 2017, 107(5): 2416-2426 DOI:10.1785/0120160393
(  0) 0) |
| [11] |
Liu C L, An C, Shan B, et al. Insights into the Kinematic Rupture of the 2015 MW8.3 Illapel, Chile, Earthquake from Joint Analysis of Geodetic, Seismological, Tsunami, and Superconductive Gravimeter Observations[J]. Journal of Geophysical Research: Solid Earth, 2018, 123(11): 9778-9799 DOI:10.1029/2018JB016065
(  0) 0) |
| [12] |
陈世仲, 李小凡, 汪文帅. 地球自由振荡的保结构模拟[J]. 地球物理学报, 2016, 59(5): 1685-1695 (Chen Shizhong, Li Xiaofan, Wang Wenshuai. Structure-Preserving Numerical Simulation for Earth's Free Oscillations[J]. Chinese Journal of Geophysics, 2016, 59(5): 1685-1695)
(  0) 0) |
| [13] |
万永革, 盛书中, 周公威, 等. 中国数字地震台网记录的苏门答腊-安达曼地震激发的地球球型自由振荡的检测[J]. 地震学报, 2007, 29(4): 369-381 (Wan Yongge, Sheng Shuzhong, Zhou Gongwei, et al. Spheroidal Oscillations of the Earth Stimulated by the Sumatra-Andaman Earthquake with CDSN Data[J]. Acta Seismologica Sinica, 2007, 29(4): 369-381)
(  0) 0) |
| [14] |
Aid K, Richards P G. Quantitative Seismology:Theory and Methods[J]. Earth Science Reviews, 1981, 17(3): 296-297
(  0) 0) |
| [15] |
江颖, 李辉, 刘子维, 等. 利用连续重力观测约束2014智利Iquique地震的震源机制解[J]. 地球物理学报, 2016, 59(3): 941-951 (Jiang Ying, Li Hui, Liu Ziwei, et al. Constraining the Focal Mechanism of the Iquique Earthquake with Observations of the Continuous Gravity Stations[J]. Chinese Journal of Geophysics, 2016, 59(3): 941-951)
(  0) 0) |
2. Key Laboratory of Earthquake Dynamics of Hebei Province, Institute of Disaster Prevention, 465 Xueyuan Street, Sanhe 065201, China
 2020, Vol. 40
2020, Vol. 40


