2. 中国科学院大学,北京市玉泉路19号甲,100049
随着现代空间大地测量技术的快速发展,地球定向参数(日长、极移和章动)的精度得到极大提高,可为深入认识地球自转变化特征提供有利条件。Gross等[1]利用1980~2000年的日长与大气数据在年际变化的高频段(1 a<周期<5 a)进行对比分析发现,大气可解释约87.3%的日长变化。然而,师思等[2]利用1979~2016年的日长与大气数据在整个年际变化频段(1 a<周期<10 a)进行分析发现,大气仅能解释约65%的日长变化,即在年际变化的低频段(5 a<周期<10 a),大气贡献可能占比较低,致使大气对整个日长年际变化的解释率降低。研究表明,在日长年际变化中,存在一个频率稳定的6 a信号,并认为其可能与地球内部的核幔耦合效应有关,Mound等[3]研究表明,该信号由核幔引力耦合效应引起。此外,Ding[4]利用AR-z谱方法从日长变化序列(1962~2018年)中探测到一个周期为8.5 a的信号,但该信号的激发源仍未明确,这从侧面说明日长年际变化还需进一步研究。
为对日长年际变化进行更细致的分析,本文采用标准Morlet小波变换方法,对日长年际变化中主要的周期信号进行识别和提取。此外,虽然许多研究表明大气与日长年际变化密切相关,但不同的研究结果显示大气对日长年际变化的影响存在差异,特别是日长年际变化低频段(5 a<周期<10 a)中信号的主要激发源尚存在争议。因此,为更加明确大气对日长年际变化的影响,本文还将通过对大气角动量序列进行处理,以进一步分析大气与日长年际变化的相关性。
1 信号提取方法为准确识别和提取日长年际变化中的信号,本文将结合使用正交Daubechies小波滤波方法、傅里叶变换和标准Morlet小波变换,同时在时间-频率两域对数据进行处理。
傅里叶变换方法可将原始序列从时域转换到频域,从而探测原始序列中可能存在的周期信号,并将结果作为下一步信号提取时的参考[5]。正交Daubechies小波滤波方法可根据需要获得特定频段的数据,以消除高频噪声和其他干扰信号,为目标信号的提取提供便利[6]。
标准Morlet小波变换(normal Morlet wavelet transform, NMWT)为本文使用的主要方法,由Liu等[7]提出,可准确地将谐波信号从包含复杂背景噪声的数据中提取出来,而无需进行逆变换,是进行调和分析的有效工具,已应用于潮位预测、极移预测以及日长6 a信号的分析中[8-11]。标准Morlet小波变换与传统小波变换均存在边缘效应,为解决该问题,基于NMWT方法提取的信号具有相位无偏特性,Duan等[10]结合传统的对称延拓方法,提出一种可有效消除NMWT边缘效应的边界极值点镜像延拓方法,简称“极值点延拓法”。极值点延拓法每次只能基于一个目标信号的边界极值点对原始数据进行对称延拓,因此NMWT方法每次只能提取一个不受边缘效应影响的目标信号,针对多个目标信号时需要重复使用上述方法。
信号提取的整体流程如下:1)使用正交Daubechies小波滤波方法对原始序列进行处理,以根据需要获得包含目标信号的特定频段;2)使用NMWT方法提取受到边缘效应影响的目标信号;3)根据提取的目标信号,使用极值点延拓法获得对称延拓后的新序列;4)使用NMWT方法从新序列中提取不受边缘效应影响的目标信号。为避免信号混频对目标信号提取造成干扰,先使用NMWT方法初步提取目标信号邻近的其他信号,然后从序列中将其剔除。
2 仿真实验分析为验证NMWT方法在提取谐波信号方面的可靠性,仿照实际日长序列构造以下复合信号:
| $ \begin{array}{l} f\left( t \right) = 0.04t + 0.001{t^2} + 0.8\cos \left( {2{\mathtt{π}}t/4.7 + 1} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;1.5{{\rm{e}}^{ - 0.015t}}\cos \left( {2{\mathtt{π}}t/6 + 0.5} \right) + \varepsilon \left( t \right) \end{array} $ |
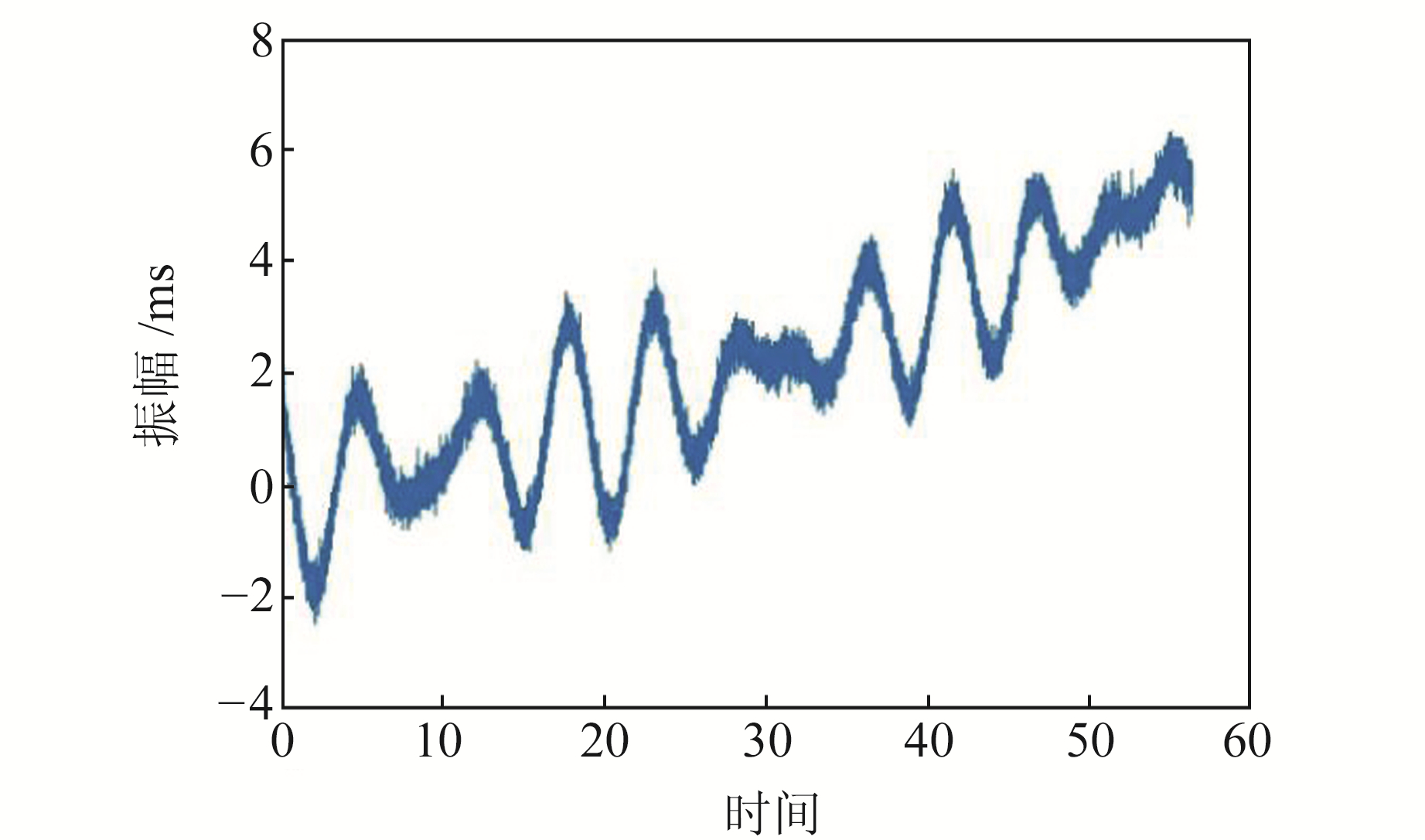
式中,t为时间变量。该复合信号主要由3部分组成,分别为趋势项h(t)=0.04t+0.001t2、纯谐波信号f1(t)=0.8cos(2πt/4.7+1)和准谐波信号f2(t)=1.5e-0.015tcos(2πt/6+0.5),ε(t)是均值为0、标准差为0.03的高斯白噪声。复合信号f(t)的时域波形如图 1所示。
|
图 1 复合信号f(t) Fig. 1 The composite signal f(t) |
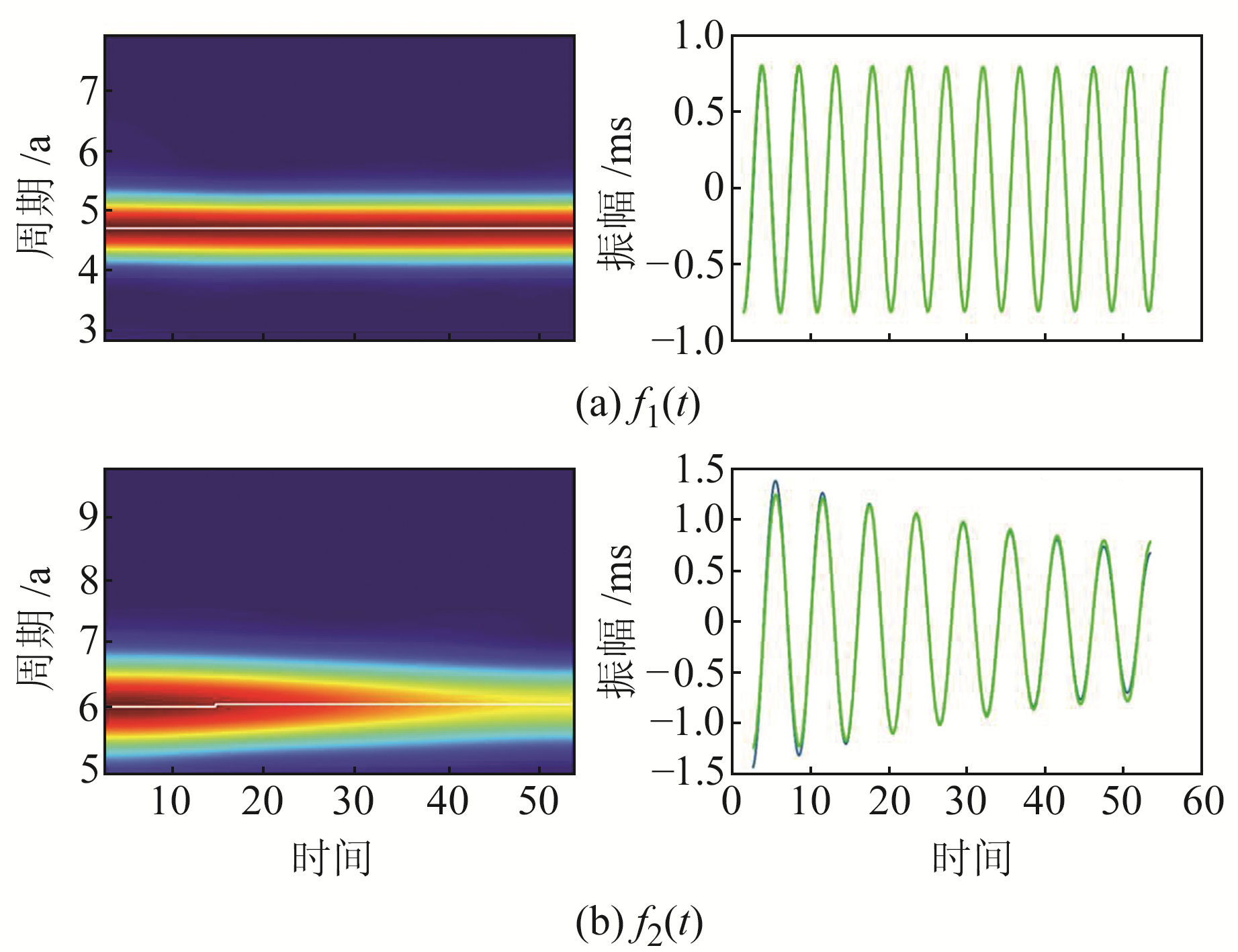
利用NMWT方法对上述复合信号f(t)进行处理,结果如图 2所示。图 2左列分别为目标谐波信号f1(t)、f2(t)的标准Morlet小波振幅谱,颜色越深表示相对振幅越大,图中白线为“脊线”,可用来识别目标信号。结果显示,小波振幅谱不仅可准确识别出目标信号周期,而且可正确反映相应目标信号振幅的长期变化趋势。图 2右列分别为目标谐波信号f1(t)、f2(t)的时域提取结果与对应原始仿真信号的比较,图中绿线为时域提取结果,蓝线为原始仿真信号。从目标谐波信号的时域提取结果对比图中可以发现,NMWT方法不仅可准确提取纯谐波信号,而且在提取振幅随时间发生变化的准谐波信号方面也具有较高精度。此外,目标谐波信号的时域提取结果在两端处与原始仿真信号基本一致,表明极值点延拓法可有效消除NMWT边缘效应。
|
图 2 目标信号f1(t)和f2(t)的标准Morlet小波振幅谱以及时域提取结果与原始仿真信号的比较 Fig. 2 The normal Morlet wavelet amplitude spectrum of target signal f1(t), f2(t) and comparison of the extracted result with the original simulation signal |
本文采用的日长变化(length-of-day variation, ΔLOD)时间序列来源于国际地球自转服务中心(IERS)发布的长期地球定向参数数据资料EOP14C04(https://www.iers.org/IERS/EN/DataProducts/EarthOrientationData/eop.html),该数据资料是通过综合处理近代空间大地测量技术资料和光学观测结果所得,具有较高的精度和系统稳定性。选取1962~2018年的日长变化序列,采样间隔为1 d。大气数据采用美国环境预报中心/国家大气研究中心(NCEP/NCAR)使用全球气象资料重新归算得到的大气角动量(atmospheric angular momentum, AAM)序列,该数据由“风项”和“气压项”两部分组成,采样间隔为6 h(https://www.iers.org/IERS/EN/DataProducts/GeophysicalFluidsData/geoFluids.html)。为便于和ΔLOD序列进行对比分析,首先需要将AAM序列按照关系式ΔLOD=[86 400 s/(CmΩ)]×ΔAAM(Ω=2π/(86 164.1 s),为地球平均自转速率;Cm=7.12×1037 kg ·m2,为地幔的轴向转动惯量)换算成与ΔLOD序列相同的量纲[12],然后按天进行简单平均得到1 d间隔的序列。ΔLOD时间序列和AAM时间序列如图 3所示。由于大气压力项对日长变化的影响较小,因此本文仅选用大气角动量数据中风项部分。

|
图 3 ΔLOD和AAM时间序列 Fig. 3 Time series of ΔLOD and AAM |
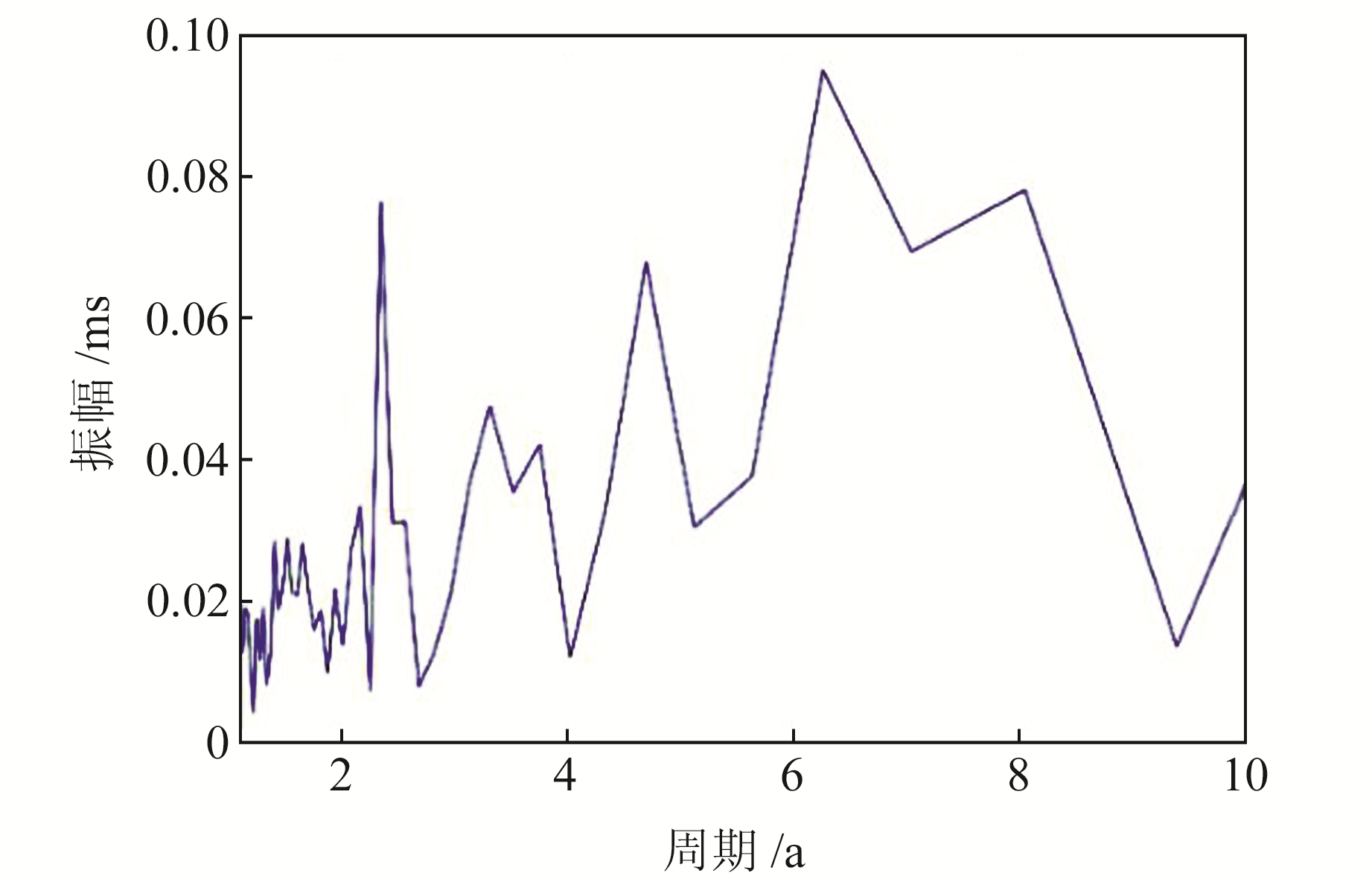
在信号提取前,首先对原始ΔLOD数据进行傅里叶变换,以探测日长年际频段中存在的明显周期信号,并将结果作为信号提取结果的参考,结果如图 4所示。图 4为ΔLOD频谱在年际频段(1 a<周期<10 a)的局部放大图,从图中可以看出,日长年际频段中存在6个主要的周期信号,其周期(和振幅)分别为2.4 a(0.08 ms)、3.3 a(0.05 ms)、3.8 a(0.04 ms)、4.7 a(0.07 ms)、6.3 a(0.10 ms)和8.1 a(0.08 ms)。
|
图 4 ΔLOD时间序列在年际频段(1 a<周期<10 a)的频谱 Fig. 4 The frequency spectrum of ΔLOD time series in interannual frequency range from 1 a to 10 a |
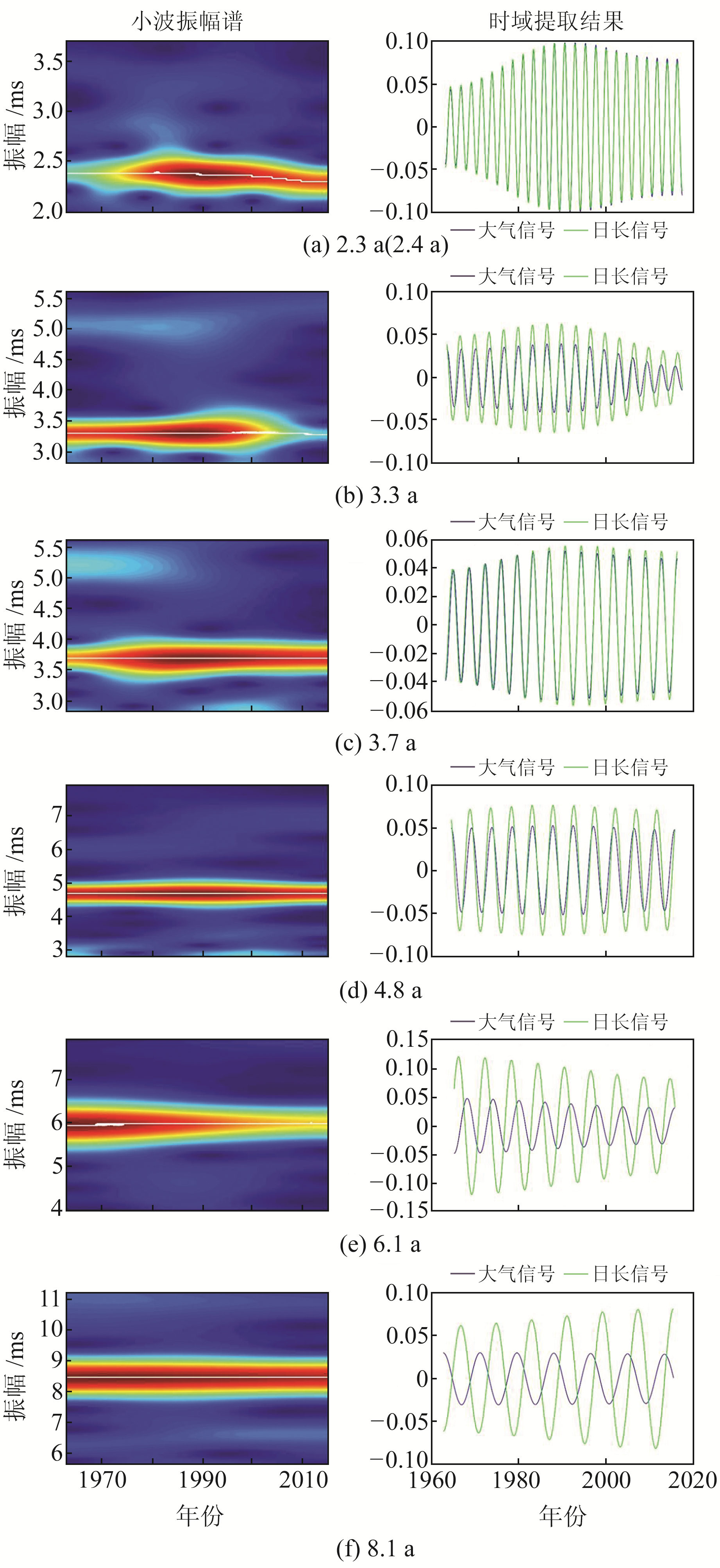
在初步确定日长变化中可能存在的年际信号后,使用标准Morlet小波变换方法对ΔLOD数据进行处理,最终识别和提取出6个日长年际信号,结果如图 5所示。图 5(a)~(f)分别为日长2.3 a(2.4 a)、3.3 a、3.7 a、4.8 a、6.1 a和8.1 a信号的标准Morlet小波振幅谱(左列)和时域提取结果(右列)。从图 5可以看出,除日长2.3 a(2.4 a)信号的频率随时间发生轻微波动(变化范围在2.3~2.4 a之间),其余日长年际信号的频率相对较稳定。此外,6个日长年际信号的振幅随时间发生不同变化。基于信号的时域提取结果,计算获得6个日长年际信号的平均振幅,依次为0.08 ms、0.05 ms、0.05 ms、0.07 ms、0.10 ms和0.07 ms。仿真实验表明,信号周期的精度为±0.1 a,信号平均振幅的精度为±0.01 ms。NMWT方法提取的结果(周期和平均振幅)与ΔLOD频谱显示的结果(图 4)非常接近,表明NMWT方法提取的日长年际信号具有可靠性。

|
图 5 日长信号的标准Morlet小波振幅谱和时域提取结果 Fig. 5 The normal Morlet wavelet amplitude spectrum and time-domain extracted result of the ΔLOD signal |
对AAM序列以及减去AAM后的ΔLOD(ΔLOD-AAM)序列进行傅里叶变换,并与原始ΔLOD序列的频谱在年际频段(1 a<周期<10 a)进行对比,结果如图 6所示。由图可知,减去AAM后的ΔLOD序列的频谱在1~5 a频段被极大削弱,而5~10 a频段的频谱受影响较小。具体到6个主要日长年际信号上,日长2.3 a(2.4 a)和3.7 a信号受大气影响程度最大,其次为3.3 a、4.8 a信号,6.1 a和8.1 a信号受影响程度最小。

|
图 6 原始ΔLOD序列、AAM序列和ΔLOD-AAM序列在年际频段(1 a<周期<10 a)的频谱对比 Fig. 6 The frequency spectrum comparison of the original ΔLOD series, AAM series and (ΔLOD-AAM) series in the interannual frequency band range from 1 a to 10 a |
由于3个序列的频谱对比结果(图 6)显示日长年际变化高频段(1 a<周期<5 a)受大气影响较大,且日长变化对大气运动过程的响应较快(即两者相位差较小),因此可以推测AAM与ΔLOD序列中相对应的4个高频年际信号(2.3 a(2.4 a)、3.3 a、3.7 a和4.8 a信号)具有相似的长期变化趋势。此外,由于4个日长高频年际信号受到大气不同程度的影响,因此还可以推测出AAM序列中4个高频年际信号的振幅与ΔLOD序列中对应信号的振幅并不一致,而是受大气影响程度越大两者振幅越接近,受大气影响程度越小则两者振幅差距越大。而日长年际变化的低频段(5 a<周期<10 a)受大气影响程度较小,原因之一可能为大气中不存在或者只存在微弱的~6 a和~8 a信号(“~”表示大约),即大气~6 a和~8 a信号的振幅可能较小;另一个原因可能为大气中存在的~6 a和~8 a信号与日长年际变化中对应的6.1 a和8.1 a信号不相关或弱相关,即两者对应信号的相位差可能较大。
为验证上述推测的正确性,仿照日长2.3 a(2.4 a)、3.3 a、3.7 a、4.8 a、6.1 a和8.1 a信号,利用NMWT方法对AAM序列中相应的信号进行提取,并将两者的时域提取结果进行比较,结果如图 7所示。图 7(a)~(f)分别为大气2.3 a(2.4 a)、3.3 a、3.7 a、4.7 a、6.0 a和8.5 a信号的标准Molret小波振幅谱(左列)以及大气和日长对应信号时域提取结果的比较(右列)。图 7(a)~(d)显示,在长期变化趋势方面,大气和日长对应的4个高频年际信号(2.3 a(2.4 a)、3.3 a、3.7 a和4.8 a信号)均非常相似;在振幅方面,大气和日长对应的2.3 a(2.4 a)和3.7 a信号的振幅非常接近,而3.3 a和4.8 a信号的振幅存在一定差距。图 7(e)和7(f)显示,大气中虽然存在6.0 a和8.5 a信号,但与日长6.1 a和8.1 a信号相比,一方面在周期和振幅上存在一定偏差,另一方面两者对应信号的相位差较大,分别为~4.5 a和~3.1 a。
|
图 7 大气信号的标准Morlet小波振幅谱以及大气和日长对应信号时域提取结果的比较 Fig. 7 The normal Morlet wavelet amplitude spectrum of atmospheric signal and comparison of extracted result of atmosphere and ΔLOD signal |
基于大气和日长年际信号的时域提取值可得到两者对应信号的相关系数,分别为0.99、0.93、0.99、0.91、-0.11和-0.56。该结果表明,大气和日长对应的4个高频年际信号(2.3 a(2.4 a)、3.3 a、3.7 a和4.8 a信号)之间存在强相关性,而大气6.0 a和8.5 a信号与日长对应的6.1 a和8.1 a信号弱相关。因此大气中虽然存在微弱的6.0 a和8.5 a信号,但并不能用来解释日长年际变化低频段(5 a<周期<10 a)中对应的信号,具体激发原因还需在其他地球物理因素中探寻。由于大气和日长存在高相关性的信号在1962~2018年时段长期变化趋势基本一致,且大气和日长数据各自独立,因此可以证明不同时段数据精度存在差异对日长年际信号的提取结果影响较小。
为定量显示大气对日长年际变化高频段(1 a<周期<5 a)中相应信号的影响,基于大气和日长4个高频年际信号的时域提取值,利用公式std(data 1)/std(data 2)×100%(std为标准差算子)分别计算大气对日长相应信号的贡献率,结果依次为99.7%、63.1%、94.7%和69.3%。该结果表明,日长2.3 a(2.4 a)和3.7 a信号几乎完全可以由大气解释,而大气也为其余2个日长信号的主要激发源。此外,虞南华等[13]研究AAM在亚季节性到年际时间尺度上对ΔLOD的激发时,证明在准2 a(23~34个月)尺度上,日长准2 a振荡几乎完全可以由大气解释,与本文结果基本一致。
4 结语本文首先通过仿真实例验证NMWT为一种有效的调和分析方法,不仅可准确提取振幅稳定的纯谐波信号,还可以较高的精度对振幅或频率随时间发生缓慢变化的准谐波信号进行提取。其次,利用NMWT方法从ΔLOD时间序列中识别和提取出6个主要的年际信号,周期分别为2.3 a(2.4 a)、3.3 a、3.7 a、4.8 a、6.1 a和8.1 a,除日长2.3 a(2.4 a)信号的频率随时间发生轻微波动(变化范围在2.3~2.4 a之间)外,其余日长年际信号的频率相对较稳定。此外,6个日长年际信号的振幅随时间发生不同变化,通过信号的时域提取值计算获得相应信号的平均振幅,结果依次为0.08 ms、0.05 ms、0.05 ms、0.07 ms、0.10 ms和0.07 ms,该结果与ΔLOD频谱显示的结果基本一致。最后,仿照提取出的日长年际信号,对大气中相应的年际信号进行提取,并基于信号的时域提取结果对两者进行相关性分析。大气与日长6个对应年际信号的相关系数分别为0.99、0.93、0.99、0.91、-0.11和-0.56,证明大气和日长对应的4个高频年际信号(2.3 a(2.4 a)、3.3 a、3.7 a和4.8 a信号)存在强相关性,而大气6.0 a和8.5 a信号与日长对应的6.1 a和8.1 a信号不相关或弱相关。因此大气中虽然存在微弱的6.0 a和8.5 a信号,但并不能用来解释日长变化中对应的6.1 a和8.1 a信号,具体激发原因还需在其他地球物理因素中寻找。大气对日长4个高频年际信号的激发贡献率分别为99.7%、63.1%、94.7%和69.3%,表明日长2.3 a(2.4 a)和3.7 a信号几乎完全可以由大气解释,而大气也为其余2个日长年际信号的主要激发源。
| [1] |
Gross R S, Fukumori I, Menemenlis D, et al. Atmospheric and Oceanic Excitation of Length-of-Day Variations during 1980-2000[J]. Journal of Geophysical Research:Solid Earth, 2004, 109(B1)
(  0) 0) |
| [2] |
师思, 周永宏, 许雪晴. 1979 - 2016年间日长变化在年际、季节性、亚季节性及高频尺度上的大气激发[J]. 天文学进展, 2017, 35(4): 448-461 (Shi Si, Zhou Yonghong, Xu Xueqing. Atmospheric Excitation of the Variation of Length of Day on Interannual, Seasonal, Sub-Seasonal and High-Frequency Timescales, 1979 - 2016[J]. Progress in Astronomy, 2017, 35(4): 448-461)
(  0) 0) |
| [3] |
Mound J E, Buffett B A. Interannual Oscillations in Length of Day: Implications for the Structure of the Mantle and Core[J]. Journal of Geophysical Research:Solid Earth, 2003, 108(B7)
(  0) 0) |
| [4] |
Ding H. Attenuation and Excitation of the ~6 Year Oscillation in the Length-of-Day Variation[J]. Earth and Planetary Science Letters, 2019, 507: 131-139 DOI:10.1016/j.epsl.2018.12.003
(  0) 0) |
| [5] |
杨丽娟, 张白桦, 叶旭桢. 快速傅里叶变换FFT及其应用[J]. 光电工程, 2004, 31(增): 1-3 (Yang Lijuan, Zhang Baihua, Ye Xuzhen. Fast Fourier Transform and Its Applications[J]. Opto-Electronic Engineering, 2004, 31(S): 1-3)
(  0) 0) |
| [6] |
魏海涛, 郑南宁, 张志华. 具有紧支撑的正交小波变换滤波器的设计原理和一种图像精确分解与重构算法[J]. 电子学报, 2000, 28(10): 17-19 (Wei Haitao, Zheng Nanning, Zhang Zhihua. Orthogonal Wavelet Transform with Compact Support Filter Design Method and an Algorithm of Image Perfect Decomposition and Reconstruction[J]. Acta Electronica Sinica, 2000, 28(10): 17-19)
(  0) 0) |
| [7] |
Liu L T, Hsu H, Grafarend E W. Normal Morlet Wavelet Transform and Its Application to the Earth's Polar Motion[J]. Journal of Geophysical Research:Solid Earth, 2007, 112(B8)
(  0) 0) |
| [8] |
Cai S, Liu L T, Wang G C. Short-Term Tidal Level Prediction Using Normal Time-Frequency Transform[J]. Ocean Engineering, 2018, 156: 489-499 DOI:10.1016/j.oceaneng.2018.03.021
(  0) 0) |
| [9] |
Su X Q, Liu L T, Hsu H, et al. Long-Term Polar Motion Prediction Using Normal Time-Frequency Transform[J]. Journal of Geodesy, 2014, 88(2): 145-155
(  0) 0) |
| [10] |
Duan P S, Liu G Y, Liu L T, et al. Recovery of the 6-Year Signal in Length of Day and Its Long-Term Decreasing Trend[J]. Earth, Planets and Space, 2015, 67: 161 DOI:10.1186/s40623-015-0328-6
(  0) 0) |
| [11] |
Li S D, Liu L T, Cai S, et al. Tidal Harmonic Analysis and Prediction with Least-Squares Estimation and Inaction Method[J]. Estuarine, Coastal and Shelf Science, 2019, 220: 196-208 DOI:10.1016/j.ecss.2019.02.047
(  0) 0) |
| [12] |
Chao B F, Yan H M. Relation between Length-of-Day Variation and Angular Momentum of Geophysical Fluids[J]. Journal of Geophysical Research:Solid Earth, 2010, 115(B10)
(  0) 0) |
| [13] |
虞南华, 郑大伟. 大气角动量资料源的变化对研究日长变化激发的贡献[J]. 天文学报, 1998, 39(2): 122-130 (Yu Nanhua, Zheng Dawei. Contribution of AAM Data Source Change to the Research on Excitation of ΔLOD[J]. Acta Astronomica Sinica, 1998, 39(2): 122-130)
(  0) 0) |
2. University of Chinese Academy of Sciences, A19 Yuquan Road, Beijing 100049, China
 2020, Vol. 40
2020, Vol. 40


