2. 国家自然资源部大地测量数据处理中心,西安市友谊东路334号,710054
水汽虽然为大气层中含量较少的气体,但变化很大,并且与众多天气现象密切相关,精确测量水汽对预警暴雨、雾霾、台风等灾害天气具有重要作用[1]。全球定位系统(global position system,GPS)具有全天候、高精度、低成本的特点,Bevis等[2]利用地基GPS进行水汽计算,提出“GPS气象学”,并且验证该方法测得的水汽误差约为5%。近年来利用GPS进行水汽探测的技术日趋成熟[3-7],并且已有不同GPS星历反演水汽含量方面的研究。段晓梅[8]以IGF的计算结果为标准,验证使用IGU实测星历和预报星历可满足近实时遥测水汽的需求。刘盼等[9]基于精密单点定位(precise point position,PPP)方法,证明利用超快速星历(预报部分)有助于实时探测水汽变化。
随着中国北斗卫星导航系统(Beidou navigation satellite system,BDS)的不断完善,现已能提供覆盖全球的高精度定位服务,并且可应用于气象研究[10]。文献[11]选取北京地区周边6个GNSS观测站,分别利用GPS和BDS计算对流层天顶总延迟(zenith total delay,ZTD),结果表明两者相差较小,偏差和标准差分别约为2 mm和5 mm。文献[12]利用PANDA软件处理亚太地区和西印度洋地区10个连续运行参考站(continuously operating reference stations,CORS)的BDS和GPS数据发现,BDS反演的水汽结果与GPS相比,偏差和标准差均小于2 mm。韩阳等[13]利用精密单点定位方法,采用GPS、DBS和GPS+BDS三种方案计算水汽,结果表明,BDS可以单独用来获取高精度的水汽结果,且GPS和BDS融合能提高水汽计算精度。高志钰等[14]使用GAMIT软件最新版本(v10.7)证明了BDS水汽反演的可行性和准确性。
武汉大学IGS分析中心提供3种不同的星历,分别为最终精密星历(WHS)、快速星历(WHR)和超快速星历(WHU),其中超快速星历中含有实测数据和预报数据[15]。国际GNSS监测评估系统(international GNSS monitoring and assessment system,IGMAS)已经给出各星历精度,分别为15 cm、20 cm、25 cm、50 cm。
本文使用GAMIT10.7软件,利用最终精密星历、快速星历和超快速星历(预报部分)进行水汽反演,并分别与GPS计算的水汽和探空数据计算的水汽进行比较,分析利用不同北斗星历反演水汽的精度。
1 大气可降水量计算方法 1.1 利用探空数据计算水汽根据各个高度上的露点温度测值,计算各个高度上的水汽压e:
| $ e = 6.107\;8{{\rm{e}}^{\frac{{a{T_d}}}{{b + {T_d}}}}} $ | (1) |
式中,a和b取值为:冰面情况下,a=9.5,b=265.49;水面情况下,a=7.5,b=237.29。比湿q可表示为:
| $ q = \frac{{622e}}{{p - 0.378e}} $ | (2) |
将各个标准等压面上的比湿进行差分计算,即可得到大气可降水量W:
| $ W = - \frac{1}{g}\sum\limits_{{p_0}}^0 {q\Delta p} $ | (3) |
将探空资料中提供的气压、温度和温度露点差代入式(1)、(2)和(3)中,即可计算出大气中的水汽含量[16-18]。
1.2 地基GNSS反演大气可降水量对流层天顶总延迟(ZTD)由静力学延迟(ZHD)和湿延迟(ZWD)组成,由于静力学延迟相对稳定,较易获取,而湿延迟会随天气发生变化,因此对流层湿延迟可由天顶总延迟减去静力学延迟得到:
| $ {\rm{ZWD = ZTD - ZHD}} $ | (4) |
静力学延迟可通过对流层延迟模型计算获得,本文选用国内精度较高的Saastamoinen模型,公式如下:
| $ \begin{array}{l} {\rm{ZH}}{{\rm{D}}_{{\rm{Saas}}}} = \frac{{0.002\;277}}{{f\left( {\varphi , H} \right)}} \times P\\ f\left( {\varphi , H} \right) = 1 - 0.002\;66 \times \cos 2\varphi - \\ \;\;\;\;\;\;\;\;0.000\;28 \times H \end{array} $ | (5) |
式中,φ为测站纬度,H为测站大地高,P为测站地面气压[19]。
综合式(4)和式(5)可得到ZWD,再将ZWD转化为PWV:
| $ \begin{array}{l} {\rm{PWV = }}\frac{\mathit{\Pi} }{\rho } \times {\rm{ZWD}}\\ \mathit{\Pi} = \frac{{{{10}^6}}}{{R\left[ {\left( {\frac{k}{{{T_m}}}} \right) + k'} \right]}} \end{array} $ | (6) |
式中,ρw为液态水密度,Tm为大气加权平均温度,R、k、k′均为常数[20]。
2 实验过程与精度分析 2.1 不同星历与探空数据分析对比本文选取陕西地区3个探空站(Yanan、Jinghe、Hanzhong)进行实验。在俄怀明大学数据网站(weather.uwyo.edu/wyoming)下载2018-01~2018-06的探空数据,采样间隔为12 h。利用MATLAB编写读取探空数据程序,并将利用式(1)~(3)计算的水汽结果记为Radio-PWV,时间分辨率为12 h。
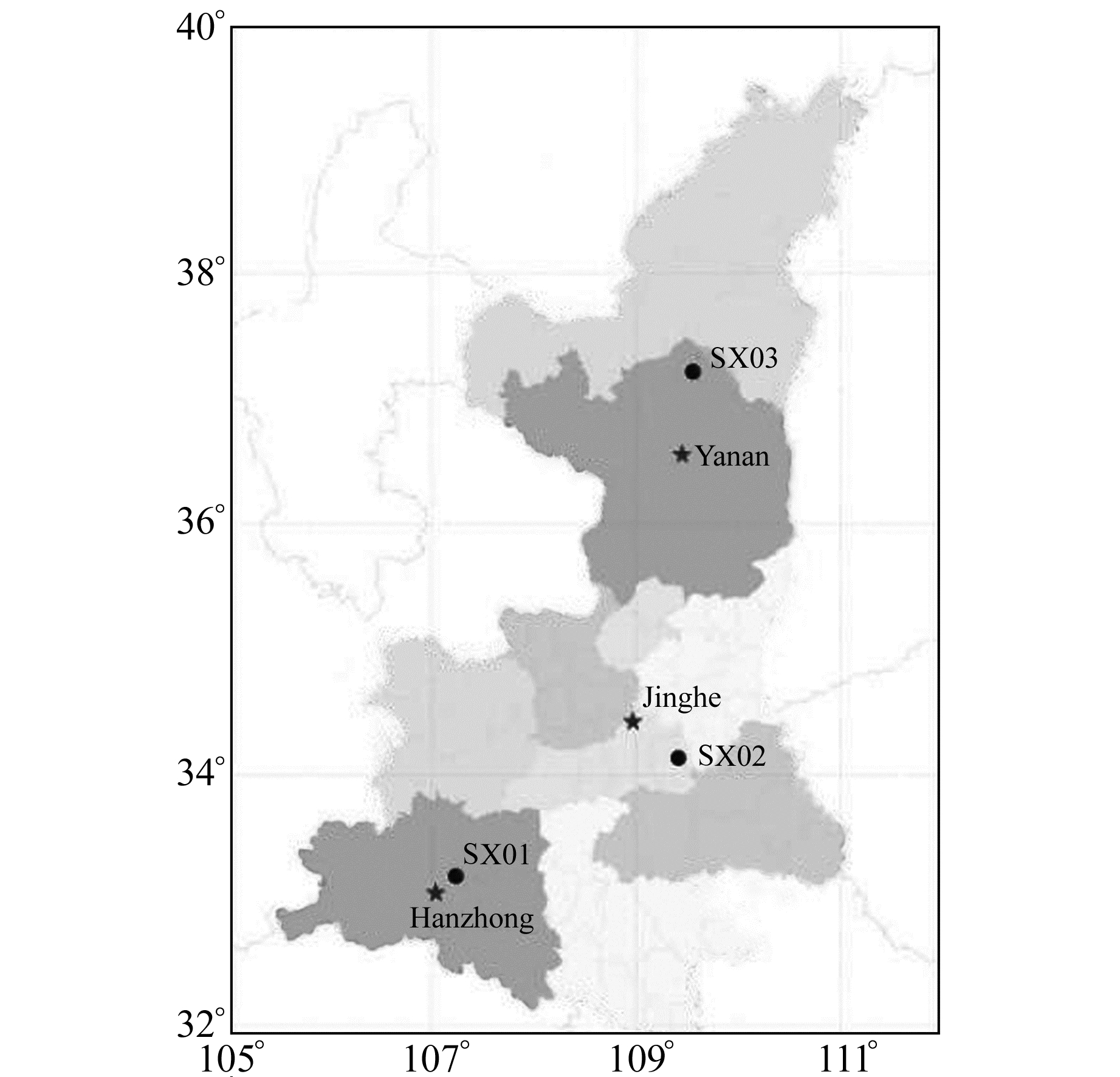
选取分别离3个探空站最近的GNSS观测站(SX01、SX02、SX03),如图 1所示。收集2018-01~2018-06共182 d的观测数据,数据采样间隔为30 s。由于上述3个观测站均装有气象仪,可获取采样间隔为1 min的气象数据。同时收集周边9个国家GNSS基准站的观测数据用于联合解算。
|
图 1 GNSS观测站和探空站位置 Fig. 1 Location of GNSS observation stations and radiosonde stations |
从武汉大学分析中心(ftp://www.igs.gnsswhu.cn/pub)下载最终精密星历、快速星历、超快速星历(提取其中的预报星历)。利用GAMIT软件进行水汽计算,得到时间分辨率为1 h的水汽结果,分别记为WHS-PWV、WHR-PWV和WHU-PWV。
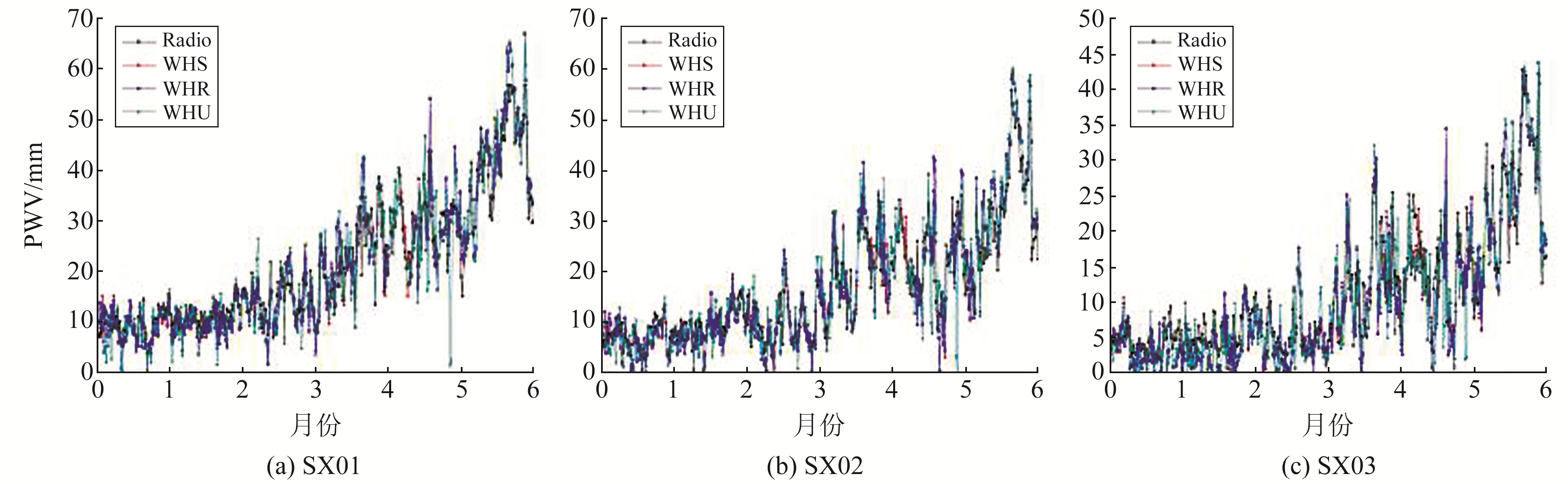
将上述3个测站利用不同星历计算的水汽与利用探空数据测得的水汽进行对比,并作出时间序列图。受探空数据制约,时间分辨率选为12 h。如图 2所示,3个测站的水汽结果整体随月份的增大而增加,呈现冬天低、夏天高的特点,与当地气候环境一致。不同星历反演的水汽值与探空数据解算的水汽结果十分接近,并且具有大致相同的变化趋势。由此可以看出,利用BDS反演水汽具有可行性。
|
图 2 不同星历与探空数据反演水汽的时间序列 Fig. 2 Time series of water vapor retrieved from different ephemeris and radiosonde data |
将3个测站不同星历解算的水汽与Radio-PWV进行线性拟合,拟合结果如图 3所示,从图中可以明显看出,3种不同星历解算的水汽与Radio-PWV有较好的拟合性。结合表 1可知,WHS- PWV和WHR-PWV精度接近,相关性也相近,均为0.95左右,其中WHS-PWV相关性更高;而WHU-PWV相关性约为0.93,相对较差。

|
图 3 3个测站不同星历与Radio-PWV的线性拟合 Fig. 3 Linear fitting of different ephemeris and radio PWV of three stations |
|
|
表 1 3个测站不同星历与Radio-PWV统计 Tab. 1 Statistics of different ephemeris and radio PWV of three stations |
表 1还包含各测站偏差(BIAS)、标准差(STD)和均方根误差(RMS),可以看出,3种不同星历计算的水汽都具有较高精度。WHS-PWV精度最高,3个测站的偏差均优于1 mm,并且各测站的标准差和均方根误差均优于5 mm;WHR-PWV与WHS-PWV相比,各项指标相差较小;WHU-PWV精度相对较差,其偏差约为1 mm,3个测站的标准差和均方根误差均优于6 mm。
2.2 不同BDS星历与GPS星历分析对比从图 1可以看出,每组探空站与GNSS观测站相距均大于10 km,不同站址可能会对水汽反演精度造成一定影响。为解决站址不一致造成的误差,本次实验收集上述3个测站的GPS观测数据,并在CDDIS官网(ftp://cddis.gsfc.nasa.gov/pub)下载IGS提供的最终精密星历(IGF)。利用GAMIT软件进行GPS基线解算以及水汽反演,得到时间分辨率为1 h的水汽结果,记为GPS-PWV。
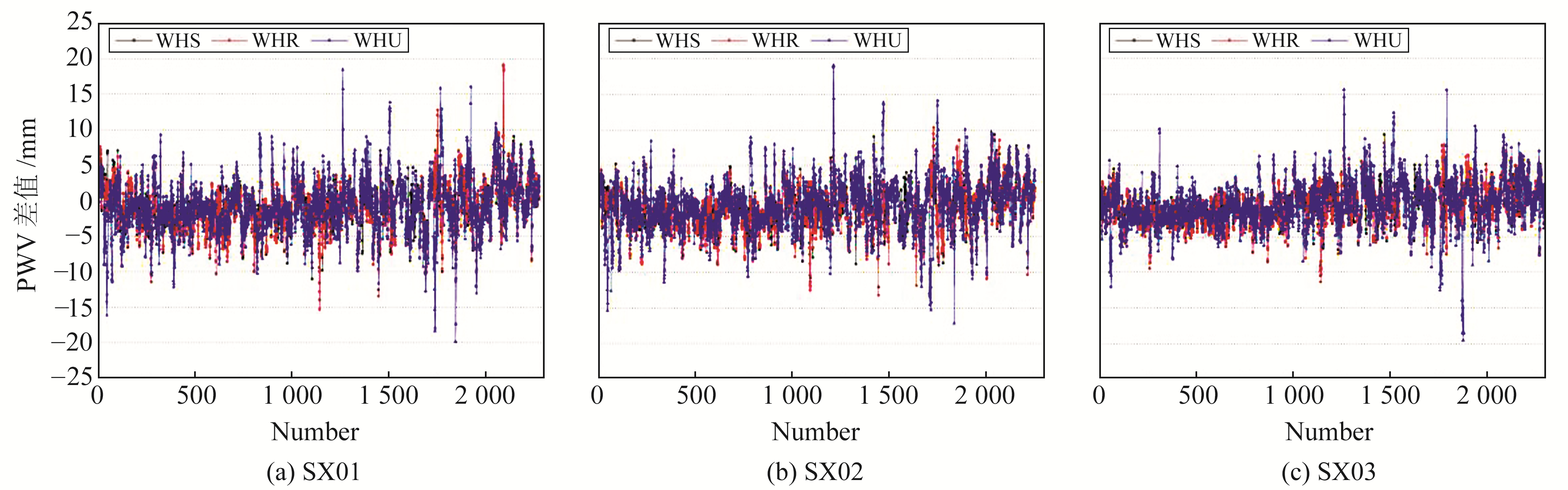
将上述3个测站利用不同BDS星历计算的水汽与GPS反演的水汽相减,并作出差值时间序列(图 4)。从图中可以看出,WHS-PWV最接近GPS-PWV,WHR-PWV结果也相对接近,而WHU-PWV精度较低,但3种BDS星历计算的水汽与GPS-PWV的变化趋势大致相同。
|
图 4 3个测站不同星历与GPS-PWV的差值时间序列 Fig. 4 Time series of difference between different ephemeris and GPS-PWV of three stations |
为更直观地表达不同BDS星历解算的PWV与GPS-PWV的差异,计算各测站水汽结果的偏差、标准差和均方根误差(表 2)。由表可见,与GPS-PWV相比,WHS-PWV的偏差均优于1 mm,且各测站的标准差和均方根误差均优于3.5 mm;WHR-PWV的结果与WHS-PWV相近,各项指标相差较小;WHU-PWV的偏差约为1 mm,3个测站的标准差和均方根误差均优于5 mm。
|
|
表 2 3个测站不同星历与GPS-PWV对比统计 Tab. 2 Comparison of different ephemeris and GPS-PWV of three stations |
将3种利用不同星历反演的水汽结果进行对比,时间分辨率为1 h。将WHR-PWV和WHU-PWV分别减去WHS-PWV,结果如图 5所示。从图 5可以看出,3个测站中WHR-PWV与WHS-PWV的差值均在±5 mm范围内,说明WHR-PWV与WHS-PWV总体吻合较好。而WHU-PWV与WHS-PWV总体吻合程度相对较差,除少数误差过大的数据外,其差值均在±10 mm范围内。其原因可能为超快速星历预报部分提供的卫星轨道精度较低,导致计算的ZTD结果较差,从而影响水汽反演的精度。

|
图 5 利用不同星历反演的PWV差值 Fig. 5 The differences of PWV retrieved by different ephemeris |
表 3为WHR-PWV与WHS-PWV、WHU-PWV与WHS-PWV之间的偏差、标准差和均方根误差。WHR-PWV与WHS-PWV的结果相似,其中各测站的偏差均较小,且标准差和均方根误差均优于1 mm;而WHU-PWV与WHS-PWV的精度相对较差。综合图 5和表 3可知,利用精密星历和快速星历反演水汽的精度相当;利用超快速星历预报部分反演水汽,其结果精度虽然不如前两种,但仍可满足气象预报要求。
|
|
表 3 不同星历产品解算的PWV对比 Tab. 3 PWV comparison of different ephemeris products |
选用陕西地区3个GNSS观测站和3个探空站2018年1~6月数据,分析用武汉大学IGS分析中心提供的3种北斗星历产品反演PWV的精度及气象预报的适用性。结果表明,不同星历反演水汽的结果与探空数据探测的结果相近。由于站址不同会引起误差,本文以GPS-PWV的结果为参考,对不同星历反演水汽的精度进行对比发现,利用事后精密星历计算的水汽精度最高,与GPS-PWV相比,各测站的偏差均优于1 mm,标准差和均方根误差均优于3.5 mm;利用快速星历计算的水汽与利用事后精密星历计算的水汽结果相似,各项指标相近;利用超快速星历预报部分计算的水汽精度相对较差,各测站偏差约为1 mm,标准差和均方根误差均优于5 mm。由此可见,利用3种不同星历解算的水汽都具有较高的准确性和可靠性,并且利用超快速星历预报部分反演水汽能为气象预报提供一定帮助。
| [1] |
尹恒毅, 郭春喜, 姚顽强, 等. 不同对流层天顶延迟模型在陕西地区的精度及适用性分析[J]. 大地测量与地球动力学, 2020, 40(4): 391-394 (Yin Hengyi, Guo Chunxi, Yao Wanqiang, et al. Accuracy and Applicability of Different Tropospheric Zenith Delay Models in Shaanxi Province[J]. Journal of Geodesy and Geodynamics, 2020, 40(4): 391-394)
(  0) 0) |
| [2] |
Bevis M, Businger S, Herring T A, et al. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System[J]. Journal of Geophysical Research Atmospheres, 1992, 97(D14): 15787-15801 DOI:10.1029/92JD01517
(  0) 0) |
| [3] |
Shi H B, Zhang R, Nie Z S, et al. Research on Variety Characteristics of Mainland China Troposphere Based on CMONOC[J]. Geodesy and Geodynamics, 2018, 9(5): 411-417 DOI:10.1016/j.geog.2018.06.007
(  0) 0) |
| [4] |
Shi H K, He X F, Wang X Y. Retrieval of PWV Based on GPS and Multi-Level Isobaric Surface Data[C].China Satellite Navigation Conference, Harbin, 2018
(  0) 0) |
| [5] |
Yang H Z, He C, Wang Z Q, et al. Reliability Analysis of European ERA5 Water Vapor Content Based on Ground-Based GPS in China[C]. Proceedings of 2019 International Conference on Wireless Communication, Network and Multimedia Engineering(WCNME 2019), Guilin, 2019
(  0) 0) |
| [6] |
胡广保, 叶世榕, 张彦祥, 等. GPS/PWV时间序列特征提取方法的研究[J]. 大地测量与地球动力学, 2019, 39(1): 36-40 (Hu Guangbao, Ye Shirong, Zhang Yanxiang, et al. Research on a Feature Extraction Method of GPS/PWV Time Series[J]. Journal of Geodesy and Geodynamics, 2019, 39(1): 36-40)
(  0) 0) |
| [7] |
王勇, 刘严萍, 李江波, 等. GPS和无线电探空的水汽变化与PM2.5/PM10变化的相关性研究[J]. 武汉大学学报:信息科学版, 2016, 41(12): 1626-1631 (Wang Yong, Liu Yanping, Li Jiangbo, et al. The Correlation between the Variation of PM2.5/PM10 and Precipitable Water Vapor Based on GPS and Radiosonde[J]. Geomatics and Information Science of Wuhan University, 2016, 41(12): 1626-1631)
(  0) 0) |
| [8] |
段晓梅.基于北斗和GPS探测水汽的数据处理和分析[D].成都: 成都信息工程大学, 2018 (Duan Xiaomei.Data Processing and Analysis on Water Vapor Detection Based on BDS and GPS[D].Chengdu: Chengdu University of Information Technology, 2018)
(  0) 0) |
| [9] |
刘盼, 刘智敏, 张明敏, 等. 不同IGS星历产品对地基GPS反演水汽的影响[J]. 测绘科学, 2018, 43(12): 17-22 (Liu Pan, Liu Zhimin, Zhang Mingmin, et al. Influence of Different IGS Ephemeris Products on GPS of Precipitable Water Vapor Inversion[J]. Science of Surveying and Mapping, 2018, 43(12): 17-22)
(  0) 0) |
| [10] |
吴旭祥, 郭秋英, 侯建辉. 基于BDS精密星历产品的水汽探测性能分析[J]. 全球定位系统, 2019, 44(5): 91-99 (Wu Xuxiang, Guo Qiuying, Hou Jianhui. Performance Analysis of Water Vapor Detection Based on BDS Precise Ephemeris Products[J]. GNSS World of China, 2019, 44(5): 91-99)
(  0) 0) |
| [11] |
Xu A G, Xu Z Q, Ge M R, et al. Estimating Zenith Tropospheric Delays from Beidou Navigation Satellite System Observations[J]. Sensors, 2013, 13(4): 4514-4526 DOI:10.3390/s130404514
(  0) 0) |
| [12] |
Li M, Li W W, Shi C, et al. Assessment of Precipitable Water Vapor Derived from Ground-Based Beidou Observations with Precise Point Positioning Approach[J]. Advances in Space Research, 2015, 55(1): 150-162 DOI:10.1016/j.asr.2014.10.010
(  0) 0) |
| [13] |
韩阳, 吕志伟, 徐剑, 等. 基于BDS/GPS观测量的大气可降水量反演精度分析[J]. 导航定位学报, 2017, 5(1): 39-45 (Han Yang, Lü Zhiwei, Xu Jian, et al. Retrieval of Precipitable Water Vapor from BDS and GPS Observations[J]. Journal of Navigation and Positioning, 2017, 5(1): 39-45)
(  0) 0) |
| [14] |
高志钰, 李建章, 刘彦军, 等. 利用BDS数据反演大气可降水量及其精度分析[J]. 测绘通报, 2019(5): 35-38 (Gao Zhiyu, Li Jianzhang, Liu Yanjun, et al. Research on the Accuracy of Atmospheric Precipitable Water Vapor with BDS[J]. Bulletin of Surveying and Mapping, 2019(5): 35-38)
(  0) 0) |
| [15] |
Su X N, Meng G J, Sun H L, et al. Positioning Performance of BDS Observation of the Crustal Movement Observation Network of China and Its Potential Application on Crustal Deformation[J]. Sensors, 2018, 18(10): 3353 DOI:10.3390/s18103353
(  0) 0) |
| [16] |
姚俊强, 杨青, 韩雪云, 等.乌鲁木齐夏季水汽日变化及其与降水的关系[C].全国云降水与人工影响天气科学会议, 乌鲁木齐, 2014 (Yao Junqiang, Yang Qing, Han Xueyun, et al.Analysis on Daily Variation of Water Vapor and Its Relationship with Rainfall in Urumqi in Summer[C].National Cloud Precipitation and Weather Modification Scientific Meeting, Beijing, 2014)
(  0) 0) |
| [17] |
潘韬, 吴绍洪, 刘玉洁, 等. 纵向岭谷区地表大气水汽含量的气候学计算[J]. 地理科学进展, 2012, 31(3): 293-302 (Pan Tao, Wu Shaohong, Liu Yujie, et al. Climatological Calculation of Land Surface Atmospheric Water Vapor Content in Longitudinal Range-Gorge Region[J]. Progress in Geography, 2012, 31(3): 293-302)
(  0) 0) |
| [18] |
杨青, 刘晓阳, 崔彩霞, 等. 塔里木盆地水汽含量的计算与特征分析[J]. 地理学报, 2010, 65(7): 853-862 (Yang Qing, Liu Xiaoyang, Cui Caixia, et al. The Computation and Characteristics Analysis of Water Vapor Contents in the Tarim Basin, China[J]. Acta Geographica Sinica, 2010, 65(7): 853-862)
(  0) 0) |
| [19] |
Saastamoinen J. Introduction to Practical Computation of Astronomical Refraction[J]. Bulletin Géodésique(1946-1975), 1972, 106(1): 383-397 DOI:10.1007/BF02522047
(  0) 0) |
| [20] |
Bevis M, Businger S, Chiswell S, et al. GPS Meteorology: Mapping Zenith Wet Delays onto Precipitable Water[J]. Journal of Applied Meteorology, 1994, 33(3): 379-386 DOI:10.1175/1520-0450(1994)033<0379:GMMZWD>2.0.CO;2
(  0) 0) |
2. Geodetic Data Processing Centre, MNR, 334 East-Youyi Road, Xi'an 710054, China
 2020, Vol. 40
2020, Vol. 40

