2. 湖南科技大学煤炭资源清洁利用与矿山环境保护湖南省重点实验室,湖南省湘潭市桃园路,411201
合成孔径雷达干涉测量(InSAR)技术因其覆盖范围广、监测精度高及受天气因素影响小等优势在矿区变形监测方面得到广泛应用[1-4]。但由于受传感器本身的限制及相干性、噪声等因素的影响,该技术在大变形区域易产生相位混叠,而按照现有的相位解缠算法无法恢复该形变相位,从而导致InSAR形变检测梯度受限,无法获取准确的形变信息[5]。因此,正确确定InSAR技术在矿区形变监测中的最大可检测梯度,对该技术在矿区中的推广应用具有重要意义。
Zebker等[6]认为,当同一像素单元内发生的形变量超出干涉波长的一半时,干涉测量结果无法反映地表真实形变。据此,Massonnet等[7]提出形变梯度的概念,并给出InSAR最大可检测形变梯度(MDDG)的理论公式,即雷达波长的一半与像素大小的比值。在实际应用中,由于地表形变信息极易被噪声掩盖,真实的MDDG远小于理论值,Baran等[8]将相干性作为变量建立新的MDDG函数模型,从而使该问题得到解决。后继学者在此基础上对影像多视因素进行研究,利用回归分析方法探寻多视与形变梯度的关系,最终建立基于多视和相干性的MDDG函数模型,极大提高了模型的检测精度,并划定了InSAR技术的可检测形变梯度范围[9-10]。然而,上述模型在实际应用中需要事先获取SAR影像计算相干性,或利用相干性+视数来判断InSAR的适宜性,在一定程度上制约了模型的检测能力,且容易造成资源浪费。同时,现有模型未考虑矿区开采的实际情况及不同地质采矿条件对开采沉陷的影响,无法在矿区开展实际应用。
本文基于不同分辨率的TerraSAR卫星数据,联合Knothe时间函数[11-12]和概率积分模型对矿区动态形变进行建模,并利用回归分析方法建立矿区InSAR最大可检测动态形变梯度函数模型,为InSAR技术在矿区形变监测的应用提供理论指导。
1 方法本文联合Knothe时间函数和概率积分法对矿区动态形变进行预计。Knothe时间函数是研究开采沉陷动态发展规律的经典理论模型,目前在开采沉陷领域已有大量实际应用[13-14],其方程可表示为[15]:
| $ W\left( t \right) = {W_0}\left( {1 - {{\rm{e}}^{ - {\rm{i}}t}}} \right) $ | (1) |
式中,c为时间影响参数,本文采用崔希民等[11]的计算方法,取c=-v/Lln0.02;W0为该地表点的最终下沉值,单位m;W(t)为该地表点在时间t的瞬时下沉值,单位m。
本文结合概率积分法原理[16],利用式(1)对矿区地表下沉进行预计,在保证回采过程中开采速度一致(v1=v2=…=vn)的前提下得到以下预计公式:
| $ \left\{ \begin{array}{l} W\left( {x, t} \right) = \varphi \left( t \right)\left[ {W\left( x \right) - W\left( {x - } \right.} \right.\\ \;\;\;\left. {\left. {{v_1}{t_1}} \right)} \right] + \varphi \left( {t - {t_1}} \right)\left[ {W\left( {x - {v_1}{t_1}} \right) - } \right.\\ \;\;\;\left. {W\left( {x - {v_1}{t_1} - {v_2}{t_2}} \right)} \right] + \cdots + \\ \varphi \left( {t - {t_1} - {t_2} - \cdots - {t_{n - 1}}} \right)\left[ {W\left( {x - } \right.} \right.\\ \;\;\;\;\left. {{v_1}{t_1} - {v_2}{t_2} - \cdots - {v_{n - 1}}{t_{n - 1}}} \right) - W\left( {x - } \right.\\ \;\;\;\;\left. {\left. {{v_1}{t_1} - {v_2}{t_2} - \cdots - {v_n}{t_n}} \right)} \right] \end{array} \right. $ | (2) |
在得到预计下沉值后将其转换为SAR数据的干涉形变相位,并进行相位缠绕处理,得到对应的模拟干涉图,再经过最小费用流解缠步骤得到对应干涉SAR数据的形变监测值。最后,将形变监测值进行过滤获取MDDG值,过滤步骤为:
1) 以预计下沉值为真值,设置阈值为真值的0.1倍,计算形变监测值与真值的差值,并将差值在阈值之下的像元作为解缠正确像元。
2) 若相邻像元均为解缠正确像元,则计算两像元间的形变梯度(即InSAR可检测的形变梯度),形变梯度计算公式为:
| $ {G_{AB}} = \left( {\Delta {D_A} - \Delta {D_B}} \right)/\Delta r $ | (3) |
式中,GAB为相邻像元A、B间的形变梯度,ΔDA和ΔDB分别为像元A和B的形变值,Δr为像元边长。
3) 在获取大量MDDG值的基础上进行经验统计和回归分析,研究形变梯度(像元间下沉值之差与像元距离之比)与开采深度、采厚及下沉系数之间的关系。回归分析所建模型以相关系数为评价指标,设置相关系数阈值为0.8,通过回归分析得到适用于不同分辨率SAR数据的MDDG模型,图 1为技术流程。
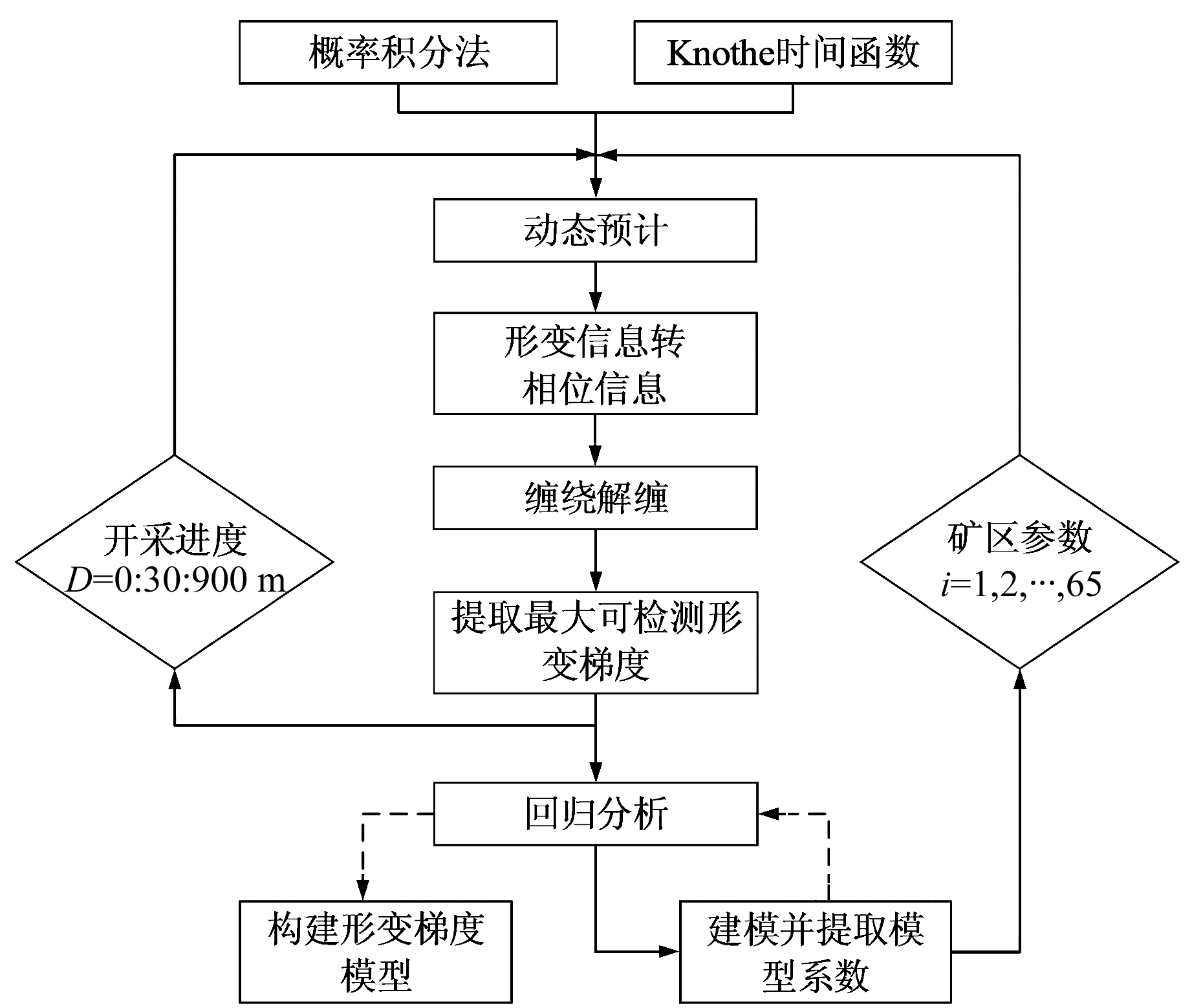
|
图 1 研究方法流程 Fig. 1 The flow chart of proposed method |
为保证选取参数的合理性,本文以文献[17]附录中给出的近水平煤层矿区参数为参考,在假定开采速度为0.92 m/d,工作面尺寸为长900 m、宽100 m不变的情况下,设置65组矿区参数(包括下沉系数q、开采深度H和开采厚度m)。表 1为部分矿区的参数选取情况。
|
|
表 1 部分矿区的参数选取 Tab. 1 Parameters selection of some mining areas |
实验过程中每开采30 m获取1次下沉值,采用Knothe时间函数动态预计开采距离在0~900 m的地表下沉情况。图 2为钱家营矿区开采过程中的地表形变情况,由于曲线过于密集,为便于分析,仅显示90 m间隔的下沉情况。

|
图 2 钱家营矿区开采过程中地表形变情况 Fig. 2 Surface deformation results during mining in Qianjiaying mining area |
从图 2可以看出,随着工作面的推进,最大下沉点位向前移动,地表下沉量也在不断增加,同时最大下沉值左侧形变梯度整体不断变大且趋于稳定,右侧形变梯度整体变小但影响范围不断扩大,进一步说明地表形变梯度随开采进度的变化而变化。
形变场生成后,通过相位反缠绕将其转换为TerraSAR卫星监测的干涉相位。图 3为不同开采进度下分辨率为1 m×1 m的TerraSAR差分干涉相位图,在相位转化过程中未加入地形相位和噪声,此时的相位信息只包含形变相位。由图可知,随着开采工作面的推进,形变范围不断变大,至开采结束时形变区域扩大为1 200 m×900 m。利用目视解译法可以看出,当开采进度为30 m时干涉条纹最为清晰,此后混叠区域逐步从中间向四周扩散,TerraSAR可检测的形变区域大多集中在矿区边缘位置。

|
图 3 不同开采阶段TerraSAR监测的干涉相位 Fig. 3 Interferometric phases monitored by TerraSAR during different mining stages |
对干涉相位进行相位解缠后得到形变信息,以式(2)得到的变形值为真值,按照图 1步骤提取不同下沉系数、开采深度及开采厚度下每个开采进度对应的MDDG值,共1 950个(65组矿区参数×30组干涉图),为后续回归分析提供数据基础。
1.2 函数模型建立 1.2.1 开采进度与MDDG的关系对1 950个MDDG值与对应开采进度进行回归分析,图 4为9个矿区的MDDG变化及拟合情况。从图中可以看出,各矿区回归模型的相关系数R均在0.95以上,且所有模拟结果中开采进度与MDDG值之间的关系具有一致性,可以用以下方程表示:
| $ y = a\left( {1 - \exp \left( { - bx} \right)} \right) $ | (4) |
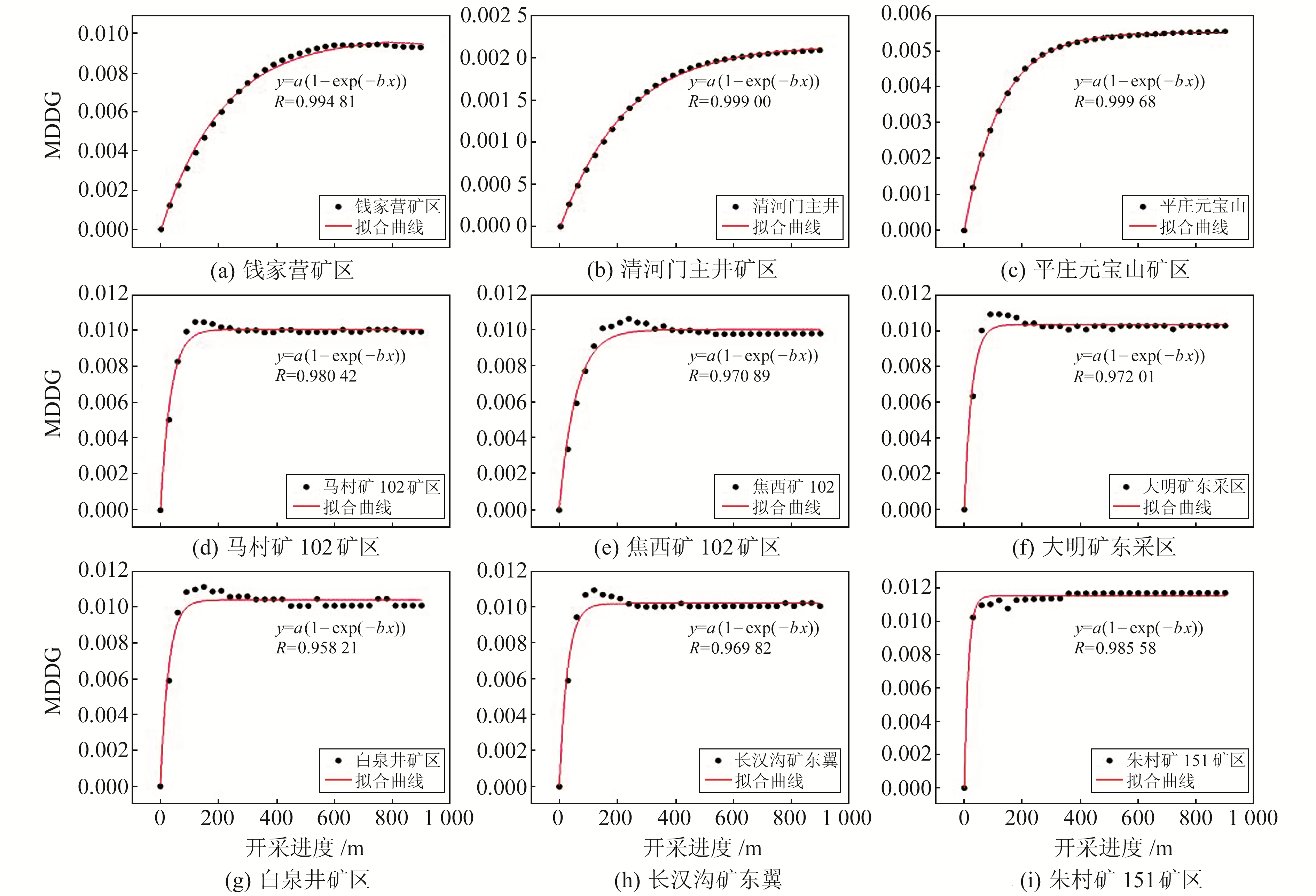
|
图 4 部分矿区动态开采过程中MDDG变化情况 Fig. 4 MDDG values during dynamic mining stages of some mining areas |
式中,y为MDDG值,x为开采进度,a、b为模型系数。
1.2.2 系数a、b与矿区参数的关系对65个矿区数据进行整理,分别统计开采深度相同、开采厚度相同或下沉系数相同但其余参数不同的矿区资料,通过固定参数法,利用回归分析研究系数a、b与其余参数的关系,分别得到开采深厚比及下沉系数与系数a之间的关系(图 5),下沉系数对系数b的影响较小(图 6),系数b仅与采深和采厚有关。图 7为开采深度及开采厚度与系数b的拟合结果。
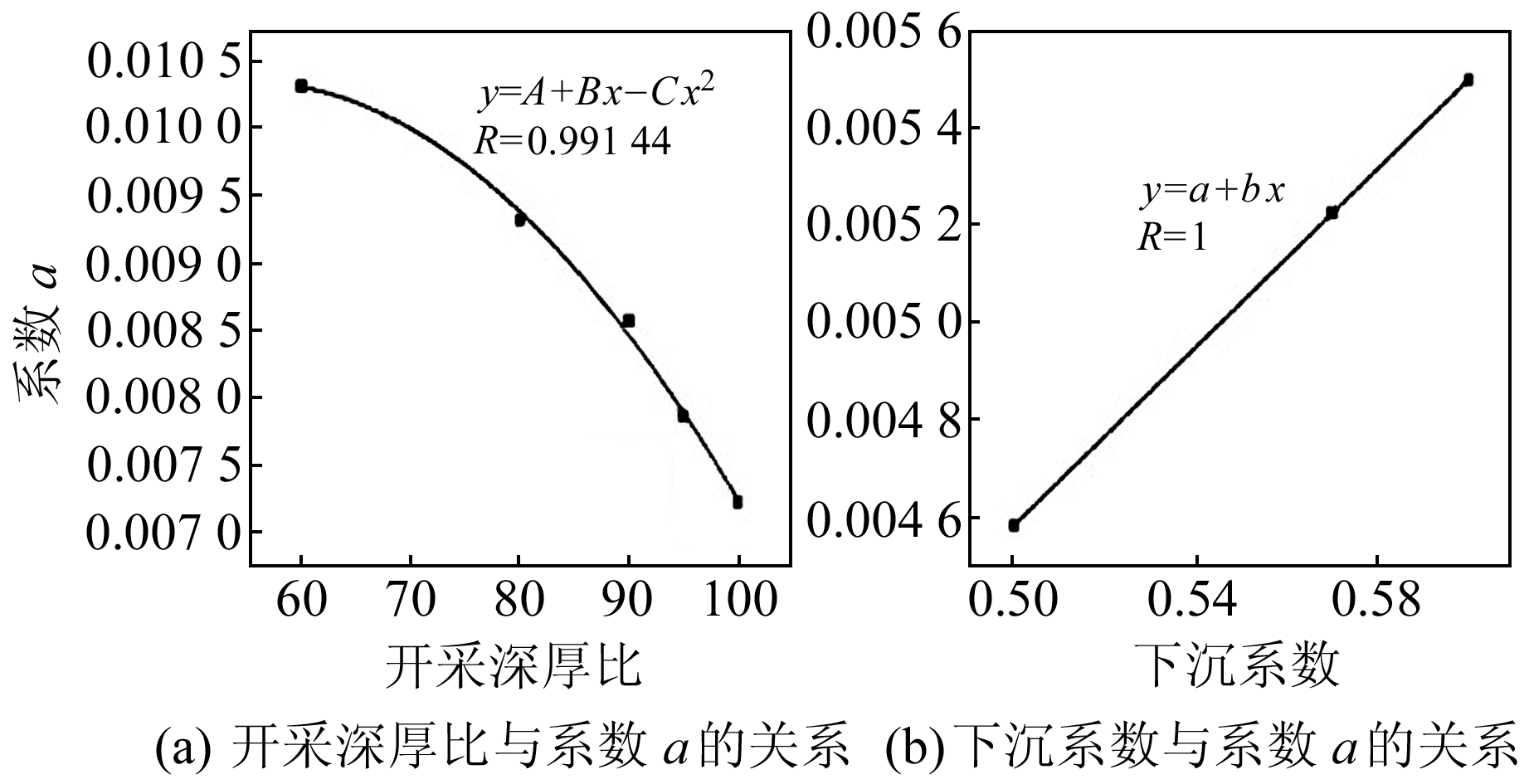
|
图 5 矿区参数与系数a的拟合情况 Fig. 5 Fitting results between mining parameters and coefficient a |
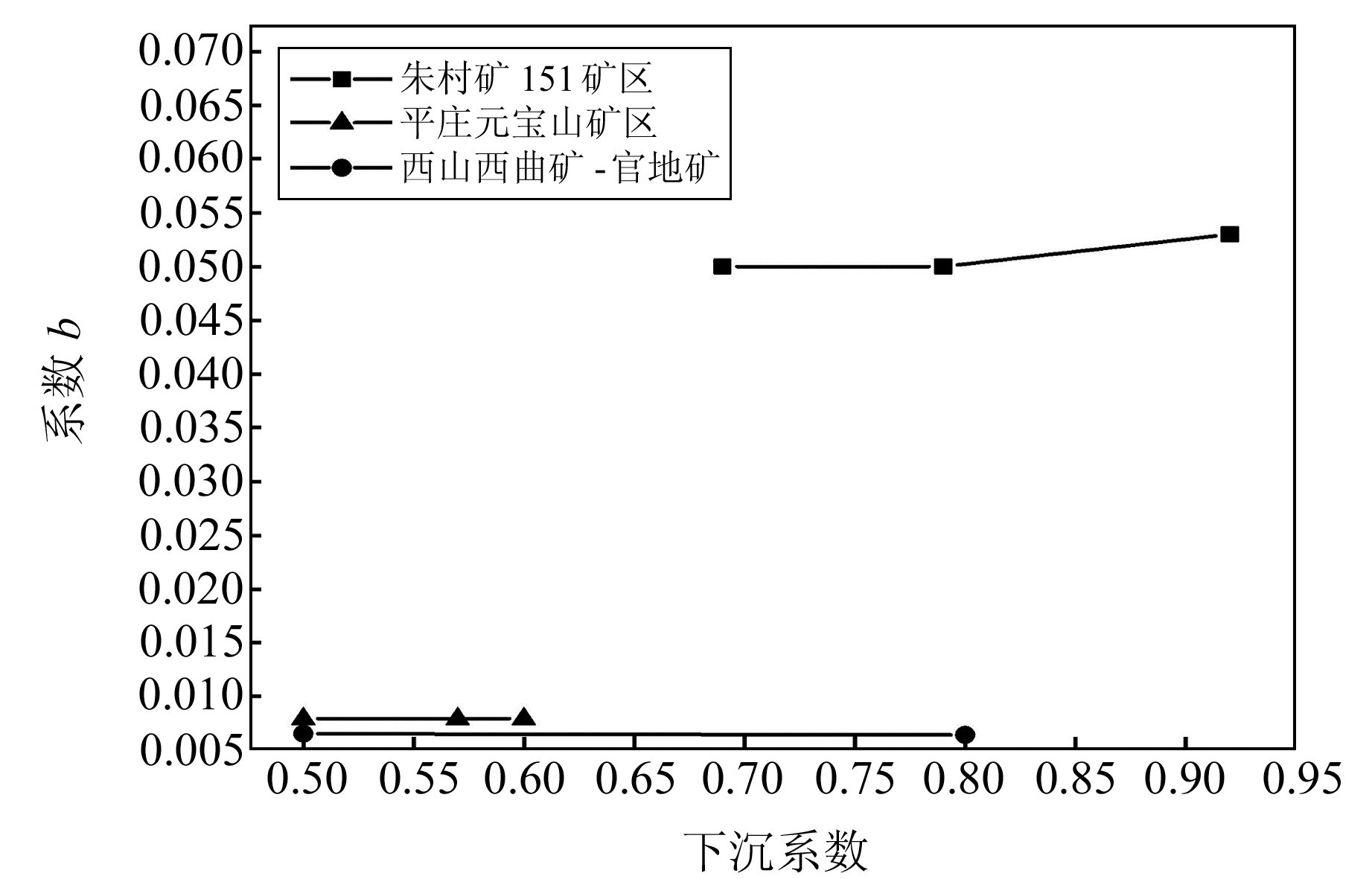
|
图 6 下沉系数与系数b之间的关系 Fig. 6 Relationship between subsidence coefficient and coefficient b |
|
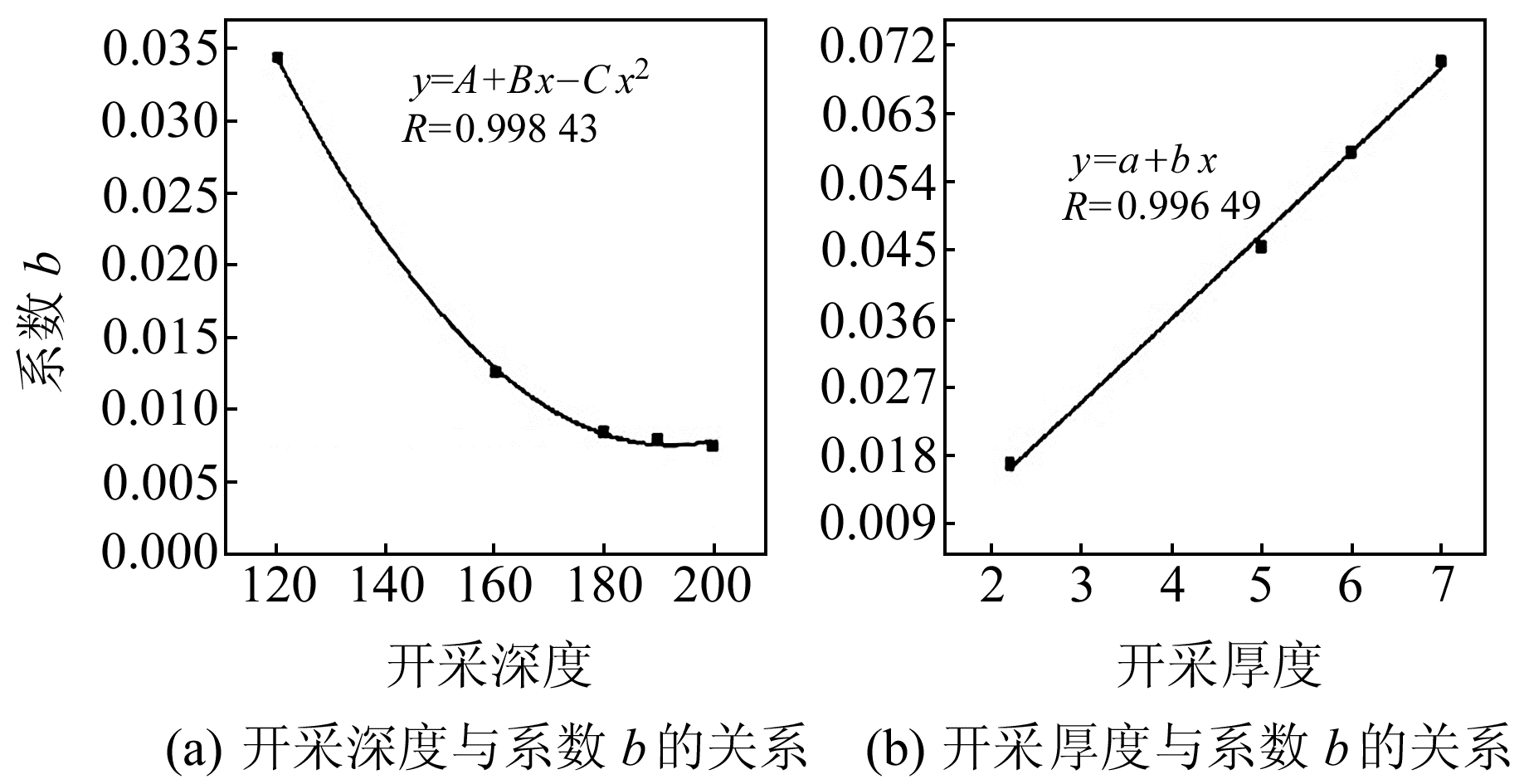
图 7 矿区参数与系数b的拟合情况 Fig. 7 Fitting results between mining parameters and coefficient b |
基于图 5的结果,对系数a与矿区参数之间的函数关系作出以下假设:
| $ a = Aq + B\left( {H/{m^2}} \right) + CH/{m^2} + D $ | (5) |
式中,q为下沉系数,H为开采深度,m为开采厚度,A、B、C、D为模型系数。
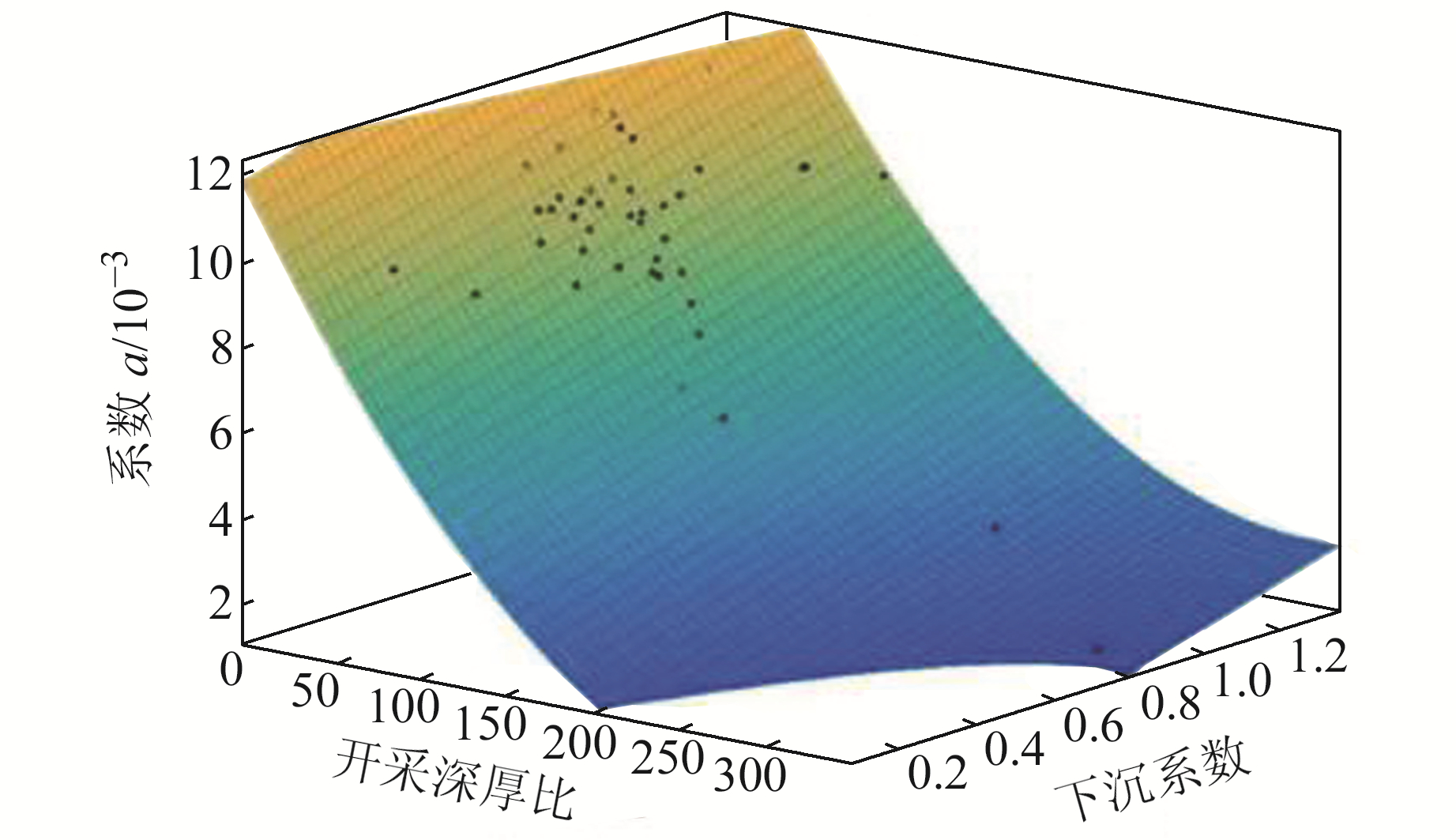
利用65个矿区数据对式(5)进行拟合分析,结果见图 8。由图可知,函数模型拟合效果显著,其相关系数为0.87,证明假设模型可以正确反映系数a与矿区参数之间的规律。式(5)中系数拟合结果为:A=2.738×10-3,B=1.105×10-7,C=-7.325×10-5,D=0.011。
|
图 8 假设模型的拟合结果 Fig. 8 Fitting result of hypothetical model |
从图 7可以看出,系数b与开采深度之间存在二次函数关系,与开采厚度之间存在线性关系。本文采用二次多项式拟合对三者关系进行回归分析,得到以下方程:
| $ \begin{array}{l} b = 0.086\;33 - 9.033 \times {10^{ - 4}}H + 0.023\;04m + \\ \;\;\;\;\;2.107 \times {10^{ - 6}}{H^2} - 7.641 \times {10^{ - 5}}Hm \end{array} $ | (6) |
结果显示,回归方程的相关系数达到0.91,说明该回归方程可以准确反映三者之间的关系。结合式(5)和式(6)可知,分辨率为1 m×1 m的TerraSAR数据最大可检测动态MDDG模型为:
| $ \begin{array}{c} {\rm{MDDG = }}\left( {2.738 \times {{10}^{ - 3}}q + 1.105} \right. \times {10^{ - 7}}\\ \left. {{{\left( {H/m} \right)}^2} - 7.325 \times {{10}^{ - 5}}H/m + 0.011} \right)\\ \left( {1 - \exp } \right.\left( { - \left( {0.086\;33 - 9.033 \times {{10}^{ - 4}}H} \right. + } \right.\\ 0.023\;04m + 2.107 \times {10^{ - 6}}{H^2} - \\ \left. {\left. {\left. {7.641 \times {{10}^{ - 5}}Hm} \right)x} \right)} \right) \end{array} $ | (7) |
利用同样方法可以得到分辨率为5 m×5 m的动态MDDG模型为:
| $ \begin{array}{c} {\rm{MDDG = }}\left( {2.738 \times {{10}^{ - 3}}q + 1.105 \times {{10}^{ - 7}}} \right.\\ {\left( {H/m} \right)^2} - 7.325 \times {10^{ - 5}}H/m + 0.011\\ \left( {1 - \exp \left( { - \left( {0.086\;33 - 9.033 \times {{10}^{ - 4}}H + } \right.} \right.} \right.\\ 0.023\;04m + 2.107 \times {10^{ - 6}}{H^2} - \\ \left. {\left. {\left. {7.641 \times {{10}^{ - 5}}Hm} \right)x} \right)} \right) \end{array} $ | (8) |
分辨率为10 m×10 m的函数模型为:
| $ \begin{array}{c} {\rm{MDDG = 0}}{\rm{.001}} \times \left( {1 - \exp } \right.\left( { - \left( {0.055\;2} \right. + } \right.\\ 3.454 \times {10^{ - 4}}H - 8.955 \times {10^{ - 3}}m - 1.6 \times {10^{ - 6}}\\ \left. {\left. {\left. {{H^2} + 5.647 \times {{10}^{ - 5}}Hm} \right)x} \right)} \right) \end{array} $ | (9) |
大柳塔煤矿位于陕西省神木县,其开采厚度约为6.94 m,开采深度为235 m,煤层倾角为1°~3°,属于近水平煤层,矿区地表随开采进度发生大梯度形变,最终形变量已超出InSAR技术可检测范围。研究区工作面平均开采速度为4 m/d,自2012-11底开采,至2013-04地表达到充分采动状态,下沉系数为0.67,选取动态开采66 d内7景TerraSAR-X和GPS数据验证动态模型的可靠性和精度,其中SAR影像参数见表 2,GPS监测资料来自矿区现场实测。沿工作面走向共布设50个GPS站点,点间距d为20 m,平面精度为10 mm+10-6d,高程精度为20 mm+10-6d。
|
|
表 2 实验所用SAR卫星参数 Tab. 2 SAR parameters used in the experiment |
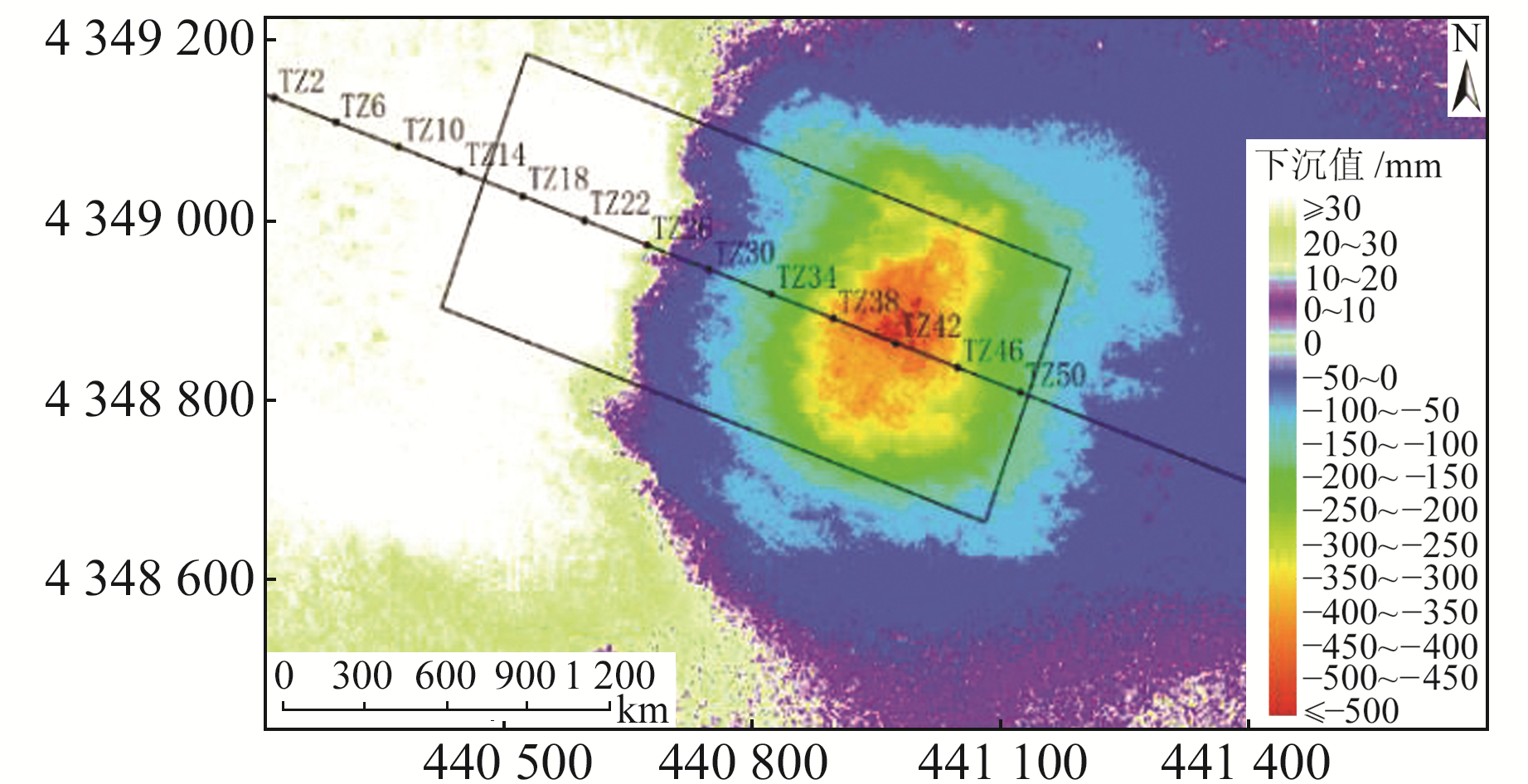
为减少时间失相关对SAR影像的影响,按照时间顺序依次进行差分干涉处理,得到6组干涉对:S1-S2、S2-S3、S3-S4、S4-S5、S5-S6、S6-S7,再依次进行累加得到时序形变结果。以2012-11-21~2013-01-26地表垂直沉降为例,具体结果见图 9。
|
图 9 开采66 d后地表沉降结果 Fig. 9 Result of surface subsidence after mining for 66 days |
本文所建模型包含1 m×1 m、5 m×5 m及10 m×10 m三种分辨率,而实际TerraSAR数据的分辨率为其近似值,且不同数据的分辨率尺寸也存在微小变化。为保证所建模型能够适用于SAR数据,需要对模型进行近似分辨率应用分析。由表 2可知,研究区SAR数据的分辨率与式(7)计算的模型(简称模型7)分辨率相近,故本文利用该数据对模型7进行分析。首先构建分辨率为0.861 m×0.909 m的MDDG模型,其公式为:
| $ \begin{array}{c} {\rm{MDDG = }}\left( {2.783 \times {{10}^{ - 3}}q + 1.3085 \times {{10}^{ - 7}}} \right.\\ \left. {{{\left( {H/m} \right)}^2} - 8.136 \times {{10}^{ - 5}}H/m + 1.177 \times {{10}^{ - 2}}} \right)\\ \left( {1 - \exp \left( { - \left( {7.057 \times {{10}^{ - 2}} - 6.813 \times {{10}^{ - 4}}H + } \right.} \right.} \right.\\ 1.657 \times {10^{ - 2}}m + 1.547 \times {10^{ - 6}}{H^2} - \\ \left. {\left. {\left. {5.5 \times {{10}^{ - 5}}Hm} \right)x} \right)} \right) \end{array} $ | (10) |
再利用式(7)和式(10)计算不同开采进度下模型的MDDG值(简称模型7和模型10),其相邻控制点的最大可检测形变差为MDDG与控制点间距(间隔20 m)的乘积,具体结果见表 3。
|
|
表 3 模型检测结果 Tab. 3 The detection results of the models |
通过表 3可以看出,模型7在近似分辨率检测中MDDG值最大不超过0.000 6,相邻控制点的最大可检测形变差不超过10 mm,2个模型的检测结果基本一致。因此,本文模型可用于近似模型分辨率下InSAR检测能力的预计。
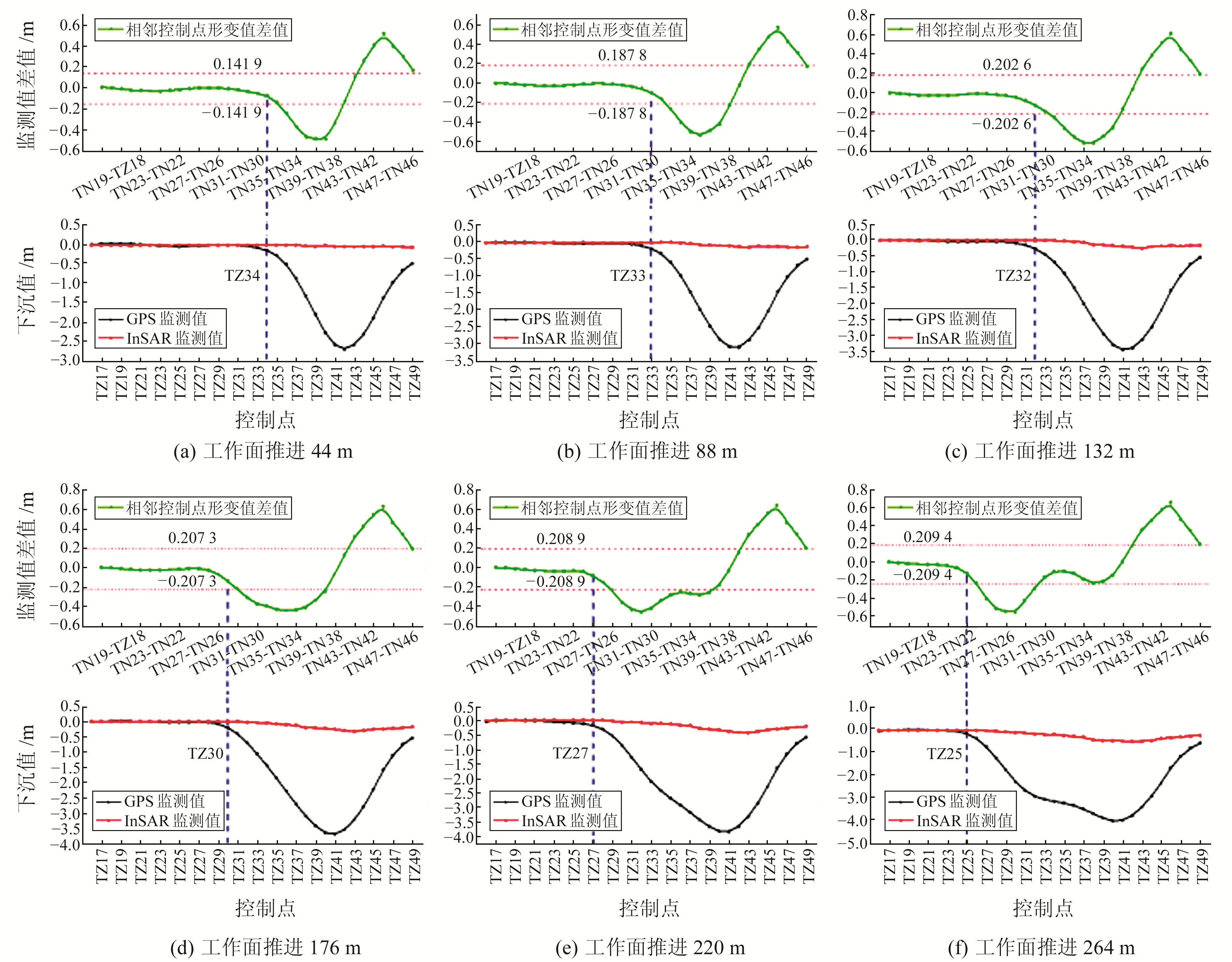
2.2 模型验证利用式(7)计算不同开采进度下InSAR的MDDG值,因为形变方向不同,形变梯度有正有负,所以模型计算的MDDG值为真实值的绝对值。将模型结果还原为实际MDDG后得到可检测区间,再以GPS监测值作为地表真实形变,若相邻GPS站点的形变差值(即形变梯度)落在模型判断区间内,则判定该区域可被InSAR检测;反之,则该区域不可被InSAR检测。由开采沉陷规律可知,地表最大沉降值的相邻控制点间的形变值差值趋近于0,该位置的监测值始终落在可检测区间内。判断中心点是否可被检测,需以相邻点的检测情况为准。可检测边界点的确定依据为边界点左右两边的相邻控制点形变值差值均在可检测区间内,动态模型的可检测预计情况如图 10所示,图中红色虚线为模型预计的InSAR可检测区间,蓝色虚线为由可检测区间转化的可检测边界。图 10子图上下2个横坐标代表的意义不同,子图上横坐标表示相邻控制点,子图下横坐标代表某一控制点,如子图(a),可检测边界经过的上横坐标值代表TZ33-TZ34,经过的下横坐标值代表TZ34。
|
图 10 动态模型的可检测预计情况 Fig. 10 Detectable predictions of the dynamic model |
由图 10可知,随着工作面的推进,地表下沉量不断增大,InSAR可检测边界向矿区边缘移动。地表沉降呈盆地状,因此靠近盆地中心位置形变梯度较大(盆地正中心除外),而盆地边缘形变梯度小,与实际监测情况一致。经检验,本文模型预测的可检测区间与实际InSAR检测区间相符,可为该技术在矿区的应用提供重要参考。
3 结语本文以65个矿区的地质采矿参数为基础,结合Knothe时间函数与概率积分法,利用TerraSAR参数模拟生成不同开采进度下的形变场,并采用回归分析方法建立适用于开采沉陷的InSAR最大可检测形变梯度模型。相较于其他形变梯度模型,该模型无需事先获取SAR影像,可减少人力物力资源的浪费,同时该模型首次实现动态开采过程中不同开采进度下MDDG的预计,应用范围更加广泛。将该模型应用于大柳塔矿区可准确预计InSAR在不同开采阶段的检测能力,从而验证了该模型的实用性,可为InSAR技术在矿区中的应用提供重要指导。
本文模型在建模时仅考虑了水平煤层,对于倾斜煤层的建模尚未涉及,并且受SAR数据源限制,仅使用TerraSAR数据建立InSAR的MDDG模型,而未考虑其他雷达卫星数据,这也是下一步研究工作的重点。
| [1] |
Li J C, Gao F, Lu J G. An Application of InSAR Time-Series Analysis for the Assessment of Mining-Induced Structural Damage in Panji Mine, China[J]. Natural Hazards, 2019, 97(1): 243-258 DOI:10.1007/s11069-019-03639-8
(  0) 0) |
| [2] |
Alam M S, Kumar D, Chatterjee R S, et al. Assessment of Land Surface Subsidence Due to Underground Metal Mining Using Integrated Spaceborne Repeat-Pass Differential Interferometric Synthetic Aperture Radar(DInSAR) Technique and Ground Based Observations[J]. Journal of the Indian Society of Remote Sensing, 2018, 46(10): 1569-1580 DOI:10.1007/s12524-018-0810-2
(  0) 0) |
| [3] |
Chen B Q, Deng K Z, Fan H D, et al. Combining SAR Interferometric Phase and Intensity Information for Monitoring of Large Gradient Deformation in Coal Mining Area[J]. European Journal of Remote Sensing, 2015, 48(1): 701-717
(  0) 0) |
| [4] |
Luo H B, Li Z H, Chen J J, et al. Integration of Range Split Spectrum Interferometry and Conventional InSAR to Monitor Large Gradient Surface Displacements[J]. International Journal of Applied Earth Observation and Geoinformation, 2019, 74: 130-137 DOI:10.1016/j.jag.2018.09.004
(  0) 0) |
| [5] |
Spagnolini U. 2-D Phase Unwrapping and Phase Aliasing[J]. Geophysics, 1993, 58(9): 1324-1334 DOI:10.1190/1.1443515
(  0) 0) |
| [6] |
Zebker H A, Villasenor J. Decorrelation in Interferometric Radar Echoes[J]. IEEE Transactions on Geoscience and Remote Sensing, 1992, 30(5): 950-959 DOI:10.1109/36.175330
(  0) 0) |
| [7] |
Massonnet D, Feigl K L. Radar Interferometry and Its Application to Changes in the Earth's Surface[J]. Reviews of Geophysics, 1998, 36(4): 441-500 DOI:10.1029/97RG03139
(  0) 0) |
| [8] |
Baran I, Stewart M, Claessens S. A New Functional Model for Determining Minimum and Maximum Detectable Deformation Gradient Resolved by Satellite Radar Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(4): 675-682 DOI:10.1109/TGRS.2004.843187
(  0) 0) |
| [9] |
Jiang M, Li Z W, Ding X L, et al. Modeling Minimum and Maximum Detectable Deformation Gradients of Interferometric SAR Measurements[J]. International Journal of Applied Earth Observation and Geoinformation, 2011, 13(5): 766-777 DOI:10.1016/j.jag.2011.05.007
(  0) 0) |
| [10] |
Wang Q J, Li Z W, Du Y N, et al. Generalized Functional Model of Maximum and Minimum Detectable Deformation Gradient for PALSAR Interferometry[J]. Transactions of Nonferrous Metals Society of China, 2014, 24(3): 824-832 DOI:10.1016/S1003-6326(14)63132-0
(  0) 0) |
| [11] |
崔希民, 缪协兴, 赵英利, 等. 论地表移动过程的时间函数[J]. 煤炭学报, 1999, 24(5): 453-456 (Cui Ximin, Miao Xiexing, Zhao Yingli, et al. Discussion on the Time Function of Time Dependent Surface Movement[J]. Journal of China Coal Society, 1999, 24(5): 453-456)
(  0) 0) |
| [12] |
崔希民, 陈立武. 沉陷大变形动态监测与力学分析[M]. 北京: 煤炭工业出版社, 2004 (Cui Ximin, Chen Liwu. Dynamic Monitoring and Mechanical Analysis of Subsidence Large Deformation[M]. Beijing: China Coal Industry Publishing House, 2004)
(  0) 0) |
| [13] |
王一, 张凯. 采动地表动态下沉的时间函数模型研究[J]. 煤矿开采, 2017, 22(5): 68-70 (Wang Yi, Zhang Kai. Study of Time Function Model of Surface Subsidence Dynamic under Mining[J]. Coal Mining Technology, 2017, 22(5): 68-70)
(  0) 0) |
| [14] |
Chen L, Zhang L G, Tang Y X, et al. Analysis of Mining-Induced Subsidence Prediction by Exponent Knothe Model Combined with InSAR and Leveling[J]. ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2018, Ⅳ-3: 53-59
(  0) 0) |
| [15] |
Kratzsch H. 采动损害及其防护[M]. 北京: 煤炭工业出版社, 1984 (Kratzsch H. Mining Damage and Its Protection[M]. Beijing: China Coal Industry Publishing House, 1984)
(  0) 0) |
| [16] |
何国清, 杨伦, 凌赓娣, 等. 矿山开采沉陷学[M]. 徐州: 中国矿业大学出版社, 1991 (He Guoqing, Yang Lun, Ling Gengdi, et al. Mining Subsidence[M]. Xuzhou: China University of Mining and Technology Press, 1991)
(  0) 0) |
| [17] |
国家煤炭工业局. 建筑物, 水体, 铁路及主要井巷煤柱留设与压煤开采规程[M]. 北京: 煤炭工业出版社, 2000 (State Bureau of Coal Industry. Rules of Coal Pillar Design and Pressure Coal Mining in Buildings, Water Bodies, Railways and Main Shafts[M]. Beijing: China Coal Industry Publishing House, 2000)
(  0) 0) |
2. Hunan Province Key Laboratory of Coal Resources Clean-Utilization and Mine Environment Protection, Hunan University of Science and Technology, Taoyuan Road, Xiangtan 411201, China
 2020, Vol. 40
2020, Vol. 40


