随着现代空间大地观测技术(如GNSS、SLR、VLBI等)和数据处理分析能力的日益提高,各种环境因素变化对大地测量要素时间序列的影响有必要进行研究。许多学者对大气、土壤水、陆地水和非潮汐负荷等环境负荷影响规律进行研究[1-3],但在研究环境负荷变化引起的地表位置变化影响时,通常忽略了环境中温度变化对测站位置变化的影响。
温度变化会产生热胀冷缩效应,从而引起地面构筑物和地壳表面基岩位置产生年周期性变化,垂直方向表现更为显著。近年来,随着观测技术的提升、连续观测数据的积累和对观测精度的高要求,部分学者开始研究温度变化对地壳三维位移及GNSS观测站垂向位移的影响[4-7]。基于前人的研究成果,本文采用气象站实测地表温度数据分析温度变化对我国新疆区域GNSS连续运行基准站垂向形变的影响,为对比温度变化与其他环境负荷对基准站周年位移的影响,结合大气负荷变化综合分析温度变化对基准站垂向形变的影响规律。
1 温度变化对垂向形变影响的物理模型地表温度变化对GNSS基准站垂直方向位移的影响,包括对地上观测墩的线性热膨胀影响和测站处基岩热传导影响两部分。GNSS基准站天线安装在混凝土观测墩顶部,既可增强观测墩稳定性,又可减小太阳光直射影响。采用地表温度变化代替观测墩周围空气温度变化,温度变化导致地面观测墩产生热胀冷缩效应,引起观测墩垂向长度季节性变化,其变化长度Δd与温度变化呈线性关系:
| $ \Delta d = \alpha \cdot h \cdot \left[ {T\left( t \right) - \bar T} \right] $ | (1) |
式中,h为地面观测墩高度,T(t)为t时刻温度,T为年平均温度值(温度变化量基准值),α=1.2×10-5为线性热膨胀系数[6]。
地表温度变化通过热传导方式引起测站底部基岩温度发生变化,导致GNSS基准站垂向位移产生年周期性变化。假设各测站所处地壳基岩为相同的均匀介质,具有相同的热传导规律,地表温度变化引起的测站基岩不同深度(向下为正)的温度变化可根据一维各向热传导方程表示为:
| $ \frac{{\partial T}}{{\partial t}} = k\frac{{{\partial ^2}T}}{{\partial {z^2}}} $ | (2) |
式中,k为均匀介质热扩散系数,与时间t和深度z(z≥0)无关;T为地表温度。T与z的边界关系公式为:
| $ \left\{ \begin{array}{l} T = \bar T + \sum\limits_{i = 1}^N {{A_i}{\rm{cos}}({\omega _i}t - {\varphi _i})} , z = 0\\ {\rm{ }}T = \bar T, z \to \infty \end{array} \right. $ | (3) |
式中,T为年平均温度值,当z=0时将地表温度变化时间序列进行Fourier谐波拟合;N为温度变化拟合谐波个数;Ai、ωi和φi为第i个谐波的振幅、角频率和初始相位[6]。
地表温度变化对GNSS连续运行基准站基岩垂向形变影响的计算公式为:
| $ \Delta h\left( t \right) = \frac{{1 + \nu }}{{1 - \nu }}\alpha \sum\limits_{i = 1}^N {{A_i}} \sqrt {\frac{k}{{{\omega _i}}}} {\rm{cos}}({\omega _i}t - \frac{{\rm{ \mathsf{ π} }}}{4} - {\varphi _i}) $ | (4) |
式中,ν为弹性介质泊松比,根据基岩类型取值0.17~0.25(如混凝土和钢材质典型值为0.2)[5]。由余弦初相可以看出,温度变化对基准站基岩垂向形变的影响相对于地表温度变化相位具有滞后性。
2 温度变化对GNSS连续运行基准站垂向形变的影响 2.1 数据整理采用中国大陆构造环境监测网络(简称“陆态网络”)位于新疆境内的GNSS连续运行基准站数据,观测时间跨度为2011~2016年,均具有超过1 a以上的连续观测记录,质量良好。通过GAMIT/GLOBK软件10.60版本进行解算,得到测站三维坐标时间序列;对坐标时间序列进行粗差剔除、移除线性趋势项、扣除平均值等处理,得到测站坐标季节性变化的时间序列。
温度变化数据采用中国地面气候资料日值数据集(V3.0)中地表 0 cm温度数据。该数据集包含中国地面824个国家级基准站和基本站自1951-01以来的气压、气温、降水量、蒸发量、相对湿度、风向风速、日照时数和0 cm地温要素日值数据。GNSS基准站与区域内气象站分布情况如图 1所示(GNSS基准站附近均有气象站分布),为更好地表征测站处温度变化,通过距离平方反比内插得到GNSS基准站温度变化时间序列。
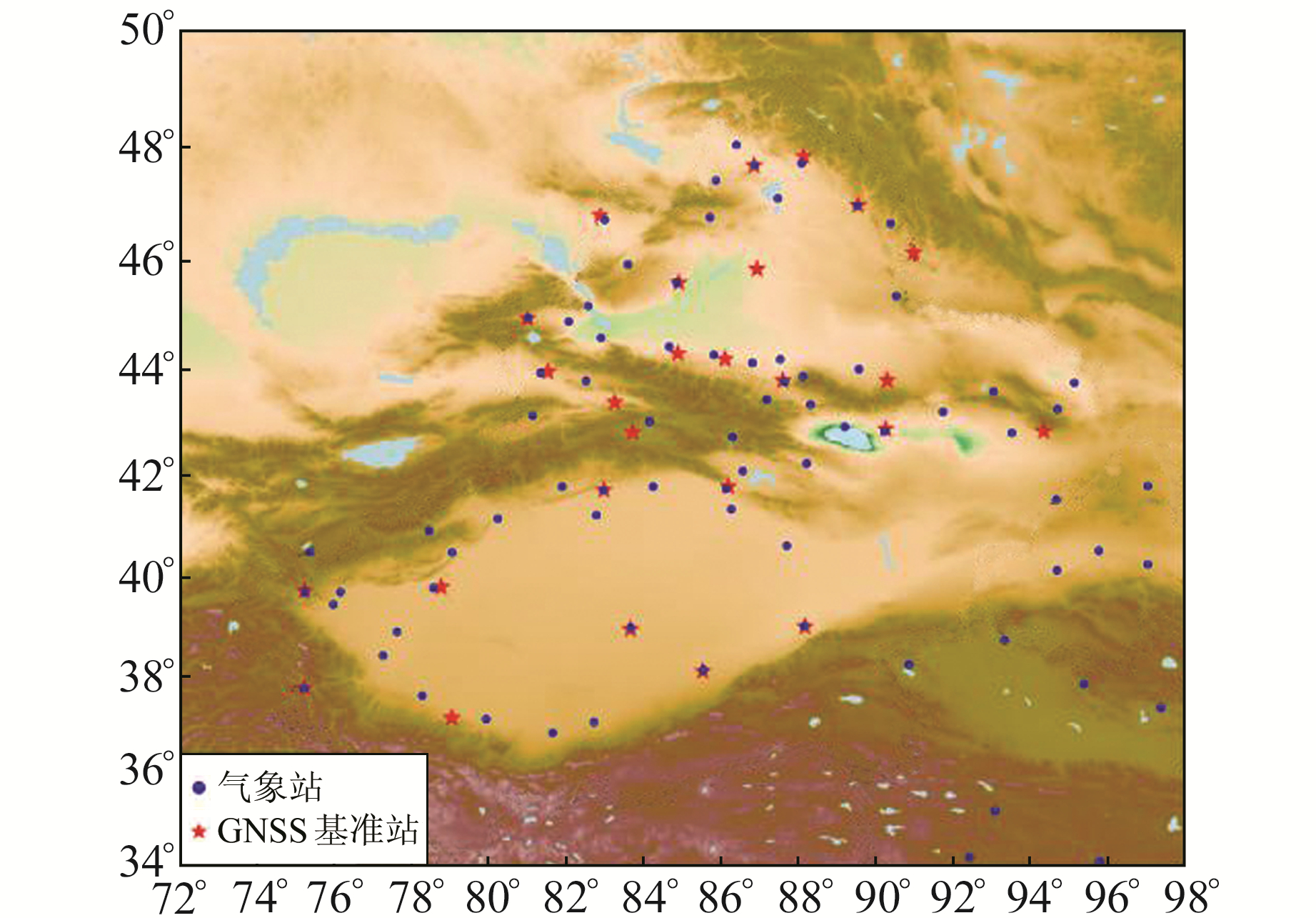
|
图 1 气象站与GNSS连续运行基准站分布 Fig. 1 Distribution of meteorological stations and GNSS continuously operating reference stations |
区域内2015-12~2016-01气象站观测数据缺失,在生成温度变化时间序列时导致GNSS基准站温度变化数据缺失。采用Fourier拟合方法,考虑周年和半周年周期变化项对温度变化时间序列进行拟合处理,将拟合值作为缺失日期的观测值。补全后XJML测站温度变化时间序列如图 2所示,从图中可以看出,补全值与观测值变化趋势具有良好的一致性,符合实际温度的变化趋势。
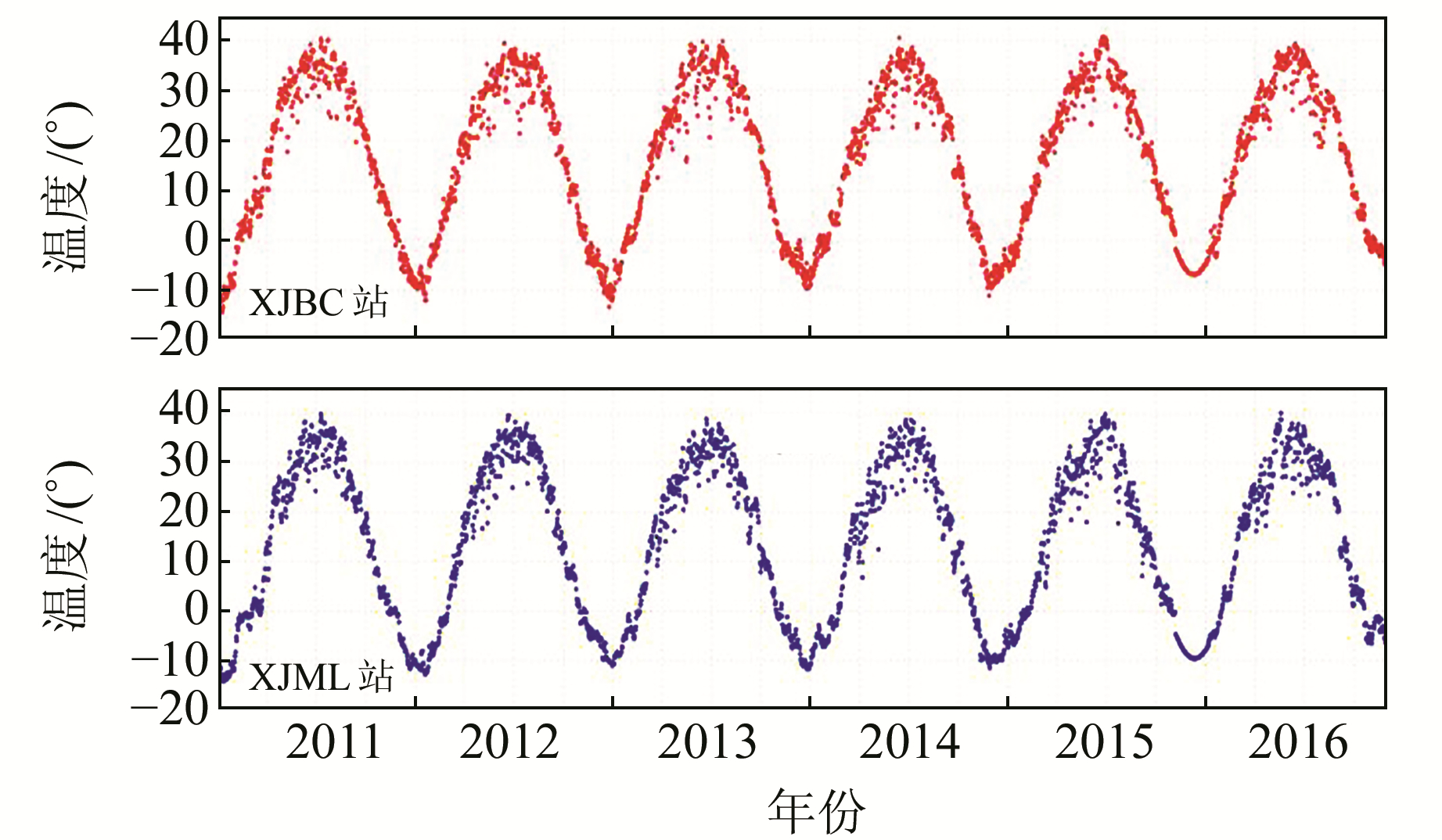
|
图 2 GNSS基准站地表温度变化时间序列 Fig. 2 Time series of surface temperature of GNSS reference stations |
陆态网GNSS基准站天线安装在观测室屋顶上方突出的观测墩顶部。为简化计算,将观测墩高度统一设定为h=4 m,T为2011年平均温度,采用式(1)计算地表温度变化对地面观测墩垂向形变的影响。结果表明,温度变化对观测墩影响的年变化量(影响量最大值减去最小值)约为1.6~2.0 mm。由于观测墩高度与温度对其垂向变化影响呈正相关,当观测墩较高时,温度变化对垂向位移的影响较大。
对地表温度变化时间序列进行Fourier谐波拟合,温度变化中周年项为主要部分,占比约85%~95%;半周年项占比约5%~15%,以下分析仅考虑周年项和半周年项。根据基岩类别确定弹性介质泊松比ν=0.2,采用式(4)计算温度变化对基岩垂向形变的影响。
采用Fourier拟合计算温度变化对基岩垂向形变的影响,拟合模型为:
| $ \begin{array}{l} y = {a_0} + {A_{周年}}{\rm{cos}}({\omega _{周年}}t + {\varphi _{周年}}) + \\ \;\;\;\;\;\;\;{A_{半周年}}{\rm{cos}}({\omega _{半周年}}t + {\varphi _{半周年}}) \end{array} $ | (5) |
式中,A、ω和φ分别为振幅、角频率和初始相位(简称初相);a0为常数项。表征拟合模型与原序列拟合度的R2均大于0.9。结果表明,温度变化对基岩垂向形变影响周年项振幅为0.65~1.01 mm,半周年项振幅为0.01~0.21 mm(约为周年项振幅10%),与文献[6]结果一致。
将温度变化对观测墩和基岩的影响相加,得到温度变化对GNSS基准站的影响(图 3)。
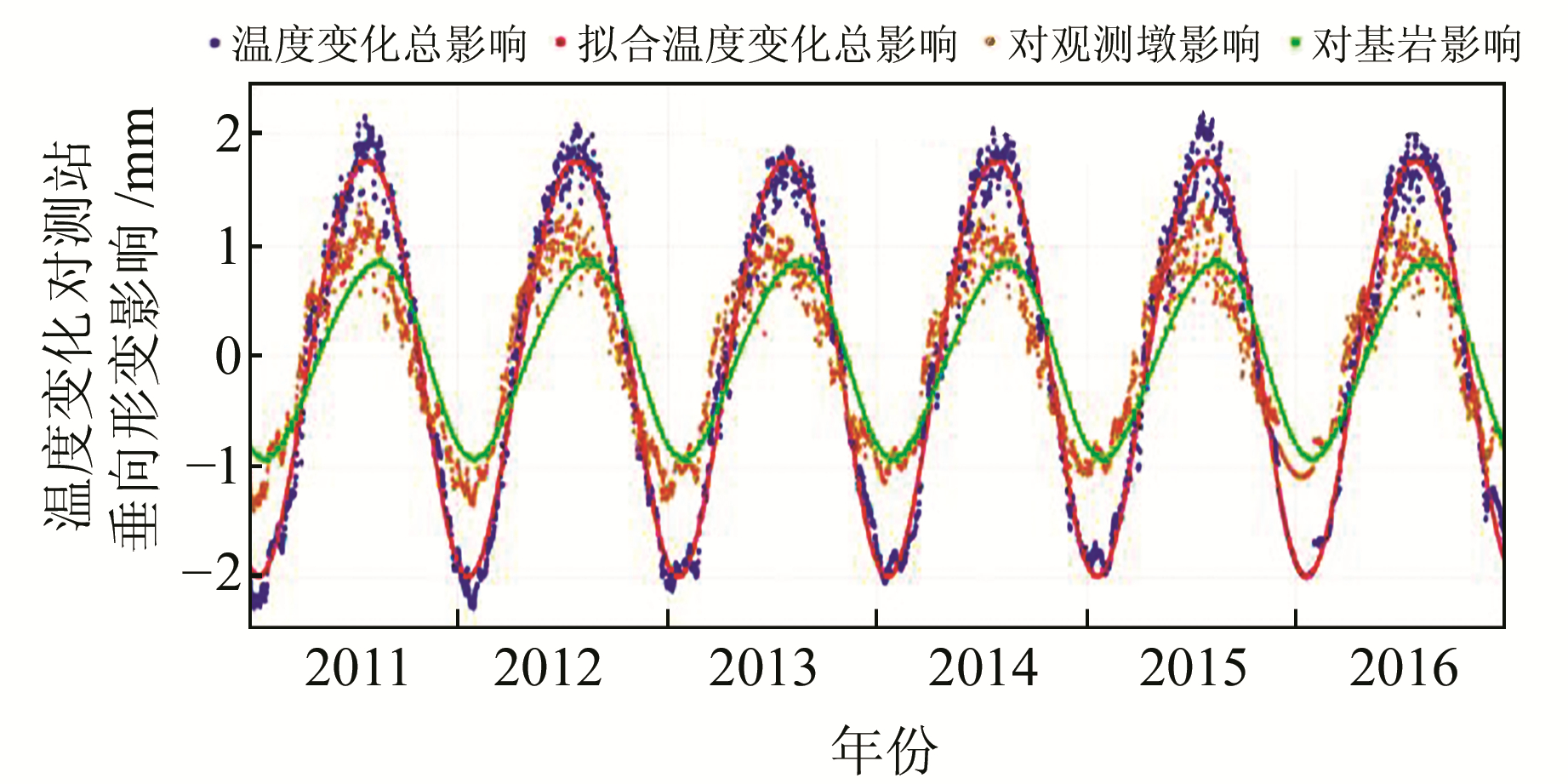
|
图 3 温度变化对XJDS站垂向形变的影响 Fig. 3 Influence of temperature change on vertical deformation of XJDS station |
针对温度变化对基准站垂向形变影响的时间序列,考虑周年和半周年周期变化进行Fourier拟合,得到周年项周期约为365 d,半周年项周期约为183 d。周年项振幅为1.4~2.1 mm,周年项初相为20.3~21.5 rad,站点间基本一致;半周年项振幅为0.01~0.33 mm,半周年项振幅约为周年项振幅的7%,统计结果见表 1。
|
|
表 1 温度变化对GNSS基准站垂向形变影响统计 Tab. 1 Statistics of influence of temperature change on vertical deformation of GNSS reference stations |
为更好地分析温度变化对GNSS基准站垂向形变的影响,统计移除温度变化影响前后的GNSS基准站垂向时间序列的RMS值,结果见表 2。从表中可以看出,24个测站RMS值减小,站点平均减小0.55 mm,减小量占比约9%;RMS值最大减小量为XJDS测站的0.84 mm,减小量占比约13%。温度变化对测站垂向形变的影响与测站垂向位置变化具有相同的变化趋势和相关性,说明温度变化是造成垂向位置季节性变化的影响因素之一,需考虑其影响。
|
|
表 2 GNSS基准站移除温度和大气负荷影响前后RMS统计 Tab. 2 RMS statistics before and after removal temperatureand atmospheric load effects of GNSS reference stations |
大气负荷变化为非构造形变影响的主要因素[1]。利用ECMWF提供的全球再分析日值数据,采用球谐系数法研究大气负荷变化(相对于2011年平均值,与温度影响的时间基准一致)对GNSS连续运行基准站垂向形变的影响[8-9](图 4)。结果表明,大气负荷对测站垂向形变的影响年变化量约为12~18 mm,上半年呈上升趋势,下半年呈下降趋势,与测站垂向位置变化和温度变化对基准站垂向位移的影响趋势基本一致。
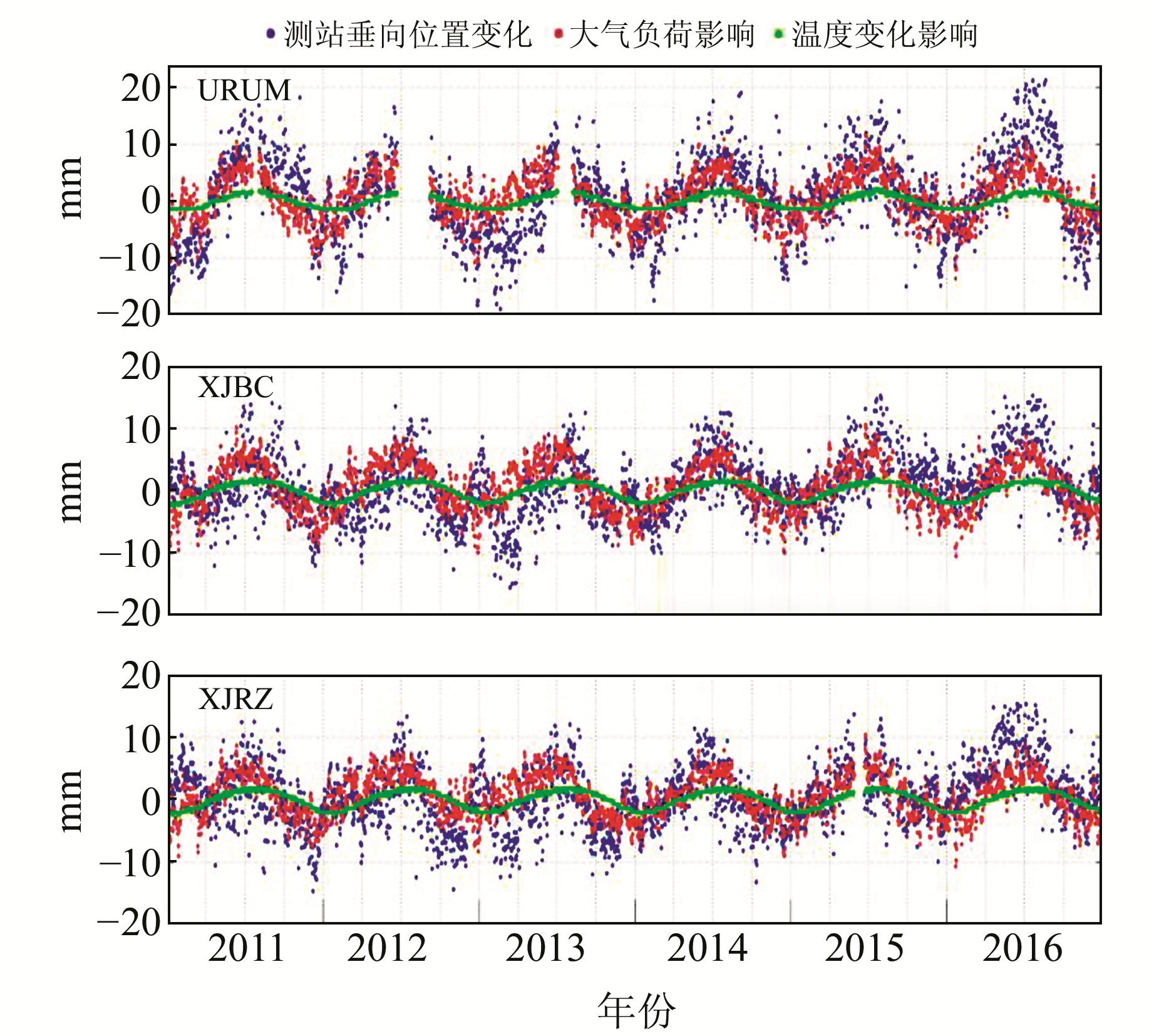
|
图 4 大气负荷和温度变化对GNSS基准站的影响 Fig. 4 Effect of atmospheric load and temperature change on GNSS reference stations |
23个测站垂向时间序列在移除大气负荷影响后RMS值减小,平均减小量约为0.75 mm,占比约12%,结果见表 2(单位mm)。TASH、XJKC和XJWU测站分别移除温度和大气负荷影响后RMS值小幅增大,从图 5可以看出,基准站垂向时间序列呈现发散无序形态,周期性变化不明显,可能导致移除温度和大气负荷影响后RMS增大。TASH测站存在异常,可能与该测站受到当地复杂环境因素影响有关[6]。
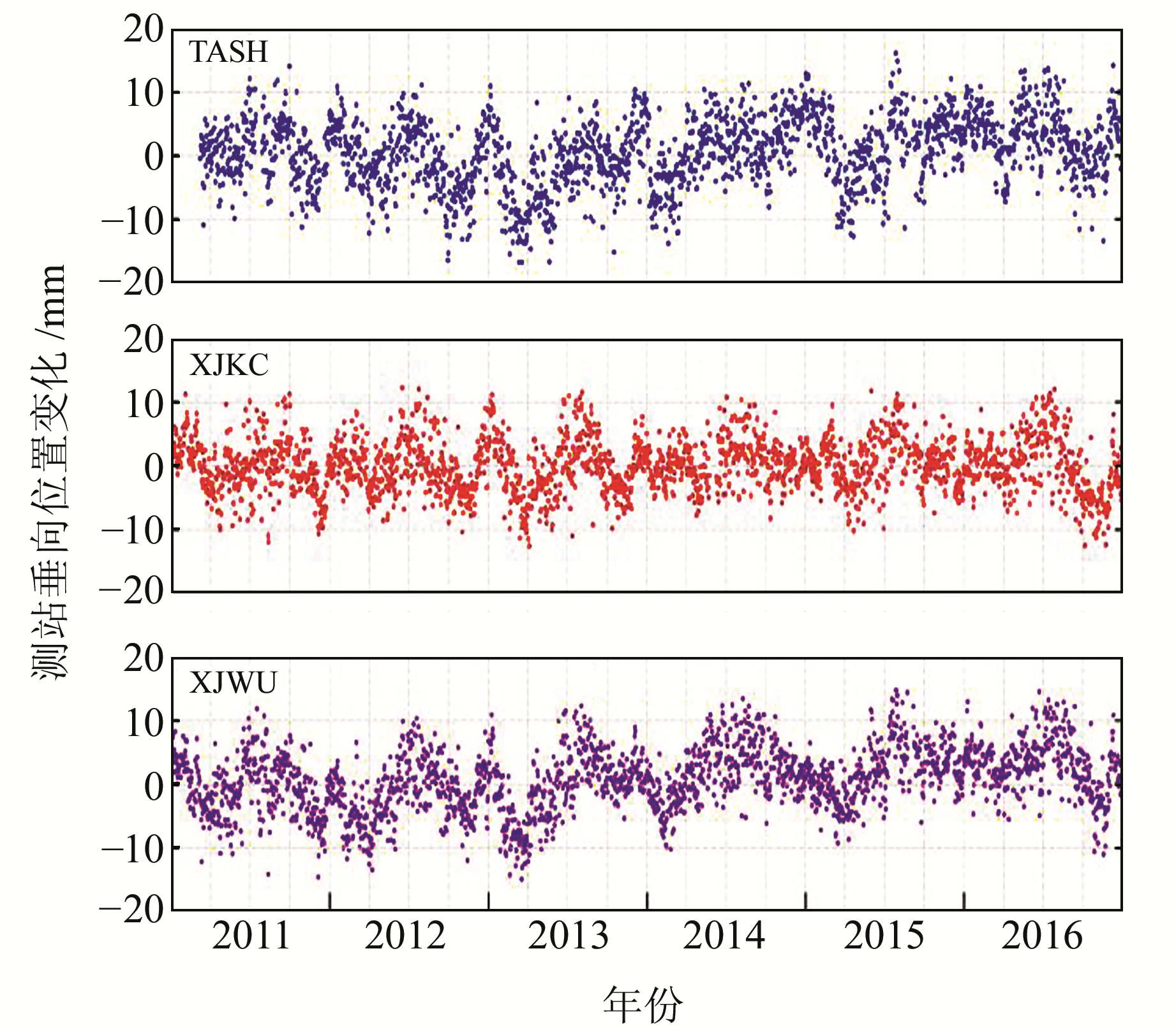
|
图 5 TASH、XJKC和XJWU测站垂向位置时间序列 Fig. 5 Vertical position time series of TASH, XJKC and XJWU stations |
统计分析GNSS基准站垂向时间序列同时移除温度和大气影响前后的RMS值变化,20个测站RMS值减小,平均减小0.82 mm,占比约13%,说明移除温度变化影响对改善测站垂向位置变化具有正反馈,考虑温度变化、大气负荷影响可进一步改善测站垂向位置变化。个别测站在分别移除温度和大气影响后RMS值降低,但同时移除会出现小幅增大,说明测站垂向位置变化会受到多种因素的综合影响,时间序列的复杂性表明各影响因素对垂向时间序列的影响机理和过程还需进一步研究。
3 结语采用中国地面气候资料日值数据集中地表温度变化数据,计算2011~2016年地表温度变化对新疆区域部分GNSS连续运行基准站垂向位移的影响,联合大气负荷变化分析温度变化对基准站垂向位置变化的影响。结果表明,温度变化对基准站垂向位置影响的周年项振幅为1.4~2.1 mm,半周年项振幅为0.01~0.33 mm,周年项振幅占主要部分。统计分析基准站垂向位置变化时间序列在移除温度变化影响前后的RMS值,24个测站RMS减小,平均减小量约为0.55 mm,精度提高约9%,表明移除温度变化影响可以改善GNSS基准站垂向位置变化。统计测站垂向位置变化时间序列同时移除温度和大气负荷变化影响前后的RMS值,20个测站RMS减小,平均减小0.82 mm,精度提高约13%,表明移除温度变化影响对改善测站垂向位置变化具有正反馈。考虑温度变化可更好地解释测站垂向位置时间序列的周期性变化,表明温度是除环境负荷因素外影响GNSS基准站垂向年周期形变的重要环境因素之一。
| [1] |
罗少聪.大气负荷效应问题研究[D].武汉: 中国科学院测量与地球物理研究所, 2003 (Luo Shaocong. Study on the Loading Effects of the Atmospheric Pressure[D]. Wuhan: Institute of Geodesy and Geophysics, CAS, 2003)
(  0) 0) |
| [2] |
朱钰.江河湖库水负荷对地壳形变和重力场变化影响研究[D].兰州: 兰州交通大学, 2018 (Zhu Yu.Study on the Influence of Crustal Deformation and Gravity Field Change Caused by Rivers, Lakes and Reservoirs[D].Lanzhou: Lanzhou Jiaotong University, 2018)
(  0) 0) |
| [3] |
王敏, 沈正康, 董大南. 非构造形变对GPS连续站位置时间序列的影响和修正[J]. 地球物理学报, 2005, 48(5): 1045-1052 (Wang Min, Shen Zhengkang, Dong Danan. Effects of Non-Tectonic Crustal Deformation on Continuous GPS Position Time Series and Correction to Them[J]. Chinese Journal of Geophysics, 2005, 48(5): 1045-1052)
(  0) 0) |
| [4] |
Dong D, Fang P, Bock Y, et al. Anatomy of Apparent Seasonal Variations from GPS-Derived Site Position Time Series[J]. Journal of Geophysical Research: Solid Earth, 2002, 107(B4)
(  0) 0) |
| [5] |
Yan H M, Chen W, Zhu Y Z, et al. Contributions of Thermal Expansion of Monuments and Nearby Bedrock to Observed GPS Height Changes[J]. Geophysical Research Letters, 2009, 36(13)
(  0) 0) |
| [6] |
闫昊明, 陈武, 朱耀仲, 等. 温度变化对我国GPS台站垂直位移的影响[J]. 地球物理学报, 2010, 53(4): 825-832 (Yan Haoming, Chen Wu, Zhu Yaozhong, et al. Thermal Effects on Vertical Displacement of GPS Stations in China[J]. Chinese Journal of Geophysics, 2010, 53(4): 825-832)
(  0) 0) |
| [7] |
Xu X Q, Dong D N, Fang M, et al. Contributions of Thermoelastic Deformation to Seasonal Variations in GPS Station Position[J]. GPS Solutions, 2017, 21(3): 1265-274 DOI:10.1007/s10291-017-0609-6
(  0) 0) |
| [8] |
王伟, 章传银, 杨强, 等. 大气负荷对区域地壳形变和重力变化的影响分析[J]. 武汉大学学报:信息科学版, 2018, 43(9): 1302-1308 (Wang Wei, Zhang Chuanyin, Yang Qiang, et al. Impact of Atmospheric Pressure Loading on Regional Crustal Deformation and Gravity Change[J]. Geomatics and Information Science of Wuhan University, 2018, 43(9): 1302-1308)
(  0) 0) |
| [9] |
王海涛, 王斌, 王伟, 等. 大气负荷对新疆地区地壳形变和地面重力变化的影响[J]. 大地测量与地球动力学, 2019, 39(2): 189-194 (Wang Haitao, Wang Bin, Wang Wei, et al. Research on the Effect of Atmospheric Pressure Load on Crust Deformation and Gravity Change in Xinjiang Region[J]. Journal of Geodesy and Geodynamics, 2019, 39(2): 189-194)
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40

