2. 武汉大学测绘学院,武汉市珞喻路129号,430079
GNSS多路径误差和随机误差与卫星中卫星钟误差、星历误差、电离层误差和对流层误差等不同,难以通过差分技术进行消除或削弱,也无法直接建立误差改正模型进行改正,是影响GNSS定位精度的主要因素[1]。因此,GNSS观测值的多路径误差和随机误差改正成为GNSS研究的难点与热点[2]。国内外部分学者[3-4]通过小波变换提取出观测值中GNSS多路径误差成分,并将其用于观测值改正,结果表明小波变换可用来削弱GNSS测量中多路径误差的影响。文献[5]和[6]确立了EMD方法分解级数的标准,并将其用来区分噪声和信息成分,可有效实现GPS多路径效应的提取。但是,EMD也存在一些不足,如缺少足够的理论支撑,存在端点效应、模态混叠等问题,这些都需要进行改进[7]。王琰等[8]对地面连续运行参考站(CORS)的多路径误差改正进行研究,建立改正经验公式,将定位精度提高30%。2013年,Gilles[9]针对经验模态分解存在端点效应、模态混叠等不足,结合小波变换的优势,提出经验小波变换(EWT)。EWT能自适应地将复杂混合信号分解成具有物理意义的分量信号,可较好地避免经验模态分解中端点效应、模态混叠现象的出现。近年来,EWT多被应用于机械故障信号分析及信号去噪,证实EWT能较好地分析复杂信号,但该方法目前在多路径误差改正领域还未得到应用。
鉴于EWT在复杂信号分析上的优势,利用GNSS观测数据中多路径误差的周日重复性特点,提出基于EWT的GNSS多路径误差改正新方法。首先利用EWT将原始信号分解成若干个经验小波函数分量,利用筛选系数将经验小波函数分量细化为含噪分量和信息分量;然后利用小波阈值算法对混合分量进行滤波,得到其含有的有用信息,与信息分量进行重构得到多路径误差改正模型,实现GNSS数据的多路径误差改正;最后利用模拟数据及GNSS实测数据验证新方法的可行性及有效性。
1 多路径误差模型提取方法的建立 1.1 基于能量熵和相关系数的含噪分量判定标准能量熵[10]值是反映信号规律性的一种指标,其值越小表明信号规律性越强。一般噪声的随机性较强而规律性较弱,因此,信号中有用成分的能量熵值小,而随机噪声的能量熵值大。相关系数是一种体现变量之间相关程度的统计指标,其取值范围为[-1, 1],数值越大表示两个变量之间的相关程度越高。
为更有效地筛选出噪声成分,结合能量熵H、相关系数R的概念,构造新的筛选系数S,其计算方式定义如下:
| $ S = \frac{H}{R} $ | (1) |
在含噪信号经EWT分解后得到的从高频到低频依次排列的若干个分量中,S发生突变时对应的函数分量为临界分量,将其之前的分量作为含噪分量。
1.2 数据去噪及多路径误差模型提取过程观测数据去噪及GNSS多路径误差模型提取步骤如下:
1) 将GNSS原始观测值通过EWT方法分解成若干个EWT分量;
2) 利用筛选系数将经验小波函数分量分解成含噪分量和信息分量;
3) 利用小波阈值算法对含噪分量进行滤波得到其含有的有用信息,并与信息分量进行重构实现GNSS观测数据去噪;
4) 将去噪后的GNSS观测值作为多路径误差;
5) 将后续相邻天的GNSS观测值减去EWT提取的多路径误差,实现GNSS多路径误差改正。
2 实验分析分别利用仿真数据及GNSS实测数据分析新方法的可行性与有效性。仿真数据包含多种分量信号及噪声混合信号,以分析基于EWT去噪方法的去噪能力,进而验证该方法用于GNSS多路径误差模型提取的有效性。利用连续3 d的GNSS观测数据,分析多路径误差提取及改正效果。
本文选定的评价标准为相关系数R、均方根误差(RMSE)以及信噪比SNR,3个指标的计算公式如下:
| $ R = \frac{{{\rm{cov}}\left[ {\overline {f\left( t \right)} y\left( t \right)} \right]}}{{{\sigma _{\overline {f(t)} }}{\sigma _{y(t)}}}} $ | (2) |
| $ {\rm{RMSE}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left[ {\overline {f\left( t \right)} - y\left( t \right)} \right]}^2}} } $ | (3) |
| $ {\rm{SNR}} = 10{\rm{lg}}\left( {\frac{{\sum\limits_{i = 1}^N {{y^2}\left( t \right)} }}{{\sum\limits_{i = 1}^N {{{\left[ {\overline {f\left( t \right)} - y\left( t \right)} \right]}^2}} }}} \right) $ | (4) |
式中,N为信号长度,f(t)为降噪后的信号,y(t)为原始信号,σf(t)和σy(t)分别为f(t)和y(t)的标准差,cov[f(t) y(t)]为f(t)和y(t)的协方差。
2.1 仿真实验与分析本文构建的仿真信号如式(5)所示,数据取样间隔为1 s,样本数为8 000。使用在原始信号中加入-2 dB、2 dB、5 dB、10 dB高斯白噪声的数据进行实验。为简洁地说明实验过程,以在原始信号中添加信噪比为5 dB的高斯白噪声的数据为例进行实验:
| $ y(t) = {\rm{sin}}\left( {\frac{{3{\rm{ \mathsf{ π} }}t}}{{2400}}} \right) + {\rm{sin}}\left( {\frac{{2{\rm{ \mathsf{ π} }}t}}{{400}}} \right) + {\rm{sin}}\left( {\frac{{5{\rm{ \mathsf{ π} }}t}}{{200}}} \right) $ | (5) |
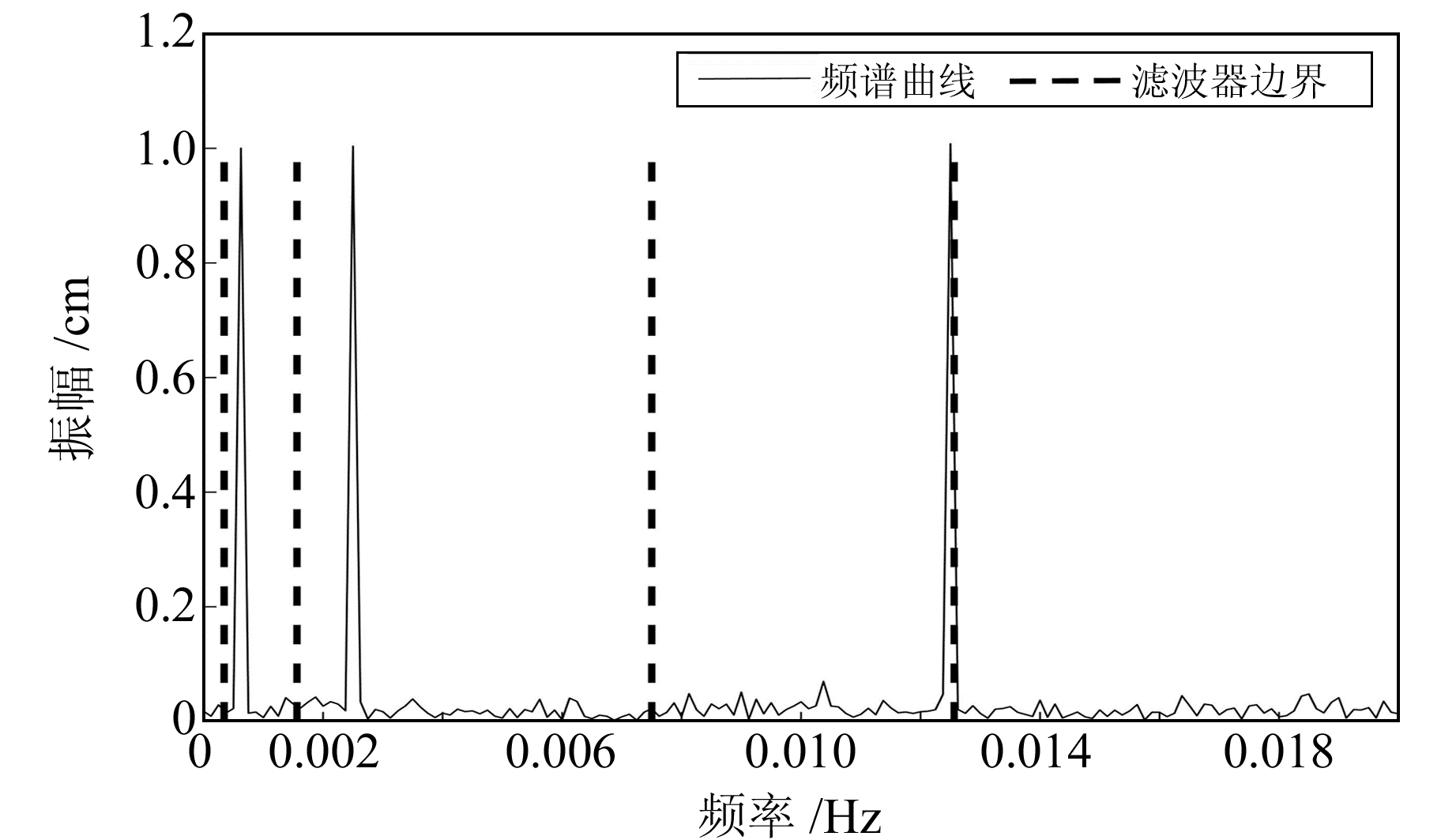
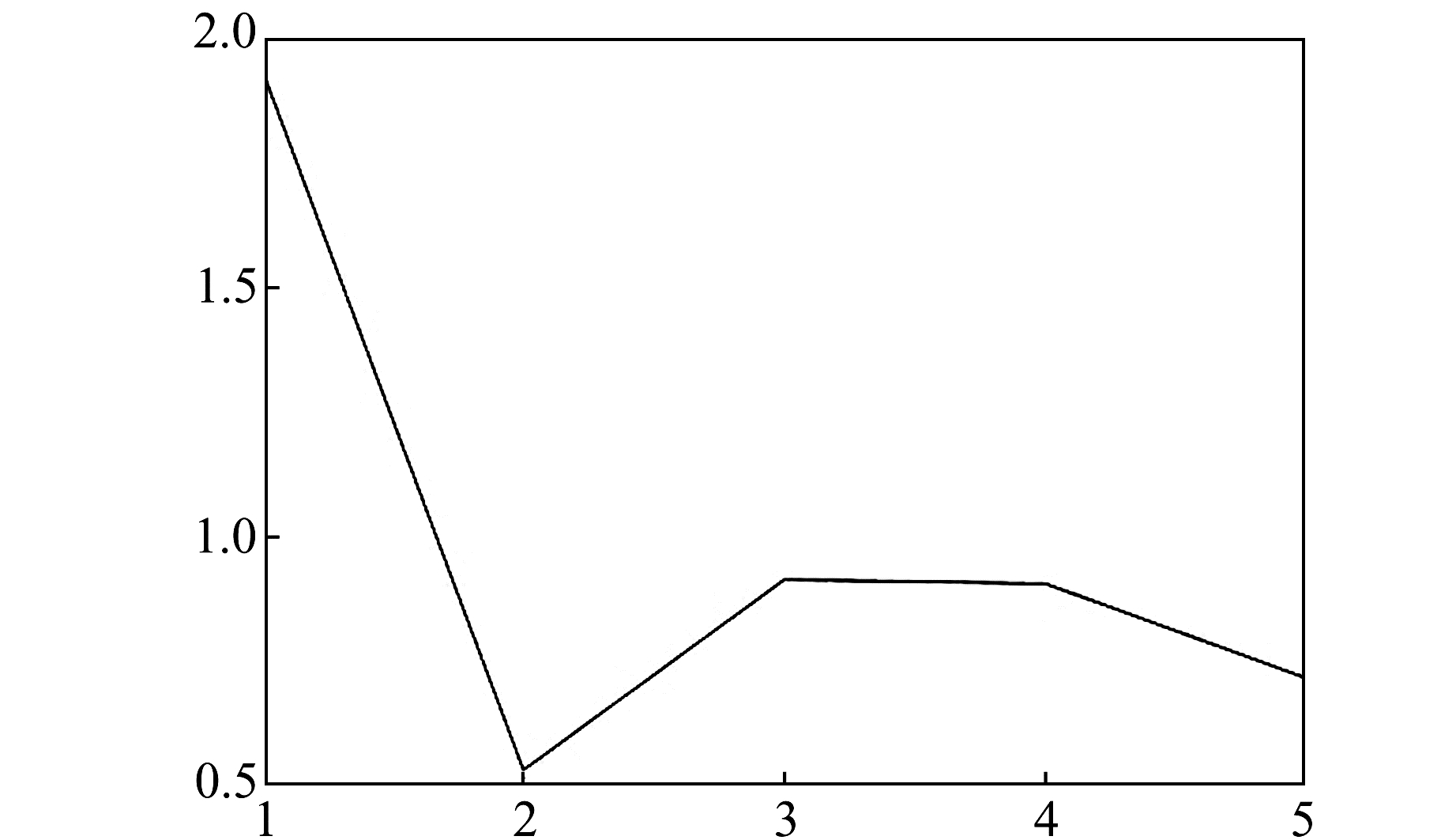
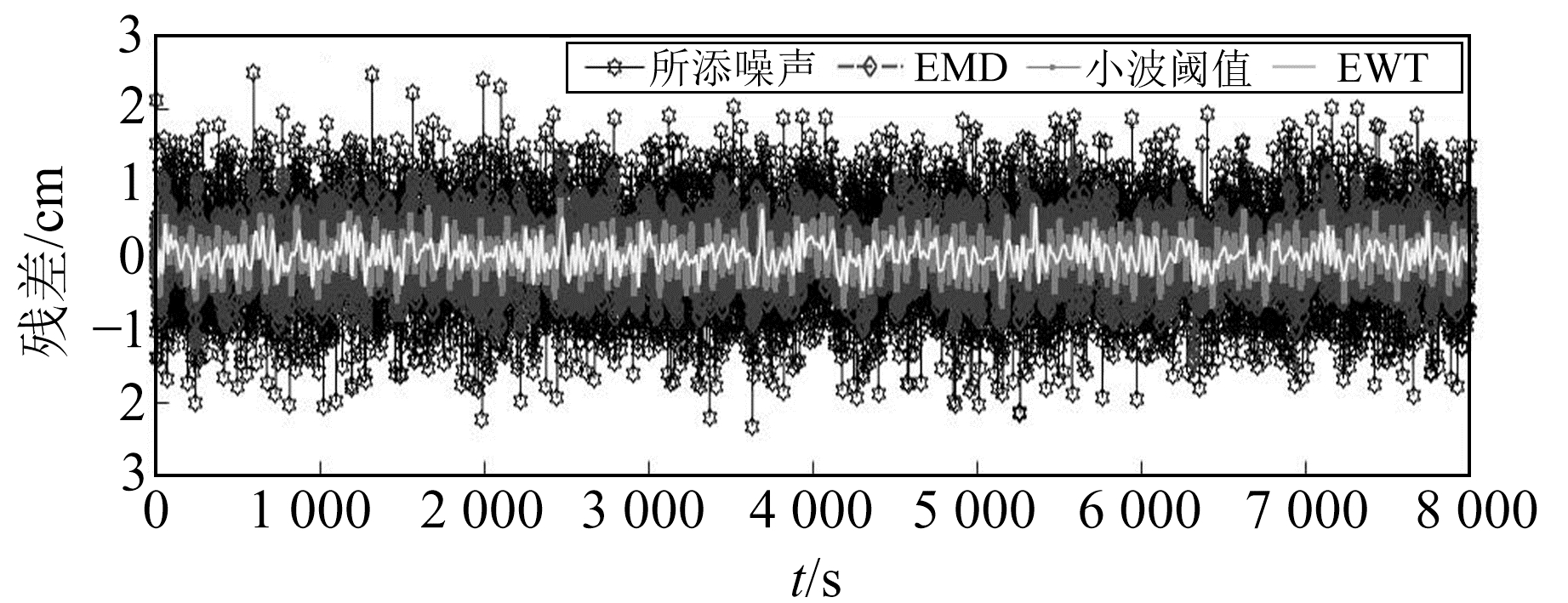
通过参考信号频谱图可更好地设置分解层数。由图 1可知,该信号含3种主要频率分量和噪声成分,因此分解层数应大于4。本文将分解层数设置为5,能较好地提取分量信号。仿真信号的筛选系数如图 2所示,在第2层发生较大变化,因此可将第1层信号作为含噪分量进行去噪处理。为了与EWT方法进行对比分析,另外使用EMD和小波阈值法对加噪的信号进行降噪。EMD降噪的具体过程与文献[1]一致;小波阈值法降噪则基于前人的经验选用db7小波基,分解层数设置为5,得到降噪后的信号。将降噪后的信号与原始参考信号作差,得到各方法降噪后依然存在的噪声,并与所添加的噪声进行对比(图 3)。从图中可以看出,EWT方法去噪后的噪声残余量比另外两种方法要小,说明其去噪效果更优。表 1为不同信噪比噪声下3种方法降噪效果的评价指标。
|
图 1 仿真信号频谱图 Fig. 1 Spectrum of simulation signal |
|
图 2 仿真信号系数筛选 Fig. 2 Coefficient screening of simulation signal |
|
图 3 去噪信号与原始参考信号的残差结果 Fig. 3 The residual results of denoised signal and original reference signal |
|
|
表 1 基于不同算法的降噪效果统计 Tab. 1 Statistics of denoising effectbased on different algorithms |
由表 1可知,随着信噪比(SNR)的增大,3种算法的RMSE值逐渐变小,EMD和小波阈值法对应的RMSE值大于EWT方法。随着噪声水平的增大,R值和SNR逐渐变小,但在添加同一噪声时,EWT方法的R值和SNR均高于EMD和小波阈值法的结果。从RMSE、R值以及降噪后的SNR值可以看出,EWT方法的降噪效果优于EMD和小波阈值法,表明改进的EWT方法具有较好的去噪效果,可应用于GNSS观测数据的多路径误差提取。
2.2 GNSS实测数据结果与分析本次实测数据采集地点位于中南大学采矿楼楼顶,接收机类型为Trimble NETR9,卫星截止高度角设置为0°。连续进行3 d观测,每天的观测时间为22 h,采样间隔为1 s,基线长度设置为6.5 m,所测数据通过GPSSM进行处理,并使用解算所得坐标与已知坐标作差得到坐标残差序列。由于本次测量时测站距离为6.5 m,经过差分处理后,对流层、电离层、钟差等误差能得到较好的消除或减弱,因此认为此时通过载波双差求解得到的坐标残差主要存在随机噪声和多路径误差。
将3 d测量得到的坐标残差序列通过恒星时轨重复周期超前特性进行对齐,并计算其相关系数(表 2)。从表中可以看出,3 d之间的坐标序列的相关系数均在0.60以上,表明对齐后的残差序列具有较强的周日重复性。因此,可利用GNSS多路径误差的周日重复性及提取的多路径误差模型对后续GNSS观测值进行多路径误差改正。
|
|
表 2 坐标残差序列相关系数 Tab. 2 Correlation coefficient of coordinate residual sequence |
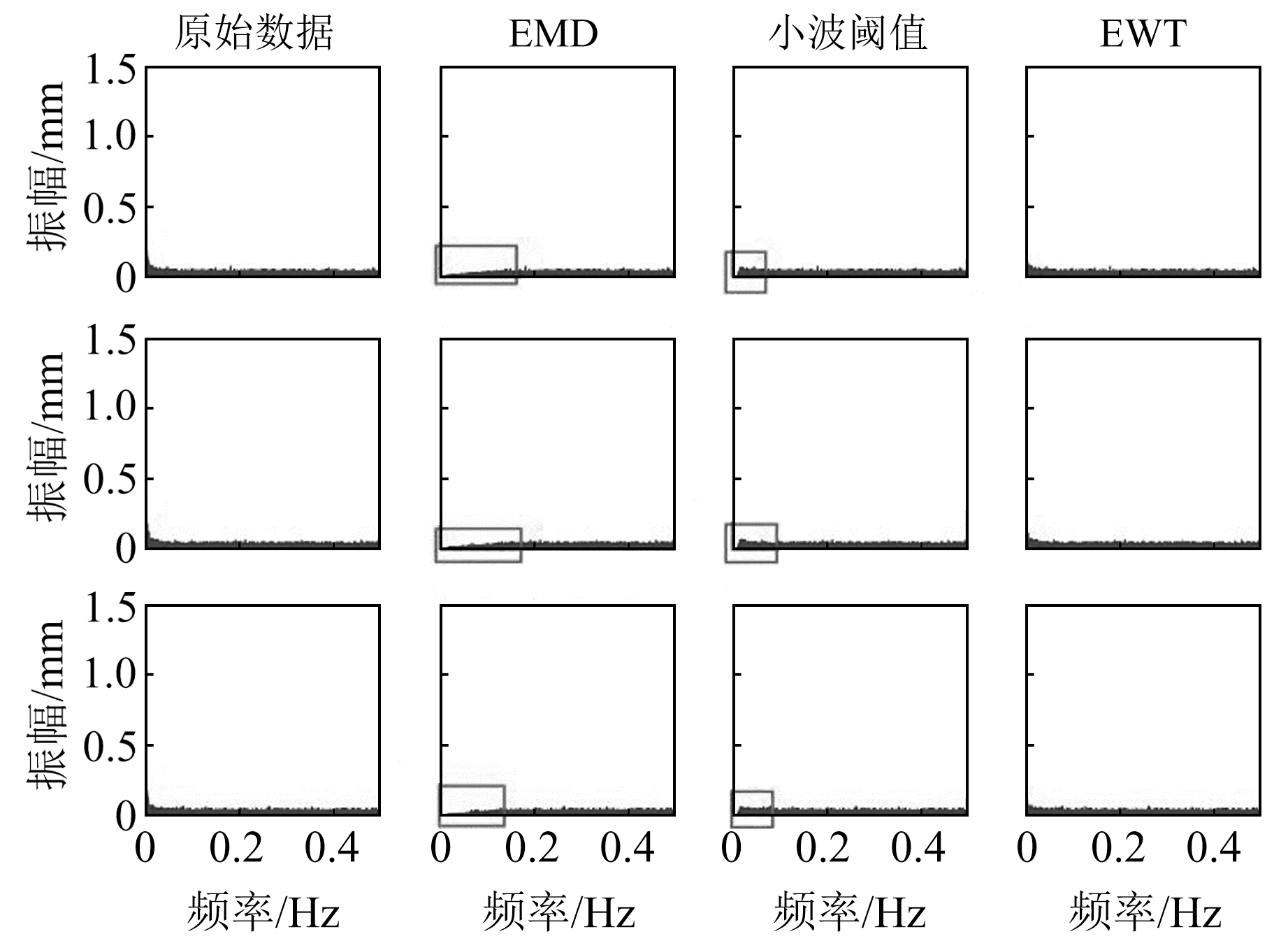
实验以Y方向为例,选取EMD、小波阈值2种方法进行对比,2种方法的细节设置与仿真实验一致。分别利用EWT、EMD及小波去噪法对GNSS坐标残差序列进行去噪,得到具体的多路径误差序列(图 4)。由图可知,EWT提取的多路径误差模型包含的噪声明显少于EMD和小波去噪方法,提取的多路径误差模型具有更高的精度。为进一步分析3种方法提取的多路径误差模型的精度,用提取的多路径误差模型改正原始坐标残差序列,得到其去除的噪声,绘制原始坐标残差序列及3种方法去除噪声的频谱图(图 5)。由图 5中GNSS坐标残差序列频谱图可知,GNSS多路径误差主要集中在低频部分,并且在整个分析频域内包含明显的随机噪声。由图 5中矩形框区域的频谱特征可知,EMD及小波方法会将低频区域的随机噪声混入其提取到的多路径误差模型中,导致提取的多路径误差模型受到噪声干扰;而EWT方法能有效去除整个频域内的随机噪声,并且剔除的噪声具有随机噪声的分布特征,EWT提取的多路径误差模型能有效剔除随机噪声的干扰,进一步表明EWT提取的多路径误差模型具有较好的精度及可靠性。

|
图 4 3个算法提取的多路径模型序列 Fig. 4 Multipath model sequence extracted by three algorithms |
|
图 5 3个算法去除的噪声频域图 Fig. 5 Noise frequency domain removed by three algorithms |
表 3为3天X、Y和H方向上的原始GNSS坐标残差序列及提取的多路径误差模型的RMSE值。由表 3可知,在X、Y和H方向上,3种算法提取的GNSS多路径误差模型的RMSE值小于原始观测值,并且EWT的效果优于EMD和小波阈值方法,能更好地去除随机噪声,证实提取的3 d GNSS多路径误差模型具有更高精度。分别计算EMD、小波方法及EWT提取的3 d多路径误差模型之间的相关性(表 4)。将表 4与表 2对比可知,EWT方法提取的3 d多路径误差模型之间具有较高的相关性,表明EWT能较好地提取多路径误差模型。EWT提取的多路径误差模型的相关性略高于EMD和小波方法,并且随时间间隔的增加相关性有所下降。
|
|
表 3 原始数据及提取的多路径误差模型的RMSE值 Tab. 3 RMSE values of original data and extracted multipath error model |
|
|
表 4 EMD、小波方法及EWT提取的3 d多路径误差模型的相关性 Tab. 4 Correlation coefficient of three days multipath error model extracted by EMD, wavelet method and EWT |
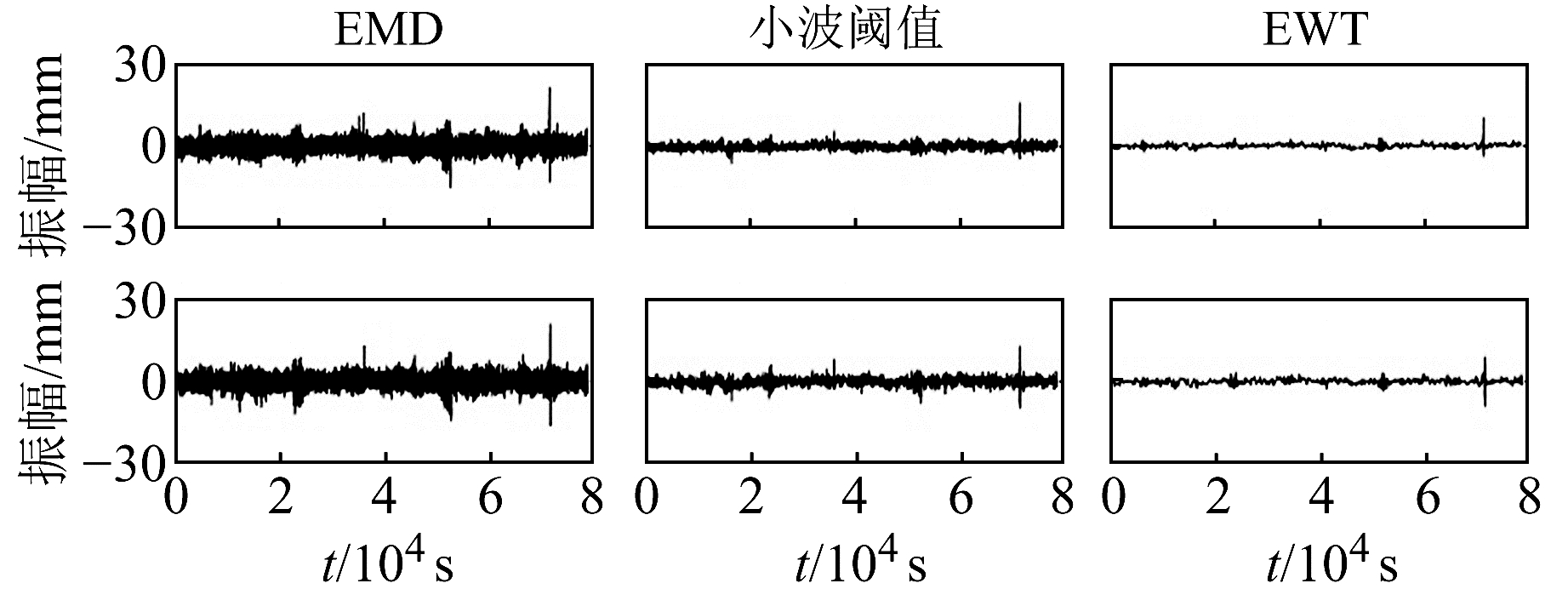
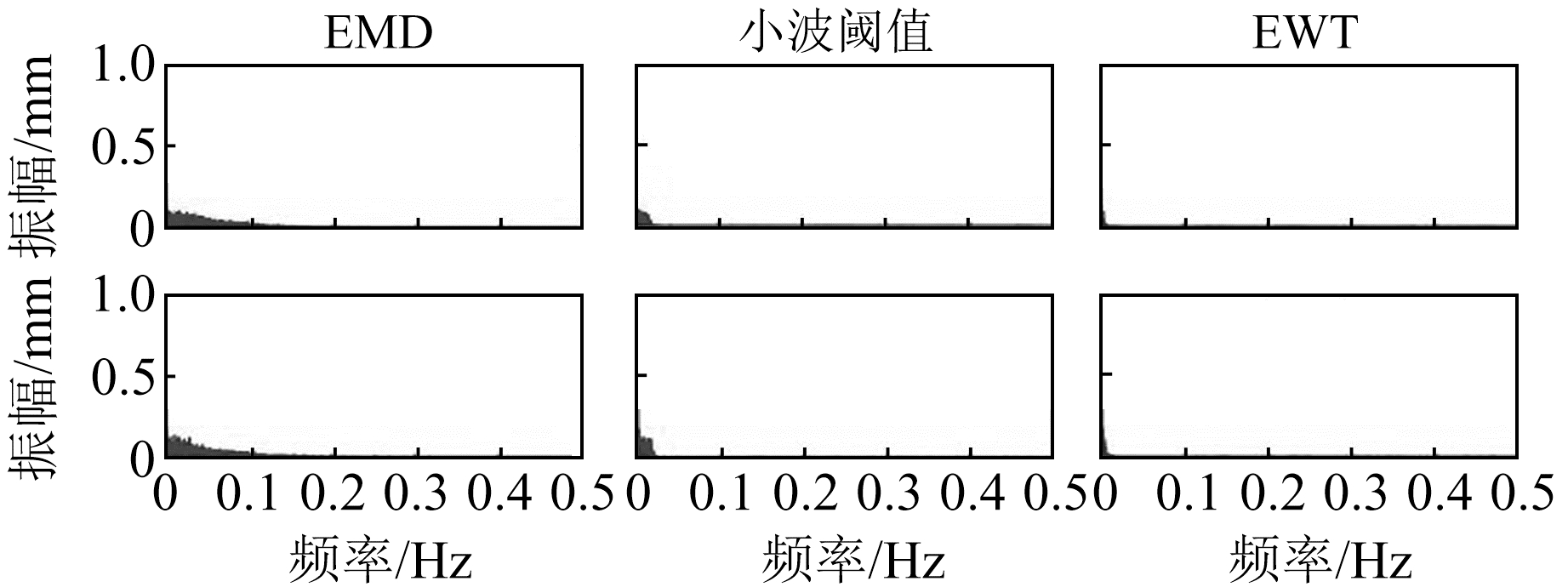
为分析利用Day1改正Day2和Day3多路径误差的效果,分别利用EMD、小波方法及EWT对Day1、Day2和Day3的坐标残差序列进行去噪,并使用Day1的多路径误差模型对Day2和Day3去噪后的序列进行改正,得到残差序列(图 6),同时绘制残差频谱图(图 7)。由图 6和图 7可知,EWT方法的残差明显小于EMD、小波方法,并且EWT方法的残差几乎不包含随机噪声,表明EWT方法能较好地提取多路径误差模型,可准确地改正Day2和Day3的多路径误差。为定量分析多路径误差的改正效果,统计残差的RMSE值(表 5)。由表 5可知,Day2改正效果优于Day3,表明随着时间的推移观测环境差异增加,导致多路径误差相关性下降。EWT方法对多路径误差的削弱效果显著优于EMD、小波方法,其在Y、X、H方向的RMSE值分别减小84%、83%、85%以上。
|
图 6 Y方向3 d多路径误差残差序列 Fig. 6 Residual sequence of three days multipath error in Y direction |
|
图 7 多路径误差模型改正后的残差序列频谱图 Fig. 7 Residual sequence spectrum of multipath error model after correction |
|
|
表 5 多路径误差模型改正残差的RMSE值 Tab. 5 RMSE values of residual sequence corrected by multipath error model |
本文将筛选系数的变化作为EWT含噪分量判定的新标准,并在此基础上构建EWT去噪新方法。通过对比新方法与EMD和小波分析法得出以下结论:1)不同信噪比情况下的模拟结果表明,新方法能有效降噪,且降噪效果优于EMD算法和小波去噪算法;2)将该方法用于GNSS多路径误差改正,实验表明,EWT方法受随机噪声的干扰程度明显小于EMD和小波方法,对多路径误差的削弱效果显著优于EMD和小波去噪方法,可较好地提高GNSS的定位精度。
| [1] |
严超, 王庆, 杨高朝, 等. EMD-RLS联合滤波算法及其在北斗多路径削弱误差中的应用[J]. 中国惯性技术学报, 2019, 27(2): 190-198 (Yan Chao, Wang Qing, Yang Gaochao, et al. EMD-RLS Combination Algorithm and Its Application in Weakening BDS Multipath Error[J]. Journal of Chinese Inertial Technology, 2019, 27(2): 190-198)
(  0) 0) |
| [2] |
Dong D N, Wang M H, Chen W, et al. Mitigation of Multipath Effect in GNSS Short Baseline Positioning by the Multipath Hemispherical Map[J]. Journal of Geodesy, 2016, 90(3): 255-262
(  0) 0) |
| [3] |
Satirapod C, Rizos C. Multipath Mitigation by Wavelet Analysis for GPS Base Station Applications[J]. Survey Review, 2005, 38(295): 2-10 DOI:10.1179/sre.2005.38.295.2
(  0) 0) |
| [4] |
Su M K, Zheng J S, Yang Y X, et al. A New Multipath Mitigation Method Based on Adaptive Thresholding Wavelet Denoising and Double Reference Shift Strategy[J]. GPS Solutions, 2018, 22(2): 40 DOI:10.1007/s10291-018-0708-z
(  0) 0) |
| [5] |
戴吾蛟, 丁晓利, 朱建军, 等. 基于经验模式分解的滤波去噪法及其在GPS多路径效应中的应用[J]. 测绘学报, 2006, 35(4): 321-327 (Dai Wujiao, Ding Xiaoli, Zhu Jianjun, et al. EMD Filter Method and Its Application in GPS Multipath[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(4): 321-327)
(  0) 0) |
| [6] |
Huang N E, Shen Z, Long S R, et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis[J]. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995 DOI:10.1098/rspa.1998.0193
(  0) 0) |
| [7] |
Li H L, Kwong S, Yang L H, et al. Hilbert-Huang Transform for Analysis of Heart Rate Variability in Cardiac Health[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2011, 8(6): 1557-1567 DOI:10.1109/TCBB.2011.43
(  0) 0) |
| [8] |
王琰, 张传定, 胡小工, 等. 一种地面连续运行参考站实时质量控制算法[J]. 仪器仪表学报, 2016, 37(11): 2506-2513 (Wang Yan, Zhang Chuanding, Hu Xiaogong, et al. Real-Time Quality Control Algorithm for Ground Continuously Operation Reference Stations[J]. Chinese Journal of Scientific Instrument, 2016, 37(11): 2506-2513)
(  0) 0) |
| [9] |
Gilles J. Empirical Wavelet Transform[J]. IEEE Transactions on Signal Processing, 2013, 61(16): 3999-4010 DOI:10.1109/TSP.2013.2265222
(  0) 0) |
| [10] |
张超, 陈建军, 郭迅. 基于EEMD能量熵和支持向量机的齿轮故障诊断方法[J]. 中南大学学报:自然科学版, 2012, 43(3): 932-939 (Zhang Chao, Chen Jianjun, Guo Xun. Gear Fault Diagnosis Method Based on Ensemble Empirical Mode Decomposition Energy Entropy and Support Vector Machine[J]. Journal of Central South University:Science and Technology, 2012, 43(3): 932-939)
(  0) 0) |
2. School of Geodesy and Geomatics, Wuhan University, 129 Luoyu Road, Wuhan 430079, China
 2020, Vol. 40
2020, Vol. 40

