2. 波恩大学大地测量与地理信息学院,波恩市努萨利17号,53121;
3. 同济大学测绘与地理信息学院,上海市四平路1239号,200092
高精度、高分辨率的地球重力场模型可为大地测量、地球物理、地震等地球科学的研究提供重要的数据支撑[1]。地球重力场模型应用的关键问题是由模型导出重力异常、高程异常等重力量的计算效率及由GNSS水准点、重力异常等实测数据全面评价重力场模型的精度,国内外学者在重力场模型精度评估与重力量快速计算等方面进行了大量研究,如利用GNSS水准数据、垂线偏差、实测重力数据、重力异常数据等对现有的重力场模型(如EGM2008等)进行精度评定[2-9]。在重力量计算研究方面,目前有ICGEM网站提供的在线计算服务[10]、基于Python+Fortran平台的Gravsoft软件[11]、ESA提供的GUT软件包[12]、基于MATLAB平台的GrafLab软件包[13-14]和IGiK-TVGMF软件包[15]及跨平台重力异常云计算软件系统OnGra[16]等,但这些软件大多只能利用重力场模型计算高程异常和重力异常等相关重力量,无法直接评估重力场模型精度及比较模型间差异。
本文基于VS2015+Intel XE 2016平台研发EGMTools软件包,可实现地球重力场模型不同阶次的精度评估及由重力场模型快速导出相关重力量等功能,同时该软件还具有为剩余地形模型(RTM)高程异常等计算提供数据预处理及不同重力场模型格式转换等功能。为提高计算效率,该软件采用OpenMP并行计算技术[17],并通过算例分析说明其主要功能。
1 原理与方法在球坐标系中,地球外部空间任意一点的扰动位T可由球谐函数展开式表示为[18]:
| $ \begin{array}{l} T\left( {\theta , \lambda , r} \right) = \frac{{GM}}{r}\left[ {\sum\limits_{n = 2}^{{N_{{\rm{max}}}}} {{{\left( {\frac{R}{r}} \right)}^n}} \sum\limits_{m = 0}^n {\left( {\Delta {{\bar C}_{nm}}{\rm{cos}}m\lambda + } \right.} } \right.\\ \left. {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\Delta {{\bar S}_{nm}}{\rm{sin}}m\lambda } \right){{\bar P}_{nm}}\left( {{\rm{cos}}\theta } \right)} \right] \end{array} $ | (1) |
式中,θ为地心余纬,λ为地心经度,r为地心向径,GM为引力常数与地球质量的乘积,R为参考椭球长半轴,ΔCnm、ΔSnm为完全规格化的n阶m次扰动位系数,Pnm(cosθ)为完全规格化的n阶m次缔合勒让德函数。其中,对于椭球面格网值重力量计算中的每个纬圈可只计算1次Pnm(cosθ),从而有效提高计算效率[19]。
1.1 模型高程异常根据Bruns公式,由扰动位T可导出高程异常ζ为:
| $ \begin{array}{l} \zeta \left( {\theta , \lambda , r} \right) = \frac{{GM}}{{r\gamma }}\left[ {\sum\limits_{n = 2}^{{N_{{\rm{max}}}}} {{{\left( {\frac{R}{r}} \right)}^n}} \sum\limits_{m = 0}^n {\left( {\Delta {{\bar C}_{nm}}{\rm{cos}}m\lambda + } \right.} } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left. {\Delta {{\bar S}_{nm}}{\rm{sin}}m\lambda } \right){{\bar P}_{nm}}({\rm{cos}}\theta )} \right] \end{array} $ | (2) |
式中,γ为计算点的正常重力值,其他参数含义同式(1)。
1.2 模型重力异常在球近似下,由扰动位T计算重力异常Δg的公式为:
| $ \begin{array}{l} \;\;\Delta g\left( {\theta , \lambda , r} \right) = \frac{{GM}}{{{r^2}}}\left[ {\sum\limits_{n = 2}^{{N_{{\rm{max}}}}} {\left( {n - 1} \right)} {{\left( {\frac{R}{r}} \right)}^n}} \right.\\ \left. {\sum\limits_{m = 0}^n {\left( {\Delta {{\bar C}_{nm}}{\rm{cos}}m\lambda + } \right.} \Delta {{\bar S}_{nm}}{\rm{sin}}m\lambda ){{\bar P}_{nm}}({\rm{cos}}\theta )} \right] \end{array} $ | (3) |
垂线偏差表示空间中任一点的铅垂线与参考椭球法线之间的夹角,分为卯酉圈分量η和子午圈分量ξ,计算公式为:
| $ \begin{array}{l} \xi \left( {\theta , \lambda , r} \right) = \frac{{GM}}{{{r^2}\gamma }}\left[ {\sum\limits_{n = 2}^{{N_{{\rm{max}}}}} {{{\left( {\frac{R}{r}} \right)}^n}} \sum\limits_{m = 0}^n {\left( {\Delta {{\bar C}_{nm}}{\rm{cos}}m\lambda + } \right.} } \right.\\ \left. {\;\;\;\;\;\;\;\;\;\;\;\;\left. {\Delta {{\bar S}_{nm}}{\rm{sin}}m\lambda } \right)\frac{{\partial {{\bar P}_{nm}}({\rm{cos}}\theta )}}{{\partial \theta }}} \right] \end{array} $ | (4) |
| $ \begin{array}{l} \;\eta \left( {\theta , \lambda , r} \right) = - \frac{{GM}}{{{r^2}\gamma {\rm{sin}}\theta }}\left[ {\sum\limits_{n = 2}^{{N_{{\rm{max}}}}} {{{\left( {\frac{R}{r}} \right)}^n}} \sum\limits_{m = 0}^n m } \right.\\ \left. {\left( { - \Delta {{\bar C}_{nm}}{\rm{sin}}m\lambda + \Delta {{\bar S}_{nm}}{\rm{cos}}m\lambda } \right){{\bar P}_{nm}}({\rm{cos}}\theta )} \right] \end{array} $ | (5) |
基于数字地形模型球谐系数可计算地形表面任意点的高程[20-21],计算公式为:
| $ \begin{array}{l} H\left( {\theta , \lambda } \right) = \sum\limits_{n = 0}^N {\sum\limits_{m = 0}^n {\left( {{{\overline {{\rm{HC}}} }_{nm}}{\rm{cos}}m\lambda + } \right.} } \\ {\rm{ }}\;\;\;\;\;\;\left. {{{\overline {{\rm{HS}}} }_{nm}}{\rm{sin}}m\lambda } \right){{\bar P}_{nm}}({\rm{cos}}\theta ) \end{array} $ | (6) |
式中,HCnm、HSnm为正规化的地形模型系数。由数字地形模型球谐系数计算得到的地形表面高程,可为RTM相关计算量的计算提供参考面。为计算陆地和海洋(或大型水域)统一的RTM,需对水域的水下地形进行统一归算(考虑水体影响),计算海洋等效岩石高HRET(sea)和大型湖泊地形HRET(lakes),其公式为:
| $ H_{{\rm{RET}}}^{{\rm{(sea)}}} = {H_{{\rm{SRT}}{{\rm{M}}_{{\rm{plus}}}}}}\left( {1 - \frac{{{\rho _s}}}{{{\rho _0}}}} \right) $ | (7) |
| $ H_{{\rm{RET}}}^{{\rm{(lakes)}}} = {H_{{\rm{SRT}}{{\rm{M}}_{{\rm{plus}}}}}} + \frac{{{\rho _l}}}{{{\rho _0}}}\left( {{H_{{\rm{surface}}}} - {H_{{\rm{SRT}}{{\rm{M}}_{{\rm{plus}}}}}}} \right) $ | (8) |
式中,ρ0为标准岩石密度2 670 kg/m3,ρs为海水密度1 030 kg/m3,ρl为淡水密度1 000 kg/m3,Hsurface为湖面高程,HSRTMplus为相对于平均海平面的海水深度。
2 EGMTools软件介绍 2.1 软件框架EGMTools软件是基于Windows10的64位操作系统,利用VS2015+Intel XE 2016平台进行开发,可移植性好。该软件集成OpenMP并行技术,主要用于重力场模型精度评估、有关重力量计算及剩余地形模型RTM重力量计算预处理等,具体功能见表 1。
|
|
表 1 EGMTools软件功能 Tab. 1 Functions of EGMTools software |
目前EGMTools软件所支持的相关数据类型及部分模型见表 2,其中软件所使用的重力场模型均可从ICGEM网站(http://icgem.gfz-potsdam.de/tom_longtime)下载,经过模型格式转换功能即可转换为EGMTools软件所能识别的模型文件格式;区域(似)大地水准面模型来自ISG网站(http://www.isgeoid.polimi.it/Geoid/reg_list.html);GNSS水准数据中GSVS2011及GSVS2014相关数据来自NGS网站;海洋重力异常数据DTU15[22]来自DTU网站(https://ftp.space.dtu.dk/pub/);RET地形模型可从网站(http://ddfe.curtin.edu.au/models/)直接下载,在数据格式准确的前提下可自行添加其他数据。
|
|
表 2 EGMTools数据及模型类型 Tab. 2 Data and model type of EGMTools |
软件计算可通过setting.ini配置文件设置有关参数,具体见图 1,其中各参数的具体含义为:1)EGMFName1为第1个重力场模型文件及路径(可作为参考模型);2)EGMFName2为第2个重力场模型文件及路径(可作为待评估模型);3)InPutDataFName(GPSPtGADOV)为输入已知重力量数据文件及路径,如相关似大地水准面数据、GNSS水准数据、DTU海洋重力异常数据及点位相关信息数据等;4)OutPutDataFName为输出结果文件的路径及名称;5)DTMFName为选择的DTM模型数据及路径;6)CalDTMFName为计算的DTM结果文件名及路径;7)Degree/Order分别为模型的最高阶次(若截断至EGMFName2模型的最高阶次,则剩余阶次采用EGMFName1模型的位系数进行填充)、开始统计精度的最低阶次、最高阶次及统计精度的阶次间隔(最后计算结果会按照对应阶次进行精度统计并输出对应阶次的格网值文件,结果可直接利用Global Mapper软件或MATLAB相关软件包进行显示);8)GridInfo为计算椭球面格网值的最小纬度、最大纬度、最小经度、最大经度、格网值纬度的分辨率及格网值经度的分辨率;9)StartRows为开始计算纬圈的行数,可记录计算格网值的位置,方便格网数据的拆分计算与合并。

|
图 1 配置文件内容 Fig. 1 Configuration file contents |
EGMTools软件可实现模型重力量计算,并比较不同模型不同阶次的空间差异及对模型精度进行评估、对相关重力场模型格式进行转换及对RTM剩余重力量计算的数据进行预处理等。本文首先对软件进行验证,再对比EGM2008模型与EIGEN-6C4模型的空间差异,利用多源实测数据对GOCO06s模型精度进行评估及对剩余地形RTM数据进行预处理来说明EGMTools软件的相关功能。
3.1 软件验证利用ICGEM网站在线计算软件,选择EIGEN-6C4模型,截断至2 160阶次,计算全球1°×1°椭球面格网重力异常值,并与EGMTools软件的计算结果进行对比,结果见图 2。
|
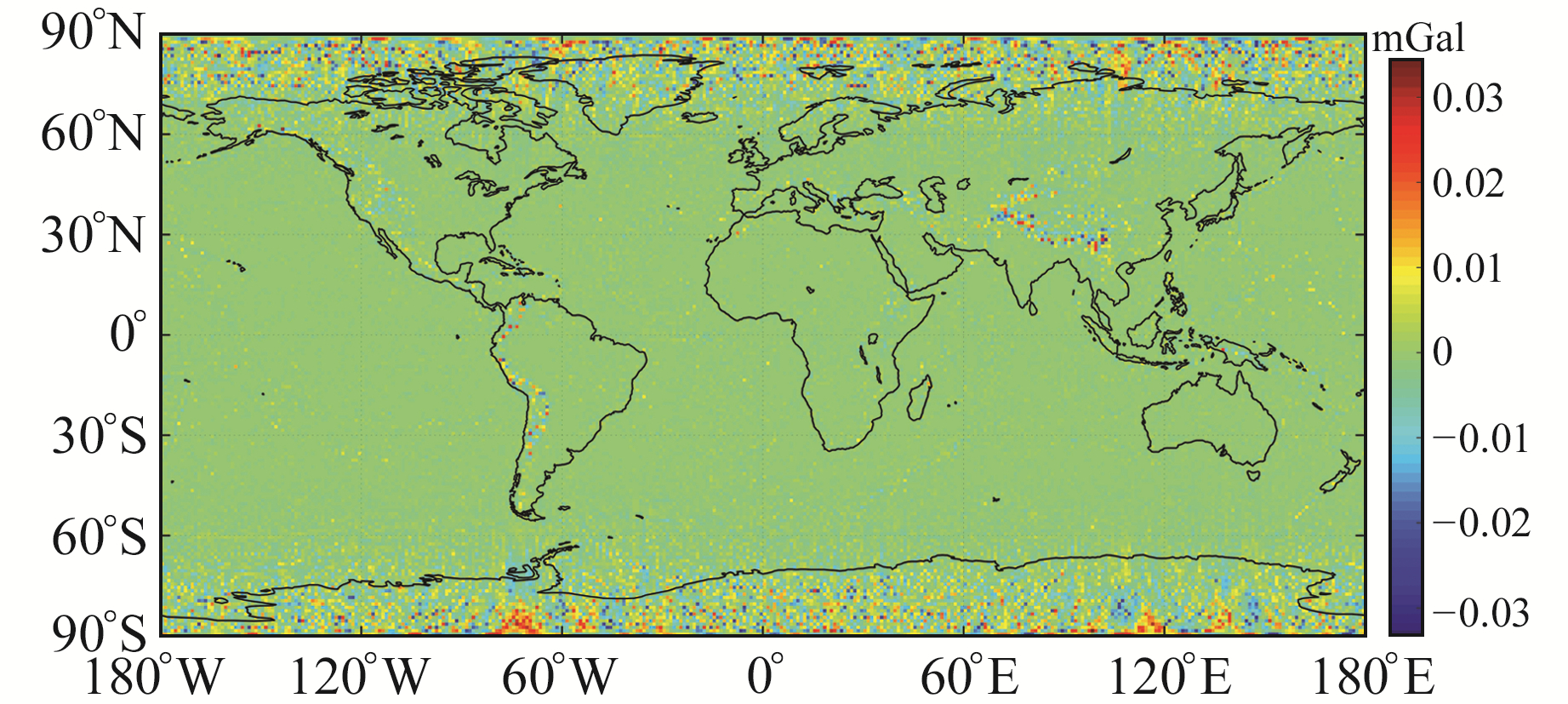
图 2 ICGEM软件与EGMTools软件重力异常差值 Fig. 2 Gravity anomaly differences between ICGEM and EGMTools software |
由图 2可知,两者的重力异常差值很小,差值标准差为±0.004 6 mGal,远小于重力异常的测量精度,表明EGMTools软件的计算结果较为可靠。
3.2 不同重力场模型空间差异比较与分析EGMTools软件可通过计算的相关重力量直接对比2个模型之间不同阶次的空间差异,可简化数据处理和人工干预流程。本文选取EGM2008模型和EIGEN-6C4模型截断至2 160阶次进行比较,计算全球1°×1°椭球面高程异常和重力异常,其格网差值结果见图 3。EGMTools软件在计算重力量的同时还能统计截断至任意阶次的模型精度,本文仅统计截断至180~2 160阶次的高程异常精度结果,具体见表 3,其中统计间隔为180阶次,可按需要在参数设置文件中输入对应的统计阶次。

|
图 3 EGM2008模型和EIGEN-6C4模型格网值差值 Fig. 3 Differences between EGM2008 and EIGEN-6C4 models |
|
|
表 3 EGM2008模型和EIGEN-6C4模型截断至任意阶次高程异常对比 Tab. 3 Comparison of height anomaly of given degree/order between EGM2008 and EIGEN-6C4 |
从图 3和表 3可知,2个模型计算的高程异常和重力异常整体上比较接近,在青藏高原、非洲、南极及南美洲等地差异稍大,而在360阶次后模型间的差异保持在一定范围内,相对精度稳定,差值标准差约为0.128 m。
3.3 利用多源实测数据评估模型精度EGMTools软件可利用多源实测数据评估模型精度,本文分别利用墨西哥GNSS水准数据(536个)、日本似大地水准面模型GSIGEO2011(分辨率为5′×7.5′)及DTU15南太平洋区域(0°~60°S,180°~270°E)重力异常数据(分辨率为5′×5′)对GOCO06s模型的精度进行评估,最高阶次取2 160阶次,并统计截断至100~300阶次的精度(截断阶次后采用EIGEN-6C4模型位系数填充至2 160阶次),统计间隔为100阶次,结果见表 4~6。
|
|
表 4 墨西哥GNSS水准数据评估GOCO06s模型精度 Tab. 4 GOCO06s model accuracy estimated with GNSS/leveling data in Mexico |
|
|
表 5 日本似大地水准面模型GSIGEO2011评估GOCO06s模型精度 Tab. 5 GOCO06s model accuracy estimatedwith GSIGEO2011 geoid model |
|
|
表 6 DTU15南太平洋区域重力异常数据评估GOCO06s模型精度 Tab. 6 GOCO06s model accuracy estimated withDTU15 gravity anomaly data in south Pacific Ocean |
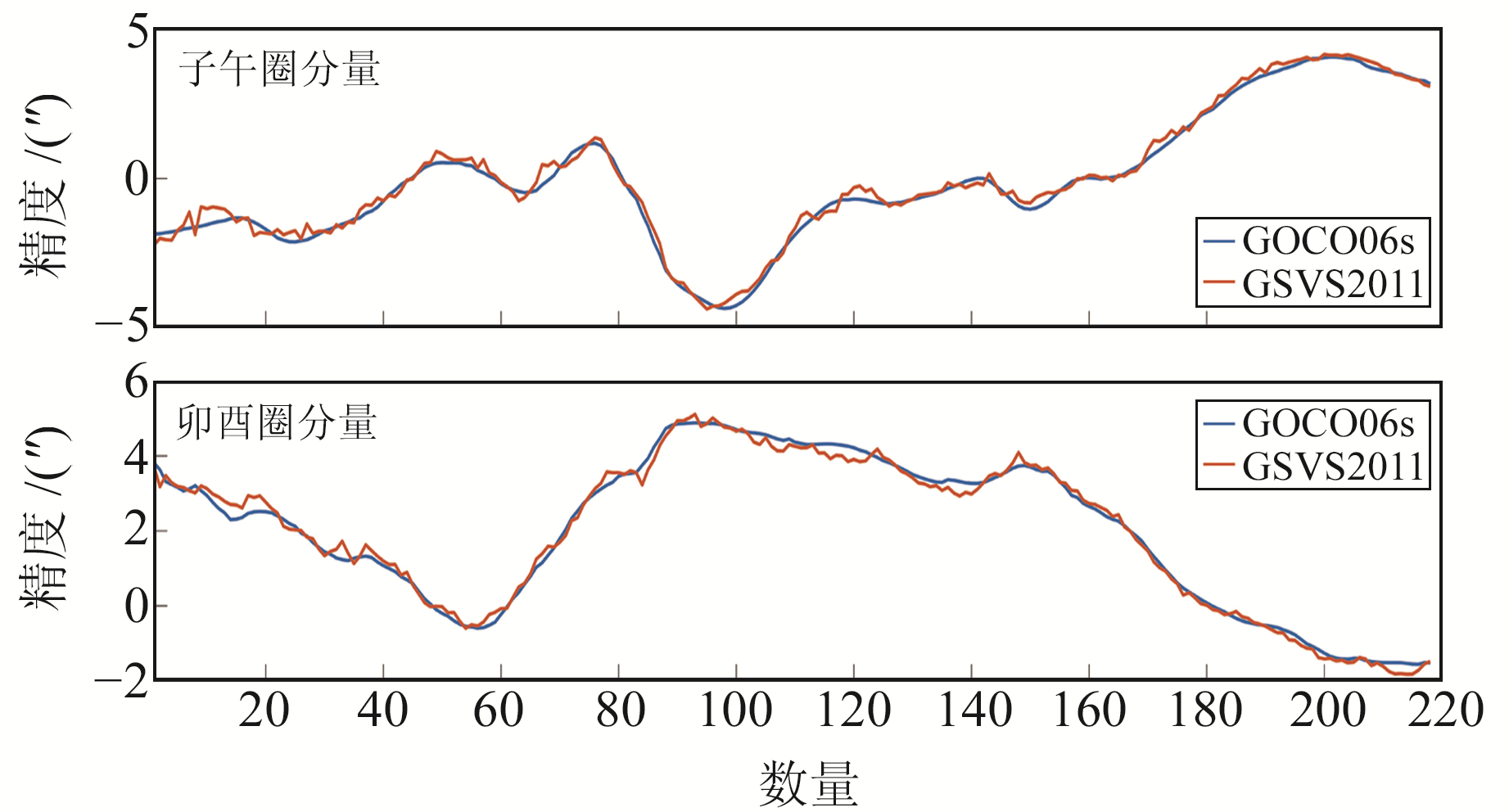
从表 4~6可以看出,经各实测数据检核,GOCO06s模型在截断至100阶次和截断至200阶次的精度相当,截断至300阶次时精度稍差,主要原因为解算GOCO06s模型采用纯卫星数据,未结合地面重力数据,导致高阶位系数精度较差[23]。基于以上结果,本文利用NGS提供的GSVS2011项目沿线218个实测垂线偏差数据对GOCO06s模型截断至200阶次(截断阶次后采用EIGEN-6C4模型位系数填充至2 160阶次)的精度进行评估,结果见图 4。由图 4可知,模型计算结果与实测值基本一致,GOCO06s模型在美国对应区域计算的子午圈分量与实测值的标准差为±0.204 7″,卯酉圈分量的标准差为±0.165 7″。
|
图 4 GSVS2011垂线偏差数据评估GOCO06s截断至200阶次模型精度 Fig. 4 Model accuracy of GOCO06s up to 200 order estimated with GSVS2011 vertical deflection data |
利用RET2012地形模型,根据式(6)截断至2 160阶次,计算15″×15″参考地形表面高程,并与15″×15″ SRTM数据进行对比,所选区域范围为24°~52°N、70°~97°E,具体结果见图 5。其中,图 5(a)为SRTM格网高程数据,图 5(b)为RET2012模型计算的地形模型高程数据,图 5(c)为剩余地形模型RTM高程数据(SRTM数据减去计算的地形表面高程),得到的剩余地形模型可直接通过Gravsoft软件计算相关重力量数据。

|
图 5 剩余地形模型计算 Fig. 5 RTM calculation |
EGMTools软件是集相关重力量计算及重力场模型评估于一体的多功能计算软件,可计算点/格网值的重力量数据,计算得到的格网值可用Global Mapper软件或MATLAB相关软件包读取。该软件还可对重力场模型进行多数据源评估,更加便捷地统计截断至任意阶次的模型精度,另外还可采用RET2012或DTM2006.0等模型进行数字地形模型高程的计算。
本文通过算例分析介绍EGMTools软件的主要功能,首先利用ICGEM网站的在线计算软件验证该软件计算结果的可靠性;再利用多源数据对GOCO06s模型精度进行评估,以此说明该软件评估不同模型不同阶次精度的便捷性;最后利用RET2012地形模型计算得到剩余地形高程数据,可直接利用Gravsoft软件计算其相关重力量,为区域似大地水准面的确定提供地形改正量。
致谢: ISG提供相关大地水准面模型,NGS提供相关GNSS水准数据和GSVS2011数据,ICGEM提供全球重力场模型,DTU提供DTU15海洋重力异常数据,在此一并表示感谢!
| [1] |
张兴福.应用低轨卫星跟踪数据反演地球重力场模型[D].上海: 同济大学, 2007 (Zhang Xingfu. The Earth's Field Model Recovery on the Basis of Satellite-to-Satellite Tracking Missions[D].Shanghai: Tongji University, 2007)
(  0) 0) |
| [2] |
章传银, 郭春喜, 陈俊勇, 等. EGM2008地球重力场模型在中国大陆适用性分析[J]. 测绘学报, 2009, 38(4): 283-289 (Zhang Chuanyin, Guo Chunxi, Chen Junyong, et al. EGM 2008 and Its Application Analysis in Chinese Mainland[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 283-289)
(  0) 0) |
| [3] |
张兴福, 刘成, 刘红新. 利用GPS/水准数据检核EGM2008重力场模型的精度[J]. 测绘通报, 2009(2): 7-9 (Zhang Xingfu, Liu Cheng, Liu Hongxin. Accuracy Validation of EGM2008 Model Using GPS/Leveling Data[J]. Bulletin of Surveying and Mapping, 2009(2): 7-9)
(  0) 0) |
| [4] |
荣敏, 周巍, 陈春旺. 重力场模型EGM2008和EGM96在中国地区的比较与评价[J]. 大地测量与地球动力学, 2009, 29(6): 123-125 (Rong Min, Zhou Wei, Chen Chunwang. Evaluation of Gravity Field Models EGM2008 and EGM96 Applied in Chinese Area[J]. Journal of Geodesy and Geodynamics, 2009, 29(6): 123-125)
(  0) 0) |
| [5] |
赵德军, 张敏利, 王强, 等. EIGEN-6C2重力场模型在中国大陆的精度分析[J]. 大地测量与地球动力学, 2014, 34(5): 21-24 (Zhao Dejun, Zhang Minli, Wang Qiang, et al. Accuracy Analyses of EIGEN-6C2 Geopotential Model in China Mainland[J]. Journal of Geodesy and Geodynamics, 2014, 34(5): 21-24)
(  0) 0) |
| [6] |
Kostelecký J, Klokočník J, Bucha B, et al. Evaluation of Gravity Field Model EIGEN-6C4 by Means of Various Functions of Gravity Potential, and by GNSS/Levelling[J]. Geoinformatics FCE CTU, 2015, 14(1): 7-28 DOI:10.14311/gi.14.1.1
(  0) 0) |
| [7] |
丁剑, 许厚泽, 章传银. 利用重力等位面特性进行地球重力场模型评价[J]. 武汉大学学报:信息科学版, 2018, 43(6): 832-839 (Ding Jian, Xu Houze, Zhang Chuanyin. To Evaluate Earth Gravitational Model Using Equigeopotential Character[J]. Geomatics and Information Science of Wuhan University, 2018, 43(6): 832-839)
(  0) 0) |
| [8] |
崔家武, 张兴福, 周波阳, 等. 利用高精度GNSS水准及垂线偏差数据分析重力场模型的误差特性[J]. 地球物理学进展, 2019, 34(5): 1728-1735 (Cui Jiawu, Zhang Xingfu, Zhou Boyang, et al. Analysis of Error Characteristics of Earth Gravity Model Using High-Precision GNSS/Leveling and Deflection of the Vertical Data[J]. Progress in Geophysics, 2019, 34(5): 1728-1735)
(  0) 0) |
| [9] |
Odera P A. Assessment of the Latest Generation GOCE-Based Global Gravity Field Models Using Height and Free-Air Gravity Anomalies over South Africa[J]. Arabian Journal of Geosciences, 2019, 12(5): 145 DOI:10.1007/s12517-019-4337-9
(  0) 0) |
| [10] |
Ince E S, Barthelmes F, Reisland S, et al. ICGEM——15 Years of Successful Collection and Distribution of Global Gravitational Models, Associated Services and Future Plans[J]. Earth System Science Data, 2019, 11(2): 647-674 DOI:10.5194/essd-11-647-2019
(  0) 0) |
| [11] |
Forsberg R, Tscherning C C. An Overview Manual for the GRAVSOFT Geodetic Gravity Field Modelling Programs[R]. Denmark: National Space Institude(DTU-Space), 2008
(  0) 0) |
| [12] |
European Space Agency. GUT User Guide and Algorithm Descriptions[Z]. 2016
(  0) 0) |
| [13] |
Bucha B, Janák J. A MATLAB-Based Graphical User Interface Program for Computing Functionals of the Geopotential up to Ultra-High Degrees and Orders[J]. Computers and Geosciences, 2013, 56: 186-196 DOI:10.1016/j.cageo.2013.03.012
(  0) 0) |
| [14] |
Bucha B, Janák J. A MATLAB-Based Graphical User Interface Program for Computing Functionals of the Geopotential up to Ultra-High Degrees and Orders: Efficient Computation at Irregular Surfaces[J]. Computers and Geosciences, 2014, 66: 219-227 DOI:10.1016/j.cageo.2014.02.005
(  0) 0) |
| [15] |
Godah W. IGiK-TVGMF: A MATLAB Package for Computing and Analysing Temporal Variations of Gravity/Mass Functionals from GRACE Satellite Based Global Geopotential Models[J]. Computers and Geosciences, 2019, 123: 47-58 DOI:10.1016/j.cageo.2018.11.008
(  0) 0) |
| [16] |
杨光亮, 申重阳, 黎哲君, 等. 重力异常场云计算软件系统[J]. 大地测量与地球动力学, 2018, 38(2): 111-115 (Yang Guangliang, Shen Chongyang, Li Zhejun, et al. Cloud Computing System of Gravity Field[J]. Journal of Geodesy and Geodynamics, 2018, 38(2): 111-115)
(  0) 0) |
| [17] |
陈秋杰, 沈云中, 张兴福. MKL和OpenMP多核并行算法解算高阶地球重力场的效率分析[J]. 大地测量与地球动力学, 2012, 32(5): 118-123 (Chen Qiujie, Shen Yunzhong, Zhang Xingfu. Analysis of Efficiency of Applying MKL and OpenMP Polynuclear Parallel Algorithms to Recovery of High Degree Earth's Gravity Field[J]. Journal of Geodesy and Geodynamics, 2012, 32(5): 118-123)
(  0) 0) |
| [18] |
Hofmann-Wellenhof B, Moritz H. Physical Geodesy[M]. San Francisco: Freeman House Publishing, 2006
(  0) 0) |
| [19] |
崔家武, 周波阳, 罗志才, 等. 利用MPI并行算法实现球谐综合的效率分析[J]. 武汉大学学报:信息科学版, 2019, 44(12): 1802-1807 (Cui Jiawu, Zhou Boyang, Luo Zhicai, et al. Efficiency Analysis of Spherical Harmonic Synthesis Based on MPI Parallel Algorithm[J]. Geomatics and Information Science of Wuhan University, 2019, 44(12): 1802-1807)
(  0) 0) |
| [20] |
Pavlis N K, Factor J K, Holmes S A. Terrain-Related Gravimetric Quantities Computed for the Next EGM[C]. Proceedings of the 1st International Symposium of the International Gravity Field Service(IGFS), Ankara, 2007
(  0) 0) |
| [21] |
张兴福, 刘成. 综合EGM2008模型和SRTM/DTM2006.0剩余地形模型的GPS高程转换方法[J]. 测绘学报, 2012, 41(1): 25-32 (Zhang Xingfu, Liu Cheng. The Approach of GPS Height Transformation Based on EGM2008 and SRTM/DTM2006.0 Residual Terrain Model[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(1): 25-32)
(  0) 0) |
| [22] |
Andersen O B, Knudsen P, Kenyon S, et al. Evaluation of the Global Altimetric Marine Gravity Field DTU15: Using Marine Gravity and GOCE Satellite Gravity[C]. International Symposium on Advancing Geodesy in a Changing World, Kobe, 2017
(  0) 0) |
| [23] |
Kvas A, Mayer-Gürr T, Krauss S, et al. The Satellite-Only Gravity Field Model GOCO06s[C]. The EGU General Assembly, Vienna, 2019
(  0) 0) |
2. Institute of Geodesy and Geo-Information, University of Bonn, 17 Nussallee, Bonn 53121, Germany;
3. College of Surveying and Geo-Informatics, Tongji University, 1239 Siping Road, Shanghai 200092, China
 2020, Vol. 40
2020, Vol. 40


