2. 高速铁路运营安全空间信息技术国家地方联合工程实验室,成都市二环路北一段111号,610031
全球质量变化及其规律是近年来科学研究的热点,自Wahr等[1]提出利用GRACE时变重力场模型估算地球表面质量变化以来,许多学者借助GRACE数据研究全球质量变化并取得进展。冰川均衡调整导致的地球内部物质运动重分布所引起的质量变化不容忽视,因此利用GRACE数据研究全球海水质量变化、极地冰川质量变化以及陆地水储量变化时都需要采用GIA模型进行扣除。不同学者[2-6]在研究同一个区域时所得到的结果存在差异,虽然数据精度和处理方法不同会造成一定的影响,但其主要原因是使用了不同的GIA模型。且上述研究主要致力于改善GRACE数据处理方法,并未对不同GIA模型改正后的结果进行对比分析,因此无法判断各种GIA模型的改正效果。本文基于GIA模型的预测结果及不确定性对各GIA模型进行比较分析,利用8种GIA模型研究其对利用GRACE数据反演全球地表质量变化的影响。在陆地区域,将扣除GIA后的GRACE结果与陆地水文模型和冰面实地监测结果进行比较;在海洋区域,通过分析陆地水及两极冰盖对海水质量变化的贡献,同时联合卫星测高与Argo海洋温盐数据集进一步对海水质量变化进行分析。综合陆地和海洋分析结果,评估各GIA模型对全球质量变化的影响。
1 数据与方法 1.1 冰川均衡调整(GIA)模型冰川均衡调整(GIA)是指粘弹性地球对末次冰期消融地表冰负荷和海水负荷变化的响应[7]。冰盖消融产生的冰水汇入海洋,引起海平面变化;同时伴随着地表冰负荷卸载和海水负荷加载,导致地球内部物质运动重分布,进而引起地球质量的变化。GIA模型的预测问题实质上为粘弹性负荷问题,研究GIA必须确定相关的冰川负荷模型(冰模型)和地幔粘滞度参考模型(地球模型)。冰模型主要是随时间变化的地表冰负荷和海水负荷,可以由相对海平面历史资料和其他一些地球物理资料得到,目前国际上针对地球整体所用的冰模型为ICE系列(ICE-4G、ICE-5G、ICE-6G);地球模型包括地球流变学参数和密度结构,其中与GIA预测最相关的流变学参数为岩石圈厚度和上、下地幔粘度,可通过调整这些参数来得到最合适的地幔粘滞度参考模型[7]。冰川均衡调整模型的适用区域存在差异,可分为全球模型和区域模型。表 1为本文所用的GIA模型。
|
|
表 1 GIA模型汇总 Tab. 1 Summary of GIA models |
美国德克萨斯大学空间研究中心CSR自2002年以来共发布多个版本的GRACE Level-2月时变重力场模型, 本文采用CSR最新发布的CSR RL06数据,时间跨度为2005-01~2014-12,共计110个月。数据为已扣除高频非潮汐大气和海洋质量变化信号、固体潮、海潮、三体引力、相对论效应、固体极潮和海洋极潮等影响的60阶正则化球谐系数。使用Sun等[16]推荐的地球质心运动模型顾及一阶项系数的影响,并使用卫星激光测距(SLR)观测的C20项来替换GRACE数据中精度较低的C20项[17]。利用Wahr等[1]的方法计算每个网格点的表面密度变化,再除以水的密度,得到用等效水高表示的表面质量变化。由于CSR发布的模型是不包含大气和海洋质量变化的时变重力场GSM模型,可直接用来计算陆地地表质量变化;而在计算海水质量变化时,可采用GSM+GAD模型,扣除GAA模型影响,保留所需的海洋信号[6]。
由于GRACE观测值的各向异性和背景模型的误差影响等,GRACE时变地球重力场模型在计算时需进行平滑滤波处理,本文采用高斯400 km的空间平滑滤波进行去噪。时变重力场数据信号经球谐截断和滤波平滑处理后会发生泄漏,本文采用Chen等[18]提出的迭代全球正向建模恢复法改正全球区域的泄漏误差。
1.3 卫星测高数据法国AVISO中心提供的月均海平面高度异常数据(mean sea level anomaly, MSLA)包含T/P、Jason-1/2、ERS-1/2和Envisat等多颗测高卫星资料,数据空间分辨率为0.25°× 0.25°,该数据已进行标准地球物理改正及大气改正,包括海洋负荷潮汐改正、极潮改正、电磁偏差改正和反变气压改正等。
1.4 Argo海洋温盐数据集Argo(array for real-time geostrophic oceanography)计划为全球海洋观测实验项目,本文在计算全球温盐比容海平面变化时,使用美国夏威夷大学国际太平洋研究中心(IPRC)、日本海洋地球科学技术中心(JAMSTEC)和美国加州大学SCRIPPS海洋研究所发布的格网化Argo资料。3家研究中心发布的数据集的时间分辨率为每月一值,空间分辨率为1°× 1°,提供0~2 000 m的三维温盐数据,其中IPRC提供的数据集在垂直方向上共分为27层,JAMSTEC共分为25层,SCRIPPS共分为58层。
1.5 水文模型GLDAS(global land data assimilation system)水文模型是由美国宇航局(NASA)、戈达德空间飞行中心(GSFC)、美国国家海洋与大气管理局(NOAA)国家环境预报中心(NCEP)联合开发的全球陆面数据同化系统,是通过地球表面实测数据、卫星观测数据、遥感数据来驱动的4个陆面过程模型,包括CLM、Mosaic、Noah、VIC。本文使用这4个模型来估算除南极和格陵兰岛以外的陆地水变化,并取4个模型计算结果的均值作为除两极以外的最终陆地水变化。
因为本文已采用全球正向建模法来迭代恢复GRACE时变重力场数据的泄漏误差,所以不对测高、温盐以及水文模式数据进行同GRACE一致的空间平滑滤波处理。
2 结果与讨论 2.1 不同GIA模型的改正值本文采用表 1中6个全球模型(ICE-5G(VM2_L90)、Paulson07、ICE-4G+RF3L20(β=0.4)、Geruo13、ICE-6G_C(VM5a)、ICE-6G_D(VM5a))和2个南极区域模型(IJ05_R2、W12a),将8个模型分别简称为ICE-5G、Paulson07、RF3L20、GW13、ICE-6G_C、ICE-6G_D、IJ05和W12a。为了比较各GIA模型在全球不同区域的质量改正值,将GIA重力场变化所反映的“等效水高”变化速率作为各GIA模型改正值进行比较。由于本文所采用的8个GIA模型在收集时并不是全部以“等效水高”变化速率形式给出,部分模型为GIA径向位移速率,所以需要先将径向位移格网进行球谐展开,再利用Wahr等[1]的方法反演出“等效水高”形式的格网。图 1为以“等效水高”形式展示的6个全球GIA模型对全球质量变化长期趋势的影响,从图中可以看出,6个全球模型在南极地区、北美洲加拿大地区、北欧3国(挪威、瑞典、芬兰)及其群岛地区的GIA改正都较为明显,并且最大改正值都位于加拿大地区,其中ICE-5G模型在加拿大地区的最大改正值达到10.18 cm/a,数值在6个全球模型中最大;RF3L20模型最大改正值为3.67 cm/a,与其他5个全球模型相比,数值最小;模型Paulson07、GW13、ICE-6G_C和ICE-6G_D最大改正值相近。

|
图 1 GIA模型对全球质量变化的影响 Fig. 1 Influence of GIA models on global mass changes |
图 2为以“等效水高”形式展示的6个全球GIA模型和2个区域GIA模型对南极地区质量变化长期趋势的影响。由图 2及表 2可知,不同GIA改正模型对南极冰盖质量变化反演结果的影响均主要体现在西南极和南极半岛,且改正值差异较大,其中全球模型的改正值大于南极区域模型。

|
图 2 GIA模型对南极质量变化的影响 Fig. 2 Influence of GIA models on mass changes in Antarctic |
|
|
表 2 GIA模型对不同区域质量的改正 Tab. 2 Mass changes correction of GIA models for different regions |
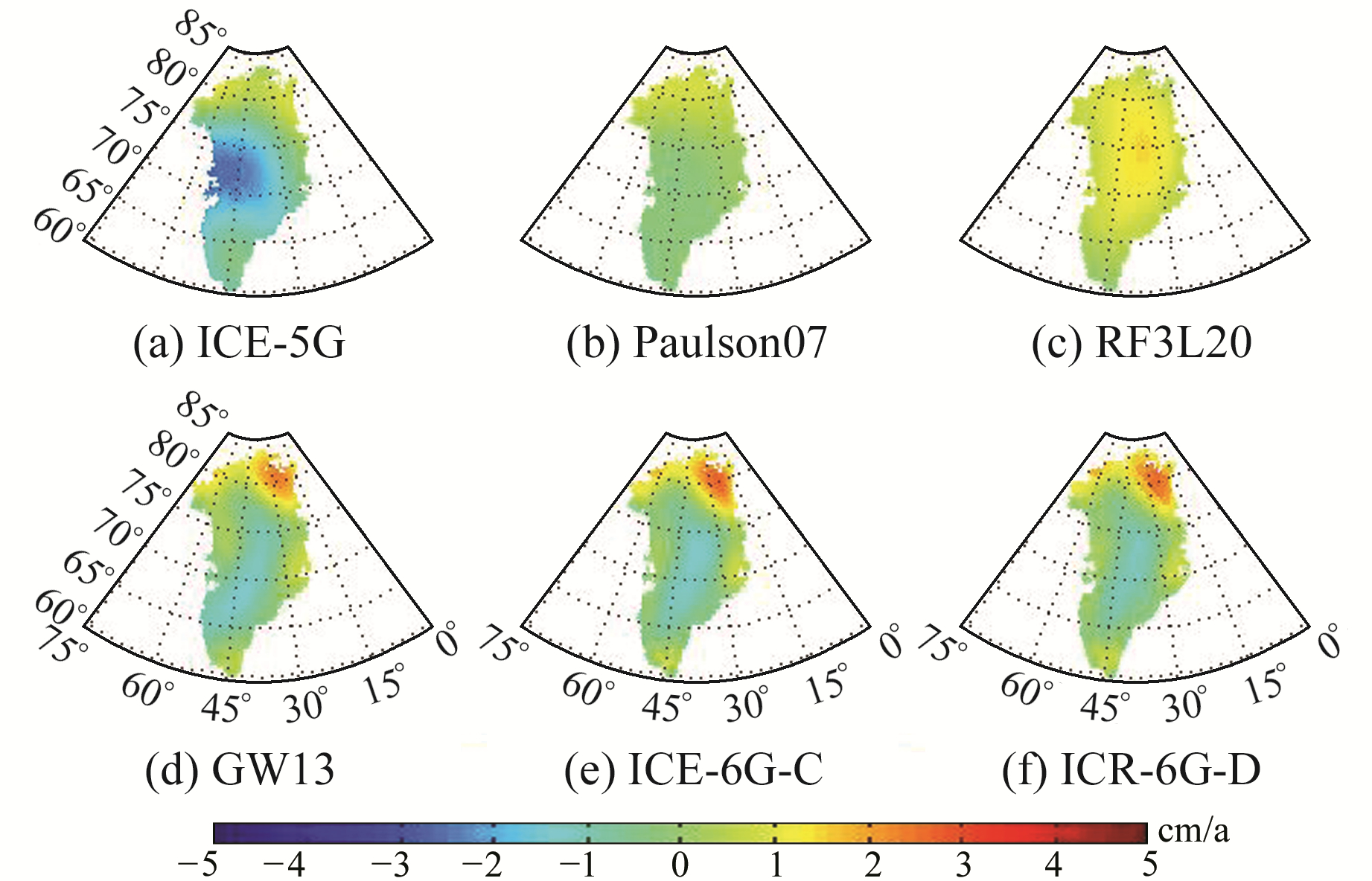
基于图 1还不能明显看出各GIA模型在格陵兰岛地区的差异,所以本文同样以“等效水高”形式展示6个全球GIA模型对格陵兰岛地区质量变化长期趋势的影响(图 3)。由图 3(a)、(c)可以看出,模型ICE-5G和RF3L20在格陵兰岛地区的改正值差异较大;由图 3(d)~(f)可以看出,模型GW13、ICE-6G_C和ICE-6G_D对整个格陵兰岛地区的改正值相近,且数值均未达到1 mm/a。结合图 1、图 3及表 2可知,各GIA模型在格陵兰岛地区质量改正值偏小。
|
图 3 GIA模型对格陵兰岛质量变化的影响 Fig. 3 Influence of GIA models on mass changes in the Greenland region |
从表 2可以看出,模型ICE-5G对海洋区域的质量改正值在6个全球模型中数值最大,为1.6 mm/a;ICE-6G_C模型次之,为1.5 mm/a;Paulson07、RF3L20、GW13和ICE-6G_D这4个模型在海洋区域的改正值相近,均在1 mm/a左右。
2.2 扣除GIA影响的全球质量变化针对§2.1的分析结果,在考虑GIA影响的前提下,联合多源数据对南极、格陵兰岛、加拿大东部、北欧3国以及海洋区域的质量变化进行对比分析。对于南极、格陵兰岛地区,可将GRACE计算的质量变化结果与国家冰雪数据中心(NSIDC)给出的结果进行对比;对于加拿大东部以及北欧3国地区,可将通过4种水文模式数据得出的结果与GRACE的计算结果作对比;对于海洋区域,由GRACE卫星重力数据反演的海水质量变化可与卫星测高解算的海平面变化减去Argo温盐数据集解算的比容海平面变化后的结果进行比较。
将GRACE数据分别用表 1中8个GIA模型进行改正后发现,格陵兰岛地区质量变化趋势差别较小。模型IJ05和W12a均利用南极GPS垂向速度来约束地球模型参数,2010年之后提出的模型GW13、ICE-6G_C和ICE-6G_D在南极地区也都利用GPS数据来约束南极GIA改正,而2010年之前提出的模型ICE-5G、Paulson07和RF3L20并未利用南极GPS隆升速度对模型进行测试和校准,所以经GW13、ICE-6G_C和ICE-6G_D模型GIA改正后的南极质量变化趋势与经IJ05和W12a模型改正后的结果相差较小,其中经模型ICE-6G_C、ICE-6G_D和IJ05改正后的南极质量变化趋势与冰面实地观测、卫星测冰ICESat等的结果一致(表 3)。
|
|
表 3 扣除GIA影响的质量变化趋势 Tab. 3 Trend of mass changes after removing GIA |
图 4为扣除GIA影响的加拿大东部和北欧3国质量变化序列,由图 4(b)及表 3可知,北欧3国经6个全球模型改正后的质量变化均呈下降趋势,这与GLDAS(4个水文模型的均值)得到的结果一致;由图 4(a)及表 3可知,除ICE-5G模型以外,加拿大东部经其他5个全球模型改正后的质量变化也呈下降趋势,也与GLDAS的结果一致。此外,经ICE-5G改正后的GRACE与GLDAS之间的相关性比其他5个模型低(表 4),而最新的ICE-6G_C和ICE-6G_D模型在ICE-5G模型基础上进行修正和约束,以适应目前所有可获得的地质和大地测量观测资料[7],所以这2个ICE系列模型在加拿大东部和北欧3国地区改正后的结果比ICE-5G模型结果更为准确。

|
图 4 扣除GIA影响的加拿大东部地区和北欧3国质量变化序列 Fig. 4 Mass change series after removing GIA of eastern Canada and the three Nordic countries |
|
|
表 4 扣除GIA影响后的GRACE与GLDAS之间的相关系数 Tab. 4 Correlation coefficient between GRACE and GLDAS after removing GIA |
陆地水和两极冰盖是影响海水质量变化的2个主要因素,通过计算这2个因素对海水质量变化的贡献来进一步分析全球海水质量变化。对于陆地水对海水质量变化趋势的贡献,取4个水文模型计算结果的均值与经GIA改正后的GRACE结果进行对比发现,除ICE-5G模型以外,其他5个全球模型与GLDAS水文模型的结果相符,对海平面的贡献均在1.20 mm/a左右(表 5,单位mm/a)。
|
|
表 5 冰盖和陆地水对海平面变化的贡献 Tab. 5 Contribution of ice sheet and land water to the sea level change |
由于受GIA影响,海洋盆地存在长期形变,所以卫星测高数据也需要扣除GIA效应,本文使用与GRACE一致的GIA模型来扣除卫星测高数据的GIA效应。图 5为扣除GIA影响后的海平面变化(其中测高-Argo表示测高数据减去3个比容海平面均值的结果),对GRACE反演的海水质量与测高-Argo的结果作相关性分析发现,经6个全球模型改正后的GRACE与测高-Argo之间的相关系数均大于0.95,表明具有极大相关性。

|
图 5 扣除GIA影响后的海平面变化 Fig. 5 Sea level changes after removing GIA |
结合陆地水和两极冰盖对海水质量变化趋势的贡献与GRACE解算的海水质量、测高海平面减去温盐比容海平面的结果发现,经模型ICE-6G_C改正后的陆地水及冰盖对海水质量变化趋势的总贡献为2.03±0.51 mm/a,与测高-Argo计算结果(2.15±0.51 mm/a)一致,但与由GRACE直接解算的海水质量变化趋势(2.62±0.54 mm/a)相差较大;经模型ICE-5G和RF3L20改正后的陆地水及冰盖对海水质量变化趋势的贡献分别为2.98±0.65 mm/a和2.71±0.49 mm/a,与由GRACE直接解算的海水质量3.03±0.61 mm/a和2.71±0.53 mm/a一致,但与测高-Argo的结果不一致;而经其他3个模型改正后,陆地水及冰盖对海水质量变化趋势的贡献与GRACE、测高-Argo的结果基本一致(表 6,单位mm/a)。
|
|
表 6 扣除GIA影响后的海水质量变化趋势 Tab. 6 Trend of ocean mass changes after removing GIA |
通过分析6个全球和2个南极区域GIA模型对全球和区域质量变化的影响,分别利用这8个模型对2005~2014年GRACE卫星重力反演的全球质量变化结果进行GIA改正。针对北美、北欧2个GIA影响较大的区域,借助地表水文模型分析这2个区域部分地区的水储量变化,并与GIA改正后的GRACE结果作比较,在扣除GIA效应后,除模型ICE-5G外,经其他5个全球模型GIA改正后的水储量变化趋势与地表水文模型一致,均呈下降趋势。针对南极区域,对8个GIA模型进行比较分析,由于2010年之后发布的模型GW13、ICE-6G_C和ICE-6G_D在南极地区均利用GPS垂向速度来约束地球模型参数,所以经这3个模型改正后的南极质量变化趋势与IJ05和W12a这2个南极区域模型改正后的结果相差较小,其中经模型ICE-6G_C、ICE-6G_D和IJ05改正后的结果与冰面实地观测、卫星测冰ICESat等结果一致。此外,对于海洋区域,经模型Paulson07、GW13和ICE-6G_D改正后的陆地水及两极冰盖对海水质量变化趋势的贡献分别与GRACE和测高-Argo的结果一致。因此,综合整个陆地和海洋分析结果认为,模型ICE-6G_D更适用于全球质量变化的研究。
| [1] |
Wahr J, Swenson S, Velicogna I. Accuracy of GRACE Mass Estimates[J]. Geophysical Research Letters, 2006, 33(6)
(  0) 0) |
| [2] |
Chen J L, Wilson C R, Blankenship D, et al. Accelerated Antarctic Ice Loss from Satellite Gravity Measurements[J]. Nature Geoscience, 2009, 2(12): 859-862 DOI:10.1038/ngeo694
(  0) 0) |
| [3] |
King M A, Bingham R J, Moore P, et al. Lower Satellite-Gravimetry Estimates of Antarctic Sea-Level Contribution[J]. Nature, 2012, 491(7 425): 586-589
(  0) 0) |
| [4] |
Schrama E J O, Wouters B, Rietbroek R. A Mascon Approach to Assess Ice Sheet and Glacier Mass Balances and Their Uncertainties from GRACE Data[J]. Journal of Geophysical Research: Solid Earth, 2014, 119(7): 6 048-6 066 DOI:10.1002/2013JB010923
(  0) 0) |
| [5] |
Cazenave A, Lombard A, Llovel W. Present-Day Sea Level Rise: A Synthesis[J]. Comptes Rendus Geoscience, 2008, 340(11): 761-770 DOI:10.1016/j.crte.2008.07.008
(  0) 0) |
| [6] |
冯伟, 钟敏, 许厚泽. 联合卫星测高、卫星重力和海洋浮标资料研究2005-2013年的全球海平面变化[J]. 地球物理学进展, 2014, 29(2): 471-477 (Feng Wei, Zhong Min, Xu Houze. Global Sea Level Changes Estimated from Satellite Altimetry, Satellite Gravimetry and Argo Data during 2005-2013[J]. Progress in Geophysics, 2014, 29(2): 471-477)
(  0) 0) |
| [7] |
马超, 李斐, 张胜凯, 等. 冰川均衡调整(GIA)模型研究进展[J]. 地球物理学进展, 2016, 31(5): 1 965-1 972 (Ma Chao, Li Fei, Zhang Shengkai, et al. Progress of Glacial Isostatic Adjustment(GIA) Models[J]. Progress in Geophysics, 2016, 31(5): 1 965-1 972)
(  0) 0) |
| [8] |
Peltier W R. Global Glacial Isostasy and the Surface of the Ice-Age Earth: The ICE-5G(VM2) Model and GRACE[J]. Annual Review of Earth and Planetary Science, 2004, 32(1): 111-149 DOI:10.1146/annurev.earth.32.082503.144359
(  0) 0) |
| [9] |
Peltier W R, Argus D F, Drummond R. Space Geodesy Constrains Ice Age Terminal Deglaciation: The Global ICE-6G_C(VM5a) Model[J]. Journal of Geophysical Research: Solid Earth, 2015, 120(1): 450-487 DOI:10.1002/2014JB011176
(  0) 0) |
| [10] |
Peltier W R, Argus D F, Drummond R. Comment on "An Assessment of the ICE-6G_C(VM5a) Glacial Isostatic Adjustment Model" by Purcell et al[J]. Journal of Geophysical Research: Solid Earth, 2018, 123(2): 2 019-2 028 DOI:10.1002/2016JB013844
(  0) 0) |
| [11] |
Paulson A, Zhong S J, Wahr J. Inference of Mantle Viscosity from GRACE and Relative Sea Level Data[J]. Geophysical Journal International, 2007, 171(2): 497-508 DOI:10.1111/j.1365-246X.2007.03556.x
(  0) 0) |
| [12] |
Wang H S, Wu P, Van der Wal W. Using Postglacial Sea Level, Crystal Velocities and Gravity-Rate-of-Change to Constrain the Influence of Thermal Effects on Mantle Lateral Heterogeneities[J]. Journal of Geodynamics, 2008, 46(3-5): 104-117 DOI:10.1016/j.jog.2008.03.003
(  0) 0) |
| [13] |
Geruo A, Wahr J, Zhong S J. Computations of the Viscoelastic Response of a 3-D Compressible Earth to Surface Loading: An Application to Glacial Isostatic Adjustment in Antarctica and Canada[J]. Geophysical Journal International, 2013, 192(2): 557-572 DOI:10.1093/gji/ggs030
(  0) 0) |
| [14] |
Ivins E R, James T S, Wahr J, et al. Antarctic Contribution to Sea Level Rise Observed by GRACE with Improved GIA Correction[J]. Journal of Geophysical Research: Solid Earth, 2013, 118(6): 3 126-3 141 DOI:10.1002/jgrb.50208
(  0) 0) |
| [15] |
Whitehouse P L, Bentley M J, Milne G A, et al. A New Glacial Isostatic Adjustment Model for Antarctica: Calibrated and Tested Using Observation of Relative Sea-Level Change and Present-Day Uplift Rates[J]. Geophysical Journal International, 2012, 190(3): 1 464-1 482 DOI:10.1111/j.1365-246X.2012.05557.x
(  0) 0) |
| [16] |
Sun Y, Riva R, Ditmar P. Optimizing Estimates of Annual Variations and Trends in Geocenter Motion and J2 from a Combination of GRACE Data and Geophysical Models[J]. Journal of Geophysical Research: Solid Earth, 2016, 121(11): 8 358-8 370
(  0) 0) |
| [17] |
Chen J L, Rodell M, Wilson C R, et al. Low Degree Spherical Harmonic Influences on Gravity Recovery and Climate Experiment(GRACE) Water Storage Estimates[J]. Geophysical Research Letters, 2005, 32(14)
(  0) 0) |
| [18] |
Chen J L, Wilson C R, Tapley B D. Contribution of Ice Sheet and Mountain Glacier Melt to Recent Sea Level Rise[J]. Nature Geoscience, 2013, 6(7): 549-552 DOI:10.1038/ngeo1829
(  0) 0) |
2. State-Province Joint Engineering Laboratory of Spatial Information Technology of High-Speed Rail Safety, 111 First Section of North-Erhuan Road, Chengdu 610031, China
 2020, Vol. 40
2020, Vol. 40


