相对重力测量一般是指测定地球表面各点之间重力值的差值,其在地质勘探和大地测量等领域发挥着重大作用。国内学者已对重力测量进行了大量研究[1-5],但以往研究中原始观测数据均是在远离城市噪声条件下采集的,数据离群值所占比例较小或不存在,满足观测精度的要求。但在城市中进行重力测量时,由于行人及车辆等外界干扰因素较多,各测站观测值波动较大,观测结果无法满足精度要求。传统的相对重力测量是在仪器稳定后连续记录3个观测值,当互差小于3 μGal时,取中值作为最终观测结果,但该方法获取的观测信息较少,且存在单一读数的随机性。而RANSAC(random sample consensus)算法在计算含有高比例离群数据的数据集时,仍能获取可靠的观测结果,具有较高的稳健性[6-7]。本文利用RANSAC算法和整体投影原理提取CG-5重力仪动态重复连续相对重力观测量,结果发现,重力观测结果精度较高,可为国家重力基础建设和重力勘探工程实践提供参考。
1 原理与方法 1.1 随机抽样一致性算法原理RANSAC算法本质上是一种数学模型参数估计算法,是对一组包含离群值的样本数据集进行迭代来计算数据的数学模型参数,以得到有效样本数据的非确定性算法。该算法通过反复选取数据中的一组随机子集来完成目标。首先将数据假设为内部值和离群值:在数据中随机抽取样本来估计模型参数,并假设为正确参数,如果某个点适用于估计模型,则认为该点为内部值,否则为离群值。然后重新估计模型参数,反复迭代,选取内部点最多的估计参数作为最优模型参数。RANSAC算法可以用最少的数据来估计整个数据集中可能蕴涵的数学模型参数,其对数据集中离群值的容忍度要高于最小二乘法等模型参数估计方法。
最优数据集的确定方法为:首先定义一个参数化的函数模型f(x|ξ),其中x为数据集D中的任意点,ξ为模型参数。RANSAC算法的目标是寻找最佳参数,使函数模型能拟合所有的数据点。若给定判定阈值参数T,则确定参数ξ内部值的数据集合为
相对重力测量是通过测量两点间的重力差值,由起算点逐点推算联测点重力值的方法和技术。假定已知控制点A的重力值gA,只需测出A、B间的重力差就可确定B点的重力值。若用相对重力仪在同一时刻多次测定A点和B点的相对重力值aA和aB,则B点的重力值gB为:
| $ {g_B} = {g_A} + \frac{1}{n}\sum\limits_{i = 1}^n {\left( {{a_{{B_i}}} - {a_{{A_i}}}} \right)} $ | (1) |
式中,n为观测次数。
2 实验设计及数据预处理本次实验采用新型自动电子读数CG-5相对重力仪,该仪器具有自动实现温度补偿、仪器倾斜改正、地震滤波、线性漂移改正、潮汐改正等功能,标称精度为5 μGal,读数分辨率为5 μGal。在西安科技大学校园南北方向主干道旁布设1条测线,A、B、C、D、E、F、G、H为测线上等间距分布的8个测点,按A→B→C→D→E→F→G→H→G→F→E→D→C→B→A顺序进行重复观测。将重力仪的采样间隔设为10 s,采样频率为6 Hz,每个测点连续观测20 min,每天观测1次,共观测4次,获取6 000多个观测数据。
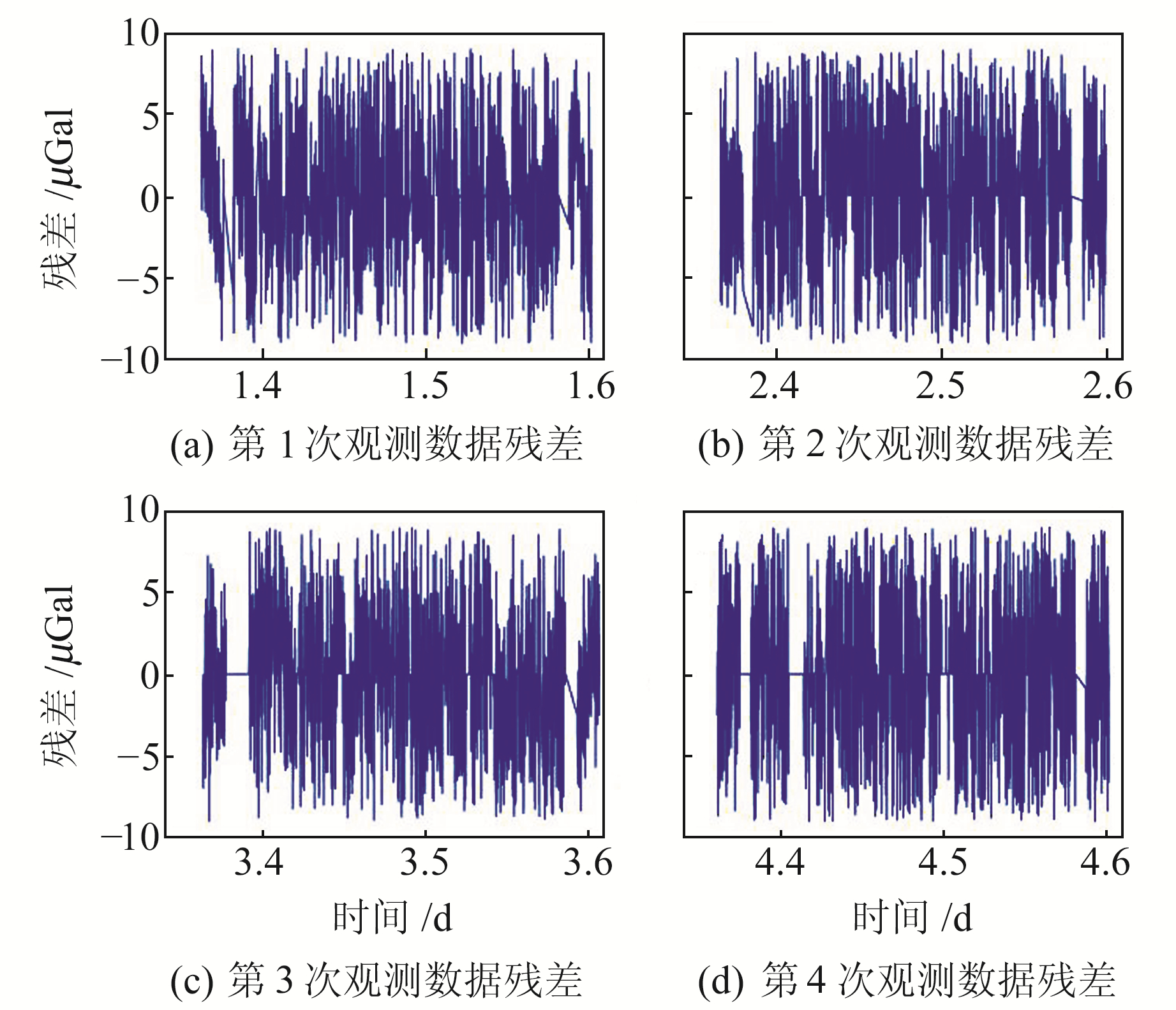
由于测线布置在主干道旁,周围行人和车辆会对观测数据造成较大影响,图 1为原始相对重力的时间序列残差,残差值范围为[-30 μGal, 30 μGal]。本文利用RANSAC算法减小重力时间序列与拟合时间序列残差的影响,根据3σ准则选择残差阈值区间为(-9 μGal, 9 μGal),残差值超出此区间的相对重力数据被认为是离群值,据此共剔除1 100多个离群值,约占观测数据总数的16%。再使用线性内插方法对数据进行插补,以第1次为例,插补前后相对重力时间序列如图 2所示,从图中可以看出,插补前后两者基本一致。图 3为剔除离群值和插补数据后的相对重力时间序列残差,残差范围为[-10 μGal, 10 μGal],残差序列较为平稳。图 1、2和3表明,离群值剔除与数据插补的效果较好。

|
图 1 原始相对重力时间序列残差 Fig. 1 Residuals of original relative gravity time series |

|
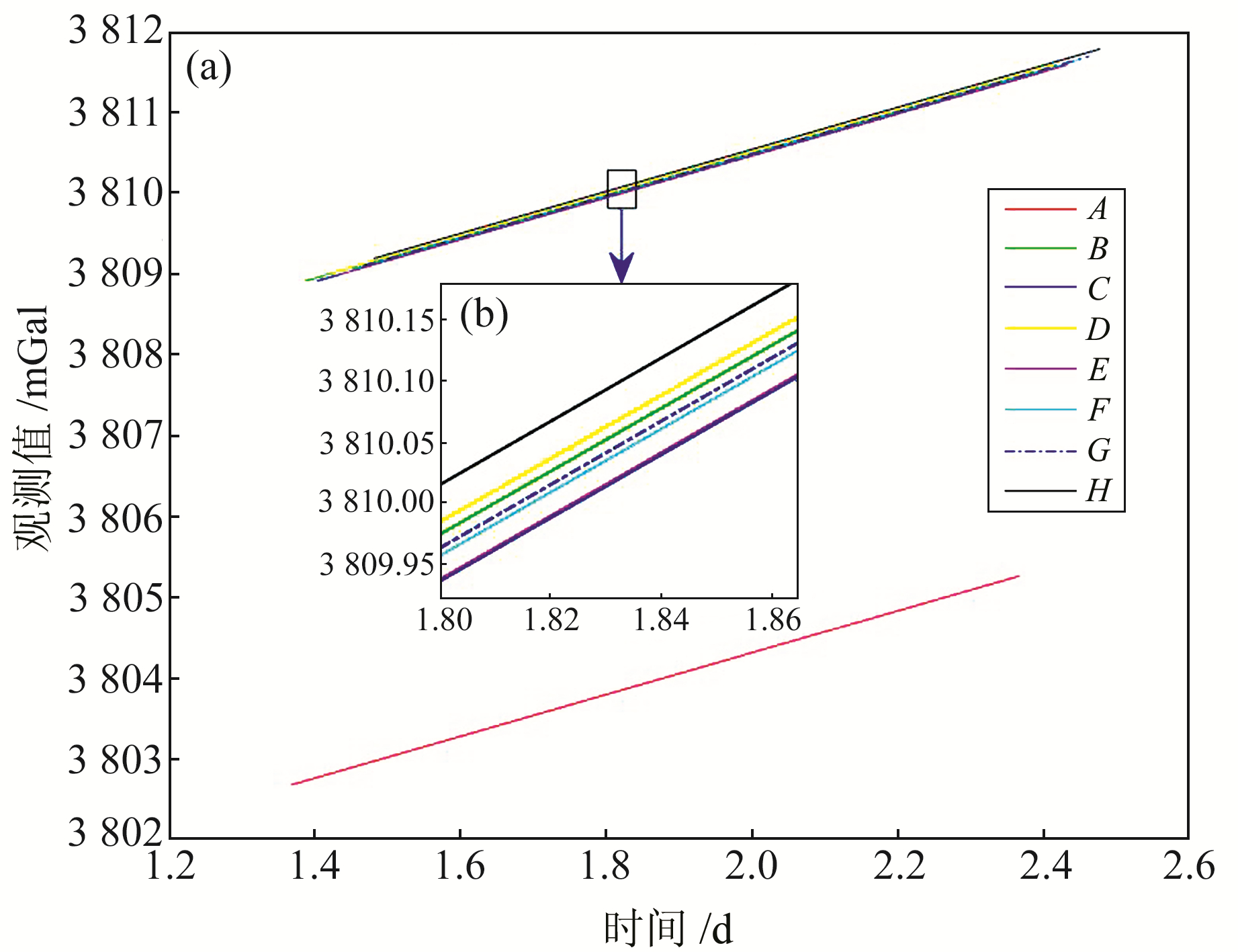
(a)为第1次插补前后相对重力时间变化序列,A、B、C…为每个测点的相对重力时间变化序列 图 2 插补前后相对重力时间序列 Fig. 2 Relative gravity time series before and after interpolation |
|
图 3 剔除离群值和插补后相对重力时间序列残差 Fig. 3 Residuals of relative gravity time series after eliminating outliers and interpolation |
在经过预处理的动态观测数据基础上,分别计算每个观测站的零点漂移率,结果见表 1和图 4。
|
|
表 1 各测站平均零漂率 Tab. 1 Average zero drift rate of each station |
|
图 4 各测站动态零漂率 Fig. 4 Dynamic zero drift rate of each station |
对原始观测数据进行预处理后可得到各观测点每次观测的时间序列,随着时间的推移,同一观测点的观测值并非常数。为更好地提取两点间的相对重力值并检验其精度,本文给出整体投影的思想:以第1次A点的往返观测值A1和A′1为固定基准,将第2、3、4次的观测结果分别逐次投影到A1和A′1上(图 5),根据式(2)计算系数Ki值;第2次的观测值A2、B2、A′2分别投影到A1、B1、A′1,第3次的观测值A3、B3、A′3分别投影到A1、B1、A′1,然后根据式(3)计算2个相同测站间不同次数的相对重力差值和残差,并检验其精度:
| $ \left[A_{1} \quad A_{1}^{'}\right]=K_{i}\left[A_{i} \quad A_{i}^{'}\right] $ | (2) |
| $ \begin{array}{llllllll} \mathit{\boldsymbol{ \boldsymbol{\varDelta} }} = {[{A_1}}&{{B_1}}&{{C_1}}&{{D_1}}&{{E_1}}&{{F_1}}&{{G_1}}&{{H_1}}&{G_1^{'} }\\ &{F_1^{'} }&{E_1^{'} }&{D_1^{'} }&{C_1^{'} }&{B_1^{'} }&{A_1^{'} }]-\\ K_{i}[A_{i} & B_{i} & C_{i} & D_{i} & E_{i} & F_{i} & G_{i} & H_{i} & G^{'}\\ &F_{i}^{'}& E_{i}^{'} &D_{i}^{'}& C_{i}^{'} &B_{i}^{'}&{_{i}^{'}}] \end{array} $ | (3) |

|
A、B、C、D分别对应各相邻测站第1、2、3、4次观测两测点间的相对重力差值 图 5 观测数据差值投影 Fig. 5 The difference projection of observed data |
式中,i=2、3、4,为观测次数,[]为向量符号,
对各观测点重复相对重力观测数据取均值,可获取相邻测点间的重力差值(即两点间的相对重力),计算两点间相对重力的残差,取绝对值最大值为段差精度,结果见表 2。计算结果表明,CG-5重力仪重复性标准差在限差之内,均优于CG-5重力仪的标称精度5 μGal,与邢乐林等[8]的研究结果一致。
|
|
表 2 相邻测点间相对重力差值及精度 Tab. 2 Relative gravity differencevalues and accuracy between adjacent points |
基于上述方法提取相对重力观测量发现,段差精度最差段为D→E,数值为4.641 μGal,标准差最差段也为D→E,数值为4.384 μGa,均小于标定精度5 μGal。为进一步验证该方法的有效性,分别对原始观测数据添加总观测量10%、20%、30%比例的离群值,利用RANSAC算法对离群值进行探测并剔除,再采用线性插值法进行补全,并计算其精度,以研究该方法对离群值的容忍度。从表 3可以看出,当离群值比例为10%时,段差精度和标准差与表 2结果大体一致,除C→D段段差精度大于5 μGal外,其他段的段差精度和标准差均优于5 μGal。而当误差比例为20%和30%时段差精度明显降低,标准差明显增大,可能与离群值比例增加导致拟合误差较大有关。
|
|
表 3 不同离群值比例下的相邻测点间相对重力差值及精度 Tab. 3 Relative gravity differencevalues and accuracy between adjacent points under different outliers ratios |
本文给出的RANSAC算法能够实现高精度重复相对重力观测量的提取,可有效避免外界或人为因素对测量数据造成的影响,具有较高的精度。基于高精度的重复相对重力观测量,利用整体投影原理对各观测点的相对重力值进行精度评定。实验结果表明,动态重力观测的残差最大值为4.641 μGal,重复性标准差最大值为4.384 μGal,均优于5 μGal。当原始观测数据包含30%的离群值时,动态重力观测的残差最大值为14.038 μGal,重复性标准差最大值为11.531 μGal,均优于15 μGal。
| [1] |
邢乐林, 王林海, 孙少安, 等. 庐山重力短基线场初值测定[J]. 大地测量与地球动力学, 2016, 36(9): 753-756 (Xing Lelin, Wang Linhai, Sun Shao'an, et al. Determination of Gravity Values for Lushan Short Gravity Calibration Baseline[J]. Journal of Geodesy and Geodynamics, 2016, 36(9): 753-756)
(  0) 0) |
| [2] |
Wang Q B, Zhou R, Sun W. Precision Analysis of Gravity Vertical Gradient Measurement Based on CG-5 Relative Gravimeter[J]. Advanced Materials Research, 2011, 301-303: 1 036-1 041 DOI:10.4028/www.scientific.net/AMR.301-303.1036
(  0) 0) |
| [3] |
郭金运, 高文宗, 于红娟, 等. 基于奇异谱分析的静态相对重力观测重力固体潮提取[J]. 地球物理学报, 2018, 61(10): 3 889-3 902 (Guo Jinyun, Gao Wenzong, Yu Hongjuan, et al. Gravity Tides Extracted from Relative Gravimetric Data with Singular Spectrum Analysis[J]. Chinese Journal of Geophysics, 2018, 61(10): 3 889-3 902)
(  0) 0) |
| [4] |
于红娟, 郭金运, 李九龙, 等. 基于主成分分析的相对重力观测零漂和固体潮提取[J]. 大地测量与地球动力学, 2015, 35(5): 906-910 (Yu Hongjuan, Guo Jinyun, Li Jiulong, et al. Zero Drift and Solid Earth Tide Extracted from Relative Gravimetric Data with Principal Component Analysis[J]. Journal of Geodesy and Geodynamics, 2015, 35(5): 906-910)
(  0) 0) |
| [5] |
祝意青, 闻学泽, 张晶, 等. 华北中部重力场的动态变化及其强震危险含义[J]. 地球物理学报, 2013, 56(2): 531-541 (Zhu Yiqing, Wen Xueze, Zhang Jing, et al. Dynamic Variation of the Gravity Field in Middle North China and Its Implication for Seismic Potential[J]. Chinese Journal of Geophysics, 2013, 56(2): 531-541)
(  0) 0) |
| [6] |
Fischler M A, Bolles R C. Random Sample Consensus : A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography[J]. Communications of the ACM, 1981, 24(6): 381-395 DOI:10.1145/358669.358692
(  0) 0) |
| [7] |
Chum O, Matas J, Kittler J. Locally Optimized RANSAC[C]. Pattern Recognition, 25th DAGM Symposium, Magdeburg, 2003
(  0) 0) |
| [8] |
邢乐林, 李辉, 夏正超, 等. CG-5重力仪零漂特性研究[J]. 地震学报, 2010, 32(3): 369-373 (Xing Lelin, Li Hui, Xia Zhengchao, et al. Study on Zero Drift Characteristics of CG-5 Gravimeter[J]. Acta Seismologica Sinica, 2010, 32(3): 369-373)
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40

